数学发展史简介

中国数学发展史概述一、中国数学的起源与早期发展据《易·系辞》记载：「上古结绳而治，后世圣人易之以书契」。

在殷墟出土的甲骨文卜辞中有很多记数的文字。

从一到十，及百、千、万是专用的记数文字，共有13个独立符号，记数用合文书写，其中有十进制制的记数法，出现最大的数字为三万。

算筹是中国古代的计算工具，而这种计算方法称为筹算。

用算筹记数，有纵、横两种方式：表示一个多位数字时，采用十进位值制，各位值的数目从左到右排列，纵横相间﹝法则是：一纵十横，百立千僵，千、十相望，万、百相当﹞，并以空位表示零。

算筹为加、减、乘、除等运算建立起良好的条件。

筹算直到十五世纪元朝末年才逐渐为珠算所取代，中国古代数学就是在筹算的基础上取得其辉煌成就的。

在几何学方面《史记·夏本记》中说夏禹治水时已使用了规、矩、准、绳等作图和测量工具，并早已发现「勾三股四弦五」这个勾股定理﹝西方称勾股定理﹞的特例。

战国时期，齐国人着的《考工记》汇总了当时手工业技术的规范，包含了一些测量的内容，并涉及到一些几何知识，例如角的概念。

战国时期的百家争鸣也促进了数学的发展，一些学派还总结和概括出与数学有关的许多抽象概念。

著名的有《墨经》中关于某些几何名词的定义和命题。

墨家还给出有穷和无穷的定义。

《庄子》记载了惠施等人的名家学说和桓团、公孙龙等辩者提出的论题，强调抽象的数学思想。

这些许多几何概念的定义、极限思想和其它数学命题是相当可贵的数学思想，但这种重视抽象性和逻辑严密性的新思想未能得到很好的继承和发展。

此外，讲述阴阳八卦，预言吉凶的《易经》已有了组合数学的萌芽，并反映出二进制的思想。

二、中国数学体系的形成与奠基这一时期包括从秦汉、魏晋、南北朝，共400年间的数学发展历史。

秦汉是中国古代数学体系的形成时期，为使不断丰富的数学知识系统化、理论化，数学方面的专书陆续出现。

现传中国历史最早的数学专著是1984年在湖北江陵张家山出土的成书于西汉初的汉简《算数书》，与其同时出土的一本汉简历谱所记乃吕后二年，所以该书的成书年代至晚是公元前186年。

数学的历史介绍数学的历史发展和重要数学家数学作为一门古老而又深刻的学科，在人类文明的历史长河中扮演着重要的角色。

从古代至今，数学不断发展演变，培育出许多伟大的数学家，他们为数学的进步做出了巨大的贡献。

本文将为大家介绍数学的历史发展并重点介绍一些重要的数学家。

一、古希腊时期数学的发展古希腊是数学史上一个重要的里程碑，许多重要的数学思想和概念都在这个时期诞生。

最为人熟知的是毕达哥拉斯学派提出的一系列数学原理，包括著名的毕达哥拉斯定理。

另外，欧几里得的《几何原本》对后世数学发展起到了巨大的影响，成为许多数学家研究的基础。

二、中世纪数学的低谷与复兴中世纪数学的发展相对较慢，部分原因是欧洲的文化环境受到了战争和政治动荡的影响。

然而，阿拉伯数学家在这个时期对数学的发展做出了重要贡献。

他们将印度和希腊的数学知识引入阿拉伯世界，并进行了整理和发展，为欧洲数学的复兴打下了基础。

著名的《阿拉伯数学传统》成为了数学史上的重要文献之一。

三、文艺复兴时期的数学突破文艺复兴时期是欧洲数学复兴的重要时期，众多数学家在这个时期涌现出来。

其中，意大利数学家斯忒芬诺为代数学的发展做出了杰出贡献，他提出了方程三次及以上的根的求解方法。

另外，日耳曼数学家勒让德也是这个时期的重要人物，他以发展微积分理论而闻名。

四、近代数学的革命近代数学的革命主要发生在17至19世纪，这一时期见证了许多基础性数学理论的诞生。

哥德巴赫猜想、费马大定理等一系列重要的数学难题在这一时期得到了提出。

著名的数学家牛顿和莱布尼茨几乎同时独立发现了微积分学，为后来的物理学和工程学等学科提供了基础。

五、现代数学的拓展与应用20世纪以来，数学已经发展成为一门庞大而复杂的学科体系。

代数学、几何学、概率论、数论等各个分支都有了独立而深入的发展。

许多著名的数学家如高斯、黎曼、庞加莱等在这个时期做出了具有重要影响的贡献。

数学的应用也广泛渗透到自然科学、工程学与经济学等领域，为人类社会的进步做出了重要贡献。

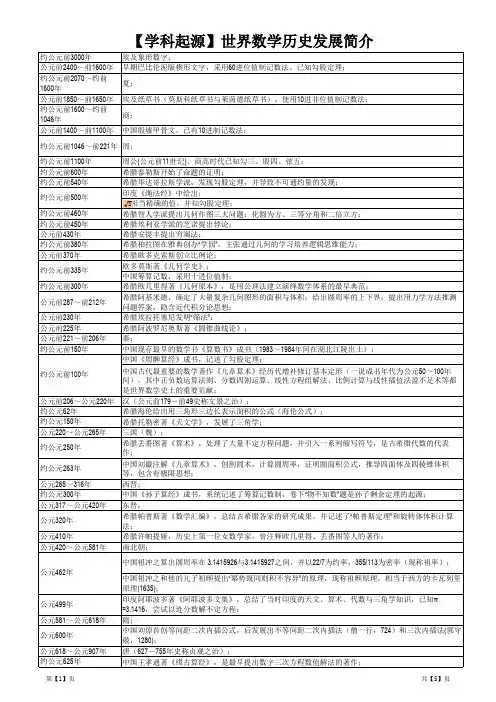
数学发展简史数学发展史大致可以分为四个阶段。

一、数学形成时期（——公元前5 世纪）建立自然数的概念，创造简单的计算法，认识简单的几何图形；算术与几何尚未分开。

二、常量数学时期（前5 世纪——公元17 世纪）也称初等数学时期，形成了初等数学的主要分支：算术、几何、代数、三角。

该时期的基本成果，构成中学数学的主要内容。

1．古希腊（前5 世纪——公元17 世纪）毕达哥拉斯——“万物皆数”欧几里得——《几何原本》阿基米德——面积、体积阿波罗尼奥斯——《圆锥曲线论》托勒密——三角学丢番图——不定方程2．东方（公元2 世纪——15 世纪）1）中国西汉（前2 世纪）——《周髀算经》、《九章算术》魏晋南北朝（公元3 世纪——5 世纪）——刘徽、祖冲之出入相补原理，割圆术，算π宋元时期（公元10 世纪——14 世纪）——宋元四大家杨辉、秦九韶、李冶、朱世杰天元术、正负开方术——高次方程数值求解；大衍总数术——一次同余式组求解2）印度现代记数法（公元8 世纪）——印度数码、有0；十进制（后经阿拉伯传入欧洲，也称阿拉伯记数法）数学与天文学交织在一起阿耶波多——《阿耶波多历数书》（公元499 年）开创弧度制度量婆罗摩笈多——《婆罗摩修正体系》、《肯特卡迪亚格》代数成就可贵婆什迦罗——《莉拉沃蒂》、《算法本源》（12 世纪）算术、代数、组合学3）阿拉伯国家（公元8 世纪——15 世纪）花粒子米——《代数学》曾长期作为欧洲的数学课本“代数”一词，即起源于此；阿拉伯语原意是“还原”，即“移项”；此后，代数学的内容，主要是解方程。

阿布尔．维法奥马尔．海亚姆阿拉伯学者在吸收、融汇、保存古希腊、印度和中国数学成果的基础上，又有他们自己的创造，使阿拉伯数学对欧洲文艺复兴时期数学的崛起，作了很好的学术准备。

3．欧洲文艺复兴时期（公元16 世纪——17 世纪）1）方程与符号意大利－塔塔利亚、卡尔丹、费拉里三次方程的求根公式法国－韦达引入符号系统，代数成为独立的学科2）透视与射影几何画家－布努雷契、柯尔比、迪勒、达．芬奇数学家－阿尔贝蒂、德沙格、帕斯卡、拉伊尔3）对数简化天文、航海方面烦杂计算，希望把乘除转化为加减。

数学史的发展脉络数学是一门古老而重要的学科，在人类文明的进程中发挥了重要的作用。

数学历经了几千年的发展，逐渐形成了今天我们所熟知的体系。

本文将从数学史的发展脉络角度，探讨数学的起源与发展，并介绍一些重要的数学里程碑。

1. 古代数学数学的起源可以追溯到公元前3000年左右的古代文明。

在古埃及、古巴比伦、古印度和古希腊等文明中，都有数学的雏形。

这些古代文明的数学主要集中在几何、代数以及计算等方面。

古埃及人发展了几何学，在建筑和土地测量中广泛应用。

他们创造了一种基于比例的方法来计算土地面积和三角形的面积。

另外，他们还用了一套类似于今天的分数系统。

古巴比伦人使用了类似于我们今天的十进制系统，并且开发了一些数学表格和算法来解决线性和二次方程。

这些成果对后来的数学发展具有重要影响。

古印度是数学发展的重要阶段，印度人在代数、几何和数字系统方面做出了许多贡献。

著名的印度数学家阿耶尔巴塔使用无穷级数来计算圆周率，他也发现了二次方程的解法，这对于后来的代数学发展产生了重大影响。

古希腊数学以其严谨的几何学而闻名，欧几里得的《几何原本》被视为古希腊几何学最重要的著作之一。

希腊人还对数学的逻辑和证明做出了重要贡献，他们开创了公理化证明的传统。

2. 中世纪数学中世纪是数学发展的相对低谷期，但也有一些重要的进展。

阿拉伯数学家在中世纪期间将古希腊和古印度数学知识传入欧洲，并为后来的数学复兴奠定了基础。

阿拉伯人引入了印度的十进制数字系统，这个系统后来直接演变为我们现在使用的阿拉伯数字系统。

他们还介绍了代数中的一些概念和方法，如解一元二次方程的方法。

同时，中世纪欧洲也出现了一些重要的数学家。

例如，莱布尼兹和牛顿独立发现了微积分学，这一发现对于科学界和工程领域产生了深远的影响。

3. 现代数学现代数学的形成可以追溯到17世纪和18世纪，这一时期被称为数学的黄金时代。

数学家们在代数、几何、概率论等领域都取得了重要的进展。

欧拉是这个时期最杰出的数学家之一，他在数论、解析数论和图论等领域有许多开创性的贡献。

数学发展简史数学发展史大致可以分为四个阶段：一、数学起源时期二、初等数学时期三、近代数学时期四、现代数学时期一、数学起源时期（远古——公元前5世纪）这一时期：建立自然数的概念；认识简单的几何图形；算术与几何尚未分开。

数学起源于四个“河谷文明”地域：非洲的尼罗河；这个区域主要是埃及王国：采用10进制，只有加法。

埃及的主要数学贡献：定义了基本的四则运算，并推广到了分数；给出了求近似平方根的方法；他们的几何知识主要是平面图形和立体图形的求积法。

西亚的底格里斯河与幼发拉底河；这个区域主要是巴比伦：采用10进制，并发明了60进制。

巴比伦王国的主要数学贡献可以归结为以下三点：度量矩形，直角三角形和等腰三角形的面积，以及圆柱体等柱体的体积；计数上，没有“零”的概念；天文学上，总结出很多天文学周期，但绝对不是科学。

中南亚的印度河与恒河；东亚的黄河与长江在四个“河谷文明”地域，当对数的认识(计数)变得越来越明确时，人们感到有必要以某种方式来表达事物的这一属性，于是导致了记数。

人类现在主要采用十进制，与“人的手指共有十个”有关。

而记数也是伴随着计数的发展而发展的。

四个“河谷文明”地域的记数归纳如下：刻痕记数是人类最早的数学活动，考古发现有3万年前的狼骨上的刻痕。

古埃及的象形数字出现在约公元前3400年；巴比伦的楔形数字出现在约公元前2400年；中国的甲骨文数字出现在约公元前1600年。

古埃及的纸草书和羊皮书及巴比伦的泥板文书记载了早期数学的内容，年代可以追溯到公元前2000年，其中甚至有“整勾股数”及二次方程求解的记录。

二、初等数学时期（前6世纪——公元16世纪）这个时期也称常量数学时期，这期间逐渐形成了初等数学的主要分支：算术、几何、代数、三角。

该时期的基本成果，构成现在中学数学的主要内容。

这一时期又分为三个阶段：古希腊；东方；欧洲文艺复兴。

下面我们分别介绍：1．古希腊（前6世纪——公元6世纪）毕达哥拉斯——“万物皆数”欧几里得——几何《原本》阿基米德——面积、体积阿波罗尼奥斯——《圆锥曲线论》托勒密——三角学丢番图——不定方程2．东方（公元2世纪——15世纪）1）中国西汉（前2世纪）——《周髀算经》、《九章算术》魏晋南北朝（公元3世纪——5世纪）——刘徽、祖冲之：出入相补原理，割圆术，算术。

数学发展史时间轴
数学发展史可以追溯到人类文明的起源，几乎与人类思维和社会发展同步进行。

下面是一个简要的数学发展史时间轴：
1. 古代数学（约公元前3000年-公元5世纪）：
古代数学主要集中在古巴比伦、古埃及、古希腊、古印度和古中国等地。

这个时期的数学主要涉及算术、几何和代数等基本概念和方法的发展。

2. 中世纪数学（公元5世纪-15世纪）：
中世纪数学主要由阿拉伯数学家和欧洲学者推动。

阿拉伯人引入了印度-阿拉伯数字系统和代数的进一步发展。

欧洲学者则致力于恢复和传播古代数学知识，推动了几何学的发展。

3. 文艺复兴时期（15世纪-17世纪）：
文艺复兴时期是数学发展的黄金时期，涌现出许多伟大的数学家。

代表性的有勒内·笛卡尔和伽利略·伽利雷，他们为代数和几何学的发展做出了重要贡献。

4. 近代数学（17世纪-19世纪）：
近代数学的突破主要来自于微积分学的发展。

牛顿和莱布尼茨同
时独立发现了微积分的基本原理。

这一时期还涌现出许多其他重要的数学家，如欧拉、高斯和拉格朗日等。

5. 现代数学（20世纪至今）：
现代数学涉及的领域非常广泛，包括数学分析、代数学、几何学、概率论、统计学、拓扑学等。

数学家们不断提出新的理论、方法和应用，推动着数学的不断发展和应用的扩展。

这只是一个简要的数学发展史时间轴，数学的发展一直在不断演进，影响着我们的生活和科学技术的进步。

西方数学发展史以下是各个时期的简要概述：1.古希腊数学（公元前600年-公元500年）：o古典希腊时期是西方数学的黄金时代，伊奥尼亚学派的泰勒斯、毕达哥拉斯学派对数论和几何有重大贡献，比如毕达哥拉斯定理。

o欧几里得编写了《几何原本》，奠定了欧氏几何的基础，包括公理化方法。

o阿基米德在静力学与浮力原理、圆周率的计算等方面做出了杰出成就。

o阿波罗尼奥斯对圆锥曲线的研究也对后世产生了深远影响。

2.中世纪数学（公元500年-1500年）：o在中世纪早期，欧洲数学的发展相对缓慢，但阿拉伯世界翻译并注解了大量的希腊数学著作，使得数学知识得以传承。

o中世纪晚期，欧洲开始出现复兴迹象，斐波那契的著作《算盘书》对商业计算和数学教育有着重要推动作用，他著名的“斐波那契数列”成为数论研究的一个经典课题。

3.文艺复兴与近代数学（1500年-1700年）：o文艺复兴时期，科学和艺术的繁荣带动了数学的发展。

笛卡尔发明了解析几何，将代数方法应用于几何问题，开辟了新的数学领域。

o帕斯卡和费马分别在概率论和数论方面做出了开创性的工作，如帕斯卡定律和费马大定理。

o牛顿和莱布尼茨独立发明了微积分，这是数学史上的一个里程碑事件，为后续物理学和其他学科提供了强大的工具。

4.18世纪到现代数学（1700年至今）：o18世纪启蒙时代的数学家如欧拉、拉格朗日和高斯等人在分析学、数论、代数学等领域取得了众多突破。

o19世纪初，随着非欧几何的发现（如黎曼几何），数学逐渐脱离了纯粹直观和经验的束缚，更加抽象和严谨。

o近代数学分支繁多，群论、拓扑学、集合论、逻辑学等新兴领域纷纷崛起，计算机科学的发展也促进了离散数学和计算数学的繁荣。

5.19世纪：o伽罗华提出了群论，为代数学开辟了新的研究方向，解决了根式解代数方程的可能性问题。

o库默尔在数论中引入理想数概念，发展了解析数论的雏形。

o戴德金和康托尔分别在实数理论与集合论方面取得了革命性进展，其中康托尔创立了现代无限集合论，并提出了著名的连续统假设。

数学史简介数学，作为人类智慧的结晶，自古以来就与人类文明的发展紧密相连。

从最初的计数和测量，到抽象的代数和几何，再到现代的计算机科学和量子力学，数学始终在各个领域发挥着重要作用。

本文将简要介绍数学的发展历程，以展示这一学科的无穷魅力。

一、古代数学数学的起源可以追溯到史前时期，当时的人们为了解决实际问题，如土地测量、天文观测等，开始研究数学。

古埃及和巴比伦是数学发展最早的地区之一，他们研究了几何学和算术，并制定了一些数学规则。

约公元前300年，古希腊数学家欧几里得发表了《几何原本》，这是一部系统地阐述了平面几何知识的著作，对后世产生了深远影响。

二、中世纪数学在中世纪，阿拉伯世界成为了数学研究的中心。

阿拉伯数学家对古希腊数学进行了翻译和传承，并在此基础上进行创新。

他们引入了印度数学中的数字系统，即阿拉伯数字，这一系统在当时比罗马数字更为先进。

阿拉伯数学家还研究了代数学，提出了方程的解法和代数符号。

三、文艺复兴时期数学文艺复兴时期，欧洲数学迅速发展。

这一时期的数学家开始研究更为复杂的数学问题，如三次方程的解法、无穷级数等。

意大利数学家伽利略和德国数学家开普勒在天文学领域取得了重要成果，为后来牛顿和莱布尼茨创立微积分奠定了基础。

四、现代数学17世纪，英国数学家牛顿和德国数学家莱布尼茨几乎同时发明了微积分。

这一学科的出现标志着现代数学的诞生。

此后，数学家们开始研究更为抽象的数学问题，如拓扑学、群论等。

19世纪，法国数学家庞加莱提出了拓扑学的基本概念，为现代几何学的发展奠定了基础。

20世纪，数学家们继续深入研究各个领域，如概率论、数论、计算机科学等，使数学得到了空前的发展。

五、数学在中国中国古代数学也有着悠久的历史。

早在商周时期，我国就有了甲骨文中的数学记载。

汉代，数学家赵爽提出了勾股定理的证明，被称为“赵爽定理”。

唐代，数学家李冶、秦九韶等人研究了高次方程的解法。

宋代，数学家贾宪、杨辉等人研究了几何学和算术。

数学的发展历史数学是一门古老而又迷人的学科，它随着人类文明的进步而不断发展。

在人类的历史长河中，数学发展经历了多个重要的阶段和里程碑。

本文将回顾数学的发展历史，带您一起走进这个充满智慧的领域。

1. 古代数学的起源数学的起源可以追溯到公元前3000年左右的古巴比伦和古埃及。

在巴比伦，人们开始研究几何学，并应用它来解决土地测量和建筑等实际问题。

古埃及人则致力于测量、计数和记录财产。

他们发明了用于扩大数字量级的系统——埃及分数系统。

2. 古希腊数学的兴起古希腊是数学史上一个重要的里程碑。

在公元前6世纪，古希腊人开始对几何学和算术进行深入研究。

毕达哥拉斯提出了一系列关于直角三角形的理论，开创了几何学研究的先河。

欧几里得则在其巨著《几何原本》中，系统地整理了希腊前人的研究成果，成为几何学的标准教材，并对后世产生深远影响。

3. 中世纪的逐渐复兴在中世纪，数学的发展出现了滞缓的趋势，但仍有一些关键性的进展。

尤其是在伊斯兰文化的影响下，阿拉伯和波斯数学家的贡献不可忽视。

穆罕默德·本·穆萨等人为代数学的发展奠定了基础，并引入了许多重要的数学概念和技术。

4. 文艺复兴时期的数学大革命文艺复兴时期，欧洲大陆经历了一场思想解放的浪潮，数学领域也不例外。

这个时期的数学家对古希腊的数学遗产进行了翻新和扩展。

尼古拉斯·科佩尼库斯在代数学中引入了符号表示法，使得代数问题的处理更加灵活高效。

同时，数学的应用范围也被扩展到物理学和天文学等领域，为科学的进步做出了巨大贡献。

5. 近现代数学的突破18世纪和19世纪是数学领域的黄金时代。

数学家们在微积分、概率论、数论和几何学等方面取得了重大突破。

如牛顿和莱布尼茨共同发现了微积分，为物理学和工程学的发展提供了坚实的基础。

高斯则在数论和代数几何学方面做出了杰出的贡献，并推动了非欧几何学的发展。

6. 当代数学的拓展和应用随着科技的进步和人类对自然规律的深入理解，数学在当代的发展变得更加广泛和深入。

数学的发展史
数学发展史可追溯到古人发现使用数字来统计物体数量的行为。

早在3000多年前，埃及人就发明了第一种数字系统。

公元前1700年，印度人发明了类似现代数学符号的符号系统，包括“ + ”、“-”、“ × ”、“÷”和根号等标记。

后来，古希腊人就利用其系统进行
形式化的数学研究，将数学从实际应用转变为理论抽象的学科。

经历了古希腊文明的发展，中世纪的数学受到了穆斯林的影响，
以独特的方法对数学进行了完善。

17世纪，1686年，英国的伽利略和
德国的斐波那契已经建立了新的数学理论体系，它不仅清晰明确地证
实了新发现的宇宙学，而且也是现代数学的基础。

18世纪，数学有了显著进步，德国数学家勃兰特开创了微积分，
拓展了古希腊时期的几何。

德国科学家博宁根据独特的方法，发现了
著名的博宁准则；而法国数学家和物理学家拉格朗日将分析几何的概
念应用到实际问题中，建立了令人惊叹的拉格朗日几何。

19世纪，海森堡、费马等俄罗斯数学家也有着重要贡献，运用所
谓的“数学分析方法”，他们把几何中的重要性质和属性抽象出来，
这就是现代数学研究的源泉。

20世纪之前，数学不断发展，深入探索
数理逻辑，发展不同类型的数论，大量新的数学定理也随之诞生。

而
20世纪以后，随着计算机的发展，数学研究也取得了非常大的进步，
数学的应用被实际应用到科学、工程、经济和社会等各个领域。

中国数学发展史中国数学发展历史可以追溯到古代，早在商代，中国人就已经开始使用字母和数字了。

随着历史的发展，中国数学也不断发展。

下面我们来一一介绍。

1.古代数学古代数学主要有三个时期：先秦时期、汉代到隋唐时期、唐宋明清时期。

在先秦时期，尚书：“六铢”之中就包含有算术运算方法。

《九章算术》是将古代运算方法集中起来的一项数学成果。

在隋唐时期，王陂算经出现，这是一部有关算术、代数、几何、人工运算和天文理论的书籍。

唐代的《数书九章》更是囊括了古代数学大量的知识和成果。

2.八股文数学八股文是中国传统文化时期的一种标志性的文章写作形式。

在明清时期，数学教育也采用了这种形式。

后来，八股文数学成为了中国古代数学的代表性成果之一，而数学分成九科也成为了这一时期的一个标志性成果。

3.古代算术古代算术指的是古人们在生产和生活中所进行的算术运算。

在《数书九章》中，有大量关于古代算术的内容。

古代算术主要包括加法、减法、乘法、除法等计算方面的知识，还包括古人们使用的算盘、草率和算具等。

4.代数学代数学是一门古老而又现代的数学学科。

最早的代数学思想可以追溯至先秦时期的“六铢”，唐代的“大衍数学”和宋代的“忘穴”等都是代数学的成果。

代数学在古代并不是一个独立的学科，而是与其他学科如几何学和算术学紧密联系在一起的。

5.数学教育古代的数学教育主要有两种形式：家教和私塾。

在家教方面，大富豪会请最好的数学家为其子弟授课。

而在私塾方面，数学家将自己的子女和其他有志于学习数学的青年聚集在一起，进行数学教育。

6.现代数学现代数学是在西方文化的影响下，从19世纪末期到20世纪初期在中国发展壮大的一门学科。

现代数学的发展主要包括微积分、概率论、数理逻辑、数论、拓扑、代数等方面。

现代数学的发展推动了许多雷同的新学科和理论的出现。

以上是有关中国数学发展史的简介。

在古代，中国数学相当发达，与世界同步。

而在现代，中国数学在与其它强国数学学者竞争的同时，被大家逐渐所认同和赞扬。

数学发展史时间轴及事件1.古埃及数学（公元前3000年-公元前1000年）数学在古埃及有着悠久的历史。

古埃及人发展出了一套完整的计数系统，以及用于计算和测量的一系列实用技术和工具。

例如，他们使用了“象形数字”来表达数值，同时发明了一种称为“祭坛测量的土地”的算法，用于计算矩形或金字塔的面积。

2.古希腊数学（公元前600年-公元500年）古希腊数学在西方数学史上占据了重要的地位。

在这个时期，出现了许多杰出的数学家，如毕达哥拉斯、欧几里得和阿基米德等。

他们为数学界的发展做出了巨大的贡献，如毕达哥拉斯提出了著名的勾股定理，欧几里得写下了著名的《几何原本》，阿基米德则发明了微积分的基本原理。

3.中世纪欧洲数学（公元500年-1500年）在中世纪欧洲，数学得到了进一步的发展。

在这个时期，出现了许多修道士和学者，如奥尔本修道士和尼科马科斯等。

他们对数学进行了深入的研究，并在代数、几何和三角学等领域取得了一些重要成果。

同时，中世纪欧洲的数学教育也变得日益重要，一些大学纷纷开设数学课程。

4.文艺复兴时期数学（公元1500年-1700年）在文艺复兴时期，数学经历了巨大的变革和发展。

人们重新审视古希腊数学，并在此基础上进行创新。

代数学逐渐成为数学的主流，同时平面几何和立体几何也得到了极大的发展。

一些重要的数学思想和方法开始形成，如极限、导数和微积分等。

在这个时期，一些重要的数学家如雷科德、韦达和牛顿等为数学界的发展做出了巨大贡献。

雷科德在其著作《大术》中系统地阐述了代数符号和算术方法，韦达则发展出了符号代数，为现代代数奠定了基础。

牛顿则在微积分和物理学等领域做出了杰出的贡献。

5.近现代数学（公元1800年至今）近现代数学的发展可以说是日新月异。

在19世纪，数学家们开始研究更抽象的问题，如数论、抽象代数和拓扑学等。

同时，概率论和统计学也得到了迅速的发展。

20世纪初，数学开始与物理学、工程学等领域紧密联系，出现了许多应用数学分支，如量子力学、计算机科学、经济学等。

数学的发展历史数学，作为一门学科，经历了漫长的发展历程。

古希腊的毕达哥拉斯学派、我国古代的算学、近代的微积分学、现代的数理逻辑等都是数学史上的重要篇章，本文将从古希腊开始，简要介绍数学发展的历史。

一、古希腊时期古希腊是古代文明的重要代表之一，也是古代数学的重要中心之一。

毕达哥拉斯学派是古希腊时期的一个著名学派，他们强调数学的重要性，并对数学的基础做出了一些贡献。

古希腊时期数学的发展主要包括以下几个方面：（一）几何学古希腊时期，几何学得到了很好的发展。

欧几里德是古希腊时期最著名的数学家之一，他根据早期希腊的几何学知识，写出了一本名为《几何原本》的巨著。

这本书主要讲述了平面几何学和立体几何学的基本理论，被誉为几何学的圣经。

欧几里德的贡献包括从公理出发发展了平面几何学，建立了如今所使用的公理体系；他对于数学的分类，也影响至今；他提出几何的递推法以及对于平面坐标系的基础建立，都是几何学中不可或缺的重要概念。

（二）代数学古希腊时期，代数学也有了一定的发展。

毕达哥拉斯学派被认为是代数学的创始学派，他们强调数的本质和有理数的存在，提出了数的概念，并且探讨了数的基本性质，以此为基础开展了整体学和方程学研究。

我们可以说，毕达哥拉斯理论的提出，为后世的数字理论提供了丰富的内容。

（三）三角学古希腊时期，三角学的基本概念已经形成并有了一定的应用。

科学家提高了三角函数的性质、以及在图形学、建筑学、天文学、地图制作等领域的实际应用。

二、中世纪中世纪，数学的发展相对缓慢，离开了古代数学之光辉，但也有一些重要的成果和贡献。

主要集中于阿拉伯数学、欧洲的代数学和三角学。

（一）阿拉伯数学阿拉伯人是拜占庭帝国的扩张者，他们将一些古希腊的数学文献翻译为阿拉伯文，在中世纪的欧陆得以广泛传播。

并且他们开展了数学的研究，特别是代数学和三角学，做出了重要的贡献。

阿拉伯人发明了一种新的计算方法“阿拉伯数字”，即我们今天所了解的数字。

阿拉伯人的贡献之一是开展了三角函数的研究、这又为后来的微积分学提供了良好的基础。

简述数学发展史数学作为一门古老而又重要的学科，其发展历程可以追溯到古代文明的起源。

从最早的数数、计算到如今的高等数学和抽象代数，数学一直在不断演变和发展。

本文将以简述数学发展史为主题，介绍数学的起源、发展和重要里程碑。

一、古代数学的起源古代数学的起源可以追溯到古埃及、巴比伦和古印度等文明。

这些文明发展了一些基本的数学概念和计算方法。

比如，古埃及人通过观察天象来制定了一套365天的日历，巴比伦人发展了一种复杂的计算方法来解决土地测量和商业交易中的问题，古印度人则发展了一套用符号表示数的系统。

二、古希腊数学的发展古希腊是数学发展史上的重要里程碑。

在古希腊，数学开始从实用的计算方法转向了理论研究。

毕达哥拉斯学派提出了著名的毕达哥拉斯定理，开启了几何学的研究。

欧几里德则系统地总结和整理了古希腊数学的成果，编写了《几何原本》，成为后世数学教材的基石。

古希腊数学的理论研究为后来的数学发展打下了基础。

三、中世纪数学的发展中世纪是数学发展的一个相对停滞的时期，主要受到宗教和哲学的影响。

然而，中世纪的阿拉伯数学家却保留了古希腊数学的传统，并且在代数学和三角学方面有了重要的贡献。

他们引入了阿拉伯数字和十进制计数法，将古希腊的几何学和印度的代数学相结合，为后来的数学发展奠定了基础。

四、文艺复兴时期的数学革新文艺复兴时期是数学发展的一个重要阶段。

在这个时期，数学开始成为一门独立的学科，并且与现实生活的应用相结合。

伽利略和笛卡尔等科学家的贡献使得数学与物理学和天文学等自然科学产生了密切的联系。

同时，数学的符号表示也得到了进一步的发展，如笛卡尔坐标系的引入使得几何学和代数学的联系更加紧密。

五、近现代数学的发展近现代数学的发展是以数学的严格化和形式化为特点的。

19世纪，数学开始从几何学和代数学中分离出来，成为一门独立的学科。

数学家们开始研究更加抽象和普遍的概念，如集合论和数理逻辑。

同时，微积分的发展也为现代科学和工程学的发展提供了强大的工具。