流体力学PPT
- 格式：ppt
- 大小：2.37 MB
- 文档页数：151
下载文档原格式
合集下载
流体力学PPT
牛顿内摩擦定律表明： 切应力与速度梯度成正比；比例系数称动力粘度。
第 20 页
职教
绪论——1.2流体的主要力学性质 3、流体的粘度
——表示流体粘滞性大小
du dy
（1） 动力粘度
( Pa s)
P(泊） 1P 0.1Pa s
（2） 运动粘度
(m 2 / s )
St : cm2 / s
/ p
β↑，压缩性↑
可知： 液体β很小
第 26 页
职教
绪论——1.2流体的主要力学性质 弹性系数： 压缩系数的倒数
E 1
第 27 页
职教
绪论——1.2流体的主要力学性质 （2）液体的热胀性 热胀系数：压强不变时，单位温度变化所引起的 体积或密度的相对变化率
V / V a T
第 21 页
职教
绪论——1.2流体的主要力学性质 4、粘性的影响因素
粘度 液体 气体
流体种类 流体温度
o 气体 温度
液体：分子内聚力是产生粘度的主要因素。 温度↑→分子间距↑→分子吸引力↓→内摩擦力↓→粘度↓ 气体：分子热运动引起的动量交换是产生粘度的主要因素。 温度↑→分子热运动↑→动量交换↑→内摩擦力↑→粘度↑
第 4 页
职教
绪论——1.1概述
应
用
重要的专业基础课程，该课程的目的是 为了学习专业课以及从事技术工作提供必要 的基础理论和实践技能
第 5 页
职教
绪论——1.1概述
主要内容
绪论 流体静力学 不可压缩一元流体动力学 流动阻力和能量损失 管路计算 附面层与绕流阻力 孔口、管嘴出流和气体射流
第 6 页
职教
流体力学ppt
概念引入： 概念引入：
位置水头 ：z 压强水头 ：p/γ 测压管水头 ：z+p/γ=C 同一容器内静止液体中， 同一容器内静止液体中， 测压管水头均相等。 测压管水头均相等。
三、压强的表示方法和度量单位
1、表示方法
（1）绝对压强Pj：以绝对真空为零点。 绝对压强P 以绝对真空为零点。 相对压强P 以大气压P 为零点。 （2）相对压强P： 以大气压Pa为零点。 工程中，通常采用相对压强， 可正可负。 工程中，通常采用相对压强，P可正可负。 绝对压强与相对压强的关系： 绝对压强与相对压强的关系：P=Pj–Pa P 为正值时： 称为正压（表压， P为正值时：Pj>Pa，称为正压（表压，即压力表 读数）。 读数）。 为负值时： 称为负压（ P为负值时：Pj<Pa，称为负压（负压的绝对值称 真空度，即真空表读数）。 真空度，即真空表读数）。 真空度（只能是正值） 真空度（只能是正值）：Pk=Pa-Pj=-P
§1－1 流体的主要力学性质 －
一、惯性
定义：惯性是物体维持原有运动状态的性质。 定义：惯性是物体维持原有运动状态的性质。 质量：表征惯性的物理量。 质量：表征惯性的物理量。 流体的质量：常以密度来反映。 流体的质量：常以密度来反映。 密度：对于均质流体， 密度：对于均质流体，单位体积的质量称为密度 ρ = m /V ，即： 重度：对于均质流体， 重度：对于均质流体，单位体积的流体所受的重 力称为流体的重力密度，简称重度。 力称为流体的重力密度，简称重度。 即：
h= p
γ
一标准大气压： 一标准大气压： 三种压强换算关系： 三种压强换算关系： 压强换算关系
101325 N / m 2 h= = 10.33m 3 9807 N / m
流体力学ppt课件
6
三、特例 ❖ 火箭在高空非常稀薄的气体中飞行以及高真空技术中，如真空泵，其分子距与设备
尺寸可以比拟，不再是可以忽略不计了。这时不能再把流体看成是连续介质来研究。 ❖ 流体性质有局部突变时，如汽化。 ❖ 研究区域很小时。
7
第三节 作用在流体表面上的力 表面力 质量力
两类作用在流体上的力：表面力和质量力
M V d M V d d V 0
V dV d
E1 pd1V 1d d p0.0 1% 25 140 2.5 18P 0 a
Vdp
13
二、流体的膨胀性 当压强一定时，流体温度变化体积改变的性质称为流体的膨胀性，膨胀性的大小用
温度膨胀系数来表示。 1.膨胀系数
单位温度增加所引起的体积相对变化量
17
三种圆板的衰减时间均相等。 库仑得出结论:衰减的原因，不是圆板与液体之间的相互摩擦 ，而是液体内部的摩擦 。
18
2.牛顿内摩擦定律
(1) 牛顿平板实验
当h和u不是很大时，两平板间沿y方向的流速呈线性分布，
uUy 或duUdy
h
h
h
dy
y U
uu+du
y
dudt
Aa
Bb
o
dy
d
d(dud)/tdtdu
3
第二节 流体作为连续介质的假设 问题的引出：
微观：流体是由大量做无规则热运动的分子所组成， 分子间存有空隙，在空间是不连续的。 宏观：一般工程中，所研究流体的空间尺度要比分子 距离大得多。
4
一、流体的连续介质假设 定义：不考虑流体分子间的间隙，把流体视为由
无数连续分布的流体微团组成的连续介质。这就是1755年欧拉提出的“连续介质 假设模型”。
三、特例 ❖ 火箭在高空非常稀薄的气体中飞行以及高真空技术中，如真空泵，其分子距与设备
尺寸可以比拟，不再是可以忽略不计了。这时不能再把流体看成是连续介质来研究。 ❖ 流体性质有局部突变时，如汽化。 ❖ 研究区域很小时。
7
第三节 作用在流体表面上的力 表面力 质量力
两类作用在流体上的力：表面力和质量力
M V d M V d d V 0
V dV d
E1 pd1V 1d d p0.0 1% 25 140 2.5 18P 0 a
Vdp
13
二、流体的膨胀性 当压强一定时，流体温度变化体积改变的性质称为流体的膨胀性，膨胀性的大小用
温度膨胀系数来表示。 1.膨胀系数
单位温度增加所引起的体积相对变化量
17
三种圆板的衰减时间均相等。 库仑得出结论:衰减的原因，不是圆板与液体之间的相互摩擦 ，而是液体内部的摩擦 。
18
2.牛顿内摩擦定律
(1) 牛顿平板实验
当h和u不是很大时，两平板间沿y方向的流速呈线性分布，
uUy 或duUdy
h
h
h
dy
y U
uu+du
y
dudt
Aa
Bb
o
dy
d
d(dud)/tdtdu
3
第二节 流体作为连续介质的假设 问题的引出：
微观：流体是由大量做无规则热运动的分子所组成， 分子间存有空隙，在空间是不连续的。 宏观：一般工程中，所研究流体的空间尺度要比分子 距离大得多。
4
一、流体的连续介质假设 定义：不考虑流体分子间的间隙，把流体视为由
无数连续分布的流体微团组成的连续介质。这就是1755年欧拉提出的“连续介质 假设模型”。
流体力学基础讲解PPT课件
措施。
05
流体流动的湍流与噪声
湍流的定义与特性
湍流定义
湍流是一种高度复杂的三维非稳态、带旋转的不规则流动。 在湍流中，流体的各种物理参数，如速度、压力、温度等都 随时间与空间发生随机的变化。
湍流特性
湍流具有随机性、不规则性、非线性和非稳定性等特性。在 湍流中，流体的速度、方向和压力等都随时间和空间发生变 化，形成复杂的涡旋结构。
环境流体流动与环境保护
要点一
环境流体流动
环境中的流体流动对环境保护具有重要影响。例如，大气 中的气流会影响污染物的扩散和迁移，水流会影响水体中 的污染物迁移和沉积等。
要点二
环境保护
通过对环境中的流体流动进行研究和模拟，可以更好地了 解污染物扩散和迁移规律，为环境保护提供科学依据。同 时，通过合理规划和设计流体流动系统，可以有效降低污 染物对环境的影响，保护生态环境。
04
流体流动的能量转换
能量的定义与分类
总结词
能量是物体做功的能力，可以分为机械能、热能、电能等。在流体力学中，主要关注的是机械能中的 动能和势能。
详细描述
能量是物体做功的能力，它有多种表现形式，如机械能、热能、电能等。在流体力学中，我们主要关 注的是机械能，它包括动能和势能两种形式。动能是流体运动所具有的能量，与流体的速度和质量有 关；势能则是由于流体所处位置而具有的能量。
流体流动噪声
流体流动过程中产生的噪声主要包括 机械噪声和流体动力噪声。机械噪声 主要由机械振动和摩擦引起，而流体 动力噪声主要由湍流和流体动力振动 引起。
噪声控制
为了减小流体流动产生的噪声，研究 者们提出了各种噪声控制方法，如改 变管道结构、添加消音器和改变流体 动力特性等。这些方法可以有效降低 流体流动产生的噪声。
05
流体流动的湍流与噪声
湍流的定义与特性
湍流定义
湍流是一种高度复杂的三维非稳态、带旋转的不规则流动。 在湍流中，流体的各种物理参数，如速度、压力、温度等都 随时间与空间发生随机的变化。
湍流特性
湍流具有随机性、不规则性、非线性和非稳定性等特性。在 湍流中，流体的速度、方向和压力等都随时间和空间发生变 化，形成复杂的涡旋结构。
环境流体流动与环境保护
要点一
环境流体流动
环境中的流体流动对环境保护具有重要影响。例如，大气 中的气流会影响污染物的扩散和迁移，水流会影响水体中 的污染物迁移和沉积等。
要点二
环境保护
通过对环境中的流体流动进行研究和模拟，可以更好地了 解污染物扩散和迁移规律，为环境保护提供科学依据。同 时，通过合理规划和设计流体流动系统，可以有效降低污 染物对环境的影响，保护生态环境。
04
流体流动的能量转换
能量的定义与分类
总结词
能量是物体做功的能力，可以分为机械能、热能、电能等。在流体力学中，主要关注的是机械能中的 动能和势能。
详细描述
能量是物体做功的能力，它有多种表现形式，如机械能、热能、电能等。在流体力学中，我们主要关 注的是机械能，它包括动能和势能两种形式。动能是流体运动所具有的能量，与流体的速度和质量有 关；势能则是由于流体所处位置而具有的能量。
流体流动噪声
流体流动过程中产生的噪声主要包括 机械噪声和流体动力噪声。机械噪声 主要由机械振动和摩擦引起，而流体 动力噪声主要由湍流和流体动力振动 引起。
噪声控制
为了减小流体流动产生的噪声，研究 者们提出了各种噪声控制方法，如改 变管道结构、添加消音器和改变流体 动力特性等。这些方法可以有效降低 流体流动产生的噪声。
流体力学(共64张PPT)
1) 柏努利方程式说明理想流体在管内做稳定流动，没有
外功参加时，任意截面上单位质量流体的总机械能即动能、
位能、静压能之和为一常数，用E表示。
即：1kg理想流体在各截面上的总机械能相等，但各种形式的机
械能却不一定相等，可以相互转换。
2) 对于实际流体，在管路内流动时，应满足：上游截面处的总机械能大于下游截面
p g 1z12 u 1 g 2W g ep g 2z22 u g 2 2g hf
JJ
kgm/s2
m N
流体输送机械对每牛顿流体所做的功
令
HeW ge,
Hf ghf
p g 1z12 u 1 g 2H ep g 2z22 ug 2 2 H f
静压头
位压头
动压头 泵的扬程（ 有效压头） 总压头
处的总机械能。
22
3)g式中z各、项 的2u 2物、理 意p 义处于g 某Z 个1 截u 2 1 面2上的p 1流 W 体e本 身g Z 所2具u 有2 22 的 能p 量2 ; hf
We和Σhf： 流体流动过程中所获得或消耗的能量〔能量损失〕;
We：输送设备对单位质量流体所做的有效功;
Ne：单位时间输送设备对流体所做的有效功，即有效功率;
u2 2
u22 2
u12 2
p v p 2 v 2 p 1 v 1
Ug Z 2 u2 pQ eW e
——稳定流动过程的总能量衡算式 18
UgZ 2 u2pQ eW e
2、流动系统的机械能衡算式——柏努利方程
1) 流动系统的机械能衡算式〔消去△U和Qe 〕
UQ'e vv12pdv热力学第一定律
26
五、柏努利方程应用
三种衡算基准
流体力学ppt课件-流体动力学
g
g
2g
水头
，
z
p
g
v2
2g
总水头， hw 水头损失
第二节 热力学第一定律——能量方程
水头线的绘制
总水头线
hw
对于理想流体，总水
1
v12 2g
2
v22 2g
头线是沿程不变的，
测压管水头线
p2
为一水平直线，对于
g
实际流体，总水头沿 程降低，但测压管水
p1 g
头线沿程有可能降低、
z2
不变或者升高。
z1
v2 A2 e2
u22 2
gz2
p2
v1A1 e1
u12 2
gz1
p1
微元流管即为流线，如果不 可压缩理想流体与外界无热 交换，热力学能为常数，则
u2 gz p 常数
2
这个方程是伯努利于1738年首先提出来的，命名为伯努利 方程。伯努利方程的物理意义是沿流线机械能守恒。
第二节 热力学第一定律——能量方程
皮托在1773年用一根弯成直角的玻璃管，测量了法国塞纳河 的流速。原理如图所示，在液体管道某截面装一个测压管和 一个两端开口弯成直角的玻璃管（皮托管），皮托管一端正 对来流，一端垂直向上，此时皮托管内液柱比测压管内液柱 高h，这是因为流体流到皮托管入口A点受到阻滞，速度降为 零，流体的动能变化为压强势能，形成驻点A，A处的压强称 为总压，与A位于同一流线且在A上游的B点未受测压管的影 响，其压强与A点测压管测得的压强相等，称为静压。
第四章 流体动力学
基本内容
• 雷诺输运公式 • 能量方程 • 动量方程 • 流体力学方程应用
第一节 雷诺输运方程
• 前面解决了流体运动的表示方法,但要在流 体上应用物理定律还有困难.
《流体力学基础》课件
流体力学的发展与前景
流体力学的历史
流体力学的发展可以追溯到古代，如亚历山大在水力学方面的研究奠定了基础。
流体力学的现状
随着计算机和数值模拟技术的发展，流体力学得到了迅速进展，推动了各个领域中的应用。
流体力学的未来
未来的流体力学研究将继续突破技术限制，深入探索流体力学领域中的未知，并应用于更多 的实际问题。
《流体力学基础》PPT课 件
流体力学是研究流体力学的基本原理和应用的学科。它涉及到流体的运动、 特性和行为，以及在各个领域中的应用。
流体力学的定义
什么是流体力学？
流体力学研究流体在宏观上的物理性质和运动规律，包括流体的压力、密度、速度、流量等。
为什么流体力学重要？
流体力学是解决涉及流体的问题和设计各类工程设备的基础，对于工程、天文学和生物学等 领域都具有重要意义。
3
流体的流动行为
流体在管道、河流、以及涡流等情况下，会产生不同的流动行为，如旋涡、沉积 和分层等。
应用案例介绍
流体力学在工程中的应用
流体力学在建筑物、水利工程、 飞行器设计等领域中有着广泛 的应用，帮助解决各种流体相 关的问题。
流体力学在天文学中的 应用
天文学中的星系、恒星和行星 的运动，以及宇宙中物质的分 布都与流体力学有着密切的关 系。
流体力学在生物学中的 应用
生物中的血液循环、鱼类的游 泳、鸟类的飞行等现象都受到 流体力学的影响，帮助揭示生 物机制。
流体力学研究的挑战
1 流体力学领域的未解之谜
2 流体力学研究的技术难题
尽管流体力学取得了许多成果，但仍有一ห้องสมุดไป่ตู้些现象和问题，如湍流、颗粒流等，尚未 完全理解。
流体力学研究需要借助先进的计算方法、 实验设备和数值模拟技术，来解决复杂的 流体问题。
《流体力学基础知识》课件
流体粘性
流体抵抗剪切力的性质，粘性大小与流体的种类和温度有关。
流动模型
根据流体的粘性和流动特性，建立各种流动模型，如层流、湍流等。
06
流体力学在工程中的应用
流体输送与管道设计
总结词
流体输送与管道设计是流体力学在工程 中的重要应用之一，主要涉及流体在管 道中的流动规律和设计原则。
VS
详细描述
在工业生产和城市供水中，需要利用流体 力学的原理进行管道设计和流体输送，以 实现高效、低能耗的流体传输。管道设计 需要考虑流体的流速、压力、粘度等参数 ，以及管道的材质、直径、长度等因素， 以确保流体输送的稳定性和可靠性。
流体力学的发展历程
要点一
总结词
流体力学的发展历程及重要事件
要点二
详细描述
流体力学的发展历程可以追溯到古代，但直到17世纪才真 正开始形成独立的学科。在17世纪到20世纪期间，许多科 学家和工程师为流体力学的发展做出了重要贡献，如伯努 利、欧拉、斯托克斯等。随着科技的发展，流体力学在理 论和实践方面都取得了巨大的进步，为人类社会的进步和 发展做出了重要贡献。
3
流体流动的连续性原理
在流场中任取一元流管，流进和流出该元流的流 量相等。
流体流动的能量传递与转换
压力能传递
流体在流动过程中，压力能可以传递给其他流体 或转化为其他形式的能量。
动能转换
流体的动能可以转换为其他形式的能量，如压能 、热能等。
热能传递
流体在流动过程中，可以与周围介质进行热能交 换，实现热量的传递。
流体流动的阻力与损失
摩擦阻力
流体在管道中流动时，由于流体的粘性和管壁的粗糙度，会产生 摩擦阻力。
局部阻力
流体在通过管道中的阀门、弯头等局部构件时，会产生局部阻力。
流体抵抗剪切力的性质，粘性大小与流体的种类和温度有关。
流动模型
根据流体的粘性和流动特性，建立各种流动模型，如层流、湍流等。
06
流体力学在工程中的应用
流体输送与管道设计
总结词
流体输送与管道设计是流体力学在工程 中的重要应用之一，主要涉及流体在管 道中的流动规律和设计原则。
VS
详细描述
在工业生产和城市供水中，需要利用流体 力学的原理进行管道设计和流体输送，以 实现高效、低能耗的流体传输。管道设计 需要考虑流体的流速、压力、粘度等参数 ，以及管道的材质、直径、长度等因素， 以确保流体输送的稳定性和可靠性。
流体力学的发展历程
要点一
总结词
流体力学的发展历程及重要事件
要点二
详细描述
流体力学的发展历程可以追溯到古代，但直到17世纪才真 正开始形成独立的学科。在17世纪到20世纪期间，许多科 学家和工程师为流体力学的发展做出了重要贡献，如伯努 利、欧拉、斯托克斯等。随着科技的发展，流体力学在理 论和实践方面都取得了巨大的进步，为人类社会的进步和 发展做出了重要贡献。
3
流体流动的连续性原理
在流场中任取一元流管，流进和流出该元流的流 量相等。
流体流动的能量传递与转换
压力能传递
流体在流动过程中，压力能可以传递给其他流体 或转化为其他形式的能量。
动能转换
流体的动能可以转换为其他形式的能量，如压能 、热能等。
热能传递
流体在流动过程中，可以与周围介质进行热能交 换，实现热量的传递。
流体流动的阻力与损失
摩擦阻力
流体在管道中流动时，由于流体的粘性和管壁的粗糙度，会产生 摩擦阻力。
局部阻力
流体在通过管道中的阀门、弯头等局部构件时，会产生局部阻力。
第一章 流体力学基础ppt课件(共105张PPT)
原
力〔垂直于作用面，记为 ii〕和两个切向 应力〔又称为剪应力，平行于作用面，记为
理
ij，i j），例如图中与z轴垂直的面上受
到的应力为 zz〔法向）、 zx和 zy〔切
电 向），它们的矢量和为：
子
课
件 τ zzix zjy zkz
返回
前页
后页
主题
西
1.1 概述
安
交 • 3 作用在流体上的力
大 化
子 课 件
返回
前页
后页
主题
西
1.2.3 静力学原理在压力和压力差测量上的应用
安
交
大 思索：若U形压差计安装在倾斜管路中，此时读数 R反
化 映了什么？
工 原
理 p1p2
p2
p1 z2
电 子
(0)gR(z2z1)g z1
课
R
件
A A’
返回
前页
后页
主题
西 1.2.3 静力学原理在压力和压力差测量上的应用
安
交 大
•
2．压差计
化 • （2〕双液柱压差计
p1
p2
工•
原•
理
电•
子•
课
件
又称微差压差计适用于压差较小的场合。
z1
1
z1
密度接近但不互溶的两种指示
液1和2 ， 1略小于 2 ；
R
扩p 大1 室p 内2 径与2 U 管1 内g 径之R 比应大于10 。 2
图 1-8 双 液 柱 压 差 计
返回
安
交 大
•
1．压力计
化 • （2〕U形压力计
pa
工 • 设U形管中指示液液面高度差为RA，1 指• 示液
流体力学基础 ppt课件
6
流体的研究意义
流体的输送：根据生产要求，往往要将流体按照生产程序 从一个设备输送到另一个设备，从而完成流体输送的任务， 实现生产的连续化。
压强、流速和流量的测量：以便更好的掌握生产状况。
为强化设备提供适宜的流动条件：为了降低传递阻力，减 小设备尺寸，材料生产中的传热、传质过程以及化学反应大 都是在流体流动下进行的。流体流动状态对这些操作有较大 影响。
➢静压头：
式中的第二项 p/ρg 称为静压头，又称为单位重量流体 的静压能。
29
静压头的意义：
，
ห้องสมุดไป่ตู้
如图所示：密闭容器，内盛 有液体，液面上方压力为p。
图 静压能的意义 说明Z1处的液体对于大气压力来说，具有上升一定高度的能力。
30
Z+ p 常数
g
位压头＋静压头＝常数
也可将上述方程各项均乘以g，可得
gZ p 常数
上式为单位质量流体的静力学基本方程式
31
3 流体静力学基本方程式的应用
一、压强测量
1 U型管液柱压差计 指示液密度 ρ0，被测流体密度
为ρ，图中 a、b两点的压力是相
等的，因为这两点都在同一种静 止液体（指示液）的同一水平面 上。通过这个关系，便可求出p1
－p2的值。
注：指示剂的选择
Ar1% (均为体积%)。试求干空气在压力为
9.81×104Pa、温度为100℃时的密度。
18
解： 首先将摄氏度换算成开尔文：
100℃＝273+100=373K
1)求干空气的平均分子量：
Mm = M１y1 + M2y2 + … + Mnyn
=32 × 0.21+28 ×0.78+39.9 × 0.01
流体的研究意义
流体的输送：根据生产要求，往往要将流体按照生产程序 从一个设备输送到另一个设备，从而完成流体输送的任务， 实现生产的连续化。
压强、流速和流量的测量：以便更好的掌握生产状况。
为强化设备提供适宜的流动条件：为了降低传递阻力，减 小设备尺寸，材料生产中的传热、传质过程以及化学反应大 都是在流体流动下进行的。流体流动状态对这些操作有较大 影响。
➢静压头：
式中的第二项 p/ρg 称为静压头，又称为单位重量流体 的静压能。
29
静压头的意义：
，
ห้องสมุดไป่ตู้
如图所示：密闭容器，内盛 有液体，液面上方压力为p。
图 静压能的意义 说明Z1处的液体对于大气压力来说，具有上升一定高度的能力。
30
Z+ p 常数
g
位压头＋静压头＝常数
也可将上述方程各项均乘以g，可得
gZ p 常数
上式为单位质量流体的静力学基本方程式
31
3 流体静力学基本方程式的应用
一、压强测量
1 U型管液柱压差计 指示液密度 ρ0，被测流体密度
为ρ，图中 a、b两点的压力是相
等的，因为这两点都在同一种静 止液体（指示液）的同一水平面 上。通过这个关系，便可求出p1
－p2的值。
注：指示剂的选择
Ar1% (均为体积%)。试求干空气在压力为
9.81×104Pa、温度为100℃时的密度。
18
解： 首先将摄氏度换算成开尔文：
100℃＝273+100=373K
1)求干空气的平均分子量：
Mm = M１y1 + M2y2 + … + Mnyn
=32 × 0.21+28 ×0.78+39.9 × 0.01
高中物理奥林匹克竞赛专题---流体力学(共88张PPT)
压强视为平均压强。因此，垂直于x轴的左、右两微元面上
的总压力分别为：
p1 pdxdydz 2 x
和
p1 p dxdydz 2 x
同理，可得到垂直于y轴的下、上两个微元面上的总压力分别
为：
p
1 2
p y
dydxdz
和
p
1 2
pp(x,y,z)
2019/9/6
6
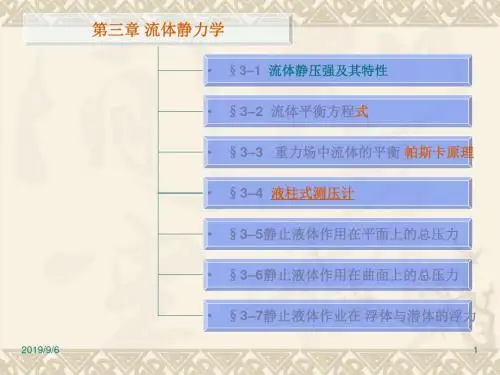
第二节 流体平衡方程式
一、流体平衡微分方程式
在静止流体中任取一边长为 dx，dy和dz的微元平行六面体
的流体微团，现在来分析作用在这流体微团上外力的平衡条 件。作用在微元平行六面体的表面力只有静压强。设微元平 行六面体中心点处的静压强为p，则作用在六个平面中心点 上的静压强可按泰勒（G.I.Taylor）级数展开，在垂直于X轴 的左、右两个平面中心点上的静压强分别为：
p y
dydxdz
2019/9/6
9
垂直于轴的后、前两个微元面上的总压力分别为：
p1pdzdxdy p1pdzdxdy
2z
2z
作用在流体微团上的外力除静压强外，还有质量力。
若流体微团的平均密度为ρ，则质量力沿三个坐标轴的分
量为
fxdxdydz fydxdydz fzdxdydz
（2）由于绝大多数气体的性质是气体绝对压强的函
数，如正压性气体ρ=ρ（p)，所以气体的压强都用
绝对压强表示。而液体的性质几乎不受压强的影响， 所以液体的压强常用计示压强表示，只有在汽化点 时，才用液体的绝对压强。
2019/9/6
30
压强的三种量度单位
（1）压强的基本定义
1 a （ 标 准 t 大 气 压 m ） 1 . 0 1 5 P 1 7 0 m 3 a 6 1 . 3 m m 0 2 O 0 3
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、液柱式测压计
（一）测压管（单管测压计）
测压管是一根两端开口的玻璃管，一端连在需要测量压 强处的容器壁上，另一端开口通大气。
A点相对压强： pA hA
优点：结构简单 缺点：测量较小的压强，20KPa以下
第 58 页
职教
流体静力学——2.5液体静压强的测量
（二）水银测压计（U形管测压计）
水银测压计是一个两端开口的U形管，弯管部分盛水银， 一端连在需要测量压强的地方，另一端通大气。
第 17 页
职教
绪论——1.2流体的主要力学性质 1、流体粘滞性分析
例：流体在圆管中流动（液体为例）
第 18 页
职教
绪论——1.2流体的主要力学性质 2、牛顿内摩擦定律
T A du
dy
式中 T—流体的内摩擦力（切向力），N； A—流层间的接触面积，m2； du/dy—垂直于流动方向上的速度梯度，1/s；
第 15 页
职教
绪论——1.2流体的主要力学性质
常见流体的密度：
表1-2
水——1000 kg/m3 空气——1.2920 kg/m3 水银——13590 kg/m3
第 16 页
职教
绪论——1.2流体的主要力学性质
（二）粘滞性
——流体内部质点（微团）或流层间如有相对运 动则产生内摩擦力（即粘滞力）以抵抗相对运动的 性质。
各种压强计量单位换算：表2-1
第 53 页
例2-4
职教
流体静力学——2.4测压管高度和测压管水头
一、液体静压强基本方 程的另一种表达形式
zA
pA
zB
pB
C(常数）
表明：在重力作用下，同种连续静止均质液体z+p/γ之和相等
第 54 页
职教
流体静力学——2.4测压管高度和测压管水头
二、液体静压强基本方程的意义
符号：p，单位：Pa
第 40 页
职教
流体静力学——2.1流体静压强及其特性
p P A
P p lim
A0 A
注意：静（总）压力P作用于受压面上，静压强p作用于受压面 上某点。
第 41 页
职教
流体静力学——2.1流体静压强及其特性
二、静压强的特性
1. 方向性
流体静压强的方向与作用面垂直并指向作用面的内法线方向。
pn
静压力
p
K
pt
切向压力
第 42 页
职教
流体静力学——2.1流体静压强及其特性
第 43 页
职教
流体静力学——2.1流体静压强及其特性
2. 大小性
作用于流体任一点静压强的大小在各个方向上均相等， 与作用面的方位无关，仅是该点坐标的函数。
p f (x, y, z)
第 44 页
职教
流体静力学——2.1流体静压强及其特性
温度↑→分子间距↑→分子吸引力↓→内摩擦力↓→粘度↓
气体：分子热运动引起的动量交换是产生粘度的主要因素。 温度↑→分子热运动↑→动量交换↑→内摩擦力↑→粘度↑
第 22 页
职教
绪论——1.2流体的主要力学性质 5、 粘度的测量 粘度计
恩格勒粘度计
第 23 页
职教
绪论——1.2流体的主要力学性质 6、牛顿流体和非牛顿流体
传递
例2-1
第 47 页
职教
流体静力学——2.2流体静压强的分布规律
（二）连通器与等压面
连通器是指相互连通的两个或几个容器 等压面是指静止液体中，压强相等的点组成的面
结论：在重力作用下，同种连续静止均质液体水平面为等压面。
第 48 页
职教
流体静力学——2.2流体静压强的分布规律
（三）分界面和自由液面
第 50 页
职教
流体静力学——2.3压强的计算基准和计量单位
一、压强的两种计算基准
1.绝对压强P′
以绝对真空（无气体分子存在）为基准点计算的压强。
2.相对压强P
以当地大气压强Pa为基准计算的压强。
p p pa
真空压强Pv（真空度）
p pa
pv pa p p
对开口容器: p h
第 51 页
（一）物理意义
z p C
比比 总 位压 比 置力 势 势势 能 能能
在重力作用下，同种连续静止液体中，各点的比位置势能与 比压力势能可相互转换，各点的总比势能保持不变。
第 55 页
职教
流体静力学——2.4测压管高度和测压管水头
（二）几何意义
z p C
位 位 测压 测
置 置 压强 压
高水 度头
管 高 度
第 32 页
职教
绪论——1.3作用在流体上的力
应力 单位面积上的表面力。
法向应力（压应力、压强）和切 向应力
p lim P A0 A
lim T
A0 A
p——法向应力，即流体所受压强，Pa τ——切向应力，即流体摩擦应力，Pa
第 33 页
职教
绪论——1.4流体的力学模型
一、连续介质与非连续介质
单位： N/m3
——表征物体重力特性的物理量
第 13 页
职教
绪论——1.2流体的主要力学性质
对于均质流体：
G
V
对于非均质流体：
lim G
V 0 V
g
第 14 页
职教
绪论——1.2流体的主要力学性质 3、影响流体密度的因素
流体种类
液体密度比气体大得多。
压力和温度
液体密度随p、t变化很小， 气体密度随p、t变化很大。
按不可压缩流体处理，如空气和烟风系统。
第 37 页
职教
知识点
流体概念及基本特性 流体的主要力学性质 作用于流体上的作用力 流体的力学模型
第 38 页
职教
流体静力学
第二章 流体静力学
第 39 页
职教
流体静力学——2.1流体静压强及其特性
一、流体静压强的定义
流体静压强：在流体内部或流体与固体壁面所存在的单位面 积上的法向作用力称为流体的压强，当流体处于静止状态时 ，流体的压强称为流体静压强
流体力学
浙江电力教育培训中心
第1页
职教
绪论——1.1概述
研究对象 研究任务 应用 主要内容 研究方法
第2页
职教
绪论——1.1概述
研究对象
流体
液体： 如电厂的水、油等 气体： 如电厂的水蒸汽、空气、烟气等
第3页
职教
绪论——1.1概述 研究任务
研究流体静止和运动时的宏观力学规律 解决工程技术问题
第4页
μ —动力粘度，Pa·s。
第 19 页
职教
绪论——1.2流体的主要力学性质 T du A dy
式中τ—切应力，即流层间单位接触面积上的内摩擦力N/ m2 ，Pa 。
牛顿内摩擦定律表明： 切应力与速度梯度成正比；比例系数称动力粘度。
第 20 页
职教
绪论——1.2流体的主要力学性质 3、流体的粘度
分界面是指两种容重不同、互不混合的液体之间的接触表面 自由液面是指静止的液体和气体接触的表面
结论：分界面、自由表面既为水平面又为等压面。
例2-2
第 49 页
职教
流体静力学——2.2流体静压强的分布规律
二、高差不大时气体压强的计算
p p0
——高差不大时气体静压强基本方程 表示空间各点气体压强相等
例2-3
连续性介质假定：
定义：不考虑流体分子间的间隙，把流体视为由无 数连续分布的流体微团组成的连续介质。
优点：可利用连续函数这一数学工具来研究流体运动规 律。
第 34 页
职教
绪论——1.4流体的力学模型
二、理想流体与粘性流体
（1）粘性流体
具有粘性的流体（μ≠0）。
（2）理想流体
忽略粘性的流体（μ=0）。
职教
流体静力学——2.3压强的计算基准和计量单位
第 52 页
职教
流体静力学——2.3压强的计算基准和计量单位
二、压强的计量单位
常用压强计量单位：
（一）用单位面积上所承受的力表示。 Pa KPa MPa 1Pa=1N/m2
（二）用液柱高度表示。 P<0.2 MPa mmH2O mmHg
（三）用大气压表示 标准大气压atm 工程大气压at
（1）牛顿流体
（μ =常数）
符合牛顿内摩擦定律的流体
如水、空气、油和水银等
（2）非牛顿流体 不符合牛顿内摩擦定律的流体
如：油漆、橡胶、糨糊、牙膏、泥浆等
第 24 页
du
dy
职教
绪论——1.2流体的主要力学性质
（三）压缩性和热胀性
流体的压缩性：P7 流体的热胀性：P7
第 25 页
职教
绪论——1.2流体的主要力学性质
单位质量力的轴向分力 ：
X FX ,Y FY , Z FZ MMM
第 31 页
职教
绪论——1.3作用在流体上的力
二、表面力
作用在被研究流体（分离体）表面上，与作用表面面积成 正比的力 ➢外力： 作用在流体边界上的外力，如大气对流体自由表面的压 力，容器壁面的反作用力 ➢内力： 流体质点相互作用而产生，如流体内压应力和切应力
（2）液体的热胀性
热胀系数：压强不变时，单位温度变化所引起的 体积或密度的相对变化率
a V /V (1/ K) T
可知：液体α很小。
a /
T
α↑，热胀性↑
注意： P、T变化很大时，要考虑体积变化，如高温高压下炉 水密度比常温常压下小。
第 28 页
职教
绪论——1.2流体的主要力学性质
2、气体的压缩性和热胀性
（一）测压管（单管测压计）
测压管是一根两端开口的玻璃管，一端连在需要测量压 强处的容器壁上，另一端开口通大气。
A点相对压强： pA hA
优点：结构简单 缺点：测量较小的压强，20KPa以下
第 58 页
职教
流体静力学——2.5液体静压强的测量
（二）水银测压计（U形管测压计）
水银测压计是一个两端开口的U形管，弯管部分盛水银， 一端连在需要测量压强的地方，另一端通大气。
第 17 页
职教
绪论——1.2流体的主要力学性质 1、流体粘滞性分析
例：流体在圆管中流动（液体为例）
第 18 页
职教
绪论——1.2流体的主要力学性质 2、牛顿内摩擦定律
T A du
dy
式中 T—流体的内摩擦力（切向力），N； A—流层间的接触面积，m2； du/dy—垂直于流动方向上的速度梯度，1/s；
第 15 页
职教
绪论——1.2流体的主要力学性质
常见流体的密度：
表1-2
水——1000 kg/m3 空气——1.2920 kg/m3 水银——13590 kg/m3
第 16 页
职教
绪论——1.2流体的主要力学性质
（二）粘滞性
——流体内部质点（微团）或流层间如有相对运 动则产生内摩擦力（即粘滞力）以抵抗相对运动的 性质。
各种压强计量单位换算：表2-1
第 53 页
例2-4
职教
流体静力学——2.4测压管高度和测压管水头
一、液体静压强基本方 程的另一种表达形式
zA
pA
zB
pB
C(常数）
表明：在重力作用下，同种连续静止均质液体z+p/γ之和相等
第 54 页
职教
流体静力学——2.4测压管高度和测压管水头
二、液体静压强基本方程的意义
符号：p，单位：Pa
第 40 页
职教
流体静力学——2.1流体静压强及其特性
p P A
P p lim
A0 A
注意：静（总）压力P作用于受压面上，静压强p作用于受压面 上某点。
第 41 页
职教
流体静力学——2.1流体静压强及其特性
二、静压强的特性
1. 方向性
流体静压强的方向与作用面垂直并指向作用面的内法线方向。
pn
静压力
p
K
pt
切向压力
第 42 页
职教
流体静力学——2.1流体静压强及其特性
第 43 页
职教
流体静力学——2.1流体静压强及其特性
2. 大小性
作用于流体任一点静压强的大小在各个方向上均相等， 与作用面的方位无关，仅是该点坐标的函数。
p f (x, y, z)
第 44 页
职教
流体静力学——2.1流体静压强及其特性
温度↑→分子间距↑→分子吸引力↓→内摩擦力↓→粘度↓
气体：分子热运动引起的动量交换是产生粘度的主要因素。 温度↑→分子热运动↑→动量交换↑→内摩擦力↑→粘度↑
第 22 页
职教
绪论——1.2流体的主要力学性质 5、 粘度的测量 粘度计
恩格勒粘度计
第 23 页
职教
绪论——1.2流体的主要力学性质 6、牛顿流体和非牛顿流体
传递
例2-1
第 47 页
职教
流体静力学——2.2流体静压强的分布规律
（二）连通器与等压面
连通器是指相互连通的两个或几个容器 等压面是指静止液体中，压强相等的点组成的面
结论：在重力作用下，同种连续静止均质液体水平面为等压面。
第 48 页
职教
流体静力学——2.2流体静压强的分布规律
（三）分界面和自由液面
第 50 页
职教
流体静力学——2.3压强的计算基准和计量单位
一、压强的两种计算基准
1.绝对压强P′
以绝对真空（无气体分子存在）为基准点计算的压强。
2.相对压强P
以当地大气压强Pa为基准计算的压强。
p p pa
真空压强Pv（真空度）
p pa
pv pa p p
对开口容器: p h
第 51 页
（一）物理意义
z p C
比比 总 位压 比 置力 势 势势 能 能能
在重力作用下，同种连续静止液体中，各点的比位置势能与 比压力势能可相互转换，各点的总比势能保持不变。
第 55 页
职教
流体静力学——2.4测压管高度和测压管水头
（二）几何意义
z p C
位 位 测压 测
置 置 压强 压
高水 度头
管 高 度
第 32 页
职教
绪论——1.3作用在流体上的力
应力 单位面积上的表面力。
法向应力（压应力、压强）和切 向应力
p lim P A0 A
lim T
A0 A
p——法向应力，即流体所受压强，Pa τ——切向应力，即流体摩擦应力，Pa
第 33 页
职教
绪论——1.4流体的力学模型
一、连续介质与非连续介质
单位： N/m3
——表征物体重力特性的物理量
第 13 页
职教
绪论——1.2流体的主要力学性质
对于均质流体：
G
V
对于非均质流体：
lim G
V 0 V
g
第 14 页
职教
绪论——1.2流体的主要力学性质 3、影响流体密度的因素
流体种类
液体密度比气体大得多。
压力和温度
液体密度随p、t变化很小， 气体密度随p、t变化很大。
按不可压缩流体处理，如空气和烟风系统。
第 37 页
职教
知识点
流体概念及基本特性 流体的主要力学性质 作用于流体上的作用力 流体的力学模型
第 38 页
职教
流体静力学
第二章 流体静力学
第 39 页
职教
流体静力学——2.1流体静压强及其特性
一、流体静压强的定义
流体静压强：在流体内部或流体与固体壁面所存在的单位面 积上的法向作用力称为流体的压强，当流体处于静止状态时 ，流体的压强称为流体静压强
流体力学
浙江电力教育培训中心
第1页
职教
绪论——1.1概述
研究对象 研究任务 应用 主要内容 研究方法
第2页
职教
绪论——1.1概述
研究对象
流体
液体： 如电厂的水、油等 气体： 如电厂的水蒸汽、空气、烟气等
第3页
职教
绪论——1.1概述 研究任务
研究流体静止和运动时的宏观力学规律 解决工程技术问题
第4页
μ —动力粘度，Pa·s。
第 19 页
职教
绪论——1.2流体的主要力学性质 T du A dy
式中τ—切应力，即流层间单位接触面积上的内摩擦力N/ m2 ，Pa 。
牛顿内摩擦定律表明： 切应力与速度梯度成正比；比例系数称动力粘度。
第 20 页
职教
绪论——1.2流体的主要力学性质 3、流体的粘度
分界面是指两种容重不同、互不混合的液体之间的接触表面 自由液面是指静止的液体和气体接触的表面
结论：分界面、自由表面既为水平面又为等压面。
例2-2
第 49 页
职教
流体静力学——2.2流体静压强的分布规律
二、高差不大时气体压强的计算
p p0
——高差不大时气体静压强基本方程 表示空间各点气体压强相等
例2-3
连续性介质假定：
定义：不考虑流体分子间的间隙，把流体视为由无 数连续分布的流体微团组成的连续介质。
优点：可利用连续函数这一数学工具来研究流体运动规 律。
第 34 页
职教
绪论——1.4流体的力学模型
二、理想流体与粘性流体
（1）粘性流体
具有粘性的流体（μ≠0）。
（2）理想流体
忽略粘性的流体（μ=0）。
职教
流体静力学——2.3压强的计算基准和计量单位
第 52 页
职教
流体静力学——2.3压强的计算基准和计量单位
二、压强的计量单位
常用压强计量单位：
（一）用单位面积上所承受的力表示。 Pa KPa MPa 1Pa=1N/m2
（二）用液柱高度表示。 P<0.2 MPa mmH2O mmHg
（三）用大气压表示 标准大气压atm 工程大气压at
（1）牛顿流体
（μ =常数）
符合牛顿内摩擦定律的流体
如水、空气、油和水银等
（2）非牛顿流体 不符合牛顿内摩擦定律的流体
如：油漆、橡胶、糨糊、牙膏、泥浆等
第 24 页
du
dy
职教
绪论——1.2流体的主要力学性质
（三）压缩性和热胀性
流体的压缩性：P7 流体的热胀性：P7
第 25 页
职教
绪论——1.2流体的主要力学性质
单位质量力的轴向分力 ：
X FX ,Y FY , Z FZ MMM
第 31 页
职教
绪论——1.3作用在流体上的力
二、表面力
作用在被研究流体（分离体）表面上，与作用表面面积成 正比的力 ➢外力： 作用在流体边界上的外力，如大气对流体自由表面的压 力，容器壁面的反作用力 ➢内力： 流体质点相互作用而产生，如流体内压应力和切应力
（2）液体的热胀性
热胀系数：压强不变时，单位温度变化所引起的 体积或密度的相对变化率
a V /V (1/ K) T
可知：液体α很小。
a /
T
α↑，热胀性↑
注意： P、T变化很大时，要考虑体积变化，如高温高压下炉 水密度比常温常压下小。
第 28 页
职教
绪论——1.2流体的主要力学性质
2、气体的压缩性和热胀性