第二节二重积分的计算
- 格式:ppt
- 大小:930.50 KB
- 文档页数:50






第二节_二重积分的计算法二重积分:在平面上规定一个有界闭合区域D,对于D上的每一点P(x,y),都有一个标量函数f(x,y)与之对应。
则二重积分的数值就是由函数f(x,y)在区域D上所有点处的函数值决定的。
二重积分一般可以表示为∬Df(x,y)dA。
计算二重积分的方法主要有以下几种:直角坐标法、极坐标法、换元积分法和累次积分法。
1.直角坐标法:针对矩形、直角三角形、抛物线和折线边界的区域,可以直接使用直角坐标法来计算二重积分。
具体步骤如下:(1)写出二重积分的累加和形式:I=ΣΣf(x,y)ΔA。
(2)将区域D分成若干小矩形,计算每个小矩形的面积ΔA。
(3)在每个小矩形上选择代表点(x,y),计算f(x,y)的函数值。
(4)将函数值与相应小矩形的面积相乘,加和求和即可得到二重积分的数值。
2.极坐标法:当具有极坐标对称性的区域时,采用极坐标法可以简化计算。
具体步骤如下:(1) 确定极坐标变换:x=r*cosθ,y=r*sinθ。
(2) 根据变换的雅可比矩阵计算面积元素dA的极坐标形式:dA=rdrdθ。
(3) 将二重积分转化为极坐标下的累次积分:I=∫∫Df(x,y)dxdy=∫∫Df(r*cosθ,r*sinθ)rdrdθ。
(4)将极坐标下的积分区域和积分限进行变换,然后按照累次积分进行计算。
3.换元积分法:当二重积分区域D的边界方程比较复杂时,可以使用换元积分法来简化计算。
具体步骤如下:(1)根据边界方程对二重积分区域D进行变换,将原来的二重积分区域映射到一个新的坐标系中的区域G。
(2)根据变换的雅可比矩阵,计算新坐标系下的面积元素dA'。
(3) 将二重积分转化为新坐标系下的累次积分:I=∫∫Df(x,y)dxdy=∫∫Gf(x(u,v),y(u,v)),J(u,v),dudv,其中J(u,v)为雅可比行列式。
(4)对新坐标系下的累次积分按照直角坐标法或极坐标法进行计算。
4.累次积分法:当二重积分区域D可以通过垂直于坐标轴的直线进行划分时,可以使用累次积分法进行计算。




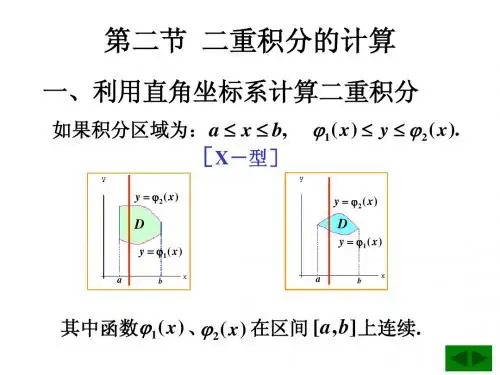
第二节 二重积分的计算法 一.本课的基本要求掌握在直角坐标系、极坐标系中二重积分的计算. 二.本课的重点、难点二重积分的计算为重点、积分限的确定为难点. 三.教学内容由⎰⎰∑→→∆=Dni iif d y x f 10),(),(lim σηξσλ;引入本次课题. 一. 直角坐标系中的累次积分法假定0),(≥y x f ,按照二重积分的几何意义⎰⎰Dd y x f σ),(的值等于以D 为底、以曲面),(y x f Z =为顶的曲顶柱体的体积.在上一章第一节我们知道区域D 的不等式组表示法通常有两种:1.⎩⎨⎧≤≤≤≤)()(21x y x bx a ϕϕ 或2.⎩⎨⎧≤≤≤≤)()(21y x y d y c ψψ 图1为方便,不妨以表示法1为例讨论.设⎰⎰Dd y x f σ),(所表示图形为图1.思路:⑴ 曲顶柱体的体积V 等于二重积分的值A .⑵ 能否找到另一种计算曲顶柱体体积V 的方法;如能找到,设其表达式为B . ⑶ 由传递关系可得到二重积分的计算方法,即A=B .在定积分的应用中我们已讨论过“平行截面面积为已知的立体的体积” 的求法.下面我们就利用其求法之一的切片法来计算二重积分⎰⎰Dd y x f σ),(所表示的柱体的体积.在区间[a,b]上任意取定一点0x ,作平行于yoz 面的平面0x x =,它与曲顶柱体相截所得截面是一个以区间[])(),(0201x x ϕϕ为底、曲线),(0y x f Z =为曲边的曲边梯形(图1中阴影部分).所以,这载面的面积为:⎰=)()(000201),()(x x dy y x f x A ϕϕ.由0x 的任意性,过区间[a,b]上任一点x 且平等yoz 面的平面截曲顶柱体所得截面的面积为:⎰=)()(21),()(x x dy y x f x A ϕϕ应用平行截面面积为已知的立体体积的求法,得曲顶柱体体积为:⎰⎰⎰==bax x badx dy y x f dx x A V )()(21]),([)(ϕϕ即⎰⎰⎰⎰=bax x Ddx dy y x f d y x f )()(21]),([),(ϕϕσ ⑴同理由表示法2可得:⎰⎰⎰⎰=dcy y Ddy dx y x f d y x f )()(21]),([),(ϕϕσ ⑵由此看到,二重积分的计算可化为两次定积分来计算.把二重积分化为两次定积分的方法称为累次积分法.在上述讨论中,我们假定0),(≥y x f ,但实际上述公式的成立并不受此条件限制. 以后我们称图1所示的积分区域为X ─型区域,后者为Y ─型区域。
§2 二重积分的计算【目的要求】1、熟练掌握先x 后y 和先y 后x 的二次积分方法;2、会熟练交换积分次序;会利用积分区域对称与被积函数的奇偶性简化二重积分的求解;3、熟练掌握先r 后θ的二次积分方法;4、会熟练地进行直角坐标系和极坐标系下二重积分的互化. 【重点难点】1、二重积分计算方法的建立;2、二重积分化为二次积分时积分限的配置;3、直角坐标系和极坐标系下二重积分的互化. 【教学内容】根据二重积分的定义来计算二重积分,对于一下特别简单的被积函数和积分区域来说是可行的,但对一般的函数和区域来说,常常是很困难的.因此,需要我们探求新的简便可行的计算方法.本节我们将介绍把二重积分化为累次积分(即两次定积分)的方法.一、利用直角坐标系计算二重积分下面我们将利用二重积分的几何意义讨论(,)d Df x y σ⎰⎰的计算问题,以下假定(,)0f x y ≥.在直角坐标系中,二重积分的面积元素d σ可表示为d d x y ,即(,)d (,)d d DDf x y f x y x y σ=⎰⎰⎰⎰.设积分区域D 可表示为不等式12,()()a x b x y x ϕϕ≤≤≤≤.xx图 7-4如图7-4所示,其中1()x ϕ,2()x ϕ在区间[],a b 上连续.这种区域的特点是:若穿过D 内部的一点与y 轴平行的直线,则该直线与区域的边界相交不超过两点,我们称之为X 型区域.按二重积分的几何意义,(,)d Df x y σ⎰⎰的值等于以D 为底,以曲面(,)z f x y =为顶的曲顶柱体的体积.我们可以应用“平行截面面积为已知的立体的体积”的方法计算这个曲顶柱体的体积.先计算截面积.为此,在区间[],a b 上任意取定一点0x ,作平行于yOz 面的平面0x x =.这平面截曲顶柱体所得的截面是一个以区间1020[(),()]x x ϕϕ为底、曲线0(,)z f x y =为曲边的曲边梯形(图7-5中阴影部分),所以这截面的面积为2010()00()()(,)d x x A x f x y y ϕϕ=⎰.一般地,过区间[],a b 上任一点x 且平行于yOz 面的平面截曲顶柱体所得截面的面积为21()()()(,)d x x A x f x y y ϕϕ=⎰.于是,应用计算平行截面面积为已知的立体的体积的方法,得曲顶柱体的体积为21()()()d (,)d d b ax abx V A x x f x y y x ϕϕ⎡⎤==⎢⎥⎣⎦⎰⎰⎰. 这个体积就是所求的二重积分的值,从而有等式21()()(,)d (,)d d bx a x Df x y f x y y x ϕϕσ⎡⎤=⎢⎥⎣⎦⎰⎰⎰⎰. (1)x图 7-5上式右端的积分叫做先对y 后对x 的二次积分,即先把x 看作常数,(,)f x y 只看作是y 的函数,并对y 计算从1()x ϕ到2()x ϕ的定积分,然后把计算结果(是关于x 的函数)对x 计算在区间[],a b 上的定积分.这个二次积分也可以记作21()()d (,)d bx ax x f x y y ϕϕ⎰⎰.因此,(1)式也可写成21()()(,)d d (,)d bx ax Df x y x f x y y ϕϕσ=⎰⎰⎰⎰, (2)这就是把二重积分化为先对y 后对x 的二次积分的公式.在上述讨论中,我们假定(,)0f x y ≥,但实际上公式(1)的成立并不受此条件的限制.类似地,如果积分区域D 可表示为不等式c yd ≤≤,12()()y x y ψψ≤≤.如图7-6所示,其中1()y ϕ、2()y ϕ在区间[],c d 上连续,那么就有21()()(,)d (,)d )d d y c y Df x y f x y x y ψψσ⎡⎤=⎢⎥⎣⎦⎰⎰⎰⎰. (3)(3)式右端的积分叫做先对x 再对y 的二次积分,该积分区域的特点是穿过D 内部的一点作与x 轴平行的直线.则该直线于区域的边界相交不超过两点,我们称之为Y 型区域.这个二次积分也可以记作21()()d (,)d dy cy y f x y x ψψ⎰⎰.因此,(3)式也可写成)(y图 7-6d21()()(,)d d (,)d dy cy Df x y y f x y x ψψσ=⎰⎰⎰⎰. (4)一般地,对于二重积分(,)d Df x y σ⎰⎰,根据积分区域D 的特点,若既是X 型又是Y 型,则公式(2)、(3)均可用,且这两个不同次序的二次积分相等,因为它们都等于同一个二重积分(,)d Df x y σ⎰⎰;若既不是X 型又不是Y 型,则我们要利用分割把区域分成几部分,使每个部分或是X 型或是Y 型.在图7-7中,把D 分成三部分,它们都是X 型区域,从而在三部分上的二重积分都可应用公式(2),再根据二重积分的性质2,它们的和就是在D 上的二重积分.下面我们通过例子来说明.例 1 计算d Dxy σ⎰⎰,其中D 是有直线1y =,2x =及y x =所围成的闭区域. 解 首先画出积分区域D (如图7-8)所示,D 既是X 型又是Y 型,因此既可以利用公式(2)也可以利用公式(4),即有两种解法,如下:解法一211d d d xDxy x xy y σ=⎰⎰⎰⎰22111()d 2xx y x =⎰ 42211()242x x =-98=. 解法二221d d d yDxy x xy y σ=⎰⎰⎰⎰22211()d 2y x y y =⎰2311(4)d 2y y y =-⎰ 42211(2)24y y =-98=. 例 2 计算d Dxy σ⎰⎰,其中D 是由抛物线2y x =及直线2y x =-所围成的闭d 图 7-7d图 7-8区域.解 首先画出积分区域D 如图7-9所示, D 既是X 型又是Y 型的,因此既可以利用公式(2)也可以利用公式(4),即有两种解法,如下: 解法一 将它看成X 型区域,则由于在 区间[0,1]及[1,4]上表示1()x ϕ的式子不同,需要分成两个小区域,我们分别记为1D 和2D ,其中{}1(,)|1D x y yx =≤≤≤, {}2(,)|21D x y x y x =-≤≤≤≤.因此,根据二重积分的性质2,有214012d d d d d d d x DDD xy xy xy x x x xy y σσσ-=+=+⎰⎰⎰⎰⎰⎰⎰⎰14220111(d (dx 22x y x x y =+⎰⎰458=.解法二 将它看成Y 型区域,则{}2(,)12,2D x y y y x y =-≤≤≤≤+,于是22222221145d d d 28y y y yDx xy y xy x yσ++--===⎰⎰⎰⎰⎰. 由此可见,利用公式(2)来计算比较麻烦.例 3 计算Dσ⎰⎰,其中D 是由直线y x =、1x =-和1y =所围成的闭区域.解 画出积分区域D (如图7-10所示),D 既是X 型的,又是Y 型的.若利用公式(2),得111d xDx y σ-=⎰⎰⎰⎰x图 7-91)31221211(1)d 3xx y x -=-+-⎰1311(||1)d 3x x -=--⎰ 13021(1)d 32x x =--=⎰.若利用公式(4),得111dy yDx σ--=⎰⎰⎰⎰, 其中关于x 的积分计算比较麻烦.所以这里用公式(2)计算较为方便.例 4 计算sin d Dyyσ⎰⎰,其中D 是由抛物线2y x =及直线y x =所围成的闭区域.解 首先画出积分区域D (如图7-11所示),D 既是X 型的,又是Y 型的. 若将D 看成X型区域,{(,)01,D x y x x y =≤≤≤≤,则10sin sin d =d d x Dyy x y y y σ⎰⎰⎰. 这个关于y 的积分不易求出原函数,因此计算无法继续下去.如果将它看成Y 型区域,{}2(,)01,D x y y y x y =≤≤≤≤,则211200sin sin sin d d d d ()d y y Dyy y x y y x y y y y y y ==-⎰⎰⎰⎰⎰ 11100cos sin d 1cos1d cos y y y y y y =--=-+⎰⎰111c o s 1(c o s )c o s d 1s i n 1y y y y =-+-=-⎰. 上述几个例子说明,在化二重积分为二次积分时,为了计算方便,需要选择图 7-10图 7-11恰当的二次积分的次序.这时,不仅需要考虑积分区域D 的形状,还要考虑被积函数(,)f x y 的特性.例 5 试证:()()0d ()d ()()d ayab x a b x a y e f x x a x e f x x --=-⎰⎰⎰,其中,a b 均为常数,且0a >.证 分析:等式左边是个先对x 再对y 的 二次积分,等式右边是个关于x 的定积分,而 被积函数是关于x 的函数,所以不妨交换积分次序,即换成先对y 再对x 的二次积分,如图 7-12所示.等式左边=()()0d ()d ()()d a a ab x a b x a xx e f x y a x e f x x --=-⎰⎰⎰.例 6 求两个底圆半径都等于R 的直交圆柱面所围成的立体的体积. 解 设这两个圆柱面的方程分别为222x y R += 及 222x z R +=.利用立体关于坐标平面的对称性,只要计算它在第一卦限部分(图7-13(a))的体积1V ,然后再乘以8就是所求立体的体积.所求立体在第一卦限部分可以看成是一个曲顶柱体,它的底为{(,)0,0D x y x R y =≤≤≤≤,图7-13(b)所示.它的顶是柱面z =.于是1DV σ=⎰⎰.图 7-12图 7-13 (a)图 7-13 (b)利用公式(2),得10d RDV x yσ==⎰⎰⎰223002()d3R Rx R x x R==-=⎰⎰.从而所求立体的体积为311683V V R==.二、利用极坐标计算二重积分有些二重积分,积分区域D的边界曲线用极坐标方程表示比较方便,而且被积函数用极坐标变量r,θ表示比较简单.这时,我们可以考虑利用极坐标来计算二重积分(,)dDf x yσ⎰⎰.我们知道平面上任意一点的极坐标(),rθ与它的直角坐标(),x y之间的变换公式为cosx rθ=,siny rθ=.按二重积分的定义1(,)d lim(,)ni i iiDf x y fλσεησ→==∆∑⎰⎰,下面我们来研究这个和的极限在极坐标系中的形式.假定从极点O出发且穿过闭区域D内部的射线与D的边界曲线相交不多于两点.我们用以极点为中心的一族同心圆:r=常数以及从极点出发的一族射线:θ=常数,把D分成n个小闭区域(图7-14).除了包含边界点的一些小闭区域外,小闭区域的面积iσ∆可计算如下:2211()22i i i i i ir r rσθθ∆=+∆⋅∆-⋅∆1(2)2i i i ir r rθ=+∆∆⋅∆()2i i ii ir r rrθ++∆=⋅∆⋅∆图7-14i i i r r θ=⋅∆⋅∆,其中i r 表示相邻两圆弧的半径的平均值.在这小闭区域内取圆周i r r =上的一点(,)i i r θ,该点的直角坐标设为i ξ,i η,则由直角坐标与极坐标之间的关系有cos i i i r ξθ=,sin i i i r ηθ=.于是11lim (,)lim (cos ,sin )nni i i i i i i i i i i i f f r r r r λλξησθθθ→→==∆=⋅∆⋅∆∑∑,即 (,)d (cos ,sin )d d DDf x y f r r r r σθθθ=⎰⎰⎰⎰.这里我们把点(,)r θ看做是在同一平面上的点(,)x y 的极坐标表示,所以上式右端的积分区域仍然记作D .由于在直角坐标系中(,)d Df x y σ⎰⎰也常记作(,)d d Df x y x y⎰⎰,所以上式又可写成 (,)d d (cos ,sin )d d DDf x y x y f r r r r θθθ=⎰⎰⎰⎰. (5)这就是二重积分的变量从直角坐标变换为极坐标的变换公式,其中d d r r θ就是极坐标系中的面积元素.公式(5)表明,要把二重积分中的变量从直角坐标变换为极坐标,只要把被积函数中的x ,y 分别换成cos r θ,sin r θ,并把直角坐标系中的面积元素d d x y 换成极坐标系中的面积元素d d r r θ即可.同样,在极坐标系下计算二重积分也要将它化为二次积分,我们根据极点与积分区域的关系分三种情况介绍.(1) 极点O 在区域D 之外,如图7-15所示,这时区域D 在θαθβ==与两条射线之间,这两条射线与区域D 的边界的交点把区域边界分为两部分,1()r r θ=,2()r r θ=.这时区域D 可以表示为{}12(,),()()D r r r r θαθβθθ=≤≤≤≤, 于是o r =图 7-15(cos ,sin )d d Df r r r r θθθ⎰⎰=21()()d (cos ,sin )dr r r f r r r βθαθθθθ⎰⎰.(2) 极点O 在区域D 的边界上,如图7-16所示,这时1()0r θ=,区域D 可以表示为{}(,),0()D r r r θαθβθ=≤≤≤≤, 于是(cos ,sin )d d d (cos ,sin )d Df r r r r f r r r r βαθθθθθθ=⎰⎰⎰.(3) 极点O 在区域D 的内部,如图7-17所示,这时区域D 可表示为{}(,)02,0()D r r r θθπθ=≤≤≤≤, 于是2()(cos ,sin )d d d (cos ,sin )d r df r r r r f r r r r πθθθθθθθ=⎰⎰⎰⎰.例 7 计算二重积分22d d 1Dx y x y++⎰⎰,其中D 是由221x y +≤所确定的圆域. 解 在极坐标中,积分区域D 可以表示为{}(,)02,01D r r θθπ=≤≤≤≤.于是,21222200d d d d d d 111D Dx y r r rr x y r r πθθ==++++⎰⎰⎰⎰⎰⎰ 221001ln(1)d 2r πθ=+⎰l n 2π=. xo 图 7-16)(θr r =图 7-17例 8计算二重积分Dσ,其中D 是圆222x y y +=围成的闭区域.解 圆222x y y +=的极坐标方程是2sin r θ=, 如图7-18所示,积分区域D 可以表示为{}(,)0,02sin D r r θθπθ=≤≤≤≤. 于是2sin 220d d d d DDr r r r πθθθθ==⎰⎰⎰⎰320088sin d (1cos )d cos 33ππθθθθ==--⎰⎰ 308132(c o s c o s )339πθθ=--=.例 9 计算二重积分22()d d x y Dex y -+⎰⎰,其中{}222(,)D x y x y R =+≤.解 在极坐标中,积分区域D 可以表示为{}(,)02,0D r r R θθπ=≤≤≤≤.于是222222()0001d d d d 2()(1)2R xy r r RR De x y e r r e e πθππ-+---==⋅-=-⎰⎰⎰⎰.例 10计算二重积分DI σ=⎰⎰,其中D 是直线y x =、2x =及上半圆周y =所围成的闭区域.解 画出积分区域D ,如图7-19所示, 它在极坐标下可表示为2(,)0,2cos 4cos D r r πθθθθ⎧⎫=≤≤≤≤⎨⎬⎩⎭.于是24cos 4302cos 0111d d (cos )d 22cos I r r r ππθθθθθθ==--⎰⎰⎰图 7-18图 7-19401(sin ln |sec tan |)2πθθθ=--+1ln 1)]2=-.三、广义二重积分若二元函数的积分区域是无界的,则类似于一元函数,我们可以先在有界区域内积分,然后通过取极限求此积分.这类积分在概率统计中有广泛的应用.例 11 计算定积分 2d x Ie x +∞--∞=⎰.解 本题如果用定积分计算,由于 2x e-的原函数不能用初等函数表示,所以算不出来.我们采用的技巧是先计算二重积分22()d d xy De x y -+⎰⎰,其中区域D 是整个平面.一方面,我们利用直角坐标系计算,可将积分区域D 表示为{}(,)|,D x y x y =-∞<<+∞-∞<<+∞,则22()d d xy De x y -+⎰⎰2222()2d d d d y =I x y x y x ey e xe +∞+∞+∞+∞-+---∞-∞-∞-∞==⎰⎰⎰⎰.另一方面,我们利用极坐标系进行计算,可将积分区域D 表示为{}(,)|02,0D r r θθπ=≤≤≤≤+∞.于是22()d d xy De x y -+⎰⎰22220d d |lim (1)r r R re r r e e πθπππ+∞--+∞-→+∞==-=-=⎰⎰. 综上,我们有2I π=,所以I =。