FFT浮点的DSP实现(精)

FFT 算法的DSP 实现对于离散傅里叶变换（DFT）的数字计算，FFT是一种有效的方法。

一般假定输入序列是复数。

当实际输入是实数时，利用对称性质可以使计算DFT 非常有效。

一个优化的实数FFT算法是一个组合以后的算法。

原始的2N个点的实输入序列组合成一个N 点的复序列，之后对复序列进行N 点的FFT 运算，最后再由N 点的复数输出拆散成2N点的复数序列，这 2 N点的复数序列与原始的2N点的实数输入序列的DFT输出一致。

使用这种方法，在组合输入和拆散输出的操作中，FFT 运算量减半。

这样利用实数FFT 算法来计算实输入序列的DFT的速度几乎是一般FFT算法的两倍。

下面用这种方法来实现一个256 点实数FFT（2N=256 ）运算。

1. 实数FFT 运算序列的存储分配如何利用有限的DSP 系统资源，合理的安排好算法使用的存储器是一个比较重要的问题。

本文中，程序代码安排在0x3000 开始的存储器中，其中0x3000~0x3080 存放中断向量表，FFT程序使用的正弦表和余弦表数据（.data段）安排在OxcOO开始的地方，变量（.bss段定义）存放在0x80 开始的地址中。

另外，本文中256 点实数FFT 程序的数据缓冲位Ox23OO~Ox23ff , FFT 变换后功率谱的计算结果存放在Ox22OO~Ox22ff 中。

连续定位.cmd 文件程序如下：MEMORY {PAGE O: IPROG: origin = Ox3O8O,len=Ox1F8OVECT: lorigin=Ox3OOO,len=Ox8OEPROG: origin=Ox38OOO,len=Ox8OOOPAGE 1:USERREGS: origin=Ox6O,len=Ox1cBIOSREGS: origin=Ox7c,len=Ox4IDATA: origin=Ox8O,len=OxB8O}SECTIONS{EDATA: origin=OxCOO,len=Ox14OO{.vectors: { } > VECT PAGE O.sysregs:.trcinit:.gblinit: { } > BIOSREGS PAGE 1 { } > IPROG PAGE O { } > IPROG PAGE O.bios:frt:{ } > IPROG PAGE O { } > IPROG PAGE O.text: { } > IPROG PAGE O.cinit: { } > IPROG PAGE O.pinit: { } > IPROG PAGE O.sysinit: { } > IPROG PAGE O.data: .bss: .far:.const: { } > EDATA PAGE 1 { } > IDATA PAGE 1 { } > IDATA PAGE 1 { } > IDATA PAGE 1.switch: { } > IDATA PAGE 1 .sysmem: { } > IDATA PAGE1•cio:{ } > IDATA PAGE1.MEM$obj: { } > IDATA PAGE1.sysheap: { } > IDATA PAGE1}2.基2实数FFT运算的算法该算法主要分为以下四步进行：1）输入数据的组合和位排序首先，原始输入的2N=256个点的实数序列复制放到标记有“ d_input_addr "的相邻单元，当成N=128点的复数序列d[n]，其中奇数地址是d[n]实部，偶数地址是d[n]的虚部，这个过程叫做组合（n为序列变量，N为常量）。

DSP实现的方法//#include "DSP281x_Device.h" // DSP281x Headerfile Include File //#include "DSP281x_Examples.h" // DSP281x Examples Include File#include <stdio.h>#include <math.h>#include <stdlib.h>#define pi atan(1.0)*4 //计算PI的值typedef struct //定义表示复数的结构体{float real;float imag;}FUSHU;FUSHU x[1024];int w[1024];FUSHU FUCHENG(FUSHU b1,FUSHU b2) //复数相乘函数{FUSHU b3;b3.real=b1.real*b2.real-b1.imag*b2.imag;b3.imag=b1.real*b2.imag+b1.imag*b2.real;return(b3);}void FFT(FUSHU *xin,int N) //FFT运算{int m,LH,I,k,J,M,K;float p,ps ;int B,N1;FUSHU w,T;M=10;//对应N值为//下面是倒序的程序LH=N/2;J=LH;N1=N-2;/*变址运算*/for(I=1;I<=N1;I++){if(I<J){T=xin[I];xin[I]=xin[J];xin[J]=T;}K=LH;while(J>=K){J=J-K;K=K/2;}J=J+K;}//下面是DIT-FFT运算程序for(m=1;m<=M;m++){B=pow(2.0,m-1);for(J=0;J<=B-1;J++){p=pow(2.0,M-m)*J;ps=2*pi/N*p;w.real=cos(ps);w.imag=-sin(ps);for(k=J;k<=N-1;k=k+pow(2.0,m)){T=FUCHENG(xin[k+B],w);xin[k+B].real=xin[k].real-T.real;xin[k+B].imag=xin[k].imag-T.imag;xin[k].real=xin[k].real+T.real;xin[k].imag=xin[k].imag+T.imag;}}}}void IFFT(FUSHU *xin,int N) //IFFT运算{int m,LH,I,k,J,M,K;float p,ps ;int B,N1;FUSHU w,T;M=10;//对应N值为//下面是倒序的程序LH=N/2;J=LH;N1=N-2;/*变址运算*/for(I=1;I<=N1;I++){if(I<J){T=xin[I];xin[I]=xin[J];xin[J]=T;}K=LH;while(J>=K){J=J-K;K=K/2;}J=J+K;}for(m=1;m<=M;m++){B=pow(2.0,m-1);for(J=0;J<=B-1;J++){p=pow(2.0,M-m)*J;ps=2*pi/N*p;w.real=cos(ps);w.imag=sin(ps);//与FFT符号相反for(k=J;k<=N-1;k=k+pow(2.0,m)){T=FUCHENG(xin[k+B],w);xin[k+B].real=xin[k].real-T.real;xin[k+B].imag=xin[k].imag-T.imag;xin[k].real=xin[k].real+T.real;xin[k].imag=xin[k].imag+T.imag;}}}for(k=0;k<N;k++)//比FFT多乘了一个常数因子/N {xin[k].real=xin[k].real/N;xin[k].imag=xin[k].imag/N;}}int main(){int n;for(n=0;n<1024;n++) //输入波形x(t) = cos(2*pi* 100*t){x[n].real=cos(2*pi*100*n/1024); //采样频率为kHzx[n].imag=0;}FFT(x,1024);//进行FFT运算for ( n=0;n<1024;n++ ){w[n]=sqrt(x[n].real*x[n].real+x[n].imag*x[n].imag);//幅度谱}IFFT(x,1024);//进行IFFT运算for(n=0;n<1024;n++)//比较逆变换之后的数据与原来的数据差{if(fabs(cos(2*pi*100*n/1024)-x[n].real)>0.001)break;}if(n<1024)puts("FFT不正确\n");if(n==1024)puts("FFT正确\n");return 0;}。

DSP实现FFT的代码FFT（快速傅里叶变换）是一种高效的算法，用于计算离散时间序列的离散傅里叶变换（DFT）。

它有广泛的应用，例如信号处理、图像处理和音频处理等领域。

以下是一个基于C语言的FFT实现的代码示例：```c#include <stdio.h>#include <math.h>//计算复数的乘积*result_real = a_real * b_real - a_imag * b_imag;*result_imag = a_real * b_imag + a_imag * b_real;//执行FFT变换（递归实现）void fft(double x_real[], double x_imag[], double X_real[], double X_imag[], int N, int step)if (step < N)fft(X_real, X_imag, x_real, x_imag, N, step * 2);fft(X_real + step, X_imag + step, x_real + step, x_imag + step, N, step * 2);for (int i = 0; i < N; i += 2 * step)double t_real = cos(-M_PI*i / N);double t_imag = sin(-M_PI*i / N);double r_real = 1;double r_imag = 0;for (int j = 0; j < step; j++)double u_real = x_real[i + j];double u_imag = x_imag[i + j];double v_real = x_real[i + j + step] * r_real - x_imag[i + j + step] * r_imag;double v_imag = x_real[i + j + step] * r_imag + x_imag[i + j + step] * r_real;x_real[i + j] = u_real + v_real;x_imag[i + j] = u_imag + v_imag;x_real[i + j + step] = u_real - v_real;x_imag[i + j + step] = u_imag - v_imag;}}}//执行FFT变换（接口函数）void perform_fft(double x_real[], double x_imag[], doubleX_real[], double X_imag[], int N)for (int i = 0; i < N; i++)X_real[i] = x_real[i];X_imag[i] = x_imag[i];}fft(x_real, x_imag, X_real, X_imag, N, 1);```要使用上述代码计算FFT变换，可以按照以下步骤进行：1. 定义输入序列数组`x_real`和`x_imag`，其中`x_real`包含实部，`x_imag`包含虚部。

快速傅立叶变换（FFT ）的实现一、实验目的1.了解FFT 的原理及算法；2.了解DSP 中FFT 的设计及编程方法；3.熟悉FFT 的调试方法；二、实验原理FFT 是一种高效实现离散付立叶变换的算法，把信号从时域变换到频域，在频域分析处理信息。

对于长度为N 的有限长序列x (n )，它的离散傅里叶变换为：(2/)j N nk N W e π-=，称为旋转因子，或蝶形因子。

在x (n )为复数序列的情况下，计算X (k )：对某个k 值，需要N 次复数乘法、(N -1)次复数加法；对所有N 个k 值，需要2N 次复数乘法和N (N -1)次复数加法。

对于N 相当大时（如1024）来说，直接计算它的DFT 所作的计算量是很大的，FFT 的基本思想在于： 利用2()j nk N N W e π-=的周期性即：k N k N N W W +=对称性：/2k k N N N W W +=-将原有的N 点序列分成两个较短的序列，这些序列的DFT 可以很简单的组合起来得到原序列的DFT 。

按时间抽取的FFT ——DIT FFT 信号流图如图5.1所示：图5.1 时间抽取的FFT —DIT FFT 信号流图FFT 算法主要分为以下四步。

第一步 输入数据的组合和位倒序∑=-=10)()(N n nk N W n x k X把输入序列作位倒序是为了在整个运算最后的输出中得到的序列是自然顺序。

第二步 实现N 点复数FFT第一级蝶形运算；第二级蝶形运算；第三级至log2N 级蝶形运算；FFT 运算中的旋转因子N W 是一个复数，可表示：为了实现旋转因子N W 的运算，在存储空间分别建立正弦表和余弦表，每个表对应从0度到180度，采用循环寻址来对正弦表和余弦表进行寻址。

第三步 功率谱的计算X (k )是由实部()R X k 和虚部()I X k 组成的复数：()()()R I X k X k jX k =+；计算功率谱时只需将FFT 变换好的数据，按照实部()R X k 和虚部()I X k 求它们的平方和，然后对平方和进行开平方运算。

数字信号处理算法的DSP实现课程报告题目：FFT反变换的DSP实现班级：信息工程1班姓名：张庆学号：200720101127日期：2010.12.25一、FFT反变换相关理论对于离散傅里叶变换(DFT)的数字计算，FFT是一种有效的方法。

一般假定输入序列是复数。

当实际输入是实数时，利用对称性质可以使计算DFT非常有效。

一个优化的实数FFT算法是一个组合以后的算法。

原始的2N个点的实输入序列组合成一个N点的复序列，之后对复序列进行N点的FFT运算，最后再由N点的复数输出拆散成2N点的复数序列，这2 N点的复数序列与原始的2N点的实数输入序列的DFT输出一致。

使用这种方法，在组合输入和拆散输出的操作中，FFT运算量减半。

这样利用实数FFT 算法来计算实输入序列的DFT的速度几乎是一般FFT算法的两倍。

二、FFT反变换DSP实现原理1.实数FFT运算序列的存储分配如何利用有限的DSP系统资源，合理的安排好算法使用的存储器是一个比较重要的问题。

本文中，程序代码安排在0x3000开始的存储器中，其中0x3000~0x3080存放中断向量表，FFT程序使用的正弦表和余弦表数据(.data段)安排在0xc00开始的地方，变量(.bss段定义) 存放在0x80开始的地址中。

另外，本文中256点实数FFT程序的数据缓冲位0x2300~0x23ff , FFT变换后功率谱的计算结果存放在0x2200~0x22ff中。

三、FFT反变换DSP实现程序说明连续定位.cmd文件程序如下：MEMORY{PAGE 0: PRGROM : origin=00080h length=00200hVECT: origin = 0xff80, len = 0x80PAGE 1: S_PRAM : origin=00060h length=00020hINTRAM1: origin=00400h length=00200hINTRAM2: origin=00800h length=00200hINTRAM3: origin=00c00h length=01000hEXTRAM1: origin=01c00h length=00400hEXTRAM2: origin=02000h length=010hEXTRAM3: o= 2100h l=500h}SECTIONS{vectors : {} > VECT PAGE 0.text : {} > PRGROM PAGE 0.data : {} > INTRAM3 PAGE 1power : {} > EXTRAM1 PAGE 1sin_tbl : {} > INTRAM1 PAGE 1cos_tbl : {} > INTRAM2 PAGE 1fft_vars: {} > S_PRAM PAGE 1stack : {} > EXTRAM2 PAGE 1.stack : {} > EXTRAM3 PAGE 1.bss : {} > EXTRAM3 PAGE 1}2. 基2实数FFT运算的算法，该算法主要分为以下四步进行：1）输入数据的组合和位排序实现数据位倒序存储的具体程序段如下：.mmregs.include "fft_size.inc".def bit_rev.ref _real_fft_input, fft_data.asg AR2,REORDERED_DA TA.asg AR3,ORIGINAL_INPUT.asg AR7,DA TA_PROC_BUF.textbit_rev:SSBX FRCTSTM #_real_fft_input,ORIGINAL_INPUT; 在AR3(ORIGINAL_INPUT)中放入输入地址STM #fft_data,DA TA_PROC_BUF; 在AR7(DA TA_PROC_BUF)中放入处理后输出的地址MVMM DA TA_PROC_BUF,REORDERED_DA TA; AR2(REORDERED_DA TA)中装入第一个位倒序数据指针STM #K_FFT_SIZE-1,BRCRPTBD bit_rev_end-1STM #K_FFT_SIZE,AR0 ; AR0的值是输入数据数目的一半MVDD *ORIGINAL_INPUT+,*REORDERED_DA TA+;将原始输入缓冲中的数据放入到位倒序缓冲中去之后,;输入缓冲(AR3)指针加1位倒序缓冲(AR2)指针也加1MVDD *ORIGINAL_INPUT-,*REORDERED_DA TA+;将原始输入缓冲中的数据放入到位倒序缓冲中去之后,;输入缓冲(AR3)指针减1位倒序缓冲(AR2)指针加1以保证位倒序寻址正确MAR *ORIGINAL_INPUT+0B ;按位倒序寻址方式修改AR3bit_rev_end:RET.end2）N 点复数FFT运算这一步中，实现FFT计算的具体程序如下：.mmregs.include "fft_size.inc".ref fft_data, d_grps_cnt, d_twid_idx, d_data_idx, sine, cosine .asg AR1,GROUP_COUNTER ;定义FFT计算的组指针.asg AR2,PX ;定义AR2为指向参加蝶形运算第一个数据的指针 .asg AR3,QX ;定义AR3为指向参加蝶形运算第二个数据的指针 .asg AR4,WR ;定义AR4为指向余弦表的指针.asg AR5,WI ;定义AR5为指向正弦表的指针.asg AR6,BUTTERFLY_COUNTER ;定义AR6为指向蝶形结的指针.asg AR7,DATA_PROC_BUF ;定义在第一步中的数据处理缓冲指针.asg AR7,STAGE_COUNTER ;定义剩下几步中的数据处理缓冲指针K_ZERO_BK .set 0K_TWID_TBL_SIZE .set 512 ; Twiddle table sizeK_DATA_IDX_1 .set 2 ; Data index for Stage 1K_DATA_IDX_2 .set 4 ; Data index for Stage 2K_DATA_IDX_3 .set 8 ; Data index for Stage 3K_FLY_COUNT_3 .set 4 ; Butterfly counter for Stage 3K_TWID_IDX_3 .set 128 ; Twiddle index for Stage 3.def fft.textfft:; Stage 1 计算FFT的第一步，两点的FFTSTM #K_ZERO_BK,BK ;让BK=0 使*ARn+0%=*ARn+0LD #-1,ASM ;为避免溢出在每一步输出时右移一位MVMM DATA_PROC_BUF,PX ;PX指向参加蝶形结运算的第一个数的实部(PR) LD *PX,16,A ;AH := PRSTM #fft_data+K_DATA_IDX_1,QX;QX指向参加蝶形结运算的第二个数的实部(QR)STM #K_FFT_SIZE/2-1,BRC ;设置块循环计数器RPTBD stage1end-1;语句重复执行的范围到地址stage1end-1处STM #K_DATA_IDX_1+1,AR0;延迟执行的两字节的指令(该指令不重复执行)SUB *QX,16,A,B ;BH := PR-QRADD *QX,16,A ;AH := PR+QRSTH A,ASM,*PX+ ;PR':= (PR+QR)/2ST B,*QX+ ;QR':= (PR-QR)/2||LD *PX,A ;AH := PISUB *QX,16,A,B ;BH := PI-QIADD *QX,16,A ;AH := PI+QISTH A,ASM,*PX+0 ;PI':= (PI+QI)/2ST B,*QX+0% ;QI':= (PI-QI)/2||LD *PX,A ;AH := next PRstage1end:; Stage 2 计算FFT的第二步，四点的FFTMVMM DATA_PROC_BUF,PX;PX 指向参加蝶形结运算第一个数据的实部(PR)STM #fft_data+K_DATA_IDX_2,QX;QX 指向参加蝶形结运算第二个数据的实部(QR)STM #K_FFT_SIZE/4-1,BRC ;设置块循环计数器LD *PX,16,A ;AH := PRRPTBD stage2end-1;语句重复执行的范围到地址stage1end-1处STM #K_DATA_IDX_2+1,AR0 ;初始化AR0 以被循环寻址;以下是第二步运算的第一个蝶形结运算过程SUB *QX,16,A,B ;BH := PR-QRADD *QX,16,A ;AH := PR+QRSTH A,ASM,*PX+ ;PR':= (PR+QR)/2ST B,*QX+ ;QR':= (PR-QR)/2||LD *PX,A ;AH := PISUB *QX,16,A,B ;BH := PI-QIADD *QX,16,A ;AH := PI+QISTH A,ASM,*PX+ ;PI':= (PI+QI)/2STH B,ASM,*QX+ ;QI':= (PI-QI)/2;以下是第二步运算的第二个蝶形结运算过程MAR *QX+ ;QX中的地址加ADD *PX,*QX,A ;AH := PR+QISUB *PX,*QX-,B ;BH := PR-QISTH A,ASM,*PX+ ;PR':= (PR+QI)/2SUB *PX,*QX,A ;AH := PI-QRST B,*QX ;QR':= (PR-QI)/2||LD *QX+,B ;BH := QRST A, *PX ;PI':= (PI-QR)/2||ADD *PX+0%,A ;AH := PI+QRST A,*QX+0% ;QI':= (PI+QR)/2||LD *PX,A ;AH := PRstage2end:; Stage 3 到 logN-1STM #K_TWID_TBL_SIZE,BK ;BK = 旋转因子表格的大小值 ST #K_TWID_IDX_3,d_twid_idx ;初始化旋转表格索引值STM #K_TWID_IDX_3,AR0 ;AR0 = 旋转表格初始索引值 STM #cosine,WR ;初始化 WR 指针STM #sine,WI ;初始化 WI 指针STM #K_LOGN-2-1,STAGE_COUNTER ;初始化步骤指针ST #K_FFT_SIZE/8-1,d_grps_cnt ;初始化组指针STM #K_FLY_COUNT_3-1,BUTTERFLY_COUNTER ;初始化蝶形结指针ST #K_DATA_IDX_3,d_data_idx ;初始化输入数据的索引stage:;以下是每一步的运算过程STM #fft_data,PX;PX 指向参加蝶形结运算第一个数据的实部(PR)LD d_data_idx, AADD *(PX),ASTLM A,QX;QX 指向参加蝶形结运算第二个数据的实部(QR)MVDK d_grps_cnt,GROUP_COUNTER ;AR1 是组个数计数器group:;以下是每一组的运算过程MVMD BUTTERFLY_COUNTER,BRC ;将每一组中的蝶形结的个数装入BRC RPTBD butterflyend-1LD *WR,T ; T := WRMPY *QX+,A ;A := QR*WR || QX*QIMACR *WI+0%,*QX-,A ;A := QR*WR+QI*WI; || QX指向QRADD *PX,16,A,B ;B := (QR*WR+QI*WI)+PRST B,*PX ;PR':=((QR*WR+QI*WI)+PR)/2||SUB *PX+,B ;B := PR-(QR*WR+QI*WI);|| QX指向QIST B,*QX ; QR':= (PR-(QR*WR+QI*WI))/2 ||MPY *QX+,A ; A := QR*WI [T=WI]; || QX->QIMASR *QX,*WR+0%,A ;A := QR*WI-QI*WRADD *PX,16,A,B ;B := (QR*WI-QI*WR)+PIST B,*QX+ ;QI':=((QR*WI-QI*WR)+PI)/2;|| QX指向QR||SUB *PX,B ;B := PI-(QR*WI-QI*WR)LD *WR,T ;T := WRST B,*PX+ ;PI':= (PI-(QR*WI-QI*WR))/2 ;|| PX指向PR||MPY *QX+,A ;A := QR*WR || QX指向QI butterflyend:; 更新指针以准备下一组蝶形结的运算PSHM AR0 ;保存AR0MVDK d_data_idx,AR0;AR0中装入在该步运算中每一组所用的蝶形结的数目MAR *PX+0 ;增加PX准备进行下一组的运算MAR *QX+0 ;增加QX准备进行下一组的运算BANZD group,*GROUP_COUNTER-;当组计数器减一后不等于零时，延迟跳转至group处POPM AR0 ;恢复AR0MAR *QX- ;修改QX以适应下一组的运算;更新指针和其他索引数据以变进入下一个步骤的运算LD d_data_idx,ASUB #1,A,B ; B = A-1STLM B,BUTTERFLY_COUNTER ;修改蝶形结个数计数器STL A,1,d_data_idx ;下一步计算的数据索引翻倍LD d_grps_cnt,ASTL A,ASM,d_grps_cnt ;下一步计算的组数目减少一半LD d_twid_idx,ASTL A,ASM,d_twid_idx ;下一步计算的旋转因子索引减少一半BANZD stage,*STAGE_COUNTER- ;AR0 = 旋转因子索引MVDK d_twid_idx,AR0Fft_end:RET ;恢复环境变量.end3）分离复数FFT的输出为奇部分和偶部分，产生最后的N=256点的复数FFT结果分离FFT输出为相关的四个序列：RP、RM、IP和IM，即偶实数、奇实数、偶虚数和奇虚数四部分，以便第四部形成最终结果。

基于DSP的FFT实现傅里叶变换（Fourier Transform）是一种将信号在时间和频率域之间进行转换的数学工具。

它可以将信号从时域转换为频域，使我们能够分析信号的频率成分。

离散傅里叶变换（Discrete Fourier Transform，DFT）是一种计算机算法，用于对离散信号进行傅里叶变换。

离散信号是由一系列采样点组成的，并且在实际应用中，离散信号更常见于数字信号处理（Digital Signal Processing，DSP）系统。

FFT（Fast Fourier Transform）是一种高效的算法，用于计算DFT。

它通过利用信号的对称性和周期性，以O(nlogn)的时间复杂度计算DFT，相比于直接计算的O(n^2)时间复杂度更为高效。

因此，FFT在数字信号处理中被广泛使用，并且是很多DSP系统中实现频谱分析的核心算法。

基于DSP的FFT实现通常采用固定点数格式进行计算，以适应数字信号的要求。

固定点数格式将浮点数表示为带有整数和小数部分的定点数，其中小数部分的位数是固定的。

这允许在硬件实现中使用更简单和更高效的运算器，并且减少了计算过程中的存储需求。

在前向变换中，基于DSP的FFT实现通常采用蝶形运算器结构，该结构通过并行计算减少了计算量。

蝶形运算器将复数乘法和加法运算相结合，以高效地计算傅里叶变换的结果。

在反向变换中，基于DSP的FFT实现使用相同的蝶形运算器结构，但需要调整一些参数来恢复时域信号。

这些参数通常是指数项，用于将频域信号的幅度和相位信息与原始时域信号进行组合。

由于DSP系统通常具有固定的计算能力和存储容量，基于DSP的FFT 实现需要考虑对资源的高效利用。

这可能包括通过流水线技术实现并行计算，使用分块技术减少存储需求，并使用低功耗算法来减少计算负载。

总结起来，基于DSP的FFT实现是一种高效的数字信号处理技术，用于将时域信号转换为频域信号。

它通过利用固定点数格式和蝶形运算器结构，以高效和准确的方式计算傅里叶变换。

STM32官方DSP的FFT库使用STMicroelectronics提供了用于STM32系列微控制器的官方DSP库，其中包括了快速傅里叶变换（FFT）的实现。

FFT是一种将时域信号转换为频域信号的算法，常用于音频处理、图像处理、通信系统等领域。

使用STM32官方DSP库中的FFT功能，需要以下几个步骤：2. 配置工程：在工程的编译选项中，确保已启用浮点运算支持。

这可以通过设置编译器选项“-u _printf_float”来实现。

3.初始化FFT配置：在使用FFT之前，需要初始化FFT的配置，包括长度、窗函数、比例缩放系数等。

例如，对于一个长度为N的FFT，可以使用arm_cfft_radix4_init_f32函数来初始化：```arm_cfft_radix4_instance_f32 S;arm_cfft_radix4_init_f32(&S, N, 0, 1);```4.执行FFT变换：在进行FFT变换之前，需要准备好输入缓冲区，并确保输出缓冲区具有足够的大小来存储FFT的结果。

例如，如果要对一个长度为N的实数序列进行FFT变换，可以使用arm_cfft_radix4_f32函数：```float32_t input[N];float32_t output[N*2];//将输入数据复制到输入缓冲区arm_cfft_radix4_f32(&S, input);//处理输出数据```注意，为了存储FFT结果中的实部和虚部，输出缓冲区的大小应为FFT长度的两倍（N*2）。

5.访问FFT结果：FFT变换的结果保存在输出缓冲区中。

对于每个频率分量，实部和虚部分别存储在相邻的位置上。

例如，要获取第n个频率分量的实部和虚部，可以使用以下代码：```float32_t re = output[2*n];float32_t im = output[2*n+1];```以上是使用STM32官方DSP库进行FFT的基本步骤。

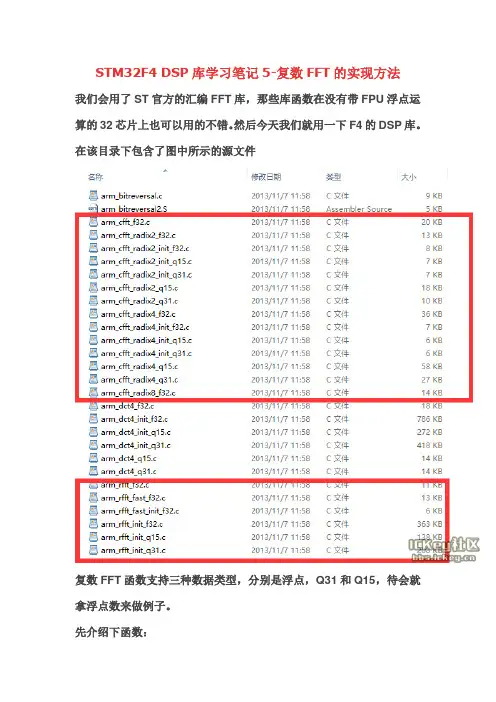
STM32F4 DSP库学习笔记5-复数FFT的实现方法我们会用了ST官方的汇编FFT库，那些库函数在没有带FPU浮点运算的32芯片上也可以用的不错。

然后今天我们就用一下F4的DSP库。

在该目录下包含了图中所示的源文件复数FFT函数支持三种数据类型，分别是浮点，Q31和Q15，待会就拿浮点数来做例子。

先介绍下函数：void arm_cfft_f32(const arm_cfft_instance_f32 * S,float32_t * p1,uint8_t ifftFlag,uint8_t bitReverseFlag);arm_cfft_instance_f32 * S是一个结构体指针这个结构体包含FFT运算的旋转因子和位反转表，就相当于一个常量，我们不用去管它。

float32_t * p1，是输入复数数组的地址，长度应该是运算点数的两倍，注意的是输入和输出共用一块缓存uint8_t ifftFlag,是运算的正反标志ifftFlag=1是反变换。

ifftFlag=0是正变换uint8_t bitReverseFlag，是flag that enables (bitReverseFlag=1) or disables (bitReverseFlag =0) bit好，然后就只要这一句话就可以计算复数的FFT正变换arm_cfft_f32(&arm_cfft_sR_f32_len1024,testInput,0, 1);计算出结果后，用下面语句就可以求出幅值了；arm_cmplx_mag_f32(testInput, testOutput, 1024);关于arm_cmplx_mag_f32(testInput, testOutput, 1024)，它的原型是：void arm_cmplx_mag_f32(float32_t * pSrc,float32_t * pDst,uint32_t numSamples);这个函数是求复数的模值float32_t * pSrc,是输入数组地址float32_t * pDst,是输出数组地址uint32_t numSamples是运算点数当然上面语句中testInput数组的长度是testOutput数组的两倍。

实验五 FFT程序设计一实验目的1 了解FFT的TMS320C54x实现的编程方法.2 掌握8-1024复数点FFT的TMS320C54x程序的使用方法.3 用FFT的TMS320C54x程序分析方波和正弦波的功率谱.二实验条件1 8-1024复数点TMS320C54x源程序fft.asm.2 8-1024复数点TMS320C54x链接命令文件fft.cmd.3正弦、余弦系数表coeff.inc.4产生正弦波信号数据文件的高级语言程序,程序名为sin_fft.exe ,5向量文件vectors.asm.三实验内容1 大致阅读fft.asm、ft.cmd、coeff.inc等文件.2 对防波输入信号进行64数点FFT.(1) T修改8—1024复数点FFT源程序fft.asm,使之执行64点FFT：●将K_FFT_SIZE 设定为64●将K_LOGN 设定为6(2)对fft.asm和vectors.asm进行过汇编.(3)链接fft.obj和vectors.obj.(4)用sin_fft.exe建立64复数点对称方波输入数据文件in.dat.3对方波输入信号进行64点FFT.f或N,重复第4步实验.(如果改变N,则需要修改fft.asm) 4改变正弦波频率f或采样频率s四实验步骤1.双击，启动CCS的仿真平台的配着选项。

选择C5410 DeviceSimulator。

2.点击project菜单栏的new选项，新建一个fft64的工程注意存储的路径。

2.把下图中用到的文件拷到工程文件目录的文件路径下。

3.在ccs平台中将用到的程序导入到平台中，点击project—>add file to project。

选择多个文件时，可以按住ctrl键。

4．将所有的程序段中的start改为_main,将fft.Asm中的K_FFT_SIZE .set 32 ;NK_LOGN .set 5 ;LOG(N)改为K_FFT_SIZE .set 64 ;NK_LOGN .set 6 ;LOG(N)5,对源文件进行编译（注意先对每个.asm文件先进行编译，以防止程序有错误），没有错误时进行链接。

FFT的DSP实现FFT（快速傅里叶变换）是一种计算离散傅里叶变换（DFT）的高效算法。

它通过利用DFT的对称性质和递归分解将计算复杂度从O(n^2)减少到O(nlogn)，其中n为信号的样本数。

DSP（数字信号处理）指的是用数字计算机或数字信号处理器对连续时间的信号进行采样、变换、滤波以及其他处理的技术和方法。

1.采样与量化：首先，将输入的模拟信号进行采样和量化。

采样将连续的模拟信号转换为离散的数字信号，量化将连续的信号幅值大小转换为离散的数值。

2. 窗函数：为了减少频谱泄漏的效应，通常在DFT之前应用窗函数对信号进行加权。

常用的窗函数有矩形窗、Hamming窗、Hanning窗等。

选择合适的窗函数可以达到有效减小频谱泄漏的目的。

3.数据流和缓冲：将经过窗函数加权的信号按照一定的时间顺序送入缓冲区。

4. 快速傅里叶变换（FFT）：将缓冲区中的数据应用FFT算法进行处理。

FFT算法将信号分解为多个较小的子问题，并通过递归将计算复杂度从O(n^2)减少到O(nlogn)。

FFT算法可以分为迭代式FFT和递归式FFT 两种形式。

5.频谱计算：通过FFT算法计算得到的频谱表示信号在频率域的分布情况。

频谱是信号在各个频率上的振幅和相位信息。

可以通过对频谱进行幅度谱或相位谱的操作来进行进一步的分析和处理。

6.频谱处理：根据具体的需求，可以对频谱进行滤波、修正、分析等操作。

滤波可用于信号降噪、频域特定频率的提取等；修正可用于频谱校正、泄漏校正等；分析可用于频谱峰值检测、频谱关键特征提取等。

7.逆变换：如果需要将频率域上的信号恢复到时域，可以通过应用逆变换（IDFT）来实现。

逆变换将频谱中的振幅和相位信息转换为原始信号的样本值。

8.输出与显示：最后，将处理后的信号输出到需要的设备或显示器上。

可以将频谱可视化展示出来，也可以将逆变换后的信号还原为音频、图像等形式的数据。

以上是FFT的DSP实现的基本步骤。

FFT在数字信号处理中被广泛应用于音频处理、图像处理、通信系统等领域。