青岛版初二数学解直角三角形测试题[1]

青岛版初中数学重点知识精选掌握知识点，多做练习题，基础知识很重要！青岛版初中数学和你一起共同进步学业有成！5.5 三角形内角和定理一、选择题:1．如图所示，在△ABC 中，∠ABC 和∠ACB 的外角平分线交于点O ，设∠BOC=a ，则∠A 等于（ ） A ．90°-2B ．90°-C ．180°-2D ．180°-α2αα2α图1图2图3图42．三角形三个内角之比为1：2：3，则该三角形三个外角之比为（ ）A ．5：4：3B ．3：2：1C ．1：2：3D ．2：3：43．已知三角形的一个外角小于和它相邻的内角，那么这个三角形是（ ） A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．以上均有可能4．等腰三角形的一个外角为110°，它的底角为（ ）A ．55°B ．70°C ．55°或70°D ．以上均有可能5．如图2，射线BA ，CA 交于点A ，连接BC ，已知AB=AC ，∠B=40°，那么x 的值是（ ）A ．40B ．60C ．80D ．100二、填空题:6．如果三角形三个外角度数之比为4：2： 3， 则这个三角形的各外角度数分别为______．7．如果一个三角形的一个外角与它的一个内角相等，这个三角形只能是_____．8．如图3所示，一个顶角为40°的等腰三角形的纸片，剪去顶角后，得到一个四边形，则∠1+∠2=______．9．如图4所示，在△ABC 中，点D 是BC 上一点，∠BAD=80°，AB=AD= DC ， 则∠C=________. 三、解答题:10．已知：如图所示，P 是△ABC 内一点，求证：∠BPC>∠BAC ．ACPB11．如图所示，△ABC 中，AD 平分∠BAC ，CD ⊥AD 于D ，AB>AC ，求证：∠ACD> ∠ABC ．12．一个等腰三角形的三个内角与顶角的一个外角之和等于260°， 求这个等腰三角形的各内角的度数．参考答案一、1．C 点拨：因为BO 平分△ABC 的一个外角，所以可知∠3=12（∠A+∠2），同理∠4=（∠1+∠A ）．又因为∠3+∠4+∠BOC=180°，12即（∠A+∠2）+（∠1+∠A ）+=180°， 1212 同时∠1+∠2+∠A=180°，即可求得∠A 的度数． 2．A 点拨：因为三角形三个内角之比为1：2：3，所以可根据三角形内角和定理求得三个内角分别为30°，60°，90°， 即与它们相邻的外角分别为150°，120°，90°，即可求得对应的外角比． 3．C 点拨：三角形的外角与其相邻的内角互补， 由于这个外角小于与它相邻的内角，所以相邻的内角必是钝角，此三角形必为钝角三角形． 4．C5．C 点拨：因为AB=AC ，所以∠B=∠C ，所以x°=40°+40°=80°，所以x=80°．二、6．160°，80°，120°点拨：三角形的外角和等于360°， 可设外角度数分别为4x°，2x°，3x°， 故可求得各外角度数．7．直角三角形 点拨：因为外角大于任何一个与它不相邻的内角，故外角只能是与和它相邻的内角相等，而两角之和为180°，故外角及其相邻的内角均为90°．8．220° 点拨：本题的结构较简单， 可利用三角形的外角与内角的等量关系转化．∠1=∠5+∠4，∠2=∠3+∠5，所以∠1+∠2=∠3+∠4+∠5+∠5=180°+40°=220 °； 也可利用四边形内角和为360°来解这道题．9．23 点拨：此题是三角形角的有关计算，因为AB=AD ．所以∠ADB=（180°-88°）×=46°．又因为AD=CD ，故∠C=1212∠ADB=23°．三、10．证明：连接AP并延长交BC于E．因为∠BPE是△BAP的一个外角，所以∠BPE>∠BAE．又因为∠CPE是△CAP 的一个外角，所以∠CPE>∠CAE．所以∠BPE+∠CPE>∠ABE+∠CAE．即∠BPC>∠BAC．点拨：本题也可延长BP，交AC于一点， 利用“三角形的外角大于与它不相邻的任一内角”来证明．11．解：因为AB>AC，所以延长CD交AB于点E，如图所示．因为AD平分∠BAC，所以∠EAD=∠CAD．因为AD⊥CD，所以∠ADE=∠ADC=90°，所以∠AED+∠EAD=∠CAD+∠ACD=90°，所以∠AED=∠ACD，又因为∠AED是△BEC 的一个外角．所以∠AED>∠ABC，所以∠ACD>∠ABC．12．解：因为等腰三角形各内角度数和为180°，所以该等腰三角形顶角的一个外角为80°，所以等腰三角形的顶角为100°，所以等腰三角形的底角为40°，40°．相信自己，就能走向成功的第一步教师不光要传授知识，还要告诉学生学会生活。

八年级数学下册第9章解直角三角形测试题导学案青岛版第9章解直角三角形测试题导学案（无答案）青岛版一、选择题（310=30）1、在Rt△ABC中，∠C=90，a=1，c=4，则sinA的值是（）A、B、C、D、2、在△ABC中，∠C=90,如果tanA=,那么sinB的值的等于（）A、B、C、D、3、在Rt△ABC中，∠C=90，若sinA=,则cosB的值为（）A、B、C、D、14、如图，为了测量河两岸A、B两点的距离，在与AB垂直的方向上取点C,测得AC=a，∠ACB=α，那么AB等于（）A、asinαB、acosαC、atanαD、acotα5、若，那么锐角α的度数是（）A、15B、30C、45D、606、AE、CF是△ABC的两条高，如果AE：CF=3：2，则sinA：sinC等于（）A、3：2B、2：3C、9:4D、4：97、如图，在△ABC中，∠C=90，∠B=50,AB=10,则BC=的长为( )A、10tan50B、10cos50C、10sin50D、8、王英同学从A地沿北偏西方向走100m到B地，再从B 地向正南方向走200m到C地，此时王英同学离A地（）A、50mB、100mC、150mD、100m9、化简=（）A、1-B、C、-1D、1-10、一艘轮船由海平面上A地出发向南偏西40的方向行驶40海里到达B地，再由B地向北偏西20方向行驶40海里到达C 地，则A、C两地相距（）A、30海里B、40海里C、50海里D、60、海里二、填空题（38=24）11、计算2sin30+2cos60+3tan45=_______、12、若sin28=cosα，则α=________、13、已知0<α<90，当α=__________时，，当α=__________时，。

14、若，则锐角α=__________。

15、在Rt△ABC中，∠C=90，，则a=__________，b=__________，c=__________，cotA=__________。

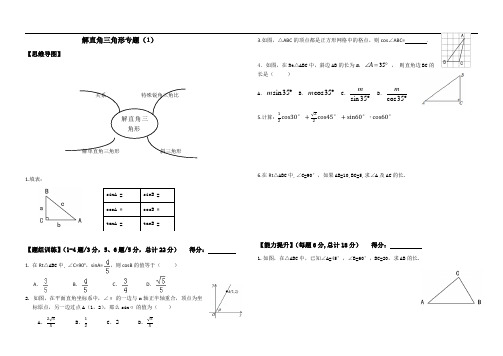
解直角三角形专题（1）【思维导图】关系 特殊锐角三角比解单直角三角形 斜三角形 1.填表：【题组训练】（1-4题/3分，5、6题/5分，总计22分） 得分：1. 在Rt △ABC 中, ∠C=90°，sinA=，则cosB 的值等于（ ）A ．B ．C ．D ．2. 如图，在平面直角坐标系中，∠α的一边与x 轴正半轴重合，顶点为坐标原点，另一边过点A （1，2），那么sinα的值为（ ）A ．2√55B ．12C ．2D ．√553.如图，△ABC 的顶点都是正方形网格中的格点，则cos ∠ABC= .4．如图，在Rt △ABC 中，斜边AB 的长为m ，35A ∠=︒ ， 则直角边BC 的长是（ ）A ．sin35m ︒B ．cos35m ︒C ．sin 35m ︒ D ．cos35m︒5.计算：12cos30°+√22cos45°+sin60°∙cos60°6.在Rt △ABC 中,∠C=90°，如果AB=10,BC=5,求∠A 及AC 的长.【能力提升】（每题6分,总计18分） 得分：1.如图，在△ABC 中，已知∠A=45°，∠B=60°，BC=20，求AB 的长.sinA = sinB = cosA = cosB = tanA =tanB =解直角三角形变式:如图，在△ABC中，已知∠A=45°，∠B=75°，BC=20，求AB的长.▲2. 已知，在△ABC中，AC=1,BC＝2，∠BCA＝135°，求tan A的值．归纳：解斜直角三角形作辅助线的标准：【当堂检测】（每题3分，共计12分）得分：1．已知α是锐角，sinα＝cos60°，则α等于（）A．30° B．45° C．60° D．不能确定 2．如图所示，A，B，C，D均在正方形网格中的格点上，∠BAD,∠CAD 分别用α和β表示．下列四个选项中正确的是（）A．sinα＝cosα B．sinα＝tanαC．sinβ＝cosβ D．sinβ＝tanβ3.在Rt△ABC中，∠B=90°，若2AB=AC,则cosC= .▲4．如图，在 ABC中，CA=CB=4，cosC=41,则tanB=（）A.210B.315C.46D.410【我的疑惑】知识点：计算类：【课后思考】已知，在△ABC中， BC＝2AC，∠BCA＝150°，求tan A的值．。

八年级下册数学解直角三角形单元试题（青岛版附答案）姓名：学号：成绩：一、填空题：（每小题3分，共30分）1、△ABC中，AB＝AC＝10cm，BC＝12cm，则cosB＝，sinB＝。

2、△ABC中，∠C＝90°，a＝6，b＝8，则sinA＝_____________.；若，00＜＜900，则＝_______。

3、在Rt△ABC中，∠C＝900，如果已知和∠B，则＝，＝。

（用锐角三角函数表示）4、若，则锐角a＝__________度5、在Rt△ABC中，∠C＝900，＝2，＝，则tan＝。

6、Rt△ABC中，∠C＝90°，，则∠B＝_________度7、已知Rt△ABC中，∠C＝900，，则∠B＝。

8、计算sin30°＋9cos600＝___________；若，则cos＝____________。

9、比较大小：sin520_________sin46010、某人沿着山坡走到山顶共走了1000米，它上升的高度为500米，这个山坡的坡度为__________，坡角为__________。

二、选择题：（每小题3分，共30分）11．直角三角形的两条边长分别为3、4，则第三条边长为()A．5B．7C．D．5或12、利用投影仪把Rt△ABC各边的长度都扩大5倍，则锐角A的各三角函数值（）A、都扩大5倍B、都缩小5倍C、没有变化D、不能确定13、在Rt△ABC中，∠C＝900，sinA＝，则tanB的值为（）A、B、C、D、14、在Rt△ABC中，∠C＝900，cosA＝，＝，则等于（）A、B、1C、2D、315、．如图，菱形ABCD的对角线AC＝6，BD＝8，∠ABD＝a，则下列结论正确的是()A．B．C．D．以上都不正确16、在Rt△ABC中，∠C＝900，下列不成立的是（）A、B、C、D、以上都不成立17、在Rt△ABC中，∠C＝900，、分别为∠A、∠B的对边，且满足则tanA的值为（）A、5或6B、2C、3D、2或318、在△ABC中，∠A∶∠B∶∠C＝1∶2∶3，则tanA＝()A、B、1C、D、19、已知A、B两点，若由A看B的仰角为，则由B看A的俯角为()A、B、C、D、20、等腰三角形的顶角A＝1200，底边BC的长为12cm,那么它的腰长是()A、cmB、cmC、cmD、6cm三、计算下列各题：（每小题4分，共24分）21、1、sin2600+cos26002、sin600－2sin300cos3003.sin300－cos24504.2cos450+5.6.四、解答下列各题：（每个4分，共24分）22、在Rt△ABC中，∠C＝900，，AB＝13，BC＝5，求sinA,cosA,tanA,23根据下列条件解直角三角形。

绝密★启用前2017-2018青岛版八年级下册数学第9章解直角三角形单元试卷注意事项：1．答题前填写好自己的姓名、班级、考号等信息2、考试时间100分钟，满分120分。

温馨提示：亲爱的同学们，考试只是检查我们对知识的掌握情况,希望你不要慌张，平心静气，不要急于下结论；下笔时，把字写得规矩些，让自己和老师都看得舒服，祝你成功！的正弦值和余弦值（）A. 都扩大2倍B. 都缩小2倍C. 都不变D. 不能确定2．（本题3分）在Rt△ABC中，∠C=90°，3sin5A ,则cos B的值为( )A. 34B.43C.35D.453．（本题3分）如图，平面直角坐标系内有一点P(3,4)，连接OP，则cos α等于（）A. 35B.45C.34D.434．（本题3分）如图，△ABC中，∠A=30°，AC=AB的长为（）A. 925．（本题3分）如图，在直角坐标系中，点A 的坐标是（2，3），则tan α的值是（ ）A. 23B. 326．（本题3分）如图，△ABC 中，∠C=90°，AD 是∠BAC 的角平分线，交BC于点D ，那么AB ACCD=（ ）A. sin ∠BACB. cos ∠BACC. tan ∠BACD. tan ∠ABC 7．（本题3分）如图，为了测量河岸A ，B 两点的距离，在与AB 垂直的方向上取点C ，测得AC=a ，∠ABC=α，那么AB 等于（ ）A. a •sin αB. a •cos αC. a •tan αD.tan a a8．（本题3分）如图，在Rt △ABC 中，∠ACB=90，CD ⊥AB ，垂足为D ，若AC=BC=2．则sin ∠ACD 的值为（ ）239．（本题3分）一人乘雪橇沿坡比滑下的距离s （米）与时间t （秒）间的关系为2102s t t =+，若滑到坡底的时间为4秒，则此人下降的高度为（ ）．A. 72mB.C. 36mD.10．（本题3分）如图，其中A ，B ，C 三地在同一直线上，D 地在A 地北偏东30°方向、在C 地北偏西45°方向．C 地在A 地北偏东75°方向．且BD=BC=30cm ．从A 地到D 地的距离是（ ）A. 303mB. 205mC. 302mD. 156m二、填空题（计32分）11．（本题4分）若sin 2α=，则锐角α=____12．（本题4分）在△ABC 中，若cosB tanA A 、∠B 为锐角，则△ABC 是_________三角形． 13．（本题4分）如图，在网格中，小正方形的边长均为1，点A 、B 、O 都在格点上，则∠OAB 的正弦值是_____．14．（本题4分）如图，小阳发现电线杆AB 的影子落在土坡的坡面CD 和地面BC 上，量得8CD =， 20BC =米， CD 与地面成30︒角，且此时测得1米的影长为2米，则电线杆的高度为=__________米．15．（本题4分）某坡面的坡度为，则坡角是__________度．16．（本题4分）已知α是锐角，且()sin 152a +︒=，则()114c o s 7π-3.14t a n 3αα-⎛⎫-++= ⎪⎝⎭__________．17．（本题4分）小明沿着坡度为1：20米的路，那么他竖直方向下降的高度为_____． 18．（本题4分）如图，在小山的东侧A 庄，有一热气球，由于受西风的影响，以每分钟35米的速度沿着与水平方向成75度角的方向飞行，40分钟时到达C 处，此时气球上的人发现气球与山顶P 点及小山西侧的B 庄在一条直线上，同时测得B 庄的俯角为30度，又在A 庄测得山顶P 的仰角为45度，求A 庄与B 庄的距离___________，山高__________．三、解答题（计58分）(1)2sin 30°＋cos 60°－tan 60°·tan 30°＋cos 245°.5|＋2·cos 30°＋（13）-1＋(9020．（本题8分）有一个角是60°的直角三角形，求它的面积y与斜边x的函数关系式．（本题8分）如图，△ABC是一仓库的屋顶的横截面，若∠B=30°，∠C=45°，21．AC=2，求线段AB的长．22．（本题8分）如图，在某建筑物AC上，挂着一宣传条幅BC，站在点F处，测得条幅顶端B的仰角为300，往条幅方向前行20米到达点E处，测得条幅，结果精确到0.1米）顶端B的仰角为600，求宣传条幅BC的长. 1.73223．（本题8分）如图，物理实验室有一单摆在左右摆动，摆动过程中选取了两个瞬时状态，从C处测得E、F两点的俯角分别为∠ACE=60°，∠BCF=45°，这时点F相对于点E升高了4cm．求该摆绳CD的长度．（精确到0.1cm，参考数据： 1.41， 1.73）24．（本题9分）如图，某高楼顶部有一信号发射塔，在矩形建筑物ABCD 的A ， C 两点处测得该塔顶端F 的仰角分别为45α∠=︒， 60β∠=︒，矩形建筑物宽度20m AD =，高度30m DC =．计算该信号发射塔顶端到地面的高度FG （结果精确到1m ， 1.73≈）．25．（本题9分）如图，贵阳市某中学数学活动小组在学习了“利用三角函数测高”后．选定测量小河对岸一幢建筑物BC 的高度．他们先在斜坡上的D 处，测得建筑物顶的仰角为30°．且D 离地面的高度DE=5m ．坡底EA=10m ，然后在A 处测得建筑物顶B 的仰角是50°，点E ，A ，C 在同一水平线上，求建筑物BC 的高．（结果保留整数）参考答案1．C【解析】∵Rt △ABC 中，若各边的长度同时都扩大2倍， ∴扩大后形成的三角形与原三角形相似， ∴锐角A 的正弦与余弦的比值不变， 故选C ．【点睛】本题产要考查相似及锐角三角函数，解答此题的关键是熟知三角函数值是一个比值，与角的边长无关. 2．C【解析】根据锐角三角函数的概念，可知正弦sinA=BC AB ，可得cosB=BCAB=sinA=35. 故选：C. 3．A【解析】试题解析：过点P 作PA x ⊥轴，则3,4,OA AP ==5,OP ==3cos .5OA OP α== 故选A. 4．C【解析】作CD ⊥AB 于D ．在直角三角形ACD 中，∠A=30°，AC=∴AD=3．在直角三角形BCD 中，tanB=2，∴BD=CD tanB=2．∴AB=AD+BD=5．故选：C．5．B【解析】如图，过点A作AB⊥x轴于B，∵A（2，3），∴OB=2，AB=3，∴tanα=ABOB=32．故选B．点睛：要求一个角的三角函数值一般将这个角放到直角三角形中去，根据定义求解，若无现成的直角三角形，一般通过辅助线构造，最常用的辅助线是作垂线段. 6．C【解析】试题分析：过点D作DE⊥AB于E，∵AD是∠BAC的角平分线，DE⊥AB于E，DC⊥AC于C，∴CD=DE，∴Rt△ADE≌Rt△ADC（HL），∴AE=AC，∴AB AC AB AECD DE--==tan∠BDE，∵∠BAC=∠BDE，（同角的余角相等）∴AB ACCD-=tan∠BDE=tan∠BAC，故选C．点睛：本题主要考查了锐角三角函数的定义；角平分线的性质，属于中等难度的题目，解决本题的关键就是通过三角形全等将未知的角转化为直角三角形中的某一个内角．在解决三角函数的题目时，很多时候有些角是不在直角三角形中，我们可以通过作垂直或者通过角度之间的关系将其转化为直角三角形中的某一个内角．7．D【解析】试题分析：根据三角函数可得：tan∠ABC=AC aAB AB=，则AB=tanaa，故选D．8．C【解析】试题分析：根据Rt △ABC 的勾股定理可得：AB=3，根据双垂直可得：∠A+∠ACD=∠A+∠B=90°，则∠ACD=∠B ，即sin ∠ACD=sin ∠B=AC AB =故选C ． 9．C【解析】已知2102S t t =+， 4t =时， 21042472m S =⨯+⨯=．再由i =可得坡脚为30°，所以117236m 22h S ==⨯=．故选C. 10．D【解析】过点D 作DH 垂直于AC ，垂足为H ，由题意可知∠DAC =75°−30°=45°， ∵△BCD 是等边三角形，∴∠DBC =60°，BD =BC =CD =30m ，∴DH =∴AD m .答：从A 地到D 地的距离是.故选：D. 11．60°【解析】根据特殊角30°，45°，60°的三角函数值，可知α的值为60°. 故答案为：60°. 12．直角【解析】cos B ＝2，tan A B =30°，∠A =60°， 所以∠C =90°.所以三角形是直角三角形. 故答案为直角.13．【解析】如图，过点O 作OC ⊥AB 的延长线于点C ，则AC=4，OC=2，在Rt △ACO 中，=∴sin ∠OAB=OC OA ==故答案为：14．(14+【解析】延长AD 交BC 的延长线于E 点，作DF ⊥BC 交BC 的延长线于点F ．根据题意可得12AB BE =． ∵8CD =米， DF BE ⊥， 30DCF ∠=︒，∴142DF CD ==米， CF == ∵28EF DF ==米．∴(28BE BC CF EF =++=+米，∴(14AB =+米． 15．60【解析】已知坡面的坡度为1:3，即可得tan 1:3α==60α=︒． 16．3【解析】∵()sin 152a +︒=， ∴α+15°=60°，即α=45°.∴原式=4cos451tan453=︒-+︒+113=++3=．17．10米【解析】试题解析：∵坡度tan α==铅直高度水平距离∴α=30°，∴下降高度=坡长×sin30°=20×12=10（米）． 故答案为：10米．18． 700【解析】试题解析：如图，过点A 作AD ⊥BC ，垂足为D ，在Rt △ACD 中，∠ACD=75°-30°=45°，AC=35×40=1400（米），∴AD=AC •sin45°．在Rt △ABD 中，∠B=30°，．又过点P 作PE ⊥AB ，垂足为E ，则AE=PE •tan45°=PE ，BE=PE •tan60°，∴∴PE=700（米）．故A 庄与B 庄的距离是700−19．（1）1；（2）11.【解析】试题分析：(1)、解决这个题目，首先我们对特殊角的三角函数值要非常熟悉，然后代入分别进行计算即可；(2)、首先根据绝对值、三角函数、负指数次幂、零次幂和算术平方根的计算法则求出各式的值，然后进行求和即可得出答案．试题解析：解：(1)原式＝2×＋－×＋＝1＋－1＋＝1. (2)原式＝5－＋2×＋3＋1＋2＝11.20．2x ． 【解析】试题分析：由sinB=AC AC AB x =，cosB=BC BC AB x =，可得sin60AC x =⋅= ， 122x BC x =⋅=，再由S △ABC =12AC ·BC 即可得到y 与x 间的函数关系式. 试题解析：∵AB=x ，∠B=60°，∠C=90°，∴AC=AB ×sin60°=2x ，BC=AB ×cos60°=2x ， 又∵S △ABC =12AC ·BC ，∴212228x y x =⨯⨯=.即y 与x 间的函数关系式为： 2y x =.21．【解析】试题分析：首先过点A 作AD ⊥BC ，根据等腰直角三角形ADC 的性质求出CD 和AD 的长度，根据Rt △ABD 的性质求出AB 的长度．试题解析：解：过点A 作AD ⊥BC ，∵∠C=45°， ∴∠DAC=45°， ∴AD=CD ， ∵AD 2+CD 2=AC 2．∴AD=， 在Rt △ABD 中，AB 2=AD 2+BD 2， ∵∠BAD=30°， ∴AB=2AD ，解得AB=2． 22．宣传条幅BC 的长为17.3米.【解析】试题分析：先由∠F=30°，∠BEC=60°解得∠EBF=30°=∠F ，从而可得BE=FE=20米，再在Rt △BEC 中由sin ∠BEC=BC BE =即可解得BC 的值.试题解析：∵∠BEC=∠F+∠EBF ，∠F=30°，∠BEC=60°，∴∠EBF=60°-30°=30°=∠F ，∴BE=FE=20（米）.∵在Rt △BEC 中，sin ∠BEC=BC BE =，∴BC=BE ×10×1.732=17.32≈17.3（米）. 23．摆绳CD 的长度为25.1cm ．【解析】试题分析：过点E 、F 作EG ⊥CD ，FH ⊥CD ，解直角三角形即可．试题解析：解：分别过点E 、F 作EG ⊥CD ，FH ⊥CD ，垂足分别为G 、H ，设摆绳CD 的长度为xcm ．则CE =CF =xcm ．由题意知：HG =4，∠CEG =60°，∠CFH =45°．在Rt △CEG 中，sin ∠CEG =CG CE，∴CG =CE •sin ∠CEG =x •sin60°，在Rt △CFH 中，sin ∠CFH =CH CF，∴CH =CF •sin ∠CFH =x •sin45°．∵HG =CG ﹣CH ，∴x •sin60°﹣x •sin45°=4，解得x =8≈25.1． 答：摆绳CD 的长度为25.1cm ．点睛：此题主要考查了解直角三角形中俯角问题的应用，根据锐角三角函数的关系得出CG 与CH 的长是解题关键．24．约有118m.【解析】试题分析：设m CG x =，在Rt △FCG 中表示出FG 的长，继而得AE 的长；在Rt △AEF 中表示出AE 的长，根据AE=EF 列出方程，解得x 的值，即可得该信号发射塔顶端到地面的高度FG 的长.试题解析：设m CG x =，∵60β∠=︒， 90CGF ∠=︒．∴FG =，∵30m DC =，∴30m EG DC ==．∴30EF FG EG =--．∵45α=︒， 90FEA ∠=︒，∴30AE FE ==-，3020x -=+，∴)251x ==．∴25175118m FG ===+≈．25．21m【解析】试题分析：过点D 作DH ⊥BC 于点M ，得出四边形DECH 是矩形，所以DH =EC ，DE =HC ，设BC 的长度为xm ，则BH =（x －5）m ，由∠BDH =30°可以求出∠DBH =60°，进而表示出DH x －5），然后表示出AC =（x －5）－10，最后由BC = tan 50°·AC 列出方程，解出x 即可.试题解析：过点D 作DH ⊥BC 于点M ，则四边形DHCE 是矩形，DH =EC ，DE =HC ，设BC 的高度为xm ，则BH =（x －5）m ，∵∠BDH =30°，∴∠DBH =60°，∴DH =BH ·tan 60°x －5），∴AC =EC －EA x －5）－10，∵∠BAC =50°，∴BC = tan 50°·AC ，∴x =tan 50°·x －5）]，解得：x ≈21，答：建筑物BC 的高约为21m ．点睛：本题关键利用待定系数法，结合锐角三角函数找出等量关系列出方程，解方程即可.。

青岛版八年级数学第二学期 第4单元 解直角三角形 质量检测题（时间：45分钟 分值：100分）2012.温馨提示：请在答题卷上作答一．单项选择题（共8小题，每小题5分，共40分）1. 甲、乙、丙三人放风筝，各人放出的风筝线长分别为60m 、50m 、40m ，线与地平面所成的角分别为30o 、45o 、60o ，假设风筝线近似看作是拉直的，则所放风筝最高的是( ).(A)甲 (B)乙 (C)丙 (D)不能确定2.已知：α为锐角，且tan α= ）(A).030α︒<<︒ (B).3045α︒<<︒ (C). 4560α︒<<︒ (D). 6090α︒<<︒3. 下列各式正确的是（ ）（A ）sin20°＋sin20°＝sin40° （B ）cot 31°＝tan （90°－59°）（C ）sin 2A ＋cos 2（90°－A ）＝1（D ）sin 2B A +＝cos 2C（其中A+B+C ＝180°）4. 已知等腰三角形顶角为120°，底上的高为5，则一腰上的高为（ ） （A ）5 （B ）52 （C ）53 （D ）105、如图，为了测量河两岸A 、B 两点的距离，在与AB 垂直的方向上取点C ，测得AC ＝a ，∠ACB ＝α，那么AB 等于（ ） A.sin a α⋅ B.cos a α⋅ C.n a ta α⋅ D.cot a α⋅6、如果sin 2α＋sin 230°＝１ 那么锐角α的度数是（ ）Ａ．１５° Ｂ．３０° Ｃ．４５° Ｄ．６０° 7、AE 、CF 是锐角△ABC 的两条高，如果AE ：CF=3：2，则sinA ：sinC 等于（ ） （A ）3：2 （B ）2：3 （C ）9：4 （D ）4：9A B C a 第5题图8、王英同学从A地沿北偏西60º方向走100m到B地，再从B地向正南方向走200m到C地，此时王英同学离A地（）（A）3100m 50m （B）100 m （C）150m （D）3二、填空题（共4小题，每小题5分，共20分，只要求填写结果）、9．1.Rt△ABC中∠C=90°，若a=8，b=6,则sinB= ；若b=25，c=30,则tanA= .10. 若锐角α、β互余且cosα＝4/5，则sinβ＝________，cosβ＝__________。

2019备战中考数学（青岛版）巩固复习-解直角三角形（含解析）一、单选题1.如图，AC是电杆AB的一根拉线，测得BC=6米，∠ACB=52°，则拉线AC的长为( )A. 米B. 米C. 6·cos52°米D.米2.如图，一块三角形空地上种草皮绿化，已知AB=20米，AC=30米，∠A=150°，草皮的售价为a元/米2，则购买草皮至少需要（）A. 450a元B. 225a元C. 150a元D. 300a元3.如图，一个斜坡长130m，坡顶离水平地面的距离为50m，那么这个斜坡的坡度为（）A. B. C. D.4.对于sin60°有下列说法：①sin60°是一个无理数；②sin60°＞sin50°；③sin60°=6sin10°．其中说法正确的有（）A. 0个B. 1个C. 2个D. 3个5.Rt△ABC中，∠C=90°，已知cosA= ，那么tanA等于（）A. B. C. D.6.如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，则sinA的值是（）A. B. C. D.7.已知∠A是锐角，且sinA=，那么锐角A的取值范围是（）A. 0°＜∠A＜30°B. 30°＜∠A＜45°C. 45°＜∠A＜60°D. 60°＜∠A＜90°8.如图，在A、B 两地之间要修一条笔直的公路，从A地测得公路走向是北偏东48°，A，B 两地同时开工，若干天后公路准确接通，若公路AB长8千米，另一条公路BC长是6千米，且BC的走向是北偏西42°，则A地到公路BC的距离是（）A. 6千米B. 8千米C. 10千米D. 14千米二、填空题9.在△ABC中，∠A,∠B都是锐角，若,，则△ABC的形状为________ 三角形.10.计算：tan60°﹣cos30°=________ .11.计算：=________12.△ABC中，AB=AC，BD为AC边上的中线，若BD等于△ABC的一边时，则tanC=________．13.用计算器计算：﹣4cos26°=________ ．（精确到0.01）14.计算tan30°tan45°=________15.我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”．如果等腰三角形的腰长为2，“内角正度值”为45°，那么该三角形的面积等于________ ．16.用科学计算器计算：﹣tan65°≈________（精确到0.01）17.如图，已知正方形ABCD的边长为2．如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D′点处，那么tan∠BAD′等于________．三、计算题18.计算：19.计算：﹣|﹣2|+（1﹣）0﹣9tan30°．四、解答题20.某校研究性学习小组测量学校旗杆AB的高度，如图在教学楼一楼C处测得旗杆顶部的仰角为60°，在教学楼五楼D处测得旗杆顶部的仰角为30°，旗杆底部与教学楼一楼在同一水平线上，已知CD=12米，求旗杆AB的高度．21.如图，我国的一艘海监船在钓鱼岛A附近沿正东方向航行，船在B点时测得钓鱼岛A在船的北偏东60°方向，船以50海里/时的速度继续航行2小时后到达C点，此时钓鱼岛A在船的北偏东30°方向．请问船继续航行多少海里与钓鱼岛A的距离最近？五、综合题22.在Rt△ABC中，∠ACB=90°（1）tanA与sinA，cosA之间有什么关系？并说明理由．（2）若23.如图，某仓储中心有一斜坡AB，其坡度为i=1：2，顶部A处的高AC为4m，B、C在同一水平地面上．（1）求斜坡AB的水平宽度BC；（2）矩形DEFG为长方体货柜的侧面图，其中DE=2.5m，EF=2m，将该货柜沿斜坡向上运送，当BF=3.5m时，求点D离地面的高．（结果保留根号）答案解析部分一、单选题1.【答案】D【考点】解直角三角形的应用【解析】【分析】根据三角函数的定义解答．【解答】∵cos∠ACB==cos52°，∴AC=米．故选：D．【点评】本题是一道实际问题，要将其转化为解直角三角形的问题，用三角函数解答．2.【答案】C【考点】解直角三角形的应用【解析】【解答】解：如图，作BA边的高CD，设与BA的延长线交于点D，∵∠BAC=150°，∴∠DAC=30°，∵CD⊥BD，AC=30m，∴CD=15m，∵AB=20m，∴S△ABC=AB×CD=×20×15=150m2，∵草皮的售价为a元/米2，∴购买这种草皮的价格：150a元．故选C．【分析】作BA边的高CD，设与BA的延长线交于点D，则∠DAC=30°，由AC=30m，求出CD=15m，然后根据三角形的面积公式推出△ABC的面积为150m2，最后根据每平方米的售价即可推出结果．3.【答案】A【考点】解直角三角形的应用﹣坡度坡角问题【解析】【解答】∵一个斜坡长130m，坡顶离水平地面的距离为50m，∴这个斜坡的水平距离为：=120m，∴这个斜坡的坡度为：50：120=5：12．故答案为：A．【分析】坡度为竖直高度与水平宽度之比，所以先通过勾股定理得到水平宽，然后求比值即可。