雷击杆塔顶时耐雷水平的计算

110kv耐雷水平110kv耐雷水平是指110kv线路在遭受雷击时能够承受的雷电过电压水平。

耐雷水平是评估线路防雷保护能力的重要指标之一，对于保障电力系统的安全稳定运行具有重要意义。

本文将从以下几个方面详细介绍110kv耐雷水平的含义、影响因素、计算方法和提高措施。

一、110kv耐雷水平的含义110kv耐雷水平是指110kv线路在遭受雷击时，能够承受的雷电过电压水平。

耐雷水平的高低直接影响到线路的防雷保护效果。

当线路遭受雷击时，雷电过电压会超过线路的绝缘水平，导致线路跳闸或设备损坏等后果，严重时甚至会影响到电力系统的稳定运行。

因此，提高110kv线路的耐雷水平对于保障电力系统的安全稳定运行具有重要意义。

二、影响110kv耐雷水平的因素影响110kv耐雷水平的因素有很多，主要包括以下几个方面：1．雷电活动的强度和频度：雷电活动的强度和频度是影响线路耐雷水平的重要因素。

一般来说，雷电活动强烈的地区，线路的耐雷水平相对较低。

2．线路绝缘水平：线路绝缘水平是决定线路耐雷水平的关键因素。

绝缘水平低的线路容易发生闪络，导致线路跳闸或设备损坏。

3．杆塔高度和地形条件：杆塔高度和地形条件也会对线路的耐雷水平产生影响。

高杆塔和复杂地形条件的线路更容易遭受雷击，因此其耐雷水平相对较低。

4．防雷保护措施：防雷保护措施的采取和效果也会对线路的耐雷水平产生影响。

例如，安装避雷器、架设耦合地线等措施可以提高线路的耐雷水平。

三、110kv耐雷水平的计算方法110kv耐雷水平的计算方法主要包括以下几种：1．统计法：根据多年的雷电活动情况和线路跳闸记录，统计出线路的耐雷水平。

这种方法简单易行，但准确度相对较低。

2．模拟法：通过模拟雷电过电压对线路的影响，计算出线路的耐雷水平。

这种方法需要建立模型并进行大量计算，但可以得到较为准确的结果。

3．工程法：根据经验公式和相关参数，计算出线路的耐雷水平。

这种方法在实际工程中应用较为广泛，但准确度受到参数选择的影响。

考点5：电力系统防雷保护5.1 输电线路的感应雷过电压一、雷击线路附近大地时，线路上的感应雷过电压1、先导在导线轴线方向上的电场强度X E 将导线两端与雷云电荷异号的正电荷，吸引到最靠近先导通道的一段导线上，成为束缚电荷。

导线上的负电荷则被排斥而向两侧运动，经线路泄露电导和系统中性点进入大地。

导线上电流很小，忽略线路工作电压，导线电位仍保持的电位。

正束缚电荷产生的电场在导线高度处被电导中负电荷产生的电场所抵消。

2、主放电先导通道中的负电荷自下而上被迅速中和，相应的电场被迅速减弱，使导线上正束缚电荷迅速释放，形成电压波向两侧传播，形成的过电压称为感应过电压的静电分量。

与此同时，由于先导通道中雷电流所产生的磁场变化而引起的感应称为感应过电压的电磁分量。

（1）当雷击点离开线路的距离s>65m 时，)(25d L KV Sh I u g ⨯⨯≈ 其中L I ：雷电流峰值（KA）；d h ：导线平均高度（m）；S：为雷击点离线路的距离。

感应过电压峰值一般最大可达300～400KV，这会引起35KV 及以下钢筋混凝土杆线路绝缘闪络。

（2）加避雷线由于屏蔽作用，感应过电压下降，导线上的感应过电压为)k 1(U U gd ,gd -=因此，避雷线离导线越近，耦合系数k 越大，U 感应越小。

二、雷击线路杆塔时，导线上的感应过电压无避雷线d ah =gd U有避雷线)1(U gd ,k ah d -=与直击雷相比，感应过电压的特点：1、极性与雷云电荷相反，一般为正极性。

2、在三相导线上同时出现，不会直接产生相间过电压。

3、 波形较缓和，波前几微秒到几十微秒，波长可达数百微秒。

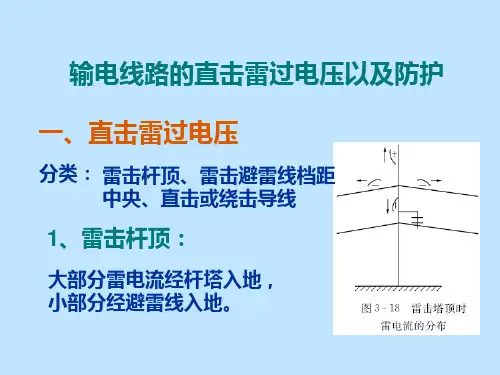
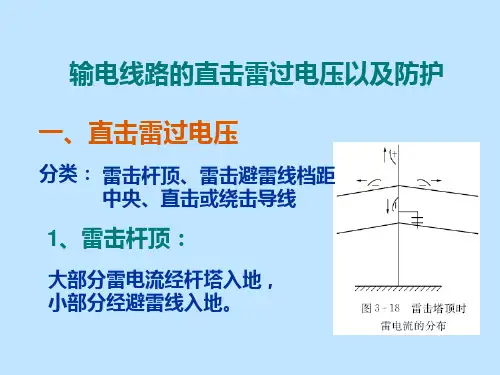
5.2 输电线路的直击雷过电压和耐雷水平一、雷击杆塔顶部1．塔顶电位塔顶电流i gt <雷电流L i ，即L i i β=gt 雷电流到达峰值时，塔顶电压有最大值6.2(ch L R U gt L td I +=β其中β为分流系数，设雷电流具有斜角波前，at i =，则t L R L L bib t ++=11β，t 取T/2，（T 1波前时间2.6us）2．导线电位和线路绝缘上的电位当塔顶电位为td U 时，在塔顶的避雷线也有同样的电位，导线上产生的耦合电压为td kU ，由于通道电磁场的作用，导线上有感应过电压)1(a k h d -, 此电压与塔顶电位极性相反，所以导线电位的幅值d U 为)1(a U U td k h k d d --=作用在线路绝缘上的总电压k)-)(1ah (U U U U d td j +=-=d td 对于斜角波前的雷电波6.2L 1LI I a T == )1)(6.26.2(ch L k h I d gt j L R U -++=ββ 3．耐雷水平的计算 耐雷水平：]6.2)6.2[)(1(ch %501d gt h k L R U I ++-=β提高耐雷水平：↓↑↓β,,R ch k ，加强线路绝缘。

可将避雷器上的电压ub近似 为一斜角平顶波。波头上升 部分斜率为侵入波的陡度， 幅值为Ub-5
只要避雷器上电压<变压器冲 击电压，则可保护
17
二、距离效应
由于避雷器离被保护设备有一段距离，在波的折反射过程中，被 保护设备的电压将不同于避雷器上的电压。
at
L
B
T
at
L
B
T l2
l1
(a)
雷电波侵入变电站的典型接线
例题：
一条220kV线路架设在平原地区，绝缘子串13片，正极性50%放电 电压为1410V；杆塔冲击接地电阻为7，避雷线半径为5.5mm， 弧垂fd＝7m，导线弧垂fd＝12m。求该线路的耐雷水平和雷击跳闸 率。 解：（1） 求耦合系数
避雷线的平均高度
导线的平均高度 h
d
h b 29 . 1
13





对于110kV以下的配电装置，绝缘水平高，可 用构架避雷针，并就近装设辅助接地装置。 对于变压器，由于最重要，因此不能装设构架 避雷针 对于35kV以下的变电站，由于绝缘水平低，故 只能装设独立避雷针，接地电阻不能超过10 发电厂厂房一般不能装设避雷针。 现在国标也推荐采用避雷线。
2 降低杆塔接地电阻
工频接地电阻一般为10-30
3
架设耦合地线
在某些雷击故障频繁的线路上，在导线下方架设一条耦合地线。 可起到分流、增加耦合的作用。
4
采用不平衡绝缘方式
在同塔双回线的情况下，采用不平衡绝缘，可避免双回线同时跳 闸而完全停电。 10
常用措施（二）：
5 6 装设自动重合闸
我国110kV以上线路自动重合闸成功率在75%-95％以上

第九章输电线路的防雷保护本章要求：输电线路的感应过电压：雷击大地和雷击杆塔时导线上感应过电压的计算输电线路上的直击雷过电压和耐雷水平建弧率及雷击跳闸率的计算。

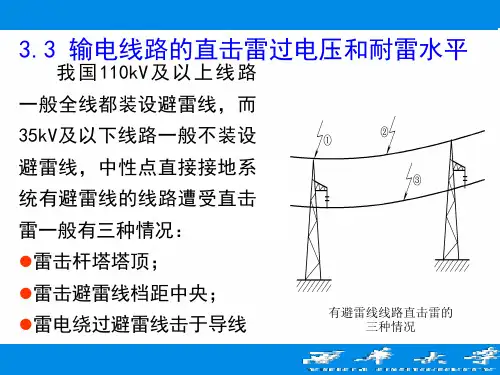
输电线路防雷措施及作用分析由于输电线路长度大，分布面广，地处旷野，易受到雷击。

输电线路上出现的大气过电压有两种：一种是雷击于输电线路引起的，称为直击雷过电压；（1）雷直击导线，无避雷线的线路最易发生，但即使有避雷线，雷电仍可能绕过避雷线的保护范围而击于导线（绕击）。

（2）雷击杆塔或避雷线强大的雷电流通过杆塔及接地电阻，使杆塔和避雷线的电位突然升高，杆塔与导线的电位差超过线路绝缘子闪络电压时绝缘子发生闪络，导线上出现很高的电压。

这种杆塔电位升高，反过来对导线放电，称为反击。

另一种是雷击线路附近地面而引起的，由于电磁感应所引起的，称为感应雷过电压。

（3）雷击输电线路附近大地：当雷击导线水平距离65m以外的大地时(更近的落雷由于线路的引雷作用而击于线路)，由于空间电磁场的急剧变化，在导线上感应出的过电压，称为感应雷过电压。

感应雷过电压的危害：（3-1）引起线路跳闸，影响正常供电由于过电压引起绝缘子闪络，导线对地短路，雷电过电压持续时间短（几十μs），继电保护装置来不及动作，但工频续流沿放电通道继续放电，在形成稳定燃烧的电弧后，则继电保护装置将使断路器跳闸，影响正常送电。

（3-2）雷电波侵入变电站导线上形成的雷电过电压波，最终将侵入变电站，经复杂的折反射后，在电气设备上出现很高的过电压，危及设备绝缘，造成事故。

输电线路防雷性能的优劣主要由耐雷水平及雷击跳闸率来衡量。

耐雷水平：雷击线路时线路绝缘不发生冲击闪络的最大雷电流的幅值，单位为KA。

线路的耐雷水平越高，线路绝缘发生冲击闪络的机会就越小。

雷击跳闸率：每100km线路每年有雷击所引起的跳闸次数。

是衡量线路防雷性能的综合指标。

线路防雷问题是一个综合的技术经济问题，在确定线路的具体防雷措施时，应根据线路的电压等级、负荷性质、系统运行方式、雷电活动的强弱、地形地貌的特点和土壤电阻率的高低等条件，特别要结合当地原有线路的运行经验通过技术经济比较来确定。

俄罗斯：80年度中已研制出110－1150kV系列合成套避雷器， 主要是用于一般超高压输电线路和紧凑型输电线路深度限制 操作过电压
此时雷电流 iL=αt =αL/Vb 间隙S承受的最大电压:
Us
UA
kUA
L b
Z0Zb 2Z0 Zb
(1 K)
感应过电压与下列因素有关:
①雷电波陡度;②档距长度;③耦合系数.
S最短间隙距离从Us的50％击穿电压得到。
Zb/2
A
Z0
❖ U50% 750SkV
❖ S (1 k) Z0Zs
750vs 2Z0 Zs
输电线路防雷技术 基础知识讲解
雷击输电线路的方式
大气过电压：
直击雷过电压：① 、②、 ③
感应雷过电压：④、②、①
其中④只对35KV以下线路有 危害
大气过电压带来的后果： 发生短路接地故障 雷电波侵入变电所，破坏设 备绝缘，造成停电事故 衡量线路防雷性能的优劣：
耐雷水平：线路遭受雷击 所能耐受不至于引起闪络 的最大雷电流（kA） 雷击跳闸率：每100km 线路每年因雷击引起的跳 闸次数
= Utd – KUtd + αhd(1-k) =(Utd +αhd) (1-K)
=[βIL(Rch+Lgt/2.6) + IL hd /2.6](1-K) =IL[β(Rch+Lgt/2.6) + hd /2.6](1-K)
4、线路绝缘子耐雷水平
当作用在线路绝缘子上的电压Uj>绝缘子串冲击闪络电压Uj50% 绝缘子将发生闪络，由于塔顶电位高于导线电位，闪络将从杆塔向 导线发展，故称为反击。 耐雷水平: 雷击杆塔时绝缘子串上承受最大雷电冲击电压所对应的雷电流:

Z0 Zb U S U A (1 k ) I L (1 k ) 2Z 0 Z b
不会出现击穿的经验公式
S 0.012 l 1
3.3.3 雷电绕击于导线时的耐雷水平
绕击率：
雷电绕过避雷线直接击中导线的概率
平原地区
lg P
lg P
h
86
3.9
3.35
3.3 输电线路的直击雷过电压和耐雷水平
我 国 110kV 及 以 上 线 路
一般全线都装设避雷线，而
35kV及以下线路一般不装设
避雷线，中性点直接接地系 统有避雷线的线路遭受直击 雷一般有三种情况： 雷击杆塔塔顶；
雷击避雷线档距中央；
雷电绕过避雷线击于导线
有避雷线线路直击雷的 三种情况
3.3.1 雷击杆塔塔项时的耐雷水平
3.3.2 雷击避雷线档距中央
3.3.3 雷电绕击于导线
返回
3.3.1 雷击杆塔塔顶时的耐雷水平
运行经验表明，雷击杆塔的次数与避雷线的根 数和经过地区的地形有关，雷击杆塔次数与雷击线 路总次数的比值称为击杆率 g ， DL/T 620—1997 标 准，击杆率g可采用下表所列数据。
击杆率g
Zb / 2 Z0 Zb U A iL Z 0 at Z0 Zb / 2 2Z 0 Z b
分析 雷击避雷线档距中央时， UA 自雷击点向两侧杆
塔移动,并于L/(2*V)的时间到达杆塔；
由于杆塔的接地作用，将出现一个负的反射波， 并经L/(2*V)的时间到达雷击点；
若此时雷电流尚未到达幅值，雷击点的电位自 负反射波到达之时开始下降，最大电位出现在 L/V时刻；
避雷线根数 平原 山丘
1 1/4 1/3

有避雷线时线路应有的耐雷水平
额定电压(kV)
35
110
220
330
500
耐雷水平I1(kA) 雷电流超过I1的概率(%)
20～30 40～75 75～110 100～150 125～175
59～46 35～14 14～6
7～2
3.8～1
2、雷击避雷线档距中央：
根据模拟试验和实际运行经验，雷击避雷线档 距 中由央于的半概 径率较较小小的(避10雷%线)。的强烈电晕衰减作用，使 过 电压波传播到杆塔时，已不足以使绝缘子串闪络 标，准通规常定只，需只要要考按虑经雷验击公避式雷S线＝对0.导01线2l+的1确反定击档问距题。 中央导、地线间的空气间距S，一般不会发生避雷 线 对导线的反击故障。
Riit
Lt
dit dt
(Rii Lt
di ) dt
Lt为杆塔等值电感，雷电流波前陡度di/dt=I/T1， 塔顶电位幅值为：
U top Ri I Lti / T1 I Ri Lt / T1
注：不同类型杆塔的等值电感不同，见表7-1； 不同电压等级及避雷线数目的β也不同，见表7-2
谢谢观看！ 2020
(2) 导线电位和绝缘子串上的电压：
雷击塔顶时，与塔顶相连的避雷线也有相同的电位 utop。负极性的雷电波沿杆塔及避雷线传播时，由 于避雷线与导线之间的电磁耦合作用，在导线上将 产生耦合电压kutop，其极性与雷电流极性相同。
另一方面，由塔顶向雷云发展的正极性雷电波，引 起空间电磁场的迅速变化，又使导线上出现与雷电 流极性相反的正的感应过电压 U g ahc (1 k) 。
提高雷击塔顶时耐雷水平的措施：
（1）一般高度杆塔（小于40m），冲击接地电阻 上压降是塔顶电位的主要成分，因此降低接地电阻 可以有效地减小塔顶电位和提高耐雷水平； （2）增大耦合系数k； （3）加强线路绝缘（提高U50%） 。

杆塔耐雷水平计算方法一、反击耐雷水平按式（1）计算()6.216.210%501av av gvt t a SUh K h h L k h h R k U I ⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-+-=ββ 式（1） 式（1）中：av h ——导线的平均高度，ma av f h h ⨯-=321 式（2）式（2）中：1h ——导线挂线点高度 a f ——导线弧垂gvh ——地线的平均高度，mg gv f h h ⨯-=322 式（3）式（3）中：2h ——地线挂线点高度 g f ——地线弧垂a h ——导线横担对地高度，m th ——杆塔高度，mK ——导线与地线间的几何耦合系数几种典型线路的几何耦合系数0K 见表1表1 典型线路的几何耦合系数0Kt L ——杆塔电感，H μ't t L h =t L 式（4）式（4）中 t h ——杆塔高度，m't L ——单位杆塔电感，m /H μ，取值见表2表2 典型杆塔的波阻抗和电感β——杆塔分流系数，取值见表3表3 杆塔分流系数k ——电晕下的耦合系数，01K k k =，其中1k 为雷击塔顶时的电晕校正系数，取值如表4表4 电晕校正系数SU R ——杆塔接地电阻，实测后应考虑1.4～1.8倍的季节系数%50U ——50％放电冲击电压二、绕击耐雷水平Z%502U I =式（5） 式（5）Z ——波阻抗，一般取100Ω。

例：忻侯Ⅰ线108＃塔型如下图，杆塔接地电阻为10Ω，导线弧垂6.6米，地线弧垂4.5米（1）避雷线平均高度：()m h b 325.4325.36=⨯-=（2）导线平均高度：(这里计算与上述表达式不一致)()m h d 1.246.6325.433=⨯--=（3）双避雷线对外侧导线的几何耦合系数：184.01022.2164ln 10005.4322ln36.129.736.121.56ln7.19.77.11.56ln 22222222220=++⨯+++++=K（4）电晕下的耦合系数：k ＝k 1k 0＝1.28×0.2＝0.256（5）杆塔电感：L t ＝36.5×0.5＝18.25(μH)（6）雷击杆塔时分流系数：β＝0.88（7）雷击杆塔时耐雷水平(当用FXBW4-500/160时)：()6.21.242.01.243216.225.1888.0256.05.3633788.0256.0121001⨯⎪⎭⎫⎝⎛⨯-+⨯⨯⎪⎭⎫⎝⎛-+⨯⨯-=I＝136.507(kA)（8）雷绕击于导线时的耐雷水平：)(2110021002kA I ==经计算可看出，108＃杆塔（ZB2-33）雷击塔顶时的耐雷水平为136.507kA ，绕击耐雷水平为21kA 。

.电磁暂态分析的理论基础1、电源合闸至单频振荡电路，在电容元件上产生的最大过电压幅值为，Ucm=稳态值+振荡幅值=稳态值+（稳态值—初始值）=2*稳态值—初始值2、导致波在传播过程产生损耗的因素主要有以下四种：1）导线电阻引起损耗；2）导线对地电导引起的损耗；3）大地电阻的损耗；4）导线发生电晕引起的损耗。

3、冲击电晕对波过程的影响对导线耦合系数的影响：发生冲击电晕后，在导线周围形成导电性能较好的电晕套，在这个电晕区内充满电荷，相当于扩大了导线的有效半径，因而与其它导线间的耦合系数也增大。

对波阻抗和波速的影响：冲击电晕将使线路波阻抗减小、波速减小对波形的影响：冲击电晕减小波的陡度、降低波的幅值的特性，有利于变电所的防雷保护。

4．一般连续式变压器绕组的αl值为5~10。

变压器绕组的末端不论接地与否，其初始电压分布均相同，按指数规律分布。

最大电位梯度出现在绕组的首端。

冲击电压波作用于变压器绕组初瞬，绕组首端的电位梯度是平均电位梯度的αl倍。

αl越大，电位分布越不均匀，相应绕组的抗冲击能力越差。

（危及变压器绕组的首端匝间绝缘）5．变压器绕组中的电磁振荡过程在10μs以内尚未发展起来，在这段时间内变压器绕组的特性主要由其纵向电容和对地电容组成的电容链决定，对首端来说相当于一个等效集中电容Cr，称为变压器的入口电容。

6．最大电位梯度均出现在绕组首端，其值等于αU0，对变压器绕组的纵绝缘（匝间绝缘）有危害。

绕组内的波过程除了与电压波的幅值有关外，还与作用在绕组上的冲击电压波形有关。

过电压波的波头时间越长（陡度越小），由于电感分流的影响，振荡过程的发展比较和缓，绕组各点的最大对地电压和纵向电位梯度都将下降；反之则振荡越激烈。

波尾也有影响，在短波作用下，振荡过程尚未充分激发起来时，外加电压已经大为减小，导致绕组各点的对地电压和电位梯度也比较低。

截波作用下绕组内的最大电位梯度将比全波作用时大，会在变压器绕组中产生很大的电位梯度，从而危及变压器绕组的纵绝缘，电力变压器不仅需要进行全波冲击耐压试验，还要通过截波耐压试验。

雷击杆塔塔顶时的过电压和耐雷水平
（3）耐雷水平的计算
I1

(1
K )

U 50% (Rch
Lgt ) 2.6

hd 2.6

雷击杆塔时的耐雷水平与分流系数，杆塔的等值电感，耦合系数及内
络电压有关
雷击避雷线档距中央时的过电压
流入雷击点的雷电流波为：
iZ
iL 1 Zb
（2）绕击跳闸率
n2 0.6hbPa P2
（四）、输电线路的防雷措施
架设避雷线 降低杆塔接地电阻 架设耦合地线 采用不平衡绝缘方式 装设自动重合闸 采用销弧线圈接地方式 装设管型避雷器 加强绝缘
三、输电线路的防雷措施
1、3~10kV线路防雷保护
不架设避雷线，可利用水泥杆的自然接地，为提高供电可 靠性可投入自动重合闸。在雷电特别强烈地区可因地制宜 采用高一电压等级的绝缘子，或顶相用针式两边改用两片 悬式绝缘子，也用采用瓷横担，以提高线路的绝缘水平。 对特殊用户应用用环形供电或不同杆双回路供电，必要时 改为电缆供电。
防止雷击闪络后建立工频短路电弧 防止线路中断供电
一、输电线路的感应雷击过电压
1、无避雷线时
当雷击点离开线路的距离大于６５米时，导线上的 感应雷过电压最大值按下式计算：
Ug 25 ILhd S
感应电压一般不超过500kV，对35kV及其以下的 水泥杆线路可能会引起闪络事故，对110kV及其以 上线路，由于线路绝缘水平较高，所以一般不会 引起闪络事故。
2
Z0
过电压为
uA

iL
Z0Zb 2Z0 Zb
（三）输电线路的雷击跳闸率 （1）建弧率
冲击闪络转为稳定工频电弧的概率称为建弧率

中央导、地线间的空气间距S，一般不会发生避雷 线 对导线的反击故障。
3、直击或绕击：
装设避雷线的线路，仍有雷绕过避雷线击于导线的 可能
发生绕击的概率称为绕击率Ka Ka与避雷线保护角α、杆塔高度h及线路通过地区 的地形地貌有关。 山区线路因地面附近电场受山坡地形影响，绕击率 约为平原线路的3倍。 虽然绕击率很小，但一旦发生绕击，产生的雷过电 压很高，即使是绝缘水平很高的超高压线路也往往 难免闪络。 (1) 雷击点电压幅值： 研究表明，雷电流通道具有分布参数特征，其波阻 抗用Z0表示。
令 U Lj U 50% ，即可求得 雷击塔顶反击时的耐雷水 平I1，即 影响I1的因素：
I1
U 50% Lt hc (1 k ) Ri T T 1 1
杆塔分流系数β，杆塔等值电感Lt，杆塔冲击接 地电阻Ri，耦合系数k和绝缘子串的U50%冲击放 电电压。
此即国标中用来估算绕击时过电压的近似公式
(2) 绕击时的耐雷水平： 令 U A U 50% ，可得绕击时的耐雷水平I2：I 2
U 50%
100
例如：采用13片XP-70型绝缘子的220kV线路绝缘子 串的U50%≈1200kV，可求得其I2＝12 kA ，大于I2的 雷电流出现概率P1≈73.1%。同理110、500kV线路 绕击时耐雷水平分别只有7、27.4kA，雷电流幅值超 过7、27.4kA的概率分别为83.3%、48.8%！
反击：本来是地（低）电位的物体，由于某种原因 导致其电位（绝对值）突然升高，当其与周围导体 的电压超过了该间隙的击穿电压或表面放电电压时 ，发生的击穿或闪络现象。
绝缘子串上 电压幅值为： (3) 耐雷水平：
U j

杆塔耐雷水平计算方法
1.杆塔耐雷水平概述
2.固定系数法
固定系数法是指根据将不同的雷电参数转化为固定的数值系数，结合
杆塔的结构参数进行计算。

根据天津市规定，固定系数法的计算公式如下：-杆塔雷电冲击可承受过流I(kA)=αS(Lxσ-λ)
-杆塔雷电冲击绕组电压U(kV)=αS(Lxσ-λ)
其中，α为雷势系数，取1.15；S为杆塔横截面积（单位：m²）；L
为杆塔高度（单位：m）；σ为大地电阻率（单位：Ω.m）；λ为杆塔附
近的基本层次雷电过程的雷电平均充电量（单位：C/m²）。

3.概率法
概率法是指根据雷电的概率分布进行统计分析，计算杆塔在不同概率
水平下的耐雷水平。

IEEE指南中介绍的概率法包括以下几个步骤：-确定雷电信号的概率分布
-选择阻抗模型
-进行雷电流和雷电绕组电压的计算
概率法的计算结果更加准确，能够更好地反映实际情况。

其优点是能
够根据具体雷电活动的特点，对杆塔进行更加精细的耐雷设计和计算。

4.其他影响因素
在杆塔耐雷水平的计算中，还需考虑以下因素：
-线路的输电能力：根据线路参数和设计要求，计算雷电过电压通过线路的能力。

-地面接地系统：合理设计接地系统，减小杆塔接地电阻，提高杆塔的抗雷性能。

-环境因素：考虑杆塔的周围环境，如空气离子浓度、湿度等对线路的影响，合理选择防雷强度等级。

综上所述，杆塔耐雷水平的计算方法可以采用固定系数法或概率法，其中概率法的计算结果更准确。

在计算中还需综合考虑线路的输电能力、接地系统和环境因素等。

通过合理的耐雷设计和计算，可以保证杆塔的安全运行和电力系统的可靠性。

第一章输电线路《线路手册》P179表3-2—3,电线风压不均匀系数和电线体型系数见P174表3—1—14和P175表3—1—15。

（二）导线应力弧垂计算注：用综合比载。

最大弧垂不等于最低点弧垂。

（三）代表档距计算、临界档距计算1、代表档距：《线路手册》P182式3-3—4，考虑悬挂点高差见式3-3-5.2、临界档距：《线路手册》P186～187式3-3-19及3—3—20。

（四）水平、垂直档距计算《线路手册》P183～184式3—3—9等. 注：悬挂点高差正负规定（五)架线观测档弧垂计算《线路手册》P210（六）塔头间隙尺寸1、悬垂子串摇摆角（或称悬垂子串风偏角）计算:《线路手册》P103注：分裂导线要乘分裂数，因为绝缘子自重无法忽略.2、导线风偏角的计算注:个人认为,用以上2个比载算出来的只是最大风偏角，如题目问实际情况下的风偏角,要用给定风速下的比载。

（七)一般档距的档距中央,导线与地线间的距离查GB50545—2010式7.0。

15 ,式中L--档距（m)档距较大时,中央导线与地线间的距离还要符合DL/T620表10。

表10 防止反击要求的大跨越档导线与避雷线间的距离(九)大档距导线与避雷线间距离的确定:查DL/T620—1997附录C,C13式（C26）：S2=≈0。

1 I《手册》P119如按上述两式选定的导线与地线间距离过大，致使大跨越杆塔在结构上发生困难或在经济上很不合理时，可考虑用几根横连线在档中将两根地线连接起来.此时，导线与避雷线之间的距离可以减小到下列数值（2—6—64）（十）线路过电压相关计算:1、雷电流幅值的概率：DL/T620—1997附录C式C12、Td=40地区每100km每年的雷击次数:3、电晕对雷电波波形的影响：DL/T620-1997附录C式C124、雷击有避雷线路杆塔顶部时耐雷水平的确定:DL/T620-1997附录C，5、绕击率的确定:DL/T620-1997附录C式C8。

P
h
86
3.35

输电线路雷击跳闸率
n n1 n2
N (gP1 P P2 )
例题
四.输电线路的防雷措施
1.架设避雷线 作用：
防止雷直击于导线； 对雷电流有分流作用，使塔顶电位下降； 对导线有耦合作用，降低雷击杆塔时绝缘子串 上电压； 对导线有屏蔽作用，可降低导线上感应电压
330kv及以上： 全线架设双避雷线 α在20度左 右
输电线路的防雷保护相 关知识讲解
衡量输电线路防雷性能的两个指标：
耐雷水平：雷击线路绝缘不发生闪络的最大 雷电流幅值
雷击跳闸率：每100km线路每年由雷击引起的 跳闸次数
一.输电线路的感应雷过电压
1.感应过电压的计算
(1).导线上方无避雷线
Ug
25
Ihd S
S:雷击点与线路的垂直距离
I:雷电流幅值
hd :导线悬挂的平均高度
(2).导线上方挂有避雷线
U
' gd
U
' gd
(1
k0
hb ) hd
(3).雷击线路杆塔时，导线上的感应过电压
无避雷线：
U gd hd
有避雷线：
U
' gd
hd (1 k0
hb hd
)
二.输电线路的直击雷过电压和耐雷水平
1.雷击杆塔塔顶 雷电流的分布
等值电路图
流经杆塔的电流
雷击处避雷线与导线间的空气隙S上承受最大电压
US U A (1 k)
l Z0Zb (1 k) b 2Z0 Zb
不会出现击穿的经验公式
S 0.012l 1
3.雷绕过避雷线击于导线或直接击于导线 等值电路图