常见晶体模型教程文件

氯化钠晶体离子晶体（1）NaCI晶胞中每个Na+等距离且最近的Cl-（即Na+配位数）为6个(2)(3)NaCI晶胞中每个CI-等距离且最近的Na+（即CI-配位数）一个晶胞内由均摊法计算出一个晶胞内占有的Na+4个; 占有的CI-4个。

在该晶体中每个Na+周围与之最接近且距离相等的Na+ 与每个Na+等距离且最近的CI-所围成的空间几何构型为CsCI晶体（注意：右侧小立方体为CsCI晶胞；左侧为8个晶胞）（1）CsCI晶胞中每个Cs+等距离且最近的C「（即Cs+配位数）为8个CsCI晶胞中每个CI-等距离且最近的Cs+（即CI-配位数）为8个，这几个Cs+在空间构成的几何构型为正方体。

（2）在每个Cs+周围与它最近的且距离相等的Cs+有6个这几个Cs+在空间构成的几何构型为正八面体。

• Cs* OCI- （3）一个晶胞内由均摊法计算出一个晶胞内占有的Cs+ 1个；占有的CI- 1个CaF2晶体（1））Ca2+立方最密堆积，F-填充在全部四面体空隙中。

（2）CaF2晶胞中每个Ca2+等距离且最近的F-（即Ca2+配位数）为8个CaF2晶胞中每个F-等距离且最近的Ca2+（即F-配位数）为4个（3）一个晶胞内由均摊法计算出一个晶胞内占有的Ca2+4个；占有的F-8个。

ZnS晶体：（1）1个ZnS晶胞中，有4 个S2「，有4个Zn2+（2）Zn2+的配位数为4个, S2_的配位数为4个O£n?，•原子晶体（1） 金刚石晶体a 每个金刚石晶胞中含有 8个碳原子，最小的碳环为 6元环，并且不在同一平面（实际为椅 式结构），碳原子为sp 3杂化，每个C 以共价键跟相邻的_4_个 C 结合，形成正四面体。

键角109° 28'b 、 每个碳原子被12个六元环共用，每个共价键被6个六元环共用c 、 12g 金刚石中有2mol 共价键，碳原子与共价键之比为 （2） Si 晶体由于Si 与碳同主族，晶体Si 的结构同金刚石的结构。

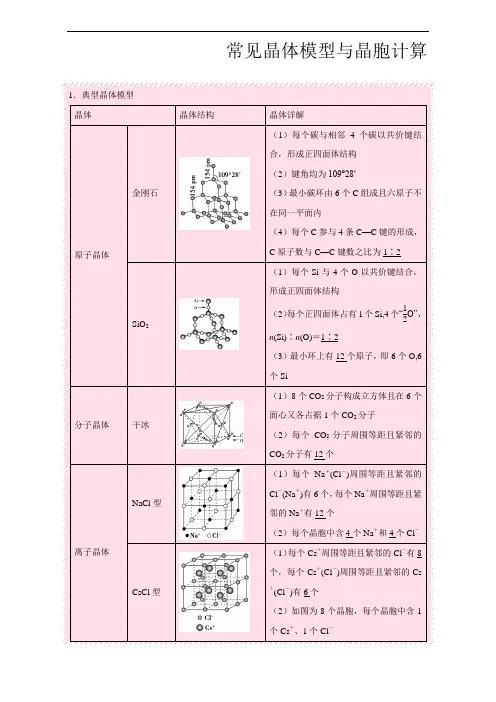
常见晶体模型与晶胞计算1．典型晶体模型晶体晶体结构晶体详解原子晶体金刚石（1）每个碳与相邻4个碳以共价键结合，形成正四面体结构（2）键角均为109°28′（3）最小碳环由6个C 组成且六原子不在同一平面内（4）每个C 参与4条C —C 键的形成，C 原子数与C —C 键数之比为1∶2SiO 2（1）每个Si 与4个O 以共价键结合，形成正四面体结构（2）每个正四面体占有1个Si,4个“12O”，n (Si)∶n (O)＝1∶2（3）最小环上有12个原子，即6个O,6个Si分子晶体干冰（1）8个CO 2分子构成立方体且在6个面心又各占据1个CO 2分子（2）每个CO 2分子周围等距且紧邻的CO 2分子有12个离子晶体NaCl 型（1）每个Na ＋(Cl －)周围等距且紧邻的Cl －(Na ＋)有6个，每个Na ＋周围等距且紧邻的Na ＋有12个（2）每个晶胞中含4个Na ＋和4个Cl －CsCl 型（1）每个Cs＋周围等距且紧邻的Cl －有8个，每个Cs ＋(Cl－)周围等距且紧邻的Cs＋(Cl－)有6个（2）如图为8个晶胞，每个晶胞中含1个Cs＋、1个Cl－金属晶体简单立方堆积典型代表Po ，配位数为6，空间利用率52%面心立方最密堆积又称为A 1型或铜型，典型代表Cu 、Ag 、Au ，配位数为12，空间利用率74%体心立方堆积又称为A 2型或钾型，典型代表Na 、K 、Fe ，配位数为8，空间利用率68%六方最密堆积又称为A3型或镁型，典型代表Mg 、Zn 、Ti ，配位数为12，空间利用率74%2．晶胞中微粒的计算方法——均摊法【重难点指数】★★★【重难点考向一】常见晶胞类型和结构特点【典型例题1】（1）【2015·高考全国卷Ⅰ，37（5）】碳有多种同素异形体，其中石墨烯与金刚石的晶体结构如图所示：石墨烯晶体金刚石晶体①在石墨烯晶体中，每个C原子连接________个六元环，每个六元环占有________个C原子。

常见晶体模型及晶胞计算晶体是由晶体胞重复堆积而成的，晶体胞是晶体的最小构造单元。

晶体的结构可以用晶胞参数表示，晶胞参数包括晶格常数、晶胞的角度、晶胞的体积等。

根据晶体的晶胞参数，可以推导出晶胞的几何形状和晶体的晶体类别。

根据晶体的晶胞形状，晶体可以分为立方晶系、四方晶系、六方晶系、正交晶系、单斜晶系和三斜晶系。

每个晶系又可以进一步分为各种晶体类别，如立方晶系下又有体心立方晶体和面心立方晶体等。

晶体模型描述了晶体的结构和排列方式。

常见的晶体模型有球模型、格点模型和球与棍模型。

1.球模型：球模型是一种简化的晶体表示方法，将晶体中的原子用球体表示，球的大小和颜色常用来表示原子的种类和其它信息。

2.格点模型：格点模型是用晶体胞中的原子位置来表示晶体结构的一种方法，晶体胞中的每个原子位置称为格点。

在格点模型中，晶体中的每个原子都用一个点来表示，这样形成了一个点阵，点阵反映了原子的排列方式。

常见的格点模型有立方格点模型、面心立方格点模型和体心立方格点模型。

3.球与棍模型：球与棍模型是一种结合了球模型和格点模型的晶体表示方法。

在球与棍模型中，每个原子用一个球来表示，不同原子之间用直线连接表示键的形成。

在进行晶胞计算时，需要确定晶体的晶胞参数。

晶胞参数可以通过实验测量得到，也可以通过计算方法获得。

晶胞计算主要包括以下几个步骤：1.实验测量：通过实验手段，如X射线衍射、电子衍射等，测量晶体的晶胞参数。

2.计算方法：根据晶体的晶胞参数和晶体的晶格类型，可以使用计算方法来预测和计算晶体的晶胞参数。

常见的计算方法有密度泛函理论（DFT）和分子力场（MM）等。

3.晶胞优化：通过晶胞优化算法，寻找晶体的最稳定结构。

晶胞优化算法可以通过改变晶胞参数、原子位置或局部结构等来寻找最低能量的晶体结构。

4.校正和验证：使用计算得到的晶胞参数进行校正和验证，与实验结果进行比较，确保计算结果的准确性和可靠性。

总之，晶体模型和晶胞计算是研究和描述晶体结构的重要工具。

MS晶体建模基本方法星期三， 2008-11-19 09：09 - Elizerbeth软件名称:Materials Studio第一种情况: 从程序自带的各种晶体及有机模型中导入体系的晶胞1．打开MS，由file〉import>structures>metals\〉pure—metals〉Fe导入Fe 的晶胞。

2．由build〉Surfaces〉cleave Surfaces打开对话框。

在对话框中输入要建立的晶面(hkl），选择position，其中depth控制晶面层数。

3．进入build〉Supercell，输入A 、B 、C的值,得到想要的超晶胞。

4．到该步骤，我们已经建立了一个周期性的超晶胞。

如果要做周期性计算,则应选择build>Crystals〉build vaccum slab，其中真空层通常选择10埃以上。

如果建立团簇模型则选择build〉Symmetry〉Non-periodic Structure，去掉模型的周期性,并跟据自己的实际需要删除部分原子，得到想要的团簇模型.5．在表面插入分子时通过菜单栏上的几个小图标添加即可.第二种情况: 手动建模，优点是可控制晶格常数。

6．首先从文献中查到晶体的晶格常数的实验值。

7．打开build>Crystals〉build crystals,可见到对话框。

在对话框中选择空间群与点群，然后在Lattice Parameter中设置晶胞基矢的长度及夹角。

8．然后打开build>Add atom，从对话框中输入坐标。

这里只需输入几个有代表性的原子的坐标，不必全部输入。

在坐标输入前首先在option页面中选择coordinate system，或者分数坐标或者卡迪尔坐标.9．以下步骤重复2-5步。

10．需要注意的是，采取什么样的团簇并不是任意的.原因是很多模型构造出来后在优化过程中往往不收敛。

要避免这个问题的办法是查阅文献，参考文献上模型进行选取,因为它们的模型通常是经过试验证实收敛的。

离子晶体氯化钠晶体（1） NaCl 晶胞中每个 Na+等距离且最近的 Cl-（即 Na+配位数）为 6 个NaCl 晶胞中每个 Cl-等距离且最近的 Na+（即 Cl-配位数）为 6 个（2）一个晶胞内由均摊法计算出一个晶胞内占有的Na+4_个；占有的 Cl-4 个。

（3）在该晶体中每个 Na+周围与之最接近且距离相等的 Na+共有 12 个；与每个 Na+等距离且最近的 Cl -所围成的空间几何构型为正八面体CsCl 晶体（注意：右侧小立方体为CsCl 晶胞；左侧为8 个晶胞）（1）+等距离且最近的-+配位数）CsCl 晶胞中每个 Cs Cl（即 Cs为 8个CsCl 晶胞中每个 Cl-等距离且最近的Cs+（即 Cl -配位数）为 8 个，这几个 Cs+在空间构成的几何构型为正方体++（2）在每个 Cs 周围与它最近的且距离相等的Cs 有。

6 个这几个 Cs+在空间构成的几何构型为正八面体（3）一个晶胞内由均摊法计算出一个晶胞内占有的。

Cs+ 1 个；占有的Cl- 1 个。

CaF2晶体（1）） Ca2+立方最密堆积， F-填充在全部四面体空隙中。

（2） CaF2晶胞中每个 Ca2+等距离且最近的 F-（即 Ca2+配位数）为 8 个CaF2晶胞中每个 F-等距离且最近的 Ca2+（即 F-配位数）为 4 个（ 3）一个晶胞内由均摊法计算出一个晶胞内占有的Ca2+4 个；占有的 F-8 个。

ZnS晶体：（1）1 个 ZnS晶胞中，有 4 个 S2－，有 4 个 Zn2＋。

（2）Zn2＋的配位数为 4 个， S2－的配位数为 4 个。

原子晶体金刚石金刚石晶胞金刚石晶胞分位置注释（ 1）金刚石晶体a、每个金刚石晶胞中含有8 个碳原子，最小的碳环为 6 元环，并且不在同一平面（实际为椅式结构），碳原子为 sp3杂化，每个 C 以共价键跟相邻的 _4_个 C 结合，形成正四面体。

键角109° 28’b、每个碳原子被 12 个六元环共用，每个共价键被 6 个六元环共用c、12g 金刚石中有 2mol 共价键，碳原子与共价键之比为1:2（2） Si 晶体由于 Si 与碳同主族，晶体Si 的结构同金刚石的结构。

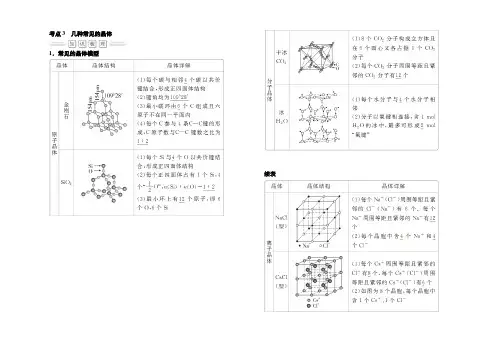
考点3几种常见的晶体1．常见的晶体模型续表2．石墨晶体石墨晶体是混合型晶体，呈层状结构。

同层内碳原子以共价键形成正六边形平面网状结构，平均每个正六边形拥有的碳原子个数是2，C 原子实行的杂化方式是sp2。

层与层之间以分子间作用力结合。

所以石墨晶体熔、沸点很高，但硬度不大，有滑腻感，能导电。

易错警示推断某种粒子四周等距且紧邻的粒子数目时，要留意运用三维想象法。

如NaCl 晶体中，Na ＋四周的Na ＋数目(Na ＋用“”表示)：每个面上有4个，共计12个。

推断正误，正确的画“√”，错误的画“×”。

(1)1 mol 金刚石和SiO 2中含有的共价键数目均为4N A 。

(×)(2)金刚石网状结构中，由共价键形成的碳原子环中，最小的环上有6个碳原子。

(√)(3)氯化钠晶体中，每个Na ＋四周距离相等且最近的Na ＋共有6个。

(×) (4)冰中包含的作用力有范德华力、氢键和共价键。

(√)(5)金属晶体能导电是由于金属晶体在外加电场作用下可失去电子。

(×)题组一 依据晶胞结构推断晶体类型 1．下图为几种晶体或晶胞的示意图：请回答下列问题：(1)上述晶体中，粒子之间以共价键结合形成的晶体是________。

(2)冰、金刚石、MgO、CaCl2、干冰5种晶体的熔点由高到低的挨次为____________________________。

(3)NaCl晶胞与MgO晶胞相同，NaCl晶体的晶格能________(填“大于”或“小于”)MgO晶体，缘由是_________________________________________________________________________________。

(4)每个Cu晶胞中实际占有________个铜原子，CaCl2晶体中Ca2＋的配位数为________。

答案(1)金刚石晶体(2)金刚石、MgO、CaCl2、冰、干冰(3)小于MgO晶体中离子的电荷数大于NaCl晶体中离子电荷数；且r(Mg2＋)<r(Na＋)、r(O2－)<r(Cl－)(4)4 8解析(1)冰晶体、干冰晶体均为分子晶体，粒子间通过分子间作用力结合成晶体，Cu晶体中微粒间通过金属键结合形成晶体，MgO和CaCl2晶体中微粒之间通过离子键结合形成晶体。

氯化钠晶体（1）NaCl晶胞中每个Na+等距离且最近的Cl-（即Na+配位数）为6个NaCl晶胞中每个Cl-等距离且最近的Na+（即Cl-配位数）为6个（2）一个晶胞内由均摊法计算出一个晶胞内占有的Na+4_个；占有的Cl-4个。

（3）在该晶体中每个Na+周围与之最接近且距离相等的Na+共有12个；与每个Na+等距离且最近的Cl-所围成的空间几何构型为正八面体CsCl晶体（注意：右侧小立方体为CsCl晶胞；左侧为8个晶胞）（1）CsCl晶胞中每个Cs+等距离且最近的Cl-（即Cs+配位数）为8个CsCl晶胞中每个Cl-等距离且最近的Cs+（即Cl-配位数）为8个，这几个Cs+在空间构成的几何构型为正方体。

（2）在每个Cs+周围与它最近的且距离相等的Cs+有6个这几个Cs+在空间构成的几何构型为正八面体。

（3）一个晶胞内由均摊法计算出一个晶胞内占有的Cs+ 1个；占有的Cl- 1个。

CaF2晶体（1））Ca2+立方最密堆积，F-填充在全部四面体空隙中。

（2）CaF2晶胞中每个Ca2+等距离且最近的F-（即Ca2+配位数）为8个CaF2晶胞中每个F-等距离且最近的Ca2+（即F-配位数）为4个（3）一个晶胞内由均摊法计算出一个晶胞内占有的Ca2+4个；占有的F-8个。

ZnS晶体：（1）1个ZnS晶胞中，有4个S2－，有4个Zn2＋。

（2）Zn2＋的配位数为4个，S2－的配位数为 4个。

Si O金刚石 金刚石晶胞 金刚石晶胞分位置注释（1）金刚石晶体a 、每个金刚石晶胞中含有8个碳原子，最小的碳环为6元环，并且不在同一平面（实际为椅 式结构），碳原子为sp 3杂化，每个C 以共价键跟相邻的_4_个C 结合，形成正四面体。

键角109°28’b 、每个碳原子被12个六元环共用，每个共价键被6个六元环共用c 、12g 金刚石中有2mol 共价键，碳原子与共价键之比为 1:2 （2）Si 晶体由于Si 与碳同主族，晶体Si 的结构同金刚石的结构。

《几种简单的晶体结构模型》教学设计一、教学目标1、知识与技能目标学生能够理解并描述常见的几种简单晶体结构模型，如简单立方、体心立方和面心立方。

掌握晶体结构中原子的排列方式和空间占有率的计算方法。

2、过程与方法目标通过观察模型和图像，培养学生的空间想象能力和抽象思维能力。

经历对晶体结构的分析和计算过程，提高学生的逻辑推理和数学运算能力。

3、情感态度与价值观目标激发学生对物质微观结构的好奇心和探索欲望。

培养学生严谨的科学态度和合作精神。

二、教学重难点1、教学重点简单立方、体心立方和面心立方晶体结构的特点。

晶体结构中原子半径、晶胞边长与空间占有率的关系。

2、教学难点对晶体结构空间概念的理解和想象。

空间占有率的计算方法。

三、教学方法1、讲授法讲解晶体结构的基本概念和模型特点。

2、直观演示法通过展示晶体结构模型、多媒体图片和动画，帮助学生建立直观的认识。

3、小组讨论法组织学生分组讨论问题，促进学生之间的交流与合作，培养学生的思维能力。

4、练习法通过课堂练习和课后作业，巩固学生所学知识，提高学生的应用能力。

四、教学过程1、导入（5 分钟）展示一些美丽的晶体图片，如钻石、水晶等，引起学生的兴趣。

提问：“这些晶体为什么会有如此规则的外形和独特的物理性质？”从而引出晶体结构的主题。

2、知识讲解（20 分钟）简单立方晶体结构展示简单立方晶体结构模型，讲解原子的排列方式。

引导学生观察并描述原子在晶胞中的位置。

体心立方晶体结构切换至体心立方晶体结构模型，对比简单立方，分析其特点。

强调体心位置原子的存在对结构的影响。

面心立方晶体结构展示面心立方晶体结构模型，引导学生观察面心位置的原子。

分析面心立方结构的紧密堆积方式。

3、小组讨论（10 分钟）分组讨论：三种晶体结构的稳定性差异及原因。

每组选派代表发言，分享讨论结果。

4、计算与推导（15 分钟）以简单立方晶体结构为例，讲解原子半径与晶胞边长的关系。

推导空间占有率的计算公式，并进行计算演示。