下载文档原格式
Document serial number [UU89WT-UU98YT-UU8CB-UUUT-UUT108]第一章导论1、什么是博弈博弈论的主要研究内容是什么2、设定一个博弈模型必须确定哪儿个方面3、举出烟草、餐饮、股市、房地产、广告、电视等行业的竞争中策略相互依存的例子。
4、"囚徒的困境”的内在根源是什么举出现实中囚徒的困境的具体例子。
5、博弈有哪些分类方法，有哪些主要的类型6、你正在考虑是否投资100万元开设一家饭店。
假设情况是这样的：你决定开，则的概率你讲收益300万元（包括投资），而的概率你将全部亏损；如果你不开，则你能保住本钱但也不会有利润，请你（a）用得益矩阵和扩展形式表示该博弈；（b）如果你是风险中性的，你会怎样选择（c）如果你是风险规避的，且期望得益的折扣系数为，你的策略选择是什么（d）如果你是风险偏好的，期望得益折算系数为，你的选择又是什么7、一逃犯从关押他的监狱中逃走，一看守奉命追捕。
如果逃犯逃跑有两条可选择的路线，看守只要追捕方向正确就一定能抓住逃犯。
逃犯逃脱可以少坐10年牢，但一旦被抓住则要加刑10年；看守抓住逃犯能得到1000元奖金。
请分别用得益矩阵和扩展形式表示该博弈，并作简单分析。
第二章完全信息静态博弈1、上策均衡、严格下策反复消去法和纳什均衡相互之间的关系是什么2、为什么说纳什均衡是博弈分析中最重要的概念3、找出现实经济或生活中可以用帕累托上策均衡、风险上策均衡分析的例子。
4、多重纳什均衡是否会影响纳什均衡的一致预测性质，对博弈分析有什么不利影响5、下面的得益矩阵表示两博弈方之间的一个静态博弈。
该博弈有没有纯策略纳什均衡t専弈的结果是什么6、求出下图中得益矩阵所表示的博弈中的混合策略纳什均衡。
7、博弈方1和2就如何分10 000元进行讨价还价。
假设确定了以下规则:双方同时提出自己要求的数额S1和S2, 0< sl,s2< 10 000,如果sl+s2W10 000,则两博弈方的要求都得到满足，即分别得到si和s2, 但如果是sl+s2>10 000,则该笔钱就被没收。
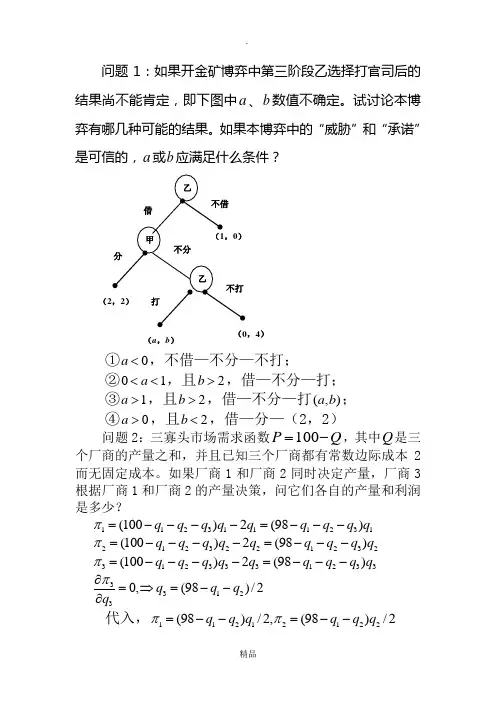
问题1：如果开金矿博弈中第三阶段乙选择打官司后的结果尚不能肯定，即下图中a 、b 数值不确定。
试讨论本博弈有哪几种可能的结果。
如果本博弈中的“威胁”和“承诺”是可信的，a 或b 应满足什么条件？①0a <，不借—不分—不打；②01a <<，且2b >，借—不分—打；③1a >，且2b >，借—不分—打(,)a b ；④0a >，且2b <，借—分—（2，2）问题2：三寡头市场需求函数Q P -=100，其中Q 是三个厂商的产量之和，并且已知三个厂商都有常数边际成本2而无固定成本。
如果厂商1和厂商2同时决定产量，厂商3根据厂商1和厂商2的产量决策，问它们各自的产量和利润是多少？1123111231(100)2(98)q q q q q q q q q π=----=---2123221232(100)2(98)q q q q q q q q q π=----=---3123331233(100)2(98)q q q q q q q q q π=----=---331230,(98)/2q q q q π∂=⇒=--∂ 代入，11212122(98)/2,(98)/2q q q q q q ππ=--=--（a ，b ） （0，4）12120,0q q ππ∂∂==∂∂，得***12398/3,49/3q q q ===***1234802/9,2401/9πππ===。
问题3：设两个博弈方之间的三阶段动态博弈如下图所示。
（1）若a 和b 分别等于100和150，该博弈的子博弈完美纳什均衡是什么？（2）T N L --是否可能成为该博弈的子博弈完美纳什均衡路径，为什么？（3）在什么情况下博弈方2会获得300单位或更高的得益？（1）博弈方1在第一阶段选择R ，在第三阶段选择S ，博弈方2在第二阶段选择M 。
（2）不可能。
T N L --带来的利益50明显小于博弈方1在第一阶段R 的得益300；无论a 和b 是什么数值，该路径都不能构成Nash 均衡，不能成为子博弈完美Nash 均衡。
问题1：如果开金矿博弈中第三阶段乙选择打官司后的结果尚不能肯定，即下图中a 、b 数值不确定。
试讨论本博弈有哪几种可能的结果。
如果本博弈中的“威胁”和“承诺”是可信的，a 或b 应满足什么条件？①0a <，不借—不分—不打；②01a <<，且2b >，借—不分—打； ③1a >，且2b >，借—不分—打(,)a b ； ④0a >，且2b <，借—分—（2，2）问题2：三寡头市场需求函数Q P -=100，其中Q 是三个厂商的产量之和，并且已知三个厂商都有常数边际成本2而无固定成本。
如果厂商1和厂商2同时决定产量，厂商3根据厂商1和厂商2的产量决策，问它们各自的产量和利润是多少？1123111231(100)2(98)q q q q q q q q q π=----=---2123221232(100)2(98)q q q q q q q q q π=----=---（a ，b ）（0，4）3123331233(100)2(98)q q q q q q q q q π=----=--- 331230,(98)/2q q q q π∂=⇒=--∂代入，11212122(98)/2,(98)/2q q q q q q ππ=--=--12120,0q q ππ∂∂==∂∂，得***12398/3,49/3q q q === ***1234802/9,2401/9πππ===。
问题3：设两个博弈方之间的三阶段动态博弈如下图所示。
（1）若a 和b 分别等于100和150，该博弈的子博弈完美纳什均衡是什么？（2）T N L --是否可能成为该博弈的子博弈完美纳什均衡路径，为什么？（3）在什么情况下博弈方2会获得300单位或更高的得益？（1）博弈方1在第一阶段选择R ，在第三阶段选择S ，博弈方2在第二阶段选择M 。
（a ，b ）50，300（2）不可能。
T N L --带来的利益50明显小于博弈方1在第一阶段R 的得益300；无论a 和b 是什么数值，该路径都不能构成Nash 均衡，不能成为子博弈完美Nash 均衡。
（3）由于T N L --不是本博弈的子博弈完美Nash 均衡，因此博弈方2不可能通过该路径实现300单位的得益，唯一有可能实现300单位及以上的得益的路径为L N S --，要使该路径成为子博弈完美Nash 均衡而且博弈方2得到300单位及以上的得益必须300,300a b >≥。
问题4：企业甲和企业乙都是彩电制造商，都可以选择生产低档产品或高档产品，每个企业在四种不同的情况下的利润如以下得益矩阵所示。
如果企业甲先于企业乙进行产品选择并投入生产，即企业乙在决定产品时已经知道企业甲的选择，而且这一点双方都清楚。
（1）用扩展型表示这一博弈。
（2）这一博弈的子博弈完美纳什均衡是什么？扩展型表示的博弈若甲选择高档，乙选择低档，甲得1000元，乙得700元；若甲选择低档，乙选择高档，那么甲得700元，乙得1000元，所以：甲的策略为：选择生产高档产品；乙的策略是：若甲选择高档，乙选择低档；若甲选择低档，乙选择高档。
本博弈的子博弈Nash均衡是：甲选择生产高档彩电，乙选择生产低档彩电。
问题5：乙向甲索要1000元，并且威胁甲如果不给就与他同归于尽。
当然甲不一定相信乙的威胁。
请用扩展型表示该博弈，并找出纯策略纳什均衡和子博弈完美纳什均衡。
两个纯策略Nash均衡：（给，实施），（不给，不实施）实施的威胁不可信，甲在第一阶段选择不给，乙在第二阶段不实施（生命诚可贵）；这是子博弈完美纳什均衡；另一个（给，实施）不可信。
问题6：两个寡头企业进行价格竞争博弈，企业1的利润函数是q c aq p ++--=21)（π，企业2的利润函数是p b q +--=22)（π，其中p 是企业1的价格，q 是企业2的价格。
求：（1）两个企业同时决策的纯策略纳什均衡； （2）企业1先决策的子博弈完美纳什均衡； （3）企业2先决策的子博弈完美纳什均衡； （4）是否存在参数c b a ,,的特定值或范围，使两个企业都希望自己先决策？ 解：（1）122()02()0p aq c pq b qππ∂=--+=∂∂=--=∂，解得：,p ab c q c =-=12,b ab c ππ==-（2）22()0q b qπ∂=--=∂，代入得到21)p ab c b π=--++（，12)0p ab c pπ∂=--+=∂（，得p ab c =-，企业1的子博弈完美纳什均衡企业1的定价p ab c =-，企业2的定价q b =，利润也与（1）相同。
与同时选择无异。
-1000，1000）（3）将p aq c =-代入222))q b p q b aq c π=--+=--+-（（ 22)0q b a qπ∂=--+=∂（，解得2aq b =+，代入得22a p abc =+-*12a b b π=+>，2*24a ab c ab c π=+->- （4）只有先决策的利润大于后决策时的利润时才有激励。
①当24a ab c ab c +->-0a ⇒≠，企业2希望先决策；②当2ab b >+时，企业1希望先决策，只要0a <都希望自己先决策。
20,0,0,024a ab b abc ab c >+>->+->，因此当0,2aa b <>-和c ab <时都能满足，这样才参数范围都希望自己先决策。
问题7：三寡头市场有倒转的需求函数为Q a Q P -=)(，其中321q q q Q ++=，i q 是厂商i 的产量。
每一个厂商生产的边际成本为常数c ，没有固定成本。
如果厂商1先选择产量1q ，厂商2和厂商3观察到1q 后同时选择2q 和3q ，问它们各自的产量和利润是多少？解：[]123()()1,2,3i i a c q q q q i π=----=21232312332020a c q q q q a c q q q q ππ∂=----=∂∂=----=∂2311()3q q a c q ==--，代入得1111()3a c q q π=--令*11110,()2d q a c dq π==-，代入得：**231()6q q a c ==-*2*2*2123111(),(),()123636a c a c a c πππ=-=-=-问题8：考虑如下的双寡头市场战略投资模型：企业1和企业2目前情况下的生产成本都是2=c 。
企业1可以引进一项新技术使单位成本降低到1=c ，该项技术需要投资f 。
在企业1作出是否投资的决策（企业2可以观察到）后，两个企业同时选择产量。
假设市场需求函数为q q p -=14)(，其中p 是市场价格，q 是两个企业的总产量。
问上述投资额f 处于什么水平时，企业1会选择引进新技术？解：以未引进技术为基准1121121222(14)2(14)2q q q q q q q q ππ=---=---，令12120q q ππ∂∂==∂∂，得12124,16q q ππ==⇒==如果引进技术，1121121222(14)(14)2q q q q fq q q q ππ=----=---令12120q q ππ∂∂==∂∂，得1211411196,,339q q f π'==⇒=- 只有引进技术后得到的利润大于未引进技术的总利润时，即196169f ->，即196521699f <-=时企业1才会引进新技术。
问题9：如果学生在考试之前全面复习，考好的概率为90%，如果学生只复习一部分重点，则有50%的概率考好。
全面复习花费的时间1001=t 小时，重点复习只需要花费202=t 小时。
学生的效用函数为：e W U 2-=，其中W 是考试成绩，有高低两种分数h W 和l W ，e 为努力学习的时间。
问老师如何才能促使学生全面复习？解：学生全面复习的期望得益10.9(200)0.1(200)0.90.1200h l h l u w w w w =⨯-+⨯-=+-学生重点复习的期望得益20.5(40)0.5(40)0.50.540h l h l u w w w w =⨯-+⨯-=+-根据激励相容的条件，12u u ≥，所以有0.90.12000.50.540h l h l w w w w +-≥+-所以：0.4()160h l w w -≥故：400h l w w -≥奖学金与学习成绩全面挂钩，才能激励学生的学习；单靠成绩没有这么大的力度。
问题10：某人正在打一场官司，不请律师肯定会输，请律师后的结果与律师的努力程度有关。
假设当律师努力工作（100小时）时有50%的概率能赢，律师不努力工作（10小时）则只有15%的概率能赢。
如果诉讼获胜可得到250万元赔偿，失败则没有赔偿。
因为委托方无法监督律师的工作，因此双方约定根据结果付费，赢官司律师可获赔偿金额的10%，失败则律师一分钱也得不到。
如果律师的效用函数为e m 05.0.-，其中m 是报酬，e 是努力小时数，且律师有机会成本5万元。
求这个博弈的均衡。
解：第三阶段，律师努力的期望得益：0.5200.557.5⨯-⨯=不努力的期望得益：0.1524.50.850.5 3.25⨯-⨯= 满足激励相容约束第二阶段：7.5 3.25&7.55>> 接受委托并努力工作第一阶段：委托，接受委托，代理人努力工作，那么0.52250.50112.50⨯+⨯=>委托是必然的选择。
打官司的人提出委托，律师接受委托并努力工作。
（225，20）（0，-5）（225，24.5）（0，-0.5）。
