图解-如何用科学计算器计算标准差
- 格式:doc
- 大小:297.00 KB
- 文档页数:3

科学计算器算标准差在统计学中,标准差是用来衡量一组数据的离散程度或者波动程度的一种统计量。
它可以帮助我们了解数据集中数值的分散程度,从而更好地理解数据的特征和规律。
在科学计算中,计算标准差是非常常见的操作,而现代科学计算器通常都具备这一功能。
下面我们将介绍如何使用科学计算器来计算标准差。
首先,我们需要明确一组数据的样本标准差和总体标准差的计算公式。
对于一组包含n个数据的样本,其样本标准差的计算公式如下:\[ s = \sqrt{\frac{\sum_{i=1}^{n}(x_i \bar{x})^2}{n-1}} \]其中,\( x_i \) 表示第i个数据点,\( \bar{x} \) 表示数据的平均值,n表示数据点的个数。
而对于一组包含n个数据的总体,其总体标准差的计算公式如下:\[ \sigma = \sqrt{\frac{\sum_{i=1}^{n}(x_i \mu)^2}{n}} \]其中,\( x_i \) 表示第i个数据点,\( \mu \) 表示总体的平均值,n表示数据点的个数。
接下来,我们将以一个具体的例子来演示如何使用科学计算器来计算标准差。
假设我们有一组数据,2, 4, 6, 8, 10。
我们首先需要计算这组数据的平均值。
然后,我们可以使用科学计算器中的统计功能来计算标准差。
在大多数科学计算器中,可以通过选择统计模式,然后输入数据,即可得到标准差的计算结果。
在计算标准差时,我们需要注意一些常见的误区。
首先,要确保输入的数据准确无误,任何一个数据点的输入错误都会导致标准差的计算结果出现偏差。
其次,要注意选择合适的标准差计算公式,根据数据是样本还是总体来选择相应的公式。
最后,要注意科学计算器的设置,确保在进行标准差计算时选择了正确的模式和参数。
总之,科学计算器可以帮助我们快速、准确地计算标准差,从而更好地理解数据的分布特征。
通过掌握科学计算器的标准差计算功能,我们可以更加高效地进行数据分析和统计处理,为科学研究和工程实践提供有力的支持。

科学计算器计算标准差在统计学中,标准差是一种用来衡量数据集中数值分散程度的统计量。
在科学计算中,我们经常需要计算标准差来评估数据的稳定性和可靠性。
本文将介绍如何使用科学计算器来计算标准差,帮助大家更好地理解和应用这一重要的统计概念。
首先,我们需要明确标准差的计算公式。
标准差的计算公式为,标准差= sqrt(Σ(xi μ)² / N),其中Σ表示求和,xi表示每个数据点,μ表示数据的均值,N表示数据点的个数。
这个公式看起来可能有些复杂,但我们可以通过科学计算器来简化计算过程。
接下来,我们将以一个具体的数据集为例,演示如何使用科学计算器来计算标准差。
假设我们有一个数据集,{3, 5, 7, 9, 11},我们将使用科学计算器来计算这个数据集的标准差。
首先,我们需要计算这个数据集的均值。
均值的计算公式为,μ = (3 + 5 + 7 + 9 + 11) / 5 = 7。
通过科学计算器,我们可以直接输入这些数值,然后按下求和符号,得到均值为7。
接下来,我们需要计算每个数据点与均值的差的平方,并将这些差的平方相加。
在科学计算器中,我们可以依次输入每个数据点与均值的差的平方,然后按下求和符号,得到这些差的平方的总和。
最后,我们需要将这些差的平方的总和除以数据点的个数,然后取平方根,即可得到标准差。
在科学计算器中,我们可以直接输入这个计算公式,得到最终的标准差。
通过上述步骤,我们成功地使用科学计算器计算出了这个数据集的标准差。
这个例子展示了科学计算器在计算标准差时的便利性和高效性,帮助我们快速准确地完成复杂的统计计算。
除了基本的计算功能,一些高级的科学计算器还提供了统计分析功能,可以直接输入数据集,然后选择计算标准差等统计量,从而更加方便地进行统计分析工作。
这些功能的存在大大简化了统计分析的流程,提高了工作效率。
总之,科学计算器在计算标准差等统计量时具有重要的作用,可以帮助我们快速准确地完成复杂的统计计算,提高工作效率。

用计算器怎么算标准差标准差是统计学中常用的一种测量数据分散程度的方法,它可以帮助我们了解数据的离散程度,对于数据分布的形状和离散程度有很强的描述能力。
在实际应用中,我们经常需要用计算器来求解标准差,下面我将介绍如何使用计算器来计算标准差。
首先,我们需要明确标准差的计算公式:标准差 = sqrt(Σ(xi μ)² / n)。
其中,Σ表示求和,xi表示每个数据点,μ表示平均值,n表示数据点的个数。
接下来,我们以一个简单的数据集为例来演示如何使用计算器来计算标准差。
假设我们有以下数据集,{2, 4, 6, 8, 10}。
第一步,我们需要计算这组数据的平均值。
使用计算器,依次输入2+4+6+8+10,然后除以5(数据点的个数),得到平均值为6。
第二步,我们需要计算每个数据点与平均值的差的平方。
依次计算(2-6)²,(4-6)²,(6-6)²,(8-6)²,(10-6)²,得到的结果分别为16,4,0,4,16。
第三步,将上一步计算的结果相加。
使用计算器,依次输入16+4+0+4+16,得到40。
第四步,将上一步计算的结果除以数据点的个数,然后求平方根。
使用计算器,依次输入40/5,得到8,然后求平方根,得到标准差为2.828。
通过以上步骤,我们成功使用计算器计算出了这组数据的标准差。
这个例子展示了如何利用计算器来进行标准差的计算,实际应用中,我们也可以通过计算器快速、准确地求解更复杂的数据集的标准差。
除了手动计算外,现代科技也提供了许多软件和工具来帮助我们计算标准差,比如Excel、Python等。
这些工具不仅可以提高计算效率,还可以减少人为错误的发生,是我们工作和学习中的好帮手。
总之,标准差是一种重要的统计量,它可以帮助我们了解数据的离散程度。
使用计算器可以快速、准确地计算标准差,对于数据分析和统计研究有着重要的意义。
希望本文的介绍能够帮助大家更好地理解和应用标准差的计算方法。

科学计算器计算标准差在统计学中,标准差是一种用来衡量数据离散程度的统计量。
它可以帮助我们了解数据的分布情况,以及数据点与平均值之间的差异程度。
在科学计算中,计算标准差是非常常见的操作,因此我们需要了解如何使用科学计算器来计算标准差。
首先,让我们来看一下标准差的计算公式:标准差= sqrt(Σ(xi μ)² / N)。
其中,Σ代表求和,xi代表每个数据点,μ代表数据的平均值,N代表数据点的个数。
这个公式看起来可能有些复杂,但是使用科学计算器来进行计算会变得非常简单。
现在,让我们来通过一个例子来演示如何使用科学计算器来计算标准差。
假设我们有一组数据,3, 5, 7, 9, 11。
首先,我们需要计算这组数据的平均值。
使用科学计算器,我们可以直接输入这组数据,然后选择“平均值”函数,计算得到平均值为7。
接下来,我们需要计算每个数据点与平均值之间的差异,并将差异的平方进行累加。
这个过程可以通过科学计算器的“平方”和“累加”功能来完成。
将每个数据点与平均值的差异进行平方,然后累加起来,得到的结果为20。
最后,我们需要将累加的结果除以数据点的个数,然后再对结果取平方根,即可得到标准差。
在科学计算器中,我们可以依次输入累加的结果、数据点的个数,然后选择“除以”和“平方根”功能,最终得到的结果为2.236。
通过这个简单的例子,我们可以看到使用科学计算器来计算标准差是非常方便和高效的。
无论是处理小规模的数据还是大规模的数据,科学计算器都能够帮助我们快速准确地完成计算。
因此,掌握科学计算器的使用方法对于进行科学计算和统计分析是非常重要的。
总之,通过本文的介绍,我们了解了标准差的计算公式以及如何使用科学计算器来计算标准差。
希望这些内容能够帮助您更好地理解标准差的概念,并掌握科学计算器的使用方法。
在实际应用中,我们可以根据具体的情况选择合适的科学计算器,以便更高效地进行数据分析和统计计算。


科学计算器计算标准差标准差是一种用来衡量数据分散程度的统计量,它可以帮助我们了解数据的离散程度和稳定性。
在科学计算中,我们经常需要计算标准差来评估数据的变化情况,以便更好地分析和理解数据。
本文将介绍如何使用科学计算器来计算标准差,帮助大家更好地掌握这一重要的统计概念。
首先,我们需要明确标准差的计算公式。
标准差的计算公式为,σ=√(∑(x-μ)²/n),其中σ表示标准差,∑表示求和,x表示每个数据点,μ表示数据的均值,n表示数据的个数。
这个公式看起来可能有些复杂,但是使用科学计算器可以轻松地进行计算。
接下来,我们将通过一个示例来演示如何使用科学计算器来计算标准差。
假设我们有一组数据,5, 7, 8, 10, 12。
我们首先需要计算这组数据的均值。
均值的计算公式为,μ=∑x/n,其中∑表示求和,x表示每个数据点,n表示数据的个数。
将这组数据代入公式中,我们可以得到均值,(5+7+8+10+12)/5=8.4。
接下来,我们需要计算每个数据点与均值的差值的平方,并将这些平方差值相加。
这一步可以使用科学计算器的求和功能来完成。
将每个数据点与均值的差值的平方相加,得到结果为,(5-8.4)²+(7-8.4)²+(8-8.4)²+(10-8.4)²+(12-8.4)²=34.8。
最后,我们需要将这个结果除以数据的个数,然后取平方根,即可得到标准差的值。
使用科学计算器的除法和平方根功能,我们可以得到标准差的值,σ=√(34.8/5)≈2.64。
通过这个示例,我们可以看到,使用科学计算器可以非常方便地计算标准差,无需手动计算,大大提高了计算的准确性和效率。
在实际的科学研究和工程计算中,我们经常需要对数据进行分析和处理,而标准差作为一种重要的统计量,可以帮助我们更好地理解数据的特性,从而做出更准确的判断和决策。
总之,科学计算器是我们在计算标准差时的得力工具,它可以帮助我们快速、准确地完成复杂的计算,提高工作效率。

科学计算器计算标准差标准差是统计学中常用的一种衡量数据离散程度的指标,它能够帮助我们了解数据的分布情况,对于科学计算器来说,计算标准差是非常常见的需求之一。
接下来,我们将介绍如何使用科学计算器来计算标准差。
首先,我们需要明确标准差的计算公式。
标准差的计算公式如下:\[ \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i\mu)^2} \]其中,\[ \sigma \] 代表标准差,\[ N \] 代表样本数量,\[ x_i \] 代表每个样本数据,\[ \mu \] 代表样本数据的平均值。
接下来,我们来演示如何使用科学计算器来计算标准差。
假设我们有一组样本数据,\[ 3, 5, 7, 9, 11 \],我们将使用科学计算器来计算这组数据的标准差。
首先,我们需要计算这组数据的平均值。
将这组数据相加并除以样本数量,即可得到平均值:\[ \mu = \frac{3+5+7+9+11}{5} = \frac{35}{5} = 7 \]接下来,我们需要计算每个样本数据与平均值的差的平方,并将其相加:\[ (3-7)^2 + (5-7)^2 + (7-7)^2 + (9-7)^2 + (11-7)^2 =16 + 4 + 0 + 4 + 16 = 40 \]然后,将上述结果除以样本数量,并取平方根,即可得到标准差:\[ \sigma = \sqrt{\frac{40}{5}} = \sqrt{8} = 2.83 \] 因此,这组数据的标准差为2.83。
通过上述演示,我们可以看到,使用科学计算器来计算标准差并不复杂。
只需要依次输入数据,按照公式进行计算,即可得到标准差的结果。
在实际应用中,我们可以根据需要,灵活运用科学计算器来计算不同数据集的标准差,从而更好地分析数据的分布情况。
总结一下,本文介绍了如何使用科学计算器来计算标准差,通过演示了解了标准差的计算过程,并且强调了科学计算器在数据分析中的重要性。

0、键位说明一、进入统计模式要开始统计计算是按以下顺序操作:mode/clR键2键进入统计计算模式,即进入SD模式。
二、计算实例计算结果按键我们通常所说的标准差就是:样本标准偏差(如下)三、数据清除要进行其他新的计算是必须按以下顺序操作:shift键mode/clR键2键=键AC键清除存储数据下面资料为赠送的地产广告语不需要的下载后可以编辑删除就可以,谢谢选择,祝您工作顺利,生活愉快!地产广告语1、让世界向往的故乡2、某沿河楼盘:生活,在水岸停泊3、一江春水一种人生4、某钱塘江边楼盘:面对潮流经典依旧5、海景房:站在家里,海是美景;站在海上,家是美景6、以山水为卖点的楼盘:山水是真正的不动产7、某城区的山腰上的楼盘:凌驾尊贵俯瞰繁华8、某地势较高的楼盘:高人,只住有高度的房子9、某学区房:不要让孩子输在起跑线上10、尾盘:最后,最珍贵11、回家就是度假的生活12、生命就该浪费在美好的事情上我们造城——2、我的工作就是享受生活——3、我家的客厅,就是我的生活名片——4、在自己的阳台看上海的未来——5、公园不在我家里我家住在公园里——6、这里的花园没有四季——7、***,装饰城市的风景——8、***,我把天空搬回家——9、房在林中,人在树下——10、生活,就是居住在别人的爱慕里——11、到〖星河湾〗看看好房子的标准——12、好生活在〖珠江〗——13、爱家的男人住〖百合〗城市岸泊:城市的岸泊,生活的小镇生活之美不缺少,在于发现情趣不在于奢华,在于精彩生活有了美感才值得思考……玫瑰庄园:山地生态,健康人生卓越地段,超大社区一种完整且完善的环境,像原生一样和谐原生景象自然天成人本理念精品建筑知名物业智能安防诚信为本实力铸造比华利山庄:海岸生活——引领世界的生活方式海岸生活——22公里的奢华海岸生活——高尚人生的序曲海岸生活——人与自然的融合苹果二十二院街:人文自然现代铺的蔓伸荣和山水美地:让世界向往的故乡香港时代:时代精英开拓未来领衔建筑,彰显尊贵绿地崴廉公寓:金桥40万平方米德国音乐艺术生活汇都国际:昆明都心,城市引擎财富之都风情之都梦幻之都文化之都商贸之都西部首座巨型商业之城颠峰商圈的原动力,缔造西部财富新领地新江湾城:绿色生态港国际智慧城新江湾城,一座承载上海新梦想的城区上海城投,全心以赴建设知识型,生态型花园城区风和日丽:入住准现楼,升值在望湾区大户,空中花园大格局下的西海岸市中心:市中心少数人的专属颠峰珍贵市中心的稀世名宅正中心城市颠峰领地颠峰勾勒稀世名宅繁华不落幕的居家风景地利皇者尽得先机稀世经典180席阳光国际公寓:阳光金桥来自纽约的生活蓝本钟宅湾:海峡西岸生态人居休闲商务区汇聚国际财富与人居梦想的绝版宝地二十一世纪是城市的世纪,二十一世纪也是海洋的世纪谁控制了海洋,谁就控制了一切站在蓝色海岸的前沿,开启一个新的地产时代东南门户海湾之心海峡西岸生态人居休闲商务区让所有财富的目光聚集钟宅湾,这里每一天都在创造历史上海A座(科维大厦):创富人生的黄金眼掘金上海!创富人生!远东大厦:花小公司的钱,做大公司的事未来城:无可挑战的优势无可限量的空间绿地集团:居住问题的答疑者,舒适生活的提案人茶马驿栈:精明置业时机享受附加值财富最大化雪山下的世外桃源茶马古道上千年清泉之乡金地格林春岸:城市精英的梦想家园繁华与宁静共存,阔绰身份不显自露建筑覆盖率仅20%,令视野更为广阔占据最佳景观位置,用高度提炼生活完美演绎自然精髓,谱写古城新篇章创新房型推陈出新,阔气空间彰显不凡365天的贴身护卫,阔度管理以您为尊金地格林小城:心没有界限,身没有界限春光永驻童话之城我的家,我的天下东渡国际:梦想建筑,建筑梦想齐鲁置业:传承经典,创新生活比天空更宽广的是人的思想创新远见生活嘉德中央公园:一群绝不妥协的居住理想家完成一座改变你对住宅想象的超越作品极至的资源整合丰富住家的生活内涵苛求的建造细节提升住家的生活品质地段优势,就是永恒价值优势设计优势,就是生活质量优势景观优势,就是生命健康优势管理优势,就是生活品味优势空中华尔兹:自然而来的气质,华尔兹的生活等级享受,没有不可逾越的极限所谓完美的习惯,是舒适空间的心情定格!临江花园:经典生活品质风景中的舞台美林别墅:源欧美经典纯自然空间住原味别墅赏园林艺术淡雅怡景温馨自然钱江时代:核心时代,核心生活核心位置创意空间优雅规划人文景观财富未来城市精神,自然风景,渗透私人空间泰达时尚广场:是球场更是剧场城市经济活力源时尚天津水舞中国未来都会休闲之居创意时尚天天嘉年华健康快乐新境界商旅新天地缔造好生意城市运营战略联盟,参与协作,多方共赢华龙碧水豪园:浪漫一次,相守一生东方莱茵:品鉴品位宜家宜人建筑一道贵族色彩品鉴一方美学空间品位一份怡然自得荡漾一股生命活力坐拥一处旺地静宅体会一种尊崇感受常青花园(新康苑):新康苑生活感受凌驾常规大非凡生活领域成功人士的生活礼遇拥有与自己身份地位相等的花园社区在属于自己的宴会餐厅里会宾邀朋只与自己品味爱好相同的成功人士为邻孩子的起步就与优越同步酒店式物管礼遇拥有[一屋两公园前后是氧吧]的美极环境水木清华:住在你心里福星惠誉(金色华府):金色华府,市府街才智名门——释放生命的金色魅力真正了解一个人,要看他的朋友,看他的对手。


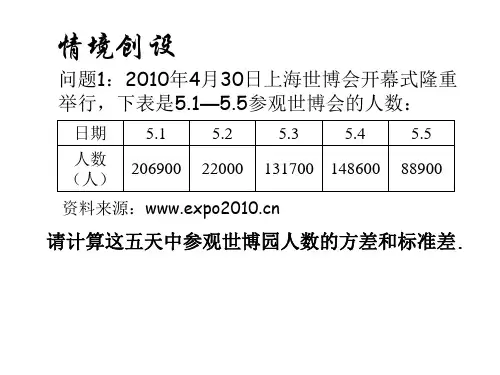
典例解析:用计算器求方差和标准差【目标导航】1.熟练掌握利用计算器求一组数据的标准差和方差.2.进一步体会计算器进行计算的优越性.【问题探究】知识点1。
体会用笔算的方法计算标准差例1.2010年4月30日上海世博会隆重举行,下表是5。
1-5.5参观世博会的人数:解析:用笔算的方法计算标准差比较繁琐,如果能够利用计算器,就会大大提高效率。
那么我们就可以借用计算器求标准差.知识点2.如何用计算器求平均数、方差和标准差例2.为了从小明和小丽两人中选拔一个参加学校军训射击比赛,现对他们的射击成绩进行了测试,10次打靶命中的环数如下:小明:10,7,8,8,8,8,8,8,9,6;小丽: 8,8,8,8,5,8,8,9,9,9计算小明和小丽命中环数的方差和标准差,哪一个人的射击成绩比较稳定?解析: (1)按开机键(2)(6个8既可以仿照P。
50方法2单个输入,也可以的方式输入)(平均数);(4(方差);(5(标准差)。
即小明射击的平均数=8,方差s2=1,标准差s=1。
(6)依次按键(7)(平均数);(。
2(方差);(。
095445115(标准差)。
即小丽射击的平均数=8,方差s2=1.2,标准差s=1。
095445115这两组数据的平均数虽然相同,但是第二组数据的方差约为1。
2,第一组数据的方差为1,因为1.2>1,所以第二组数据的离散程度较大,小明射击成绩比小丽稳定。
尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be someunsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
科学计算器算标准差标准差是一种用来衡量数据分散程度的统计量,它能够告诉我们数据集中的值与平均值之间的差异程度。
在科学计算中,我们经常需要计算标准差来评估数据的稳定性和可靠性。
本文将介绍如何使用科学计算器来计算标准差,帮助大家更好地理解和运用这一重要的统计量。
首先,我们需要明确标准差的计算公式。
标准差的计算公式如下:\[ \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i\bar{x})^2} \]其中,σ代表标准差,N代表数据集的样本数量,xi代表第i 个数据点,而 \(\bar{x}\) 代表数据集的平均值。
接下来,我们将以一个具体的数据集为例,来演示如何使用科学计算器来计算标准差。
假设我们有以下数据集,{3, 6, 9, 12, 15}。
首先,我们需要计算这组数据的平均值。
平均值的计算公式如下:\[ \bar{x} = \frac{3+6+9+12+15}{5} = \frac{45}{5} = 9 \]得到平均值为9。
接下来,我们需要计算每个数据点与平均值之间的差异,并将差异的平方进行累加。
计算过程如下:\[ (3-9)^2 + (6-9)^2 + (9-9)^2 + (12-9)^2 + (15-9)^2 \]\[ = 36 + 9 + 0 + 9 + 36 \]\[ = 90 \]然后,我们需要将累加的结果除以样本数量,并取平方根,即可得到标准差:\[ \sigma = \sqrt{\frac{90}{5}} = \sqrt{18} \]\[ \sigma \approx 4.24 \]因此,这组数据的标准差约为4.24。
在实际的科学计算中,我们可能会遇到更复杂的数据集和更繁琐的计算过程。
这时,科学计算器就显得尤为重要了。
现代科学计算器通常具有复杂的统计计算功能,可以帮助我们快速、准确地计算标准差等统计量。
在使用科学计算器进行标准差计算时,我们只需要依次输入数据点,按下相应的统计计算按钮,即可得到标准差的计算结果,极大地提高了我们的工作效率。
卡西欧计算器计算标准差标准差是统计学中常用的一种测量数据离散程度的指标,它能够帮助我们了解数据的分布情况,对于数据分析和比较具有重要意义。
在实际的工作和学习中,我们经常需要使用计算器来进行标准差的计算。
而卡西欧计算器作为一款常用的科学计算器,可以很方便地进行标准差的计算。
下面我们将介绍如何使用卡西欧计算器来计算标准差。
首先,我们需要明确标准差的计算公式:标准差 = 根号下( (∑(X-μ)²) / N )。
其中,X代表每个数据点,μ代表数据的平均值,N代表数据的个数。
接下来,我们以一个简单的数据集为例来进行计算。
假设我们有一个数据集,3, 5, 7, 9, 11。
我们首先需要计算这组数据的平均值。
在卡西欧计算器上,我们可以按照以下步骤进行计算:1. 输入数据集的每个数据点,3 → 5 → 7 → 9 → 11。
2. 按下“=”键,计算出数据的总和,35。
3. 再按下“n”键,输入数据的个数,5。
4. 按下“=”键,计算出数据的平均值,7。
得到数据的平均值为7。
接下来,我们需要计算每个数据点与平均值的差的平方,并将它们相加。
在卡西欧计算器上,可以按照以下步骤进行计算:1. 输入第一个数据点与平均值的差的平方,(3-7)²。
2. 按下“M+”键,将结果存储到内存中。
3. 依次输入剩下的数据点与平均值的差的平方,并按下“M+”键,将结果累加到内存中。
4. 最后按下“MR”键,将内存中的结果取出,得到数据点与平均值的差的平方的总和,32。
得到数据点与平均值的差的平方的总和为32。
最后,我们需要将这个总和除以数据的个数,然后取平方根,即可得到标准差。
在卡西欧计算器上,可以按照以下步骤进行计算:1. 输入数据点与平均值的差的平方的总和,32。
2. 按下“n-1”键,将数据的个数减1,4。
3. 按下“=”键,计算出方差,8。
4. 最后按下“√”键,得到标准差,2.83。
通过以上步骤,我们成功地使用卡西欧计算器计算出了这组数据的标准差,结果为2.83。