TOPKAPI模型的应用及与新安江模型的比较研究
- 格式:pdf
- 大小:355.86 KB
- 文档页数:5


新安江模型与总径流线性响应模型的应用对比研究
蔡素芳;梅亚东;陈洋波
【期刊名称】《中国农村水利水电》
【年(卷),期】2009()9
【摘要】建立了三水源新安江模型和总径流线性响应模型,并应用于广东省的4个小型流域。
根据同一流域对不同洪水等级具有不同调蓄能力的特点,提出了分类法率定新安江模型参数;从5个精度度量标准对2类模型的应用效果进行了较深入的对比分析。
结果表明,分类法率定新安江模型参数能够得到更合理的参数,有助于提高预报精度,且新安江模型在研究流域的适用性时优于总径流线性响应模型。
【总页数】4页(P79-81)
【关键词】新安江模型;总径流线性响应模型;分类法
【作者】蔡素芳;梅亚东;陈洋波
【作者单位】武汉大学水资源与水电工程科学国家重点实验室;中山大学水资源与环境系
【正文语种】中文
【中图分类】TV124
【相关文献】
1.多输入单输出总径流线性响应模型在黄河玛曲站的应用 [J], 喇承龙;孔令峰;史彦斌
2.总径流线性响应模型与线性扰动模型 [J], 王厥谋;文康;梁康辰
3.总径流线性响应模型与线性扰动模型 [J], 文康;梁庚辰
4.总径流非线性响应模型的应用研究 [J], 王继伟;王真荣
5.VIC模型与新安江模型径流模拟对比研究 [J], 张兰影;庞博;徐宗学;何睿
因版权原因,仅展示原文概要,查看原文内容请购买。

基于GIS的分布式托普卡匹水文模型在洪水预报中的应用刘志雨
【期刊名称】《水利学报》
【年(卷),期】2004(000)005
【摘要】本文对托普卡匹(TOPKAPI)水文模型进行了改进,增加了植物截留、降水下渗、土壤水深层渗漏、地下径流等计算模块,并对壤中流计算模块作了相应的调整,将TOPKAPI模型改进成一个较完整的分布式流域水文模型.该改进后的TOPKAPI模型应用于面积约为1万km2的息县以上淮河流域1998年、2002年和2003年汛期洪水的模拟,模型确定性系数均在0.84以上,模拟成果令人满意.该模型可应用于洪水预报、土地利用和环境影响评价、洪水极值分析、无资料地区水文模拟计算等.
【总页数】6页(P70-75)
【作者】刘志雨
【作者单位】水利部水文局,北京,100053
【正文语种】中文
【中图分类】TV124
【相关文献】
1.MIKE SHE 分布式水文模型在广东省中小河流洪水预报中的应用展望 [J], 陈国轩;梁海涛;林蓉璇
2.分布式水文模型在半干旱地区洪水预报中的应用 [J], 董红
3.分布式水文模型在洪水预报中的应用研究综述 [J], 梁钟元;贾仰文;李开杰;牛存稳;王浩
4.基于GIS的DEM和分布式水文模型的应用比较 [J], 李致家;张珂;姚成
5.分布式水文模型在淮河洪泽湖以上流域洪水预报中的应用 [J], 宋玉;李致家;杨涛因版权原因,仅展示原文概要,查看原文内容请购买。

半湿润半干旱地区TOPKAPI模型的洪水模拟
刘玉环;李致家;刘志雨;张艳玲
【期刊名称】《水力发电》
【年(卷),期】2016(042)001
【摘要】为了探索分布式水文模型在半干旱半湿润地区的应用效果,选用基于物理的分布式水文模型TOPKAPI,研究其在国内中小流域的适用性.选取半湿润地区马渡王流域、板桥流域及半干旱地区志丹流域作为典型研究流域,分析2000年~2010年的8场洪水模拟精度等特征值.结果表明,模型在半湿润地区取得较好的应用效果,验证了模型的合理性和适用性;而在半干旱地区模拟精度较差,适用性不好,但可用于中小河流洪水模拟,基本满足流域洪水预警的应用要求.
【总页数】5页(P18-22)
【作者】刘玉环;李致家;刘志雨;张艳玲
【作者单位】河海大学水文水资源学院,江苏南京210098;河海大学水文水资源学院,江苏南京210098;水利部水文局,北京100053;陕西省水文水资源勘测局,陕西西安710068
【正文语种】中文
【中图分类】TV122.5;O141.4
【相关文献】
1.半干旱半湿润地区洪水预报模型适用性研究 [J], 刘郁;赵兰兰;马丁
2.基于TOPKAPI模型的湿润流域洪水模拟 [J], 徐杰; 李致家; 马亚楠; 胡友兵
3.基于TOPKAPI模型的湿润流域洪水模拟 [J], 徐杰;李致家;马亚楠;胡友兵
4.洪水预报智能模型在中国半干旱半湿润区的应用对比 [J], 张珂;牛杰帆;李曦;晁丽君
5.LSPC模型在半干旱半湿润地区多年连续日径流模拟中的应用 [J], 余翔;黄津辉;林超
因版权原因,仅展示原文概要,查看原文内容请购买。

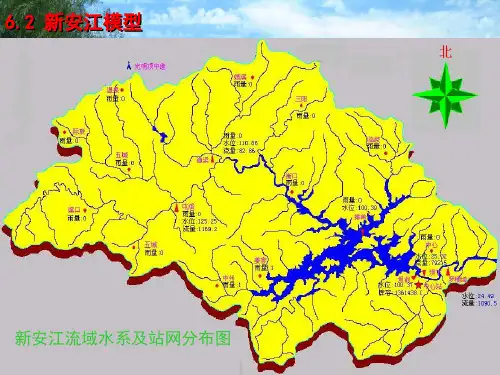
2新安江流域水文模型60年代初,河海大学(原华东水利学院)水文系赵人俊等开始研究蓄满产流模型,配合必然的汇流计算,将模型应用于水文预报和水文设计。
1973年,他们在对新安江水库做入库流量预报的工作中,把他们的体会归纳成一个完整的降雨径流流域模型——新安江模型。
模型可用于湿润地域和半湿润地域的湿润季节径流模拟和计算。
最初的新安江模型为两水源模型,只能模拟地表径流和地下径流。
80年代初期,模型研制者将萨克拉门托模型与水箱模型中,用线性水库函数划分水源的概念引入新安江模型,提出了三水源新安江模型,模型能够模拟地面径流、壤中流、地下径流。
1984至1986年,又提出了四水源新安江模型,能够模拟地面径流、壤中流、快速地下径流和慢速地下径流。
三水源新安江模型一样应用成效较好,但模拟地下水丰硕地域的日径流进程精度不够理想。
在新安江三模型中增加慢速地下水结构就成为四水源新安江模型。
当流域面积较小时,新安江模型采纳集总模型,当面积较大时,采纳分块模型。
分块模型把流域分成许多块单元流域,对每一个单元流域做产、汇计算,取得单元流域的出口流量进程。
再进行出口以下的河道洪水演算,求得流域出口的流量进程。
把每一个单元流域的出流进程相加,就求得了流域出口的总出流进程。
划分单元流域的要紧目的是处置降雨散布的不均匀性,因此单元流域应当大小适当,使得每块面积上的降雨散布比较均匀。
并有一定数量的雨量站。
第二尽可能使单元流域与自然流域相一致,以便于分析与处置问题,并便于利用已有的小流域水文资料。
若是流域内有大中型水库,那么水库以上的集水面积即应作为一个单元流域。
因为各单元流域的产汇、流计算方式大体相同,以下只讨论一个单元流域的情形。
新安江模型包括4个计算环节:蒸散发计算;流域产流计算;径流划分;汇流计算。
4个计算环节别离概化了流域降雨径流的要紧产、汇流物理进程。
流域蒸散发计算各类水源的蒸散发计算模型都可采纳两层蒸发模型或两层蒸发模型,一样依如实际情形选用。


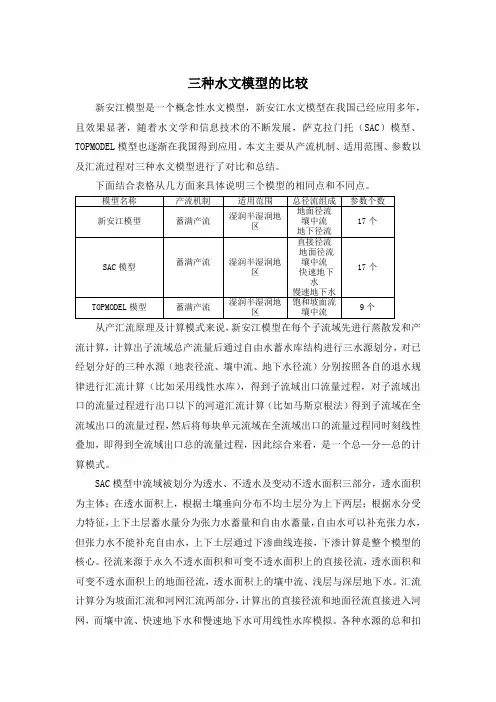
三种水文模型的比较新安江模型是一个概念性水文模型,新安江水文模型在我国已经应用多年,且效果显著,随着水文学和信息技术的不断发展,萨克拉门托(SAC)模型、TOPMODEL模型也逐渐在我国得到应用。
本文主要从产流机制、适用范围、参数以及汇流过程对三种水文模型进行了对比和总结。
下面结合表格从几方面来具体说明三个模型的相同点和不同点。
从产汇流原理及计算模式来说,新安江模型在每个子流域先进行蒸散发和产流计算,计算出子流域总产流量后通过自由水蓄水库结构进行三水源划分,对已经划分好的三种水源(地表径流、壤中流、地下水径流)分别按照各自的退水规律进行汇流计算(比如采用线性水库),得到子流域出口流量过程,对子流域出口的流量过程进行出口以下的河道汇流计算(比如马斯京根法)得到子流域在全流域出口的流量过程,然后将每块单元流域在全流域出口的流量过程同时刻线性叠加,即得到全流域出口总的流量过程,因此综合来看,是一个总—分—总的计算模式。
SAC模型中流域被划分为透水、不透水及变动不透水面积三部分,透水面积为主体;在透水面积上,根据土壤垂向分布不均土层分为上下两层;根据水分受力特征,上下土层蓄水量分为张力水蓄量和自由水蓄量,自由水可以补充张力水,但张力水不能补充自由水,上下土层通过下渗曲线连接,下渗计算是整个模型的核心。
径流来源于永久不透水面积和可变不透水面积上的直接径流,透水面积和可变不透水面积上的地面径流,透水面积上的壤中流、浅层与深层地下水。
汇流计算分为坡面汇流和河网汇流两部分,计算出的直接径流和地面径流直接进入河网,而壤中流、快速地下水和慢速地下水可用线性水库模拟。
各种水源的总和扣除时段内的水面蒸发4E ,即得河网总入流。
河网汇流一般采用无因次单位线。
总的来看是一个分—总的过程。
新安江模型在每个子流域先进行蒸散发和产流计算,计算出子流域总产流量后通过自由水蓄水库结构进行三水源划分,对已经划分好的三种水源(地表径流、壤中流、地下水径流)分别按照各自的退水规律进行汇流计算(比如采用线性水库),得到子流域出口流量过程,对子流域出口的流量过程进行出口以下的河道汇流计算(比如马斯京根法)得到子流域在全流域出口的流量过程,然后将每块单元流域在全流域出口的流量过程同时刻线性叠加,即得到全流域出口总的流量过程,因此综合来看,是一个总—分—总的计算模式。

TOPMODEL模型与NAM模型在中小流域的比较研究周景舒;张行南;夏达忠
【期刊名称】《重庆理工大学学报(自然科学版)》
【年(卷),期】2017(031)002
【摘要】选取NAM模型代表集总式概念模型,TOPMODEL模型代表半分布式模型,从模型基本原理模型结构、输入、参数率定以及模拟结果等方面对两个模型进行比较.结果表明:在梓潼流域上,TOPMODEL和NAM模拟的径流深相对误差均在20%以下,预报项目按照确定性系数达到了乙级精度,且两个模型相差不大,故TOPMODEL及NAM模型均能适用于梓潼流域.
【总页数】7页(P67-72,101)
【作者】周景舒;张行南;夏达忠
【作者单位】河海大学水文水资源学院,南京210098;河海大学水文水资源学院,南京210098;河海大学水资源高效利用与工程安全国家工程研究中心,南京210098;河海大学水文水资源学院,南京210098;河海大学水资源高效利用与工程安全国家工程研究中心,南京210098
【正文语种】中文
【中图分类】TV21
【相关文献】
1.新安江模型与DHSVM在中小流域的比较研究 [J], 潘宇微;张行南;夏达忠;石超
2.TOPMODEL模型与NAM模型在中小流域的比较研究 [J], 周景舒;张行南;夏达
忠;
3.GTOPMODEL模型与TOPMODEL模型比较 [J], 张珂;李致家;包红军
4.BP神经网络与NAM模型在西营流域的比较研究 [J], 王万祯;王超;孙嘉辉;宋培兵
5.基于TOPMODEL的分布式水文模型在中小流域的应用研究 [J], 李振亚;黄国新;肖凤林;胡玲玲;王淑梅;王娇
因版权原因,仅展示原文概要,查看原文内容请购买。

三个水文模型在英那河史家堡流域的应用作者:蒋燕解河海李显鸿来源:《硅谷》2010年第16期摘要: 英那河地处北方半湿润地区,其降水的显著特点是在时空上分布极不均匀。
由于降水分布不均,该地区洪涝及干旱灾害很严重。
因此研究该地区的洪水预报对该地区的防汛抗旱工作、水资源的合理利用与保护、水利工程建设与管理及工农业生产与人民生活等方面有着重要的意义。
研究选用新安江模型、API模型和TOPMODEL对英那河上英那河史家堡流域的产汇流规律及洪水预报进行研究应用,并对三个模型在研究区域应用的结果进行比较分析。
关键词: 新安江模型;API模型;TOPMODEL;半湿润地区;洪水模拟中图分类号:TV21文献标识码:A文章编号:1671-7597(2010)0820126-01洪水预报技术从经验性阶段走向近代科学阶段开始在20世纪30年代,经验方法虽然操作简单,但缺少数理根据,逻辑不够准确,随着计算机技术的发展及系统理论在洪水预报中的应用,洪水预报技术开始得到了迅速发展,便随之产生了流域降雨径流模型的概念。
本研究选用三水源新安江模型、前期雨量指数模型(API模型)和TOPMODEL对英那河上英那河史家堡流域的产汇流规律及洪水预报方法进行了研究。
研究目标是试图通过不同的模型在英那河水库流域模拟情况的比较分析,从而找出它们之间的差异,分析研究哪种水文模型比较适用于该流域。
1 模型介绍1.1 新安江模型新安江模型是一个概念性模型。
计算主要分为蒸发、产流、分水源和汇流几个计算部分。
其中蒸散发分为三层:上层、下层和深层;产流采用蓄满产流概念;水源分为地表径流、壤中径流和地下径流三种水源;汇流分为坡地、河网汇流两个阶段。
1.2 API模型API模型又称前期雨量指数[3](antecedent precipitation index)模型,由五变数降雨径流相关图发展形成,其实用的表达形式是传统的降雨径流相关图,所以又称降雨径流经验相关法。
四种水文模型的比较四种水文模型的比较摘要:水文模型是用数学的语言对现实水文过程进行模拟和预报,在进行水文规律的探讨和解决水文及生产实际问题中起着重要作用。
本文分别介绍了新安江模型、萨克拉门托(SAC)模型、SWAT模型以及TOPMODEL模型,并对这四种水文模型的蒸发计算、产流机制、汇流计算、适用流域、参数以及模型特点等不同方面进行了比较分析。
并结合对着4种模型之间的比较,作出了总结分析和展望。
关键词:新安江模型;SAC模型;SWAT模型; TOPMODEL模型;模型比较引言流域水文模型在进行水文规律研究和解决生产实际问题中起着重要的作用。
新安江模型是一个概念性水文模型,1973年由赵人俊教授领导的研究组在编制新安江预报方案时,汇集了当时在产汇流理论方面的成果,并结合大流域洪水预报的特点,设计出的我国第一个完整的流域水文模型,至今仍在我国湿润和半湿润地区的洪水预报中得到广泛应用;萨克拉门托水文模型,简称SAC 模型,是R.C.伯纳什(Burnash)和R.L.费雷尔(Ferral )以及RA麦圭儿(Mcguire )于20世纪60年代末至70年代初研制的,是一个连续模拟模型,模型研制完成时间相对较晚,其功能较为完善,兼有蓄满产流和超渗产流,广泛应用于美国水文预报中;SWAT模型是美国农业部农业研究中心研制开发的用于模拟预测土地利用及土地管理方式对流域水量、水质过程影响的分布式流域水文模型;TOPMODEL为基于地形的半分布式流域水文模型,于1979年由Beven和Kirkby提出,其主要特征是将数字高程模型(DEM )的广泛适用性与水文模型及地理信息系统(GIS)相结合,基于DEM数据推求地形指数,并以此来反映下垫面的空间变化对流域水文循环过程的影响,描述水流趋势。
本文对这四中水文模型从蒸发计算、产汇流计算、适用流域以及参数等方面进行分析比较,并得出结论。
1模型简介1.1新安江模型新安江模型是赵人俊等在对新安江水库做入库流量预报工作中,归纳成的一个完整的降雨径流模型。
三种水文模型的比较新安江模型是一个概念性水文模型,新安江水文模型在我国已经应用多年,且效果显著,随着水文学和信息技术的不断发展,萨克拉门托(SAC)模型、TOPMODEL模型也逐渐在我国得到应用。
本文主要从产流机制、适用范围、参数以及汇流过程对三种水文模型进行了对比和总结。
下面结合表格从几方面来具体说明三个模型的相同点和不同点。
从产汇流原理及计算模式来说,新安江模型在每个子流域先进行蒸散发和产流计算,计算出子流域总产流量后通过自由水蓄水库结构进行三水源划分,对已经划分好的三种水源(地表径流、壤中流、地下水径流)分别按照各自的退水规律进行汇流计算(比如采用线性水库),得到子流域出口流量过程,对子流域出口的流量过程进行出口以下的河道汇流计算(比如马斯京根法)得到子流域在全流域出口的流量过程,然后将每块单元流域在全流域出口的流量过程同时刻线性叠加,即得到全流域出口总的流量过程,因此综合来看,是一个总—分—总的计算模式。
SAC模型中流域被划分为透水、不透水及变动不透水面积三部分,透水面积为主体;在透水面积上,根据土壤垂向分布不均土层分为上下两层;根据水分受力特征,上下土层蓄水量分为张力水蓄量和自由水蓄量,自由水可以补充张力水,但张力水不能补充自由水,上下土层通过下渗曲线连接,下渗计算是整个模型的核心。
径流来源于永久不透水面积和可变不透水面积上的直接径流,透水面积和可变不透水面积上的地面径流,透水面积上的壤中流、浅层与深层地下水。
汇流计算分为坡面汇流和河网汇流两部分,计算出的直接径流和地面径流直接进入河网,而壤中流、快速地下水和慢速地下水可用线性水库模拟。
各种水源的总和扣除时段内的水面蒸发4E ,即得河网总入流。
河网汇流一般采用无因次单位线。
总的来看是一个分—总的过程。
新安江模型在每个子流域先进行蒸散发和产流计算,计算出子流域总产流量后通过自由水蓄水库结构进行三水源划分,对已经划分好的三种水源(地表径流、壤中流、地下水径流)分别按照各自的退水规律进行汇流计算(比如采用线性水库),得到子流域出口流量过程,对子流域出口的流量过程进行出口以下的河道汇流计算(比如马斯京根法)得到子流域在全流域出口的流量过程,然后将每块单元流域在全流域出口的流量过程同时刻线性叠加,即得到全流域出口总的流量过程,因此综合来看,是一个总—分—总的计算模式。
四种水文模型的比较摘要:水文模型是用数学的语言对现实水文过程进行模拟和预报,在进行水文规律的探讨和解决水文及生产实际问题中起着重要作用。
本文分别介绍了新安江模型、萨克拉门托(SAC)模型、SWAT模型以及TOPMODEL模型,并对这四种水文模型的蒸发计算、产流机制、汇流计算、适用流域、参数以及模型特点等不同方面进行了比较分析。
并结合对着4种模型之间的比较,作出了总结分析和展望。
关键词:新安江模型;SAC模型;SWA T模型;TOPMODEL模型;模型比较引言流域水文模型在进行水文规律研究和解决生产实际问题中起着重要的作用。
新安江模型是一个概念性水文模型,1973年由赵人俊教授领导的研究组在编制新安江预报方案时,汇集了当时在产汇流理论方面的成果,并结合大流域洪水预报的特点,设计出的我国第一个完整的流域水文模型,至今仍在我国湿润和半湿润地区的洪水预报中得到广泛应用;萨克拉门托水文模型,简称SAC模型,是R.C.伯纳什(Burnash)和R.L.费雷尔(Ferral)以及R.A.麦圭儿(Mcguire)于20世纪60年代末至70年代初研制的,是一个连续模拟模型,模型研制完成时间相对较晚,其功能较为完善,兼有蓄满产流和超渗产流,广泛应用于美国水文预报中;SWAT模型是美国农业部农业研究中心研制开发的用于模拟预测土地利用及土地管理方式对流域水量、水质过程影响的分布式流域水文模型;TOPMODEL为基于地形的半分布式流域水文模型,于1979年由Beven和Kirkby提出,其主要特征是将数字高程模型(DEM)的广泛适用性与水文模型及地理信息系统(GIS)相结合,基于DEM数据推求地形指数,并以此来反映下垫面的空间变化对流域水文循环过程的影响,描述水流趋势。
本文对这四中水文模型从蒸发计算、产汇流计算、适用流域以及参数等方面进行分析比较,并得出结论。
1模型简介1.1新安江模型新安江模型是赵人俊等在对新安江水库做入库流量预报工作中,归纳成的一个完整的降雨径流模型。
基于API模型与新安江模型的察尔森水库洪水预报作者:张露张佳宾梁国华孙亚来源:《南水北调与水利科技》2015年第06期摘要:察尔森水库承担着兴安盟地区的防洪、灌溉和供水等任务,其洪水预报具有重要的研究意义。
考虑到下垫面条件和降雨分布特征的影响,单一模型或同组参数在该地区很难取得理想的洪水模拟效果,尝试引入分单元新安江模型与API模型分别对察尔森水库洪水进行预报,并分析总结两模型在该地区的适用性。
结果表明:两种模型预报结果都较好,且对于大暴雨洪水预报效果更理想;当前期土壤湿润时,分单元新安江模型预报效果更好;当前期土壤干旱、降雨强度较大时,API模型预报效果优于分单元新安江模型。
实际作业时根据需要选择模型进行预报,有利于察尔森水库合理调度,提高水库经济效益。
关键词:察尔森水库;洪水预报;新安江模型;API模型中图分类号:TV213 文献标志码:A 文章编号:1672-1683(2015)06-1056-04Abstract:Chaersen reservoir undertakes the important tasks for the hinggan league area,such as irrigation,flood control and so on,its flood forecasting is significance.Due to the hydrogeological condition and characteristics of rainfall distribution,it is difficult to obtain a better simulation by the single model or a set of parameters.This paper used unit Xin′anjiang model and API model to forecast Chaersen reservoir flood respectively,and analyzed the applicability of the two models in the region.The results showed that forecast results by the models all met the requirement of the operational,and especially the heavy flood effect is better;If the antecedent soil is moist,both models were applicable,particularly the Xin′anjiang;If the antecedent soil is drought and rainfall intensity was larger,the Xin′anjiang model i s not applicable,it was supposed to choose the API model to forecast.Therefore,it is necessary for us to choose proper model according to the hydrogeological conditions and the characteristics of rainfall distribution to improve the flood forecast accuracy and to direct reservoir regulation,in order to improve the economic effectiveness.Key words:Chaersen reservoir;flood forecast;Xin′anjiang model;API model洪水预报是减轻洪涝灾害和提高洪水资源利用率的重要手段,较高精度的洪水预报成果可以充分发挥水库的综合利用效益。
第47卷第3期2019年5月河海大学学报(自然科学版)Journal of Hohai University(Natural Sciences)Vol.47No.3May 2019DOI :10.3876/j.issn.10001980.2019.03.001 基金项目:国家重点研发计划(2016YFC0402705);国家自然科学基金(51679061);中央高校基本科研业务费专项(2016B04714)作者简介:姚成(1982 ),男,副教授,博士,主要从事水文模型与水文预报研究㊂E⁃mail:yaocheng@引用本文:姚成,邱桢毅,李致家,等.API 模型和新安江模型的参数区域化研究与应用[J].河海大学学报(自然科学版),2019,47(3):189⁃194.YAO Cheng,QIU Zhenyi,LI Zhijia,et al.Parameter regionalization study and application of API model and Xin’anjiang model[J].Journal of Hohai University(Natural Sciences),2019,47(3):189⁃194.API 模型和新安江模型的参数区域化研究与应用姚 成1,邱桢毅1,李致家1,胡维登1,许 洁2(1.河海大学水文水资源学院,江苏南京 210098;2.安徽省水文局,安徽合肥 230022)摘要:为了将API 模型与新安江模型更好地应用于无资料地区,将API 模型和新安江模型应用于大别山区及皖南山区的29个中小流域,对模型参数在研究区的区域规律进行研究,通过中小河流新建水文测站对参数区域化的成果进行实证研究㊂结果表明:API 模型与新安江模型均能较好地用于研究区中小流域的洪水模拟;逐步回归分析法能有效地推求模型的敏感参数;基于空间邻近与逐步回归分析相结合的参数区域化方法,API 模型与新安江模型在新建水文测站次洪模拟中的平均确定性系数分别达到0.92和0.86,该方法能有效地推求研究区无资料流域API 模型与新安江模型的参数㊂关键词:API 模型;新安江模型;无资料地区;参数区域化;空间邻近法;逐步回归分析法;新建水文测站中图分类号:P338 文献标志码:A 文章编号:10001980(2019)03018906Parameter regionalization study and application of API model and Xin ’anjiang modelYAO Cheng 1,QIU Zhenyi 1,LI Zhijia 1,HU Weideng 1,XU Jie 2(1.College of Hydrology and Water Resources ,Hohai University ,Nanjing 210098,China ;2.Hydrology Bureau of Anhui Province ,Hefei 230022,China )Abstract :In order to better apply the API model and Xin’anjiang model to the ungauged regions,the parameter regionalization study and its application were conducted in this paper.Here,the API model and Xin’anjiang model were applied to small and medium⁃sized basins in the Dabie Mountain area and South Anhui Mountain area,the regional regularity of model parameters in the selected area was studied,and the result of regionalization was verified by the new hydrological station for the small and medium⁃sized rivers.The results show that both API model and Xin’anjiang model can be used to simulate the flood runoff in the study area;stepwise regression analysis can effectively deduce the sensitive parameters;based on the parameter regionalization method combining spatial proximity and stepwise regression analysis,the average deterministic coefficients for hourly API model and Xin’anjiang model simulations in the new hydrological station are 0.92and 0.86,respectively.Therefore,this method can effectively deduce the parameters of API model and Xin’anjiang model in the ungauged basins of selected area.Key words :API model;Xin’anjiang model;ungauged regions;parameter regionalization;spatial proximity;stepwise regression analysis;new hydrological station水文模型作为水文预报的计算工具,一直是水文工作者研究的重点㊂随着研究的不断开展,水文模型的研究已在有水文资料的地区取得了较好的进展[1⁃2]㊂其中,传统的API 模型与新安江模型经过长期的优化改进,在国内已经取得了广泛的应用,尤其是在湿润与半湿润地区,取得了较高的预报精度[3⁃4]㊂然而,模型091河海大学学报(自然科学版)第47卷参数的推求问题限制了API模型和新安江模型在无资料地区的进一步应用㊂因此,有效地解决API模型与新安江模型在无资料地区的参数推求问题,对于无资料地区的水文预报具有重要意义㊂在模型参数推求过程中,3种典型的参数区域化方法被广泛使用,即空间邻近法㊁回归分析法以及物理相似法[5]㊂而自2003年国际水文科学协会(IAHS)提出无资料流域水文预报(PUB)计划以来,模型参数推求方面的研究取得了一定的进展[6]㊂Oudin等[7]将基于TOPMODEL与GR4J模型的回归分析㊁空间邻近㊁物理相似3种方法进行试验,结果显示空间邻近法最优;Reichl等[8]基于SIMHYD模型对物理相似法加以优化,结果显示经过改进的物理相似法优于空间邻近以及回归分析法;Zhang等[9]基于改进新安江模型对空间邻近与物理相似法进行整合,结果表明两者相结合的方法较传统的参数区域化方法对结果有一定改善㊂由此可见,参数区域化方法的优化与结合是有必要的㊂此外,对于参数区域化方法的验证通常采用交叉验证,没有对无资料地区的未来资料序列进行实际检验㊂与此同时,近年来无资料流域新建成了大量的水文测站㊂新建水文测站资料序列较短,难以进行参数的率定,但可以通过有限的最新资料对参数区域化方法推求的参数结果进行实际检验㊂本文选择大别山区及皖南山区为研究区,将API模型与新安江模型应用于研究区的29个中小流域,并且采用空间邻近与逐步回归分析相结合的参数区域化方法估计研究区内无资料流域的水文模型参数,旨在验证2种模型在研究区中小流域适用性的同时,通过新建水文测站检验此方法用于推求研究区无资料流域模型参数的有效性,改善API模型㊁新安江模型在无资料流域应用困难的现状,并为参数区域化方法的研究提供一定的借鉴㊂1 研究区概况及数据资料研究区为安徽省大别山区及皖南山区,属亚热带湿润季风气候,夏季雨量充沛,年平均降雨量1200~ 1500mm,年均蒸发量600~800mm㊂基于水文资料系列㊁流域代表性等因素,本文在研究区选取周家河㊁张冲等29个独立的中小流域作为研究对象,流域面积介于4.71~887.88km2之间,均为自然闭合流域,受水工建筑物的影响较小㊂为率定API模型新安江模型的参数,选取这29个中小流域的实测水文资料,包括逐日流量与雨量㊁时段流量与雨量以及蒸发数据等,其中流量㊁雨量的时段长均为1h㊂为便于比较模型模拟结果与实测数据,模型模拟的时段长取1h㊂为提取流域的属性因子用于逐步回归分析,本文选用研究区中小流域的数字高程数据,资料来自于中国科学院计算机网络信息中心国际科学数据镜像网站,精度为90m×90m,数据采集时间为2000年㊂通过地理信息系统软件提取了流域面积㊁河网密度㊁平均高程㊁面积坡度等12种流域的属性因子㊂2 API模型与新安江模型简介2.1 API模型API模型又称前期雨量指数模型,模型产流部分采用前期雨量指数和降雨量计算,汇流部分采用Nash 单位线计算[10]㊂API模型的参数有:流域最大初损值I m㊁前期雨量指数消退系数k以及Nash汇流参数N和K(N为线性水库个数,K为线性水库的蓄泄系数)㊂2.2 新安江模型新安江模型[11]是典型的概念性水文模型,模型的结构主要分为4个模块:(a)蒸散发模块,参数有K c㊁W um㊁W lm㊁C;(b)产流模块,参数有W m㊁B㊁I mp;(c)水源划分模块,参数有S m㊁E x㊁K g㊁K i;(d)汇流模块,参数有C i㊁C g㊁C s㊁L㊁X,参数的物理意义见文献[12]㊂2.3 模型应用API模型与新安江模型在29个流域的应用结果用于检验模型在研究区的适用性㊂模型参数的率定采用SCE⁃UA算法,该优化算法稳定性好㊁收敛速度快,且应用较好[13]㊂选用洪峰相对误差㊁确定性系数对模拟结果进行评价㊂依据GB/T22482 2008‘水文情报预报规范“,洪峰相对误差在20%以内为合格㊂图1为29个流域次洪模拟结果箱型图,显示了洪峰合格率㊁确定性系数均值的最小值㊁下四分位数㊁中位数㊁上四分位数㊁最大值,体现了API模型与新安江模型在29个流域模拟精度的变幅㊂由图1可知,API模型与新安江模型在29个流域次洪模拟结果的洪峰合格率均在60%以上,确定性系数均值都在0.6以上㊂经统计:API模型应用于29个流域的平均洪峰合格率和平均确定性系数分别为第3期姚 成,等 API 模型和新安江模型的参数区域化研究与应用77.45%和0.72;新安江模型应用于29个流域的平均洪峰合格率和平均确定性系数分别为83.72%和0.84㊂模型应用结果表明API 模型新安江模型均能较好地用于研究区中小流域的洪水模拟,且新安江模型可以取得相对更高的模拟精度㊂图1 API 模型和新安江模型次洪模型模拟结果统计箱型图Fig.1 Statistical boxplots of the simulating results by API model and Xin 爷anjiang model3 参数区域化及其验证3.1 参数区域化空间邻近法是指建立在已知数据分布存在一定地理规律的基础上,通过已知点或其分区综合数据,推求该区域任一点或者分区数据的方法㊂模型参数通常具有一定物理意义,能够反映流域的自然地理综合特征㊂而流域自然地理特征是经过气候地形等长时间作用演化的结果,故其具有一定的区域相似性[14]㊂正是区域相似性使得水文模型参数在空间分布上具有一定的规律,这也是空间邻近法能用于推求模型参数的前提条件㊂本文采用的空间邻近法为反距离权重法[15],该法在模型参数推求中应用较好㊂此外,回归分析法作为参数区域化最常用的方法之一,其参数推求结果的好坏主要取决于模型参数与流域属性因子间是否存在较好的关联性,所选取的流域属性因子也需要能够反映出流域的自然地理特征㊂在选取流域属性因子的过程中,本文采用的是逐步回归分析法[16⁃17]㊂逐步回归分析法不但剔除了引起多重共线性的变量,还能确保最后得到的自变量集是最优的㊂图2 计算K 值与率定K 值对比Fig.2 Comparison between calculated and rating values of KAPI 模型参数确定时,首先固定参数k 与N ,k 与N 一般为常数,分别取0.85和3[18]㊂其次利用反距离权重法推求参数I m ,降雨径流移用邻近流域的相关关系㊂最后通过逐步回归分析方法获得公式计算参数K ㊂其中,根据芮孝芳[18]对Nash 模型参数的分析,K 与流域的地形地貌条件相关㊂故本文以K 为因变量,流域属性因子为自变量,通过逐步回归分析,得到K 与流域地貌特征的定量关系:K =5.534S -0.236area (1)式中:S area 流域面积坡度,dm /km 2㊂通过逐步回归分析法得到的计算K 值与率定K 值近乎相等(图2),但可以明显看出金家流域的计算值严重偏离率定值㊂据流域勘查发现,金家流域范围内存在东方红水库,该水库对径流有一定的调节作用㊂在参数率定过程当中,水库的调节作用已体现在实测洪水资料中㊂而在对该流域进行K 值计算时并未考虑水191291河海大学学报(自然科学版)第47卷库的调节作用,故导致计算值远小于率定值㊂此外,发现金家流域的洪水资料中大洪水仅一场,且场次洪水资料较少,率定值可能存在一定的偏差㊂基于上述原因,对除金家流域外的参数计算结果进行统计,计算K 值与率定K值的平均绝对误差为0.29㊂因而,在不存在水工建筑物影响或者影响较小的情况下,可以在研究区采用此公式计算K值㊂从物理层面分析,流域汇流过程中很重要的一部分是流域对净雨再分配中的水动力扩散作用,水动力扩散对于地表净雨汇流的影响主要体现在水流速度沿不同方向的差异性,这与流域的地形地貌有密切联系㊂式(1)中的流域面积坡度通过影响水动力扩散作用来改变地表净雨的再分配,从而影响了参数K的大小㊂新安江模型参数确定时,为降低 异参同效”影响,首先对不敏感参数W m㊁W um㊁W lm㊁B㊁C㊁I mp㊁E x采用固定赋值的方法,不再进行优选;其次利用反距离权重法推求参数K c㊁S m㊁K g㊁K i㊁C g㊁C i㊁X;最后通过逐步回归分析方法获得公式计算参数:河网蓄水消退系数C s㊁滞时L㊂根据赵人俊等[19]对新安江模型参数的分析, C s㊁L由河网地貌条件决定㊂故本文分别以C s㊁L为因变量,流域属性因子为自变量,通过逐步回归分析,得到了C s㊁L与流域地貌特征的定量关系:C s=exp(-0.2867A0.252426.72-0.99ln S area-3.185ln H平均-9.55ln P P)(2)式中:H平均 流域平均高程,m;P P 流域河网密度,km/km2;A 流域面积,km2㊂L=0.005A+0.516(3) 图3为逐步回归分析法得到的计算C s值与率定C s值对比结果,结果显示计算C s值与率定C s值整体误差较小,平均绝对误差为0.07,但孙家桥与舒家流域的偏差较大,分别达到0.37和0.17㊂分析发现:孙家桥流域面积较小㊁主河道长较短;舒家流域面积偏小,主河道长偏短,流域的河道平均坡度非常大㊂流域面积小㊁主河道长较短㊁河道平均坡度大这3个方面的原因可能造成流域的调蓄能力较差,从而使模型率定的C s 值较小㊂另外,孙家桥与舒家流域的面积均较小,而在面积较大的流域,杨山岭以及沙埠流域计算结果非常好㊂通过误差变化发现,误差整体上随着流域面积的减小呈现增大趋势,即误差与流域面积大体上呈现反比关系㊂造成这种误差现象的原因除异参同效以及模型结构所带来的不确定因素外,可能与小流域特定的地质条件和地貌结构有关㊂因此可以在研究区采用式(2)计算C s值,且应用于面积较大的流域效果更好㊂图3 计算C s值与率定C s值的对比Fig.3 Comparison between calculated and rating values of C sL的计算公式恰为一元线性回归,其回归模型的相关系数R2=0.64,表明该回归模型因变量与自变量之间的相关性程度较好㊂经统计:计算值L与率定值L的误差绝对值控制在3h之内,平均误差为0.74h,误差较小㊂且式(3)只含有一个因变量,可很好地避免变量之间的相关性,可以在研究区采用式(3)计算L㊂3.2 参数区域化成果在新建水文站的验证本文选取研究区内的祁门流域对参数区域化成果进行验证㊂通过空间邻近与逐步回归分析相结合的参数区域化方法推求,祁门流域的模型参数均已得到㊂祁门作为中小河流新建水文测站,于2014年建立,仅有2015 2016年间3场洪水资料㊂基于研究区参数区域化的成果,本文采用API与新安江模型对这3场洪水进行模拟,模拟结果统计见表1,洪水过程模拟见图4㊂由表1可知:API模型3场洪水的洪峰相对误差均小于20%,洪峰合格率为100%,洪峰平均相对误差水平为6.71%;3场洪水的确定性系数均大于0.8,平均确定性系数为0.92㊂新安江模型有2场洪水的洪峰相对误差小于20%,洪峰合格率为66.67%,洪峰平均相对误差水平为10.49%;3场洪水的确定性系数均大于第3期姚 成,等 API 模型和新安江模型的参数区域化研究与应用表1 API 模型与新安江模型在祁门流域的模拟结果Table 1 Simulating results of API model and Xin ’anjiang model in the Qimen Basin洪号实测洪峰/(m 3㊃s -1)计算洪峰/(m 3㊃s -1)洪峰相对误差/%确定性系数新安江模型API 模型新安江模型API 模型新安江模型API 模型2015060708492.00456.44427.40-7.23-13.130.870.882016041923469.00483.83474.60 3.16 1.190.870.952016061811676.83819.55716.2021.09 5.820.830.94图4 祁门流域洪水过程模拟Fig.4 Simulation of flood process in the Qimen Basin0.8,平均确定性系数为0.86㊂由图4所示的3场洪水过程可知:API 模型的洪水模拟过程在涨洪初期流量略微高于实测,退水存在陡落现象,洪峰与实测较为接近,整体模拟效果较好;新安江模型的2016061811号模拟洪水洪峰与实测偏差较大,且3场洪水均略微滞后,但洪水过程线形状与实测较为一致;在整体上,API 模型的模拟效果略优于新安江模型㊂由此可见,API 模型和新安江模型均能够较好地模拟祁门流域的洪水过程,但新安江模型在祁门流域的模拟效果较API 模型稍差,这与前文模型在研究区29个中小流域的模拟结果有所差异㊂造成该现象的原因可能是:(a)API 模型结构简单,需要率定的参数较少,有效的参数推求方法对于模拟效果起到了决定性的作用㊂而新安江模型结构比较复杂,需要率定的参数较多,参数推求的准确性对于模拟结果并非是唯一的因素㊂因为影响模拟结果的是参数组合而不是单一参数,参数之间有复杂的联系,多个参数微小差异的组合可能会引起较大的影响,即 异参同效”现象;(b)祁门作为新建水文测站,历史资料有限,3场洪水的模拟结果具有一定的不确定性㊂4 结 语将API 模型和新安江模型应用于安徽省大别山区及皖南山区的29个中小流域,在参数区域化方法上做出了新的尝试,采用空间邻近与逐步回归分析相结合的方法对研究区的模型参数开展区域化㊂在参数区域化成果验证过程中,采用中小河流新建水文测站㊂研究结果表明:(a)API 模型和新安江模型均能较好地用于研究区中小流域的洪水模拟;(b)逐步回归分析法能有效地推求模型敏感参数K ㊁C s ㊁L ;(c)基于空间邻近与逐步回归分析相结合的参数区域化方法,API 模型和新安江模型在新建水文测站次洪模拟中的平均确定性系数分别达到0.92和0.86,该方法能有效地推求研究区无资料流域API 模型和新安江模型的参数㊂此外,尽管研究得出了上述有用的结论,但仍需更多的新建水文测站及其实测资料来验证以便得到可靠性更高的结论,这都有待于在今后的研究中进行㊂参考文献:[1]芮孝芳,蒋成煜,张金存.流域水文模型的发展[J].水文,2006,26(3):22⁃26.(RUI Xiaofang,JIANG Chengyu,ZHANG Jincun.Development of watershed hydrologic models[J].Journal of China Hydrology,2006,26(3):22⁃26.(in Chinese))391491河海大学学报(自然科学版)第47卷[2]李致家,姚成,张珂,等.基于网格的精细化降雨径流水文模型及其在洪水预报中的应用[J].河海大学学报(自然科学版),2017,45(6):471⁃480.(LI Zhijia,YAO Cheng,ZHANG Ke,et al.Research and application of the high⁃resolution rainfall runoff hydrological model in flood forecasting[J].Journal of Hohai University(Natural Sciences),2017,45(6):471⁃480.(in Chinese))[3]张建云.中国水文预报技术发展的回顾与思考[J].水科学进展,2010,21(4):435⁃443.(ZHANG Jiangyun.Review andreflection on China's hydrological forecasting technique[J].Advances in Water Science,2010,21(4):435⁃443.(in Chinese)) [4]杨殿亮,许畅,钟华.沂河临沂站洪水预报影响因素分析[J].水利规划与设计,2017(12):33⁃35.(YANG Dianliang,XUChang,ZHONG Hua.Analysis of factors effecting flood prediction of Linyi station in Qihe River[J].Water Resources Planning and Design,2017(12):33⁃35.(in Chinese))[5]MERZ R,BLOSCHLl G.Regionalisation of catchment model parameters[J].Journal of Hydrology,2004,287(1):95⁃123.[6]SIVAPALAN M,TAKEUCHI K,FRANKS S W,et al.IAHS decade on predictions in ungauged basins(PUB),2003⁃2012:shaping an exciting future for the hydrological sciences[J].International Association of Scientific Hydrology Bulletin,2003,48(6):857⁃880.[7]OUDIN L,ANDREASSIAN V,CHARLES P,et al.Spatial proximity,physical similarity,regression and ungaged catchments:acomparison of regionalization approaches based on913French catchments[J].Water Resources Research,2008,44(3):893⁃897.[8]REICHL J P C,WESTERN A W,MCINTYRE N R,et al.Optimization of a similarity measure for estimating ungauged streamflow[J].Water Resources Research,2009,45(10):208⁃225.[9]ZHANG Yongqiang,CHIEW F H S.Relative merits of different methods for runoff predictions in ungauged catchments[J].WaterResources Research,2009,45(45):4542⁃4548.[10]SITTNER W T,SCHAUSS C E,MONRO J C.Continuous hydrograph synthesis with an API⁃type hydrologic model[J].WaterResources Research,1969,5(5):1007⁃1022.[11]赵人俊.流域水文模拟:新安江模型与陕北模型[M].北京:水利电力出版社,1984.[12]包为民.水文预报[M].4版.北京:中国水利水电出版社,2009.[13]董洁平,李致家,戴健男.基于SCE⁃UA算法的新安江模型参数优化及应用[J].河海大学学报(自然科学版),2012,40(5):485⁃490.(DONG Jieping,LI Zhijia,DAI Jiangnan.Application of SCE⁃UA algorithm to optimization of Xin’anjiang modelparameters[J].Journal of Hohai University(Natural Sciences),2012,40(5):485⁃490.(in Chinese))[14]姚成,章玉霞,李致家,等.无资料地区水文模拟及相似性分析[J].河海大学学报(自然科学版),2013,41(2):108⁃113.(YAO Cheng,ZHANG Yuxia,LI Zhijia,et al.Hydrological simulations and similarities in ungauged basins[J].Journal of Hohai University(Natural Sciences),2013,41(2):108⁃113.(in Chinese))[15]DUAN Ping,SHENG Yehua,JIA L I,et al.Adaptive IDW interpolation method and its application in the temperature field[J].Geographical Research,2014,196:31⁃38.[16]游士兵,严研.逐步回归分析法及其应用[J].统计与决策,2017(14):31⁃35.(YOU Shibing,YAN Yan.Stepwiseregression analysis and its application[J].Statistics&Decision,2017(14):31⁃35.(in Chinese))[17]王卫光,陆文君,邢万秋,等.黄河流域Budyko方程参数n演变规律及其归因研究[J].水资源保护,2018,34(2):7⁃13.(WANG Weiguang,LU Wenjun,XING Wanqiu,et al.Analysis of change and attribution of Budyko equation parameter n in Yellow River[J].Water Resources Protection,2018,34(2):7⁃13.(in Chinese))[18]芮孝芳.利用地形地貌资料确定Nash模型参数的研究[J].水文,1999,19(3):6⁃10.(RUI Xiaofang.A study ondetermining the parameters of the nash model using geomorphological data[J].Journal of China Hydrology,1999,19(3):6⁃10.(in Chinese))[19]赵人俊,王佩兰.新安江模型参数的分析[J].水文,1988,8(6):4⁃11.(ZHAO Renjun,WANG Peilan.Study on parametersof Xinanjiang model[J].Journal of China Hydrology,1988,8(6):4⁃11.(in Chinese))(收稿日期:20180525 编辑:张志琴)。