非稳态导热习题

“非稳态导热”例题例题1：一温度为20℃的圆钢，长度为0.3m ，直径为60mm ，在一温度为1250℃的加热炉内被加热。

已知圆钢的导热系数为35 W/(m ∙K)，密度为7800kg/m 3，比热容为0.460J/(kg ∙K)，加热炉长为6m ，圆钢在其中匀速通过，其表面和炉内烟气间的表面传热系数为100 W/(m 2∙K)。

现欲将该圆钢加热到850℃，试求该圆钢在加热炉内的通过速度。

解 特征尺寸A V /为m 0136.0)1060(14.3413.0)1060(14.33.0)1060(14.3414124133322=⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯=⨯+=---d dL L d A V πππ 则毕渥数v Bi 为05.0211.01.0039.0350136.0100)/(v =⨯=<=⨯==M A V h Bi λ 因此可以采用集总参数法求解。

θθρτ0ln hA cV= 即s548.14 1250850125020ln 100)10460.0(78003=--⨯⨯=τ则该圆钢在加热炉内的通过速度为m /s 0109.014.5486===τL v例题2：两块厚度均为30mm 的无限大平板，初始温度为20℃，分别用铜和钢制成。

平板两侧表面的温度突然上升至60℃，计算使两板中心温度均达到56℃时两板所需时间之比。

已知铜和钢的热扩散率分别为610103-⨯m 2/s 和6109.12-⨯m 2/s 。

(125.0==铜钢钢铜a a ττ)例题3：无内热源、常物性的二维导热物体在某一瞬时的温度分布为x y t cos 22=。

试说明该导热物体在x =0，y =1处的温度是随时间增加而逐渐升高，还是逐渐降低？例题4：一初始温度为20℃的钢板，厚度为10cm ，密度为为7800kg/m 3，比热容为460.5 J/(kg ∙K)，导热系数为53.5W/(m ∙K)，放置到温度为1200℃的加热炉中加热，钢板与烟气间的表面传热系数为407 W/(m 2∙K)。

公用设备工程师-专业基础（暖通空调、动力）-传热学-2.3非稳态导热[单选题]1.在非稳态导热过程中，瞬态导热过程根据温度的变化特性可以分为三个不同的阶段，下列说法中不正确的是()（江南博哥）。

[2014年真题]A.在0.2＜Fo＜∞的时间区域内，过余温度的对数值随时间线性变化B.Fo＜0.2的时间区域内，温度变化受初始条件影响最大C.最初的瞬态过程是无规则的，无法用非稳态导热微分方程描述D.如果变化过程中物体的Bi数很小，则可以将物体温度当作空间分布均匀计算正确答案：C参考解析：非稳态的三个阶段中，初始阶段和正规状态阶段是以傅里叶数Fo＝0.2为界限。

A项，在正规状态阶段（0.2＜Fo＜∞），过余温度的对数值随时间按线性规律变化；B项，Fo＜0.2为初始阶段，该阶段内受初始条件影响较大，且各个部分的变化规律不相同；C项，非稳态的导热微分方程在描述非稳态问题时并未有条件限制，即便是最初阶段也是可描述的；D项，毕渥准则数Bi 为导热热阻与对流热阻的比值，当Bi较小时，说明物体的导热热阻接近为零，因此可以将物体温度当作空间分布均匀计算。

[单选题]2.当固体导热过程Bi数趋于无限大时，描述该物体导热性质的正确说法是()。

[2016年真题]A.物体温度可以近似等于流体温度B.物体内部导热能力远大于物体换热能力C.物体内部温度变化速度相对较快D.边界壁面温度等于流体温度正确答案：D参考解析：毕渥准则（Bi＝hδ/λ）表示物体内部导热热阻（δ/λ）与物体表面对流换热热阻（1/h）的比值，固体导热过程Bi数趋于无限大时，导热热阻远远大于对流换热热阻，这意味着表面传热系数趋于无限大，即对流换热的热阻趋于零，但内部导热热阻的大小无法确定，这时物体的表面温度几乎从冷却过程一开始便立即降低到流体的温度，即边界壁面温度等于流体温度，而物体内部的温度变化未可知。

D.对于普通圆柱体L＝R，R为半径正确答案：D参考解析：毕渥准则的公式为：Bi＝hL/λ。

非稳态导热问题例：一厚46.2mm温度278K的奶油，由冷藏室移至298K环境中，奶油盛于容器中，顶面与环境接触，各侧面及底面均绝热，试计算5小时后，奶油顶面、中心面及底面的温度。

k=0.197w/m.k,C=2300J/kg.K,ρ=998kg/m3, h=8.52w/m2.K例：一直径较大的火箭发动机喷管，壁厚8mm，密度8600kg/m3，k=26w/m.K，C=545J/kg.K，在静态实验中初始温度27°C的管壁与此1800°C的高温燃汽接触，h=2050w/m2.K，若壁面能承受最高温度为1010°C，假设外侧完全绝热，试求火箭发动机能允许运行的时间。

例：直径50mm长1.2m的轴，在炉内加热达到均匀温度427°C，将其一端面投入38°C的冷却剂中淬火，轴表面与冷却剂之间的h为340w/m2K, 若轴的k=26w/m.K，α=0.031m2/h，求出1.25分钟后轴距表面0.01m处的温度（以及端面的中心温度）例：钢锭尺寸长0.5m, 宽0.7m, 高1m，k=40.5w/m.K, α=0.722×10-5m2/s, 求钢锭置入炉温1200°C的加热炉中4小时后最低温度和最高温度之差，其初始温度为20°C，h=348w/m2.K。

例：某材料用热处理法进行改性，如果该材料加工成5mm半径的球体，在炉内加热到400o C，将其从炉内移出进行两步冷却。

第一步移出后在20o C的空气中冷却经历一段时间ta, 使球体的中心温度达到335o C，如果对流换热系数为10w/m2k ；第二步是将第一步冷却后球体放到20o C的水浴中进行冷却，若对流换热系数为6000/m2k。

试计算（1）第一步需要的时间；（2）第二步将中心温度从335o C降至50o C所需要的时间。

,3/30006−1000,/==ρ20==α×10kkgKWmKsmJc.6,66kg/2m/。

第三阶段 建立新的稳态阶段， 理论上需要无限长
t
H
1
时间
物体各处的温度达
t
0
G
F A B E C D
到新的稳态
两类非稳态导热的区别：瞬态导热存在着有区别的 三个不同阶段，而周期性导热不存在。
5 热量变化
Φ 1－－板左侧导入的热流量 Φ 2－－板右侧导出的热流量
各阶段热流量的特征： 不规则情况阶段段：Φ1急剧减小，Φ2保持不变；
物体的温度随时间的推移逐渐趋近于恒定的值
着重讨论瞬态非稳态导热。
非稳态导热过程中在热量传递方向上不
同位臵处的导热量是不同的；
不同位臵间导热量的差别用于（或来自）
该两个位臵间内能随时间的变化，这是 区别与稳态导热的一个特点。
对非稳态导热一般不能用热阻的方法来
作问题的定量分析。
3 温度分布
h Bi 1h
（3） / 与 1/ h 的数值比较接近
平板中不同时刻的温度分布
介于上述两种极端情况之间。 两个热阻的相对大小对于物体
中非稳态导热的温度场的变化 具有重要影响。 引入表征这两个热阻比值的无 量纲数毕渥数。 Bi h
1h

近似分析法
a
L2
exp Bi Fo 0
0
exp Bi Fo 0
Bi Fo
应用集总参数法时，物体过余温度随时间的变化 关系是一条负自然指数曲线，或者无因次温度的 对数与时间的关系是一条负斜率直线
3.2.2 导热量计算式、时间常数与傅立叶数
1、导热量计算

hA Vc 0
Q Φ ( )d (t0 t ) hAe

④ 某一时刻物体表面的热流量或从某一时刻起经一定时间后表面传递的总热量。
5
2）求解方法：主要有分析解法、数值解法、图解法和热电模拟法等。 本章仅介绍分析解法，而且只针对第三类B、C下一维非稳态导热的求解。
二、一维非稳态导热的分析解及诺谟图
工程上常见的非稳态导热问题分以下三种：
一维非稳态导热问题：
无限大平壁 无限长圆柱体
一、概 述
1.1 定义：非稳态导热是指发生在非稳态温度场内的导热过程。
其数学表达式为：t f (x, y, z, )
按照其过程进行的特点，可分为以下二种：
（1）周期性非稳态导热：导热物体内的温度随时间周期性地 变化。
（2）非周期性非稳态导热（瞬态导热）：物体内的温度随时 间不断的 升高或降低。
2
1.2 非稳态导热过程的特点
大平壁非稳态导热分析
由左侧表面导入的热量到达右侧表面之前的一段时间。
② 正常情况阶段。
当左侧表面导入的热量到达右侧表面之后，使右侧壁温不断升高，直到它达
到新的平衡状态的这段时间。
4
B）大平壁两侧被加热过程
一初始温度均匀为t0的无限大平壁，突 然投入到温度为tf的热流体中对称加热。平 壁内发生了非稳态导热过程。平壁中的温
1.3 求解的目的和方法
1） 求解非稳态导热问题主要目的有四个：
① 物体的某一部分从初始温度上升或下降到某一确定温度所需的时间，或经某 一时间后物体各部分的温度是否上升或下降到某一指定值；
② 物体在非稳态导热过程中温度分布，为求材料热应力和热变形提供必要资料； ③ 物体在非稳态导热过程中的温升速率；
二维非稳态导热问题：短圆柱体、长的方柱体
三维非稳态导热问题：短方柱体、长方体

Bi hl ≤0.1
时、物体中最大与最小的过余温度之差小于5%，对于一 般工程计算，此时已经足然特确地可以认为整个物体温度 均匀。按照这样要求，由于l=V/A对圆柱有球分别是半轻 的1/2与1/3、因而如果以l作为Bi数的特征长度，则该Bi数 对平板、国柱与球应该分别小于0.1、0.05和0. 033。
方程中指数的量纲：
hA
W m2K
m2
w1
Vc
kg m3
Jkg K
[
m3
]
J
s
第三章 非稳态导热
9
即与 1 的量纲相同，当 Vc 时，则
hA
hA
1 Vc
此时，
e1 36.8%
0
称
Vc
hA
为时间常数，用 c 表示。
第三章 非稳态导热
10
如果导热体的热容量（ Vc ）小、换热条件好（h大），
有一直径为 5cm 的钢球，初始温度为 450 ℃，将其突然置 于温度为 30 ℃空气中。设钢球表面与周围环境间的总换热 系数为 24w/（m2 . K），试计算钢球冷却到 300 ℃所需的 时间。已知钢球的 c=0.48kJ/(kg·K ) , ρ =7753kg/m3 , λ =33w/(m. K ).
Fo
l2
a
换热时间 边界热扰动扩散到l 2面积上所需的时间
无量纲 热阻
Fo越大，热扰动就能越深入地传播到物体 内部，因而，物体各点地温度就越接近周
围介质的温度。
无量纲 时间
第三章 非稳态导热
12
对于平板、圆柱、球的一维非稳态第三类边界条件条件下 的导热问题，当按特征长度
l= 、厚度为2 的平板，
l=R、圆柱 l=R.球 定义的Bi数满足

分析解

分析解为：
无穷级数之和
x, x 2 a Cn exp n 2 cos n 0 n 1
式中
4sin n Cn 2n sin 2n
μn称为特征值，是以下超越方程的根：
n tan n

原因是：由非稳态过程的特点造成的

非稳态过程的特点（以厚为dx的微元平壁为例）
——进入微元平壁的热量一边被吸收（蓄热），一边
被传导

——吸收的结果：不但使进、出平壁的热量不等，而
且导致自身温度升高

——传导的结果：热量能够影响到的区域，平壁温度
都将发生变化

首先，受流体加热的影响，壁面两侧的温度立即发生

引入过余温度θ=t-t∞后的数学模型：
2 a 2 x
0 x , 0
| 0 0 t0 t f
| x 0 0 x
| x h | x x
求解是数学问题，方法很多。典型的分离变量法、
Laplace变换方法等

从平壁放入流体中的那一刻起，壁面
就具有和流体相同的温度
h Bi 1h

随时间的推移，平壁内各点的温度逐 渐升高而最终趋于t∞

这时第三类边界条件可转化为第一类 边界条件
h Bi 1h

当Bi→0时，即物体内部的导热热阻δ/λ远小于表面的对
流热阻1/h，可以忽略物体内部的导热热阻
h

x, x 2 a Cn exp n 2 cos n 0 n 1
4sin n Cn 2n sin 2n

(b)
36 .8%
可以得出内部热阻可被忽略的非稳 态导热过程具有以下二个特点： （1）物体温度 随时间按指数函数关系下降，如 图所示，开始下降快，随后变化减慢。
0
， t t f 0，即t t f
Tτ
集总参数系统θ -τ曲线
τ
（2）物体温度随周围流体温度变化的快慢与该物体的时间常数Tτ有关。 什么是时间常数？式（b）中 ρcV/（hA） 具有时间的量纲，此外，对于常物 性物体，一旦几何尺寸确定（ V/A 确定）， ρcV/（hA） 的值也就确定了。 cV T 在以上二个意义上，把 ρcV/（hA） 称为时间常数，记为Tτ，即 。 hA
代人（a）式得 cV
Ah(t t f ) V
集总参数系统的微分方程
dt ＝ Ah (t t f ) d
（2）根据能量守恒定律：物体内能（焓）的变化等于物体表面对外散去的热量：
cV
dt ＝Ah (t t f ) d
3
求解微分方程：
引入过余温
初始条件：
t tf
d ＝ Ah ， 上式变成 cV d
o


d
hAo (
cV
hA

o
)(e
hA cV
hA cV
o
1)
Φ的单位—W或kW； Qτ的单位—J或kJ。
cVo (1 e
)
请大家思考：瞬时的传热量Φ和总传热量Qτ的单位是什么？
7
三、集总参数法的适用条件
集总参数法比较简单，但应用它是有条件的，必须满足： Bi
1 R R 2l V BiV Bi 0.05 L 2 2 2Rl A

alpha1=3/(2600*1150); alpha2=0.2/(600*200); for j=2:50 A1(j,j)=(dr^2)/(alpha1* dt)- dr/r(j)+2; end for j=1:150 A2(j,j+1)=-1; end A1(1,1)=500+3/dr; A2(1,2)=-3/dr; A3=zeros(151,151); for j=1:150 A3(j+1,j)= dr /r(j+1)-1; end for j=52:150 A1(j,j)=( dr ^2)/(alpha2* dt)- dr /r(j)+2; end A1(51,51)=-(3+0.2); A2(51,52)=0.2; A3(51,50)=3; A=A1+A2+A3; A(151,151)=1; A(151,150)=-1; b=zeros(151,1,2500); L=-1*tril(A,-1); U=-1*triu(A,1); D=diag(diag(A)); j=1; x(:,:,1)=1; for n=2:2000 b(1,1,n)=0; %由前一时间循环结果给下一时间的方程组 b 赋值
程序清单（以保温层 d=0.05m 为例）
dr=0.0005; dt=1; M=2600*1150*( dr)^2/ dt; N=600*200*( dr)^2/ dt; for i=1 : 151 r(i)=0.025+(i-1)* dr; end T=ones(151,2500); x=zeros(151,150,2500); A1=eye(151,151); A2=zeros(151,151);
保温层内侧温度提高，其余基本一致。 2） d=0.060 m > d0

2010年12月26日 年 月 日
11
§２ 对流边界条件下非稳态导热 二、集总参数法（Bi→0） 集总参数法（ ）
3.能量平衡分析： 能量平衡分析： 能量平衡分析
− ρVcdt = hA(t − t f )dτ
4.温度场： 温度场： 温度场
hA θ = θ 0 exp − ρcV τ
2010年12月26日 年 月 日
8
§２ 对流边界条件下非稳态导热 一、毕渥准则数Bi 毕渥准则数
λ = hL Bi = 1 λ
h L
物体内部导热热阻与表 面复合换热热阻的相对大 为定型尺寸。 小，L为定型尺寸。 为定型尺寸 其大小将影响温度场的 特点。 特点。
2010年12月26日 年 月 日 9
每课一题
厨师在炒鸡肉丝时要品尝一 下咸淡，于是他从100℃ 100℃的 下咸淡，于是他从100℃的 热炒锅中取出一鸡肉丝， 热炒锅中取出一鸡肉丝，用 口吹了一会，待其降至65℃ 口吹了一会，待其降至65℃ 时再放入口中。 时再放入口中。试估算厨师 需要吹多长时间？ 需要吹多长时间？
2010年12月26日 年 月 日
§２ 对流边界条件下非稳态导热
Bi数对非稳态温度场的影响 Bi数对非稳态温度场的影响
集总热容情况
2010年12月26日 年 月 日
第三类边界条件
第一类边界条件
10
§２ 对流边界条件下非稳态导热 二、集总参数法（Bi→0） 集总参数法（ ）
1.集总热容 集总热容 2.集总参数法 集总参数法 即忽略物体内部导热热阻， 即忽略物体内部导热热阻 ， 将其看作集 总热容来定量分析瞬态非稳态导热过程 的方法
2010年12月26日 年 月 日

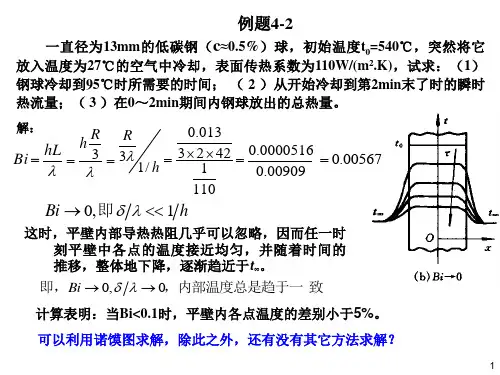
课后作业-3.3 非稳态导热过程分析1. （P67 思考题4）初温为0t 、厚为2δ的大平壁一侧绝热，另一侧：（a ）与温度为1t （01t t >）的流体相接触；（b ）壁面温度突然升高为1t 。

试画出几个时刻大平壁内的温度分布曲线，并比较其异同。

解：如图所示：因为大平壁一侧绝热，故考虑将大平壁沿一侧对称过去，厚度变为4δ。

条件（a ）时，τ=τ1时刻曲线较陡，τ=τ2时刻曲线相对平缓，τ=τ3时刻曲线相对τ=τ2时刻更平缓，τ=τ4时刻曲线已非常平缓。

但需注意，在τ=τ1至τ4时刻，大平壁另一侧温度一直无法到达t1，均在t1以下，τ=τ2、τ3、τ4时刻曲线形状都是超越曲线，而τ=τ1时刻曲线形状为一条超越曲线加一条直线加两者之间的一个间断点。

条件（b ）同理，只不过条件（b ）在τ=τ1至τ4时刻，其另一侧壁面温度都是从t1开始。

最终结果图保留一半也可以。

2.（P68 习题3-5）一厚10mm的大平壁（满足集总参数法求解的条件），初温为300℃，密度为7800kg/m²,比热容为0.47kJ/（kg·℃），导热系数为45W/（m ·K ），一侧有恒定热流q=100W/m ²流入，另一侧与20℃的空气对流换热，表面传热系数为70W/（m ²·K ）。

试求3min 后平壁的温度。

解：由能量守恒定理可知：()∞--=t t hA qA d dt c V τρ ① 单位面积大平壁的体积为：301.0101.0m A S V =⨯=•=则由①得：()⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--=+-=•∴-⨯⨯-=•⨯⨯⨯71503666771507015007036660201701001047.0780001.03t d dt t t d dt t d dt τττ故 对两边进行积分，有：()τττ36667ln 36667715030071500300-=-∴-=-⎰⎰t tt d t dt 令180=τ，则：975.218=t ℃。

第三章 非稳态导热习题例3.1一腾空置于室内地板上的平板电热器，加在其上的电功率以对流换热和辐射换热的方式全部损失于室内。

电热器表面和周围空气的平均对流换热系数为h ，且为常数，室内的空气温度和四壁、天花板及地板的温度相同,均为t f 。

电热器假定为均质的固体,密度为ρ，比热为c ，体积为V , 表面积为A ，表面假定为黑体，因其导热系数足够大，内部温度均布.通电时其温度为t 0。

试写出该电热器断电后温度随时间变化的数学描述. ［解] 根据题意，电热器内部温度均布,因此可用集中参数分析法处理。

电热器以辐射换热方式散失的热量为：44r f ()A T T σΦ=- （1）以对流换热方式的热量为：c f ()hA T T Φ=- (2）电热器断电后无内热源,根据能量守恒定律，散失的热量应等于电热器能量的减少。

若只考虑电热器的热力学能r c d d TcVρτ-Φ-Φ= (3） 因此,相应的微分方程式为：44f f d ()()d TA T T hA T T cVσρτ-+-=- （4) 初始条件为：τ=0， t =t 0 （5）上述两式即为该电热器断电后温度随时间变化的数学描述。

例 3.2 电路中所用的保险丝因其导热系数很大而直径很小可视为温度均布的细长圆柱体，电流的热效应可视为均匀的内热源。

如果仅考虑由于对流换热的散热量,保险丝表面和温度为t f 的周围空气之间的平均对流换热系数为h ，且为常数。

试求该保险丝通电后温度随时间的变化规律.［解］ 根据题意，保险丝内部温度均布,因此可用集中参数分析法处理. 保险丝表面以对流换热方式散失的热量为：c f ()hA T T Φ=- （1）保险丝的内热源为：Q 0=IR 2 （2）式中：I -—保险丝通过的电流，(A ）； R -—保险丝的电阻，Ω。

根据能量守恒，散失的热量与内热源所转变成的热量的和应等于保险丝能量的变化。

若只考虑保险丝的热力学能c 0d d TQ cVρτ-Φ+= （3）因此,相应的微分方程式为：2f d ()d ThA T T I R cVρτ--=- （4） 初始条件为：τ=0, t =t f (5)上述两式即为该保险丝通电后温度随时间变化的数学描述.令2f I Rt t hAθ=--，则上述微分方程改写为d d ρθθτ=-cV hA (6）该微分方程的解为θθτθρ=-=-00exp()exp(BiFo)hAcV(7） 以温度t 表示该解τρ--=---22f 0f (）exp()I R I R hAt t t t hA hA cV（8）由初始条件τ=0， t 0= t f ，该式可写为τρ-=--2f [1exp()]I R hAt t hA cV（9）上式即为该保险丝通电后温度随时间的变化规律，从中可以看出内热源对保险丝的温度变化的作用.例3.3 一块厚10 mm 的纯铝板置于温度为10 ℃的空气中，铝板和空气之间的平均对流换热系数h =10 W/(m 2·K ），且为常数.求该铝板从100 ℃降到20 ℃所需时间及当时的热流密度。

第3章思考题1. 试说明集总参数法的物理概念及数学处理的特点答：当内外热阻之比趋于零时，影响换热的主要环节是在边界上的换热能力。

而内部由于热阻很小而温度趋于均匀，以至于不需要关心温度在空间的分布，温度只是时间的函数， 数学描述上由偏微分方程转化为常微分方程、大大降低了求解难度。

2. 在用热电偶测定气流的非稳态温度场时,怎么才能改善热电偶的温度响应特性? 答：要改善热电偶的温度响应特性，即最大限度降低热电偶的时间常数hA cv c ρτ=,形状上要降低体面比，要选择热容小的材料，要强化热电偶表面的对流换热。

3. 试说明”无限大平板”物理概念,并举出一二个可以按无限大平板处理的非稳态导热问题 答；所谓“无限大”平板，是指其长宽尺度远大于其厚度，从边缘交换的热量可以忽略 不计，当平板两侧换热均匀时，热量只垂直于板面方向流动。

如薄板两侧均匀加热或冷却、 炉墙或冷库的保温层导热等情况可以按无限大平板处理。

4. 什么叫非稳态导热的正规状态或充分发展阶段?这一阶段在物理过程及数学处理上都有些什么特点?答：非稳态导热过程进行到一定程度,初始温度分布的影响就会消失，虽然各点温度仍 随时间变化,但过余温度的比值已与时间无关，只是几何位置(δ/x )和边界条件(Bi 数)的函数，亦即无量纲温度分布不变，这一阶段称为正规状况阶段或充分发展阶段。

这一阶段的数学处理十分便利，温度分布计算只需取无穷级数的首项进行计算。

5. 有人认为,当非稳态导热过程经历时间很长时,采用图3-7记算所得的结果是错误的.理由是： 这个图表明,物体中各点的过余温度的比值与几何位置及Bi 有关,而与时间无关.但当时间趋于无限大时,物体中各点的温度应趋近流体温度,所以两者是有矛盾的。

你是否同意这种看法,说明你的理由。

答：我不同意这种看法，因为随着时间的推移，虽然物体中各点过余温度的比值不变 但各点温度的绝对值在无限接近。

这与物体中各点温度趋近流体温度的事实并不矛盾。

传热学3-7章问答题及答案第三章非稳态热传导一、名词解释非稳态导热：物体的温度随时间而变化的导热过程称为非稳态导热。

数Bi ：Bi 数是物体内部导热热阻λδ与表面上换热热阻h 1之比的相对值，即：λδh Bi =o F 数：傅里叶准则数2τl a Fo =，非稳态过程的无量纲时间，表征过程进行的深度。

二、解答题和分析题1、数Bi 、o F 数、时间常数c τ的公式及物理意义。

答：数Bi ：λδh Bi =，表示固体内部导热热阻与界面上换热热阻之比。

2τl a Fo =，非稳态过程的无量纲时间，表征过程进行的深度。

hA cVc ρτ=，c τ数值上等于过余温度为初始过余温度的36.8%时所经历的时间。

2、0→Bi 和∞→Bi 各代表什么样的换热条件？有人认为0→Bi 代表了绝热工况，是否正确，为什么？答：1）0→Bi 时，物体表面的换热热阻远大于物体内部导热热阻。

说明换热热阻主要在边界，物体内部导热热阻几乎可以忽略，因而任一时刻物体内部的温度分布趋于均匀，并随时间的推移整体地下降。

可以用集总参数法进行分析求解。

2）∞→Bi 时，物体表面的换热热阻远小于物体内部导热热阻。

在这种情况下，非稳态导热过程刚开始进行的一瞬间，物体的表面温度就等于周围介质的温度。

但是，因为物体内部导热热阻较大，所以物体内部各处的温度相差较大，随着时间的推移，物体内部各点的温度逐渐下降。

在这种情况下，物体的冷却或加热过程的强度只决定于物体的性质和几何尺寸。

3）认为0→Bi 代表绝热工况是不正确的，0→Bi 的工况是指边界热阻相对于内部热阻较大，而绝热工况下边界热阻无限大。

3、厚度为δ2，导热系数为λ，初始温度均匀并为0t 的无限大平板，两侧突然暴露在温度为∞t ，表面换热系数为h 的流体中。

试从热阻的角度分析0→Bi 、∞→Bi 平板内部温度如何变化，并定性画出此时平板内部的温度随时间的变化示意曲线。

答：1）0→Bi 时，平板表面的换热热阻远大于其内部导热热阻。

0
.
23
12

分别为：
.436
0
.20

1
2 1


s
0
.
46
1


t

t

q

1400

884
.
2


1116
.
8
℃
2
w


1
1
.
436
1

➢ 将求出的t2 与原假设的t2 相比较，若两者相差甚大，需重新计算。
重设t2=1120℃，计算的方法同上，中间过程略去，可以得到：
➢

s

0
.46
单位面积热阻：（1）导热热阻S/λ;
（2）对流给热热阻1/α
Si
多层：温度分布；热通量；界面温度的求解；
单位面积热阻:（1）导热热阻

i
（2）对流给热热阻1/ α
小
➢
结
对于一维圆筒壁：
单层：温度分布；热流量；
单位长度热阻:（1）导热热阻
1
d
ln 2
2 d 1
1
（2）对流给热热阻 d
多层：温度分布；热流量；界面温度的求解；
di1
1
单位长度热阻:（1）导热热阻
ln
2 d
i
i
（2）对流给热热阻 1
d
➢ 对于有内热源的情况：
温度分布，热通量或热流量均不为常数
热阻分析法的适用范围：一维、稳态、无内热源的情况。
临界绝热层：
2 x
dc
2
内容结构
1 稳态导热

第一章、基本内容：1、一双层玻璃窗，宽1.1m，高1.2m，厚3mm，导热系数为1.05W/(m·K)；中间空气层厚5MM，设空气隙仅起导热作用，导热系数为0.026W/(m·K)。

室内空气温度为25℃。

表面传热系数为20W/(m2·K)；室外空气温度为-10℃，表面传热系数为15W/(m2·K)。

试计算通过双层玻璃窗的散热量，并与单层玻璃窗相比较。

假定在两种情况下室内、外空气温度及表面传热系数相同。

解：(1)双层玻璃窗情形，由传热过程计算式：显然，单层玻璃窃的散热量是双层玻璃窗的2.6倍。

因此，北方的冬天常常采用双层玻璃窗使室内保温。

2、一外径为0.3m，壁厚为5mm的圆管，长为5m，外表面平均温度为80℃。

200℃的空气在管外横向掠过，表面传热系数为80W/(m2·K)。

入口温度为20℃的水以0.1m/s的平均速度在管内流动。

如果过程处于稳态，试确定水的出口温度。

水的比定压热容为4184J/(kg·K)，密度为980kg/m3。

解：(1)管外空气与管子之间的对流换热量：(2)由于过程处于稳态，管外空气所加的热量由管内水带走，因此，其中Ac为管内流通截面积。

故出口温度为：3、白天，地球表面接受来自太阳的辐射热流密度为669W/m2。

设地表空气与地面向的表面传热系数为30W/(m2·K)，空气温度为20℃。

设地球可以看成黑体表面，且地球对太空的辐射可看成是对0K黑体空间的辐射。

试确定地球表面的平衡温度。

解：由热平衡关系，地球接受来自太阳的辐射热量以两种方式散掉，即与空气的对流换热及与太空的辐射换热，设过程为稳态，有：。

将代入上式，得第二章、导热理论基础及稳态导热部分1、一直径为d。

，单位体积内热源的生成热Φ的实心长圆柱体，向温度为t∞的流体散热，表面传热系数为h。

试列出圆柱体中稳态温度场的微分方程式及定解条件。

解：()KTKTKmWhmWqskyf,293,30,66922==•==KTc300≈(2)单层玻璃窗情形：2、金属实心长棒通电加热,单位长度的热功率等于Φl(单位是W/m)，材料的导热系数λ，表面发射率ε、周围气体温度为t f，辐射环境温度为T sur，表面传热系数h均已知，棒的初始温度为t0。

Unsteady-state Conduction1应用背景•工业:金属热处理---淬火动力机械开车、关车精密机床的热变形•民用:地球气温的变化医疗中检测温度范围---激光手术(热疗法)生物传热---温度震荡3522xt t ∂∂=∂∂ατ0)0(t t ===τ∞===t t )0(τ],,,,,),[(0h x t t f t t λατδ∞∞−=−∞∞−−=Θt t t t 0δxX =λδh B i =20δατ=F ),,(o i F B X f =Θ过余温度比6Analytical solution for 1-D transient heat conductionFor an infinite plateλ=consta=const h=constIn a symmetrical system, we can just analyze half of itHeat fluxΦ－－板左侧导入的热流量1Φ－－板右侧导出的热流量216？？<Bi<∞什么是无量纲数？基本思想：当所研究的问题非常复杂，涉及到的参数很多，为了减少问题所涉及的参数，于是人们将这样一些参数组合起来，使之能表征一类物理现象，或物理过程的主要特征，并且没有量纲。

因此，这样的无量纲数又被称为特征数，或者准则数，比如，毕渥数又称毕渥准则。

以后会陆续遇到许多类似的准则数。

特征数涉及到的几何尺度称为特征长度，一般用符号l 表示。

对于一个特征数，应该掌握其定义式＋物理意义，以及定义式中各个参数的意义。

192124用诺谟求解非稳态导热问题的思路1,已知时间，求温度分布及热量mθθ2、已知温度分布，求时间25•Question: A large plate of steel 20.0cm thick and initially at 20℃is suddenly exposed to the heating environment of 1000℃with a heat transfer coefficient of 174W/m2.℃. Calculate the time required for the plate to attain a temperature of 500℃at the surface.(α=0.555×10-5m2/s, λ=34.8W/m.℃)When Bi=0.1, μ1=0.3111 radBi=0.5, μ1=0.6533 radBi=1.0, μ1=0.8603 rad2629For a random body,τ=0, t=t 0It is suddenly immersed into a cool fluid that t= t ∞<t 0Using energy conservation principal,τρd dtVct t hA -)(=−∞过余温度— ∞−=t t θ, thencq d dt vρτ=dθhA =− dτ θ ρVcIntegral⇒ ⇒hA τ ∫θ0 = − ∫0 dτ θ ρVcθdθ⇒Where,hA θ ln =− τ θ0 ρVc⇒θ t − t∞ Θ= = =e θ 0 t0 − t∞−hA τ ρVchA hV λA2 τ= ⋅ 2 τ ρcV λA V ρc = h(V A)λaτ ⋅ = Biv ⋅ Fov 2 (V A)Bi v =h (V A )λaτ Fo v = (V A ) 2θ =e θ0Where,hA τ − ρ Vc=e− Bi v ⋅ Fo vThe temperature field is an exponential curve⎡ W ⎤ ⎡ 2⎤ ⋅ m ⎢ ⎥ 2 hA w 1 ⎣m K⎦ ⎣ ⎦ = = = J s ρVc ⎡ kg ⎤ ⎡ Jkg ⎤ 3 ⎢ 3 ⎥⋅⎢ K ⎥[m ] ⎣m ⎦ ⎣ ⎦32Thant means whenτ=ρVchA，thenhA τ⋅ =1 ρVcθ = e −1 = 36.8% θ0ρVc上式表明：当传热时间等于hA 余温度已经达到了初始过余温度的36.8％。