直流电动机的模型

《直流电动机模型》把直流电能转换成机械能，并输出机械转矩的电动机称为直流电动机，它用动力设备的最大特点是转矩大，能够均匀平滑地调节转速。

因此，在需要调节转速的生产机械，常用直流电动机来拖动。

直流电机直流电机外形图直流电机接线盒（红色接正极S黑色損负直流电源正极（红色）硅整流变压器直流电源负极（黑色）直流伺服电动机它使用直流电源的伺服电动机，实质上就是他励直流电动机，主磁极磁场绕组的励磁电流由另外的直流电源供电，与电枢电路没有电的联接。

定子由硅钢片冲制迭压而成，磁极和磁轭相连，它的优点是调速范围宽广而平滑，利用电枢控制，可有直线性的调速特性，超支转矩大，反应灵敏，缺点是有换向器和电刷的滑动接触，常因接触不良，而影响运行的稳定性。

电源攝头（接入220V电源）直流伺服电机直流电机接线盒直流电源正根（红色）直流伺服电机外形图（红色接正极、黒色摄负《自整角电动机》此自整角电机为两极的隐极式结构，为获得较好的参数配合，提高运行性能，三相整步绕组放在定子铁心上，励磁绕组放在转子铁心上，并由两组电刷、戈U环引出。

定子各相绕组轴线在空间互差120度。

自整角机外形图三相绕线式电动机模型本模型外壳为透明有机玻璃制作，它一般由转轴、转子绕组、端盖、轴承、定子绕组、转子、定子、集电环、电刷、刷架、出线盒等组成。

其定子结构与鼠笼电动机一样，接成三相对称绕组，直接通入三相交流电。

绕线型转子绕组由绝缘导线制成绕组元件，嵌放在转子铁心槽内，然后连接成对称的三相绕组，一般采用星形连接，三相引出线接到固定在转轴上三个互相绝缘的集电环上，由集电环上的电刷引出与外面接线端子连接。

也可直接闭路，亦可在转子回路中接入附加电阻。

以改善起动性能和对电机调速。

可宜接短接、可接入电湄（出厂时为直灘接）把插头插入低压电源11插座，便可演示绕线电动机外观图三相同步电动机模型模型外壳为透明有机玻璃制成，它主要有定子、转子两大部分组成，其定子和异步电动机定子结构相似，磁极装在转子上，三相绕组装在定子上。

永磁⽆刷直流电机的数学模型 ⽆刷直流电机绕组中产⽣的感应电动势与电机转速匝数成正⽐，电枢绕组串联公式为 其中，E为⽆刷直流电机电枢感应线电动势（V）；p为电机的极对数；α为极弧系数；W为电枢绕组每相串联的匝数；φ为每极磁通（Wb）；n为转速（r／min）。

在反电动势E和极对数p已经确定的情况下，为使电机具有较⼤的调速范围，就须限制电枢绕组的匝数W。

因此，磁悬浮飞轮电机绕组电感和电阻都⾮常⼩，使得电机在运⾏过程中，相电流可能存在不连续状态。

假定电机定⼦三相完全对称，空间上互差120°电⾓度；三相绕组电阻、电感参数完全相同；转⼦永磁体产⽣的⽓隙磁场为⽅波，三相绕组反电动势为梯形波；忽略定⼦绕组电枢反应的影响；电机⽓隙磁导均匀，磁路不饱和，不计涡流损耗；电枢绕组间互感忽略。

公式中，Va、Vb、Vc和Vn分别为三相端电压和中点电压（V），R和E为三相电枢绕组电阻（Ω）和电感（H），Ea、Eb和Ec为三相反电动势（V），ia、ib．和ic为三相绕组电流（A）。

可将⽆刷直流电机每相绕组等效为电阻、电感和反电动势串联。

⽆刷直流电机绕组采⽤三相星形结构，数学模型⽅程如式(2-2)所⽰： 在电机运⾏过程中，电磁转矩的表达式为 电机的机械运动⽅程为 式中，Te和TL分别为电磁转矩和负载转矩（Nm）；J为转⼦的转动惯量（kg·2m）；f为阻尼系数（N·m·s）。

电机设计反电动势为梯形波，其平顶宽度为120°电⾓度，梯形波的幅值与电机的转速成正⽐。

其中，反电动势系数乃e由以下公式计算为 电机转⼦每运⾏60°电⾓度进⾏⼀次换相，因此在每个电⾓度周期中，三相绕组反电动势有6个状态。

电机运⾏过程中瞬态功耗的公式为 其中，Ω为电机⾓速度，P为功耗。

永磁⽆刷直流电机的控制可分为三相半控、三相全控两种。

三相半控电路的特点简单，－个可控硅控制⼀相的通断，每个绕组只通电1／3的时间，另外2／3时间处于断开状态，没有得到充分的利⽤。

直流电机工作原理图解一.直流电机的物理模型图解释。

这是分析直流电机的物理模型图。

其中，固定部分有磁铁，这里称作主磁极；固定部分还有电刷。

转动部分有环形铁心和绕在环形铁心上的绕组。

(其中2个小圆圈是为了方便表示该位置上的导体电势或电流的方向而设置的)上图表示一台最简单的两极直流电机模型，它的固定部分（定子）上，装设了一对直流励磁的静止的主磁极N和S，在旋转部分（转子）上装设电枢铁心。

定子与转子之间有一气隙。

在电枢铁心上放置了由A和X两根导体连成的电枢线圈，线圈的首端和末端分别连到两个圆弧形的铜片上，此铜片称为换向片。

换向片之间互相绝缘，由换向片构成的整体称为换向器。

换向器固定在转轴上，换向片与转轴之间亦互相绝缘。

在换向片上放置着一对固定不动的电刷B1和B2，当电枢旋转时，电枢线圈通过换向片和电刷与外电路接通。

二.直流发电机的工作原理直流发电机是机械能转换为直流电能的电气设备。

如何转换？分以下步骤说明：设原动机拖动转子以每分转n转转动；电机内部的固定部分要有磁场。

这个磁场可以是如图示的磁铁也可以是磁极铁心上绕套线圈，再通过直流电产生磁场。

其中 If 称之为励磁电流。

这种线圈每个磁极上有一个，也就是，电机有几个磁极就有几个励磁线圈，这几个线圈串联（或并联）起来就构成了励磁绕组。

这里要注意各线圈通过电流的方向不可出错。

在以上条件下环外导体将感应电势，其大小与磁通密度 B 、导体的有效长度 l 和导体切割磁场速度 v 三者的乘积成正比，其方向用右手定则判断。

但是要注意某一根转子导体的电势性质是交流电。

而经电刷输出的电动势确是直流电了。

这便是直流发电机的工作原理。

如下动画演示：三.直流电动机的工作原理直流电动机的原理图对上一页所示的直流电机，如果去掉原动机，并给两个电刷加上直流电源，如上图（a）所示，则有直流电流从电刷 A 流入，经过线圈abcd，从电刷 B 流出，根据电磁力定律，载流导体ab和cd收到电磁力的作用，其方向可由左手定则判定，两段导体受到的力形成了一个转矩，使得转子逆时针转动。

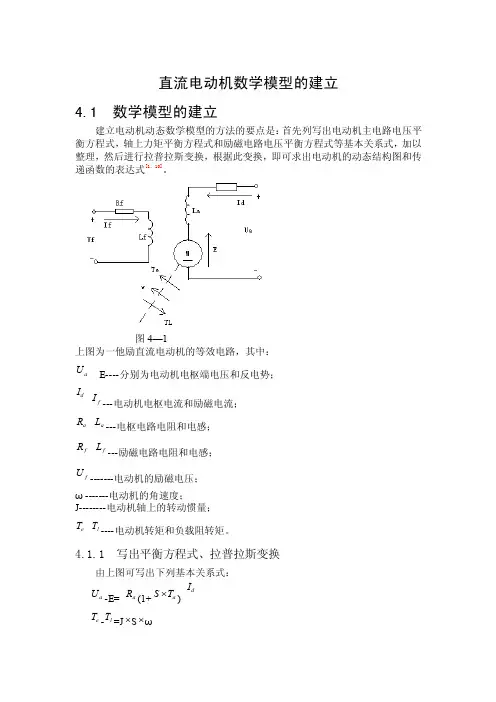
直流电动机数学模型的建立4.1 数学模型的建立建立电动机动态数学模型的方法的要点是：首先列写出电动机主电路电压平衡方程式，轴上力矩平衡方程式和励磁电路电压平衡方程式等基本关系式，加以整理，然后进行拉普拉斯变换，根据此变换，即可求出电动机的动态结构图和传递函数的表达式[1，10]。

图4—1上图为一他励直流电动机的等效电路，其中：a U E----分别为电动机电枢端电压和反电势；d I f I ---电动机电枢电流和励磁电流；a R a L ---电枢电路电阻和电感；fR f L ---励磁电路电阻和电感； f U -------电动机的励磁电压；ω-------电动机的角速度；J--------电动机轴上的转动惯量；e T l T ----电动机转矩和负载阻转矩。

4.1.1 写出平衡方程式、拉普拉斯变换由上图可写出下列基本关系式：a U -E= a R (1+a T S ⨯) d Ie T -l T =J ⨯S ⨯ωf U = f R ()f f I T S ⨯⨯+1E=ωωφ⨯⨯⨯=⨯⨯f e I M p KTe=df d m I I M p I K ⨯⨯⨯=⨯⨯φ 其中:a a a R L T = 为电枢电路时间常数；f f f R L T = 为励磁电路时间常数；p 为电动机磁极对数；M 为励磁绕组和电枢绕组的互感；4.1.2 动态结构图将S=d/dt 看作算子，则上述诸式也就是它们的拉氏变换。

所以由上式可画出直流电动机的结构。

如图4—2所示。

图4—2如果将讨论的问题限制在稳态工作点附近的小偏差情况，经过化简，可得此时系统的增量方程为：d a a a I T S R E U ⨯⨯+⨯=-)1(ω⨯⨯=-S J T T l ef f f f I T S R U ⨯⨯+⨯=)1( 00Ω⨯⨯⨯+⨯⨯⨯=f f I M p I M p E ω0d f d f e I I M p I I M p T ⨯⨯⨯+⨯⨯⨯= 为简化起见，式中表示增量的下标1已删去。

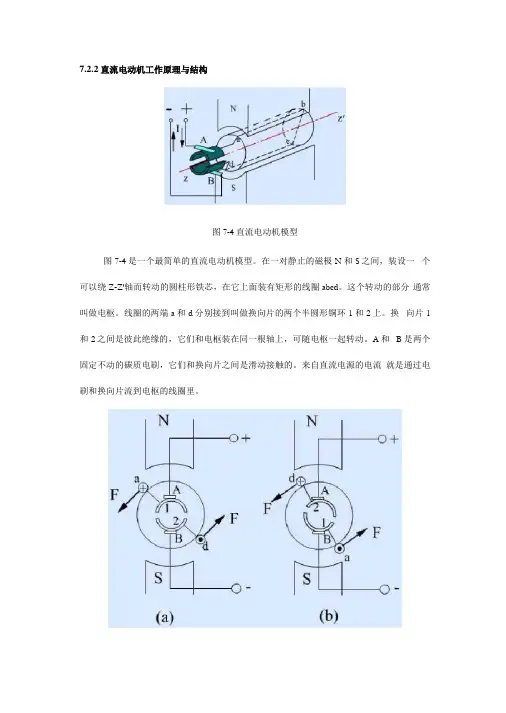
7.2.2直流电动机工作原理与结构图7-4直流电动机模型图7-4是一个最简单的直流电动机模型。

在一对静止的磁极N和S之间，装设一个可以绕Z-Z'轴而转动的圆柱形铁芯，在它上面装有矩形的线圈abcd。

这个转动的部分通常叫做电枢。

线圈的两端a和d分别接到叫做换向片的两个半圆形铜环1和2上。

换向片1和2之间是彼此绝缘的，它们和电枢装在同一根轴上，可随电枢一起转动。

A和B是两个固定不动的碳质电刷，它们和换向片之间是滑动接触的。

来自直流电源的电流就是通过电刷和换向片流到电枢的线圈里。

图7-5换向器在直流电机中的作用当电刷A和B分别与直流电源的正极和负极接通时，电流从电刷人流入，而从电刷B流出。

这时线圈中的电流方向是从a流向b,再从c流向d。

我们知道，载流导体在磁场中要受到电磁力，其方向由左手定则来决定。

当电枢在图7-5(a)所示的位置时，线圈ab 边的电流从a流向b,用于表示，cd边的电流从c流向d,用。

表示。

根据左手定则可以判断出，ab边受力的方向是从右向左，而cd边受力的方向是从左向右。

这样，在电枢上就产生了反时针方向的转矩，因此电枢就将沿着反时针方向转动起来。

当电枢转到使线圈的ab边从N极下面进入$极，而cd边从S极下面进入N极时，与线圈a端联接的换向片1跟电刷B接触，而与线圈d端联接的换向片2跟电刷A接触，如图7-5 (b)所示。

这样，线圈内的电流方向变为从d流向c,再从b流向a,从而保持在N极下面的导体中的电流方向不变。

因此转矩的方向也不改变，电枢仍然按照原来的反时针方向继续旋转。

由此可以看出，换向片和电刷在直流电机中起着改换电枢线圈中电流方向的作用。

直流电机工作原理和结构一、直流电机工作原理直流发电机的工作原理直流电动机的工作原理电机的可逆运行原理两个定理与两个定则1、电磁感应定理在磁场中运动的导体将会感应电势，若磁场、体和导体的运动方向三者互相垂直，则作用导体中感应的电势大小为： e = B・l・v电势的方向用右手定则2.电磁力定律载流导体在磁场中将会受到力的作用，若磁场与载流导体互相垂直（见下图），作用在导体上的电磁力大小为：f = B」・i力的方向用左手定则（一）直流发电机的工作原理1.直流发电机的原理模型time01.1. A亘樵发电机工作原理电刷引击电势无书感题也势如LE 直流发电机工作原理2.发电机工作原理a、直流电势产生用电动机拖动电枢使之逆时针方向恒速转动，线圈边a b和c d分别切割不同极性磁极下的磁力线，感应产生电动势直流发电机的工作原理就是把电枢线圈中感应产生的交变电动势，靠换向器配合电刷的换向作用，使之从电刷端引出时变为直流电动势因为电刷A通过换向片所引出的电动势始终是切割N极磁力线的线圈边中的电动势。

直流电机的模型建立与参数辨识直流电机是一种常见的电动机，广泛应用于各个领域，如工业生产、交通运输和家用电器等。

为了控制和优化直流电机的性能，我们需要建立一个准确的数学模型，并确定模型的参数。

本文将详细介绍直流电机的模型建立与参数辨识方法。

1. 直流电机模型直流电机可以简化为一种旋转的能量转换装置，它将直流电能转换为机械能。

直流电机模型通常分为两种：简化模型和详细模型。

简化模型是基于电机的基本原理和假设，通过几个关键参数来近似描述电机的行为。

其中最常用的模型是电力模型和电流模型。

电力模型假设电机转速保持恒定，可以通过电源电压和电机电流来估算电机输出的功率。

电流模型假设电机的电压保持恒定，可以通过电流和转矩关系来估算电机的转速。

详细模型则更加精确，考虑了电机的动态响应，包括电枢电压、反电动势、电感和电阻等因素。

详细模型可以通过Kirchhoff电路定律和电机的物理特性方程来建立。

其中最常用的是Laplace域模型和状态空间模型。

2. 直流电机参数辨识方法直流电机的参数辨识是指通过实验数据来确定模型的参数，以准确描述电机的动态行为。

常用的参数辨识方法有试验法和辨识法。

试验法是通过对电机进行一系列实验观测，采集电机的输入输出数据，并应用数学统计方法来估计参数值。

试验法需要在实际工作条件下进行，确保测试环境的准确性和稳定性。

辨识法是一种基于最优化理论的方法，通过对已知输入输出数据进行数学建模，并利用最小二乘法或其它最优化算法来求解最优参数。

辨识法可以基于频域或时域数据进行辨识，常用的方法有傅里叶变换法、极小二乘法和卡尔曼滤波法等。

辨识方法的选择应根据实际需求和可用数据的特点来确定。

试验法较为简单，适用于实验室环境下的实际测试；辨识法更加精确，适用于手头有大量数据并希望得到相对准确的参数估计的情况。

3. 直流电机参数辨识的挑战直流电机参数辨识虽然在理论上可行，但实际上会面临一些挑战。

首先，直流电机的参数具有不确定性和非线性，由于摩擦力、磁阻力和电机内部热量等因素的影响，电机的参数在不同操作条件下会有所变化。