下载文档原格式
电流型PWM整流器的SVPWM控制及仿真研究王鹤霖;程启明;郭凯;李明;陈根【摘要】为解决三相电流型PWM整流器的拓扑结构带来的系统阶次增加、并联谐振等问题,详细介绍了三相CSR的空间电流矢量的控制方法,包括系统的数学建模、控制策略、信号发生和实现调制等.在Matlab/Simulink软件平台进行了三相CSR 双闭环解耦SVPWM控制方法的仿真,并通过与传统的SPWM控制方法进行对比,验证了该控制方法具有更好的动、静态特性,且动态响应快,能有效抑制网侧谐波,实现单位功率因数运行.该方法为三相CSR的控制方法提供了新思路,具有一定的理论和实际应用价值.【期刊名称】《自动化仪表》【年(卷),期】2016(037)001【总页数】5页(P16-20)【关键词】PWM整流器;空间电流矢量;双闭环解耦控制;电压型PWM整流器;空间矢量脉宽调制【作者】王鹤霖;程启明;郭凯;李明;陈根【作者单位】上海电力学院自动化工程学院,上海200090;上海电力学院自动化工程学院,上海200090;上海电力学院自动化工程学院,上海200090;上海电力学院自动化工程学院,上海200090;上海电力学院自动化工程学院,上海200090【正文语种】中文【中图分类】TP273;TH71近年来，基于电流型PWM整流器(current source PWM rectifier，CSR)同电压型PWM整流器(voltage source PWM rectifier，VSR)相比，具有输入功率因数可调、谐波电流抑制、短路保护和降压等优点，目前已在超导储能、电池组充电、电能质量调节器等场合有着广泛的应用[1]。
在拓扑组成上，电压型和电流型PWM整流器具有对偶的结构特征，因此基于VSR的一些先进控制策略可以同理直接移植至CSR控制中去，如电压定向控制、预测模型控制、直接功率控制等[2] 。
但是，由于CSR在交流输入侧增加了LC滤波环节，不仅增加了系统阶次，而且会引起并联谐振的问题，这就给系统中各控制参数的确定和优化增加了难度，因此有关CSR的控制策略优化方面还需进一步深入研究[3]。
收稿日期:2004-09-06作者简介:李燕(1973)),女,广西人,讲师,硕士,研究方向:电力电子与运动控制,DSP 技术。
文章编号:1003-6199(2004)04-0067-03基于DSP 的恒压频比控制SVPWM 方式的研究和实现李 燕1,林忠岳2,田 茂2(1.广西民族学院电子与通信工程系,广西南宁 530006;2.广西大学电气工程学院,广西南宁 530004)摘 要:电压空间矢量(SVPW M )调制方式把逆变器和电机看作一个整体处理,具有所得模型简单,便于数字化实现,并具有转矩脉动小、噪声低、电压利用率高等优点。
近年来在变频调速系统中逐渐得到了应用和重视。
本文叙述了空间电压矢量的基本原理,讨论了不对称SVPWM 波形及两种对称SVPWM 波形的产生方法及优缺点。
利用数字信号处理器TM S 320F240产生基于恒压频比控制的对称S VPWM 调制波形,实验结果表明S VPWM 的调制波,和准优化PW M 有异曲同工之处,其实质也是一种带谐波注入的调制方法。
关键词:电压空间矢量;V/F(恒压频比)控制;DSP(数字信号处理器)中图分类号:TM 921 文献标识码:AResearch and Realize the S VPWM under V/F Control Based on DSPLI Yan 1,LIN Zhong -yue 2,TIAN Mao2(1.Department of Electronic and T elecommunication,Guangx i U niversity for Nationalities,Nanning 530006,China;2.College of Electrical Eng ineering,Guang xi University,Nanning 530004,China)Abstract:Th e inverter and motor is Treated as one part in voltage space-vector.So it has simple model and can be reali z ed using di gital tech -nic.Low torque pulse,low noise and high using rate of voltage is the advantage of SVPWM.The fundamental principle of voltage space-vector (S VPWM )is recounted in this paper.The present paper discusses advantages and disadvantages betw een asymmetrical SVPWM w ave and sym met -rical SVPWM w ave.The method of producing S VPWM is al so presented.Symmetrical S VPW M w ave under V/F control is produced using digital signal processor TM S320F240i n the paper.T he w ave produced by SVPWM is similar with optimizati on PW M.Key words :voltage space-vector;V/F control;DS P1 引言变频调速系统目前应用最为广泛的是恒压频比(U /F)控制。
基于SVPWM的无刷直流电机控制策略的研究作者：贺海波来源：《科学与财富》2018年第14期摘要：方波控制下无刷直流电机（BLDCM）运行过程中转矩脉动大、换相噪声明显。
针对上述问题，提出了基于SVPWM的无刷直流电机磁场定向控制策略。
通过转子磁场定向，实现了无刷直流电机电磁转矩与转子磁链的自然解耦。
建立Smulink仿真平台完成对所提算法的建模，进一步验证了控制方案的可行性，通过对比仿真波形曲线可知，矢量控制下电机达到稳态所需上升时间较短，能较快速跟随目标转速，有较好的动态调速性能，同时抗干扰动性能力强，电机稳定性更好，转矩脉动更小。
关键词：无刷直流电机；SVPWM；磁场定向；0 引言无刷直流电机（BLDCM）相比于有刷直流电机及交流电机具有其自身的许多优点，如调速性能优良，动态响应迅速，速度/扭矩性能好以及使用寿命长等。
现今，无刷直流电机在汽车、家电、计算机、工业、医疗、航空航天等领域得到了广泛应用[1，2]。
由于传统PID控制器具有算法简单、稳定和可靠性高等优点，因此广泛应用于速度控制系统[3]。
传统的无刷直流电机一般都采用方波控制，算法简单，易于控制，但噪声高，而且转矩脉动大，对电机控制效率不高[4]。
本文从电机的动态数学模型出发，推导了高性能调速方案的控制模型。
通过与传统的方波控制比较，证明利用矢量控制来控制BLDCM更具优越性。
并利用Simulink搭建无刷直流电机矢量控制系统图，得到转速、电流和转矩的仿真波形，并对实验数据进行理论分析，进一步验证了控制方案的可行性。
1 无刷直流电机数学模型以两相导通星型连接的三相六状态作为研究对象建立数学模型，需做以下假设[5]：1、参数相同且保持恒定，电机的气隙磁感应强度在空间呈梯形分布；2、忽略定子铁心齿槽效应和空间谐波；3、定子与转子之间气隙均匀，不计磁路饱和，不考虑电枢反应。
4、不计涡流和磁滞损耗，转子上没有阻尼绕组；通过电机的电压方程经过Clark变换和Park变换得到在同步旋转坐标系下的数学模型。
![一种基于FPGA的简化SVPWM算法的实现方法[发明专利]](https://img.taocdn.com/s1/m/3d54ecbb85868762caaedd3383c4bb4cf7ecb730.png)
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号 (43)申请公布日 (21)申请号 201911009938.9(22)申请日 2019.10.22(71)申请人 哈尔滨理工大学地址 150080 黑龙江省哈尔滨市南岗区学府路52号(72)发明人 勾金雷 田晓华 王建民 (74)专利代理机构 哈尔滨市松花江专利商标事务所 23109代理人 杨立超(51)Int.Cl.H02P 27/12(2006.01)H02P 6/08(2016.01)(54)发明名称一种基于FPGA的简化SVPWM算法的实现方法(57)摘要一种基于FPGA的简化SVPWM算法的实现方法，涉及逆变器控制技术领域。
本发明为了解决采用传统SVPWM算法利用FPGA实现时存在运算过程计算量较大、占用大量逻辑单元、运算速度较低的问题。
定义两电平三相电压源逆变器电路逆变电路，简化SVPWM算法扇区判断条件，简化SVPWM算法相邻矢量作用时间。
本发明方法运算过程计算量较小，不会占用大量逻辑单元，运算速度较高。
使用简化SVPWM算法，直接用三相电压进行扇区判断，并计算相邻矢量作用时间。
本发明通过modelsim仿真验证了其可行性。
权利要求书4页 说明书9页 附图8页CN 110649860 A 2020.01.03C N 110649860A1.一种基于FPGA的简化SVPWM算法的实现方法，其特征在于：所述方法的具体过程为：步骤一、定义两电平三相电压源逆变器电路逆变电路定义6个开关量Sa、Sb、Sc、Sa′、Sb′、Sc′，表示逆变器中六个功率开关器件的开断；前三个参数是上桥臂开关量，代表0或1，0代表关断，1代表开启；后三个参数是下桥臂开关量，代表0或1，0代表关断，1代表开启；当上桥臂的开关器件导通时，Sa、Sb、Sc为1，其下桥臂的开关器件关断，即Sa′、Sb′、Sc′为0；反之，当Sa、Sb、Sc为0时，下桥臂的开关器件开通，即Sa′、Sb′、Sc′为1；逆变器同一桥臂中的开关器件不会发生同时开通或关断的情况，逆变器一共就拥有8种开关状态组合；交流侧相电压与开关函数之间关系为：式中：U dc表示直流母线电压；s a、s b、s c表示三个上桥臂开关量；V AN、V BN、V CN表示交流侧相电压；对于不同的开关状态组合可得到8个基本电压空间矢量，逆变器的8种开关模式就对应8个电压空间矢量，各矢量为：将(2)式进行简化，如(3)式：将逆变器每个开关状态所对应的输出相电压代人(3)式，则电压源型逆变器能够输出的电压空间矢量共有8个，分别命名为V0(000)，V1(001)，V2(010)，V3(011)，V4(100)，V5 (101)，V6(110)，V7(111)；其中V0(000)、V7(111)所对应的输出电压为零，称其为零矢量；其余6个所对应的输出电压不为零，称其为有效矢量；有效矢量的幅值均为2U dc/3；j代表虚部；6个有效矢量相互之间的夹角为60°，将整个平面分成6个扇区；SVPWM通过这八个空间矢量去等效参考电压空间矢量U out，进而在电动机空间形成圆形旋转磁场；步骤二、简化SVPWM算法扇区判断条件为方便计算简化(3)式得：由欧拉公式对(6)式进行变换为:由式(7)可知步骤三、简化SVPWM算法相邻矢量作用时间。
SVPWM算法研究与试验应用SVPWM算法是一种针对空间矢量调制技术的高级控制算法，用于对三相交流电机进行精密控制。
该算法可以通过改变参考电压矢量的相位和大小，控制电机的电流和速度，并且具有较高的动态响应能力和控制精度。
SVPWM算法的基本原理是通过将三相交流电压转换为一个空间矢量，并将其控制在一个特定的方向和大小，从而实现电机驱动控制。
具体而言，该算法将三相电压看作一个三角形，通过通过调整参考电压的大小和相位，控制电机的电流和速度。
其中，电机的电流和速度与参考电压的相位差和大小有关。
SVPWM算法适用于多种交流电机驱动控制，如变频空调、电动汽车、电动机、风电等领域，广泛应用于工业自动化和控制系统中。
在实际应用中，为了提高算法的可靠性和灵活性，通常需要通过建立基于SVPWM算法的电机模型和控制系统，进行动态仿真和试验分析，以验证控制算法的性能和有效性。
在电机控制系统中，SVPWM算法通常与其他控制算法组合使用，如PID控制、电流矢量控制、位置控制等，实现更加稳定和高效的电机驱动控制。
同时，也需要针对不同应用场景和电机参数调整控制系统的参数和配置，以保证控制系统的效率和精度。
总之，SVPWM算法作为一种高级控制算法，在工业自动化和控制系统中具有广泛的应用前景。
通过建立电机模型和控制系统，可以实现SVPWM算法的实验验证和优化，同时也可以使控制系统更加灵活和智能，为电机控制和工业应用带来更大的价值和效益。
为了更好地了解市场变化和消费者需求，许多公司会收集大量的数据并进行分析。
以下是一些可能的相关数据，以及对其进行分析的例子。
1. 销售额数据：通过对销售额数据进行分析，公司可以了解销售趋势和产品受欢迎程度。
例如，如果一家服装公司发现一种特定的衣服款式最近的销售额增加了很多，那么他们可能会考虑生产更多这种衣服款式。
2. 消费者调研数据：消费者调研数据可以帮助公司了解消费者的喜好和需求，从而制定更好的营销策略和产品开发计划。
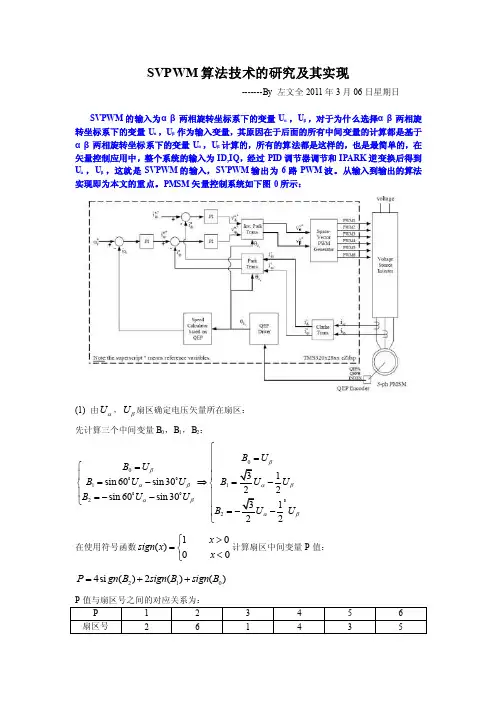
SVPWM 算法技术的研究及其实现-------By 左文全2011年3月06日星期日SVPWM 的输入为αβ两相旋转坐标系下的变量U α，U β，对于为什么选择αβ两相旋转坐标系下的变量U α，U β作为输入变量，其原因在于后面的所有中间变量的计算都是基于αβ两相旋转坐标系下的变量U α，U β计算的，所有的算法都是这样的，也是最简单的，在矢量控制应用中，整个系统的输入为ID,IQ ，经过PID 调节器调节和IPARK 逆变换后得到U α，U β，这就是SVPWM 的输入，SVPWM 输出为6路PWM 波。
从输入到输出的算法实现即为本文的重点。
PMSM 矢量控制系统如下图0所示：(1) 由U α，U β扇区确定电压矢量所在扇区： 先计算三个中间变量B 0，B 1，B 2：0011221sin 60sin 3022sin 60sin 30122B U B U B U U B U B U U B U ββαβαβαβαβ⎧⎪=⎧=⎪⎪⎪=-⇒=-⎨⎨⎪⎪=--⎩⎪=--⎪⎩在使用符号函数1()0x sign x x >⎧=⎨<⎩计算扇区中间变量P 值： 2104si ()2()()P gn B sign B sign B =++P 值与扇区号之间的对应关系为：图1 扇区分布图2扇区变量P与扇区SECTOR之间对应关系图3 扇区变量P与扇区SECTOR之间关系(2)确定单位矢量切换时间t1，t2：先计算三个中间变量X，Y，Z：1212X UY UZ Uβαβαβ⎧⎪=⎪⎪=+⎨⎪⎪=+⎪⎩如果t1+t2>1，则11122212ttt tttt t⎧=⎪+⎪⎨⎪=⎪+⎩；如果t1+t2<1，则t1,t2保持不变。
（这里用到的UALFA,UBETA 都是标幺值，计算出的t1，t2都是占空比）图4 T1，T2的波形图5 T1，T2的波形(3)利用t1,t2计算切换点T a，T b，T c：先计算中间变量Taon，Tbon，Tcon：1212(1)/2(0~1)aon bon a con b T t t T T t T T t=--⎧⎪=+⎨⎪=+⎩，则不同扇区内切换点T a ，T b ，T c 可有下表得到：(0.5)*2(0.5)*2(1~1)(0.5)*2a ab b cc T T T T T T =-⎧⎪=--⎨⎪=-⎩ 范围改变设PWM 周期为T pwm ，则T1PRD=T pwm /2：EvaRegs.CMPR1 = (int16)(T1Period/2+T1Period*Ta/2);EvaRegs.CMPR2 = (int16)(T1Period/2+T1Period*Tb/2);EvaRegs.CMPR3 = (int16)(T1Period/2+T1Period*Tc/2);图5 Taon，Tbon，Tcon的波形图6 Ta，Tb，Tc的波形图7 Ta，Tb，Tc的波形(4)接负载仿真：图4 负载相电流波形图5 负载相电压，线电压波形图6 示波器上滤波后负载相电压，线电压波形图7 总体仿真模型SVPWM实现的核心程序：//================================================================================ //IPark变换UD,UQ-->UALFA,UBETA获得给定信号//================================================================================ Ualfa = _IQmpy(Ud,Cosine) - _IQmpy(Uq,Sine);Ubeta = _IQmpy(Uq,Cosine) + _IQmpy(Ud,Sine);//================================================================================ //通过UALFA,UBETA确定扇区变量P//================================================================================ B0=Ubeta;B1=_IQmpy(_IQ(0.8660254),Ualfa)- _IQmpy(_IQ(0.5),Ubeta);// 0.8660254 = sqrt(3)/2B2=_IQmpy(_IQ(-0.8660254),Ualfa)- _IQmpy(_IQ(0.5),Ubeta); // 0.8660254 = sqrt(3)/2if(B0>_IQ(0)) P0=1;else P0=0;if(B1>_IQ(0)) P1=1;else P1=0;if(B2>_IQ(0)) P2=1;else P2=0;P=P0+2*P1+4*P2;//================================================================================ //通过扇区变量P确定扇区Sector//================================================================================ if(P==1) Sector=2;else if(P==2) Sector=6;else if(P==3) Sector=1;else if(P==4) Sector=4;else if(P==5) Sector=3;else if(P==6) Sector=5;if(i<256){Temp4[i]=P;Temp5[i]=Sector;//利用CCS Graph观察前先保证语句前的“//”号已经去掉i=i+1;if(i>=256) i=0;//利用CCS Graph观察扇区变量P与扇区}//================================================================================ //根据扇区Sector计算Ta,Tb,Tc//================================================================================ X=Ubeta;Y=_IQmpy(_IQ(0.8660254),Ualfa)+ _IQmpy(_IQ(0.5),Ubeta);// 0.8660254 = sqrt(3)/2Z=_IQmpy(_IQ(-0.8660254),Ualfa)+ _IQmpy(_IQ(0.5),Ubeta); // 0.8660254 = sqrt(3)/2if(Sector==1){t1=-Z;t2=X;Taon=_IQmpy(_IQ(0.5),(_IQ(1)-t1-t2));Tbon=Taon+t1;Tcon=Tbon+t2;Ta=Taon;Tb=Tbon;}else if(Sector==2){t1=Z;t2=Y;Taon=_IQmpy(_IQ(0.5),(_IQ(1)-t1-t2));Tbon=Taon+t1;Tcon=Tbon+t2;Ta=Tbon;Tb=Taon;Tc=Tcon;}else if(Sector==3){t1=X;t2=-Y;Taon=_IQmpy(_IQ(0.5),(_IQ(1)-t1-t2));Tbon=Taon+t1;Tcon=Tbon+t2;Ta=Tcon;Tb=Taon;Tc=Tbon;}else if(Sector==4){t1=-X;t2=Z;Taon=_IQmpy(_IQ(0.5),(_IQ(1)-t1-t2));Tbon=Taon+t1;Tcon=Tbon+t2;Ta=Tcon;Tc=Taon;}else if(Sector==5){t1=-Y;t2=-Z;Taon=_IQmpy(_IQ(0.5),(_IQ(1)-t1-t2));Tbon=Taon+t1;Tcon=Tbon+t2;Ta=Tbon;Tb=Tcon;Tc=Taon;}else if(Sector==6){t1=Y;t2=-X;Taon=_IQmpy(_IQ(0.5),(_IQ(1)-t1-t2));Tbon=Taon+t1;Tcon=Tbon+t2;Ta=Taon;Tb=Tcon;Tc=Tbon;}//================================================================================ //根据占空比Ta,Tb,Tc计算全比较器持?//================================================================================ Ta=_IQmpy(_IQ(2),(Ta-_IQ(0.5)));Tb=_IQmpy(_IQ(2),(Tb-_IQ(0.5)));Tc=_IQmpy(_IQ(2),(Tc-_IQ(0.5)));Tmp = (int32)T1Period*(int32)Modulation; // Q15 = Q0*Q15，占空比设置MPeriod = (int16)(Tmp>>15); // Q0 = (Q15->Q0)Tmp = (int32)MPeriod*(int32)Ta; // Q15 = Q0*Q15，计算全比较器CMPR1赋值EvaRegs.CMPR1 = (int16)(Tmp>>16) + (int16)(MPeriod>>1); // Q0 = (Q15->Q0)/2 + (Q0/2)Tmp = (int32)MPeriod*(int32)Tb; // Q15 = Q0*Q15，计算全比较器CMPR2赋值EvaRegs.CMPR2 = (int16)(Tmp>>16) + (int16)(MPeriod>>1); // Q0 = (Q15->Q0)/2 + (Q0/2)Tmp = (int32)MPeriod*(int32)Tc; // Q15 = Q0*Q15，计算全比较器CMPR3赋值EvaRegs.CMPR3 = (int16)(Tmp>>16) + (int16)(MPeriod>>1); // Q0 = (Q15->Q0)/2 + (Q0/2)本文主要基于TI公司C2000系列F2812例程中的说明文件svgen_dq.pdf编写而成，主要是帮助SVPWM初学者。
SVPWM控制算法及代码实现本文针对SVPWM控制算法实现过程进行详细推导，已及对最终PWM模块输出进行完整图解，并根据SVPWM实行过程附带对应源代码，以便深入理解分析SVPWM算法。
SVPWM技术目的：通过基本空间矢量对应的开关状态组合，得到一个给定的参考电压矢量U ref。
电压矢量以ω=2πf角速度旋转，旋转一周时间T= 1/f；若载波频率为f s,则频率比n = f s/f。
如此将一个周期切割为n个小增量，则每个增量角度为∆θ = 2π/n = 2πf/f s = 2πT s/T。
1.基本矢量推导以扇区Ⅰ为例，如图1-1，将U4、U6及零矢量（U0和U7）合成U ref，其中U4和U6分别作用时间为T4和T6，零矢量作用时间为T0，于是有：T s=T4+T6+T0(1-1)U ref T s=U4T4+U6T6(1-2)图1-1 扇区Ⅰ的电压矢量合成与分解图图1-2 电压矢量图在α/β参考坐标系中，令U ref和U4的夹角为θ，则可以得到：Uα=T4T s |U4|+T6T s|U6|cosπ3(1-3)Uβ=T6T s |U6|sinπ3(1-4)由于|U4| = |U6| = 2Udc/3，从而计算出T4和T6，如下T4=√3T sU dc (√32Uα−12Uβ)(1-5)T6=√3T sU dcUβ(1-6)则零矢量电压所分配时间为（7段式）：T0=T7=(T s−T4−T6)/2(1-7)同理，可计算出其它扇区矢量作用时间如表1-1所示：表1-12.扇区判断通过上述对扇区矢量时间的推导可知实现SVPWM调制的实时信号，但实现SVPWM调制的首要条件是知道参考电压U ref所在的区间位置，才能利用所在扇区的相邻两电压矢量和适当的零矢量来合成参考电压矢量。
因此，空间矢量调制的第一步则是通过已知的参量来判断空间电压矢量所处的扇区。
由于计算扇区矢量作用时间使用到Uα和Uβ，且Uα和Uβ可由Clarke变换轻易获取，通过此参量不仅可以判断空间电压矢量所处扇区，还可以获得扇区矢量作用时间。
