基于曲率驱动的类双线性图像快速插值方法

图像缩放算法及速度优化——（⼆）双线性插值 双线性插值作为OpenCV中默认使⽤的图像缩放算法，其效果和速度都是不错的。

并且效果也⽐较稳定，计算复杂度并不算太⾼。

我看了很多⽹上的算法，⾃⼰也没看太懂，下⾯是从⽹上找的双线性插值算法的讲解。

“图像的双线性插值放⼤算法中，⽬标图像中新创造的象素值，是由源图像位置在它附近的2*2区域4个邻近象素的值通过加权平均计算得出的。

双线性内插值算法放⼤后的图像质量较⾼，不会出现像素值不连续的的情况。

然⽽次算法具有低通滤波器的性质，使⾼频分量受损，所以可能会使图像轮廓在⼀定程度上变得模糊。

” 下⾯还是根据我⾃⼰的理解来继续讲述吧，相信读者中有很多⾼⼿，希望读者能给予我指点⼀下，让我也能更明⽩⼀些。

双线性插值算法和最近邻插值算法⽐较类似。

在最近邻插值算法中，⽬标图像中的某个点(x,y)是去源图像中找最邻近的⼀个点(x0, y0)即可。

⽬标图像中的点(x, y)对应于源图像中的点(x0',y0')，x0'、y0'很可能不是整数，⽽是⼩数，⽽最近邻插值算法是找其邻近整型值(int(x0'+0.5f),int(y0'+0.5f))（上篇⽂章中没有进⾏四舍五⼊）。

我们现在找x0', y0'所在位置旁边的四个点，根据这四个点与(x0',y0')距离的关系计算⽬标图像中(x,y)⼀点的像素值。

算法描述如下：(1)计算源图像与⽬标图像宽与⾼的⽐例w0 : 表⽰源图像的宽度h0 : 表⽰源图像的⾼度w1 : 表⽰⽬标图像的宽度h1 : 表⽰⽬标图像的⾼度float fw = float(w0-1)/(w1-1);float fh = float(h0-1)/(h1-1);(2)针对⽬标图像的⼀个点(x, y),计算在源图像中的对应坐标，结果为浮点数。

float x0 = x * fw;float y0 = y * fh;int x1 = int(x0);int x2 = x1 + 1;int y1 = int(y0);int y2 = y1+1;所求的源图像中的四个点坐标为(x1, y1) (x1, y2) (x2, y1) (x2,y2)(3)求周围四个点所占的权重⽐值如上图，fx1 = x0 - x1;fx2 = 1.0f - fx1;fy1 = y0 - y1;fy2 = 1.0f - fy1;float s1 = fx1*fy1;float s2 = fx2*fy1;float s3 = fx2*fy2;float s4 = fx1*fy2;我们以value(坐标)来代表取得此点的坐标值，则:value(x0,y0) = value(x2,y2)*s1+value(x1,y2)*s2+value(x1,y1)*s3+value(x2,y1)*s4;如果对上述运算不够明⽩的话，可以这样来求。

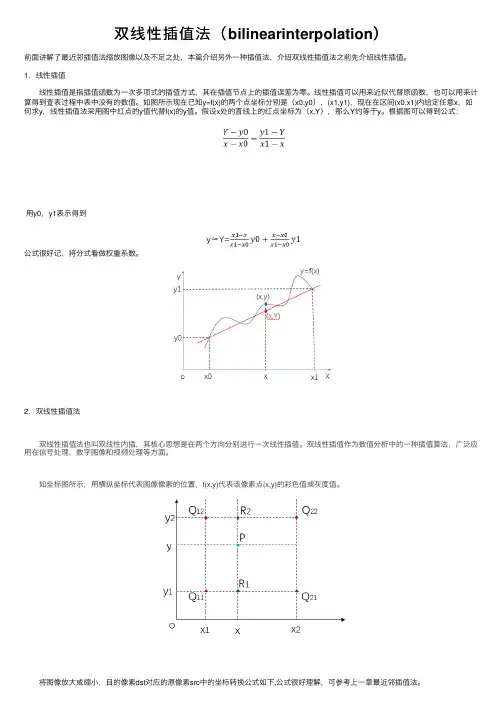
双线性插值法（bilinearinterpolation）前⾯讲解了最近邻插值法缩放图像以及不⾜之处，本篇介绍另外⼀种插值法，介绍双线性插值法之前先介绍线性插值。

1. 线性插值 线性插值是指插值函数为⼀次多项式的插值⽅式，其在插值节点上的插值误差为零。

线性插值可以⽤来近似代替原函数，也可以⽤来计算得到查表过程中表中没有的数值。

如图所⽰现在已知y=f(x)的两个点坐标分别是（x0,y0），(x1,y1)，现在在区间(x0,x1)内给定任意x，如何求y，线性插值法采⽤图中红点的y值代替f(x)的y值。

假设x处的直线上的红点坐标为（x,Y），那么Y约等于y。

根据图可以得到公式：⽤y0，y1表⽰得到公式很好记，将分式看做权重系数。

2. 双线性插值法 双线性插值法也叫双线性内插，其核⼼思想是在两个⽅向分别进⾏⼀次线性插值。

双线性插值作为数值分析中的⼀种插值算法，⼴泛应⽤在信号处理，数字图像和视频处理等⽅⾯。

如坐标图所⽰，⽤横纵坐标代表图像像素的位置，f(x,y)代表该像素点(x,y)的彩⾊值或灰度值。

将图像放⼤或缩⼩，⽬的像素dst对应的原像素src中的坐标转换公式如下,公式很好理解，可参考上⼀章最近邻插值法。

srcX=dstX*(srcWidth/dstWidth) srcY=dstY*(srcHeight/dstHeight) 上式中，dstX与dstY为⽬标图像的某个像素的横纵坐标，dstWidth与dstHeight为⽬标图像的长与宽；srcWidth与srcHeight为原图像的宽度与⾼度。

srcX，srcY为⽬标图像在该点（dstX，dstY）对应的原图像的坐标。

现在假设⽬标图像的像素点(x’，y’)映射到原图像中是(x,y)，也就是图中的P点。

设Q11 = (x1, y1)、Q12 = (x1, y2)、Q21 = (x2, y1) 、Q22 = (x2, y2)，图中Q11,Q12,Q21,Q22分别为距离P点的最近的四个点。

基于CFA模式的一种改进型双线性图像插值算法
朱磊;毛欢
【期刊名称】《电子测量技术》
【年(卷),期】2009()8
【摘要】本文介绍了图像传感器常用的CFA模式原理,针对该图像模式常用插值算法的缺陷,提出了一种基于图像相关性和简单边缘检测的改进型双线性插值算法。

该算法具有算法简单,插值效果好,节约处理器指令周期等特点,可用于带有图像传感器的嵌入式系统中。

【总页数】4页(P122-125)
【关键词】图像插值;CFA模式;图像传感器;双线性插值
【作者】朱磊;毛欢
【作者单位】西安工程大学电子信息学院
【正文语种】中文
【中图分类】TP319
【相关文献】
1.一种改进的双线性插值图像放大算法 [J], 龚昌来;杨冬涛
2.一种改进的双线性插值图像放大算法 [J], 李永艳;付志兵
3.一种基于矢量方法的彩色图像双线性插值算法 [J], 方凯;李德华;金良海;朱美能
4.一种基于邻点法、双线性插值法和三次样条插值法的图片放缩聚合算法研究 [J],
金凯文
5.一种基于CFA插值系数熵的图像来源取证算法 [J], 谢建;潘晓中
因版权原因，仅展示原文概要，查看原文内容请购买。

图像插值技术——双线性插值法在图像处理中，如果需要对图像进⾏缩放，⼀般可以采取插值法，最常⽤的就是双线性插值法。

本⽂⾸先从数学⾓度推导了⼀维线性插值和⼆维线性插值的计算过程，并总结了规律。

随后将其应⽤到图像的双线性插值上，利⽤Matlab编程进⾏图像的缩放验证，实验证明，⼆维线性插值能够对图像做出较好的缩放效果。

数学⾓度的线性插值⼀维线性插值假设有⼀个⼀元函数 y=f(x) , 已知曲线上的两点，A 和 B 的坐标分别为 (x0,y0) 、(x1,y1) 。

现在要在A 和 B 之间通过插值计算出⼀个点 P ,若已知 P点的横坐标 x，如何求出 P点的纵坐标 y ?这⾥我们的插值之所以叫做线性插值，就是因为我们假定了 P 点落在 A 点和 B 点的连线上,使得他们的坐标之间满⾜线性关系。

所以，根据初中的知识，可以得到下⾯的等式：y−y0 y1−y0=x−x0 x1−x0这⾥我们令：α=x−x0 x1−x0于是，我们可以得到P点的纵坐标 y 的表达式：y=(1−α)f(x0)+αf(x1)⼆维线性插值⼀维线性插值可以扩展到⼆维的情况。

假设有⼀个⼆元函数 z=f(x,y) , 已知曲⾯上的四点，A 、B 、C、D的坐标分别为 (x0,y0) 、(x1,y0) 、(x1,y1)、(x0,y1) 。

现在要在A 、B 、C、D之间通过插值计算出⼀个点 P ,若已知 P点的坐标 (x,y)，如何求出 P点的函数值坐标 z ?这⾥我们依旧可以仿照⼀维线性插值，进⾏计算。

假设先计算 y 轴⽅向的插值点 P0 和 P1 ,则根据上⾯的推导过程，且令α=y−y0 y1−y0则， P0 的取值 z0为：z0=(1−α)f(x0,y0)+αf(x0,y1) P1 的取值 z1为：z1=(1−α)f(x1,y0)+αf(x1,y1)再计算 x 轴⽅向的插值点 P，令β=x−x0 x1−x0则 P 的取值 z为：z=(1−β)z0+βz1整理得到下⾯的式⼦：z =(1−β)(1−α)f x 0,y 0+αf x 0,y 1+β(1−α)f x 1,y 0+αf x 1,y 1=(1−β)(1−α)f x 0,y 0+(1−β)αf x 0,y 1+β(1−α)f x 1,y 0+βαf x 1,y 1⼩结由⼀维线性插值过渡到⼆维线性插值，我们发现，⼆者在表达式上有相似的规律：⼀维线性插值：y =f (x )α=x p −x 0x 1−x 0y p =(1−α)f x 0+αf x 1⼆维线性插值：z =f (x ,y )α=x p −x 0x 1−x 0,β=y p −y 0y 1−y 0z p =(1−β)(1−α)f x 0,y 0+(1−β)αf x 0,y 1+β(1−α)f x 1,y 0+βαf x 1,y 1图像中的双线性插值我们可以⽤函数来表⽰⼀幅图像（假设为单通道）。

双线性插值图像插值 ⽬前，终端显⽰器都由点阵的像素点构成，在表现⾮⽔平或者竖直的直线时，必然会出现直线的歪曲，即锯齿效应。

位图经过缩放、旋转等变换，都会使锯齿效应增强。

尤其当显⽰分辨率过低时，在表现⾮⽔平或竖直的直线以及明显边缘时，离散的像素点间灰度值缺少过渡，会有很明显的锯齿。

对于这种情况，我们需要对图像边缘进⾏柔化处理，使图像边缘看起来更平滑，更接近现实。

同样的，依空间坐标变换⽅法，计算得到的对应点坐标通常不是整数，如果简单地使⽤取整或者最邻近插值的⽅法得到⽬标图像，⽬标图像会有⽐较明显的锯齿效应。

对于这个问题，在处理过程中通常是采⽤双线性插值或双三次插值。

在均衡算法速度与图像质量的情况下，更倾向于使⽤双三次插值⽅法来完成图像处理中的灰度级插值。

最近邻插值 最近邻插值算法⼜称零阶插值，它是⼀种⽐较容易实现且算法复杂度较低的插值算法，其原理是取待插值点周围4个相邻像素点中欧式距离最短的⼀个邻点的灰度值作为该点的灰度值。

由于仅⽤对该插值点影响最⼤的（即最近的）像素的灰度值作为该点的值，没有考虑其他相邻像素的影响，因此插值后得到的图像容易产⽣块效应，造成图像模糊，放⼤效果⼀般不够理想。

双线性插值 双线性插值是有两个变量的插值函数的线性插值扩展，其核⼼思想是在两个⽅向分别进⾏⼀次线性插值。

其原理是待插点像素值取原图像中与其相邻的４个点像素值的⽔平、垂直两个⽅向上的线性内插，即根据待采样点与周围４个邻点的距离确定相应的权重，从⽽计算出待采样点的像素值。

根本上来说，双线性插值算法是⼀种加权算法，如图所⽰。

它以到最近四个像素点的距离为参考权值，经两次线性插值，综合得到当前点的灰度值。

计算公式如下： 从公式中我们可以看出，⽬标点的灰度值由周围四个像素点依权值取平均得到，有低通滤波的效果，故⽽能够起到抗锯齿的效果。

但此种插值⽅法中没有考虑相邻点间灰度值变化率的影响，因此具有低通滤波器的性质，会使放⼤后图像的重要细节受到损失，图像变得模糊不清。

三种插值算法最近邻插值法的双线性内插值:对于图像中一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v,其中 i 、 j 均为非负整数, u 、 v 为 [0,1区间的浮点数,则这个像素得值f(i+u,j+v 可由原图像中坐标为 (i,j、 (i+1,j、 (i,j+1、 (i+1,j+1所对应的周围四个像素的值决定,即:f(i+u,j+v = (1-u(1-vf(i,j + (1-uvf(i,j+1 + u(1-vf(i+1,j + uvf(i+1,j+1其中 f(i,j表示源图像 (i,j处的的像素值,以此类推这就是双线性内插值法。

双线性内插值法计算量大,但缩放后图像质量高, 不会出现像素值不连续的的情况。

由于双线性插值具有低通滤波器的性质, 使高频分量受损,所以可能会使图像轮廓在一定程度上变得模糊插值的计算方法有很多, 比较常用的有最近像素插值算法、双线性插值算法、双三次插值算法和分形算法的四种。

其中, 最近像素插值算法是最简单的一种插值算法, 这种方法是当图片放大时, 缺少的像素通过直接使用与之最接近的原有像素的颜色生成, 也就是说照搬旁边的像素。

如图 1所示,当图片扩大时,要增加 X 点处的像素,由于 X 点与 A 、 B 这两个有效像素中的 B 点最接近,因此 X 点会直接照搬B 点的像素,从而使到 X 点生成的效果与 B 点一样。

虽然这种算法简单, 因此处理的速度很快, 但结果通常会产生明显可见的锯齿, 效果往往不佳。

双线性插值算法, 是指输出的图像的每个像素都是原图中四个像素运算的结果, 由于它是从原图四个像素中运算的, 因此这种算法很大程度上消除了锯齿现象, 而且效果也比较好。

双三次插值算法是双线性插值算法的改进算法,它输出图像的每个像素都是原图 16个像素运算的结果, 由于效果好, 运算速度也不慢, 因而这种插值方法是一种很常见的算法, 普遍用在图像编辑软件、打印机驱动和数码相机上。

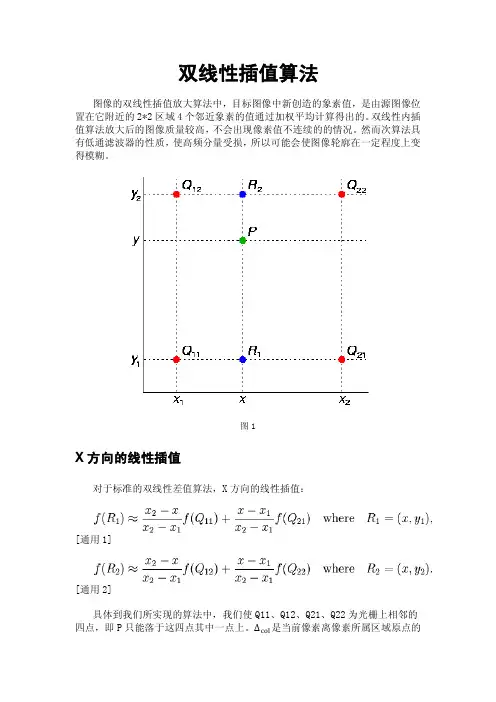
双线性插值算法
双线性插值（Bilinear Interpolation）是一种非常常见的插值算法，它可以用来插值两个或多个维度的数据，广泛应用于图像处理、机器学习等领域。

双线性插值的基本原理是：从数据中取出四个点，比如a、b、c、d，然后在这四个点上构建一个双线性曲面，曲面的函数为：f(x,y)=ax+by+cxy+d，其中a,b,c,d是待求的系数。

双线性插值的具体过程是：首先确定子区域的四个顶点，比如：a(x1,y1),b(x1,y2),c(x2,y1),d(x2,y2)，接着在这四个顶点上求出曲面的函数，即：f(x,y)=ax+by+cxy+d，其中a,b,c,d是待求的系数，我们可以用矩阵求解法来解出这四个系数。

最后，对于子区域内的任一点，都可以用双线性插值算法来求出它的函数值：
f(x,y)=ax+by+cxy+d。

双线性插值算法的优势在于它可以用来插值两个或多个维度的数据，而且插值的精度高，可以达到很好的效果。

此外，双线性插值算法的运算速度也比较快，不需要太多的计算量，因此在实际应用中得到了广泛的应用。

综上所述，双线性插值算法是一种高效、精确的插值算法，广泛应用于图像处理、机器学习等领域。

它可以用来插值两个或多个维度
的数据，插值精度高，且运算速度快。

使用图像处理技术实现图像插值的方法图像插值是一种常用的图像处理技术，它通过在已知像素值的基础上，推断出未知像素的值，从而提高图像的分辨率。

在计算机视觉、图像处理和计算机图形学领域，图像插值被广泛应用于图像放大、图像重建、图像修复等任务中。

本文将介绍几种常见的图像插值方法，并探讨它们的优缺点。

第一种常见的图像插值方法是最近邻插值。

该方法简单直观，在放大图像时，每个新像素只采用其最近的已知像素的值。

最近邻插值的优点是计算速度快，适用于实时图像处理。

然而，最近邻插值方法会导致图像出现锯齿状的伪影，因为它没有考虑像素间的渐变过程。

第二种常见的图像插值方法是双线性插值。

相比于最近邻插值，双线性插值对像素间的渐变进行了考虑。

它利用已知像素周围的4个像素值进行加权平均，得到新像素的值。

这种插值方法克服了最近邻插值的锯齿伪影问题，使图像看起来更加平滑。

然而，双线性插值的计算量较大，在处理大型图像时可能会影响性能。

第三种常见的图像插值方法是双三次插值。

双三次插值在双线性插值的基础上进行了改进，增加了更多的已知像素进行加权平均。

它通过拟合像素周围16个像素值的二次曲线来计算新像素的值。

与双线性插值相比，双三次插值能够更好地保留图像的细节和纹理信息。

然而，双三次插值会导致图像出现一些模糊效果，尤其是在处理边缘和细节部分时。

除了上述常见的图像插值方法，还有一些更高级的插值方法，如 Lanczos 插值、B样条插值等。

这些方法考虑了更多像素的权重分布，能够更准确地估计未知像素的值。

在特定的应用场景下，它们能够取得更好的效果。

然而，这些高级插值方法也更加复杂，计算量更高。

在实际应用中，选择合适的图像插值方法需要根据具体的需求和限制来决定。

如果对计算性能要求较高，可选择最近邻插值或双线性插值；如果对图像质量要求较高，可以考虑双三次插值或其他高级插值方法。

还可以结合不同的插值方法，根据图像的不同区域或特征选择最适合的方法。

综上所述，图像插值是一种重要的图像处理技术，它通过推测未知像素的值来提高图像的分辨率。

基于曲率驱动的类双线性图像快速插值方法路锦正;张启衡;徐智勇;彭真明【期刊名称】《光电工程》【年(卷),期】2011(038)004【摘要】To satisfy fast image zooming requirement with preserving edge-sharpness, a quasi-bilinear algorithm based on profile curvature of brightness surface is introduced. Firstly, in view of inherent low-pass property of bilinear, an amendatory formula is established via including pixel variation. Then, for obtaining the dominant direction of neighboring pixels, image coordinate and its brightness are treated as surface when gray value being simulated as altitude of earth surface. Lastly, magnitudes of curvatures of specified direction is regarded as adjustment reference of structures type of image, such as edge or texture. Therefore, weights of direction of a pair of two pixels average can be adaptively evaluated according to several thresholds of curvatures. Experiment results of synthetic data demonstrate that, comparedwith other similar techniques, Power Signal to Noise Ratio (PSNR) gain of image twice-interpolated is 7.8 dB, and improvement of Structural Similarity (SSIM) is 0.1. Especially, arithmetic type of proposed algorithm is simple, and its complexity is relatively low, thus it is convenient to real-time application over fixed platform.%为实现保持图像边缘锐度的快速插值放大,提出了基于图像曲面曲率信息的类双线性插值方法.首先鉴于双线性插值的低通滤波固有特性,引入像素的值变化以构造类双线性插值模型;为获得相邻像素点的方向趋势,将灰度值模拟为地表高程并与二维坐标形成空间曲面;最后以指定方向的曲面的剖面曲率作为图像边缘等结构类型的判别依据,自适应优化两组两像点均值的方向权重从而获得丰富的像素插值先验.合成图像的两倍插值实验显示,峰值信噪比PSNR提高7.8dB,图像框架相似性SSIM改善0.1.本方法计算类型简单且复杂度低,易于定点平台的实时应用.【总页数】8页(P108-114,123)【作者】路锦正;张启衡;徐智勇;彭真明【作者单位】中国科学院光电技术研究所,成都,610209;电子科技大学,光电信息学院,成都,610054;中国科学院研究生院,北京,100049;中国科学院光电技术研究所,成都,610209;中国科学院光电技术研究所,成都,610209;电子科技大学,光电信息学院,成都,610054【正文语种】中文【中图分类】TP391.4【相关文献】1.基于统计特征的彩色图像快速插值方法 [J], 刘晓松;杨新;汪进2.基于曲率驱动模型的图像修复算法 [J], 李世银;冯瑾;陈燕;卢兆林3.基于GFS的双线性快速模糊增强图像边界检测新算法 [J], 韩培友;郝重阳;董桂云4.基于曲率驱动的p-harmonic模型图像修复算法 [J], 王艳琴;吴爱弟5.基于曲率驱动的p-harmonic模型图像修复算法 [J], 王艳琴;吴爱弟;因版权原因，仅展示原文概要，查看原文内容请购买。

双线性插值算法的一种快速实现方式
陈宝平;赵俊岚;尹志凌
【期刊名称】《北京电子科技学院学报》
【年(卷),期】2004(012)004
【摘要】几何运算要求对图像进行灰度值插值,双线性算法可产生令人满意的效果,但是程序较复杂,运行时间较长.本文提出了双线性插值算法的一种快速实现方式,该方式便于编程,计算效率高,运行速度快.
【总页数】3页(P21-23)
【作者】陈宝平;赵俊岚;尹志凌
【作者单位】内蒙古财经学院,信息管理系,呼和浩特,010050;内蒙古财经学院,信息管理系,呼和浩特,010050;内蒙古师范大学,计算机科学与技术系,呼和浩特,010022【正文语种】中文
【中图分类】TP919.81
【相关文献】
1.基于双线性插值算法的缩放IP核设计 [J], 邹学瑜;刘昌禄;胡敬营
2.一种基于矢量方法的彩色图像双线性插值算法 [J], 方凯;李德华;金良海;朱美能
3.基于DSP的双线性插值算法在图像旋转中的应用 [J], 尹雪; 刘思念; 袁春梅; 周杰
4.结合双线性插值与局部均值的红外图像插值算法 [J], 黄元忠;廖小华;卢庆华
5.基于CFA模式的一种改进型双线性图像插值算法 [J], 朱磊;毛欢
因版权原因，仅展示原文概要，查看原文内容请购买。

基于双线性插值的图像缩放在GPU上的实现
王平;全吉成;赵柏宇
【期刊名称】《微电子学与计算机》
【年(卷),期】2016(33)11
【摘要】针对传统的在CPU上实现的基于双线性插值的图像缩放存在速度慢等问题,利用GPU高性能并行计算优势,实现了在GPU上基于双线性插值的快速缩放.此算法将目标图像的每个像素分配给GPU中每个线程同时执行,提高插值效率.从实验结果可以看出,此算法在放大图像时,随着图像分辨率的增大,GPU的插值速度相对CPU单线程和多线程的插值速度显著提高,能很好达到实时缩放图像的效果.【总页数】4页(P129-132)
【关键词】GPU;双线性插值;并行算法;图像缩放
【作者】王平;全吉成;赵柏宇
【作者单位】空军航空大学航空航天情报系
【正文语种】中文
【中图分类】TP391
【相关文献】
1.基于双线性插值法的图像缩放算法的设计与实现 [J], 张洋
2.基于双线性插值的图像缩放算法的研究与实现 [J], 王森;杨克俭
3.基于历史模拟法的风险价值算法在GPU上的实现和优化 [J], 张劼;文敏华;林新华;孟德龙;陆豪
4.基于FMM-PM方法的宇宙N体模拟在GPU上
的实现和优化 [J], 扶月月;王武;王乔
5.基于FMM-PM方法的宇宙N体模拟在GPU上的实现和优化 [J], 扶月月;王武;王乔
因版权原因，仅展示原文概要，查看原文内容请购买。