当前位置：文档之家 › 传递函数的基本性质

传递函数的基本性质

  • 格式：pptx
  • 大小：207.83 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

自动控制原理传递函数知识点总结

自动控制原理传递函数知识点总结

自动控制原理传递函数知识点总结自动控制原理是研究自动控制系统中信号传递、处理、转换等基本理论和方法的学科。

传递函数是描述线性时不变系统的数学模型，它对于分析和设计控制系统起着重要的作用。

下面将对自动控制原理中关于传递函数的知识点进行总结。

一、传递函数的定义传递函数是用来描述线性时不变系统输入-输出关系的数学函数。

对于连续时间系统，传递函数可以表示为：G(s) = Y(s) / X(s)其中，G(s)为传递函数，Y(s)为系统的输出信号，X(s)为系统的输入信号，s为复变量。

对于离散时间系统，传递函数可以表示为：G(z) = Y(z) / X(z)其中，G(z)为传递函数，Y(z)为系统的输出信号，X(z)为系统的输入信号，z为复变量。

二、传递函数的性质1. 时域特性：传递函数可以通过拉氏变换将时域的微分、积分方程转换为频域的代数方程，从而简化系统的分析和设计。

2. 稳定性：传递函数的稳定性与其极点位置有关。

当所有极点均位于左半平面时，传递函数是稳定的；当存在极点位于右半平面时，传递函数是不稳定的。

3. 零点和极点：传递函数的零点是使得传递函数为零的点，极点是使得传递函数无穷大的点。

零点和极点的位置对系统的动态性能和稳定性有重要影响。

4. 频率响应：传递函数的频率响应是指系统对不同频率输入信号的响应特性。

频率响应可以通过传递函数的频域分析获得，包括幅频特性和相频特性。

三、传递函数的常见形式1. 一阶系统传递函数：一阶系统的传递函数形式为：G(s) = K / (s + a)其中，K为传递函数的增益，a为系统的时间常数。

2. 二阶系统传递函数：二阶系统的传递函数形式为：G(s) = K / (s^2 + 2ζω_ns + ω_n^2)其中，K为传递函数的增益，ζ为阻尼比，ω_n为自然频率。

3. 传递函数的因果性：因果系统的传递函数在复平面上的极点全部位于左半平面，即Re(s) < 0。

非因果系统的传递函数在复平面上的极点存在于右半平面，即Re(s) > 0。

2-4 线性系统的传递函数

2-4 线性系统的传递函数
1
0
T
t
11
惯性环节的实例如下图所示。
R C uc
ur
(a)
在图(a)所示的电路中，输出电压uc与输入电 压ur间的微分方程为
du c T + uc = ur dt
式中T=RC，为电路的时间常数。
12
if uf
Rf
Lf
(b)
在图(b)所示的直流电机的激磁电路中，当 以激磁电压uf为输入量、以激磁电流if为输出量 时，其电路方程为
G (s) = R(s) =
m m −1 1 0
a n s + a n −1 s
n
n −1
+ …… + a1 s + a 0
( 2 − 50 )
可见，传递函数是由系统微分方程经拉氏变换而引出 的。 系统输入、输出及传递函数之间的相互关系可用 下图表示，输出是由输入经过G(s)的传递而得到的， 因此称G(s)为传递函数。因为传递函数是在零初始条 件下定义的，故在初始条件为零时，它才能完全表征 系统的动态性能。
+ (a)
C ic uc
ur n θ
(b)
ur 在图(a)中，因为 i c = i = R
容两端电压，所以有
uc = 1 c
而输出电压uc近似等于电
∫ i c dt =
在图(b)中，以电动机的转速n(转/分)为输入量， 以减速齿轮带动负载运动的轴的角位移θ为输出量， 可得微分方程 1
θ (t ) =
§2-4 线性系统的传递函数
控制系统的微分方程，是时域中描述系统动态性 能的数学模型，求解微分方程可以得到在给定外界作 用及初始条件下系统的输出响应，并可通过响应曲线 直观地反映出系统的动态过程。但系统的参数或结构 形式有变化，微分方程及其解都会同时变化，不便于 对系统进行分析与研究。 根据求解微分方程的拉氏变换法，可以得到系统 的另一种数学模型——传递函数。它不仅可以表征系 统的动态特性，而且可以方便地研究系统的参数或结 构的变化对系统性能所产生的影响。在经典控制理论 中广泛应用的根轨迹法和频率法，就是在传递函数基 础上建立起来的。

自动控制原理--传递函数的定义及性质和表示形式

自动控制原理--传递函数的定义及性质和表示形式
K*:=b0/a0，称为根轨迹增益；N(S)=0为系统 特征方程
传 递 函 数的表示形式
3.时间常数形式（尾1型 ）
G(s)
bm (1s 1)( 2s2
an (T1s 1)(T2s2
22s 1)( is 1) 2T2s 1)(Tjs 1)
m
K bm K * am
(zi )
1 n
称 G(s)的开环增益。
传递函数
传递函数的定义及性质 传 递 函 数的表示形式
传 递 函 数的定义
对于n阶系统，线性微分方程的一般形式为：
a d n c(t) a d n1 c(t) a d c(t) a c(t)
0 dt n
dt1 n1
dt n1
n
b d m r(t) b d m1 r(t) b d r(t) b r(t)
另外实际系统总有惯性，因此实际系统中有n>＝m，n称 为系统的阶数
传递函数的性质
7）传递函数是系统单位脉冲响应的Laplace变换。
定义 g(t) 为系统单位脉冲作用下的系统输出：
当 r(t) (t) 时，系统的输出c(t)称为 g(t)
此时，L[r(t)] L[ (t)] 1 所以：
C(s) G(s)R(s) G(s) c(t) g(t) L1[C(s)] L1[G(s)R(s)] L1[G(s)]
( p j )
1
i ,Tj 称时间常数。
传递函数的性质
G(s)
C(s) R(s)
b0sm a0 s n
b1sm1 a1sn1
bm1s an1s
bm an
5）传递函数的概念主要适用于单输入单输出系统。
若系统有多个输入信号，在求传递函数时，除了一

2.2 传递函数

2.2 传递函数

3、典型环节的形式
G (s) K
( s 1) (T s 1)
j 1 j i 1 n i
m
上式中 τi──分子各因子的时间常数 ； Tj──分母各因子的时间常数 ；
K ──时间常数形式传递函数的增益；通常称为传递系数。
五、传递函数的求取
1、解析法
建立微分方程，根据微分方程按定义求取
介绍一种方法：复阻抗法
i
U R
du iC dt
i
1 udt L
U (s) I (s) R
U (s) I (s) Z (s)
I ( s) CsU ( s) U ( s )
1 Cs
1 Cs
I (s)
U (s) Ls
R
Ls
1 , Ls 分别成为电阻、电容和电感的复阻抗 把 R, Cs
传递函数是经典控制理论中最重要的数学模型之 一。利用传递函数，在系统的分析和综合中可解决如 下问题：
不必求解微分方程就可以研究初始条件为零的系统在输 入信号作用下的动态过程。 可以研究系统参数变化或结构变化对系统动态过程的影 响，因而使分析系统的问题大为简化。 可以把对系统性能的要求转化为对系统传递函数的要求， 使综合问题易于实现。
11/17/2013 8:53:46 PM
3
一、定义
零初始条件下，线性定常系统输出量的拉氏变换 与输入量的拉氏变换之比，称为该系统的传递函数，
记为G(s)，即：
L[ y (t )] Y ( s ) G( s) L[r (t )] R( s )
意义：
R( s )
G (s )
Y ( s)
Y (s) R(s)G(s)
1 1 Y ( s) G s) R s) （ （ Ts 1 s

数学模型-传递函数

数学模型-传递函数

1 1 ， j ，Ti zj pi ( pi )
( z j )
m
(3) 二项式表示法：
如 p1 . p2为一对共轭复数，则有
1 1 2 ( s p1 )( s p2 ) s 2 n s n 2
1 1 2 2 或 (T1 s 1)(T2 s 1) T s 2Ts 1
当初始条件为零时有：
3
第二章 数学模型
传 递 函 数(续)
C ( s ) b0 s m b1 s m 1 bm 1 s bm 则G ( s ) R( s ) a 0 s n a 1 s n 1 a n 1 s a n
s j 为复数， G (s ) 是复变量s 的函数， 故称为复放大系数。
i 1
m
(s z )
当s
z j时，G(s) = 0. z j 为传函的零点。
10
当 s pi 时，G(s) = , pi 为传函的极点。
第二章 数学模型
而 K g b0 ——传递系数。(根轨迹中叫根轨迹增益)
a0
(2）时间常数表示法：
bm d m s m d m 1 s m 1 d 1 s 1 G( s ) a n c n s n c n 1 s n 1 c 1 s 1
其传递函数为
6. 齿轮系
m
Z1
Z2
c
第二章 数学模型
§2-2 传 递 函 数
用拉氏变换求解微分方程，虽思路清晰,简单实用,但 如果系统参数改变，特征方程及其解都会随之改变。 要了解参数变化对系统动态响应的影响，就必须多次 计算，方程阶次愈高，计算工作量越大，故引入另一 种数模—传递函数。它是控制理论中的重要概念和工具， 也是经典理论中两大分支—根轨迹和频率响应的 基础。利用传递函数不必求解微方就可研究初始条件 为零的系统在输入信号作用下的动态过程。

自控理论 2-2传递函数

自控理论 2-2传递函数

当 ui ( t ) = 1( t )时,
− t 1 −1 τs 则u0 ( t ) = L ⋅ =e τ τs + 1 s 1
图2-8 RC电路 电路
当 τ << 1 时，可近似认为 G ( s ) ≈ τs
5. 振荡环节
d 2 c( t ) dc( t ) 2 T + 2ζT + c( t ) = Kr ( t ) 2 dt dt
运放 2
U 2 ( s ) τs + 1 G2 ( s) = = U 1 ( s) Ts
( 2 − 38)
式中
τ = R3C
T = R2C
功放
U a ( s) G3 ( s) = = K2 U 2 ( s)
( 2 − 39)
附:电枢控制直流电动机的微分方程 电枢控制直流电动机的微分方程
dmc d 2n dn TaTm 2 + Tm + n = K u ua − K m (Ta + mc ) dt dt dt La ; 电磁时间常数 Ta = Ra 传递系数 1 Ku = Ce 机电时间常数 Tm Km = J ( 2 − 10)
m m −1
∏ (s − z
j =1 n i =1
m
j
)
∏ (s − p )
i
式中
z j ( j = 1 , 2 L m )为传递函数的零点； 为传递函数的零点； p i ( i = 1 , 2 L n )为传递函数的极点； 为传递函数的极点； K 1 = b0 为传递系数或根轨迹增 益。
② 时间常数表达式
n≥m
当初始条件均为零时，两边取拉氏变换 当初始条件均为零时，
(s

传递函数及其性质

传递函数及其性质

2-6 传递函数求解控制系统的微分方程，可以得到在确定的初始条件及外作用下系统输出响应的表达式，并可画出时间响应曲线，因而可直观地反映出系统的动态过程。

如果系统的参数发生变化，则微分方程及其解均会随之而变。

为了分析参数的变化对系统输出响应的影响，就需要进行多次重复的计算。

微分方程的阶次愈高，这种计算愈复杂。

因此，仅仅从系统分析的角度来看，就会发现采用微分方程这种数学模型，当系统阶次较高时，是相当不方便的。

以后将会看到，对于系统的综合校正及设计，采用微分方程这一种数学模型将会遇到更大的困难。

目前在经典控制理论中广泛使用的分析设计方法——频率法和根轨迹法，不是直接求解微分方程，而是采用与微分方程有关的另一种数学模型——传递函数，间接地分析系统结构参数对响应的影响。

所以传递函数是一个极其重要的基本概念。

一、传递函数的概念及定义在[例2-7]中，曾建立了RC 网络微分方程，并用拉氏变换法对微分方程进行了求解。

其微分方程（2-44）为)()(t u t u dtdu RC r c c =+ 假定初始值0)0(=c u ，对微分方程进行拉氏变换，则有)()()1(s U s U RCs r c =+网络输出的拉氏变换式为)(11)(s U RCs s U r c += （2-48）这是一个以s 为变量的代数方程，方程右端是两部分的乘积；一部分是)(s U r ，这是外作用（输入量）的拉氏变换式，随)(t u r 的形式而改变；另一部分是11+RCs ，完全由网络的结构参数确定。

将上式（2-48）改写成如下形式 11)()(+=RCs s U s U r c 令11)(+=RCs s G ，则输出的拉氏变换式可写成 )()()(s U s G s U r c =可见，如果)(s U r 给定，则输出)(s U c 的特性完全由)(s G 决定。

)(s G 反映了系统（网络）自身的动态本质。

这很显然，因为)(s G 是由微分方程经拉氏变换得到的，而拉氏变换又是一种线性变换，只是将变量从实数t 域变换（映射）到复数s 域，所得结果不会改变原方程所反映的系统本质，对照)(s G 与原微分方程（2-44）的形式，也可看出二者的联系。

传递函数求增益

传递函数求增益

传递函数求增益1. 什么是传递函数求增益传递函数求增益是信号处理中的一种方法，用于描述系统对输入信号的放大或衰减程度。

传递函数是输入输出之间的关系，可以通过传递函数求取系统的增益。

在控制系统设计和信号处理中，传递函数求增益是非常重要的一项技术。

2. 传递函数的定义和性质传递函数是描述系统输入输出关系的函数，一般用H(s)表示，其中s是复变量。

传递函数的定义如下：H(s) = Y(s) / X(s)其中，Y(s)是系统的输出信号的拉普拉斯变换，X(s)是系统的输入信号的拉普拉斯变换。

传递函数具有以下性质：•线性性：传递函数具有线性性质，即系统的输出是输入的线性组合。

•时不变性：传递函数具有时不变性质，即系统的输出不随时间变化。

•因果性：传递函数具有因果性质，即系统的输出只依赖于当前和过去的输入。

•稳定性：传递函数具有稳定性质，即系统的输出有界。

3. 传递函数求增益的方法传递函数求增益的方法有多种，下面介绍几种常用的方法：3.1 频域法频域法是一种常用的传递函数求增益的方法，它通过对系统的输入输出信号进行频谱分析来求取增益。

具体步骤如下：1.对系统的输入信号进行傅里叶变换，得到输入信号的频谱。

2.对系统的输出信号进行傅里叶变换，得到输出信号的频谱。

3.将输出信号的频谱除以输入信号的频谱，得到系统的传递函数。

4.根据传递函数的定义，求取系统的增益。

3.2 时域法时域法是另一种常用的传递函数求增益的方法，它通过对系统的输入输出信号进行时域分析来求取增益。

具体步骤如下：1.对系统的输入信号进行拉普拉斯变换，得到输入信号的拉普拉斯变换。

2.对系统的输出信号进行拉普拉斯变换，得到输出信号的拉普拉斯变换。

3.将输出信号的拉普拉斯变换除以输入信号的拉普拉斯变换，得到系统的传递函数。

4.根据传递函数的定义，求取系统的增益。

3.3 实验法实验法是一种直接测量系统输入输出信号的方法，通过实验来求取系统的增益。

具体步骤如下：1.设计一个合适的实验，确定系统的输入信号和输出信号。

传递函数h(w)表达式

传递函数h(w)表达式

传递函数h(w)表达式传递函数h(w)在信号处理和控制系统中扮演着重要的角色，它可以用来描述从输入信号到输出信号的转换过程。

在本文中，我们将深入探讨传递函数h(w)的定义、表达式及其性质。

一、传递函数h(w)的定义传递函数h(w)定义为输出信号Y(s)与输入信号X(s)的拉氏变换的比值，即：h(w) = Y(s) / X(s)其中，s是复数变量，w是实数变量。

二、传递函数h(w)的表达式传递函数h(w)可以用多种形式表示，下面列举其中三种常见的表达式：1. 一阶系统的传递函数表达式:h(w) = k / (1 + jwT1)其中k为系统增益，T1为时间常数，j为虚数单位。

2. 二阶系统的传递函数表达式:h(w) = k / (1 + 2ξjwT1 - w^2T1^2)其中k为系统增益，T1为时间常数，ξ为系统阻尼比。

3. 低通滤波器的传递函数表达式:h(w) = 1 / (1 + jw/ωc)其中ωc为截止频率。

三、传递函数h(w)的性质1. 线性性：传递函数h(w)具有线性性质，即故障率相加等于总故障率。

2. 相位性：传递函数h(w)具有相位性质，信号在传输过程中的相位延迟可以通过传递函数h(w)来描述。

3. 带通性：传递函数h(w)能够描述信号在频率响应范围内的放大或衰减情况。

4. 稳定性：对于连续系统，传递函数h(w)是稳定的，当系统极点都在s左半平面时，系统是稳定的。

5. Fourier性：传递函数h(w)满足Fourier变换定理，即在频率域中，将传递函数h(w)乘以输入信号X(s)的拉普拉斯变换就能得到输出信号Y(s)的拉普拉斯变换。

总之，传递函数h(w)在系统分析和设计中扮演着重要的角色，它不仅形象地描述了系统特性，还能优化系统获得更好的性能。

因此，深入了解传递函数h(w)的定义、表达式和性质是非常有帮助的。

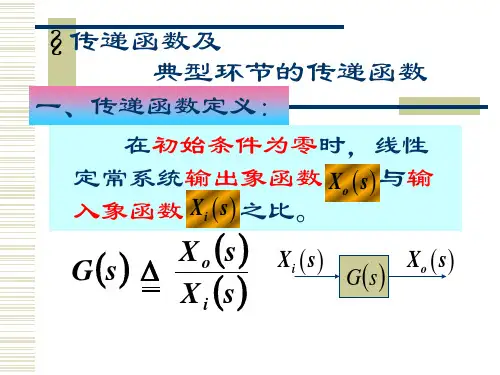
传递函数及方块图剖析

传递函数及方块图剖析

则G(s) = Uo s = RCS
(RC = T
K 1
Ui s RCS + 1
K = 1)
Gs k
4 积分环节
s
时间域方程
xo t k xi t dt
X o s
k
X i s
s
X o s X i s
k s
例9
i2(t)
i1(t) ui(t)
R
A
B
C
_
K0 +
uo(t)
ui (t) = -C duo (t)
传递函数及 典型环节的传递函数
一、传递函数定义：
在初始条件为零时，线性
定常系统输出象函数 Xo s与输 入象函数 Xi s 之比。
Gs
X o s Xi s
Xi s Gs Xo s
设线性定常系统的微分方程为：
a
0
xon
t
a1
x
n1
o
t
a
n1
x
o
t
a
n
x
o
t
b0
x
m
i
t
b1
x
m
i
1
t
bm 1
x i
t
则G(s) = Uo s =
1
Ui s RCS + 1
(RC = T)
例4
弹簧-阻尼系统
K
xi
t
xo
t
D
dxo
dt
t
KXi s KXo s DsXo s
Gs
Xo s Xi s
K Ds
K
D
1 s 1
K
Gs Ks

第四章控制系统的传递函数

第四章控制系统的传递函数

其中，
n
1 T
——环节的 固有频率
To 2
1 T
——环节的 阻尼比
如果0≤ξ<1，二阶环节称为振荡环节
例7 图示是由质量m、阻尼c、弹簧k组成的动力系统. 求G(s)
依动力平衡原理有 Xi(t) k m c
Xo(t)
d 2 xo dxo m 2 c kxo kxi dt dt
因此，系统的传递函数就是系统单位脉冲响应 的拉氏变换。
一般地,传递函数的表达式为
X o ( s) ao s n a1s n1 a2 s n2 an G( s ) X i ( s) bo s m b1s m1 b2 s m2 bm
2. 传递函数的性质
k
k为比例环节的增益或称为放大系数
例1
解
ni(t)
z1
求一对齿轮传动的传递函数 no z1 k ∴G(s)=k ni z2
最基本的运算放大器
no(t)
z2
例2
i 1= i 2
ei ea ea eo R1 R2
ei eo R1 R2
ei
R2 R1 e i2 a Ko a i3 i1 +
ZL=Ls
3.电容元件
dUC iC C dt
ZC(s) = 1/sC
例5
下图是一个由运算放大器组成的积分器， 求G(s)。 C R i + uc 取拉氏变换 uo Ui(s) R
Zc
i
+ Uo(s)
ui
解：
1 uc idt c
I ( s) U c ( s) cs
K s
1 Zc cs
ms2 X o ( s) csX o (s) kXo ( s) kXi (sG( s) 2 ms cs k

朱玉华自动控制原理第2章 数学模型2-3

朱玉华自动控制原理第2章 数学模型2-3

G(s) C(s) ……① R(s)
若已知线性定常系统的微分方程为
a0
d nc(t) dt n
a1
d n1c(t) dt n1
an1
dc(t) dt
anc(t)
b0
d mr(t) dt m
b1
d m1r(t) dt m1
bm1
dr(t) dt
bmr(t)
式中，c(t)为输出量，r(t)为输入量。
§2.3 传 递 函 数
一、传递函数的基本概念
指导思想：在零初始条件下，通过拉氏变换，将微分 方程变为s域（复数域）内的代数方程，在s 域内研究系统 的运动规律。必要时，通过拉氏反变换转化为时域形式。
s域（复数域）内的代数方程（即数学模型），称为 传递函数。
1、传递函数的定义
在初始条件为零时，线性定常系统输出量的拉氏变换与 输入量的拉氏变换之比，定义为该系统的传递函数。
RC
du0 (t) dt
u0 (t)
RC
dui (t) dt
G(s) RCs Td s RCs 1 Td s 1
只有当Td<<1时，才有G(s)≈Tds，实际的微分环节趋 于理想微分环节
再如:RL网络,其电路方程为
du0 (t) dt
R L
u0 (t)
dui (t) dt
G(s) Ls Td s Ls 1 Td s 1
如
G(s)
C(s) R(s)
b1s a0s2
b2 a1s
a2
S的代数方程：
(a0s2 a1s a2 )C(s) (b1s b2 )R(s)
用 d 置换s后得相应的微分方程 dt
a0
d 2c(t) dt 2

第六章 传递函数

第六章 传递函数

第六章 传递函数对于线性定常系统，传递函数是常用的一种数学模型，它是在拉氏变换的基础上建立的。

用传递函数描述系统可以免去求解微分方程的麻烦，间接地分析系统结构及参数与系统性能的关系，并且可以根据传递函数在复平面上的形状直接判断系统的动态性能，找出改善系统品质的方法。

因此，传递函数是经典控制理论的基础，是一个极其重要的基本概念。

第一节 传递函数的定义一、传递函数的定义1、定义对于线性定常系统，在零初始条件下，系统输出量的拉氏变换与输入量的拉()()C s R s ==零初始条件输出信号的拉氏变换传递函数输入信号的拉氏变换2、推导设线性定常系统的微分方程的一般形式为1011110111()()()()()()()()n n n n nn m m m m mm d d d a c t a c t a c t a c t dtdtdtd d d b r t b r t b r t b r t dtdtdt------++⋅⋅⋅++=++⋅⋅⋅++◆ 式中c(t)是系统输出量，r(t)是系统输入量，r(t)、c(t)及其各阶导数在t=0时的值均为零，即零初始条件。

◆a ， 1a ，…，na 及b ， 1b ，…，mb 均为系统结构参数所决定的实常数。

对上式中各项分别求拉氏变换，并令C(s)＝L[c(t)]，R(s)=L[r(t)]，可得s 的代数方程为：11011011[]()[]()nn mm n n m m a s a sa s a C sb sb sb s b R s ----++⋅⋅⋅++=++⋅⋅⋅++于是，由定义得到系统的传递函数为：10111011()()()()()m m m m nn n nb s b sb s b C s M s G s R s a s a sa s a N s ----++⋅⋅⋅++===++⋅⋅⋅++其中，1011()m m m m M s b s b s b s b --=++⋅⋅⋅++ 1011()n n n n N s a s a s a s a --=++⋅⋅⋅++ N(s)=0称为系统的特征方程，其根称为系统特征根。

传递函数

传递函数
R ＋ i (t ) u r (t ) C u c (t ) L ＋
－
－
第二节 传递函数
解：由图列微分方程
2u R L d du ur 解： 输入量： c c + u = u 得 c r RC dt + LC + 2 dt i uc 输出量： C 拉氏变换： ur
+ uc -
RCsUc(s) + LCs2 Uc (s) + U c (s ) 根据基尔霍夫定律：
第二节 传递函数
式中： K 0 — 为放大系数 传递函数性质： S = S1 , S2 · · · , Sn — 传递函数的极点 （ 4 ）传递函数是在零初始条件下定义的， （1）传递函数只适用于线性定常系统。 S = 不能反映非零初始条件下系统的运 Z1 , Z2 · · · , Zm — 传递函数的零点 动过程。 传递函数分母多项式就是相应微分方 （2）传递函数取决于系统的结构和参数， 将传递函数中的分子与分母多项式分 程的特征多项式，传递函数的极点就是微 与外施信号的大小和形式无关。 别用因式连乘的形式来表示，即 分方程的特征根。 （3）传递函数一般为复变量S 的有理分式。 K0 (s –z1 ) (s –z2 ) · · · (s – z m ) G (s ) = (s – s 1 ) ( s – s 2 பைடு நூலகம் · · · (s –sn ) n>=m
根据传递函数的定义有
C ( s) bm s m bm1s m1 b1s b0 G( s ) R( s) an s n an1s n1 a1s a0
第二节 传递函数
二、传递函数的求取 传递函数以般有三种方法求取：1、直接计算法， 2、阻抗法，3、动态结构图法（下一节在讲）。 1、2两种一起讲 例题1、求图示RLC电路的传递函数。

传递函数h(s)

传递函数h(s)

传递函数h(s)传递函数h(s)是控制工程中的一个重要概念，它能够描述一个系统的输入、输出之间的关系，被广泛地用于系统建模和控制器设计中。

本文将从以下几个方面介绍传递函数h(s)的相关内容。

1. 什么是传递函数h(s)传递函数h(s)被定义为系统输出与输入之间的比值，其中s表示Laplace变换的复频域变量。

传递函数h(s)通常表示成以下形式：h(s)=Y(s)/X(s)其中Y(s)为系统输出的Laplace变换，X(s)为系统输入的Laplace变换。

2. 传递函数h(s)的意义传递函数h(s)描述了输入信号在系统内传输和处理的方式，可以揭示系统的动态特性和频率响应特性。

其中，系统的动态特性包括零极点分布、系统阶数等内容；频率响应特性包括截止频率、幅频特性、相频特性等内容。

3. 传递函数h(s)的性质传递函数h(s)具有多种性质，下面介绍其中几个重要性质。

（1）时域特性：传递函数h(s)的逆Laplace变换可以得到系统的时间响应，这个响应包括系统的稳态响应和暂态响应。

（2）稳定性：当传递函数h(s)的所有极点均位于s平面的左半面时，系统是稳定的，否则系统是不稳定的。

（3）因果性：当传递函数h(s)是因果传递函数时，系统是因果的，否则系统是非因果的。

4. 传递函数h(s)的应用传递函数h(s)广泛应用于系统建模和控制器设计中。

在系统建模中，传递函数h(s)可以用来描述电路、机械系统、化学反应等各种物理系统；在控制器设计中，传递函数h(s)可以用来设计比例-积分-微分（PID）控制器、模型预测控制器、自适应控制器等各种控制器。

总之，传递函数h(s)是控制工程中不可或缺的重要概念，理解和掌握传递函数h(s)的相关内容，对于系统建模和控制器设计具有重大的意义。

传递函数的性质

传递函数的性质

传递函数的性质传递函数是一种常用的数学概念，它广泛应用在电路理论、控制理论、系统的分析和设计中。

传递函数的性质对电路、控制、信号处理以及生物学等领域有着重要意义。

传递函数是指一个函数，它可以描述输入信号对输出信号的变化。

它也称为传递系数，可以清楚地表示输出信号动态的变化状态。

传递函数的主要作用是分析和描述系统的状态，可以用来研究系统的性能，在电子工程、计算机工程、生物学等领域都有重要意义。

传递函数是系统动态特性的重要参数，它可以描述系统的输入信号对输出信号的变化。

系统的传递函数通常是一个分母多项式，它可以清楚地表达系统的输出信号如何变化，也可以用它来研究系统的稳定性、敏感性、有效性和效果等性能特性。

传递函数的性质可分为幅频特性和空间特性两类。

幅频特性是指传递函数的输出信号随输入信号频率的变化，其空间特性描述了传递函数的输出信号随时间变化的特性。

通常来讲，传递函数具有以下性质：(1)益：传递函数的增益是指输出信号与输入信号的大小比值，它表示了传递函数的增益特性，增益数值越大表示系统的响应能力越强；(2)位：传递函数的相位是指输出信号相对与输入信号的相位差，它表示了传递函数的相位特性，相位角越大表示系统的响应时间越长；(3)抗：传递函数的阻抗是指系统相对于输入信号的阻抗，它表示了系统的阻抗特性，阻抗数值越小表示系统的阻抗能力越低；(4)对性：传递函数的相对性是指系统对输入信号的变化反应能力，它表示了系统的相对特性，相对性数值越大表示系统对输入信号的变化反应能力越强。

传递函数的性质是一个重要的系统特性，可以用来研究系统的动态特性，可以根据系统的动态特性来分析和控制系统的性能。

因此，传递函数的性质也是系统设计和分析的重要参数，是系统的技术分析的重要基础。

综上所述，传递函数的性质对于理解和分析系统的状态有重要意义，在电路、控制、信号处理以及生物学等领域中都有广泛的应用。

它们可以帮助我们更加清楚地描述系统的性能，并为系统的设计与分析提供良好的参考依据。

控制系统中的传递函数分析

控制系统中的传递函数分析

控制系统中的传递函数分析传递函数是控制系统中的重要概念，用于描述输入信号与输出信号之间的关系。

通过对传递函数的分析，我们可以深入了解控制系统的性能和稳定性。

本文将对控制系统中的传递函数进行详细分析与讨论。

一、传递函数的定义及表示在控制系统中，传递函数是描述输入信号与输出信号之间关系的数学模型。

通常由拉普拉斯变换表示，可以表示为以下形式：G(s) = Y(s) / X(s)其中，G(s)为传递函数，Y(s)为输出信号的拉普拉斯变换，X(s)为输入信号的拉普拉斯变换。

二、传递函数的性质传递函数具有以下几个重要的性质：1. 线性性质：传递函数具有线性特性，即满足叠加原理，对于两个输入信号分别为X1(s)和X2(s)，输出信号分别为Y1(s)和Y2(s)，则对应的传递函数分别为G1(s)和G2(s)，则有：G(a*X1(s) + b*X2(s)) = a*G1(s) + b*G2(s)其中，a和b为常数。

2. 时不变性：传递函数具有时不变性，即传递函数对于输入信号的响应不随时间变化而变化。

3. 因果性：传递函数具有因果性，即输入信号的响应只依赖于当前及过去的输入信号，而不依赖于未来的输入信号。

4. 稳定性：传递函数的稳定性可以通过判断系统的极点位置来确定。

当所有极点的实部均为负数时，传递函数是稳定的。

三、传递函数的频域分析传递函数可以通过频域分析进行研究和理解。

1. 幅频特性：通过传递函数的模来描述系统的幅频特性。

传递函数的模为：|G(s)| = sqrt((Re(G(s)))^2 + (Im(G(s)))^2)其中，Re(G(s))为传递函数的实部，Im(G(s))为传递函数的虚部。

幅频特性可以反映系统对不同频率信号的增益情况。

2. 相频特性：通过传递函数的相位角来描述系统的相频特性。

传递函数的相位角为：arg(G(s)) = atan(Im(G(s)) / Re(G(s)))相频特性可以反映系统对不同频率信号的相位变化情况。

《自动控制原理》第二章传递函数

《自动控制原理》第二章传递函数

输出信号的拉氏变换 传递函数 = 输入信号的拉氏变换 零初始条件
C ( s) G(s) = R( s)
autocumt@ 1 中国矿业大学信电学院
一、 传递函数的定义和主要性质
设线性定常系统由下述n阶线性常微分方程描述： 设线性定常系统由下述n阶线性常微分方程描述：
dn d n −1 d a 0 n c (t ) + a1 n −1 c (t ) + ⋅ ⋅ ⋅ + a n −1 c (t ) + a n c (t ) dt dt dt d m −1 d dm = b0 m r (t ) + b1 m −1 r (t ) + ⋅ ⋅ ⋅ + bm −1 r (t ) + bm r (t ) dt dt dt
autocumt@
15
中国矿业大学信电学院
自动控制原理
4、振荡环节
特点：包含两个独立的储能元件，当输入量发生变化时，两个 包含两个独立的储能元件，当输入量发生变化时， 包含两个独立的储能元件 储能元件的能量进行交换，使输出带有振荡的性质。 储能元件的能量进行交换，使输出带有振荡的性质。
z1 n 2 (t) = n1 (t) z2
G(s) = N 2 (s) z1 = =K N1 (s) z 2
传递函数： 传递函数：
autocumt@
9
中国矿业大学信电学院
其它一些比例环节
自动控制原理
R2 R1
r (t )
Ec
R
c (t )
ic (t )
r1
r2
r (t )
c(t )
C
例：积分电路 积分电路
i1 (t )
R1

自动控制原理--传递函数相关知识

自动控制原理--传递函数相关知识

26.5
1
s 17.25
17.25
26.5
s (s 17.25)2 (26.5)2 (s 17.25)2 (26.5)2
所以
y(t)
1 e17.25t
cos 26.5t 17.25 e17.25t 26.5
sin 26.5t
1 e17.25t
cos
26.5t
17.25 26.5
sin
26.5t
D(s) a0sn a1sn1 an1s an D(s) 0即是系统的特征方程。
G(s) N (s) b0 (s z1)(s z2 ) (s zm ) D(s) a0 (s p1)(s p2 ) (s pn )
s zi (i 1, 2 m)是N (s) 0的根，称为传递 函数的零点，s pi (i 1, 2 n)是D(s) 0的根 是传递函数的极点。
因为组成系统的元部件或多或少存在惯 性，所以G(s)的分母阶次大于等于分子阶 次，即 n,是m有理真分式，若 ,我们m 就 n 说这是物理不可实现的系统。
二、传递函数的性质
(1)传递函数是一种数学模型，是对微分方程在零初始条件 下进行拉氏变换得到的；
(2)传递函数与微分方程一一对应；
(3)传递函数描述了系统的外部特性。不反映系统的内部物 理结构的有关信息；
R(s)
式中 ——环节的时间常数。
特点：输出量正比输入量变化的速度，能预示输 入信号的变化趋势。
实例：测速发电机输出电压与输入角度间的传递 函数即为微分环节。
5）振荡环节：其输出量和输入量的关系，由下面的 二阶微分方程式来表示。
T2
d 2 y(t) dt 2
2 T
dy (t ) dt
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Uc (s)
1 RCs
U 1
r
(s)
RC RCs
1
uc
(0)
(2.18)
当输入为阶跃电压ur(t)= u0·1(t)时，对Uc(s)求拉氏反变换，即得 uc(t)的变化规律:
大量资料 天天更新
uc
(t)
u0
(1
e
t RC
)
uc
(0)e
t RC
式中第一项称为零状态响应， 由U(t)决定的分量； 第二项称为零输入响应， 由初始电压Uc (0)决定的 分量。
第二节 控制系统的复数域数学模型
一、传递函数的概念 二、传递函数的性质 三、典型环节及其传递函数
大量资料 天天更新
引言
• 控制系统的微分方程：是在时域描述系统动态性能的数 学模型，在给定外作用及初始条件下，求解微分方程可以 得到系统的输出响应。但如果系统的某个参数变化或者结 构形式改变时，便需要重新列写并求解微分方程。
(2.19)
图2-5表示各分量的变化曲线， 电容电压Uc (t)即为两者的合成。
图2-5 RC网络的阶跃响应曲线
大量资料 天天更新
在式(2.19 )中，如果把初始电压Uc(0)也视为一个输入作用，
则根据线性系统的叠加原理，可以分别研究在输入电压Ur(t)
和初始电压Uc(0)作用时，电路的输出响应。若Uc(0) =0，则
• 传递函数：对线性常微分方程进行拉氏变换，得到的系统 在复数域的数学模型----传递函数。 传递函数不仅可以表征系统的动态特性，而且可以研 究系统的结构或参数变化时对系统性能的影响。传递函数 是经典控制理论中最基本、最重要的概念
大量资料 天天更新
一、传递函数的概念
图2-4所示的RC电路中电
容的端电压Uc (t) 。根据克
图2-4 RC 电路
现在对上述微分方程两端进行拉氏变换，并考虑电容上的 初始电压Uc (0)，得:
RCsUc (s) RCuc (0) Uc (s) Ur (s) (2.17)
式中 Uc(s)—— 输出电Uc(t)的拉氏变换； Ur(s)—— 输入电压Ur(t)的拉氏变换。
由上式求出Uc(s)的表达式:
希霍夫定律，可列写如下
微分方程：
i(t)R uc (t) ur (t)
(2.14)
uc (t )
1 C
i(t)dt
(2.15)
消去中间变量i(t)，得到输入Ur (t) 与 方输程出: Uc(t) 之间的线性定常微分
RC
duc (t) dt
uc
(t )
ur
(t )
(2.16)
大量资料 天天更新
线性（或线性化）定常系统在零初始条件下，输出量的拉氏 变换与输入量的拉氏变换之比称为传递函数。
大量资料 天天更新
若线性定常系统由下述n阶微分方程描述：
an
dn dt n
c(t)
an1
d n 1 dt n1
c(t)
a1
d dt
c(t
)
a0c(t
)
(2.22)
式中bcm(dtd)tm是m r系(t)统 b输m1出ddt量mm11，r(rt()t)是系 b统1 dd输t r入(t)量 b，0r(at)i
1.传递函数是复变量s的有理真分式函数，分子的阶数m小
于或等于分母的阶数n （m≤n） ，且所有系数均为实数。
2.传递函数只取决于系统和元件的结构和参数，与外作用 及初始条件无关。
3.传递函数的零、极点分布图也表征了系统的动态性能。 将式(2.23)中分子多项式及分母多 项式因式分解后，写为如 下形式：
一般zi，pi可以为实数，也可 为复数，且若为复数，必共 轭成对出现。
将零、极点标在复平面 上，则得到传递函数的零极 点分布图，如图2-7所示。
图中零点用“o”表示，极点 用“X ”表示。
图2-7
s2 G(s) (s 3)(s2 2s 2)
零极点分布图
大量资料 天天更新
4. 若令式(2.23)中s = 0，则：
有:
Hale Waihona Puke Uc (s)1 RCs
U 1
r
(s)
(2.20)
当输入电压ur(t)一定时，电路输出响应的拉氏变换Uc(s)完全由 1/(RCs+1)所确定，式(2.20)亦可写为:
Uc(s) 1 Ur (s) RCs 1
(2.21)
当初始电压为零时，电路输出函数的拉氏变换Uc(s)与输入 函数拉氏变换Ur(s)之比，是一个只与电路结构及参数有关的函数 。
(i=1,2,…,n), bj(j=1,2,…,m)是与系统构参数有关的常系
数。
令C(s)=L[c(t)]，R(s)=L[r(t)]，在初始条件为零时，对式 (2.22)进行拉氏变换，可得到s的代数方程：
[ansn an1sn1 a1s a0 ]C(s)
[bmsm bm1sm1 b1s b0 ]R(s)
G(s) C(s) k (s z1)(s z2 ) (s zm ) R(s) (s p1)(s p2 ) (s pn )
(2.24)
大量资料 天天更新
式中k为常数，-z1,…,-zm为传
递函数分子多项式方程的m个 根，称之为传递函数的零点 ；-p1,…,-pn为分母多项式方程 的n个根，称为传递函数的极 点。
大量资料 天天更新
由传递函数的定义，线性定常系统的传递函数：
G(s)
C(s) R(s)
bm s m an s n
bm1sm1 an1sn1
b1s b0 M (s) a1s a0 D(s)
(2.23)
式中 M(s)= bmsm+bm-1sm-1+…+b1s+b0为传递函数的分子多项式； D(s)= ansn+an-1sn-1+…+a1s+a0为传递函数的分母多项式。
传递函数是在初始条件为零（或称零初始条件）时定义的。 控制系统的零初始条件有两方面的含义，一系统输入量及其各 阶导数在t =0时的值均为零；二系统输出量及其各阶导数在t =0 时的值也为零。
大量资料 天天更新
二、传递函数的性质
从线性定常系统传递函数的定义式(2.23)可知，传递函数具 有以下性质：
大量资料 天天更新
式(2.21)来表征电路本身特性，称做传递函数，记为： G(s) 1 Ts 1
式中T=RC。显然，传递函 数G(s)确立了电路输入电压 与输出电压之间的关系。
图2-6 传递函数
传递函数可用图2-6表示。该图表明了电路中电压的传递 关系，即输入电压Ur(s)，经过G(s)的传递，得到输出电压 Uc(s)=G(s)Ur(s) 。