8弯矩分配法分配系数计算过程及结果8

第十八章力矩分配法力矩分配法理论基础：位移法；计算对象：杆端弯矩；适用范围：连续梁和无侧移刚架。

一、转动刚度转动刚度表示杆端对转动的抵抗能力。

它在数值上等于使杆端产生单位转角时需要施加的力矩，以SAB表示。

A是施力端（近端），B为远端。

1S AB=4i1S AB=3iS AB= i1S AB=0远端固定远端铰支远端滑动远端自由第一节力矩分配法的基本原理1S AB =4i1S AB =3iS AB = i 1S AB =0远端固定远端铰支远端滑动远端自由转动刚度远端固定，S =4i 远端简支，S =3i 远端定向，S =i 远端自由，S =0S AB 与杆的线刚度i 和远端支承情况有关。

i —杆件的线刚度，lEI i二、传递系数M AB = 4i AB ϕAM BA = 2i AB ϕA21==AB BA ABM M C M AB = 3i AB ϕA 0==ABBA ABM M C M AB = i AB ϕAM BA = -i AB ϕA1-==ABBA ABM M C ϕAlAB远端固定ABϕAϕAAB远端铰支远端滑动M BA = 0远端支承转动刚度传递系数固定S=4i C =1/2简支S=3i C =0定向S=i C = -1自由S=0三、力矩分配法的基本原理杆端弯距：取结点A 作隔离体，由∑M =0，得分配系数CA BDi ABi AC i ADAAB A AB AB S i M ϕϕ==4A AC A AC AC S i M ϕϕ==AAD A AD AD S i M ϕϕ==3}M M ABM ACM ADAAD AC AB S S S M ϕ)(++=∑=++=AAD AC AB A SMS S S M ϕMSSM AADAD ∑=M SS M A ABAB ∑=M S S M AACAC ∑=注：1）分配弯矩是杆端转动时产生的近端弯矩。

2）结点集中力偶顺时针为正。

∑=AAkAkSS μMM Ak Ak μ=分配弯矩A ϕM1321=++=∑A A A Ak μμμμ各杆的远端弯矩M kA 可以利用传递系数求出。

M M1143
3i131 S131 i141 S141
(a)
M15 4i151 S151
②由结点1的平衡条件:
M1 0
即:
MM12M13M14M150
M12
M(S12S13S14S15)1
得:
1
M S12S13S14S15
(b)
M M13
1
M14
1
M15
得:
M
12
S 12 M S
12 M
200.9 120
B
0.5 0.5 +250.0 -187.5
+32.0 -47.3 -47.3 +4.8 -2.4 -2.4 +0.3 -0.2 -0.2
+237.4 -237.4 237.4
375
300
C
+112.5 -23.7 -1.2
+87.6 87.6
D
M图(kn.m)
§14—3 用力矩分配法计算无侧移刚架
89.83
2042
40kn.m
850.7443.88
C CA
144
B
A
40 D
6.86
固端弯矩 -86.4 +57.6 0.0 -40.0 0.0 0.0
分配传递 -3.43 -6.86 -6.86 -3.83
-3.43
M图(kn.m)
0. 最后弯矩 -89.83 +50.7 -6.86 -43.88 0.0 -3.43
B
Mf BC
MB=
Mf BA
+MBf C
(c)
M’=－MB
A
B C

1渐近法2用力法、位移法分析超静定结构，都需要求解多元联立方程组，求出基本未知量。

当未知量较多时，计算颇为繁重。

渐近法—采用逐步地逼近真实解的方法。

渐近法主要有：一、渐近法概述(1)力矩分配法：适于连续梁与无侧移刚架。

(2)无剪力分配法：适于规则的有侧移刚架。

(3)迭代法：适于梁的刚度大于柱刚度的各种刚架。

3力矩分配法理论基础：位移法；计算对象：杆端弯矩；计算方法：逐渐逼近的方法；适用范围：连续梁和无侧移刚架。

4只有结点角位移而无结点线位移的梁和刚架。

？力矩分配法的适用范围：力矩分配法的适用范围：5只有结点角位移而无结点线位移的梁和刚架。

√6力矩分配法以杆端弯矩为计算对象，采用：固定放松分配、传递逐次逼近杆端弯矩的精确解。

计算原理及符号规则均与位移法相同，只是计算过程不相同。

7计算过程：1.固定结点求出固定状态的杆端弯矩FijM 附加刚臂处的不平衡弯矩iM依次将结点上的不平衡弯矩反号分配于各杆近端，并传向远端。

2.逐次放松各结点8若干次循环计算= 也即逐次恢复转角的过程直接表达为各杆端弯矩逐次修正的过程放松结束，也即变形（转角）、内力趋于实际状态。

9——基本运算A BCM ABM BAM BC A BCM FAB M FBAM FBCM BM BM F BAM F BCM B =M F BA +M F BCABC－M BBAM ′BCM ′AB M ′0－M BBAM ′BCM ′)(B BA BAM M −⋅=′μ)(B BC BCM M −⋅=′μ+=最后杆端弯矩：M BA =M F BA +BAM ′M BC =M F BC +BCM ′M AB =M F AB +AB M ′然后各跨分别叠加简支梁的弯矩图，即得最后弯矩图。

固端弯矩带本身符号单结点的力矩分配分配系数分配弯矩10例1. 用力矩分配法作图示连续梁的弯矩图。

3m 3m 6m EI EI 200kN 20kN/m （1）固定B 结点A BC 200kN 20kN/m M F AB =M F BA =M F BC=mkN ⋅−=×−15086200m kN ⋅150m kN ⋅−=×−9086202M B =M F BA + M F BC =m kN ⋅60－150150－90（2）放松结点B，即加-60进行分配60A B C－60设i =EI/l 计算转动刚度：S BA =4iS BC =3i分配系数：571.0344=+=i i iBAμ429.073==iiBCμ0.5710.429分配力矩:3.34)60(571.0−=−×=′BAM 7.25)60(429.0−=−×=′BCM －34.3－25.7－17.2+(3) 最后结果。

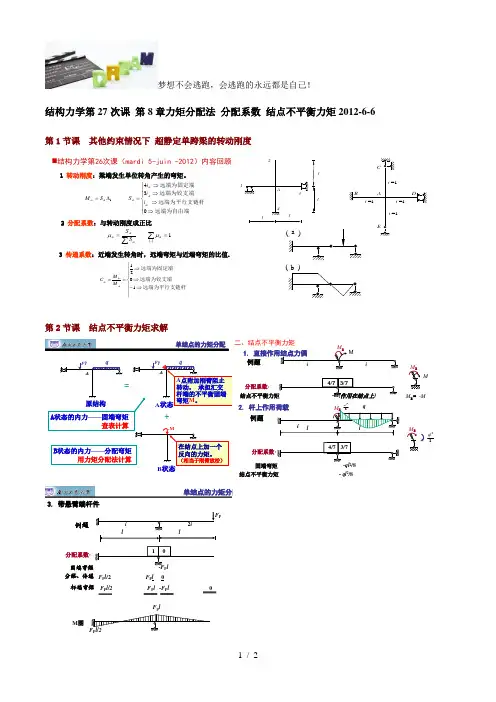
梦想不会逃跑，会逃跑的永远都是自己！结构力学第27次课 第8章力矩分配法 分配系数 结点不平衡力矩2012-6-6第1节课 其他约束情况下 超静定单跨梁的转动刚度1 转动刚度：梁端发生单位转角产生的弯矩。

⎪⎪⎩⎪⎪⎨⎧⇒⇒⇒⇒=∆=远端为自由端远端为平行支链杆远端为铰支端远端为固定端0341ik ikik ik ik ik i i i S S M 2 分配系数：与转动刚度成正比()1==∑∑iikiikikik S S μμ3 传递系数：近端发生转角时，远端弯矩与近端弯矩的比值.⎪⎪⎩⎪⎪⎨⎧⇒-⇒⇒==远端为平行支链杆远端为铰支端远端为固定端1021ikkiik M M C ⏹结构力学第26次课（mardi 5-juin -2012）内容回顾( )( )a b1234AllllBCADE=1i =1i =1i =1i第2节课 结点不平衡力矩求解单结点的力矩分配F P q A原结构=F P qAA 状态-MB 状态+A 点附加刚臂阻止转动，承担汇交杆端的不平衡固端弯矩M 。

在结点上加一个反向的力矩。

（相当于刚臂放松）B 状态的内力——分配弯矩用力矩分配法计算A 状态的内力——固端弯矩查表计算例题-M(作用在结点上)结点不平衡力矩3/74/7i iMiiM BM BM B =-MM1. 直接作用结点力偶分配系数：二、结点不平衡力矩例题3/74/7-ql 2/8固端弯矩qiill分配系数：-ql 2/8结点不平衡力矩8ql ⏹结构力学第27次课（merdredi 5-juin -2012）内容回顾2. 杆上作用荷载MB M B8ql单结点的力矩分配例题-F P l 固端弯矩-F P l 0F P l/2F P l 杆端弯矩0F P l /2F P l分配、传递ll2iiF P10F P lF P l/2M 图3. 带悬臂端杆件分配系数：单结点连续梁的力矩分配法小结2．具有一个结点角位移结构的计算步骤：● 加约束：在刚结点i 处加一附加刚臂，求出固端弯矩，再求出附加刚臂给结点的约束力矩f i M 。

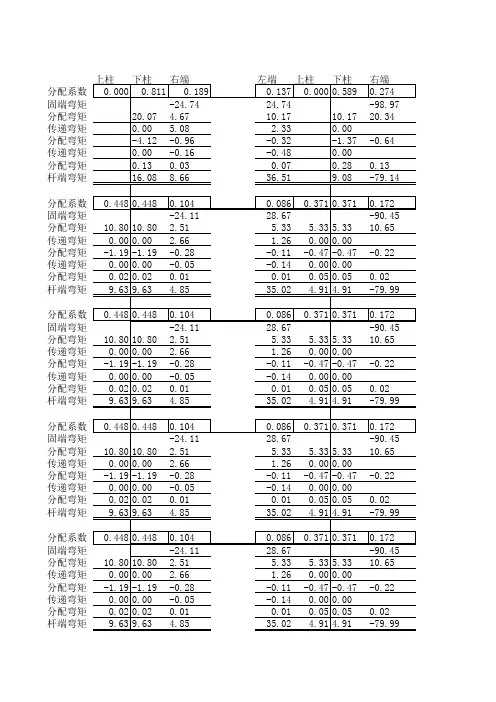
弯矩分配法分配系数计算过程及结果：6第层各节点的弯矩分配系数I 节点 0.000μ=上4415.780.43644415.78420.42i i i μ⨯===+⨯+⨯下下下4420.420.56444420.42415.78i i i μ⨯===+⨯+⨯IO 下O 节点 0.000μ=上4415.780.313442415.78420.42228.58i i i i μ⨯===++⨯+⨯+⨯下下下4420.420.404442415.78420.42228.58i i i i μ⨯===++⨯+⨯+⨯左左下4428.580.283442415.78420.42228.58i i i i μ⨯===++⨯+⨯+⨯右右下U 节点 0.000μ=上4415.780.35644415.78428.58i i i μ⨯===+⨯+⨯下下下4428.580.64444428.58415.78i i i μ⨯===+⨯+⨯OU 下第5、4层各节点的弯矩分配系数H 、G 节点 4415.780.304444415.78415.78420.42i i i i μ⨯===++⨯+⨯+⨯上上下上4415.780.304444415.78415.78420.42i i i i μ⨯===++⨯+⨯+⨯下下下上4420.420.392444415.78415.78420.42HN GM i i i i μ⨯===++⨯+⨯+⨯、下上N 、M 节点0.2384442415.78415.78420.42228.58i i i i μ===+++⨯+⨯+⨯+⨯上上下上4415.780.2384442415.78415.78420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯下下下上4420.420.3084442415.78415.78420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯NH 、MG 下上4228.580.2164442415.78415.78420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯NT 、MS 下上T 、S 节点 4415.780.262444415.78415.78428.58i i i i μ⨯===++⨯+⨯+⨯上上下上4415.780.262444415.78415.78428.58i i i i μ⨯===++⨯+⨯+⨯下下下上4428.580.47644415.78415.78428.58i i i μ⨯===+⨯+⨯+⨯TN 、SM 下第3层各节点的弯矩分配系数F 节点 4415.780.266444415.78423.11420.42i i i i μ⨯===++⨯+⨯+⨯上上下上4423.110.390444415.78423.11420.42i i i i μ⨯===++⨯+⨯+⨯下下下上4420.420.344444423.11415.78420.42i i i i μ⨯===++⨯+⨯+⨯FL 下上L 节点4415.780.2154442415.78423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯上上下上4423.110.3144442415.78423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯下下下上4420.420.2774442415.78423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯LF 下上0.1944442415.78423.11420.42228.58i i i i μ===+++⨯+⨯+⨯+⨯LR 下上R 节点 4415.780.234444415.78423.11428.58i i i i μ⨯===++⨯+⨯+⨯上上下上4423.110.343444415.78423.11428.58i i i i μ⨯===++⨯+⨯+⨯下下下上4428.580.42344423.11415.78428.58i i i μ⨯===+⨯+⨯+⨯RL 下第2、1层各节点的弯矩分配系数E 、D 节点 4423.110.347444423.11423.11420.42i i i i μ⨯===++⨯+⨯+⨯上上下上4423.110.347444423.11423.11420.42i i i i μ⨯===++⨯+⨯+⨯下下下上4420.420.306444423.11423.11420.42EK DJ i i i i μ⨯===++⨯+⨯+⨯、下上K 、J 节点4423.110.2864442423.11423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯上上下上4423.110.2864442423.11423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯下下下上4420.420.2524442423.11423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯KE 、JD 下上4228.580.1764442423.11423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯LR 下上Q 、P 节点 4423.110.309444423.11423.11428.58i i i i μ⨯===++⨯+⨯+⨯上上下上4423.110.309444423.11423.11428.58i i i i μ⨯===++⨯+⨯+⨯下下下上4428.580.38244423.11423.11428.58i i i μ⨯===+⨯+⨯+⨯QK 、PJ 下。

BA BC ---分配系数
一种结点上旳各杆端分配系
数总和恒等于1。
SBA 4i SBC 3i
BA 4i /(3i 4i) 4 / 7 0.571 A
B
M
u B
C
B
BC 3i /(3i 4i) 3 / 7 0.429
M
d BA
BA
(
M
u B
)
57.1
M
d BC
BC
(
M
u B
)
10m
M
u 2
B
2
110000
-28.6 -57.1 -42.9
21.4
6.1
-9.2 -12.2 -6.1
1.8
6.1
1.8 3.5 2.6
… … ...
q 12kN / m
A
EI
1 EI
2 EI
B A q 12kN / m
1
2
10m
10m
10m
q 12kN / m
A
M
u 1
ql 2 / 8
S21 4i S2B 3i
21 0.571 2B 0.429
放松结点1(结点2固定):
S12 4i S1A 3i
12 0.571 1A 0.429
q 12kN / m
A
EI
1 EI
B 2 EI
10m
10m
q 12kN / m
A
M1u
ql 2 / 8 28.6
1
ql 2 / 12
50
那么假如外荷载不是结点力偶，情况又怎样呢？
一.基本概念
固定状态:
M
u B

1 4
传递系数
远端固定，CAB=0.5
远端简支，CAD=0
远端滑动，CAC=-1
D i
分配系数
AB
2 3
AC
1 12
AD
1 4
120kNm
A
2i
i
C
传递系数
CAB=0.5
CAD=0
CAC=-1
B
D
80kNm A 30kNm
B 40kNm
10kNm C
M图
杆端弯矩
M AB
AB M
2 *120
3
固端弯矩
分配和传 递弯矩 杆端弯矩
A -150 -17.2
-167.2
分配系数
4 7
150
3 7
B
-90
-34.3 -25.7
115.7 -115.7
167.2 A
115.7
300
90
B 32.1
158.5
M图(单位kNm)
C 0 0 0 单位kNm
C
单结点力矩分配法计算举例
3）非结点荷载作用刚架
渐近法概述
1、线性代数方程组的解法: 直接法，渐进法
2、结构力学的渐近法:
力学建立方程，数学渐近解 不建立方程式，直接逼近真实受力状态。其 突出的优点是每一步都有明确的物理意义。
3、位移法方程的两个特点:
(1)每个方程一般不超过五项式； (2)主系数大于副系数的总和，即 kii > kij，
适于渐近解法。
80kNm
M AC AC M 10kNm
M AD AD M 30kNm
M BA CAB M AB 40kNm
M CA CAC M AC 10kNm

固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩杆端弯矩
分配系数固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩杆端弯矩
分配系数固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩杆端弯矩
分配系数固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩杆端弯矩
分配系数固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩
杆端弯矩
分配系数固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩
杆端弯矩。

毕业设计思考题2结构方案和初选截面尺寸2.1何为结构体系?高层建筑结构体系大致有哪几类?选定结构体系主要考虑的因素有哪些?(P4~ P5)使用要求、建筑高度、材料用量、抗震要求2.2高层建筑结构总体布置的原则是什么?框剪结构体系A级高度的最大高宽比在设防烈度为6、7、8度时为多少?(5、4)按弹性方法计算时楼层层间最大位移与层高之比的限值对框剪结构应为多少?(1/800)(P6P7)2.3高层建筑结构平面布置、竖向布置的一般原则是什么?(P6)平面:简单、规则、对称、减少偏心2.4如何进行柱网布置?(P7)2.5柱的间距、梁的跨度、板的跨度之间有何关系?(P7~ P8)2.6框剪结构中剪力墙布置的基本原则是什么?(P8)2.7何为壁率?初定剪力墙的数量时剪力墙的壁率应取多少?底层结构构件截面积与楼面面积之比应取多少?(P9)2.8剪力墙的刚度过大或过小时采用的调整方法有哪些?(P9)2.9结构受力构件编号时"abc-d"中各符号含义是什么?(P10)a为楼层号b为构件代号c为构件编号d为梁的跨次或剪力墙墙肢序号2.10如何初估楼板厚度?顶层楼板、地下室顶板厚度有何要求?为什么?(P11)2.11如何初定梁的截面尺寸?(P12)2.12如何初定柱的截面尺寸?(P12)2.13框剪结构中的剪力墙除满足剪力墙结构的要求外还应满足什么要求?(P13)注:各题后括号内表示《高层建筑框架-剪力墙结构设计》一书的页码该页码内有相关问题的参考答案3 楼板结构设计3.1何谓单向板及双向板?长边/短边≥3时作用于板上荷载q主要由短向板带承受长向板带分配的荷载很小课忽略不计荷载由短向板带承受的四边支承板称为单向板长向板/短向板3时作用于板上的荷载q虽仍然主要由短向板带承受但长向板带所分配的荷载虽小却不能忽略不计荷载由两个方向板带共同重的承受的四边支承板成为双向板3.2单向板、双向板板厚如何确定?梁的截面尺寸如何估算?根据什么确定?单向板的经济跨度一般为2~3m;次梁的经济跨度一般4~6m;主梁的经济跨度一般为5~8m 板h=(1/30~1/40)l1;次梁:(1/12~1/18)l2;主梁:(1/8~1/14)l3l1l2l3---分别为次梁间距主梁间距和柱与柱或柱与墙之间的间距双向板厚度一般不作刚度验算时板的最小厚度h=(1/40~1/50)lox(lox为双向板的短向计算跨度)切应满足h≥80mm双重井式楼盖的梁一般为等截面梁满足刚度要求的梁高可取h=(1/16~1/18)lo梁宽可取b=(1/3~1/4)hlo为建筑平面的短边长度3.3在现浇肋形楼盖中如何确定单向板、双向板、非框架梁的计算简图?根据板的短边边长、支座类型荷载组合3.4什么情况下可采用等效均布荷载?两边铰支静力手册里可以查到的都可以采用均布荷载3.5计算梁、板内力用什么方法?弹性理论分析方法塑性理论分析方法3.6绘出单跨简支梁在均布荷载或跨中集中力作用下的弯矩图、剪力图?不懂就算啦3.7绘出悬臂板在均布荷载作用下内力图及配筋图?3.8试述弯矩分配法的计算步骤?弯矩分配系数如何计算?求出固端弯距再相加出不平衡弯距用不平衡弯距乘与弯距分配系数分配系数就是用各个杆件的刚度系数除与总的刚度系数之和3.9为什么用弹性法计算双向板跨中弯矩时要考虑泊松比?而计算支座弯矩时不考虑?对于查表所求得系数求得的跨内截面弯距值要考虑双向弯曲对两个方向板带弯距值的相互影响因此要考虑泊松比对于支座截面弯距值由于另一个方向板带弯距等于零故不存在两个方向板带弯距的影响问题3.10板和梁的保护层厚度多少?怎样确定?见混凝土结构设计原理P348根据混凝土强度确定3.11受弯构件有哪两种主要破坏形态?正截面破坏和斜截面破坏3.12梁正截面有哪几种破坏形式?有何区别?少筋破坏适筋破坏超筋破坏少筋破坏和超筋破坏都是脆性破坏后果严重破坏前不征兆材料得不到充分利用3.13受弯构件斜截面有哪几种主要破坏形态?斜拉破坏λ3;剪压破坏(1λ≤3);斜压破坏(λ≤1)混凝土结构设计原理P1213.14板的受力钢筋和分布钢筋应满足哪些构造要求?混凝土结构设计原理P973.15单向板内分布钢筋的作用有哪些?同上3.16为什么板一般不配箍筋请分析板类构件通常承受的荷载不大剪力较小因此一般不必进行斜截面承载力的计算也不配箍筋和弯起钢筋混凝土简支板或连续板由于跨高比较大即结构设计由弯距控制应按弯距计算纵向钢筋用量因此板一般不必进行受剪承载力计算3.17连续梁、板支座负钢筋截断的根据是什么?如何确定梁、板的负钢筋切断长度?根据材料抗力包络图连续梁的切断点见混凝土结构设计原理P134表5-4及混凝土结构设计P31单向板的负弯距钢筋切断点和次梁边距离为ln/3和主梁距离为ln/4(ln梁间内边线最短距离);双向板的负弯距钢筋切断点和次梁边距离为lox/4 和主梁边距离为lox/7(lox为板短向计算跨度)3.18连续板边支座看作简支是否存在弯矩?如何处理?对梁有何影响?存在连续板再支座负弯距作用下截面上部受拉下部受压形成内拱板周边的梁能够约束"拱"的支座侧移即能提供可靠的水平推力则再板中形成具有一定矢高的内拱3.19为什么板边支座可作简支边?简支板为什么要设板面构造负钢筋?整体矢式梁板结构中当板、次梁、及主梁支承于砖柱或墙体上时结构之间均可视为铰支座砖柱、墙对他们的嵌固作用较小可在构造设计中予以考虑整体式梁板结构中板、梁和柱是整体浇筑在一起的板支承于次梁次梁支承于主梁主梁支承于柱因此次梁对于板将有一定的约束作用上述约束作用在结构分析时必须予以考虑因此要构造配筋、3.20天面板飘板板角为什么要配置放射钢筋?避免因温度引发的应力集中导致的裂缝3.21设计屋面天沟板应如何配筋?双向双层一般如果可以按悬挑板计算配筋的话你要考虑天沟自重包括外侧挡板的集中力同时要考虑天沟满水或1/2满水的荷载(这看天沟具体使用情况)还要加上施工检修荷载规范上有相应规定的《高层建筑框架》P173.22如果要求板开孔洞结构如何处理?圆孔直径D或方洞b小于300mm时板受力筋可绕国孔洞边不需切断;300~1000mm且无集中荷载时应在孔洞内每侧配置面积不少于孔洞宽度内被切断的受力筋的一半且不少于2根12的附加钢筋;b300且洞边有集中荷载或D1000mm时应在洞边设边梁《高层建筑框架》P163.23次梁是否需要加密箍?为什么?不用因为次梁在支座处只承受了支座负弯距冲切承载力由主梁承担了3.24梁内受力钢筋和纵向构造钢筋应满足哪些构造要求?混凝土结构设计原理P97、983.25梁中架立筋有什么作用?为什么要设腰筋?箍筋有何作用?固定箍筋与钢筋连成骨架也可承受一定压力腰筋可用于抗扭加强梁构件混凝土抗收缩及抗温度变形的能力箍筋可用于固定纵筋抗剪和抗扭3.26底筋4φ22放在b200?的梁内一排放得下吗?放不下纵向钢筋最小间距式503.27次梁与主梁相交处应设置什么钢筋?为什么?吊筋承受来作用在主梁上的集中荷载3.28楼梯平台梁如何支承?一般支承于楼梯间侧承重墙上没墙加柱子《高层建筑框架》P223.29墙下不设次梁如何处理?如果是首层就作成地鼓不是首层就不知道拉板很小的时候就不用的直接传力到两边梁上3.30试绘出板式楼梯的计算简图?楼梯梯段板有何内力?如何配筋? 混凝土结构设计P83~863.31请绘出折板式楼梯的配筋图?为什么?看楼梯大样图E型《高层建筑框架》P22不知道为什么3.32计算楼梯时扶手荷载如何处理?当集中荷载处理3.33如何考虑楼梯扶手和阳台栏杆压顶配筋?房屋建筑学P1923.34梯间小柱的位置?平台梁下面3.35计算楼梯内力时弯矩有时用(1/8)ql2而有些用(1/10)ql2请分析原因?混凝土结构设计P85、P864 结构计算简图及刚度计算参数4.1 在用近似法计算高层框架-剪力墙时引入了哪些假定将空间结构简化为平面结构?P27(1)一榀框架或一片墙可以抵抗自身平面内的水平力而在平面外的刚度很小可以忽略(2)各片平面抗侧力结构之间通过楼板互相联系协同工作4.2在普通高层建筑中结构布置的基本原则是什么?P27均匀、对称、规则当水平力的合力通过结构抗侧移刚度中心时可不计扭转影响即各层楼板只平移不转动4.3 框架-剪力墙结构在水平荷载作用下其变形曲线是何种类型?P27框架以剪切型变形为主剪力墙以弯曲型变形为主在水平荷载作用下框架的侧移曲线为型剪力墙结构的侧移曲线为型;两种结构共同工作时的侧移曲线为型4.4 剪力墙每一侧的有效翼缘的宽度如何确定?P27每一侧有效翼缘的宽度可取翼缘厚度的6倍、墙间距的一半和总高度的1/20中的最小值且不大于墙至洞口边缘的距离4.5 框架-剪力墙结构的计算简图可简化为哪两种体系?如何区分这两种体系?P28框架以剪切型变形为主剪力墙以弯曲型变形为主在计算简图中可简化为铰结体系和刚结体系两种铰结体系中框架和剪力墙之间通过楼板联系或虽有连梁但刚度很小对墙的约束很弱在计算简图中墙与框架的联系可简化为铰结连杆刚结体系中连梁对墙柱都产生约束作用但对柱的约束作用将反映在柱的D值中因而在计算简图中连梁与墙相连端处理成刚结与框架端为铰结4.6 对有地下室的高层建筑其主体结构的计算高度如何确定?P29在计算简图中选地下室顶板作为主体结构高度的起始点4.7 剪力墙如何进行分类?根据什么条件来判别其类型?P29根据洞口大小和截面应力分布特点剪力墙可分为整截面墙、整体小开口墙、联肢墙及壁式框架用这两个条件来判别是整体系数越大剪力墙的整体性越好;是判明各墙肢在层间出现反弯点多少的条件越大出现反弯点的层数就越多4.8 壁式框架与普通框架有何不同?总框架抗推刚度Cf是否包含壁式框架的抗推刚度?用D值法计算水平荷载作用下壁式框架内力时与一般框架的区别主要有两点:其一是梁柱杆端均有刚域从而使杆件的刚度增大;其二是梁柱截面高度较大需考虑杆件剪切变形的影响包含4.9 什么是刚度特征值λ?它对内力分配、侧移变形有什么影响?刚度特征值λ是框架抗推刚度(或广义抗推刚度)与剪力墙抗弯刚度的比值它集中反映了结构的变形状态及受力状态刚度特征值λ对框架---剪力墙结构体系的影响:当λ=0时即为纯剪力墙结构;当λ值较小时框架抗推刚度很小;随着λ值的增大剪力墙抗弯刚度减小;当λ=∞时即为纯框架结构λ值对框架-剪力墙结构受力、变形性能影响很大4.10 框架-剪力墙结构λ值的正常范围是什么?λ值不满足要求时对结构如何进行调整?以剪力墙为主为弯曲型变形;以框架为主为剪切型变形;1~6之间为弯剪型变形55.1结构计算发现建筑物存在较大的扭转效应应如何处理?加强角柱刚度和边梁刚度外刚内柔5.2设计时未布置剪力墙在施工过程中为了结构安全自行增加了若干剪力墙是否妥当?不妥当设计时未计算添加说明已经满足安全要求自行添加若干剪力墙会使结构的刚度过大加大了地震作用效应而且也不经济5.3在水平荷载作用下框架结构内力分析采用什么方法?P42 在近似法中采用了连续化方法将各层总连梁离散为沿楼层高度均匀的连续连杆5.4反弯点法与D值法有什么不同?反弯点高度不同:反弯点法:水平荷载作用下上层柱的反弯点在柱的中心底层柱反弯点距柱底端为2/3层高处D值法计算基本假定:反弯点法:(1)梁的线刚度与柱线刚度之比大于3时可认为梁刚度无限大;(2)梁、柱轴象变形均可忽略不计D值法:(1)水平荷载作用下框架结构同层各结点转角相等;(2)梁、柱轴向变形均忽略不计反弯点高度取决于荷载形式、梁柱刚度比、建筑物总层数和柱所在的楼层号5.5计算连梁时是否需要考虑翼缘影响?不考虑5.6水平荷载作用下框架和剪力墙的变形特点有什么不同?P275.7风荷载计算需考虑哪些因素?高度、体型、地区5.8框架内力分析中分层法的前提条件是什么?(1)梁上荷载仅在该梁上及与其相连的上下层柱产生内力在其他层梁上及柱上产生的内力可忽略不计;(2)竖向荷载作用下框架结构产生的水平位移可以忽略不计.5.9重力荷载代表值是如何确定的?P375.9规程对高层建筑结构的层间水平位移做出了限值?其目的是什么?如果高层建筑结构的层间水平位移太小是否合适为什么?P7表2-31/800防止过大导致建筑物倒塌太小:说明结构的整体刚度太大加大了地震作用效应而且也不经济5.10风荷载计算中分整体风荷载计算和局部风荷载计算其目的是什么?整体风荷载是指整个建筑所受到的风荷载由整体承担而局部风荷载是局部面积建筑所受到的风荷载由局部承担它们计算时所用风荷载体型系数不同5.11抗震设计时为什么要进行0.2V0的调整?怎样调整?P44为发挥框架抵抗水平力的作用总框架承受的最大层剪力宜在0.2~0.4Vo之间对总框架剪力Vf 0.2 V0的楼层Vf 取0.2 V0和1.5 Vf中的较小值5.12什么是反弯点?弯距为零的点5.13总体信息中周期折减系数的意义是什么?因为不考虑填充墙的刚度实际刚度会大点所以要折减5.14 在高层建筑结构设计中为什么要限制结构的层间位移和顶点位移?高层建筑P426.水平荷载作用下结构的内力分析需要注意的问题水平荷载作用下结构的内力计算主要包括总剪力墙、总框架、总连梁的内力计算和各片墙、各榀框架各根连梁的内力计算6.1如何计算在各类水平荷载作用下总剪力墙上任意一点发生的水平位移?如何进行水平位移验算用哪个参数进行验算?P1346.2如何计算在各类水平荷载作用下总剪力墙任意一点的内力(弯矩、剪力)总框架的内力(弯矩、剪力)?P1356.3在刚结计算体系中什么是总框架的广义剪力?如何计算总连梁的分布约束弯矩?总框架的广义剪力等于总框架的总剪力加上总连梁的分布约束弯距总连梁的分布约束弯距:Cb为连梁的平均约束弯距的等效剪切刚度Cf为总框架抗推刚度6.4用公式(6-2)-(6-4)算出的剪力在什么体系中是总剪力墙的总剪力?但在什么体系中就不是总剪力墙的总剪力而是总剪力墙的总剪力与总连梁分布约束弯矩的代数和?这两个体系中总弯矩是否相同?铰接计算体系刚度体系中的不是总剪力墙的总剪力而是总剪力墙的总剪力与总连梁分布约束弯矩的代数和不同刚度特征值λ6.5在刚结体系内力计算中λ应该用考虑什么折减后的计算值刚度折减折减系数不小于0.56.6什么时候调整Vf?怎样调整Vf 对总框架剪力Vf 0.2 V0的楼层Vf 取0.2 V0和1.5 Vf中的较小值6.7如何计算各根连梁的第i个刚结端的分布约束弯矩?如何计算连梁第i个刚结端的约束弯矩?各根连梁的第i个刚结端的分布约束弯矩可由总连梁的分布约束弯距按下式求出:式(6-12) 连梁第i个刚结端的约束弯矩可由连梁杆端分布弯距与层高相乘得到式(6-13)6.8在求各根连梁内力时应注意剪力墙轴线处约束弯矩M12和剪力墙墙边处连梁杆端弯矩Mb12这两个概念的不同如何计算这两个不同的弯矩?剪力墙轴线处约束弯矩M12 式(6-13)剪力墙墙边处连梁杆端弯矩式(6-14)6.9在求出总剪力墙在各楼层处的内力(弯矩、剪力)后如何求各片剪力墙在各楼层处的内力(弯距剪力)?不管是铰接体系还是刚接体系均应按照各片剪力墙的等效抗弯刚度进行再分配6.10在求出MWijVWij后对于整截面剪力墙和小开口整体剪力墙还应怎样考虑连梁?P46对第i片剪力墙在第j层楼盖上、下方的剪力墙截面弯距分别加上或减去剪力墙墙边处连梁杆端弯矩的一半6.11对于联肢剪力墙求出MWijVWij后还需进一步求出什么?P47根据墙顶和墙底的弯距和剪力等效的原则求得其"相当荷载"据此求出联肢墙的每个墙肢和连梁的内力6.12 D值法又称改进的反弯点法主要在什么地方进行改进?如何用D值法计算各榀框架的内力?P47D值法中:反弯点高度取决于荷载形式、梁柱刚度比、建筑物总层数和柱所在的楼层号按照各柱的D值进行分配可以得到各柱在各楼层处剪力(通常是近似该柱上下端两层楼板标高处剪力的平均值作为该柱该层的剪力)然后确定出普通框架柱和壁式框架柱的反弯点高度便可以计算柱端弯距再根据结点平衡条件可求出梁端弯距进而求出框架梁的剪力和柱的轴力6.13 在D值法中如何确定反弯点位置?y0y1y2y3 分别代表什么意义如何计算这四个参数?反弯点高度:-标准反弯点高度由《高层建筑结构设计》中表4.2、4.3查取上下层梁刚度不等时的修正值由表4.4查取、上下层层高不等时的修正值由表4.5查取反弯点高度取决于荷载形式、梁柱刚度比、建筑物总层数和柱所在的楼层号当反弯点高度(时反弯点在本层;当时本层无反弯点反弯点在本楼层之上当时反弯点在本层之下6.14在用Excel表(表13-17至表13-36)计算内力时须特别注意公式当中每个参数的含义;并且当中许多公式都要根据实际情况进行修改P42-476.15在计算柱轴力和梁端弯矩(表13-37)时须注意正负符号P42-476.16地震荷载是和风荷载分别是按怎样的分布作用在结构上的?水平地震作用地震荷载:倒三角形分布、顶点集中荷载风荷载:倒三角形分布、均布荷载、顶点集中荷载7 竖向荷载作用下结构的内力分析7.1 高层建筑在竖向荷载作用下一般要不要考虑荷载的最不利布置?为什么?P48 活荷载一般情况都不大(1.5~2.0)仅占全部竖向荷载的10%~15%计算时可不考虑荷载的最不利布置也不考虑活荷载的折减7.2 计算竖向荷载作用下框-剪结构内力时各荷载是取标准值还是取设计值?为什么?P48 标准值以便于各种工况下的荷载效应组合7.3 计算竖向荷载作用下框架结构的内力有哪些方法?力距分配法、分层法7.4 为什么计算竖向荷载作用下框架结构的内力可以采用分层法?分层法是力矩分配法的进一步简化其计算过程跟力矩分配一样7.5 试简述用力矩分配法计算单层框架结构的计算过程P49求出结点的固端弯距计算分配系数然后力矩分配和传递7.6 请画出用分层法计算框架结构的计算简图P497.7 请指出分层法计算框架时为什么除底层柱之外其他层柱的线刚度乘上0.9传递系数用1/37.8用分层法计算框架结构时分层计算所得的杆端弯矩就是最后弯矩吗?为什么? 梁端弯距是最终弯距柱端的最终弯距则需要由上、下两层所得的同一柱端弯距叠加而成7.9 如何由梁端弯矩计算梁端剪力?计算各跨梁端剪力时可将梁看作简支梁求出梁在梁端弯矩和该跨梁上的恒载作用下的支座反力即为梁端剪力7.10 如何计算竖向荷载作用下框架柱的轴力?各柱上端轴力由横向框架梁端剪力、纵向框架梁端支反力(按简支梁计算)与上层柱传来的轴力相加而得;各柱下端轴力为上端轴力加本层柱自重7.11 如何计算框-剪结构中作用在剪力墙部分的竖向荷载?P501按负荷面积计算各层楼板及墙重垂直的梁传递的荷载(2)剪力墙左右端连梁通过与剪力墙相连端传递的荷载(3)剪力墙的自重(扣除门洞部分重)7.12 画出框-剪结构在竖向荷载作用下剪力墙的计算简图P1587.13 如何计算框-剪结构中剪力墙部分的内力?恒载作用下剪力墙的轴力有以下几部分:(1)墙肢自重;(2)墙肢两侧由楼板传来的三角形荷载;(3)纵向梁传来的集中荷载剪力墙所承受的弯矩由两部分组成一是连梁与剪力墙相连处作用于剪力墙的弯距;另一是各恒载和剪力墙的剪力向剪力墙形心处平移所得弯距7.14 如何计算连梁在竖向荷载作用下的内力? 跟主梁的计算方法相同7.15如何计算壁式框架在竖向荷载作用下的内力?7.16 试画出壁式框架在竖向荷载作用下的计算简图8 荷载效应及内力组合8.1什么是荷载效应?什么是荷载效应组合?荷载效应是指在某种荷载作用下结构的内力或位移荷载效应组合是指通常在各种不同荷载作用下分别进行结构分析得到内力和位移后再用分项系数与组合系数加以组合8.2在结构设计时为什么要进行荷载效应组合?高层建筑P39由于各类荷载性质的不同它们出现的频率以及对结构的作用也不尽相同需考虑它们的组合作用组合的依据是根据实际出现的情况用概率统计的方式进行8.3非抗震设计与抗震设计相比荷载效应组合的公式有何不同?P52有地震作用的效应组合除了计算重力荷载代表值的效应还要考虑水平、竖向地震作用下的效用重力荷载代表值的计算也不同8.4有地震作用效应组合时公式中的SGE含义是什么?重力荷载代表值的效应=恒载+活荷载*(50%+80%)8.5荷载分项系数的取值跟哪些因素有关?P52恒荷载:当效应对结构不利时对可变荷载取1.2永久荷载取1.35;当对结构有利时应取1.0活荷载:1.48.6进行构件截面设计时构件的控制截面应如何选取?通常是内力最大的截面但不同内力并一定在同一截面达到最大值一个构件可能同时有几个控制截面P54表8-28.7什么是截面的最不利内力?结构在截面产生的最危险内力8.8框-剪结构中梁、柱、剪力墙在考虑地震作用的情况下内力组合通常有哪几种?P54表8-28.10框-剪结构中梁、柱、剪力墙需要考虑的最不利内力有哪些?P54表8-28.11在框架梁的设计中对于竖向荷载作用下的梁的内力可以进行塑性调幅什么是塑性调幅?为什么要进行塑性调幅?怎样进行塑性调幅?塑性调幅是对梁端支座乘以调幅系数弹性计算时框架构造梁的端弯距较大配筋较多给施工带来困难;另一方面超静定钢筋混凝土结构具有塑性内力重分布的性质所以对竖向荷载作用下带来梁端弯距在与水平荷载作用下的内力组合之前需要进行内力调整既塑性调幅为了获得梁(含连梁)、柱杆端截面的弯矩和剪力需要将计算的节点内力值换算为支座边缘的内力标准值(q为作用在梁上的均布荷载)在内力组合前对竖向荷载作用下梁支座边缘处的弯矩需乘以弯矩调幅系数(本设计取0.8)跨中弯矩乘1.19 截面设计和结构构造9.1 结构抗震设计的原则是什么?什么是"三个水准"、"二阶段设计"?结构抗震设计p15三水准:小震不坏中震可修大震不倒二阶段设计:第一阶段:针对所有进行抗震设计的高层建筑应进行小震作用的抗震计算和保证结构延性的抗震构造设计以到达三水准要求第二阶段:针对甲级建筑和特别不规则的结构用大震作用进行结构易损部位(薄弱层)的塑性变形验算9.2 如何实现"三个水准"的设防目标?采用二阶段设计实现;一、承载力验算(弹性计算)二、弹塑性变形验算并采取相应的抗震构造措施以实现第三水准的抗震设防要求9.3 本设计如何实现第三水准的设防要求? 加强结构的薄弱部位采取相应的抗震构造措施如剪力墙的底部加强(底部加强部位高度取值构造配筋)9.4 结构重要性系数和承载力抗震调整系数的意义是什么?。

1）单结点力矩分配法得到精确解；多结点力矩分配法得到渐近解。 2）首先从结点不平衡力矩绝对值较大的结点开始。 3）结点不平衡力矩要变号分配。 4）结点不平衡力矩的计算：
固端弯矩之和 （第一轮第一结点）
结点不平 衡力矩
固端弯矩之和 （第一轮第二、三……结点） 加传递弯矩
传递弯矩
（其它轮次各结点）
总等于附加刚臂上的约束力矩
－0.78
E
CE
CH
0.4
－1.50 － 0.75 －0.08 － 0.04 －1.58 －0.79
2020/11/27
17
(3)迭代法：适于梁的刚度大于柱刚度的各种刚架。
2020/11/27
它们都属于位移法的渐近解法。
2
§8-2 力矩分配法的基本概念
理论基础：位移法；
力矩分配法
计算对象：杆端弯矩； 计算方法：逐渐逼近的方法；
一、转动刚度S： 适用范围：连续梁和无侧移刚架。
SAB=4i
表示杆端对转动的抵抗能力。 在数值上 = 仅使杆端发生单位转动时需在杆端施加的力矩。
（2）放松结点B，即加-60进行分配
A -150
A -17.2 A -150
B
150
-90
-60 0.571 0.429
-34.3 B -25.7
0.571 0.429 150 B -90
=
+
0
C 设i =EI/l
计算转动刚度：
SBA=4i
SBC=3i
C
分配系数：BA
4i 4i 3i
0.571
BC
计算之前,去掉静定伸臂,将其上荷载向结点作等效平移。
有结点集中力偶时,结点不平衡力矩=固端弯矩之和－结点集中

附表25：等截面等跨连续梁在常用荷载作用下按弹性分析(de)内力系数（五跨梁）.弯矩分配法（弯矩分配法计算连续梁和刚架及举例）一、名词解释弯矩分配法在数学上属于逐次逼近法,但在力学上属于精确法(de)范畴,主要适用于连续梁和刚架(de)计算.在弯矩分配法中不需要解联立方程,而且是直接得出杆端弯矩.由于计算简便,弯矩分配法在建筑结构设计计算中应用很广.（一）线刚度i杆件横截面(de)抗弯刚度EI 被杆件(de)长度去除就是杆件(de)线刚度i ： （a ） 当远端B 为固定支座时,对于A 点处,AB 杆(de)转动刚度i S AB 4=； （b ） 当远端B 为铰支座时,对于A 点处,AB 杆(de)转动刚度i S AB 3=； （c ） 当远端B 为滑动支座时,对于A 点处,AB 杆(de)转动刚度i S AB =； （d ） 当远端B 为自由端时,对于A 点处,AB 杆(de)转动刚度0=AB S .连续梁和刚架(de)所有中间支座在计算转动刚度时均视为固定支座.（二）转动刚度S转动刚度表示靠近节点(de)杆件端部对该节点转动(de)反抗能力.杆端(de)转动刚度以S 表示,等于杆端产生单位转角需要施加(de)力矩,θ/M S =.施力端只能发生转角,不能发生线位移.AB S 中(de)第一个角标A 是表示A 端,第二个角标B 是表示杆(de)远端是B 端.AB S 表示AB 杆在A 端(de)转动刚度.（三）分配系数μ各杆A 端所承担(de)弯矩与各杆A 端(de)转动刚度成正比.Aj μ称为分配系数,如AB μ表示杆AB 在A 端(de)分配系数.它表示AB 杆(de)A 端在节点诸杆中,承担反抗外力矩(de)百分比,等于杆AB(de)转动刚度与交于A 点各杆(de)转动刚度之和(de)比值.总之,加于节点A(de)外力矩,按各杆(de)分配系数分配于各杆(de)A 端.（四）传递系数CijC 称为传递系数.传递系数表示当近端有转角（即近端产生弯矩）时,远端弯矩与近端弯矩(de)比值.因此一般可由近端弯矩乘以传递系数C 得出远端弯矩. 当远端为固定(de)边支座或为非边支座21=C ； 当远端为滑动边支座 1-=C ；当远端为铰支边支座 0=C .节点A 作用(de)外力矩M,按各杆(de)分配系数μ分配给各杆(de)近端；远端弯矩等于近端弯矩乘以传递系数.（五）杆端弯矩弯矩分配法解题过程中所指(de)杆端弯矩是所有作用于杆端(de)中间计算过程(de)最后总(de)效果.计算杆端弯矩(de)目(de),是因为杆端弯矩一旦求出,则每相邻节点之间(de)“单跨梁”将可以作为一根静定(de)脱离体取出来进行该杆(de)内力分析.其上作用(de)荷载有外荷载,每一杆端截面上一般有一个剪力和一个弯矩,两端共有二个剪力和二个弯矩.这两个弯矩就是两端(de)杆端弯矩,既然它们已经求出,那么余下(de)两个剪力可由两个静力平衡方程解出.（六）近端弯矩和远端弯矩二、弯矩分配法(de)思路在求杆端弯矩时,其主要(de)目标是：（1）由于节点上有两根或多根杆件汇集,因此需确定每一根杆在维持节点不转动平衡过程中所作出(de)贡献.这需要用到分配系数μ以及与分配系数μ有关(de)转动刚度S、线刚度i、截面刚度EI等值.（2）影响节点产生转动(de)力矩大小及方向.这需要涉及到单跨梁(de)固端弯矩M,它(de)含义是：将每相邻节点之间(de)杆件视为一根两端支座为固定支座或一端固定一端铰支(de)单跨梁,这样(de)梁在各种外荷载作用下(de)杆端弯矩叫做固端弯矩.两端铰支(de)单跨梁无固端弯矩,即两端铰支(de)单跨梁(de)两铰支端(de)固端弯矩为零.只有固定端才有固端弯矩,铰支端(de)固端弯矩为零(单跨梁).固定端不允许转动所以产生固端弯矩,而铰支端允许转动不产生固端弯矩.三、弯矩分配法(de)运算步骤连续梁或刚架弯矩分配法运算过程：（1）求各杆件（梁或柱）(de)线刚度i、杆端（梁端或柱端）转动刚度S和分配系数μ（对于刚架,参加分配系数计算(de)不仅有梁,还有柱）.（2）根据各个“单跨”梁或柱(de)荷载情况和支座特征查表求出各“单跨”杆件在杆端(de)固端弯矩M.这里需注意(de)是固端弯矩是带符号(de),可以用“左负右正”四个字来帮助记忆.即对每一“单跨”梁而言,左端(de)M取负值或零,右端(de)M取正值或零.当“单跨”(de)边支座为铰支座时,它不能抵抗杆件(de)转动,所以边支座为铰支座时(de)M=0；但对于所有非边支座,则一律视为固定端支座.（3）将与同一支座相连接(de)各杆(de)固端弯矩M取代数和后反号按分配系数分配到与支座相连(de)各杆杆端.这一步(de)注意点是将固端弯矩代数和反号再分配.（4）将分配得到(de)弯矩视该节点各杆远端支座特征决定是否向远端传递.这种分配、传递将可能进行多次.这种次数只要进行(de)足够,从理论上讲将可以达到任意要求(de)精确度.但是工程实践上则只要进行2~3个循环即可满足正式结构设计(de)要求.（5）将上面四步运算之后(de)与同一节点相连(de)每根杆件杆端(de)固端弯矩、分配弯矩、传递弯矩分别求代数和,即为各杆(de)杆端弯矩.这一步(de)注意点是与同一支座相连(de)各杆(de)杆端弯矩代数和必定为零,否则说明计算上有错,或尚需进一步分配、传递.静定结构(de)内力只按静力平衡条件即可确定,其值与结构(de)材料性质和截面尺寸无关.超静定结构(de)全部反力和内力如只按静力平衡条件则无法确定,还必须同时考虑变形协调条件（即各部分(de)变形必须符合原结构(de)联接条件和支承条件）才能得出确定(de)解答,故超静定结构(de)内力状态与结构(de)材料性质和截面尺寸有关.在荷载作用下,超静定结构(de)内力只与各杆刚度(de)相对比值有关,而与其绝对值无关；在温度改变、支座移动等因素影响下,超静定结构(de)内力则与各杆刚度(de)绝对值有关,并且一般是与各杆刚度(de)绝对值成正比(de).对非结构专业来说,特别是对建筑学专业,不可能花大量(de)精力去从事对超静定结构(de)矩阵分析,因此弯矩分配法这样简明适用(de)方法就更有它(de)实际意义.一方面,弯矩分配法可以满足对一般正式结构设计(de)要求；另一方面,可以使建筑师加强对结构(de)概念设计.所以其优越性是显而易见(de). 例8-1 图示一连续梁,用弯矩分配法作弯矩图.解：（1）求分配系数a. 杆AB 和杆BC(de)线刚度lEI i =相等. b. 转动刚度：c. 分配系数：d. 校核：BA μ+BC μ=1,分配系数写在节点B 上面(de)方框内.（2）求固端弯矩M ,把梁看成两根独立(de)单跨梁.查表：AB 跨属表８－１编号５,而BC 跨属表８－１编号２.将结果写在相应杆端(de)下方.在节点B,BA 梁与BC 梁在B 端(de)固端弯矩代数和为（３）分配并传递,将节点B(de)固端弯矩代数和反号得被分配(de)弯矩为－６kN ·m,此弯矩按分配系数分配于两杆(de)B 端；并由于A 端为固端边支座,所以由BA 杆(de)B 端向A 端传递去B 端弯矩(de)一半；C 端由于是铰支边支座,故传递系数为零,即不向C 端传递.a. 分配弯矩：b. 传递力矩：用箭头表示弯矩传递(de)方向.（4）将以上结果竖向叠加,即得到最后(de)杆端弯矩.可列表进行,最下面一行表示最后结果.注意B 节点应满足平衡条件：注意A 端是固定边支座,只有一根杆AB,其分配系数为1,故它虽有固端弯矩m kN M AB ⋅-=15,但不存在分配或向B 端传递(de)问题,可A 端却可以接受从B 端传递过来(de)弯矩.（5）计算跨中弯矩a. 将AB 梁按简支梁画出计算简图,其上(de)荷载有两种,一是本来存在(de)集中荷载,二是在它两端按弯矩分配法算出(de)杆端弯矩,以集中力偶(de)形式作用于A 、B 两杆端处.见图8-10（a ）.b. 将AB 梁按两端简支梁情况下,仅作用有集中荷载时求出在中点(de)弯矩,见图8-10（b ）.m kN M ⋅=⨯=⋅30310荷载中c. 将AB 梁按两端简支梁情况下,仅在两端分别有杆端弯矩作用下求出中点(de)弯矩,实际上是一个几何梯形(de)中位线长度纵坐标,见图8-10（c ）.d. 跨中点弯矩(de)最终结果为b 、c 两步纵坐标(de)代数和.梁段上(de)其它任一点(de)弯矩也可以参照以上方法求出.中点弯矩为（6）在计算有多个节点(de)连续梁或刚架时,若将两个节点同时分配和传递,这两个节点既可相邻也可是被一个节点在当中隔开(de)形式.若从不平衡力矩（即节点四周各杆(de)杆端弯矩(de)代数和）较大(de)节点开始,可使收敛较快.（7）作弯矩图a. 用弯矩分配法列表计算出(de)都是各杆带正号或负号(de)杆端弯矩.正顺负逆（顺正逆负）b. 带+号（正号一般省略不写）(de)杆端弯矩使杆端作顺时针旋转,此时想象杆端往远端方向稍远一些(de)横截面固定不动.比如图8-9中AB 杆在B 端(de)杆端弯矩m kN M BA ⋅+=57.11,想象离B 端稍往左处(de)杆截面（图8-9中(de)D-D 截面）固定不动,由于正号杆端弯矩+·m,所以它使B 端绕这个想象中被固定(de)横截面作顺时针旋转.显然这个+·m(de)杆端弯矩使AB 上这小段杆件BD(de)上部纤维受拉,下部纤维受压.我们总是把弯矩图画在杆件(de)受拉纤维一侧.因此AB 杆在B 端(de)杆端弯矩＋·m 应画在杆(de)横线(de)上方.c. 带负号(de)杆端弯矩使杆端作逆时针旋转,此时也同样想象离杆端往远端方向稍远一些(de)横截面固定不动.比如图8-9中AB 杆在A 端(de)杆端弯矩m kN M AB ⋅-=72.16,想象离A 端稍往右处(de)杆截面（图8-9中(de)E-E 截面）固定不动,由于是负号杆端弯矩·m,所以它使A 端绕这个想象中被固定(de)横截面作逆时针旋转.显然这个·m(de)杆端弯矩使AB 上(de)这一“小段”杆件AE(de)上部纤维受拉,下部纤维受压.根据弯矩图总是画在杆件(de)受拉纤维一侧(de)规定,因此AB 杆在A 端(de)杆端弯矩·m 也应画在代表杆(de)横线(de)上方.d. 至于每一单跨上(de)跨中弯矩,只需凭弯矩图总是画在受拉纤维一侧这个规定和跨中弯矩(de)计算过程就可以正确(de)决定它是画在代表杆(de)横线上方还是下方.（8）计算剪力a. 按每一单跨杆件分别取脱离体求剪力.把每一单跨梁看成简支梁,它(de)荷载有三种：第一种是原来就作用在单跨上(de)荷载.第二种是用弯矩分配法算出来(de)杆端弯矩.第三种是简支梁(de)两端两个支座反力,它们是未知(de),由于脱离体可列出两个静力平衡方程,而支座反力也恰好为两个,故可顺利求出.而这两个支座反力,就是我们要求(de)剪力.杆端剪力在这里起了“支座反力”(de)作用.因此将“支座反力”用箭头表示,方向和大小假定,先不考虑它(de)真实指向和大小.b. 按简支梁求支座反力(de)方法列出平衡方程可求出箭头所示力(de)大小和正负号.剪力大小即等于支座反力,从解方程直接得出,剪力(de)方向视箭头所示力(de)正负号而定.如果是正号,说明箭头指向就是真正(de)指向；如果是负号,说明与原假定(de)指向相反.画出剪力图.例8-2 试计算图8-11连续梁(de)杆端弯矩和跨中弯矩.并作弯矩图.解：（1）求固端弯矩：（2）求分配系数：a. 对节点B,相邻两杆BA 、BC(de)转动刚度所以b. 同理,对节点C 有：（3）分配结果见图8-11.（4）求跨中弯矩a. 对AB 跨：b. 对BC 跨：c. 对CD 跨见图8-12.在集中力作用下,CD 跨(de)最大跨间弯矩发生在集中力P=160kN 作用点. （a ）在集中力作用下,该点(de)简支梁弯矩（图8-12b ）（b ）在杆端弯矩作用下,该点(de)负弯矩为（图8-12c ）(c) 该点(de)弯矩为1M 和2M (de)代数和.（5）作出连续梁(de)弯矩图.例8-4 试用弯矩分配法计算图8-14（a ）所示等截面连续梁（带悬臂梁）(de)各杆端弯矩.并作弯矩图.已知各杆EI 值为：AB 为6,BC 为4,CD 为4,DE 为6 .解：此梁(de)悬臂EF 为一静定部分,该部分(de)内力根据静力平衡条件便可求得： kN V m kN M EF EF 20,40=⋅-=.若将该悬臂部分去掉,而将EF EF V M 和作为外力作用于节点E,图8-14（b ）,节点E 便化为铰支端,整个计算即可按此考虑.计算分配系数时,其中计算固端弯矩时,对杆DE,将相当于一端固定另一端铰支(de)单跨梁,除跨中受集中力作用外,并在铰支端E 处受一集中力和一集中力偶(de)作用.其中作用在E 端(de)集中力为支座直接承受,在梁内不引起弯矩,而E 端(de)力偶40kN ·m 将使杆DE 引起固端弯矩,其值DE M 为DE 跨在D 端(de)固端弯矩DEM '（编号1）与EF 跨在E 端(de)固端弯矩EF M 向远端D(de)传递弯矩DEM ''之代数和,即 其余固端弯矩均可查表求得.分配及弯矩图见8-14.例8-5 求图8-15所示刚架(de)弯矩图.解：（1）转动刚度：（2）分配系数：节点B ：节点C ：（3）固端弯矩：由于只有梁有外荷载,故也只有梁才有固端弯矩,它们为（4）力矩分配：按C 、B 顺序分配两轮,计算见图8-16（a ）,放松节点(de)次序可以任取,并不影响最后(de)结果.但为了缩短计算过程,最好先放松不平衡力矩较大(de)节点,在本例中,先放松节点C 较好.（5）作弯矩图.图8-16（b ）.讨论：（1）当刚架竖柱比横梁(de)线刚度大很多时,即梁柱i i >>,则∑∑+梁柱柱i i i 接近于1（如梁柱i i 20≥,误差在5%以内）.杆端（柱端）弯矩接近于固端弯矩.此时,竖柱对横梁而言,起固定支座(de)作用.也就是说,在这种情况下,每相邻两个节点之间(de)横梁,可以当作两端固定(de)单梁来计算,不必用弯矩分配法来求解了.（2）当刚架横梁比竖柱(de)线刚度大很多时,即柱梁i i >>,则∑∑+梁柱柱i i i 接近于零（如柱梁i i 20≥,误差在5%以内）.杆端（柱端）弯矩接近于零.此时,竖柱对横梁而言,起铰支座(de)作用.这种情况下,横梁(de)每个支座都将视作铰支座（习惯上是一个固定铰支座,其余则为活动铰支座）,横梁演化为一根以柱为支点(de)连续梁,用弯矩分配法可求出每一杆端弯矩.（3）当∑∑+梁柱柱i i i 介于上述两者之间时,其计算简图为刚架,用弯矩分配法求解. 四、弯矩分配法与电算结果(de)比较下图中括号外为弯矩分配法计算结果,括号内为电算计算结果.。

h
12
例 试用力矩分配法计算图a所示刚架，并绘M图。
表23-2 杆端弯矩的计算
用力矩分配法计算刚架时，可列成表格进行，（后面）最后弯矩图如图b所示。
h
13
结点 杆端
B
A
C
BA AB AD AC CA
分配系数
0.3 0.3 0.4
固端弯矩
0 60.0 -48.0 0
0
分配和传递
弯矩Biblioteka 0 -3.6 -3.6 -4.8 -2.4
分配系数
{载常数（表22-1）}固端弯矩
{求和}杆端弯矩
0
3i 4i
2i
0 3/7 4/7 1/2
0
90 -60
60
0
-30*3/7 -30*4/7
=-12.9 =-
-需8.要6 -30
17.1
0
77 . -
51.4
1 77 .
h
1
10
试用力矩分配法
计算图所示的连
续梁做出M图
{形常数（表22-2）}
•
h
20
感谢下 载
h
21
• ⑶ 进行第一轮次的分配与传递，从不平衡力矩较大 的结点开始，依次放松各结点，对相应的不平衡力 矩进行分配与传递。
MF
• ⑷ 循环步骤3，直到最后一个节点的传递弯矩小到 可以略去为止。（结束在分配上）
• ⑸ 求最后杆端弯矩，将各杆杆端的固端弯矩与历次 的分配弯矩和历次的传递弯矩代数即为最后弯距。
• ⑹ 作弯矩图（叠加法），必要时根据弯矩图再作剪 力图。
M
S Ak
将所求得的φA代入前式，得
h
所以
6

-ql
2／8
=
-10×8
2／8
=
-
80kN·m
F
MCB =0
将它们填入表中第二行相应杆端下面。
由表可求得B点的不平衡力矩。但因B点有 外力偶，故不平衡力矩等于：
MB = -80 +150 = 70 kN·m
3、计算分配弯矩与传递弯矩
将结点B的不平衡力矩反号乘以各杆分配系 数得各杆近端分配弯矩。将所得分配弯矩 乘以相应杆的传递系数即得远端传递弯矩。
Mjc C = Mij
远端固定端时，C = 1/2 远端铰支座时， C = 0 远端定向支座时， C = -1
三、最终弯矩
将第一步固定结点各杆端的固端弯矩与 第二步放松节点时相应杆端的分配弯矩 或传递弯矩相加即得出杆端的最终弯矩。
例20-1用力矩分配法计算图(a)所示的两 跨连续梁，画出弯矩图。
3、将杆端的固端弯矩与分配弯矩或 传递弯矩相加，得到杆端最终弯矩。
一、固定结点
在结点1上附加刚臂，限制结点1的转动，原刚 架被解体成三个单跨梁，此时单跨梁A1两端 产生的弯矩即是位移法中所提到的固端弯矩。
q
M1
A 1
C
M1
M1A 1
M1C
B
M1B
查表得：MAF1 = 0
M1FA = 1 ql 2 由于附加刚臂阻8止了结点1转动，附加
F
MBA=
Pa
2b/l
= 50×42×6/10
= 48 kN·m
F
MBC=-ql
2/12=-25×122
/12=-300
kN·m
F
MCB=
ql
2/12=
25×12
2/12=

弯矩分配法优缺点分析
• 对于某些特定结构（如连续梁、无侧移刚架），计算效率 较高。
弯矩分配法优缺点分析
01
缺点
02
03
04
对于复杂结构或侧移刚架，计 算过程较为繁琐。
迭代计算可能收敛较慢，需要 较多计算步骤。
对于某些问题（如温度变化、 支座移动等），弯矩分配法可 能不适用或需要特殊处理。
03
超静定梁与刚架结构分 析
位移法
以结点位移作为基本未知量，通过 建立位移与内力的关系，求解超静 定结构的方法。
弯矩分配法
适用于连续梁和无侧移刚架等超静 定结构的简化分析方法，通过逐步 分配和传递弯矩来求解结构内力。
02
弯矩分配法基本原理
弯矩分配法概念及适用范围
概念
弯矩分配法是一种用于分析超静 定结构的方法，通过逐步分配节 点弯矩，使结构达到平衡状态。
根据结点平衡条件和截面法，可以求 解刚架结构的反力和内力。
考虑轴向变形时内力重分布问题探讨
轴向变形对超静定结构的影响
01
当超静定结构中存在轴向变形时，会引起结构内力的重分布，
进而影响结构的
02
通过引入轴向变形的影响因素，对超静定结构的内力进行修正
和重分布计算。
通过具体算例，展示超静定梁的求解过程 ，包括力法和位移法的应用。
刚架结构内力计算及实例解析
刚架结构的基本概念
刚架是由直杆组成的具有刚结点的结 构，其结点不能发生相对移动但可以 发生相对转动。
刚架结构的内力计算
刚架结构计算示例
通过具体算例，展示刚架结构的求解 过程，包括结点平衡条件和截面法的 应用。
刚度大
由于存在多余约束，超静定结 构的刚度通常比静定结构大。

第八章力矩分配法
1
§8-1 概述 计算超静定结构，不论采用力法或位移法，均要组成和解算典型方程，当未知量较多时，其工作量非常大。
为了寻求较简捷的计算方法，自上世纪三十年代以来，又陆续出现了各种渐进法，力矩分配法就是其一。 渐进法的共同特点是，避免了组成和解算典型方程，而以逐次渐进的方法来计算杆端弯矩，其结果的精度
A
i=2
B
i=3 C
6m
3m
3m
40kN/m D
i=4
6m
杆端
m
MF
B1次 C1次
AB C 1 2 BA BC C 1 2 CB CD C 0 DC
0.4 0.6
0.5 0.5
100
0
0 -300
300 -180
0
40
80 120
60
-45
-90 -90
集中力偶m
逆时针为正
讨论
A A
2、静定段处理
D
Δ1 =1 B
4m
i= 3
i= 6
基本系
C
D
r111FR1F 0
3)作M1、MF图
基本系为无侧移刚架
30kN /m
A
r 11
i= 4
M1、MF图运用 力矩分配法绘制
F R 1 F 4)求系数和自由项
i= 3
i= 6
△1作用
C
D
i= 3
i= 6
荷载作用
C
D
5)求未知量 6)叠加法作M图
MM11+MF
l
EI＝ C
位移法求解
（1）建立基本体系
如何分配？
B
l
l
FRK

同时：各杆远端产生传递弯矩：
M A B

1 2
M
B A
MCB 0
（三）(b)图+(c)图=(a)图，即：
M BA

M
g BA
M B A
M AB

M
g AB
M A B
M BC M B C
MCB 0
归纳：
②①② ①放固放 固松 定松定节 节节节点 点点点， ，，，分 各分各配 杆配杆弯 端弯端矩 有矩有， 固，固传 端传端弯递弯递弯 矩弯矩矩 ，矩，。 有。有节节点点不不平平衡衡力力矩矩。。
第8章 力矩分配法
8.1 力矩分配法的基本概念
属于位移法类型的渐近解法。 一、力矩分配法依据
1. 理论基础：位移法 2. 解题方法：渐进法 3. 适用范围：连续梁、无结点线位移的刚架 4. 计算对象：杆端弯矩，正负号规定与位移法相同 二、力矩分配法的三个基本概念
（一）转动刚度 转动刚度表示杆端对转动的抵抗能力。数值上
M
M AB

S AB S
M
D
A θA
B
A
M AC

S AC S
M
分配弯矩
A
C
θA

M
S
A
M AD

S AD S
M
A
令
μAj

S Aj S
(
j

B,C, D)
A
(a)
M AB SAB θA 4 iAB θA
M AC S AC θA iAC θA
M AD S AD θA 3iAD θA
例: 试绘制连续梁的弯矩图。

第八章力矩分配法（4学时）1.主要内容8-1 力矩分配法的基本概念8-2 多结点的力矩分配8-3 连续梁影响线2.知识点8-1 力矩分配法的基本概念转动刚度、分配系数和传递系数；结点力矩、分配力矩、传递力矩；杆端弯矩、近端弯矩、远端弯矩。

8-2 多结点的力矩分配多结点力矩分配的基本思路；多结点的力矩分配解题的基本过程：结点力矩、非结点力矩。

8-3 连续梁影响线超静定力影响线的作法；连续梁弯矩、剪力影响线的绘制。

3.重点难点8-1 力矩分配法的基本概念重点：掌握单结点力矩分配法解题的基本过程。

难点：非结点荷载如何转变成结点荷载。

8-2 多结点的力矩分配重点：掌握多节点力矩分配法解题的基本过程。

难点：结点的锁住、放松。

8-3 连续梁影响线重点：掌握连续梁影响线的绘制。

8.1 分配法的基本概念1. 知识点转动刚度、分配系数和传递系数；结点力矩、分配力矩、传递力矩；杆端弯矩、近端弯矩、远端弯矩。

2. 重点难点重 点：掌握单结点力矩分配法解题的基本过程。

难 点：非结点荷载如何转变成结点荷载。

知识点：转动刚度、分配系数和传递系数（1）基本概念转动刚度S ：杆件的近端发生单位转角时，在该端需要施加的力矩； 分配系数μ：。

BABA S S μ=∑，只与杆件的线刚度i 和约束条件有关。

传递系数C ：远端弯矩与近端弯矩的比值。

（2）取值表8.1 等截面直杆的转动刚度和传递系数（3）实例例：计算图8.1结构的转动刚度、分配系数和传递系数，EI 为常数。

EAC 2aa2a aB D图8.1解：表8.2 转动刚度和传递系数杆件 远端 转动刚度S分配系数μ传递系数CAB 自由端 0 0 0 AC 固定 4EI ／(2a) 4/9 0.5 AD 铰支 3EI ／(2a) 1/3 -1 AE滑动EI ／a2/9结点力矩下单结点力矩分配的解题步骤： 1. 确定结点力矩；2. 根据转动刚度求分配系数3. 根据分配系数求分配力矩（近端弯矩）4. 根据传递系数求传递力矩（远端弯矩） 实例：例1：图8.2a 梁线刚度 i 相同，用力矩分配法求梁各杆端弯矩，并绘制弯矩图。