下载文档原格式
医学统计学方法试题及答案（一）1.呈对数正态分布的数值变量资料，描述集中趋势的指标最宜选用（）A.几何均数B.众数C.算术均数D.调和均数E.中位数2.某课题组获得某校新入学大学男生腹部皮下脂肪厚度(cm)和身高(cm)资料，现比较这两个变量的离散趋势，最佳的指标是（）A.变异系数B.全距C.方差或标准差D.偏度系数E.四分位数间距3.研究者预比较两种中成药对口腔溃疡的治疗效果是否有差别，用“有效、一般、无效”作为评价疗效的指标。
宜采用的统计分析方法是（）A.t检验B.方差分析C.Z检验D.秩和检验E.回归分析4.不是四分位数间距特点的是（）A.适用条件同中位数B.反映数值变量资料的离散趋势C.较极差稳定D.考虑了每个变量值的变异情况E.不受两端极大值、极小值的影响5.对于正偏态分布的资料，M与X的关系为（）A.M=XB.M<XC.M>XD.M=2XE.M与X无确定关系6.某种人群(如成年男子)的某个生理指标(如收缩压)或生化指标(如血糖水平)的正常值范围一般指（）A.该指标在所有人中的波动范围B.该指标在所有正常人中的波动范围C.该指标在绝大部分正常人中的波动范围D.该指标在少部分正常人中的波动范围E.该指标在一个人不同时间的波动范围7.对于一组经对数变换后亦不服从正态分布的偏态分布资料，描述该组的离散趋势应选用（）A.方差B.样本标准差C.总体标准差D.四分位数间距E.变异系数8.不是正态分布特征的是（）A.曲线位于横轴上方均数处最高B.以零为中心，左右对称C.均数为其位置参数D.标准差为其变异度参数E.正态分布曲线下面积有一定分布规律9.某病住院日的频数分布呈单峰分布。
平均住院日为10日。
中位数为5日，则住院日的分布是（）A.正态分布B.正偏态分布C.负偏态分布D.左偏态分布E.对称分布10.下列指标为相对比的是（）A.中位数B.几何均数C.均数D.标准差E.变异系数11.某高校测得1100名20岁健康男大学生的身高，经检验资料服从正态分布，其均值为172cm，标准差为4cm，求得的区间(172-2.58×4,172+2.58×4)称为身高的（）A.99%医学参考值范围B.95%医学参考值范围C.99%总体均数可信区间D.95%总体均数可信区间E.97.5%总体均数可信区间12.正态分布是（）A.以+值为中心的频数分布B.以参数为中心的频数分布C.以变量为中心的频数分布D.以观察例数为中心的频数分布E.以均数为中心的频数分布13.计算相对数的目的是（）A.为了进行显著性检验B.为了表示绝对水平C.为了便于比较D.为了表示实际水平E.为了表示相对水平14.对计数资料进行统计描述的主要指标是（）A.平均数B.相对数C.标准差D.变异系数E.中位数15.说明两个有关联的同类指标的比即为（）A.率B.相对比C.构成比D.频率E.频数16.说明某事物内部各组成部分的比重或分布的指标称为（）A.率B.标准差C.频率D.相对比E.构成比17.说明某现象发生强度的指标为（）A.全距B.相对比C.率D.均数E.比值比18.假设检验的目的是（）A.检验参数估计的准确度B.检验参数估计的糖确度C.检验总体参数是否不同D.检验样本统计量是否不同E.检验样本统计量与总体参数是否不同19.某医生治疗了两例视网膜炎患者，1例有效，说法错误的是（）A.总有效率为50%B.最好用绝对数表示C.必须用率表示时，应同时给出其可信区间D.分母太小，用相对数不可靠E.最好是增大样本量在进行统计描述20.经调查甲乙两地的冠心病粗死亡率均为4/105，经统一年龄构成后，甲地标化率为4.5/105，乙地为3.8/105。
《医学统计学》计算分析题参考答案孙振球主编. 医学统计学.第3版. 北京：人民卫生出版社，2010第二章计量资料的统计描述计算分析题（P26）1. 根据某单位的体检资料，116名正常成年女子的血清甘油三酯测量结果如下，请据此资料：（1）描述集中趋势应选择何指标？并计算之。
（2）描述离散趋势应选择何指标？并计算之。
（3）求该地正常成年女子血清甘油三酯的95%参考值范围。
（4）试估计该地正常成年女子血清甘油三脂在0.8mmol/L以下者及1.5mmol/L者各占正常成年女子总人数的百分比？表2-1某单位116名正常成年女子的血清甘油三酯（mmol/L）测量结果组段频数0.6~ 10.7~ 30.8~ 90.9~ 131.0~ 191.1~ 251.2~ 181.3~ 131.4~ 91.5~ 51.6~1.7 1合计116（1）数据文件数值变量名：组段，频数；用Compute产生新变量“组中值”（也可直接输入组中值）。
（2）操作步骤Analyze èData èWeight Cases ；Weight Cases by 频数。
Analyze èDescriptives èDescriptives ；将“组中值”选入V ariable 框中；单击OK 。
（3）结果解释表2-1显示某单位116名正常成年女子的血清甘油三酯测量结果呈正态分布，故选择均数描述集中趋势，选择标准差描述离散趋势。
某单位116名正常成年女子的血清甘油三酯测量结果的均数为1.16（mmol/L ），标准差为0.20（mmol/L ）；该地正常成年女子血清甘油三酯的95%参考值范围是（0.77，1.55）mmol/L 。
计算过程根据公式s x 96.1±，即1.16±1.96×0.20。
该单位正常成年女子血清甘油三酯在0.8 mmol/L 以下者估计占总人数的3.59％，1.5 mmol/L 以下者估计占总人数的95.54％。
医药数理统计课后答案【篇一：医药数理统计(第二版)第七章习题解答】>1、解答（1）问题分析本题涉及一个因素a——接种方式，分三种方式，看作三个水平——a1,a2,a3 考察同一随机变量x——伤寒病菌的存活时间（天数）目的是接种方式对伤寒病菌的存活时间是否有显著影响。
将三种接种方式下伤寒病菌的存活时间分别记为x1,x2,x3，题目已知从三个总体中分别抽取的样本容量分别为10，9，11假定三总体x1,x2,x3均服从正态分布，且具有相同的方差，即xi~n(?i,?2),i?1,2,3这样，要考察三种接种方式下伤寒病菌的存活时间是否存在显著差异，体现为同时比较三总体的均值是否相等，构成一个假设检验问题，检验的原假设和备择假设如下：h0:?1??2??3， h0:?1,?2,?3不全相等由此，我们可以利用单因素方差分析解决问题。
（2）数据输入利用spss处理，定义两个变量（存活时间，接种方式），将30个存活时间数据均输在变量“存活时间”列，在“接种方式”列用“1”，“2”，“3”表示三种不同分数据的输入格式。
（3）数据处理点击analyze →compare means→ one-way anova 处理结果（方差分析表）（4）结果分析组间离差平方和 ssa?70.429 自由度df1?3?1?2 组内离差平方和sse?13.7 自由度df2?10?9?11?3?27 737组间均方msa?ssa/df1?35.215 组内均方mse?sse/df2?5.101检验统计量观测值f0?msa/mse?6.903检验p值，p?p{f?f0}?0.004（即自由度为（2，27）的f分布f0点右侧尾部的概率）。
选取显著水平??0.01，由于检验p值小于显著水平，数据支持拒绝原假设的结论，认为不同的接种方式其伤寒病菌的存活时间存在非常显著差别。
2、解答（1）问题分析问题涉及一个因素（药物成分含量的检测方法），分4个水平。
医学统计学课后习题答案第一章医学统计中的基本概念练习题一、单向选择题1. 医学统计学研究的对象是A. 医学中的小概率事件B. 各种类型的数据C. 动物和人的本质D. 疾病的预防与治疗E．有变异的医学事件2. 用样本推论总体，具有代表性的样本指的是A．总体中最容易获得的部分个体B．在总体中随意抽取任意个体C．挑选总体中的有代表性的部分个体D．用配对方法抽取的部分个体E．依照随机原则抽取总体中的部分个体3. 下列观测结果属于等级资料的是A．收缩压测量值B．脉搏数C．住院天数D．病情程度E．四种血型4. 随机误差指的是A. 测量不准引起的误差B. 由操作失误引起的误差C. 选择样本不当引起的误差D. 选择总体不当引起的误差E. 由偶然因素引起的误差5. 收集资料不可避免的误差是A. 随机误差B. 系统误差C. 过失误差D. 记录误差E．仪器故障误差答案: E E D E A二、简答题常见的三类误差是什么？应采取什么措施和方法加以控制？[参考答案]常见的三类误差是：（1）系统误差：在收集资料过程中，由于仪器初始状态未调整到零、标准试剂未经校正、医生掌握疗效标准偏高或偏低等原因，可造成观察结果倾向性的偏大或偏小，这叫系统误差。
要尽量查明其原因，必须克服。
（2）随机测量误差：在收集原始资料过程中，即使仪器初始状态及标准试剂已经校正，但是，由于各种偶然因素的影响也会造成同一对象多次测定的结果不完全一致。
譬如，实验操作员操作技术不稳定，不同实验操作员之间的操作差异，电压不稳及环境温度差异等因素造成测量结果的误差。
对于这种误差应采取相应的措施加以控制，至少应控制在一定的允许范围内。
一般可以用技术培训、指定固定实验操作员、加强责任感教育及购置一定精度的稳压器、恒温装置等措施，从而达到控制的目的。
（3）抽样误差：即使在消除了系统误差，并把随机测量误差控制在允许范围内，样本均数（或其它统计量）与总体均数（或其它参数）之间仍可能有差异。
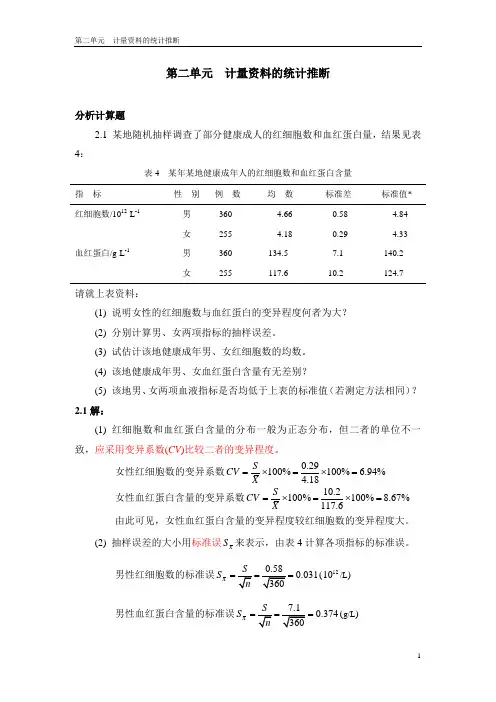
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数 标准差 标准值* 红细胞数/1012·L -1 男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
第二单元 计量资料的统计推断分析计算题某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数标准差 标准值*红细胞数/1012·L -1 男 360女 255 血红蛋白/g ·L -1 男 360女255请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大 (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同） 解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
该地男性红细胞数总体均数的95%可信区间为：－× , ＋×，即 , 1210/L 。
该地女性红细胞数总体均数的95%可信区间为：－× , ＋×，即 , 1210/L 。
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别例 数 均 数 标准差 标准值* 红细胞数/1012·L -1男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L )男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
该地男性红细胞数总体均数的95%可信区间为：(4.66－1.96×0.031 , 4.66＋1.96×0.031)，即(4.60 , 4.72)1210/L 。
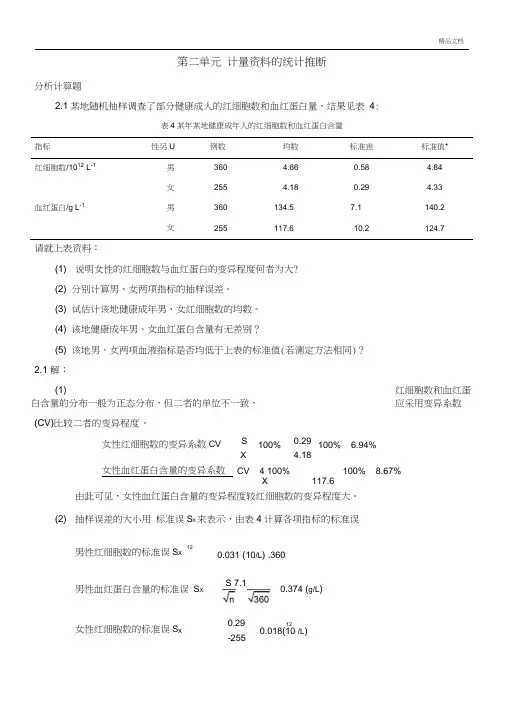
第二单元计量资料的统计推断分析计算题2.1某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4:表4某年某地健康成年人的红细胞数和血红蛋白含量指标性另U例数均数标准差标准值*红细胞数/1012L-1男360 4.660.58 4.84女255 4.180.29 4.33血红蛋白/g L-1男360134.57.1140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大?(2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值(若测定方法相同)？2.1 解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV)比较二者的变异程度。
女性红细胞数的变异系数CV S100%0.29100% 6.94%X 4.18女性血红蛋白含量的变异系数CV 4 100%100% 8.67%X117.6由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误S X来表示，由表4计算各项指标的标准误120.031 (10/L) .360男性红细胞数的标准误S X男性血红蛋白含量的标准误S X0.374 (g/L)女性红细胞数的标准误S X 0.29-255120.018(10 /L) S 7.1(3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100,可视为大样本 未知，但n 足够大，故总体均数的区间估计按(X u /2S X ,X u /2S X )计算。
该地男性红细胞数总体均数的 95%可信区间为:(4.66- 1.96 @031 , 4.66+ 1.96 @031),即(4.60,4.72)10%。
该地女性红细胞数总体均数的 95%可信区间为：(4.18 - 1.96 0.018,4.18+ 1.96 0.018), 即卩(4.14,4.22)1012/L 。
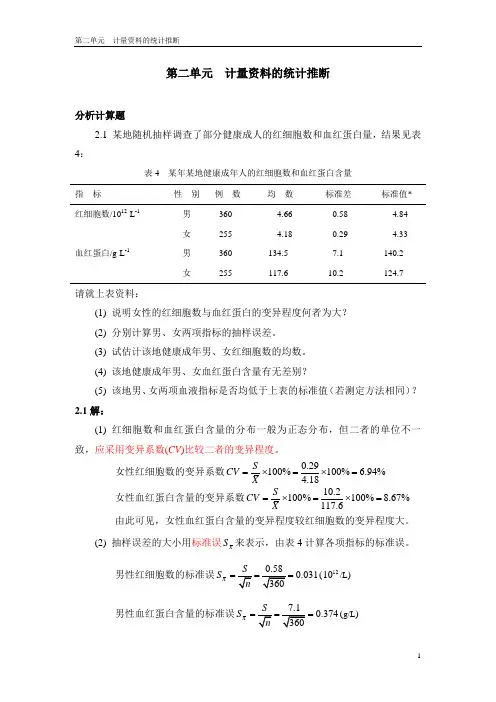
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数 标准差 标准值* 红细胞数/1012·L -1 男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数 标准差 标准值* 红细胞数/1012·L -1 男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯= 由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L )男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数 标准差 标准值* 红细胞数/1012·L -1 男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
该地男性红细胞数总体均数的95%可信区间为：(4.66－1.96×0.031 , 4.66＋1.96×0.031)，即(4.60 , 4.72)1210/L 。
该地女性红细胞数总体均数的95%可信区间为：(4.18－1.96×0.018 , 4.18＋1.96×0.018)，即(4.14 , 4.22)1210/L 。
(4) 两成组大样本均数的比较，用u 检验。
1) 建立检验假设，确定检验水准H 0：12μμ=，即该地健康成年男、女血红蛋白含量均数无差别 H 1：12μμ≠，即该地健康成年男、女血红蛋白含量均数有差别0.05α=2) 计算检验统计量22.829X X u ===3) 确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.001，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地健康成年男、女的血红蛋白含量均数不同，男性高于女性。
(5) 样本均数与已知总体均数的比较，因样本含量较大，均作近似u 检验。
1) 男性红细胞数与标准值的比较 ① 建立检验假设，确定检验水准H 0：0μμ=，即该地男性红细胞数的均数等于标准值H 1：0μμ<，即该地男性红细胞数的均数低于标准值 单侧0.05α= ② 计算检验统计量0 4.66 4.845.8060.031X X t S μ--===- ③ 确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地男性红细胞数的均数低于标准值。
2) 男性血红蛋白含量与标准值的比较 ① 建立检验假设，确定检验水准H 0：0μμ=，即该地男性血红蛋白含量的均数等于标准值 H 1：0μμ<，即该地男性血红蛋白含量的均数低于标准值 单侧0.05α= ② 计算检验统计量0134.5140.215.2410.374X X t S μ--===- ③ 确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地男性血红蛋白含量的均数低于标准值。
3) 女性红细胞数与标准值的比较 ① 建立检验假设，确定检验水准H 0：0μμ=，即该地女性红细胞数的均数等于标准值 H 1：0μμ<，即该地女性红细胞数的均数低于标准值 单侧0.05α= ② 计算检验统计量0 4.18 4.338.3330.018X X t S μ--===-③ 确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地女性红细胞数的均数低于标准值。
4) 女性血红蛋白含量与标准值的比较 ① 建立检验假设，确定检验水准H 0：0μμ=，即该地女性血红蛋白含量的均数等于标准值 H 1：0μμ<，即该地女性血红蛋白含量的均数低于标准值 单侧0.05α= ② 计算检验统计量0117.6124.711.1110.639X X t S μ--===- ③ 确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地女性血红蛋白含量的均数低于标准值。
2.2 为了解某高寒地区小学生血红蛋白含量的平均水平，某人于1993年6月随机抽取了该地小学生708名，算得其血红蛋白均数为103.5g/L ，标准差为1.59g/L 。
试求该地小学生血红蛋白均数的95%可信区间。
2.2解：σ未知，n 足够大时，总体均数的区间估计可用(/2/2X X X u S X u S αα-+ , )。
该地小学生血红蛋白含量均数的95％可信区间为：(103.5 1.96103.5 1.96-+, )，即(103.38 , 103.62)g/L 。
2.3 一药厂为了解其生产的某药物（同一批次）之有效成分含量是否符合国家规定的标准，随机抽取了该药10片，得其样本均数为103.0mg ，标准差为2.22mg 。
试估计该批药剂有效成分的平均含量。
2.3解：该批药剂有效成分的平均含量的点值估计为103.0 mg 。
σ未知且n 很小时，总体均数的区间估计可用()/2,/2,X X X t S X t S αναν-+ , 估计。
查t 界值表得t 0.05/2,9=2.262，该批药剂有效成分的平均含量的95％可信区间为：(103.0 2.262103.0 2.262-+, ，即(101.41 , 104.59)mg 。
2.4 152例麻疹患儿病后血清抗体滴度倒数的分布如表5，试作总体几何均数的点值估计和95%区间估计。
表5 152例麻疹患儿病后血清抗体滴度倒数的分布滴度倒数 1 2 4 8 16 32 64 128 256 512 1024 合计 人 数171031334224311522.4解：将原始数据取常用对数后记为X ，则152 1.85970.44250.0359X n X S S ====，，，，用(/2/2X X X u S X u S αα-+，)估计，则滴度倒数对数值的总体均数的95％可信区间为：(1.8597 1.960.0359 1.8597 1.960.0359-⨯+⨯ , )，即(1.7893 , 1.9301)。
所以滴度倒数的总体几何均数的点估计值为： 1.8597101072.39X ==，滴度倒数的总体几何均数的95%区间估计为( 1.7893 1.93011010, )，即(61.56 , 85.13)。
SPSS 操作 数据录入：打开SPSS Data Editor 窗口，点击Variable View 标签，定义要输入的变量x 和f ；再点击Data View 标签，录入数据（见图2.4.1，图2.4.2）。
图2..4.1 Variable View窗口内定义要输入的变量x和f图2.4.2 Data View窗口内录入数据分析：Transform Compute…Target Variable：键入logxNumeric Expression：LG10(x) 将原始数据取对数值OKData Weight Cases…Weight cases by Frequency Variable：f 权重为fOKAnalyze Descriptive Statistics Explore… 探索性分析Dependent list：logx 分析变量logx Display：StatisticsS tatistics…：Descriptives 统计描述注：最后得到结果是原始数据对数值的均数及其95%可信区间。
2.5 某口腔医生欲比较“个别取模器龈下取模技术”与“传统硅橡胶取模方法”两种取模技术精度的差异，在12名病人口中分别用两种方法制取印模，在体视显微镜下测量标志点到龈沟底的距离，结果如表6，问两种取模方法结果有无差异？表6 12个病人口腔某测量标志点到龈沟底的距离/cm病例号个别取模器龈下取模技术传统硅橡胶取模方法1 0.626 0.6142 0.627 0.6263 0.670 0.6544 0.548 0.5495 0.590 0.5746 0.603 0.5877 0.605 0.6028 0.347 0.3389 0.768 0.75910 0.576 0.57211 0.330 0.31812 0.233 0.2192.5解：本题为配对设计的两样本均数的比较，采用配对t检验。
表2.5.1 12个病人口腔某测量标志点到龈沟底的距离/cm(1) 建立检验假设，确定检验水准H 0：0d μ=，即两种取模方法结果无差异 H 1：0d μ≠，即两种取模方法结果有差异0.05α=(2) 计算检验统计量两种取模方法结果的差值d 的计算见表2.5.1。
120.00930.00610.0018d d n d S S ====， ，， 00.00935.1670.0018d d t S -=== 112111n ν=-=-=(3) 确定P 值，作出统计推断查t 界值表得P <0.001，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为两种取模方法结果有差异，个别取模器龈下取模法标志点到龈沟底的距离略高于传统硅胶取模法。
病例号 个别取模器龈下取模1d传统硅橡胶取模法2d12d d d =-1 0.626 0.614 0.012 2 0.627 0.626 0.0013 0.670 0.654 0.016 4 0.548 0.549 -0.0015 0.590 0.574 0.016 6 0.603 0.587 0.016 7 0.605 0.602 0.0038 0.347 0.338 0.009 9 0.768 0.759 0.009 10 0.576 0.572 0.004 11 0.330 0.318 0.012 120.2330.2190.014SPSS操作数据录入：打开SPSS Data Editor窗口，点击Variable View标签，定义要输入的变量x1和x2；再点击Data View标签，录入数据（见图2.5.1，图2.5.2）。
