活性污泥反应动力学及其应用

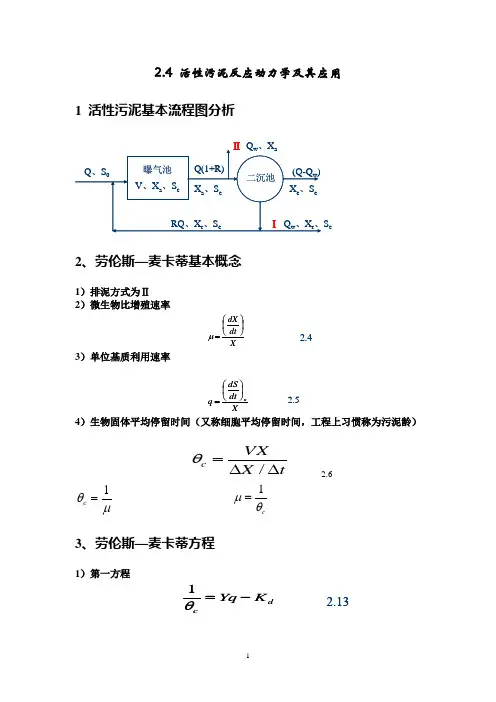
2.4 活性污泥反应动力学及其应用1 活性污泥基本流程图分析S e2、劳伦斯—麦卡蒂基本概念1）排泥方式为Ⅱ2）微生物比增殖速率⎛μXdt dX ⎪⎭⎫ ⎝= 2.43）单位基质利用速率⎛=Xdt dS q u ⎪⎭⎫ ⎝ 2.54）生物固体平均停留时间（又称细胞平均停留时间，工程上习惯称为污泥龄）tX VXc ∆∆=/θ 2.6μθ1=ccθμ1=3、劳伦斯—麦卡蒂方程1）第一方程dcK Yq -=θ12.132）第二方程K =⎫⎛S S X q dt dS s au+⎪⎭ ⎝m ax 2.154、劳伦斯—麦卡蒂基本方程式的应用1）确立处理水基质浓度（S e ）与生物固体平均停留时间（θc ）之间的关系（1）全混流⎫=K K ⎪⎪⎭⎝⎛+-⎪⎪⎭⎫⎝⎛+dcd c s eYv K S θθ11m ax 2.16（2）推流式S 对推流式deos e o e o cK S K S S S S v Y-+--=ln)()(1m ax θ 2.172）确立微生物浓度（X ）与生物固体平均停留时间θc 之间的关系（1）全混流)1()(c d e o c K S S Y t X θθ+-=2.18（2）推流 X对推流式（反应器内微生物浓度采用其平均值）。

)1()(c d e o c K S S Y t X θθ+-=2.193）确立活性污泥回流比（R ）与生物固体平均停留时间（θc ）之间的关系)1(=++-dt dXV X R Q RQX a r⎪⎪⎭⎫⎝⎛-+=a r c X X R R V Q 11θ 10S V IX r 6m a x)(=4）总产率（Y ）与表现产率（Y obs ）之间的关系()q X dt dS X dtdX dS dXdt dS dt dXY uu uμ=⎪⎭⎫⎝⎛==⎪⎭⎫⎝⎛=dX ()uobsdS Y '=2.23=11cd d c obs K Y K Y Y θμθ++⨯=2.245）θc 值与Se 值及E 的关系1dc K Yv -=m ax m in)(θ 2.266）（2.32）式便于用以求定曝气池的容积（V ）qX S S Q V a e )(0-=5、动力学参数的测定maxmax 011v S v K S S tXe S e +⎪⎪⎭⎫ ⎝⎛∙⎪⎪⎭⎫ ⎝⎛=-dcK Yq -=θ16、例题。

活性污泥法污水处理数学模型的发展和应用活性污泥法污水处理数学模型的发展和应用污水处理是国家和社会发展中的一个重要环节。

随着工业化和城市化进程的加快，污水处理厂的建设和运行愈加重要。

活性污泥法是目前应用最广泛的一种污水处理技术，它通过活性污泥微生物群落的代谢活动来去除水中的有机物质和氮、磷等污染物。

为了更好地设计和运行活性污泥法污水处理系统，科学家们开展了大量的研究，并发展了一系列的数学模型。

本文将探讨活性污泥法污水处理数学模型的发展和应用。

首先，要了解活性污泥法的基本原理。

在活性污泥法污水处理系统中，活性污泥是核心元素。

活性污泥中的微生物以有机物为能源，通过氧化、还原反应分解有机物，从而将污水中的有机物质降解为水和二氧化碳。

此外，活性污泥还可以通过硝化和反硝化过程将水中的氨氮转化为硝酸盐和氮气，并通过磷酸盐的沉淀去除水中的磷。

因此，了解活性污泥的代谢特性和微生物群落结构对于优化污水处理系统非常重要。

由于活性污泥法处理系统的复杂性和实际运行中的不确定性，传统经验模型的优化和改进已经不能满足实际需求。

因此，科学家们开始研究并发展了数学模型，以预测和模拟活性污泥法处理系统的性能。

这些数学模型包括质量平衡模型、动力学模型和群体动力学模型等。

质量平衡模型是最基本的数学模型之一，它基于质量守恒原理，以质量浓度的变化作为变量，描述污水中有机物质和污染物的传输和转化。

质量平衡模型可以用来优化活性污泥污染物的去除效率，提高系统的稳定性和可靠性。

然而，质量平衡模型无法描述微生物群落的动态变化和相互作用。

为了更好地描述活性污泥法处理系统中微生物的动态行为，科学家们发展了动力学模型。

动力学模型以微生物群落的代谢过程为基础，通过微分方程组描述了有机物质和污染物的转化动力学。

这些模型可以用来预测系统的稳态和响应速度，优化供碳、氮和磷源的进料方式，提高活性污泥的处理效率。

群体动力学模型是动力学模型的进一步发展，它考虑了微生物群体内部的异质性和互作。

浅谈好氧活性污泥法在污水治理中的应用随着城市化程度的不断深化，人口压力的逐步提高。

我国环境污染的情况也越来越严峻。

党和国家已经将环境保护确立为我国的基本国策之一。

目前，按照要素分类，环境污染主要包括大气污染、水体污染和土壤污染。

针对水体污染的治理，直接关系到人民群众的用水健康和环境的可持续发展。

传统的污水处理方法，较难直接分解污染物，残留量较高，容易造成二次污染；同时，成本较高，设备较为复杂。

而欠发达地区通常使用的方法是利用自然水体的自身净化能力对受到污染的水体进行净化，这种方法对自然环境的破坏较大，过多依赖水体的自然净化能力，不符合可持续发展的战略目标。

而新兴的微生物活性污泥法，因为其设备简单，投资较低，污水净化效率高，二次污染少等优势，得到了广泛的应用与认可。

并在实践中不断发展。

一、水体自净和活性污泥法自然界中的水体是存在自我净化的能力的。

当水体中存在一些有机污染物的时候。

水中的浮游生物、紫外线照射等影响因素就可以使有污染性的有机物转变为无害的简单物质。

使水体质量恢复到受到污染之前的水平。

这就是水体自净。

但是，水体自净是存在一个污染浓度的上限的。

也就是说，自然界的水体存在一定的自净容量。

超过自净容量的水体污染就不能被水体的自净能力所消化。

因此，自净容量就是指在水体正常生物循环过程中能够净化有机污染物的最大数量。

基于以上思路，我们可以人为扩大水体的自净容量。

这就引出了活性污泥法在污水处理中的应用。

活性污泥法，是利用活性污泥中的好氧生物，对污水中的污染物进行氧化还原。

使之变为无害化产物的过程。

将曝气池与二次沉淀池进行串联，并且将污泥管与之回联。

使得二次沉淀池中沉淀的污泥回流到曝气池中。

使这些污泥以及其中的活性成分能够在曝气池中起到凝聚、吸附的作用。

同时，其中的微生物能够使曝气池中的有害化学成分进行氧化分解。

这就是活性污泥法的基本原理和概念。

二、活性污泥法的基本原理活性污泥法是利用悬浮生长的微生物絮体处理废水的一类好氧生物处理方法，生物絮体称活性污泥。

活性污泥法的反应动力学原理及其应用活性污泥法（activated sludge process）是一种常见的生物处理废水的方法，广泛应用于污水处理厂。

它的反应动力学原理涉及到生物物理和化学反应过程，其应用可以有效去除污水中的有机物、氮、磷等污染物。

接触氧化污泥法是将污水与活性污泥充分接触，通过氧化降解有机物。

在这个过程中，有机物首先被吸附到污泥团聚体的表面，然后被微生物降解。

微生物通过对有机物进行代谢，产生酶来催化有机物的降解。

反应过程中，溶解氧和微生物是限制因素。

溶解氧的供应主要通过曝气作用，污水中的氧被转移到活性污泥颗粒上，为微生物呼吸提供氧气。

间歇氧化污泥法是将污水与活性污泥进行间歇接触和氧化降解。

在间歇氧化污泥法中，活性污泥以混合液的形式存在，定期进入污泥沉淀池进行沉淀。

通过周期性地供氧和去除微生物产物，可以提高微生物的降解效率。

间歇氧化污泥法可以减小活性污泥容积，减少处理设备和设备的尺寸。

活性污泥法的应用非常广泛。

首先，它可用于去除污水中的有机物。

微生物通过分解有机物来获取能量，降解有机物为二氧化碳和水，从而达到去除有机物的目的。

其次，活性污泥法也可用于去除污水中的氮和磷。

氮有机物在细菌的作用下，先转化为氨氮，然后转化为亚硝酸盐和硝酸盐。

磷则被微生物分离吸附到活性污泥中。

最后，活性污泥法还可用于去除重金属和其他有害物质。

然而，对于有害物质的降解程度则受到微生物菌群的结构和活性因素的限制。

除了以上应用，活性污泥法还可用于废水的预处理、提高水体的自净能力、生物氮除磷等。

此外，活性污泥法还可以与其他处理方法结合使用，如沉淀、过滤和气浮等，以更好地达到废水处理的目的。

总之，活性污泥法是一种基于微生物代谢的处理方法，通过微生物的作用和生物反应动力学原理，可以有效去除污水中的有机物、氮、磷等污染物，具有广泛的应用前景。

活性污泥法水处理过程的反应动力学研究随着工业和城市化的发展，人们对于水的需求越来越高，同时，水污染也变得越来越严重。

为了保障人民健康和维护生态环境，水处理成为至关重要的问题。

活性污泥法是一种常用的水处理方法，也是较为有效的污水处理技术之一。

反应动力学研究是活性污泥法水处理过程的重要组成部分，本文将从反应动力学的角度探讨活性污泥法水处理的研究现状及未来发展趋势。

一、活性污泥法的工艺原理和优势活性污泥法是一种将生物技术应用于水处理的方法，主要利用微生物对污水中的有毒有害物质进行降解，从而实现排放标准的水质。

其中，活性污泥是通过让微生物在一定温度、pH值、搅拌条件下生长繁殖形成的。

该方法在研究和应用中不断地被改进和完善，现已成为一种稳定、节能、环保的高效水处理工艺。

活性污泥法具有的优势主要包括以下几点：1. 处理能力强。

活性污泥法能够同时处理多种污染物，将多种有机物转化为无机物，消除氨氮及硝酸盐等有害物质。

同时，活性污泥法的处理效率很高，可将有机物质降解至90%以上。

2. 适应性强。

活性污泥法可适用于多种污染物类型及浓度，适应性广泛。

通过调节污泥的数量、质量、新陈代谢和清除机能，能够处理不同种类何浓度的废水。

3. 运行费用低。

相比于其他的水处理工艺，活性污泥法的运行费用较低，并且处理效果稳定可靠。

此外，工艺过程中能够利用氧气和碳源，从而达到省能减排的目的。

4. 适用范围广。

活性污泥法可广泛应用于染料、电镀、造纸、农业等行业的水处理问题。

二、活性污泥法水处理过程的反应动力学研究活性污泥法经过多年的应用和研究，涵盖了处理剂量、污泥浓度、温度、pH 值、水质、紫外线辐照等众多因素。

其中，反应动力学研究最为重要。

反应动力学以重心反应动力学和区域反应动力学为主要研究方法，可以通过实验及建模进行研究。

重心反应动力学的研究方法主要基于化学反应速率法，以化学反应中活性物质的浓度为研究对象，将废水的水质状况与活性污泥的活动状况作为反应动力学的研究对象，在探讨废水对活性污泥的影响、污泥流出指数、反应动力学常数等方面有较为广泛的应用。

13.3 活性污泥反应动力学及应用13.3.1 概述活性污泥反应动力学能够通过数学式定量地或半定量地揭示活性污泥系统内有机物降解、污泥增长、耗氧等作用与各项设计参数、运行参数以及环境因素之间的关系。

在活性污泥法系统中主要考虑有机物降解速度、微生物增长速度和溶解氧利用速度。

目前，动力学研究主要内容包括：（1）有机底物降解速度与有机物浓度、活性污泥微生物量之间的关系。

（2）活性污泥微生物的增殖速度与有机底物浓度、微生物量之间的关系。

（3）微生物的耗氧速率与有机物降解、微生物量之间的关系。

13.3.2 反应动力学的理论基础（1）有机物降解与活性污泥微生物增殖曝气池是一个完整的反应体系，池内微生物增殖是微生物合成反应和内援代谢两项胜利活动的综合结果，即：微生物增殖速率= 降解有机物合成的生物量速率—内源代谢速率式中，Y——产率系数，即微生物降解1kgBOD所合成的MLSS量，kgMLSS/kgBOD；K d——自身氧化率，即微生物内源代谢的自身减少率；对于完全混合式活性污泥系统，曝气池中的微生物量物料平衡关系式如下：每日池内微生物污泥增殖量=每日生成的微生物量—每日自身氧化掉的量∴式中，S0——原水BOD浓度；S e——处理出水BOD浓度；Q——日处理水量，m3/d；V——曝气池容积，m3；X——曝气池中污泥平均浓度，mg/L。

两边除以VX ，式子变为而q称为BOD比降解速率，其量纲与污泥负荷相同，单位一般用kgBOD/（kgMLSS?d）表示。

即，θc为泥龄。

可见高去除负荷下，污泥增长很快，导致排泥加快，污泥龄就短，生物向不够丰富，因此原水的可生化性要好。

对于一个稳定的反应体系，Y、K d是常数，可以设计实验获得。

一般生活污水类水质，Y=0.5~0.65，K d=0.05~0.1；部分工业废水的Y、K d值见设计手册。

（2）有机物降解与需氧量同样，曝气池内，因为降解有机物，就要消耗溶解氧O2，同时微生物内源代谢也消耗溶解氧。

4-2活性污泥法反应动力学一、概述 研究目的：定量或半定量地揭示系统内有机物降解、污泥增长、耗氧等作用与各项设计参数、运行参数以及环境因素之间的关系；研究内容:（1）基质降解的动力学，涉及基质降解与基质浓度、生物量等因素的关系； （2）微生物增长动力学，涉及微生物增长与基质浓度、生物量、增长常数等因素的关系； （3）还研究底物降解与生物量增长、底物降解与需氧、营养要求等的关系。

模型假设:①曝气池为完全混合式； ②在稳定状态下； ③进水和出水无微生物；④二沉池中微不发生微生物对有机物的降解； ⑤底物浓度用可降解的有机物浓度表示； ⑥温度不变，进水有机物成分性质不变 二、有机底物降解动力学 1、米氏方程1913年，德国化学家Michaelis 和Menten 根据中间产物学说对酶促反映的动力学进行研究，提出表示整个反应中底物浓度和反应速度关系公式——米氏方程。

在酶促反应中，在低浓度底物情况下，反应相对于底物是一级反应（first order reaction ）；而当底物浓度处于中间范围时，反应是混合级反应（mixed order reaction ）。

当底物浓度增加时，反应由一级反应向零级反应（zero order reaction ）过渡。

maxm v S v K S=+ V max —最大反应速度。

S —反应中底物浓度。

K m —米氏常数；表示反应达到1/2V max 的底物浓度，mol/L ，由酶的性质决定，与酶的浓度无关。

2、Monod 方程1942年Monod 在纯培养的单一底物的试验中发现微生物的增殖速度与底物浓度之关系符合米氏方程。

max S S K Sμμ=+ 微生物比增殖速率：单位质量微生物的增殖速率，T -1；u max —微生物最大比增殖速度，T -1。

K S —饱和常数u=1/2u max 时的底物浓度，或称半速率常数。

S —有机底物浓度。

1950年采用异养微生物群体(混合培养)和单一基质的试验，提出微生物比增长速率max 1S S dXX dtK Sμμ==+假定u=rv ，u max =rv max ，则maxmax 1S S S S dSv v r r K S K S X dtμμ====-++ 得Monod 方程：max S dSXSv dtK S-=+Monod 方程的两个推论： ①高底物浓度S 》K S ，max dSv X dt-=，有机物降解速率=v max ，与底物浓度无关，零级反应。

（1）比较莫诺方程、米门方程的异同点。

答：莫诺方程和米门方程形式十分相似，但它们表达的意思完全不同。

①莫诺方程：式中，μ——微生物的比增长速度，即单位生物量的增长速度；μmax——微生物最大比增长速度；K s——半饱和常数，为当时的底物浓度，质量/容积；S——单一限制性底物浓度。

莫诺方程描述的是微生物比生长速度与单一限制性底物存在的关系，适用于单一限制性基质，不存在抑制的情况。

②米门方程：式中，v——反应速度；K m——米氏常数；V max——酶被底物饱和时的反应速度；[S]——底物浓度。

米门方程描述的是一个酶促反应的起始速度与底物浓度关系的速度方程，适用于单一基质酶促反应，不存在抑制的情况。

（2）试推导米门方程表达式v=vmax S/(S+Km)。

答：首先定义[E t]为酶的总浓度，即[E t]= [E]+ [ES]；则ES的生成速率为k1[E][S] = k1 ([E t] - [ES]) [S]；而ES的分解速率为k-1[ES] + k2[ES]；根据稳态假说，当反应处于稳态时，ES 的生成与分解速率相等，即k1 ([E t] - [ES]) [S]= k-1[ES] + k2[ES]经过移项等操作后，可以得到一个关于[ES]的方程，即[ES]=k1[E t][S] / (k1[S]+ k-1 + k2)右边的分式分子分母同时除以k1，可得[ES]/k1=[E t][S] / ([S]+(k-1 + k2)/k1) 此时将(k-1 + k2)/k1定义为米氏常数(Michaelis constant，K m)，因此方程可写为[ES]=[E t][S]/(K m+[S])产物的生成速率取决于[ES]，即v= k2[ES]所以原方程又可以改写为v= k2[E t][S]/(K m+[S])当酶分子达到饱和，所有酶分子都结合上底物，即[E t] = [ES]时，反应速率达到最大。

此时最大反应速率V max = k2[E t] ，所以原方程又可写为v=v max S/(S+K m)，其中S即为[S]. 推导完成。