C++几何图形面积周长计算

小学六年级数学几何形的面积与周长计算规则总结几何形是数学中的重要概念之一，它涵盖了各种形状的图形，如矩形、三角形和圆形等。

在小学六年级数学课程中，学生需要学习如何计算这些几何形的面积和周长。

本文将对小学六年级数学几何形的面积与周长计算规则进行总结，以帮助学生更好地掌握这些知识。

一、矩形的面积和周长计算规则矩形是一种具有四个直角的四边形，它的两组相对边分别相等。

计算矩形的面积和周长需要掌握以下规则：1. 面积计算规则：矩形的面积等于长乘以宽。

设矩形的长为L，宽为W，则矩形的面积S = L × W。

2. 周长计算规则：矩形的周长等于两倍的长加两倍的宽。

设矩形的长为L，宽为W，则矩形的周长P = 2L + 2W。

二、三角形的面积和周长计算规则三角形是一种具有三条边和三个内角的图形。

计算三角形的面积和周长需要掌握以下规则：1. 面积计算规则：三角形的面积等于底边乘以高再除以2。

设三角形的底边为B，高为H，则三角形的面积S = (B × H)/2。

2. 周长计算规则：三角形的周长等于三条边的长度之和。

设三角形的三边长分别为a、b、c，则三角形的周长P = a + b + c。

三、圆形的面积和周长计算规则圆形是一种具有无限多个点到中心点距离相等的图形。

计算圆形的面积和周长需要掌握以下规则：1. 面积计算规则：圆形的面积等于半径的平方乘以π（pi）。

设圆形的半径为R，则圆形的面积S = πR²。

2. 周长计算规则：圆形的周长也称为圆周，等于直径乘以π。

设圆形的直径为D，则圆形的周长C = πD。

综上所述，小学六年级数学几何形的面积与周长计算规则可以归纳为以上三种常见几何形的计算公式。

学生在计算时应根据所给图形的形状，选用相应的计算规则进行求解。

通过反复练习和实际应用，学生将能够熟练掌握这些计算方法，提升数学水平。

长方形的周长面积
长方形是数学中一个经常被提及的基本几何图形，它由四条边所组成，是一种具有四个直角的多边形。

下面我们来讲一下长方形的周长
面积。

一、长方形的定义
长方形是一种具有四个直角的多边形，它的四条边分别被称为长、宽、对边和邻边。

根据定义，长方形的对边相等，邻边相等。

二、长方形的周长
长方形的周长是指长方形四条边的总长度。

可以用公式C= 2(L+W)来
计算。

其中，C表示长方形的周长，L表示长方形的长度，W表示长方形的宽度。

三、长方形的面积
长方形的面积是指长方形内部的所有空间面积之和。

可以用公式A=
L×W来计算。

其中，A表示长方形的面积，L表示长方形的长度，W
表示长方形的宽度。

四、周长和面积的关系
周长和面积是两个基本的几何概念，它们在许多数学问题中都有重要
的应用。

在长方形中，周长和面积之间也有一定的关系。

具体来说，
当长方形的长度和宽度固定时，长方形的周长和面积呈现出一种负相
关的关系：周长越大，面积越小；周长越小，面积越大。

五、长方形在生活中的应用
长方形是一种常见的几何图形，在我们生活中也有许多应用。

例如，我们常用的书本、门、窗、桌子、电视机等家具，都可以看做是长方形。

此外，在建筑、工程、农业、地理等领域中，长方形也有广泛的应用。

六、结语
长方形是一种简单而又重要的几何图形，它在数学和实际问题中都有着广泛的应用。

通过了解长方形的定义、周长、面积和应用等方面的知识，可以帮助我们更好地理解和应用长方形。

圆的周长计算公式有哪些
圆是一个几何图形，具有许多特性，其中之一是其周长。

圆的周长是
指围绕圆的线段的总长度。

圆的周长可以通过半径或直径来计算。

以下是
一些计算圆周长的公式：
1.使用半径计算圆周长：
圆的周长公式：C=2πr
2.使用直径计算圆周长：
圆的周长公式：C=πd
上述两个公式是最基本的计算圆周长的方法。

根据需要，可以选择使
用半径或直径来计算圆的周长。

不仅可以使用这两个公式计算圆周长，还可以使用其他参数（如面积）来计算。

下面是一些使用其他参数计算圆周长的方法：
1.使用面积计算圆周长：
首先，我们需要使用面积公式S=πr^2计算圆的面积。

然后，可以使
用面积公式和半径来计算圆的周长。

圆的周长公式：C=2π√(S/π)
2.使用圆弧长度计算圆周长：
当我们知道圆上的圆弧长度时，可以使用圆弧长度与圆心角度数的关
系来计算圆的周长。

圆的周长公式：C=(l/α)*360°
其中，C表示圆的周长，l表示圆上的圆弧长度，α表示圆心角的度数，360°表示一个完整的圆。

3.使用弧度计算圆周长：
在数学中，常用弧度作为角度度量单位，圆的周长可以使用弧度和半径进行计算。

圆的周长公式：C=2πr（以弧度计）
这些是一些计算圆周长的公式。

根据需要，可以选择适合的公式进行计算。

无论使用哪种公式，都需要了解圆的基本概念和参数，如半径、直径、面积、圆心角度数等。

同时，需要注意使用正确的单位和数值精度来计算圆的周长。

几何图形面积公式三角形：=ah÷2三角形的面积=底×高÷2 S三=S×2÷h三角形的底=面积×2÷高 a三三角形的高=面积×2÷底 h=S×2÷a三四边形：=2（a+b）长方形的周长=（长+宽）×2 C长正方形的周长=边长×4 C=4a正=ab长方形的面积=长×宽S长正方形的面积=边长×边长S=a2正=ah平行四边形的面积=底×高S平平行四边形的底=面积÷高a=S÷h平=S÷a平行四边形的高=面积÷底h平梯形：梯形的面积=(上底+下底)×高÷2 S=（a+b）h÷2梯=S×2÷（a+b）梯形的高=面积×2÷（上底+下底） h梯上底+下底=面积×2÷高 a+b=S×2÷h=S×2÷h－b 梯形的上底=面积×2÷高－下底 a梯=S×2÷h－a 梯形的下底=面积×2÷高－上底 b梯钢管堆成梯形的形状，要算钢管的根数，就按梯形的面积公式计算，其中最上层是上底，最下层是下底，中间层数就是高。

总根数=（顶层根数+底层根数）×层数÷2 层数=（底层-顶层+1 ）。

圆周长与面积的计算公式全文共四篇示例，供您参考第一篇示例：圆是几何图形中常见的形状之一，它具有很多特性和性质。

圆周长和面积的计算是圆的重要属性之一，也是初中数学学习的基本部分。

在实际生活中，我们经常会遇到需要计算圆的周长与面积的情况，比如建筑工程领域、地理测量领域等。

本文将详细介绍圆的周长和面积的计算公式，并探讨它们的性质和应用。

让我们从圆的周长开始讨论。

圆的周长是指圆的边界的长度，也就是圆的周长是圆的边界一周的长度。

当圆的半径为r时，圆的周长的计算公式为：C=2πr，其中π是一个数学常数，大约为3.14159。

通过圆的周长计算公式，我们可以得出一些结论。

圆的周长与半径r成正比，也就是说，随着半径r的增大，圆的周长也会增加；反之，半径减小时，圆的周长也会减小。

圆的周长与π成正比，也就是说，无论圆的半径大小如何，圆的周长与π的值相关。

接下来，让我们来讨论圆的面积的计算。

圆的面积是指圆内部的区域的大小，也就是圆的面积可以简单理解为圆内部所占的平方单位的数量。

当圆的半径为r时，圆的面积的计算公式为：A=πr²。

通过圆的面积计算公式，我们同样可以得出一些结论。

圆的面积与半径r的平方成正比，也就是说，随着半径r的增大，圆的面积也会增加；反之，半径减小时，圆的面积也会减小。

圆的面积与π成正比，也就是说，无论圆的半径大小如何，圆的面积与π的值相关。

在实际应用中，圆的周长和面积的计算公式有着广泛的应用。

在地理测量领域，我们可以利用圆的周长和面积的计算公式来计算地球表面上的长度和面积，从而帮助我们更准确地理解地球的地貌和分布。

在建筑工程领域，我们可以利用圆的周长和面积的计算公式来计算圆形建筑物的周长和面积，从而帮助我们更精准地规划和设计建筑。

除了单纯的计算，圆的周长和面积的性质也经常被应用于解决实际问题。

在数学建模中，我们可以利用圆的周长和面积的计算公式来建立数学模型，解决诸如液体容器的容积计算、圆形运动的路径规划等实际问题。

圆的面积和周长计算圆是几何中的一个基本图形，具有无限的对称性和独特的美感。

在数学中，我们经常需要计算圆的面积和周长，这对于解决实际问题和理解圆的性质都非常重要。

本文将介绍如何计算圆的面积和周长，并提供一些实际应用的例子。

一、圆的面积计算圆的面积是指圆所包围的平面区域的大小。

要计算圆的面积，我们需要知道圆的半径。

半径是从圆心到圆上任一点的距离，通常用字母r 表示。

圆的面积计算公式为：A = πr²其中，A表示圆的面积，π是一个数学常数，约等于3.14159，r是圆的半径。

例如，如果一个圆的半径为5cm，那么它的面积可以计算如下：A = π × 5²= 3.14159 × 25≈ 78.54所以，这个圆的面积约为78.54平方厘米。

二、圆的周长计算圆的周长是指圆周上的长度。

要计算圆的周长，我们同样需要知道圆的半径。

圆的周长计算公式为：C = 2πr其中，C表示圆的周长，π为数学常数，r为圆的半径。

以前述半径为5cm的圆为例，它的周长可以计算如下：C = 2π × 5= 2 × 3.14159 × 5≈ 31.42所以，这个圆的周长约为31.42厘米。

三、圆的面积和周长的实际应用圆的面积和周长计算在实际生活和工作中有很多应用。

以下是两个常见的例子：1. 圆的面积和周长在工程建设中的应用在建筑、道路和轨道等工程建设中，需要合理安排各种设施和材料的使用，并进行施工计划和预算。

圆的面积和周长计算可以帮助工程师确定建筑物的基础尺寸、道路的曲线半径、轨道的半径等。

通过计算圆的面积和周长，可以精确控制工程的尺寸，确保工程质量。

2. 圆的面积和周长在日常生活中的应用除了工程建设，圆的面积和周长计算也在日常生活中有很多应用。

例如，我们经常使用圆桌，计算桌面的面积可以帮助我们选择合适大小的桌布；计算圆饼的面积可以帮助我们确定合适的切割方法；计算花坛的面积可以帮助我们购买足够的土壤和植物。

圆的周长与面积的计算圆是一种常见的几何图形，具有许多独特的特性，其中包括周长和面积的计算。

在本文中，我们将介绍如何计算圆的周长和面积，并提供一些实际应用的例子。

一、圆的周长的计算圆的周长是指圆的边界长度，也就是围绕圆的一条闭合曲线的长度。

圆的周长可以通过圆的半径或直径进行计算。

1. 使用半径计算圆的周长圆的周长可以使用以下公式进行计算：C = 2πr，其中C表示圆的周长，π表示圆周率，r表示圆的半径。

例如，如果一个圆的半径为5厘米，则其周长可以计算为：C = 2π× 5 = 10π cm。

2. 使用直径计算圆的周长圆的周长也可以使用直径进行计算。

直径是圆的边界上任意两点之间的距离，也是圆的最长直径。

根据直径的定义，圆的周长等于直径乘以π。

因此，使用以下公式可以计算圆的周长：C = πd，其中C表示圆的周长，π表示圆周率，d表示圆的直径。

例如，如果一个圆的直径为10厘米，则其周长可以计算为：C = π× 10 = 10π cm。

二、圆的面积的计算圆的面积是指圆内部的平面区域的大小。

圆的面积可以通过圆的半径或直径进行计算。

1. 使用半径计算圆的面积圆的面积可以使用以下公式进行计算：A = πr^2，其中A表示圆的面积，π表示圆周率，r表示圆的半径。

例如，如果一个圆的半径为3厘米，则其面积可以计算为：A = π × 3^2 = 9π cm^2。

2. 使用直径计算圆的面积圆的面积也可以使用直径进行计算。

直径是圆的边界上任意两点之间的距离，也是圆的最长直径。

根据圆的面积定义，圆的面积等于半径平方乘以π。

因此，使用以下公式可以计算圆的面积：A = π(d/2)^2，其中A表示圆的面积，π表示圆周率，d表示圆的直径。

例如，如果一个圆的直径为6厘米，则其面积可以计算为：A = π ×(6/2)^2 = 9π cm^2。

三、实际应用示例圆的周长和面积的计算在日常生活中有许多实际应用。

面积和周长：图形的面积和周长计算面积和周长是几何学中两个重要的概念，用来描述图形的大小和形状。

准确计算图形的面积和周长对于很多领域都是必不可少的，比如建筑设计、土木工程、农业规划等等。

在本文中，我们将介绍一些常见图形的面积和周长计算方法，帮助您准确计算各种图形的尺寸。

一、三角形三角形是最基本的图形之一，它由三条线段组成。

计算三角形的面积可以使用海伦公式或基础公式。

海伦公式适用于已知三边长度的情况，公式为：面积= √(s × (s-a) × (s-b) × (s-c))其中，s是三角形的半周长，即s = (a + b + c) / 2，a、b、c分别为三角形的三边长度。

基础公式适用于已知底和高的情况，公式为：面积 = 0.5 ×底 ×高计算三角形的周长很简单，只需要将三边长度相加即可。

二、矩形矩形是一个拥有四个直角的四边形。

计算矩形的面积和周长非常简单，只需要根据矩形的长和宽使用下列公式：面积 = 长 ×宽周长 = 2 × (长 + 宽)三、正方形正方形是一种特殊的矩形，所有四条边的长度相等。

正方形的面积和周长的计算方法与矩形相同：面积 = 边长 ×边长周长 = 4 ×边长四、圆形圆形是一个没有直角的几何图形，其特点是所有点到圆心的距离相等。

计算圆的面积和周长需要使用圆周率π，一般取3.14或3.14159。

计算圆形的面积和周长公式如下：面积= π × 半径 ×半径周长= 2 × π × 半径五、椭圆椭圆是一个拉长的圆形，其周长和面积的计算较为复杂。

椭圆的面积计算公式如下：面积= π × 长半轴 ×短半轴其中，长半轴和短半轴分别是椭圆的长和短轴的一半。

椭圆的周长计算没有简单的公式，可以使用数值积分等方法进行近似计算。

六、其他图形除了上述常见图形外，还有许多其他复杂的图形，如梯形、扇形、六边形等。

V＝S底h
＝πr2h
空心圆柱
R－外圆半径
r－内圆半径
h－高
V＝πh(R2-r2)
直圆锥
r－底半径
h－高
S侧=πr(r2+h2)1/2＝πrL
S表＝S全= S侧+πr2＝πrL+πr2＝πr(L+r)
V＝ πr2h
几何图形面积体积周长计算公式
1、平面图形
名称
符号
周长C和面积S
正方形
a—边长
C＝4a
S＝a2
长方形
a和b－边长
C＝2(a+b)
S＝ab
三角形
a,b,c－三边长
h－a边上的高
S＝ ah
C＝a+b+c
平行四边形
a,b－边长
h－a边的高
S＝ah
CHale Waihona Puke 2(a+b)菱形D－长对角线长
d－短对角线长
a－边长
S＝ Dd
S＝ah
C＝4a
梯形
a和b－上、下底长
h－高
m－中位线长
S＝ (a+b)h
＝mh
圆
r－半径
d－直径
C＝πd＝2πr
S＝πr2
＝ πd2
扇形
r—扇形半径
n—圆心角度数
C＝2r＋2πr× L= πr
S＝ πr2= Lr
圆环
R－外圆半径
r－内圆半径
D－外圆直径
d－内圆直径
S＝π(R2-r2)
＝ π(D2-d2)
2、立方图形
名称
符号
面积S和体积V
正方体
a－边长
S＝6a2
V＝a3

已知周长求面积的计算公式圆周率π作为数学运算的重要参数，在很多几何计算中都起到了重要作用。

圆形是一种常见的几何图形，其周长和面积的计算公式也非常重要，许多几何计算中都使用到它们。

今天我们就来讨论如何根据圆的周长来求出其面积的计算公式。

1.先，需要知道的是圆的周长公式，即C=2πr，这里C表示圆的周长，r表示圆的半径。

根据这个公式，可以知道，如果我们已知圆的周长，那么就可以根据公式计算出圆的半径。

2.算出圆的半径以后，要求出圆的面积，就要用到圆形面积公式，即S=πr。

这里S表示圆的面积，π和r分别表示圆周率和圆的半径。

3.样，当我们已知一个圆的周长时，就可以根据上述公式求出圆的半径和面积。

例如，已知圆的周长为12m，那么圆的半径r=12/2π，圆的面积S=π(12/2π)=9π。

圆形是数学中一种常见的几何图形，其周长和面积的计算公式也都是一种重要的知识点。

在实际的几何计算中，当获得一个圆的周长时，可以根据已知周长求面积的计算公式，先求出该圆的半径，再求出该圆的面积。

因此，掌握这种计算公式对正确地解决问题是非常重要的。

从蒙氏三角公式到欧拉公式，从极限的概念到快速求根，圆周率π无疑是一个伟大的发明，也是数学中的一大神奇。

从理论上讲，π的值是无限的，但在实际的计算中，由于计算机的运算能力，我们只能精确到小数点后某一位数，而在平时的学习工作中，也可以根据公式或者一些计算规律来获得很高精度的值。

另外，要使用已知周长求面积的计算公式，还要注意单位的正确使用，比如圆的周长单位是米或者厘米、圆的面积单位是平方米或者平方厘米等。

只有正确使用单位，才能得出正确的结果。

总之，已知周长求面积的计算公式是一个非常重要的公式，它可以帮助我们解决许多几何问题，在实际应用中也发挥了重要作用。

圆形周长和面积的计算公式，是数学中基本知识，也是日常计算几何图形参数的重要工具，应该牢记其计算公式，掌握正确使用单位的方法，从而正确计算出正确的结果。

几何常用周长面积体积公式咱们从小学开始，就跟各种几何图形打交道啦。

什么三角形、正方形、圆形，还有后来的长方体、正方体、圆柱体等等。

这些图形都有自己的周长、面积、体积公式，可别小瞧它们，用处大着呢！先来说说周长。

周长就是图形一圈的长度。

比如咱们常见的正方形，它的周长公式就是边长乘以 4。

我记得有一次，我带着小侄子在公园里玩，看到一个正方形的花坛。

小侄子好奇地问我：“叔叔，这个花坛一圈有多长啊？”我就告诉他，咱们只要量一下其中一条边的长度，然后乘以 4 就知道啦。

量了一下，边长是 3 米，那周长就是 3×4 = 12 米。

小侄子似懂非懂地点点头，看着他那可爱的模样，我觉得数学真有趣，能在生活中随时派上用场。

再说说长方形的周长公式，是长加宽的和乘以 2。

有一回，我帮朋友装修房子，要给一个长方形的房间铺地毯，就得先知道房间的周长，量好了长是 5 米，宽是 3 米，那周长就是（5 + 3）× 2 = 16 米，这样就能算出需要多少米长的地毯边条啦。

接下来是圆形的周长，公式是2πr 或者πd，这里的 r 是半径，d 是直径，π 呢，通常取 3.14。

我有次去买自行车，看到车轮上的花纹，就想到了这个公式。

车轮的直径大约是 60 厘米，那周长就是 3.14×60 = 188.4 厘米，这就大概能知道车轮转一圈能走多远啦。

说完了周长，再聊聊面积。

正方形的面积公式是边长乘以边长。

我家有块正方形的小桌布，边长是 2 米，那面积就是 2×2 = 4 平方米。

长方形的面积是长乘以宽。

像我之前说的那个房间，面积就是 5×3 = 15 平方米。

三角形的面积是底乘以高除以 2。

有次在路边看到工人在测量一块三角形的广告牌，底是 4 米，高是 3 米，面积就是 4×3÷2 = 6 平方米。

圆形的面积公式是πr²。

过年的时候家里做汤圆，我看着那圆圆的汤圆，就想到了这个公式。

小学数学图形求阴影部分面积方法总结我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形。

我们的面积及周长都有相应的公式直接计算。

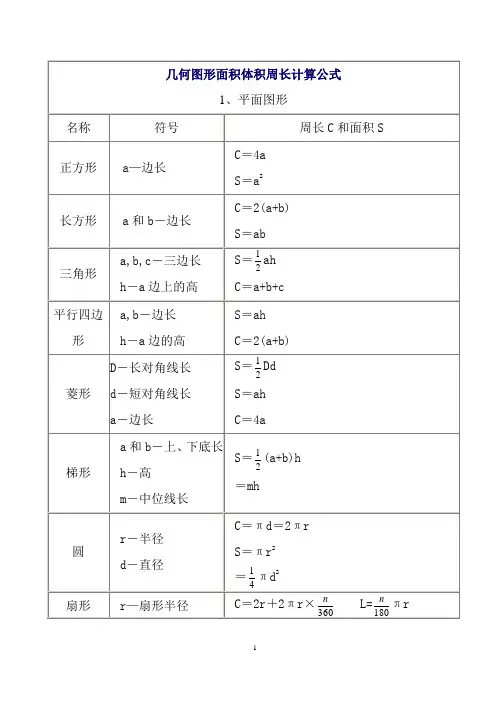
如下表：1、几何图形计算公式：1) 正方形：周长＝边长×4 C=4a面积=边长×边长S=a×a2) 正方体：表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3) 长方形：周长=(长+宽)×2 C=2(a+b) 面积=长×宽S=ab4)长方体：表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh) 体积=长×宽×高V=abh5)三角形：面积=底×高÷2 s=ah÷26)平行四边形：面积=底×高s=ah7)梯形：面积=(上底+下底)×高÷2 s=(a+b)×h÷28)圆形：周长=直径×Π=2×Π×半径C=πd=2πr面积=半径×半径×π9)圆柱体：侧面积=底面周长×高表面积=侧面积+底面积×2体积=底面积×高10)圆锥体：体积=底面积×高÷32、面积求解大致分为以下几类：从整体图形中减去局部；割补法：将不规则图形通过割补，转化成规则图形。

实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

求圆的周长和面积的c++编程1. 前言圆是我们日常生活中经常遇到的几何图形之一，求解圆的周长和面积是数学中的基本问题之一。

在计算机编程中，我们可以利用c++语言来编写程序，求解圆的周长和面积。

2. 圆的周长和面积公式在编程之前，我们首先需要了解圆的周长和面积的计算公式。

圆的周长计算公式为：C = 2 * π * r，圆的面积计算公式为：S = π * r^2，其中π为圆周率，r为圆的半径。

3. 利用c++编程求解圆的周长和面积下面我们将利用c++语言来编写程序，求解圆的周长和面积。

```c++#include <iostream>using namespace std;const double PI = 3.14159;double calculateCirclePerimeter(double radius) {return 2 * PI * radius;}double calculateCircleArea(double radius) {return PI * radius * radius;}int main() {double radius;cout << "请输入圆的半径：";cin >> radius;double perimeter = calculateCirclePerimeter(radius);double area = calculateCircleArea(radius);cout << "圆的周长为：" << perimeter << endl;cout << "圆的面积为：" << area << endl;return 0;}```在上面的c++程序中，我们首先定义了圆周率π的常量，并编写了两个函数分别用于计算圆的周长和面积。

圆计算公式圆的计算公式。

圆是数学中非常重要的一个几何图形，它在日常生活中也有着广泛的应用。

在数学中，我们经常需要计算圆的各种属性，比如周长、面积、直径、半径等。

为了更好地理解圆的计算公式，本文将介绍一些常见的计算公式，并且给出相关的推导过程和例题。

1. 圆的周长计算公式。

圆的周长是指圆的边界的长度，通常用C表示。

圆的周长计算公式为：C = 2πr。

其中，r表示圆的半径，π是一个数学常数，约为3.14159。

推导过程，圆的周长可以看作是圆的直径乘以π，而直径是半径的两倍，因此圆的周长就是2πr。

例题，如果一个圆的半径为5cm，那么它的周长是多少？解，根据圆的周长计算公式，C = 2πr，代入r=5，得到C = 2π5 = 10π≈31.42cm。

2. 圆的面积计算公式。

圆的面积是指圆内部的区域的大小，通常用A表示。

圆的面积计算公式为：A = πr²。

推导过程，圆的面积可以看作是圆的半径的平方乘以π，因此圆的面积就是πr²。

例题，如果一个圆的半径为6cm，那么它的面积是多少？解，根据圆的面积计算公式，A = πr²，代入r=6，得到A = π6² = 36π≈113.1cm²。

3. 圆的直径计算公式。

圆的直径是指圆的边界通过圆心的两个点之间的距离，通常用d表示。

圆的直径计算公式为：d = 2r。

其中，r表示圆的半径。

推导过程，圆的直径是圆的半径的两倍，因此圆的直径就是2r。

例题，如果一个圆的直径为10cm，那么它的半径是多少？解，根据圆的直径计算公式，d = 2r，代入d=10，得到10 = 2r，解得r = 5。

4. 圆的周长和面积的关系。

通过上面的介绍，我们知道了圆的周长和面积的计算公式，现在我们来看一下它们之间的关系。

假设一个圆的周长为C，半径为r，面积为A，那么有以下关系：C = 2πr。

A = πr²。

可以看出，圆的周长和面积都与圆的半径r有关，而且都包含了π这个常数。

面积周长体积公式大全一、面积的概念及公式面积是指一个二维图形所覆盖的表面大小。

通常用单位面积（如平方米、平方厘米）来表示。

不同的几何图形有不同的计算公式。

1.矩形的面积公式:矩形是一个有四个直角的四边形，其对边互相平行且相等。

矩形的面积等于它的长度与宽度的乘积。

公式为：面积=长×宽。

2.正方形的面积公式:正方形是一个四边形，其四个边相等且都是直角。

正方形的面积等于边长的平方。

公式为：面积=边长×边长，或面积=边长²。

3.三角形的面积公式:三角形是一个有三条边和三个内角的图形，根据边和高的关系，有不同的计算公式。

-使用底和高计算三角形的面积：面积=1/2×底×高。

-使用三边计算三角形的面积：根据海伦公式，面积=√[s(s-a)(s-b)(s-c)]，其中s是三角形的半周长，a、b、c是三角形的三边。

4.圆的面积公式:圆是一个平面上的图形，其上任意两点之间的距离都相等。

圆的面积等于半径的平方乘以π。

公式为：面积=半径²×π，或面积=径²×π。

二、周长的概念及公式周长是指一个图形的边界长度，通常用单位长度（如米、厘米）来表示。

几何图形的周长与图形的形状有关。

1.矩形的周长公式:矩形的周长等于两个长度与两个宽度的和。

公式为：周长=2×(长度+宽度)。

2.正方形的周长公式:正方形的周长等于四个边长的和。

公式为：周长=4×边长。

3.三角形的周长公式:三角形的周长等于三个边长的和。

公式为：周长=边1+边2+边34.圆的周长公式:圆的周长也被称为圆周长或弧长，等于圆的半径乘以2再乘以π。

公式为：周长=直径×π，或周长=2×半径×π。

三、体积的概念及公式体积是指立体图形所包围的空间大小，通常用单位体积（如立方米、立方厘米）来表示。

几何图形的体积与其形状和尺寸有关。

1.长方体的体积公式:长方体是一个有六个面的立体图形，其中每一对相对面都是平行且相等的矩形。

几何图形的面积与周长计算一、面积计算1.矩形的面积：矩形的面积等于长乘以宽。

2.正方形的面积：正方形的面积等于边长的平方。

3.三角形的面积：三角形的面积等于底乘以高除以2。

4.平行四边形的面积：平行四边形的面积等于底乘以高。

5.梯形的面积：梯形的面积等于上底加下底乘以高除以2。

6.圆的面积：圆的面积等于π乘以半径的平方。

7.扇形的面积：扇形的面积等于π乘以半径的平方乘以弧度除以360度。

二、周长计算1.矩形的周长：矩形的周长等于长加宽的两倍。

2.正方形的周长：正方形的周长等于边长的四倍。

3.三角形的周长：三角形的周长等于三边之和。

4.平行四边形的周长：平行四边形的周长等于两对平行边之和的两倍。

5.梯形的周长：梯形的周长等于上底加下底加两腰的长度。

6.圆的周长：圆的周长等于2乘以π乘以半径。

7.扇形的周长：扇形的周长等于弧长加上两倍的半径。

以上就是几何图形的面积与周长计算的相关知识点，希望对你有所帮助。

习题及方法：1.习题：计算一个边长为5厘米的正方形的面积和周长。

方法：正方形的面积等于边长的平方，所以面积=5厘米 * 5厘米 = 25平方厘米。

正方形的周长等于边长的四倍，所以周长=5厘米 * 4 = 20厘米。

答案：面积=25平方厘米，周长=20厘米。

2.习题：计算一个长为8厘米，宽为4厘米的矩形的面积和周长。

方法：矩形的面积等于长乘以宽，所以面积=8厘米 * 4厘米 = 32平方厘米。

矩形的周长等于长加宽的两倍，所以周长=(8厘米 + 4厘米) * 2 = 24厘米。

答案：面积=32平方厘米，周长=24厘米。

3.习题：计算一个底为6厘米，高为4厘米的三角形的面积和周长。

方法：三角形的面积等于底乘以高除以2，所以面积=6厘米 * 4厘米 / 2 = 12平方厘米。

三角形的周长等于三边之和，所以周长=6厘米 + 4厘米 + 5厘米 = 15厘米。

答案：面积=12平方厘米，周长=15厘米。

4.习题：计算一个底为10厘米，高为5厘米的梯形的面积和周长。

几何体的周长面积体积公式大全几何体是指在三维空间中存在的由点、线、面组成的实体。

常见的几何体包括圆、矩形、正方形、三角形、圆柱体、圆锥体、球体等。

每个几何体都有其特定的性质，如周长、面积和体积等。

下面是关于常见几何体的周长、面积和体积公式的详细解析：1. 圆（Circles）：周长公式：C=2πr，其中r为半径。

面积公式：A=πr²，其中r为半径。

2. 矩形（Rectangle）：周长公式：C=2(a+b)，其中a和b为矩形的两条边长。

面积公式：A = ab，其中a和b为矩形的两条边长。

3. 正方形（Square）：周长公式：C=4s，其中s为正方形的边长。

面积公式：A=s²，其中s为正方形的边长。

4. 三角形（Triangle）：周长公式：C=a+b+c，其中a、b和c为三角形的三条边长。

面积公式：A = 0.5bh，其中b为三角形的底边长，h为对应的高。

5. 圆柱体（Cylinder）：侧面积公式：A = 2πrh，其中r为圆柱体的底圆半径，h为圆柱体的高。

底面积公式：B=πr²，其中r为圆柱体的底圆半径。

体积公式：V=Bh=πr²h，其中B为底面积，h为圆柱体的高。

6. 圆锥体（Cone）：侧面积公式：A = πrl，其中r为圆锥体的底圆半径，l为圆锥体的斜边。

底面积公式：B=πr²，其中r为圆锥体的底圆半径。

体积公式：V=(1/3)Bh=(1/3)πr²h，其中B为底面积，h为圆锥体的高。

7. 球体（Sphere）：表面积公式：A=4πr²，其中r为球体的半径。

体积公式：V=(4/3)πr³，其中r为球体的半径。

除了上述几何体，还有其他复杂的几何体，如棱柱体、棱锥体和多面体等。

它们的周长、面积和体积公式相对复杂，需要根据具体几何体的形状来计算。

总结起来，了解几何体的周长、面积和体积公式对于解决与几何相关的问题非常重要。