第五章 三维实体网格划分
- 格式：doc
- 大小：509.00 KB
- 文档页数：14
下载文档原格式
合集下载
hyperworks有限元仿真-第5章_1D网格划分
hyperworks有限元仿真-第5章_1D⽹格划分V1D⽹格划分本章介绍“Practical Finite Element Analysis”⼀书中的部分内容。
Matthias Goelke审查了本⽂并添加了部分内容。
5.1 何时使⽤1D单元某⼀维度的尺⼨相⽐另外两个维度⼤很多：单元形状–线⽤户提供的数据–剩下两个维度的尺⼨，截⾯积单元类型–⼆⼒杆、杆、梁、管、轴对称壳等实际应⽤–长轴、梁、销连接、连接单元5.2 刚度矩阵推导什么是刚度以及为什么我们在FEA中需要它？刚度‘K’定义为⼒/长度（单位N/mm）。
物理意义–刚度等于产⽣单位位移所需要的⼒。
刚度取决于⼏何形状以及材料属性。
铸铁低碳钢铝考虑3个⼏何尺⼨完全相同的⼆⼒杆–铸铁、低碳钢和铝。
如果我们测量产⽣1mm位移所需要的⼒，铸铁需要的⼒最⼤，然后依次是低碳钢和铝，即KCI > KMS > KAl。
低碳钢低碳钢低碳钢现在考虑3个相同材料不同截⾯的⼆⼒杆。
同样，产⽣单位位移所需要的⼒是不同的。
所以，刚度不仅依赖于材料，也依赖于⼏何形状。
刚度矩阵的重要性- 对于结构分析，刚度是⼀个⾮常重要的属性。
线性静态分析的⽅程是[F] = [K] [D]。
⼒通常是已知的，位移是未知的，⽽刚度是单元的特有属性。
这就意味着如果我们⽤公式表达⼀个给定形状的刚度矩阵，⽐如线、四边形或者四⾯体，那我们就可以通过⽹格划分来表达任何⼏何形状并使⽤⽅程F = K D求解。
公式表达刚度矩阵的⽅法：1) 直接法2) 变分法3) 加权残值法直接法很容易理解，但是很难⽤电脑程序表达。
⽽变分法和加权残值法很难理解，但是从编程的⾓度来说很简单。
这就是为什么所有的软件要么使⽤变分法，要么使⽤加权残值法。
直接法推导⼆⼒杆单元的刚度矩阵：直接法推导刚度矩阵的⽅法：对于⼀个给定的单元，假设有n个⾃由度（⽐如，⼀个quad4单元的所有⾃由度= 4*6 = 24）。
步骤1）假设第⼀个⾃由度≠ 0，并且其它所有⾃由度= 0。
三维实体网格模流分析介绍及应用(转载)
三维实体网格模流分析介绍及应用(台湾)科盛科技股份公司张政亿刘文斌摘要：由于塑料射出产品大多为薄壳产品，因此在模流分析上多使用薄壳模型(shell model)并指定厚度；或用STL格式模型，再依薄壳理论分析之。
但由于薄壳理论的简化太多，在先天有诸多的限制，无法完全仿真塑料流动上的的所有现象;再加上部份的塑料件实为粗厚件，其厚度已超出薄壳理论的范围，且网格厚度定义不易，种种的误差累积可能会使分析结果的参考性变低。
新一代的三维模流分析技术，使用三度空间的实体元素，不需做任何厚度的假设；再加上统御方程式不做任何的减化。
可忠实的表现出所有塑料流动上的现象，其参考性也大为提高。
本文即藉由Moldex3D以及数个实际案例来说明三维模流分析技术的优异性能。
关键词 : 三维模流分析、Moldex3D、shell model、薄壳理论一、案例因为使用实际3D理论来求解，因此对于塑料射出的应用不再局限于薄壳件，应用的范围更为广泛，且所得到的结果更为准确，在此列举连结器─如图1及图2所示、手机上盖─如图3及图4所示的实际短射与Moldex3D分析结果比较以供参考。
下文中并将列举不同案例以说明3D模流分析在实际产品上的应用。
图1、连接器产品模流分析与短射样品比较图2、连接器产品模流分析与短射样品比较图3、手机外壳产品模流分析与短射样品比较图4、手机外壳产品模流分析与短射样品比较A.喷流现象非薄壳件的一个常见的流动现象为喷流(jetting)，通常这种现象会在成品表面留下皱折的痕迹。
以薄壳理论为基础的mid-plane及STL 网格对于这种肇因于厚件及高射速的流动现象均无法做正确的仿真。
本案例的几何如图5; 一模四穴含流道的体积约为635c.c.，充填时间为5秒，每一穴的每秒流率约为32c.c.，对一般射出而言并不算高速，但因为本案例几何造形不属于薄壳件，如此射速已足以让熔胶突出模壁表面，依此即可预测此处将有熔胶皱折的喷流现象产生。
第5章网格划分讲述介绍
5.1 网格的类型
Moldflow是注塑新产品成型仿真及分析的软件，其基本核心的思 想是有限元的方法。也可以这样说，有限元方法就是利用假想的 线或面将连续介质的内部和边界分割成有限数量的、有限大小的 单元体来处理。这样一来，把一个连续的相对大的整体简化成有 限个小的单元体，从而得到与真实结构相近的模型。在数值计算 和处理就是在这些小的单元体的模型上进行的。为了便于直观， 在Moldflow，将这些单元叫做网格（mesh）。
5.4 本章小结
本章主要介绍了在Moldflow中网格的三种类型、创建一个工程、 网格如何划分、网格的状态统计以及网格统计作息的意义和注意 点。本章学习的重点和难点是三种网格的应用范围、网格的划分、 网格统计信息的意义能力， 明辨是非的能力。 所以我们要勤恳读书，广泛阅读， 古人说“书中自有黄金屋。 ”通过阅读科技书籍，我们能丰富知识， 培养逻辑思维能力； 通过阅读文学作品，我们能提高文学鉴赏水平， 培养文学情趣； 通过阅读报刊，我们能增长见识，扩大自己的知识面。 有许多书籍还能培养我们的道德情操， 给我们巨大的精神力量， 鼓舞我们前进。
第5章 网格划分
Moldflow采用的是有限元的分析技术，它模拟塑料注塑成型过程 的充填、保压和冷却。它预测塑料熔体在流道、浇口和型腔中的 流动、冷却以及可能将要发生的缺陷。它可以优化浇口位置、数 量，优化注塑成型工艺参数。它可以发现可能发生的一些制品的 缺陷。本章主要讲Moldflow中模型网格的一些基本知识和如何划 分网格，为Moldflow的分析打下基础。
5.1.3 表面网格
表面网格（Fusion）与中面网格（Midplane）不同。它是创建在模 型的外表面上的，也是由三个节点组成的三角形单元形成的网格。 其优缺点介于实体网格（3D）与中面网格（Midplane）之间。图 5.3是删除一个表面网格中的一个三角形单元后看到的情况。此类 网格形成在模型的外表面，是由三角形单元组成的。
第五章ANSYS优化设计
第五章ANSYS 优化设计拓扑优化拓扑优化是指形状优化，也称为外形优化，其目的是寻找载荷作用下的物体最佳材料分配方案，最大刚度设计。
拓扑优化的原理是在满足结构体积缩减量的条件下使结构的柔度极小化。
极小化的结构柔度实际就是要求结构的刚度最大化。
ANSYS提供的拓扑优化技术用于确定系统的最佳几何形状，其原理是系统材料发挥最大利用率，同时确保诸如整体刚度、自振频率等在满足工程要求的条件下获得极大或极小值。
优化参数：不需要人工定义优化参数，而是自动将材料分布当作优化参数。
目标函数：是在满足给定的实际约束条件下（如体积减小等）需要极大或极小化的参数，通常采用的目标函数是结构柔量能量(the energy of structure compliance)极小化和基频最大等。
支持的单元类型：二维实体单元：PLANE2、PLANE82，用于平面应力或轴对称问题；三维实体单元：SOLID92、SOLID95；壳单元：SHELL93。
特别提醒：1、ANSYS程序只对单元类型编号等于1的单元部分进行拓扑优化，对于单元类型编号等于或大于2的单元网格不进行拓扑优化。
2、（1）拓扑优化只能基于线性结构静力分析或模态分析，其它分析类型暂时还不支持。
（2）ANSYS实际提供的拓扑优化为基于线性结构静力分析的最大静态刚度拓扑优化设计和基于模态分析的最大动态刚度优化设计，同时需要达到体积最小化目的。
（3）采用单载荷步或多载荷步的线性结构静力分析时，施加相应的载荷和边界条件。
采用模态频率分析，仅仅施加边界条件。
3、拓扑优化的结果对网格划分密度非常敏感，较细密的网格可以产生更加清晰、确定的拓扑结果，但计算会随着单元规模的增加而需要更多的收敛时间；相反，较粗的网格会生成模糊、不确定的拓扑结果。
另外，拓扑优化结果对载荷情况十分敏感，有时很小的载荷变化将导致拓扑优化结果的巨大差异。
优化设计1． 简介举例：如何在原材料消耗最少情况下，使水杯的容积最大。
3维实体ansys应力分析中的单元选择和网格划分
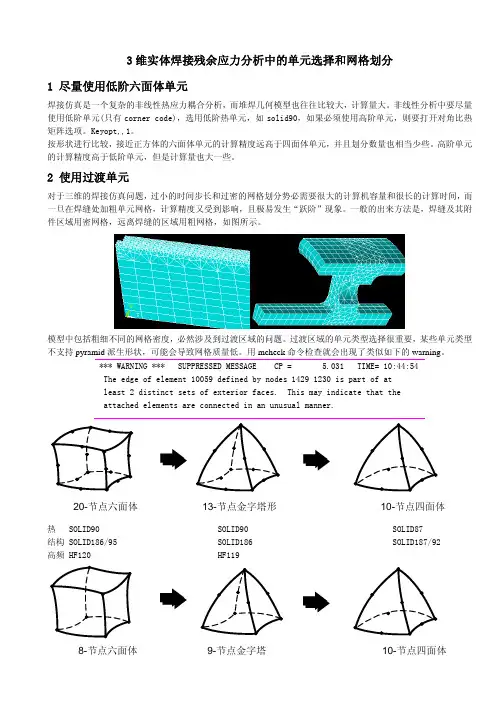
3维实体焊接残余应力分析中的单元选择和网格划分1 尽量使用低阶六面体单元焊接仿真是一个复杂的非线性热应力耦合分析，而堆焊几何模型也往往比较大，计算量大。
非线性分析中要尽量使用低阶单元(只有corner code)，选用低阶热单元，如solid90，如果必须使用高阶单元，则要打开对角比热矩阵选项。
Keyopt,,1。
按形状进行比较，接近正方体的六面体单元的计算精度远高于四面体单元，并且划分数量也相当少些。
高阶单元的计算精度高于低阶单元，但是计算量也大一些。
2 使用过渡单元对于三维的焊接仿真问题，过小的时间步长和过密的网格划分势必需要很大的计算机容量和很长的计算时间，而一旦在焊缝处加粗单元网格，计算精度又受到影响，且极易发生“跃阶”现象。
一般的出来方法是，焊缝及其附件区域用密网格，远离焊缝的区域用粗网格，如图所示。
模型中包括粗细不同的网格密度，必然涉及到过渡区域的问题。
过渡区域的单元类型选择很重要，某些单元类型不支持pyramid 派生形状，可能会导致网格质量低。
用mcheck 命令检查就会出现了类似如下的warning 。
*** WARNING *** SUPPRESSED MESSAGE CP = 5.031 TIME= 10:44:54 The edge of element 10059 defined by nodes 1429 1230 is part of at least 2 distinct sets of exterior faces. This may indicate that the attached elements are connected in an unusual manner.热 SOLID90 SOLID90 SOLID87 结构 SOLID186/95 SOLID186 SOLID187/92 高频 HF120 HF11910-节点四面体13-节点金字塔形20-节点六面体8-节点六面体9-节点金字塔 10-节点四面体热 SOLID70 SOLID90 SOLID87结构 SOLID185/45 SOLID186 SOLID187/92过渡单元： 热SOLID90 结构SOLID186 （一般不选用一阶六面体单元作为过渡单元）自由网格往往数量多质量差，映射网格却不容易实现。
三维网格分割--基础知识
三维网格分割经典聚类算法
模糊聚类分割算法：2003 年，Katz 等人提出了模糊聚类的层次分解算法，将 复杂模型进行由粗到精，得到分割片层次树，一层一层的处理，最终分割成边 界线平滑、有意义的若干个较为简单的部分。层次树的根表示整个网络模型 S。 在每个节点，首先确定需要进一步分割为更精细分割片的数目，然后执行个Kway 分割。优点：该算法可以得到有意义的部分子模型，且没有出现锯齿现象， 算法也不会产生过分分割效果。
W
F 2,1
N2 j 1
W , j 表示表示的第j个列向量W，
,h , j W WW h X h2
Xh
2 F
WhTWh
1,1
三维网格分割组合分割-亲和力聚合谱聚类
亲和力聚合谱聚类（AASC）：寻求描述网格过分割面片多特征融合的亲和矩 阵，利用谱聚类算法对所有补丁块进行一致分割。
分割准 则
三维网格分割及其相关基本概念
表面测地线距离：是指三维模型的两个顶点在模型表面的最短距离，它不仅可以有 效的克服三维模型噪声的干扰，而且与三维模型的坐标系方向无关。但不易计算， 常用特征描述之间的欧氏距离代替。
欧几里德距离：两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离：
亲和力聚合谱聚类实现过程：
谱聚类划分数据到m个互不相交的类，寻找索引向量F f1, f2 , , fn ,满足
min W
f1 , , fn i, j
kij
fi , f j
2
F D W F
s.t. F DF 1 利用Lu Du = 1,2 , 令亲和矩阵相关权值为
5.2.3D网格的划分
3D网格的划分例一，这个例子主要讲的是模型的拆分技巧和方法，以及一些划分3D网格的方法。
在一般情况下都要讲模型进行拆分，否则是不能进行划分的。
1，划分网格前个几何整理1，调入几何模型，qtrpisp.igs，如下图2，点击Geom页面下的lines面板3，进入create line字面板，作如下的一条直线4，点击return，退出这个面板5，点击Geom页面下的surface edit面板6，进入trim with line子面板，点击黄色的surf键选择下图中的三个面7，点击黄色的lines键，选择刚刚制作的那条线8，在sweep trim lines下面的指针中选择，along a vector9，在to trim through下面的指针中选择entire surface10，在下面的选择集中选择，z-axis，点击trim，结果如下在选择的三个面中出现绿色的线，这三个面被拆分11，同样在这个子面板中，surfs选择下图中的面，12，点击黄色的lines，选择下图中的线结果如下13，仍然在trim with lines 子面板中，surfs选择下图中的面线选择下图中的线，在sweep trim lines下面的指针中选择norm to surface点击trim，结果如下。
14，用同样的方法，将下面的面切开，过程和结果如下。
15，点击进入surface edit面板下面的trim with nodes子面板，分割如下的面点击两个端点，结果如下2，开始划分网格1，点击进入collcetors面板，创建以下几个compShell_1,shell_2,shell_3,shell_4,solid_1solid_2,solid_3,solid_4,分别赋予相应的颜色1，1对下面的划分有两种方法，下面是第一种方法1，点击进入2D页面下的automesh，面板2，进入create mesh子面板，在旁边的选择集中选择surf，点击下图中的面点击mesh，3，在elements size=后面的输入框中，输入2.5，点击左边的reclae all，点击mesh 4，点击图中的中子数，左键点击为加，右键点击为减，结果如下图5，点击return，形成网格1．2划分的第二种方法1，点击进入永久菜单中的global面板，使shell_1成为当前comp2，点击进入Geom 页面下的surface edet面板3，进入trim with nodes子面板，将曲面分成如下的三部分4，点击进入2D页面下的spline面板，使用mesh ，w/o，surf，创建如下的网格（如果一边的种子点很少，一边很多的话，就用鼠标左键按住种子点向上拖是增加，向下拖是减少）划分完之后比较两者的优劣（以下接第二种方法）6，点击进入Geom页面下的distance面板，测量一下图中的线的距离图中的线的距离为7.57，点击永久菜单中的global面板，在element size=后面的输入框中输入2，点击return 退出这个面板8，点击Geom页面下的geom cleanup面板，在左边的子面板中选edges，在下面的三个子面板中选则toggele，（大家也可以试试跳过这一步，看看结果）9，点击途中的两条线，这两条线变成蓝色，被抑制10，使solid_1为当前的comp11，点击3D页面下的solid map面板12，在source geom.的选择集中选在surf，点击网格所在的面13，在destination geom.的选择集中选择lines，点击图中的几条线，along geom选择none，elem选择shell_1的网格14，点击mesh结果如下15，点击这个面板右下角的equiv/faces键，结果如下16，点击disp观察生成的faces comp17，点击organize面板，选择底面上的网格，移到shell_2中18，删掉faces这个comp结果如下19，进入3D页面下的solid map面板，在source geom.的选择集中选择包围shell_2的几条边线，在destination geom.的选择集中选择底面，along geom.选择none，elems 选择shell_2，在density=后面的输入框中输入5，生成如下的网格（设置也如下图）20，删掉shell_2 的网格，但不要删掉shell_2这个comp21，使shell_2成为当前的comp，创建如下的网格21，创建网格，当前comp为shell_3，如下图22，点击进入3D面板中的solid map面板，创建如下的网格23.1在下图的面上创建如下的网格（从这步起可以有两种方法）方法一2，点击3D页面下的spin面板3，进入spin elems子面板，选择刚才创建的elems4，在下面的方向选择器中，选择y-axis，base点选择外圆的圆心点，在angle后面的输入框中输入90，on spin=后面的输入框中输入26，点击spin+，结果如下图可以使用line drag，方法如下：1，点击3D面板下面的line drag面板，进入drag elems子面板，drag后面的elems按键高亮，选择shell_42，点击along旁边的line list按键，选择一条圆周线，如下图在on drag=后面的输入框中输入26，点击drag，如果如下这两种方法虽然可以做出来网格，但是在圆心的部分的网格的质量很差，如下图所以在圆心的部分不用这样的方法，看另外一种方法。
三维实体网格自适应划分算法_张文明
(x1, y1) ， (x2 , y2 ) ，则新节点Nn的位置为
⎧⎪xn = (x1 + x2 ) 2 ∓ L2e − (l1 2)2 ( y2 − y1) l1 ⎨
(9)
⎪⎩ yn = ( y1 + y2 ) 2 ∓ L2e − (l1 2)2 (x2 − x1) l1
式中 l1 = (x2 − x1)2 + ( y2 − y1)2 ，(xn , yn ) 有两个解， 位于B的两侧，选取位于同一侧的解。将以上坐标 变换至三维空间，便形成了一新的节点，对新节点 Delaunay三角化，又形成新的Delaunay三角单元， 采用上述方法循环交替，便可实现对三维实体每一 个平面进行剖分。平面上生成的节点即为三维实体 平面边界的节点集。
Abstract：The high grade grid division is the key of the three dimensional modeling research. Based on analysis to the three dimensional geometry and the physical characteristics, a three dimensional grid division encryption rule is introduced. Through the research of grid refinement region and the grid node algorithm, a dynamic node unit integration three dimensional grid adaptive division algorithm is designed on the basis of on Delaunay triangulation. With the preprocessing of the object, the nodes are optimized by using Delaunay triangulation and characteristic centralized region is refined locally. Compared with traditional method, this algorithm has obvious superiority in computation and accuracy. Through grid division to the machine parts and optimized grid density distribution, the results can accurately describe the three dimensional entity geometrical physique characteristic and the physical characteristic distribution. Experiment verifies the validity of this method, thus providing the basic guarantee to more in-depth researches of entity characters. Key words：Three dimensional entity Adaptive Local mesh refinement Mesh generation
三维网格分割的经典方法
三维网格分割的经典方法摘要：本文针对三维网格分割问题，提出一个经典的方法。
该方法基于微分几何和测地距离。
在算法中，将面片类型相同的顶点分割在一起。
测地距离利用顶点之间的最短路径表示，这里可以利用一些经典的算法求最短路径，如Dijkstra 算法。
但是当网格的数量很多时，Dijkstra 算法的效率很低。
因此，此算法避免了在整个网格上应用最短路径算法，在局部网格中求最短路径，从而减少了计算量。
本文在人造物体的三维网格模型以及分子结构中验证了该方法的有效性。
关键字：几何算法 面片分割 测地距离简介3D 物体的三维网格表示法具有很多的应用。
例如，在图像分析中，表示利用深度图像重建的物体表面。
此外，在复杂物体和场景的建模和可视化中也有广泛的应用。
在网格面片的分析中，网格分割已经成为一个关注的问题。
网格分割也就是将网格上相互接近并且具有相似曲率的顶点分成一组。
网格分割在很多方面具有重要的应用。
特征提取，模型匹配等。
Mangan 和Whitaker 提出三维网格分割的分水岭算法。
Razdan 和Bae 扩展了此算法，将基于点元（voxel-based ）和分水岭算法相结合，来分割三角网格。
这两种方法在分割中都需要计算整个曲率，然后在局部曲率最小处建立初始分割。
然而，在某些物体中，局部曲率的最小值是很难确定的。
因此，在这里提出一个初始分割的新方法。
在该算法中，应用基于面片的类型信息的网格区域增长方法，对顶点进行初始分割。
利用高斯曲率和平均曲率对顶点所在的面片进行分类。
这里利用离散微分几何计算高斯曲率和平均曲率。
通过本文提出的新方法来求得测地距离。
文章结构：第二部分，介绍网格面片的曲率分析和面片分类。
第三部分，详述本文的分割算法。
第四部分，实验以及其分割结果。
第五部分，结论。
2 面片分析在面片分析中，首先计算高斯曲率和平均曲率，然后利用它们进行面片分类。
顶点P 0的高斯曲率K 的计算公式如下：，A K θρ∆= ，∑-=∆i i 2θπθ ∑=ii A A ， A 为相邻三角形T i ( i =1，2，3，…)的面积总和。
三维网格分割--基础知识汇总
特征描述符：用来描述图形几何特征的符号。如高斯曲率（GC）、外直径特征函 数（SDF）、平均测地距离（AGD）、保角因子（CF）、图形文脉（SC），其中 GC、AGD和CF描述三维网格的外部特征，而SDF和SC描述三维网格的内部特征。
刚性：物体外部形状不随着移动等外界因素发生变化（如平移、旋转） 非刚性：物体会在外界因素的影响下形状发生变化（如缩放） 鲁棒性（robustness）：即稳健性，表征控制系统对特性或参数摄动的不敏感性。
区均域值生漂长移法(：MS选)：定通不过同迭区代域搜的索种特子征元空素间（中如样顶本点点、最三密角集曲的面区片域信，息搜等索）点，沿然 后着在样种本子点区密域度的增周加围的根方据向一漂定移的到生局长部规密则度进最行大区点域。生优长点，：直该到方覆法盖完整全个依区靠域 为特止征。空优间点中：的思样想本简点单进，行实分现析速，度无快需；先缺验点知：识易，产收生敛过速分度割快。。
H
min F Wh Pcons W1,W2, ,WH
W1 , ,WH h1
s.t. Wh 0 diag Wh 0, h 1, 2, , H
其中：Pcons W1,W 2,
,WH
W W
2,1
1,1
单特征组合分 割W：1 求11解亲W和1矩1阵2 可转化为W如1 下N 2优化问 题：
三维网格分割及其相关基本概念
相似性
度量 分
割
的
特征选
一 般
择
分割算 法选取
过
程
结果验 证
分割准 则
三维网格分割及其相关基本概念
表面测地线距离：是指三维模型的两个顶点在模型表面的最短距离，它不仅可以有
效的克服三维模型噪声的干扰，而且与三维模型的坐标系方向无关。但不易计算， 常用特征描述之间的欧氏距离代替。
刚性：物体外部形状不随着移动等外界因素发生变化（如平移、旋转） 非刚性：物体会在外界因素的影响下形状发生变化（如缩放） 鲁棒性（robustness）：即稳健性，表征控制系统对特性或参数摄动的不敏感性。
区均域值生漂长移法(：MS选)：定通不过同迭区代域搜的索种特子征元空素间（中如样顶本点点、最三密角集曲的面区片域信，息搜等索）点，沿然 后着在样种本子点区密域度的增周加围的根方据向一漂定移的到生局长部规密则度进最行大区点域。生优长点，：直该到方覆法盖完整全个依区靠域 为特止征。空优间点中：的思样想本简点单进，行实分现析速，度无快需；先缺验点知：识易，产收生敛过速分度割快。。
H
min F Wh Pcons W1,W2, ,WH
W1 , ,WH h1
s.t. Wh 0 diag Wh 0, h 1, 2, , H
其中：Pcons W1,W 2,
,WH
W W
2,1
1,1
单特征组合分 割W：1 求11解亲W和1矩1阵2 可转化为W如1 下N 2优化问 题：
三维网格分割及其相关基本概念
相似性
度量 分
割
的
特征选
一 般
择
分割算 法选取
过
程
结果验 证
分割准 则
三维网格分割及其相关基本概念
表面测地线距离：是指三维模型的两个顶点在模型表面的最短距离，它不仅可以有
效的克服三维模型噪声的干扰，而且与三维模型的坐标系方向无关。但不易计算， 常用特征描述之间的欧氏距离代替。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五章三维实体网格划分本章讲述三维实体网格划分。
包括三部分内容：●生成四面体网格零件：对实体指定线性或者2次四面体网格。
●四面体网格填充器：通过从曲面网格生成四面体网格来对实体划分网格。
●扫描实体网格：通过从曲面网格生成六面体或者楔形网格对实体划分网格。
5．1 生成3D零件网格本节说明如何使用四面体网格划分方法生成3D网格。
在【Generative Structural Analysis】（通用结构分析）工作台和【Advanced Meshing Tools】（高级网格划分工具）工作台都有本命令。
根据用户安装的产品不同，显示的选项是不同的：●【Generative Structural Analysis】（通用结构分析）或者【FEM Surface】（曲面网格划分）系列产品。
●【FEM Solid】（有限元实体划分）系列产品。
5.1.1 【Generative Structural Analysis】（通用结构分析）或者【FEM Surface】（曲面网格划分）系列产品在通常的用户中，一般安装的是第一种情形。
在这种设置下，无论是在通用结构分析工作台还是高级划分工具工作台，定义3D网格的零件时，弹出的对话框只有两个选项卡。
（1）点击【Meshing Methods】（网格划分方法）工具栏内的【Octree Tetrahedron Mesher】（四面体网格划分器）按钮，如图5－1所示。
如果用户在【Generative Structural Analysis】（通用结构分析）工作台，则需要点击【Model Manager】工具栏内的【Octree Tetrahedron Mesher】（四面体网格划分器）按钮，如图5－2所示。
图5－1【Octree Tetrahedron Mesher】（四面体网格划分器）按钮图5－2（2）在图形区选择要划分网格的实体零件。
选择后弹出【OCTREE Tetrahedron Mesh】（四面体网格划分器）对话框，如图5－3所示。
注意！只能选择属于【PartBody】下的元素。
●【Global】选项卡：可以修改网格全局参数。
●【Local】选项卡：创建局部网格参数。
（3）在对话框的选项内输入相应的数值。
在本例中，在【Size】（尺寸）数值栏内输入20mm。
（4）点击对话框内的【确定】按钮，生成新的网格零件，并且在模型树上显示出新的网格零件名称，如图5－4所示。
图5－3【OCTREE Tetrahedron Mesh】（四面体网格划分器）对话框图5－4模型树上显示出新的网格零件名称注意！3D网格可以手动删除或者添加。
5.1.2【FEM Solid】（有限元实体划分）系列产品下面说明安装【FEM Solid】（有限元实体划分）系列产品时的情况。
在这种设置下，无论是在通用结构分析工作台还是高级划分工具工作台，定义3D网格的零件时，弹出的对话框有4个选项卡。
（1）点击【Meshing Methods】（网格划分方法）工具栏内的【Octree Tetrahedron Mesher】（四面体网格划分器）按钮。
如果用户在【Generative Structural Analysis】（通用结构分析）工作台，则需要点击【Model Manager】工具栏内的【Octree TetrahedronMesher】（四面体网格划分器）按钮。
（2）在图形区选择要划分网格的实体零件。
选择后弹出【OCTREE Tetrahedron Mesh】（四面体网格划分器）对话框，如图5－5所示。
注意！只能选择属于【PartBody】下的元素。
●【Global】选项卡：可以修改网格全局参数。
⏹【Size】（网格尺寸）：允许用户定义网格的尺寸（以mm为单位）。
⏹【Absolute sag】绝对垂度：网格和几何图形之间的最大间隙，如图5－6所示。
图5－5【OCTREE Tetrahedron Mesh】（四面体网格划分器）对话框图5－6绝对垂度示意图⏹【Proportional sag】比例垂度：局部绝对垂度与局部网格长度的比例。
比例垂度值＝局部绝对垂度值/局部网格棱边长度值注意！绝对垂度和比例垂度可以修改局部网格棱边长度值。
用户可以使用绝对垂度和比例垂度两个值，在实际应用中，程序采用两个数字中约束严格的一个值。
⏹【Element type】单元类型：允许用户选择单元的类型（Linear线性单元，或者Parabolic二次单元）●【Local】局部选项卡用户可以添加局部网格参数，例如垂度、尺寸或者在零件上的分布参数。
为了添加局部参数，先在【A vail abl e specs】（可使用的特定参数栏）点击选择希望添加的参数，如图5－7所示，然后点击【A dd】（添加）按钮。
⏹【Local size】（局部尺寸）：用户可以修改名称、支承和数值，如图5－8所示。
图5－7【A vailable specs】（可使用的特定参数栏）内的选项图5－8【Local Mesh size】（局部网格尺寸）对话框⏹【Local sag】（局部垂度）：用户可以修改名称、支承和数值，如图5－9所示。
⏹【Edges distribution】（棱边上的分布）：允许用户定义在某一特定棱边上局部节点分布。
为完成该功能:选择【Edges di stri buti on】（棱边上的分布）选项，然后点击【Add】（添加）按钮。
弹出【Edges di stri bution】（棱边上的分布）对话框，如图5－10所示。
图5－9【Local Mesh sag】（局部网格垂度）对话框图5－10【Edges di stributi on】（棱边上的分布）对话框在图形区选择指定节点分布的棱边，然后输入要分割的棱边数量。
【Edges Di stri buti on.1】特征出现在模型树上，同时所选择棱边上出现节点，如图5－11所示。
点击【Local Mesh Distribution】局部网格分布对话框内的【确定】按钮。
⏹【Imposed points】强制点：允许用户选择一些点，在划分网格时强制考虑这些选择的点。
注意！在此种情况下，用户选择的点必须是在形状设计工作台或者零件工作台创建的点。
只有在曲线上或者曲面上的点，才能够选择使用。
点所在的支承元素必须是所划分的几何的一部分。
为完成该功能:选择【Local imposed points】局部强制加点选项，然后点击【Add】（添加）按钮。
弹出【Imposed Points】强制点对话框，如图5－12所示。
图5－11选择棱边上出现节点图5－12【Imposed Points】强制点对话框从模型树（在Open B ody组下面）选择点，作为划分网格上强制添加的点。
点击【Imposed Points】强制点对话框内的【确定】按钮。
为了编辑已经创建的局部网格分布，用户需要双击模型树上的【Local Nodes Di stributi on】对象，然后从弹出的【Local Mesh Distribution】（局部网格分布）对话框中修改参数。
●【Quality】（质量）选项卡⏹【Criteria】（标注）：允许用户选择一个标准（Shape形状、Skewness偏斜度、Strech伸展）⏹【Intermediate nodes parameters】（中间节点参数）：只有在选择【Paraboli c】（二次）网格时，才可以使用本选项。
该选项允许用户选择二次网格中间节点的位置（Jacobian雅可比，Warp翘曲）。
几何图形和中间节点之间的距离值是雅可比值或者是翘曲值。
图5－13【Quality】（质量）选项卡显示内容图5－14 几何图形和中间节点之间的距离值●【Others】（其它）选项卡：图5－15 【Others】（其它）选项卡显示内容⏹【Details simplification】（简化的细节）：允许用户移除小的网格。
⏹【Geometry size limit】（几何尺寸限值）：允许用户指定由网格划分器忽略的最大单元尺寸值。
注意！如果所有曲面的棱边都小于几何尺寸限值，该曲面将被划分器忽略。
⏹【Mesh edges suppression】（网格棱边抑制）：移除小的棱边（在划分网格之后）没有网格棱边抑制采用网格棱边抑制图5－16 不采用和采用网格棱边抑制的比较注意！有时会发生网格棱边抑制导致违背约束条件。
⏹【Global interior size:】（全局内部尺寸）：允许用户指定网格最大内部尺寸。
注意！如果全局内部尺寸小于在【Si ze】（尺寸）栏定义的数值，【Si ze】（尺寸）栏的数值将降低到全局内部尺寸值。
⏹【Min. size for sag specs】（指定垂度的最小值）：允许用户指定由于垂度指定值产生的网格优化中的最小网格尺寸。
⏹【Max. number of attempts】（最多尝试次数）：对于复杂的几何形状，如果在划分网格时，需要进行多次尝试，允许用户强制指定一个最多尝试次数。
1.选择需要的参数。
在本例题中，保留默认的参数。
2.点击【Apply】（应用）按钮。
弹出【Computation Status】（计算状态）对话框，并在零件上生成网格。
为了更好地显示网格，可以将几何体隐藏起来。
在左边的模型树上右击【Li nks Manager.1】对象，然后在弹出的快捷菜点中选择【Hide/Show】（隐藏/显示）选项。
最终生成的网格如图5－17所示。
在模型树上出现【OCTREE Tetrahedron Mesh.1: Part.1】对象，如图5－18所示。
图5－17最终生成的网格图5－18【OCTREE Tetrahedron Mesh.1: Part.1】对象3.点击对话框内的【OK】（确定）按钮为了编辑网格模型，可以双击模型树上的【OCTREE Tetrahedron Mesh.1: Part.1】对象，双击后，弹出【OCTREE Tetrahedron Mesh】（OCTREE四面体网格）对话框。
5.2四面体网格填充器本节说明如何从表面网格创建生成四面体网格。
四面体网格过滤器从曲面网格（三角形壳单元或者四边形壳单元）创建生成体积网格（线性四面体网格或者二次四面体网格）。
本项功能必须在FEM Solid (FMD)产品下执行。
在创建实体网格前，有两个必要条件：（1）要确保曲面网格是封闭且连续的。
（2）要确保曲面网格没有交叉干涉。
用户可以使用【检查干涉】功能，先对曲面网格进行检查。
●3D网格的质量依赖于2D网格的质量。
在创建3D网格前，要确保2D网格质量是好的。
●使用本功能前，必须先有一个曲面网格。
曲面网格可以与几何形状关联，也可以不关联。