圆锥曲线全部公式及概念
- 格式:docx
- 大小:368.09 KB
- 文档页数:11

卜人入州八九几市潮王学校数学概念、方法、题型、易误点技巧总结——圆锥曲线1.圆锥曲线的两个定义:〔1〕第一定义中要重视“括号〞内的限制条件:椭圆中,与两个定点F,F的间隔的和等于常数,且此常数一定要大于,当常数等于时,轨迹是线段F F,当常数小于时,无轨迹;双曲线中,与两定点F,F的间隔的差的绝对值等于常数,且此常数一定要小于|F F|,定义中的“绝对值〞与<|F F|不可无视。
假设=|F F|,那么轨迹是以F,F为端点的两条射线,假设﹥|F F|,那么轨迹不存在。
假设去掉定义中的绝对值那么轨迹仅表示双曲线的一支。
比方:①定点,在满足以下条件的平面上动点P的轨迹中是椭圆的是A.B.C.D.〔答:C〕;②方程表示的曲线是_____〔答:双曲线的左支〕〔2〕第二定义中要注意定点和定直线是相应的焦点和准线,且“点点距为分子、点线距为分母〞,其商即是离心率。
圆锥曲线的第二定义,给出了圆锥曲线上的点到焦点间隔与此点到相应准线间隔间的关系,要擅长运用第二定义对它们进展互相转化。
如点及抛物线上一动点P〔x,y〕,那么y+|PQ|的最小值是_____〔答:2〕2.圆锥曲线的HY方程〔HY方程是指中心〔顶点〕在原点,坐标轴为对称轴时的HY位置的方程〕:〔1〕椭圆:焦点在轴上时〔〕〔参数方程,其中为参数〕,焦点在轴上时=1〔〕。
方程表示椭圆的充要条件是什么?〔ABC≠0,且A,B,C同号,A≠B〕。
比方:①方程表示椭圆,那么的取值范围为____〔答:〕;②假设,且,那么的最大值是____,的最小值是___〔答:〕〔2〕双曲线:焦点在轴上:=1,焦点在轴上:=1〔〕。
方程表示双曲线的充要条件是什么?〔ABC≠0,且A,B异号〕。
比方:①双曲线的离心率等于,且与椭圆有公一共焦点,那么该双曲线的方程_______〔答:〕;②设中心在坐标原点,焦点、在坐标轴上,离心率的双曲线C过点,那么C的方程为_______〔答:〕〔3〕抛物线:开口向右时,开口向左时,开口向上时,开口向下时。

圆锥曲线1.椭圆22221(0)x y a b a b +=>>的参数方程是cos sin x a y b θθ=⎧⎨=⎩ 离心率c e a ==准线到中心的距离为2a c ,焦点到对应准线的距离(焦准距)2b p c =. 通径的一半(焦参数):2b a.2.椭圆22221(0)x y a b a b+=>>焦半径公式及两焦半径与焦距构成三角形的面积:21()a PF e x a ex c =+=+,22()a PF e x a ex c =-=-;1221tan 2F PF F PFS b ∆∠=.3.椭圆的的内外部: (1)点00(,)P x y 在椭圆22221(0)x y a b a b +=>>的内部2200221x y a b⇔+<.(2)点00(,)P x y 在椭圆22221(0)x y a b a b +=>>的外部2200221x y a b⇔+>.4.双曲线22221(0,0)x y a b a b -=>>的离心率c e a ==2a c ,焦点到对应准线的距离(焦准距)2p c = 通径的一半(焦参数):2b a焦半径公式21|()|||a PF e x a ex c =+=+,22|()|||a PF e x a ex c=-=-,两焦半径与焦距构成三角形的面积1221cot 2F PF F PF S b ∆∠=.5.双曲线的内外部: (1)点00(,)P x y 在双曲线22221(0,0)x y a b a b -=>>的内部2200221x y a b⇔->.(2)点00(,)P x y 在双曲线22221(0,0)x y a b a b -=>>的外部2200221x y a b⇔-<.6.双曲线的方程与渐近线方程的关系:(1)若双曲线方程为12222=-b y a x ⇒渐近线方程:22220x y a b -=⇔x aby ±=.(2)若渐近线方程为x aby ±=⇔0=±b y a x ⇒双曲线可设为λ=-2222b y a x .(3)若双曲线与12222=-b y a x 有公共渐近线,可设为λ=-2222bya x(0>λ,焦点在x 轴上;0<λ,焦点在y 轴上). (4) 焦点到渐近线的距离总是b7.抛物线px y 22=的焦半径公式:抛物线22(0)y px p =>焦半径02p CF x =+. 过焦点弦长p x x p x p x CD ++=+++=212122.8.抛物线px y 22=上的动点可设为P ),2(2 y py 或2(2,2)P pt pt P (,)x y ,其中 22y px =.9.二次函数2224()24b ac b y ax bx c a x a a-=++=++(0)a ≠的图象是抛物线:(1)顶点坐标为24(,)24b ac b a a --;(2)焦点的坐标为241(,)24b ac b a a -+-;(3)准线方程是2414ac b y a--=. 10.以抛物线上的点为圆心,焦半径为半径的圆必与准线相切;以抛物线焦点弦为直径的圆,必与准线相切;以抛物线的焦半径为直径的圆必与过顶点垂直于轴的直线相切.11.直线与圆锥曲线相交的弦长公式: AB =1212||||AB x x y y ==-=-(弦端点A ),(),,(2211y x B y x ,由方程⎩⎨⎧=+=0)y ,x (F b kx y 消去y 得到02=++c bx ax ,0∆>,α为直线AB 的倾斜角,k 为直线的斜率,12||x x -=12.圆锥曲线的两类对称问题:(1)曲线(,)0F x y =关于点00(,)P x y 成中心对称的曲线是00(2-,2)0F x x y y -=. (2)曲线(,)0F x y =关于直线0Ax By C ++=成轴对称的曲线是22222()2()(,)0A Ax By C B Ax By C F x y A B A B ++++--=++.特别地,曲线(,)0F x y =关于原点O 成中心对称的曲线是(,)0F x y --=. 曲线(,)0F x y =关于直线x 轴对称的曲线是(,)0F x y -=. 曲线(,)0F x y =关于直线y 轴对称的曲线是(,)0F x y -=. 曲线(,)0F x y =关于直线y x =轴对称的曲线是(,)0F y x =. 曲线(,)0F x y =关于直线y x =-轴对称的曲线是(,)0F y x --=.13.圆锥曲线的第二定义:动点M 到定点F 的距离与到定直线l 的距离之比为常数e ,若01e <<,M 的轨迹为椭圆;若1e =,M 的轨迹为抛物线;若1e >,M 的轨迹为双曲线.注意:1、还记得圆锥曲线的两种定义吗?解有关题是否会联想到这两个定义? 2、还记得圆锥曲线方程中的:(1)在椭圆中:a 是长半轴,b 是短半轴,c 是半焦距,其中222b ac =-,,(01)ce e a=<<是离心率,2a c 是准心距,2b c 是准焦距, 2b a是半通径.(2)在双曲线中:a 是实半轴,b 是虚半轴,c 是半焦距,其中222b c a =-,,(1)c e e a=>是离心率,2a c 是准心距,2b c 是准焦距, 2b a是半通径.(3)在抛物线中:p 是准焦距,也是半通径.3、在利用圆锥曲线统一定义解题时,你是否注意到定义中的定比的分子分母的顺序?(到定点的距离比到定直线的距离)4、离心率的大小与曲线的形状有何关系(圆扁程度,张口大小)?等轴双曲线的离心率是多少?(e =5、在用圆锥曲线与直线联立求解时,消元后得到的方程中要注意:二次项的系数是否为零?判别式的限制.(求交点,弦长,中点,斜率,对称,存在性问题都在下进行).注意:尤其在求双曲线与直线的交点时:当0∆>时:直线与双曲线有两个交点(包括直线与双曲线一支交于两点和直线与双曲线两支各交于一点两种情况);当0∆=时,直线与双曲线有且只有一个交点(此时称指向与双曲线相切),反之,当直线与双曲线只有一个交点时,直线与双曲线不一定相切,此时直线与双曲线的一条渐近线平行,当0∆<时,直线与双曲线没有交点.6、椭圆中,注意焦点、中心、短轴端点所组成的直角三角形.此时222a b c =+. 7、通径是抛物线的所有焦点弦中最短的弦.(想一想在双曲线中的结论?) 8、你知道椭圆、双曲线标准方程中,,a b c 之间关系的差异吗?9、如果直线与双曲线的渐近线平行时,直线与双曲线相交,只有一个交点;如果直线与抛物线的轴平行时,直线与抛物线相交,只有一个交点.此时两个方程联立,消元后为方程变为一次方程.椭圆练习1.过椭圆12222=+by a x (a>b>0)的左焦点F 1任做一条不与长轴重合的弦AB,F 2为椭圆的右焦点,则△ABF 1的周长是( ) (A)2a (B)4a (C)2b (D)4b2.设b a b a b a +=+∈则,62,,22R 的最小值是( ) (A)22-(B)335-(C)-3(D)27-3.椭圆的两个焦点和短轴的两个顶点,是一个含600角的菱形的四个顶点,则椭圆的离心率为( ) (A )21 (B )23 (C )33 (D )21或23 4.设常数m>0,椭圆x 2+m 2y 2=m 2的长轴是短轴的两倍,则m 的值等于( ) (A )2 (B )2 (C )2或21 (D )2或225.过椭圆22221x y a b+=(0a b >>)的左焦点1F 作x 轴的垂线交椭圆于点P ,2F 为右焦点,若1260F PF ∠=,则椭圆的离心率为( ) (A)212 (D)136.如果椭圆的两个焦点将长轴分成三等份,那么这个椭圆的两条准线间的距离是焦距的( )(A )18倍 (B )12倍 (C )9倍 (D )4倍7.当关于x,y 的方程x 2sin α-y 2cos α=1表示的曲线为椭圆时,方程(x+cos α)2+(y+ sin α)2=1所表示的圆的圆心在( ) (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限8.已知椭圆的焦点为F 1,F 2,P 是椭圆上的一个动点,如果延长F 1P 到Q,使得|PQ|=|PF 2|,那么动点Q 的轨迹是( ) (A )圆 (B )椭圆 (C )直线 (D )其它9.已知椭圆14922=+y x 与圆(x-a)2+y 2=9有公共点, 则a 的取值范围是( )(A)-6<a <6 (B)0<a≤5 (C)a 2<25 (D)|a|≤610.设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是( ) (A)2 (B)12(C)2(D1 11.在椭圆12222=+by a x 上取三点,其横坐标满足x 1+x 3=2x 2,三点依次与某一焦点连结的线段长为r 1,r 2,r 3,则有( ) (A )r 1,r 2,r 3成等差数列 (B )231211r r r =+ (C )r 1,r 2,r 3成等比数列 (C )以上都不对 12.已知椭圆22:12x C y +=的右焦点为F ,右准线为l ,点A l ∈,线段AF 交C 于点B ,若3FA FB =,则||AF13.已知1F 、2F 是椭圆的两个焦点,满足120MF MF ⋅=的点M 总在椭圆内部,则椭圆离心率的取值范围是( ) (A)(0,1) (B)1(0,]2(C)(D)14.一个椭圆中心在原点,焦点12F F 、在x 轴上,P (2)是椭圆上一点,且1122||||||PF F F PF 、、成等差数列,则椭圆方程为( ) (A )22186x y += (B )221166x y += (C )22184x y += (D )221164x y +=15.若椭圆19822=++y a x 的离心率是21,则a 的值为————————. 16.椭圆x 2cos 2α+y 2=1(0<α<π,α≠2π)的半长轴=——————,半短轴=——————,半焦距=——————,离心率=——————. 17.已知椭圆22221(0)x y a b a b +=>>的左、右焦点分别为12(,0),(,0)F c F c -,若椭圆上存在一点P 使1221sin sin a c PF F PF F =,则该椭圆的离心率的取值范围为 .18.M 是椭圆14922=+y x 上的一点,F 1,F 2 是椭圆的焦点,且∠F 1MF 2=900,则△F 1MF 2的面积等于——————. 19.与圆(x+1)2+y 2=1相外切,且与圆(x -1)2+y 2=9相内切的动圆圆心的轨迹方程是——————20.设椭圆⎪⎩⎪⎨⎧==ααsin 32cos 4y x (α为参数)上一点P 与x 轴正向所成角∠POx=3π,则点P 的坐标是__.21.在平面直角坐标系xOy 中,椭圆22221(0)y x a b a b+=>>的焦距为2c ,以O 为圆心,a 为半径作圆M ,若过2(0)a P c ,作圆M 的两条切线相互垂直,则椭圆的离心率为22.已知直线l :y=mx+b,椭圆C:22)1(ax -+y 2=1,若对任意实数m,l 与C 总有公共点,则a,b 应满足的条件是 .23.椭圆4cos 2sin x y ϕϕ=⎧⎨=⎩(ϕ为参数)上点到直线20x y -=的最大距离是 .24.12F F 、是椭圆2214x y +=的左、右焦点,点P 在椭圆上运动,则12||||PF PF ⋅的最大值是 .25.已知椭圆焦点为F 1(0,-22),F 2(0, 22),长轴长为6, 过焦点的弦的长等于短轴长,求这焦点弦的倾斜角.26.在椭圆191622=+y x 上求一点M ,使它到直线l:3x+4y -50=0的距离最大或最小. 27.在△ABC 中,BC=24,AC 、AB 的两条中线之和为39,求△ABC 的重心轨迹方程.29.椭圆12222=+by a x 与x 轴、y 轴正方向相交于A 、B ,在第一象限内的椭圆上求一点C ,使得四边形OACB 的面积最大.30.点A 、B 分别是椭圆1202362=+y x 长轴的左、右端点,点F 是椭圆的右焦点,点P 在椭圆上,且位于x 轴上方,PF PA ⊥.(1)求点P 的坐标;(2)设M 是椭圆长轴AB 上的一点,M 到直线AP 的距离等于||MB ,求椭圆上的点到点M 的距离d 的最小值.双曲线练习1.F 1、F 2为双曲线1422-=-y x 的两个焦点,点P 在双曲线上,且∠F 1PF 2=90°,则△F 1PF 2的面积是________________.2.双曲线焦点在y 轴上,且一个焦点在直线5x -2y +20=0上,两焦点关于原点对称,35=a c ,则此双曲线的方程是________.3.已知双曲线22163x y -=的焦点为1F 、2F ,点M 在双曲线上且1MF x ⊥轴,则1F 到直线2F M 的距离为________________.4.已知双曲线22ax -22b y =1(a >0,b >0)的右焦点为F ,右准线与一条渐近线交于点A ,△OAF 的面积为22a (O为原点),则两条渐近线的夹角为______________________.5.已知定点A 、B 且|AB|=4,动点P 满足|PA|-|PB|=3,则|PA|的最小值是_________________.6.已知F 1、F 2是双曲线)0,0(12222>>=-b a by a x 的两焦点,以线段F 1F 2为边作正三角形MF 1F 2,若边MF 1的中点在双曲线上,则双曲线的离心率是_________________.7.过双曲线22221x y a b-=(a >0,b >0)的左焦点且垂直于x 轴的直线与双曲线相交于M 、N 两点,以MN 为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_________.8.双曲线112422=-y x 上点P 到左焦点的距离为6,这样的点有______个. 9.直线y=x+3与曲线14||92=-x x y 的交点个数是 .10.双曲线的两准线间的距离是焦距的53,则此双曲线的离心率为 .11.已知双曲线的渐近线方程是x y 32±=,且双曲线过点(3,4),则双曲线的离心率为 ,双曲线的方程为 . 12.设连接共轭双曲线四个顶点和四个焦点所成两个四边形的面积分别为S 1,S 2,则(21S S )max 为 . 13.已知双曲线的两个焦点坐标为F 1(0,-10), F 2(0,10)且一条渐近线方程是430x y -=,则双曲线的标准方程为14.已知双曲线经过)3,453(-A ,且与另一双曲线116922=-y x ,有共同的渐近线,则此双曲线的标准方程是 .15.已知双曲线的一条渐近线方程是043=+y x ,焦点是椭圆12510022=+y x 与坐标轴的交点,则双曲线的标准方程是 .16.已知双曲线的两条渐近线所夹的锐角是60︒,则此双曲线的离心率为 . 9.直线y x =-1被双曲线,3222=-y x 所截得弦的中点坐标是 ,弦长是 .17.已知关于x ,y 的二次方程4814)16()4(222+-=-+-m m y m x m 表示的是双曲线,则m 的取值范围是 .18.已知双曲线方程为191622=-y x ,经过它的右焦点F 2,作一条直线,使直线与双曲线恰好有一个交点,则该直线的斜率是 .19.已知双曲线方程为422=-x y ,过一点P (0,1),作一直线l ,使l 与双曲线无交点,则直线l 的斜率k 的集合是 .20.双曲线191622=-y x 右支上一点P 到左右两个焦点的距离之比是5:3,则P 点右准线的距离为_____________. 21.以230x y ±=为渐近线,且经过点(1 , 2)的双曲线是 .22.双曲线的离心率e =2,则它的一个顶点把焦点之间的线段分成长、短两段的比是 .23.双曲线1322=-y x 的渐近线中,斜率较小的一条渐近线的倾斜角为 . 24.若双曲线2222by a x -=1的一条渐近线的倾斜角为锐角α,则双曲线的离心率为____________.25.已知双曲线的渐近线方程为043=±y x ,一条准线的方程为0335=+y ,则双曲线方程 .26.双曲线1422=+k y x 的离心率e ∈(,)12,则k 的取值范围是______________.27.椭圆14222=+a y x 与双曲线1222=-y a x 的焦点相同,则a = . 28.如图,OA 是双曲线的实半轴,OB 是虚半轴,F 为焦点, 且∠=︒BAO 30,S ABF∆=)336(21-,则该双曲线方程是 . 29.已知双曲线的中心在原点,以坐标轴为对称轴,且与圆x y 2217+=相交于点A (4 , -1),若圆在点A 的切线与双曲线的渐近线平行,求此双曲线的方程.30.双曲线与椭圆1362722=+y x 有共同的焦点,它们的一个交点的纵坐标为4,求双曲线的方程.31.直线231+=x y 与双曲线14922=-y x 的两个交点与原点构成三角形,求此三角形的面积.32.已知双曲线b x a y a b 222222-=上有一点P ,焦点为F 1、F 2,且∠=F PF 12α,求证:2221αctg b S PF F ·=∆.33.斜率为2的直线l 被双曲线12322=-y x 截得的弦长为1552,求直线l 的方程. 34.已知P 为双曲线x y 2244-=上的动点,Q 是圆41)2(22=-+y x 上的动点,求PQ 的最小值。

圆锥曲线公式大全(总7页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--圆锥曲线知识考点一、直线与方程1、倾斜角与斜率:1212180<α≤0(tan x x y y --==)α 2、直线方程:⑴点斜式:直线l 经过点),(000y x P ,且斜率为k : ()00x x k y y -=- ⑵斜截式:已知直线l 的斜率为k ,且与y 轴的交点为),0(b :b kx y += ⑶两点式:已知两点),(),,(222211y x P x x P 其中),(2121y y x x ≠≠:121121y y y y x x x x --=-- ⑷截距式:已知直线l 与x 轴的交点为A )0,(a ,与y 轴的交点为B ),0(b :1x y a b+= ⑸一般式:0=++C By Ax (A 、B 不同时为0, 斜率BAk -=,y 轴截距为BC -) (6)k 不存在⇔a x b a x o=⇔⇔=)的直线方程为过(轴垂直,90α3、直线之间的关系:222111:,:b x k y l b x k y l +=+=⑴平行:{⇔⇔≠=21212121//b b k k k k l l 且都不存在,212121C C B B A A ≠=⑵垂直:{⇔⇔⊥-=⇔-==21212111.021k k k k k k l l 不存在,02121=+B B A A⑶平行系方程:与直线0=++C By Ax 平行的方程设为:0=++m By Ax⑷垂直系方程:与直线0=++C By Ax 垂直的方程设为:0=++n Ay Bx⑸定点(交点)系方程:过两条直线:,0:22221111=++=++C y B x A l C y B x A l 的交点的方程设为:0)(222111=+++++C y B x A C y B x A λ反之直线0)(222111=+++++C y B x A C y B x A λ中,λ取任何一切实数R ,则直线一定过定点),(00y x ,即0:,0:22221111=++=++C y B x A l C y B x A l 两条直线的交点),(0y x4、距离公式:(1)两点间距离公式:两点),(),,(222211y x P x x P :()()21221221y y x x P P -+-=(2)点到直线距离公式:点),(00y x P 到直线0:=++C By Ax l 的距离为2200BA CBy Ax d +++=(3)两平行线间的距离公式:1l :01=++C By Ax 与2l :02=++C By Ax 平行,则2221BA C C d +-=二、圆与方程 1、圆的方程:⑴标准方程:()()222r b y a x =-+- 其中圆心为(,)a b ,半径为r .⑵一般方程:022=++++F Ey Dx y x (0422>-+F E D )其中圆心为(,)22D E --,半径为r =2、直线与圆的位置关系 点),(00y x 和圆222)()(r b y a x =-+-的位置关系有三种:222222222)()()(rb y a x r b y a x rb y a x >-+-⇔=-+-⇔<-+-⇔)(点在圆外)(点在圆上)(点在圆内直线0=++C By Ax 与圆222)()(r b y a x =-+-的位置关系有三种:0<∆⇔⇔>相离r d ; 0=∆⇔⇔=相切r d ;0>∆⇔⇔<相交r d .切线方程:(1)当点),(00y x P 在圆222r y x =+上⇔200r y y x x =+ 圆222)()(r b y a x =-+-⇔200))(())((r b y b y a x a x =--+-- (2)当点),(00y x P 在圆222r y x =+外,则设直线方程()00x x k y y -=-,并利用d=r 求出斜率,即可求出直线方程【备注:切线方程一定是两条,考虑特殊直线k 不存在】④弦长公式:222||d r AB -=2212121()4k x x x x =+-- 3、两圆位置关系:21O O d =⑴外离:r R d +> ⇔有4条公切线 ⑵外切:r R d += ⇔有3条公切线 ⑶相交:r R d r R +<<- ⇔有2条公切线 ⑷内切:r R d -= ⇔有1条公切线 ⑸内含:r R d -< ⇔有0条公切线三、圆锥曲线与方程1.椭圆焦点的位置 焦点在x 轴上 焦点在y 轴上图形标准方程()222210x y a b a b+=>> ()222210y x a b a b+=>> 第一定义到两定点21F F 、的距离之和等于常数2a ,即21||||2MF MF a +=(212||a F F >)第二定义 与一定点的距离和到一定直线的距离之比为常数e ,即(01)MFe e d=<< 范围a x a -≤≤且b y b -≤≤ b x b -≤≤且a y a -≤≤2.双曲线顶点 ()1,0a A -、()2,0a A ()10,b B -、()20,b B ()10,a A -、()20,a A()1,0b B -、()2,0b B轴长 长轴的长2a = 短轴的长2b = 对称性 关于x 轴、y 轴对称,关于原点中心对称焦点 ()1,0F c -、()2,0F c ()10,F c -、()20,F c焦距 222122()F F c c a b ==-离心率 22222221(01)c c a b b e e a a a a-====-<<准线方程 2a x c=±2a y c=±焦半径 0,0()M x y 左焦半径:10MF a ex =+ 右焦半径:20MF a ex =-下焦半径:10MF a ey =+ 上焦半径:20MF a ey =-焦点三角形面积12212tan()2MF F S b F MF θθ∆==∠021s 21y c in PF PF •=••=θ 通径过焦点且垂直于长轴的弦叫通径: ab 22焦点的位置焦点在x 轴上 焦点在y 轴上图形标准方程()222210,0x y a b a b -=>> ()222210,0y x a b a b -=>> 第一定义到两定点21F F 、的距离之差的绝对值等于常数2a ,即21||||2MF MF a -=(2102||a F F <<) 第二定义 与一定点的距离和到一定直线的距离之比为常数e ,即(1)MFe e d=>【备注】1、双曲线和其渐近线得关系:由双曲线求渐进线:x a b y a x b y a x b y b y a x b y a x ±=⇒±=⇒=⇒=-⇒=-22222222222201由渐进线求双曲线:λ=-⇒=-⇒=⇒±=⇒±=2222222222220by a x b y a x a x b y a x b y x a b y2.等轴双曲线⇔实轴和虚轴等长的双曲线⇔其离心率e =2⇔渐近线x ±=y⇔方程设为λ=-22y x2、求弦长的方法: ①求交点,利用两点间距离公式求弦长; ②弦长公式 ) (消y x x x x k x x k l ]4))[(1(1212212212-++=-+=五、.直线与圆锥曲线的关系1、直线与圆锥曲线的关系如:直线y =kx +b 与椭圆x 2a 2+y 2b2=1 (a >b >0)的位置关系:图形标准方程 22y px = ()0p >22y px =- ()0p >22x py = ()0p >22x py =- ()0p >开口方向 向右 向左 向上 向下定义 与一定点F 和一条定直线l 的距离相等的点的轨迹叫做抛物线(定点F 不在定直线l 上)顶点 ()0,0离心率 1e =对称轴 x 轴y 轴范围0x ≥0x ≤0y ≥0y ≤焦点 ,02p F ⎛⎫ ⎪⎝⎭ ,02p F ⎛⎫- ⎪⎝⎭ 0,2p F ⎛⎫ ⎪⎝⎭0,2p F ⎛⎫- ⎪⎝⎭准线方程 2px =-2px =2p y =-2p y =焦半径 0,0()M x y 02pMF x =+02pMF x =-+02pMF y =+02p MF y =-+通径 过抛物线的焦点且垂直于对称轴的弦称为通径:2HH p '=焦点弦长 公式 12AB x x p =++参数p几何意义参数p 表示焦点到准线的距离,p 越大,开口越阔直线与椭圆相交?⎩⎨⎧ y =kx +bx 2a 2+y2b 2=1⇔有2组实数解,即Δ>0.直线与椭圆相切?⎩⎨⎧ y =kx +bx 2a 2+y2b 2=1⇔有1组实数解,即Δ=0,直线与椭圆相离⎩⎨⎧y =kx +bx 2a 2+y2b 2=1⇔没有实数解,即Δ<【备注】(1)韦达定理(根与系数的关系){AB x AC x C By Ax x -=+=⇔=++2121x .x 210x 的两根方程和则有21221214)(||xx x x x x -+=-(2){b kx y bkx y +=+=1122则有下列结论b x x k y y ++=+)(2121)(2121x x k y y -=-22121221)(b x x k x x k y y +++=③、与弦的中点有关的问题常用“点差法”:把弦的两端点坐标代入圆锥曲线方程,作差→弦的斜率与中点的关系;0202y a x b k -=(椭圆) 0202y a x b k =(双曲线)3、关于抛物线焦点弦的几个结论(了解)设AB 为过抛物线22(0)y px p =>焦点的弦,1122(,)(,)A x y B x y 、,直线AB 的倾斜角为θ,则⑴ 221212,;4p x x y y p ==- ⑵ 22;sin p AB θ=⑶ 以AB 为直径的圆与准线相切;π;⑸112. ||||FA FB P+=⑷焦点F对A B、在准线上射影的张角为2。
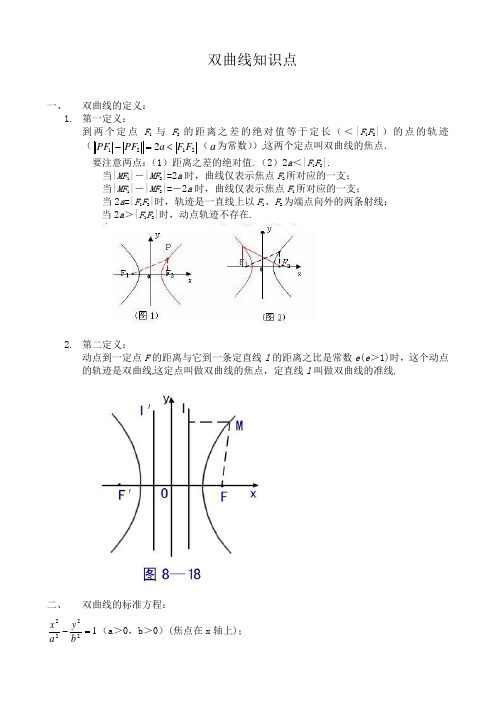
双曲线知识点一、 双曲线的定义:1. 第一定义:到两个定点F 1与F 2的距离之差的绝对值等于定长(<|F 1F 2|)的点的轨迹(21212F F a PF PF <=-(a 为常数))这两个定点叫双曲线的焦点.要注意两点:(1)距离之差的绝对值.(2)2a <|F 1F 2|.当|MF 1|-|MF 2|=2a 时,曲线仅表示焦点F 2所对应的一支; 当|MF 1|-|MF 2|=-2a 时,曲线仅表示焦点F 1所对应的一支;当2a =|F 1F 2|时,轨迹是一直线上以F 1、F 2为端点向外的两条射线;当2a >|F 1F 2|时,动点轨迹不存在.2. 第二定义:动点到一定点F 的距离与它到一条定直线l 的距离之比是常数e (e >1)时,这个动点的轨迹是双曲线这定点叫做双曲线的焦点,定直线l 叫做双曲线的准线二、双曲线的标准方程:12222=-by a x (a >0,b >0)(焦点在x 轴上);12222=-bx a y (a >0,b >0)(焦点在y 轴上); 1. 如果2x 项的系数是正数,则焦点在x 轴上;如果2y 项的系数是正数,则焦点在y 轴上. a 不一定大于b.2. 与双曲线12222=-by a x 共焦点的双曲线系方程是12222=--+k b y k a x 3. 双曲线方程也可设为:221(0)x y mn m n-=> 例题:已知双曲线C 和椭圆221169x y +=有相同的焦点,且过(3,4)P 点,求双曲线C 的轨迹方程。
三、点与双曲线的位置关系,直线与双曲线的位置关系: 1 点与双曲线:点00(,)P x y 在双曲线22221(0,0)x y a b a b -=>>的内部2200221x y a b ⇔->点00(,)P x y 在双曲线22221(0,0)x y a b a b -=>>的外部2200221x y a b ⇔-<点00(,)P x y 在双曲线22221(0,0)x y a b a b -=>>上220022-=1x y a b⇔2 直线与双曲线:(代数法)设直线:l y kx m =+,双曲线)0,0(12222>>=-b a by a x 联立解得02)(222222222=----b a m a mkx a x k a b1) 0m =时,b bk a a-<<直线与双曲线交于两点(左支一个点右支一个点);b k a ≥,bk a≤-,或k 不存在时直线与双曲线没有交点;2) 0m ≠时,k 存在时,若0222=-k a ba bk ±=,直线与双曲线渐近线平行,直线与双曲线相交于一点;若2220b a k -≠,222222222(2)4()()a mk b a k a m a b ∆=-----2222224()a b m b a k =+-0∆>时,22220m b a k +->,直线与双曲线相交于两点; 0∆<时,22220m b a k +-<,直线与双曲线相离,没有交点;0∆=时22220m b a k +-=,2222m b k a +=直线与双曲线有一个交点; 若k 不存在,a m a -<<时,直线与双曲线没有交点; m a m a ><-或直线与双曲线相交于两点; 3. 过定点的直线与双曲线的位置关系:设直线:l y kx m =+过定点00(,)P x y ,双曲线)0,0(12222>>=-b a by a x1).当点00(,)P x y 在双曲线内部时:b bk a a-<<,直线与双曲线两支各有一个交点; a bk ±=,直线与双曲线渐近线平行,直线与双曲线相交于一点;b k a >或bk a<-或k 不存在时直线与双曲线的一支有两个交点;2).当点00(,)P x y 在双曲线上时:bk a =±或2020b x k a y =,直线与双曲线只交于点00(,)P x y ;b bk a a-<<直线与双曲线交于两点(左支一个点右支一个点); 2020b x k a y >(00y ≠)或2020b x b k a a y <<(00y ≠)或bk a <-或k 不存在,直线与双曲线在一支上有两个交点; 当00y ≠时,bk a =±或k 不存在,直线与双曲线只交于点00(,)P x y ;b k a >或bk a <-时直线与双曲线的一支有两个交点;b bk a a-<<直线与双曲线交于两点(左支一个点右支一个点); 3).当点00(,)P x y 在双曲线外部时:当()0,0P 时,b bk a a -<<,直线与双曲线两支各有一个交点; b k a ≥或bk a≤或k 不存在,直线与双曲线没有交点;当点0m ≠时,k =时,过点00(,)P x y 的直线与双曲线相切 bk a=±时,直线与双曲线只交于一点;几何法:直线与渐近线的位置关系例:过点(0,3)P 的直线l 和双曲线22:14y C x -=,仅有一个公共点,求直线l 的方程。

1. 椭圆l τ + ∑- = i(a>b>O)的参数方程是V Cr Zr 2,2»2准线到中心的距离为L ,焦点到对应准线的距离(焦准距)p =—・通径的一半(焦参数):丄.C Ca2 22. 椭圆∆τ + l τ = l(rt >∕7>θ)焦半径公式及两焦半径与焦距构成三角形的面积: Cr Zr| PF l | = e(x + —) = a+ ex , ∖PF 21 = e(-— X) = U-ex ↑ S 斗严;=b 2 tan '丫 F22 223.椭圆的的内外部:(1)点PesyO)在椭圆丄v + L = l(α>b>0)的内部O⅛- + ⅛<l. Cr 泸Cr b'2 2 2 2(2)点 P(X o o to)在椭圆上τ +丄r = l(α>b>O)的外部 <≠>⅛ + ⅛>ι.Cr Zr Cr Zr的距离(焦准距)P = — •通径的一半(焦参数):— C a5. 双曲线的内外部:(1)点P(X o o tO)在双曲线=Cr Ir/2 2 2 2 ⑵点P(X (P y 0)在双曲线一一二~ = l(α > 0,b > 0)的外部o —⅛■-汙V1・Cr IrCr Zr6. 双曲线的方程与渐近线方程的关系:(1)若双曲线方程为二一二=1二>渐近线方程:Δ1-22 = O^> y = ±-χ・α~ Ir Cr 少a-> 2A χ∙ V r β,V*⑵若渐近线方程为y = ±-x<=>-±- = O=>¾曲线可设为r — — = λ・ a a b Cr Zr2 22 2⑶若双曲线与亠一亠=1有公共渐近线,可设为=T 一亠=λCr XCr Ir(λ>0,焦点在X 轴上;九<0,焦点在y 轴上)・ (4)焦点到渐近线的距离总是b ∙7. 抛物线y 2= 2px 的焦半径公式:拋物线y 2=2px(p>0)焦半径ICFI = X O + -^・ 过焦点弦长IcQl = “+上+心+ £ = “+“ + 〃 . 2 2 28. 拋物线y 2 = IPX JL 的动点可设为P(±-,儿)或P(2∕"[2p∕) P(x , V ),其中y 2= 2PX ・2 P '•、 b A ,ac — b~9. 二次函数y = ax 1 +bx + c = a(x + —)2+ ------------- (a ≠ 0)的图象是抛物线:(1 )顶点坐标为Ia 4aZb 4“C — b~ z. .. ... I . . h ^CIC — /?" +1、 Z -S Λ /V ∙ z t , CT^CIC — b~ — 1 ,—:——):(2)焦点的坐标为,——; ---------------- ):(3)准线万程是y = IABl = 5J(1+^2)(X 2 "ΛI )2 =I 比 _兀21 Vl +tan 2 a =I y l _y 21 √l + c^t 2ay = kx + b . .α(弦端点ACv 1,y 1X B(X^y 2),由方程<消去y 得到αL +bx + c = O 9 Δ>0, α为直线AB 的圆锥曲线X = Cl COS θ 亠 亠 C• 离心率£ =—= y = bs ∖nθ aV»*■ C 4. 双曲线亠一 — = 1(« > 0.Z? > 0)的离心^e =— a ∕Γa • 2ι2 「,准线到中心的距离为∙,焦点到对应准线 焦半径公式\PF }\ =I e(x + —) I=I a + <?xI, ∖PF 2∖ =I e(-^x) I=I a-ex ∖9 C 两焦半径与焦距构成三角形的面积S λj.ιp l .y = b 2 COt 'F'] F .2 22L = l(">0d>0)的内部 o ⅛-4>l. • - Cr Zr2a 4a2a 4a" 4a10. 以抛物线上的点为圆心,焦半径为半径的圆必与准线相切:以拋物线焦点弦为直径的圆,必与准线相切; 以抛物线的焦半径为直径的圆必与过顶点垂直于轴的直线相切・11. 直线与圆锥曲线相交的弦长公式:IABI = √(x 1-x 2)2+(y 1-y 2)2或F(x,y) = O倾斜角,&为直线的斜率,I召I= J(XI +心)‘ _4召心・12.圆锥曲线的两类对称问题:(1)曲线F(X,y) = O关于点P(X o,儿)成中心对称的曲线是F(2x0-x t2y0 -y)=0.(2)曲线F(X,y) = 0关于直线Av + Bv + C = O成轴对称的曲线是—2A(Ar + By+ C) 2B(Ax + By + C)x CFa ------ —R——、y --------- -V———)=0・√Γ+歹A" + B'特别地,曲线F(X9 y) = 0关于原点O成中心对称的曲线是F(-x,-y) = 0・曲线F(X9 y) = 0关于直线X轴对称的曲线是F(X^y) = 0.曲线F(X9 y) = 0关于直线y轴对称的曲线是F(-x, y) = 0・曲线F(X9 y) = 0关于直线y = x轴对称的曲线是F{y.x) = 0.曲线F(X,y) = 0关于直线y = -x轴对称的曲线是F(-y,-x) = 0・13 •圆锥曲线的第二定艾:动点M到定点F的距离与到定直线/的距离之比为常数£,若0 VfVl, M的轨迹为椭圆;若e = ∖9 M的轨迹为抛物线;若e>∖9 M的轨迹为双曲线.注意:J还记得圆锥曲线的两种定义吗解有关题是否会联想到这两个定狡2、还记得圆锥曲线方程中的:2(1)在椭圆中:α是长半轴,〃是短半轴,C是半焦距,其中b2 =a2-C29 f = (Ovwvl)是离心率,—a C• 2. 2是准心距,-L是准焦距,-L是半通径.C a2(2)在双曲线中:"是实半轴,b是虚半轴,C是半焦距,其中b2 =c2-a29 e = -∖e>l)是离心率,L是a C准心距,伫是准焦距,冬是半通径.C a(3)在抛物线中:0是准焦距,也是半通径.3、在利用圆锥曲线统一定狡解题吋,你是否注意到定艾中的定比的分子分母的顺序(到定点的距离比到定直线的距离)4、离心率的大小与曲线的形状有何关系(圆扁程度,张口大小)等轴双曲线的离心率是多少(0 = √Σ)5、在用圖锥曲线与直线联立求解时,消元后得到的方程中要注意:二次项的系数是否为零判别式A 2 0的限制. (求交点,弦长,中点,斜率,对称,存在性问题都在Δ >0下进行).注意:尤其在求双曲线与直线的交点时:当A>0时:直线与双曲线有两个交点(包括直线与双曲线一支交于两点和直线与双曲线两支各交于一点两种情况):当A = O时,直线与双曲线有且只有一个交点(此时称指向与双曲线相切),反之,当直线与双曲线只有一个交点时,直线与双曲线不一定相切,此时直线与双曲线的一条渐近线平行,当AvO时,直线与双曲线没有交点.6、椭圆中,注意焦点.中心.短轴端点所组成的直角三角形•此时Cr =b2+c2・7、通径是抛物线的所有焦点弦中最短的弦.(想一想在双曲线中的结论)8、你知道椭圆、双曲线标准方程中aj∖c之间关系的差异吗9、如果直线与双曲线的渐近线平行吋,直线与双曲线相交,只有一个交点;如果直线与拋扬线的轴平行时,直线与抛物线相交,只有一个交点•此时两个方程联立,消元后为方程变为一次方程.椭圆练习1・过椭圆二+二=1 (a>b>O)的左焦点F I任做一条不与长轴重合的弦AB, F2为椭圆的右焦点,則AABA的周长是/ b^( )(A)2a (B)4a (C)2b (D) 4b2•设a,beR.a2+2b2 =6,则α + b 的最小值是( )(A) - 2√2 (B)-垃(0-3 (D)-2323. 椭圆的两个焦点和短轴的两个顶点,是一个含60°角的菱形的四个顶点,则椭圆的离心率为( )(A)丄 (B)遇 (C)遇 (D)丄或遇2 23 2 24. 设常数m>0,椭圆x 2+m 2y 2=m 2的长轴是短轴的两倍,則m 的值等于( )(A) 2(B) √2(C) 2 或丄 (D) √Σ 或空2 22 25. 过椭圆二+ L = l(°>b> 0)的左焦点片作X 轴的垂线交椭圆于点P,化为右焦点,若ZF i PF. = 60 ,则Cr "椭圆的离心率为()(A)^⑻迟 (C)I(D)I23236. 如果椭圆的两个焦点将长轴分成三等份,那么这个椭圆的两条准线间的距离是焦距的() (A) 18 倍 (B) 12 倍 (C) 9 倍 (D) 4 倍7. 当关于X, y 的方程X 2Sin^ -y 2COSCr=I 表示的曲线为椭圆时,方程(x+cos α)'+(y+ Sinaf)Jl 所表示的圆的國心在()(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限8. 已知椭圆的焦点为F b F 2,P 是椭圆上的一个动点,如果延长F 卩到Q,使得I PQ I=I PF 2I,那么动点Q 的轨迹是( )(A)圆 (B)椭圆 (C)直线 (D)其它9. 已知椭圆—÷-= 1与圆(χ-a)⅛Λ=9有公共点,则a 的取值范围是()9 4 (A)-6<a<6(B)0<a≤5(C)a 2<25(D) ∣a∣≤610•设椭圆的两个焦点分别为F-、F 2,过F?作椭圆长轴的垂线交椭圆于点P,若AFPFz 为等腰直角三角形,则椭 圆的离心率是()(A)YZ(B)幺二! (C) 2-√2(D) √2-l2 2SS11. 在椭圆—÷γ-≈ 1上取三点,其横坐标满足X I +×3=2X 2,三点依次与某一焦点连结的线段长为r b r 2, r 3,则有 α∙ b・I I 7()(A) r b r 2, r 3成等差数列 (B)丄+丄=二 (C) r b r 2,r 3^等比数列 (C)以上都不对 12•已知椭圆C ι- + y 2= 1的右焦点为F,右准线为/,点Ae/ ,线段4F 交C 于点B,若FA = 3FB, »■]2伍若椭圆之+「I 的离心率是、则W*16 •椭圆X 2COs 2 α +y 2=1 (0< a <ΛR, a≠ y )的半长轴= ------- ,半短轴= -------- ,半焦距= -------- ,离心率= ----------------- = --------- ,則该椭圆的离心率的取值范围为 ____________________ ・(A) (0.1)(B) (0.1)(0(0,#)(D)哼,1)13.已知片、耳是椭國的两个焦点,满足・"庁=0的点M 总在椭圆内部•则椭圆离心率的取值范围是()14. 一个椭圆中心在原点,焦点斤、C 在X 轴上,P (2, √J)是椭圆上一点,且1卩斤1、1斥巴I 、IP 耳I 成等差数列,則椭圆方程为()(A) ⅞4- ⑻护汀<C) ⅜÷⅞ = ∙ I 丽二()(A) √2 (B) 2 (C)^(D) 317.已知椭圆⅛4= ↑(a>b>O)的左、 右焦点分别为斤(一c,0),耳(c,0), 若椭圆上存在一点P 使Sin PI71F2 Sin PF l F X是椭圆二+ 2_ = i上的一A,F I,F2是椭圆的焦点,且ZF I MF2=9O o,则ZkFNF?的面积等于9 419•与圆(x+1)2+y2=1相外切,且与IS(X-I)2÷y2=9相内切的动圆圆心的轨迹方程是X = 4COSa , …Ir20•设椭圆( L (□为参数)上一点P与X轴正向所成角ZPOx=-, 点P的坐标是y = 2√3 Sin a 321.在平面直角坐标系.9y中,椭E)4÷4 = 1G∕>∕7>O)的焦距为2c,以0为圆心,为半径作圆M ,若过P(Qe) Cr Iy C作圆M的两条切线相互垂直,则椭圆的离心率为 _________________22•已知直线/ : y=mx+b,椭圆C: (A ^.I)÷y2=1,若对任意实数叫/与C总有公共点,則a, b应满足的条件“是 _________ •23•椭圆F=4cos0 (。

最全圆锥曲线知识点总结的定义是指平面内一个动点P到两个定点F1,F2的距离之和等于常数(PF1+PF2=2a>F1F2),那么这个动点P的轨迹就是椭圆。
这两个定点被称为椭圆的焦点,两焦点的距离被称为椭圆的焦距。
注意:如果PF1+PF2=F1F2,则动点P的轨迹是线段F1F2;如果PF1+PF2<F1F2,则动点P的轨迹无图形。
2)对于椭圆,如果焦点在x轴上,那么它的参数方程是x=acosθ,y=bsinθ(其中θ为参数),如果焦点在y轴上,那么它的参数方程是y=acosθ,x=bsinθ。
如果椭圆的标准方程是x2/a2+y2/b2=1(a>b>0),那么它的范围是−a≤x≤a,−b≤y≤b,焦点是两个点(±c,0),对称中心是(0,0),顶点是(±a,0)和(0,±b),长轴长为2a,短轴长为2b,离心率为e=c/a,椭圆即为0<e<1的情况。
3)关于直线与椭圆的位置关系,如果点P(x,y)在椭圆外,那么a2+b2>1;如果点P(x,y)在椭圆上,那么a2+b2=1;如果点P(x,y)在椭圆内,那么a2+b2<1.4)焦点三角形是指椭圆上的一点与两个焦点构成的三角形。
5)弦长公式是指如果直线y=kx+b与圆锥曲线相交于两点A、B,且x1、x2分别为A、B的横坐标,那么AB=√[1+k2(x1−x2)2]。
如果y1、y2分别为A、B的纵坐标,则AB=√[1+k2(y1−y2)2]。
如果弦AB所在直线方程设为x=ky+b,则AB=√[1+k2(y1−y2)2]。
6)圆锥曲线的中点弦问题可以用“韦达定理”或“点差法”求解。
在椭圆中,以P(x,b2x,y)为中点的弦所在直线的斜率k=−a2y。
1.已知椭圆 $m x^2 + n y^2 = 1$ 与直线 $x+y=1$ 相交于$A,B$ 两点,点 $C$ 是 $AB$ 的中点,且 $AB=2\sqrt{2}$,求椭圆的方程,若 $OC$ 的斜率为 $\frac{1}{2}$,求 $m,n$ 的值。
圆锥曲线知识点整理圆锥曲线是高中数学中的重要内容,包括椭圆、双曲线和抛物线。
下面我们来详细整理一下圆锥曲线的相关知识点。
一、椭圆1、定义平面内与两个定点 F₁、F₂的距离之和等于常数(大于|F₁F₂|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2、标准方程焦点在 x 轴上:\(\frac{x^2}{a^2} +\frac{y^2}{b^2} =1\)(\(a > b > 0\)),其中\(a\)为长半轴长,\(b\)为短半轴长,\(c\)为半焦距,满足\(c^2 = a^2 b^2\)。
焦点在y 轴上:\(\frac{y^2}{a^2} +\frac{x^2}{b^2} =1\)(\(a > b > 0\))3、椭圆的性质(1)范围:对于焦点在 x 轴上的椭圆,\(a \leq x \leq a\),\(b \leq y \leq b\);对于焦点在 y 轴上的椭圆,\(b \leq x \leq b\),\(a \leq y \leq a\)。
(2)对称性:椭圆关于 x 轴、y 轴和原点对称。
(3)顶点:椭圆有四个顶点,焦点在 x 轴上时,顶点坐标为\((\pm a, 0)\),\((0, \pm b)\);焦点在 y 轴上时,顶点坐标为\((0, \pm a)\),\((\pm b, 0)\)。
(4)离心率:椭圆的离心率\(e =\frac{c}{a}\),\(0 < e < 1\),\(e\)越接近 0,椭圆越接近于圆;\(e\)越接近 1,椭圆越扁。
二、双曲线1、定义平面内与两个定点 F₁、F₂的距离之差的绝对值等于常数(小于|F₁F₂|)的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,两焦点间的距离叫做焦距。
2、标准方程焦点在 x 轴上:\(\frac{x^2}{a^2} \frac{y^2}{b^2} = 1\),其中\(a > 0\),\(b > 0\),\(c^2 = a^2 + b^2\)。
圆锥曲线公式及知识点总结圆锥曲线的统一定义:到定点的距离与到定直线的距离的商是常数e的点的轨迹。
数学里有很多公式,为了帮助大家更好的学习数学,小编特地为大家整理了圆锥曲线公式及知识点总结,希望对大家的数学学习有帮助。
圆锥曲线公式:椭圆1、中心在原点,焦点在x轴上的椭圆标准方程:其中x²/a²+y²/b²=1,其中a>b>0,c²=a²-b²2、中心在原点,焦点在y轴上的椭圆标准方程:y²/a²+x²/b²=1,其中a>b>0,c²=a²-b²参数方程:x=acosθ;y=bsinθ(θ为参数,0≤θ≤2π)圆锥曲线公式:双曲线1、中心在原点,焦点在x轴上的双曲线标准方程:x²/a-y²/b²=1,其中a>0,b>0,c²=a²+b².2、中心在原点,焦点在y轴上的双曲线标准方程:y²/a²-x²/b²=1,其中a>0,b>0,c²=a²+b².参数方程:x=asecθ;y=btanθ(θ为参数)圆锥曲线公式:抛物线参数方程:x=2pt²;y=2pt(t为参数)t=1/tanθ(tanθ为曲线上点与坐标原点确定直线的斜率)特别地,t可等于0直角坐标:y=ax²+bx+c(开口方向为y轴,a≠0)x=ay²+by+c(开口方向为x轴,a≠0)离心率椭圆,双曲线,抛物线这些圆锥曲线有统一的定义:平面上,到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。
且当01时为双曲线。
圆锥曲线公式知识点总结圆锥曲线椭圆双曲线抛物线标准方程x²/a²+y²/b²=1(a>b>0)x²/a²-y²/b²=1(a>0,b>0)y²=2px(p>0)范围x∈[-a,a]x∈(-∞,-a]∪[a,+∞)x∈[0,+∞)y∈[-b,b]y∈Ry∈R对称性关于x轴,y轴,原点对称关于x轴,y轴,原点对称关于x轴对称顶点(a,0),(-a,0),(0,b),(0,-b)(a,0),(-a,0)(0,0)焦点(c,0),(-c,0)(c,0),(-c,0) (p/2,0)【其中c²=a²-b²】【其中c²=a²+b²】准线x=±a²/cx=±a²/cx=-p/2渐近线——————y=±(b/a)x—————离心率。
《圆锥曲线公式汇总》《圆锥曲线公式汇总》一、椭圆1.标准方程:a2x2+b2y2=1 (焦点在x轴上,a>b>0;焦点在y轴上,b>a>0)2.焦点坐标:F1(−c,0),F2(c,0) (c为焦距的一半,c2=a2−b2)3.离心率:e=ac (0<e<1)4.焦点到曲线上任意一点的距离之和:PF1+PF2=2a5.焦点到曲线上任意一点的距离之差:∣PF1−PF2∣=2a2−b26.曲线上的点到焦点的距离与到准线的距离之比:dPF=e (d为准线到原点的距离)7.准线方程:x=±ca2 (焦点在x轴上);y=±ca2 (焦点在y轴上)8.通径长(过焦点且垂直于长轴的弦长):a2b29.短轴端点到焦点的距离:a10.焦点三角形的面积:S=b2tan(2θ) (θ为焦点三角形的顶角)二、双曲线1.标准方程:a2x2−b2y2=1 (焦点在x轴上,a>0,b>0);a2y2−b2x2=1 (焦点在y轴上,a>0,b>0)2.焦点坐标:F1(−c,0),F2(c,0) (c为焦距的一半,c2=a2+b2)3.离心率:e=ac (e>1)4.焦点到曲线上任意一点的距离之差的绝对值:∣PF1−PF2∣=2a5.焦点到曲线上任意一点的距离之和:PF1+PF2=2a2+b26.曲线上的点到焦点的距离与到准线的距离之比:dPF=e (d为准线到原点的距离)7.准线方程:x=±ca2 (焦点在x轴上);y=±ca2 (焦点在y轴上)8.通径长(过焦点且垂直于实轴的弦长):a2b29.实轴端点到焦点的距离:c−a10.焦点三角形的面积:S=tan(2θ)b2 (θ为焦点三角形的顶角)三、抛物线1.标准方程:y2=4px (焦点在x轴上,p为焦准距);x2=4py (焦点在y轴上,p为焦准距)2.焦点坐标:F(2p,0) (焦点在x轴上);F(0,2p) (焦点在y轴上)3.准线方程:x=−2p (焦点在x轴上);y=−2p (焦点在y轴上)4.曲线上任意一点到焦点的距离等于到准线的距离:PF=d (d为准线到原点的距离)。
圆锥曲线公式及知识点总结(详解)(实用版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的实用资料,如小学资料、初中资料、高中资料、大学资料、文言文、中考资料、高考资料、近义词、反义词、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this store provides you with various types of practical materials, such as primary school materials, junior high school materials, senior high school materials, university materials, classical Chinese, senior high school examination materials, college entrance examination materials, synonyms, antonyms, other materials, etc. If you want to know different data formats and writing methods, please pay attention!圆锥曲线公式及知识点总结(详解)圆锥曲线的统一概念:到定点的距离与到定直线的距离的商是常数e的点的轨迹。
圆锥曲线1.椭圆22221(0)x y a b a b +=>>的参数方程是cos sin x a y b θθ=⎧⎨=⎩离心率c e a ==准线到中心的距离为2a c,焦点到对应准线的距离(焦准距)2b p c =. 通径的一半(焦参数):2b a.2.椭圆22221(0)x y a b a b+=>>焦半径公式及两焦半径与焦距构成三角形的面积:21()a PF e x a ex c =+=+,22()a PF e x a ex c =-=-;1221tan 2F PF F PFS b ∆∠=.3.椭圆的的内外部: (1)点00(,)P x y 在椭圆22221(0)x y a b a b+=>>的内部2200221x y a b⇔+<. (2)点00(,)P x y 在椭圆22221(0)x y a b a b +=>>的外部2200221x y a b ⇔+>.4.双曲线22221(0,0)x y a b a b -=>>的离心率c e a ==,准线到中心的距离为2a c ,焦点到对应准线的距离(焦准距)2p c = 通径的一半(焦参数):2b a焦半径公式21|()|||a PF e x a ex c =+=+,22|()|||a PF e x a ex c=-=-,两焦半径与焦距构成三角形的面积1221cot 2F PF F PFS b ∆∠=.5.双曲线的内外部: (1)点00(,)P x y 在双曲线22221(0,0)x y a b a b-=>>的内部2200221x y a b⇔->. (2)点00(,)P x y 在双曲线22221(0,0)x y a b a b -=>>的外部2200221x y a b⇔-<.6.双曲线的方程与渐近线方程的关系:(1)若双曲线方程为12222=-b y a x ⇒渐近线方程:22220x y a b -=⇔x ab y ±=.(2)若渐近线方程为x aby ±=⇔0=±b y a x ⇒双曲线可设为λ=-2222b y a x .(3)若双曲线与12222=-b y a x 有公共渐近线,可设为λ=-2222by a x(0>λ,焦点在x 轴上;0<λ,焦点在y 轴上). (4) 焦点到渐近线的距离总是b7.抛物线px y 22=的焦半径公式:抛物线22(0)y p x p =>焦半径02pCF x =+. 过焦点弦长p x x px p x CD ++=+++=212122. 8.抛物线px y 22=上的动点可设为P ),2(2y py或2(2,2)P pt pt P (,)x y ,其中22y px =.9.二次函数2224()24b ac b y ax bx c a x a a-=++=++(0)a ≠的图象是抛物线:(1)顶点坐标为24(,)24b ac b a a --;(2)焦点的坐标为241(,)24b ac b a a-+-;(3)准线方程是2414ac b y a--=.10.以抛物线上的点为圆心,焦半径为半径的圆必与准线相切;以抛物线焦点弦为直径的圆,必与准线相切;以抛物线的焦半径为直径的圆必与过顶点垂直于轴的直线相切.11.直线与圆锥曲线相交的弦长公式: AB =(弦端点A ),(),,(2211y x B y x ,由方程⎩⎨⎧=+=0)y ,x (F bkx y 消去y 得到02=++c bx ax ,0∆>,α为直线AB 的倾斜角,k 为直线的斜率,12||x x -=12.圆锥曲线的两类对称问题:(1)曲线(,)0F x y =关于点00(,)P x y 成中心对称的曲线是00(2-,2)0F x x y y -=. (2)曲线(,)0F x y =关于直线0Ax By C ++=成轴对称的曲线是22222()2()(,)0A Ax By C B Ax By C F x y A B A B ++++--=++.特别地,曲线(,)0F x y =关于原点O 成中心对称的曲线是(,)0F x y --=. 曲线(,)0F x y =关于直线x 轴对称的曲线是(,)0F x y -=. 曲线(,)0F x y =关于直线y 轴对称的曲线是(,)0F x y -=. 曲线(,)0F x y =关于直线y x =轴对称的曲线是(,)0F y x =. 曲线(,)0F x y =关于直线y x =-轴对称的曲线是(,)0F y x --=.13.圆锥曲线的第二定义:动点M 到定点F 的距离与到定直线l 的距离之比为常数e ,若01e <<,M 的轨迹为椭圆;若1e =,M 的轨迹为抛物线;若1e >,M 的轨迹为双曲线.注意:1、还记得圆锥曲线的两种定义吗?解有关题是否会联想到这两个定义?2、还记得圆锥曲线方程中的:(1)在椭圆中:a 是长半轴,b 是短半轴,c 是半焦距,其中222b a c =-,,(01)ce e a=<<是离心率,2a c 是准心距,2b c 是准焦距, 2b a 是半通径.(2)在双曲线中:a 是实半轴,b 是虚半轴,c 是半焦距,其中222b c a =-,,(1)ce e a=>是离心率,2a c 是准心距,2b c 是准焦距, 2b a是半通径.(3)在抛物线中:p 是准焦距,也是半通径.3、在利用圆锥曲线统一定义解题时,你是否注意到定义中的定比的分子分母的顺序?(到定点的距离比到定直线的距离)4、离心率的大小与曲线的形状有何关系(圆扁程度,张口大小)?等轴双曲线的离心率是多少?(e =5、在用圆锥曲线与直线联立求解时,消元后得到的方程中要注意:二次项的系数是否为零?判别式的限制.(求交点,弦长,中点,斜率,对称,存在性问题都在下进行).注意:尤其在求双曲线与直线的交点时:当0∆>时:直线与双曲线有两个交点(包括直线与双曲线一支交于两点和直线与双曲线两支各交于一点两种情况);当0∆=时,直线与双曲线有且只有一个交点(此时称指向与双曲线相切),反之,当直线与双曲线只有一个交点时,直线与双曲线不一定相切,此时直线与双曲线的一条渐近线平行,当0∆<时,直线与双曲线没有交点.6、椭圆中,注意焦点、中心、短轴端点所组成的直角三角形.此时222a b c =+.7、通径是抛物线的所有焦点弦中最短的弦.(想一想在双曲线中的结论?)8、你知道椭圆、双曲线标准方程中,,a b c 之间关系的差异吗?9、如果直线与双曲线的渐近线平行时,直线与双曲线相交,只有一个交点;如果直线与抛物线的轴平行时,直线与抛物线相交,只有一个交点.此时两个方程联立,消元后为方程变为一次方程.椭圆练习1.过椭圆12222=+b y a x (a>b>0)的左焦点F 1任做一条不与长轴重合的弦AB,F 2为椭圆的右焦点,则△ABF 1的周长是( ) (A)2a (B)4a (C)2b (D)4b 2.设b a b a b a +=+∈则,62,,22R 的最小值是( )(A)22-(B)335- (C)-3(D)27-3.椭圆的两个焦点和短轴的两个顶点,是一个含600角的菱形的四个顶点,则椭圆的离心率为( ) (A )21 (B )23 (C )33 (D )21或234.设常数m>0,椭圆x 2+m 2y 2=m 2的长轴是短轴的两倍,则m 的值等于( ) (A )2 (B )2(C )2或21 (D )2或225.过椭圆22221x y a b+=(0a b >>)的左焦点1F 作x 轴的垂线交椭圆于点P ,2F 为右焦点,若1260F PF ∠=,则椭圆的离心率为( ) (A)212(D)136.如果椭圆的两个焦点将长轴分成三等份,那么这个椭圆的两条准线间的距离是焦距的( )(A )18倍 (B )12倍 (C )9倍 (D )4倍7.当关于x,y 的方程x 2sin α-y 2cos α=1表示的曲线为椭圆时,方程(x+cos α)2+(y+ sin α)2=1所表示的圆的圆心在( ) (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限8.已知椭圆的焦点为F 1,F 2,P 是椭圆上的一个动点,如果延长F 1P 到Q,使得|PQ|=|PF 2|,那么动点Q 的轨迹是( ) (A )圆 (B )椭圆 (C )直线 (D )其它 9.已知椭圆14922=+y x 与圆(x-a)2+y 2=9有公共点, 则a 的取值范围是( )(A)-6<a<6 (B)0<a≤5 (C)a 2<25 (D)|a|≤610.设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是( ) (A )2 (B )12(C )2(D111.在椭圆12222=+b y a x 上取三点,其横坐标满足x 1+x 3=2x 2,三点依次与某一焦点连结的线段长为r 1,r 2,r 3,则有( ) (A )r 1,r 2,r 3成等差数列 (B )231211r r r =+ (C )r 1,r 2,r 3成等比数列 (C )以上都不对12.已知椭圆22:12x C y +=的右焦点为F ,右准线为l ,点A l ∈,线段AF 交C 于点B ,若3FA FB =,则||AF(D) 3 13.已知1F 、2F 是椭圆的两个焦点,满足120MF MF ⋅=的点M 总在椭圆内部,则椭圆离心率的取值范围是( )(A)(0,1) (B)1(0,]2(C)(D) 14.一个椭圆中心在原点,焦点12F F 、在x 轴上,P (2,)是椭圆上一点,且1122||||||PF F F PF 、、成等差数列,则椭圆方程为( ) (A )22186x y += (B )221166x y +=(C )22184x y += (D )221164x y += 15.若椭圆19822=++y a x 的离心率是21,则a 的值为————————.16.椭圆x 2cos 2α+y 2=1(0<α<π,α≠2π)的半长轴=——————,半短轴=——————,半焦距=——————,离心率=——————.17.已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12(,0),(,0)F c F c -,若椭圆上存在一点P 使1221sin sin a cPF F PF F =,则该椭圆的离心率的取值范围为 .18.M 是椭圆14922=+y x 上的一点,F 1,F 2 是椭圆的焦点,且∠F 1MF 2=900,则△F 1MF 2的面积等于——————.19.与圆(x+1)2+y 2=1相外切,且与圆(x -1)2+y 2=9相内切的动圆圆心的轨迹方程是——————20.设椭圆⎪⎩⎪⎨⎧==ααsin 32cos 4y x (α为参数)上一点P 与x 轴正向所成角∠POx=3π,则点P 的坐标是__.21.在平面直角坐标系xOy 中,椭圆22221(0)y x a b a b+=>>的焦距为2c ,以O 为圆心,a 为半径作圆M ,若过2(0)aP c,作圆M 的两条切线相互垂直,则椭圆的离心率为22.已知直线l :y=mx+b,椭圆C:22)1(ax -+y 2=1,若对任意实数m,l 与C 总有公共点,则a,b 应满足的条件是 . 23.椭圆4c o s2s i n x y ϕϕ=⎧⎨=⎩(ϕ为参数)上点到直线20x y -的最大距离是 . 24.12F F 、是椭圆2214x y +=的左、右焦点,点P 在椭圆上运动,则12||||PF PF ⋅的最大值是 .25.已知椭圆焦点为F 1(0,-22),F 2(0, 22),长轴长为6, 过焦点的弦的长等于短轴长,求这焦点弦的倾斜角.26.在椭圆191622=+y x 上求一点M ,使它到直线l:3x+4y -50=0的距离最大或最小.27.在△ABC 中,BC=24,AC 、AB 的两条中线之和为39,求△ABC 的重心轨迹方程. 29.椭圆12222=+b y a x 与x 轴、y 轴正方向相交于A 、B ,在第一象限内的椭圆上求一点C ,使得四边形OACB 的面积最大. 30.点A 、B 分别是椭圆1202362=+y x 长轴的左、右端点,点F 是椭圆的右焦点,点P 在椭圆上,且位于x 轴上方,PF PA ⊥.(1)求点P 的坐标;(2)设M 是椭圆长轴AB 上的一点,M 到直线AP 的距离等于||MB ,求椭圆上的点到点M 的距离d 的最小值.双曲线练习1.F 1、F 2为双曲线1422-=-y x 的两个焦点,点P 在双曲线上,且∠F 1PF 2=90°,则△F 1PF 2的面积是________________.2.双曲线焦点在y 轴上,且一个焦点在直线5x -2y +20=0上,两焦点关于原点对称,35=a c,则此双曲线的方程是________. 3.已知双曲线22163x y -=的焦点为1F 、2F ,点M 在双曲线上且1MF x ⊥轴,则1F 到直线2F M 的距离为________________.4.已知双曲线22a x -22b y =1(a >0,b >0)的右焦点为F ,右准线与一条渐近线交于点A ,△OAF的面积为22a (O 为原点),则两条渐近线的夹角为______________________.5.已知定点A 、B 且|AB|=4,动点P 满足|PA|-|PB|=3,则|PA|的最小值是_________________.6.已知F 1、F 2是双曲线)0,0(12222>>=-b a by a x 的两焦点,以线段F 1F 2为边作正三角形MF 1F 2,若边MF 1的中点在双曲线上,则双曲线的离心率是_________________.7.过双曲线22221x y a b-=(a >0,b >0)的左焦点且垂直于x 轴的直线与双曲线相交于M 、N 两点,以MN 为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_________.8.双曲线112422=-y x 上点P 到左焦点的距离为6,这样的点有______个. 9.直线y=x+3与曲线14||92=-x x y 的交点个数是 . 10.双曲线的两准线间的距离是焦距的53,则此双曲线的离心率为 . 11.已知双曲线的渐近线方程是x y 32±=,且双曲线过点(3,4),则双曲线的离心率为 ,双曲线的方程为 .12.设连接共轭双曲线四个顶点和四个焦点所成两个四边形的面积分别为S 1,S 2,则(21S S )max 为 .13.已知双曲线的两个焦点坐标为F 1(0,-10), F 2(0,10)且一条渐近线方程是430x y -=,则双曲线的标准方程为14.已知双曲线经过)3,453(-A ,且与另一双曲线116922=-y x ,有共同的渐近线,则此双曲线的标准方程是 .15.已知双曲线的一条渐近线方程是043=+y x ,焦点是椭圆12510022=+y x 与坐标轴的交点,则双曲线的标准方程是 .16.已知双曲线的两条渐近线所夹的锐角是60︒,则此双曲线的离心率为 . 9.直线y x =-1被双曲线,3222=-y x所截得弦的中点坐标是 ,弦长是 .17.已知关于x ,y 的二次方程4814)16()4(222+-=-+-m m y m x m 表示的是双曲线,则m的取值范围是 .18.已知双曲线方程为191622=-y x ,经过它的右焦点F 2,作一条直线,使直线与双曲线恰好有一个交点,则该直线的斜率是 . 19.已知双曲线方程为422=-x y,过一点P (0,1),作一直线l ,使l 与双曲线无交点,则直线l 的斜率k 的集合是 .20.双曲线191622=-y x 右支上一点P 到左右两个焦点的距离之比是5:3,则P 点右准线的距离为_____________.21.以230x y ±=为渐近线,且经过点(1?,?2)的双曲线是 .22.双曲线的离心率e =2,则它的一个顶点把焦点之间的线段分成长、短两段的比是 .23.双曲线1322=-y x 的渐近线中,斜率较小的一条渐近线的倾斜角为 .24.若双曲线2222b y a x -=1的一条渐近线的倾斜角为锐角α,则双曲线的离心率为____________.25.已知双曲线的渐近线方程为043=±y x ,一条准线的方程为0335=+y ,则双曲线方程 . 26.双曲线1422=+ky x 的离心率e ∈(,)12,则k 的取值范围是______________.27.椭圆14222=+a y x 与双曲线1222=-y a x 的焦点相同,则a = .28.如图,OA 是双曲线的实半轴,OB 是虚半轴,F 为焦点, 且∠=︒BAO 30,S ABF ∆=)336(21-,则该双曲线方程是 . 29.已知双曲线的中心在原点,以坐标轴为对称轴,且与圆x y 2217+=相交于点A (4?,?-1),若圆在点A 的切线与双曲线的渐近线平行,求此双曲线的方程.30.双曲线与椭圆1362722=+y x 有共同的焦点,它们的一个交点的纵坐标为4,求双曲线的方程.31.直线231+=x y 与双曲线14922=-y x 的两个交点与原点构成三角形,求此三角形的面积.32.已知双曲线b x a y a b 222222-=上有一点P ,焦点为F 1、F 2,且∠=F PF 12α,求证:2221αctgb S PF F ·=∆.33.斜率为2的直线l 被双曲线12322=-y x 截得的弦长为1552,求直线l 的方程.34.已知P 为双曲线x y 2244-=上的动点,Q 是圆41)2(22=-+y x 上的动点,求PQ 的最小值。