数值微分与数值积分练习题

(3) 被积函数f(x)没有具体的解析表达式, 其函数关系由表格或图形表示.对于这些情况, 要计算积分的准确值都是十分困难的. 由此可见, 通过原函数来计算积分有它的局限性, 因而研究一种新的积分方法来解决Newton-Leibniz公式所不能或很难解决的积分问题,这时需要用数值解法来建立求积分的近似计算方法.但是点ξ的具体位置一般是未知的, 因而的值也是未知的, 称为f (x )在区间[a ,b ]上的平均高度.那么只要对平均高度提供一种算法，相应地就获得一种数值求积方法)(ξf )(ξf )(ξf定义4.1如果某个求积公式对于次数不大于m 的多项式均能准确的成立,但对于m+1次多项式就不一定准确，则称该求积公式具有m 次代数精度.从而验证求积公式的代数精度时,只需验证该求积公式对是否成立即可.12,,,,,1)(+=m m x x x x x f 4.1.2 代数精度的概念mm xa x a x a a x f ++++= 2210)(注：由于次数不大于m 的多项式可以表示为例4.2验证梯形公式的代数精度.练习4.1验证中矩形公式和Simpson公式的代数精度.（2）先用某个简单函数近似逼近f (x ), 用代替原被积函数f (x )，即)(x ϕ)(x ϕ⎰⎰≈babadxx dx x f )()(ϕ要求：函数应对f (x )有充分的逼近程度,并且容易计算其积分.)(x ϕ由于多项式能很好地逼近连续函数,且又容易计算积分,因此将选取为插值多项式, 这样f (x )的积分就可以用其插值多项式的积分来近似代替)(x ϕ以此构造数值算法.定理4.1n +1个节点的求积公式至少有n 次代数精度的充要条件是它是插值型的.()nn k k k I A f x ==∑代入插值求积公式(4.6)有()0()()k nn n k k I b a C f x ==-∑称为Newton-Cotes 求积公式,称为Cotes 系数()kn C (2)显然, 是不依赖于积分区间[a ,b ]以及被积函数f (x )的常数,只要给出n ,就可以算出Cotes 系数.()kn C (1)容易验证()01nn kk C==∑注(4.7)4.2.2 偶阶求积公式的代数精度n阶Newton-Cotes公式至少具有n次代数精度梯形公式(一阶Newton-Cotes公式)具有1次代数精度Simpson公式(二阶Newton-Cotes公式)具有3次代数精度定理4.2当n为偶数时, Newton-Cotes公式(4.7)至少有n+1次代数精度.4.2.4 复化求积法及其收敛性由梯形、Simpson和Cotes求积公式余项可知，随着求积节点数的增多，对应公式的精度也会相应提高.但由于n≥8时的Newton-Cotes公式开始出现负值的Cotes 系数.根据误差理论的分析研究,当积分公式出现负系数时,可能导致舍入误差增大,并且往往难以估计.因此不能用增加求积节点数的方法来提高计算精度.在实际应用中,通常将积分区间分成若干个小区间,在每个小区间上采用低阶求积公式,然后把所有小区间上的计算结果加起来得到整个区间上的求积公式,这就是复化求积公式的基本思想.常用的复化求积公式有复化梯形公式和复化Simpson 公式.。

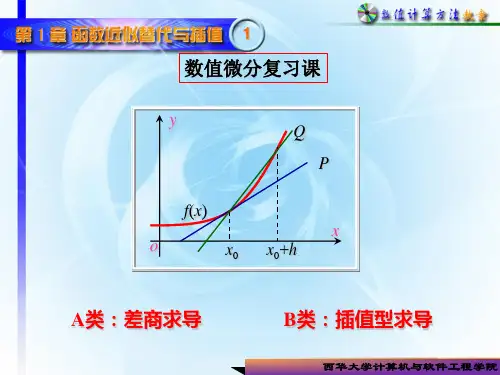
数值积分与数值微分习题课数值积分与数值微分习题课一、已知012113,,424x x x ===，给出以这3个点为求积节点在[]0.1上的插值型求积公式解：过这3个点的插值多项式基函数为()()()()()()()()()()()()()()()()120201020212101201222021120,0,1,2k k x x x x l x x x x x x x x x l x x x x x x x x x l x x x x x A l x dx k --=----=----=--==?()()()()()()()()()()()()11120000102110210010121012020211322411133424413144111 3324241142x x x x x x A dx dx x x x x x x x x x x A dx dx x x x x x x x x x x A dx x x x x ?-- --?===---- ???-- --?===----- ???-- ??--==--??102313134442dx ??=--故所求的插值型求积公式为211123343234f x dx f f f ≈-+ ? ? ???????二、确定求积公式()()(11158059f x dx f f f -??≈++??的代数精度，它是Gauss 公式吗？证明：求积公式中系数与节点全部给定，直接检验依次取()23451,,,,,f x x x x x x =，有[](111112151815191058059dx xdx --==?+?+==?+?+??(((221221331331441441551551215805391058059215805591058059x dx x dx x dx x dx ----??==?+?+??==?+?+??==?+?+??==?+?+??本题已经达到2n-1=5。

数值分析练习题及答案数值分析练习题及答案数值分析是应用数学的一个分支，它研究如何使用数值方法解决实际问题。

在数值分析的学习过程中，练习题是非常重要的一部分，通过练习题的完成，我们可以更好地理解和掌握数值分析的原理和方法。

本文将给出一些数值分析的练习题及其答案，希望对读者有所帮助。

一、插值与拟合1. 插值是指根据已知数据点的函数值，通过某种方法推导出在这些数据点之间的函数值。

请问插值的目的是什么？答案：插值的目的是通过已知数据点的函数值，推导出在这些数据点之间的函数值，以便于我们在这些数据点之间进行计算和分析。

2. 拟合是指根据已知数据点的函数值，通过某种方法找到一个函数，使得该函数与这些数据点尽可能接近。

请问拟合的目的是什么？答案：拟合的目的是通过已知数据点的函数值，找到一个函数，使得该函数与这些数据点尽可能接近，以便于我们对数据的趋势和规律进行分析和预测。

二、数值积分1. 数值积分是指通过数值方法计算一个函数在某个区间上的积分值。

请问数值积分的应用领域有哪些？答案：数值积分在科学计算、工程设计、金融分析等领域都有广泛的应用。

例如，在物理学中，数值积分可以用来计算物体的质心、重心等重要物理量；在金融分析中，数值积分可以用来计算期权的价格和风险价值等。

2. 辛普森法则是一种常用的数值积分方法，它通过将积分区间划分为若干个小区间，并在每个小区间上使用一个二次多项式来逼近被积函数。

请问辛普森法则的原理是什么？答案：辛普森法则的原理是通过将积分区间划分为若干个小区间，并在每个小区间上使用一个二次多项式来逼近被积函数。

然后，通过对这些小区间上的二次多项式进行积分，最后将这些积分值加起来，就可以得到整个积分区间上的积分值。

三、数值微分1. 数值微分是指通过数值方法计算一个函数在某个点处的导数值。

请问数值微分的作用是什么？答案：数值微分的作用是通过数值方法计算一个函数在某个点处的导数值，以便于我们对函数的变化趋势和规律进行分析和预测。

第7章 数值微分与数值积分一、填空题1. 设()11=f ，()22=f ，()03=f ，由数值微分的三点求导公式得到()≈'1f .2. 已知()11=f ，()53=f ，()35-=f ，由Simpson 求积公式求得()≈⎰dx x f 51. 3. 计算积分dx x ⎰10.5，取4位有效数字. 用梯形公式计算求得的近似值为 ，用Simpson 公式计算求得的近似值为 ；梯形公式的代数精度为 ，Simpson 公式的代数精度为 . 4. 若用复化梯形公式计算⎰10dx e x，要求误差不超过610-，至少用 个求积节点（利用余项公式估计）.二、单选题1. 等距二点求导公式()≈'1x f ( ).A ．()()0101x x x f x f --B ．()()1001x x x f x f --C ．()()1001x x x f x f -+D ．()()0101x x x f x f +- 2. 5个节点的Newton-Cotes 求积公式，至少具有的代数精度次数为( ).A ．5B ．4C ．6D ．3三、判断题1. 求积公式的精度随着代数精度的增加而提高. （ ）2. 当8≥n 时，Newton-Cotes 求积公式会发生数值不稳定性. （ ）四、计算题1. 求积公式为()()()[]⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-++-≈⎰-21211111f f B f f A dx x f ，求A 、B 使求积公式的代数精度尽量高，并求其代数精度.2. 已知数值积分公式为()()()[]()()[]h f f h h f f h dx x f h '-'++≈⎰00220λ，试确定积分公式中的参数λ，使其代数精确度尽量高，并其其代数精确度.3. 取4个等距节点，用复化梯形公式求⎰10dx e x 的近似值（取四位小数），并求该近似值有效数字的位数.五、综合题 1. 判断数值求积公式[])2()1(23)( 30f f dx x f +≈⎰是否为插值型求积公式，给出原因.2. 取5个等距节点，分别用复化梯形公式和复化Simpson 公式计算积分dx x ⎰+202211的近似值（保留四位小数）.。

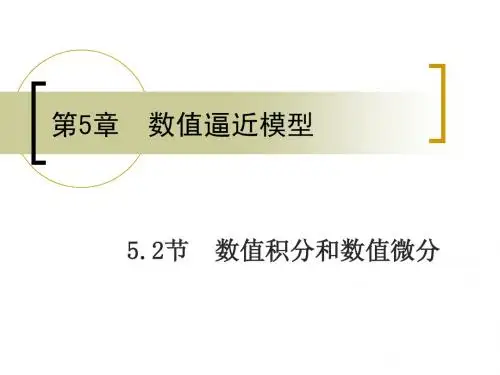
4.1数值第４章数值微分与积分微分【4.1.1】已知x 2.5 2.6 2.7 2.8 2.9y12.182513.463714.879716.444618.1741（1）用前差、后差和中心差求 2.7x =的一阶导数值（2）用中心差求 2.7x =的二阶导数值【4.1.2】用泰勒展开()()()()()()()2312!3!i i i i i f x f x f x f x f x x x x +¢¢¢¢¢¢=+D +D +D +K\*MERGEFORMAT (1.1)()()()()()()()2312!3!i i i i i f x f x f x f x f x x x x -¢¢¢¢¢¢=-D +D -D +K\*MERGEFORMAT (1.2)（1）推导微分公式()()()()1i i i f x f x f x O x x+-¢=+D D ()()()()1i i i f x f x f x O x x--¢=+D D ()()()()2112i i i f x f x f x O x x+--¢=+D D ()()()()()()1122i i i i f x f x f x f x O x x +--+¢¢@+D D 另外：()()()()()()()()()()111112''2i i i i i i i i i i f x f x f x f x f x f x h h f x h h f x f x f x h +-++-----¢¢»=-+=【4.1.3】采用泰勒展开方法确定下列数值微分公式0000(,)()()(2)x h af x bf x h cf x h f =++++提示：取00(,)'()x h f x f =，00(,)''()x h f x f =【解】2300001()()'()''()()2f x h f x hf x h f x O h +=+++230000(2)()2'()2''()()f x h f x hf x h f x O h +=+++00023000()()(2)1()()(2)'()(2)''()max(,,)()2af x bf x h cf x h a b c f x b c hf x b c h f x a b c O h ++++=+++++++如果：（1）取00(,)'()x h f x f =，则有关系：210; (2)1; (2)02a b c b c h b c h ++=+=+=得到：123,,c b a =-==-（2）取00(,)''()x h f x f =，则有关系：210; (2)0; (2)12a b c b c h b c h ++=+=+=得到：222121,,c b a ==-=【4.1.4】（1）二阶微分写为：11/2211/21/22()2()()''()(/2)()2()()''()(/2)j j j j j j j j f x f x f x f x h f x f x f x f x h +++++-+=-+=\*MERGEFORMAT (1.3)有什么区别（2）1/2111/2211/2()()'(()()/)'()/2''(2)()2()()/2j j j j j j j j j j f x f x f x f x h f f x f x x h hf x f x f x h h ++++++---==-=-+\*MERGEFORMAT (1.4)结果对否，为什么？【解】对于（1.3）式23111()()'()''()'''()26j j j j j f x f x hf x h f x h f x +=++++L \*MERGEFORMAT (1.5)231/2111()()'()(/2)''()(/2)'''()226j j j j j f x f x hf x h f x h f x +=++++L \*MERGEFORMAT (1.6)将2(1.6)(1.5)´-,得，（非对称，一阶精度），对称，二阶精度）对于（1.4）式应该是1/2111/221()()()()'()'()/2''()()2()()/4j j j j j j j j j j f x f x f x f x h f f x f x x hhx f hf f x x h +++++--=--==-+\*MERGEFORMAT (1.7)11'()()()j j j f x f x f x h++=-,即差分定义要围绕j x 点，而（1.4）式中1'()j f x +的下一步定义111/2()('())/2j j j f x f x f x h +++-=与j x 点无关，结果是错的。