卡平方测验
- 格式:doc
- 大小:630.00 KB
- 文档页数:13


第八章卡平方(χ2)测验知识目标:●理解卡平方(χ2)的概念;●掌握适合性测验的方法;●掌握独立性测验的方法;●了解卡平方(χ2)的可加性和联合分析。
能力目标:●学会适合性测验的方法;●学会独立性测验的方法;前面介绍了数量性状资料的统计分析方法。
在生物和农业科学研究中,还有许多质量性状的资料,这样的资料可以转化为次数资料。
间断性变数的计数资料也可整理为次数资料。
凡是试验结果用次数表示的资料,皆称为次数资料。
次数资料的统计分析方法有二项分布的正态接近法和卡平方(χ2)测验法等。
本章主要介绍卡平方测验。
第一节卡平方(χ2)测验一、卡平方(χ2)概念为了便于理解,现结合一实例说明χ2统计量的意义。
菠菜雌雄株的性比为1:1,今观测200株菠菜,其中有92棵雌株,108棵雄株。
按1:1的性比计算,雌、雄株均应为100株。
以O表示实际观察次数,E表示理论次数,可将上述情况列成表8-1。
表8-1 菠菜雌雄株实际观测株数与理论株数的比较性别观测株数O理论株数EO-E(O-E)2/E雌92(O1)100(E1)-8 0.64雄108(O2)100(E2)8 0.64合计200 200 0 1.28从表8-1看到,实际观察次数与理论次数存在一定的差异,这里雌、雄各相差8株。
这个差异是属于抽样误差,还是菠菜雌雄性比发生了实质性的变化?要回答这个问题,首先需要确定一个统计量用以表示实际观察次数与理论次数偏离的程度,然后判断这一偏离程度是否属于抽样误差,即进行显著性测验。
为了度量实际观察次数与理论次数偏离的程度,最简单的办法是求出实际观察次数与理论次数的差数。
从表8-1看出:O1-E1= 8,O 2-E 2=8,由于这两个差数之和为0, 显然不能用这两个差数之和来表示实际观察次数与理论次数的偏离程度。
为了避免正、负抵消,可将两个差数O 1-E 1、O 2-E 2平方后再相加,即计算∑-2)(E O ,其值越大,实际观察次数与理论次数相差亦越大,反之则越小。


卡平方测验公式
卡方检验(Chi-Square Test)是一种常用于统计学研究中的检验方法,用于判断两个分类变量之间是否存在关联性。
卡方检验的公式为:
χ²=Σ(Oi−Ei)²/Ei
其中,χ²代表卡方值,Oi代表观察值,Ei代表期望值。
观察值是指实际观察到的数据,期望值是指在假设两个变量没有关联的情况下,根据样本的总数和各分类的比例计算出的预期值。
卡方检验的原理是比较观察值与期望值的差异是否显著。
如果观察值与期望值的差异很大,就表明两个变量之间存在关联性,并且卡方值会很大。
如果差异不显著,就表明两个变量之间没有关联性,并且卡方值会接近于0。
在实际应用中,卡方检验常用于分析定类变量之间的关系。
例如,研究不同性别对健康状况的影响,可以将性别和健康状况分别作为两个分类变量,并通过卡方检验来确定它们之间是否存在关联性。



卡平方测验
实验目的
1.以提供的数据练习计算x2值,并测定其是否近似理论假设的期望比值。
2.依据相应自由度,检验计算所得x2值。
3.熟练掌握x2值的计算和利用x2值评估实验结果
实验原理
卡平方(x2)测验的目的是以吻合度断定所获得的资料与理论上期望的比值是否满足或近似,也就是x2测验可以测定所得数据是否偏离吻合概率。
显然,如果偏差小是因为偶然机会,偏差大则不是出于偶然机会。
卡平方x2测验试图为我们解决这个问题:“骗差小到何种程度才可以认为只是出于偶然机会。
”卡平方x2值的公式如下:
x2 =∑(O-E)2/E
这里的o是特定表现型个体的观察数目;E是这一表现型在理论上期望的数目;∑是各种表现型(O-E)2/E的累加值。
例如,高茎番茄和矮茎番茄杂交,F1全为高茎,F2有102株高茎和44株矮茎。
这些资料是否符合3:1的概率?回答这个问题必须计算x2值,把计算过程综合整理于表2-1。
2
计算所得的x值为2.0548,x值意味着什么呢?如果实际观察值(O)精确等于理论期望值(E),x2值为 0,是一个完满的好适度。
于是x2值小,表明观察结果接近期望比率;x2值大,表明观察结果与期望比率存在明显差异。
一般统计学家把P=1/20或P=0.05定为显著水平。
当两组变数自由度为1时,卡平方x2值为3.841的概率是0,05,观察值与期望值相抵触。
在刚才的实例中x2=2.0548,它小于允许最大值x2 =3.841,P>0.05。
因而可以认为偏差只是偶然机会,实验数据符合3:1的概率的假设。
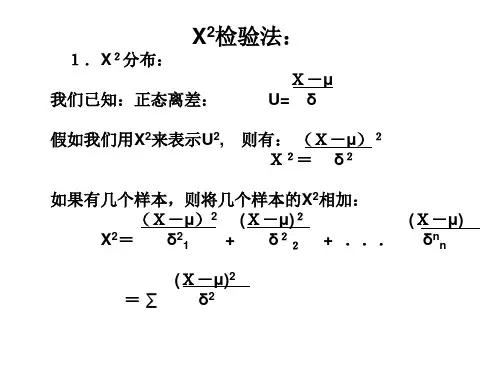

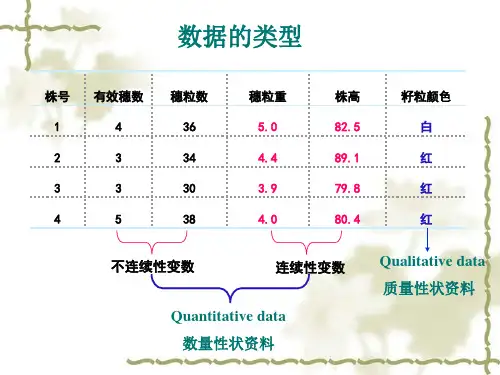

小题教学计划2.5 卡平方(χ2)测验一、次数资料的2χ测验凡试验结果出现多少次、多少回来表示的资料称为次数资料或计数资料。
在农业试验中,不论是质量性状还是数量性状,有些性状以次数表示是方便而合理的,这就要找出一个相应的概率分布测验次数资料。
一般采用2χ测验法。
卡平方(2χ)测验这一数学方法,就是判断质量性状的次数资料的某种假设的理论次数与实际次数出现的差异,是属于偶然因素产生的,还是必然的结果?因此2χ测验必须有明确的假设,然后计算实际发生的现象与假设进行比较,以确定假设的概率值,再承认或推翻假设,这同以前所讲的显著性测验的步骤是完全一样的。
(一)2χ的计算方法例题1:菠菜的雌株与雄株的比例为1:1,今观察200株菠菜,其中雌株92株,雄株108株,试测验此二数是否符合1:1的性别比例,如下表1表1 菠菜雌株与雄株的观察株数与理论株数性别 观察株数 (O ) 理论株数(E ) O-E EE O 2)(-雌 92(O 1) 100(E 1) -8 0.64 雄 108(O 2) 100(E 2) 8 0.64 总和 200(n ) 200(n ) 0 1.28计算公式是:2χ=EE O k21)(-∑ O=实际观察数 E=理论次数 k=组数从上式可以看出:2χ值是偏差与理论次数之比值的总和,用以度量观察次数与理论次数的相差程度,当偏差(O-E )愈大时,其卡平方值愈大,说明观察次数和理论次数愈不符合;当偏差愈小时,其卡平方值愈小,观察次数与理论次数愈接近;当2χ=0时,说明观察值与理论值完全符合。
因离差总和等于零,必须对(O-E )加以平方,以免除偏差正负值的影响,因此上式的分子为(O-E )2。
而分母用理论次数。
(二)2χ分布及显著性测验 1、2χ的分布2χ分布曲线可用下列方式表示:y=2212/2221]2/2[21χυυχυ---e)()(!)(上式中的υ为自由度,e 为自然对数的底数,即2.71828。
第八章卡平方(χ2)测验知识目标:●理解卡平方(χ2)的概念;●掌握适合性测验的方法;●掌握独立性测验的方法;●了解卡平方(χ2)的可加性和联合分析。
能力目标:●学会适合性测验的方法;●学会独立性测验的方法;前面介绍了数量性状资料的统计分析方法。
在生物和农业科学研究中,还有许多质量性状的资料,这样的资料可以转化为次数资料。
间断性变数的计数资料也可整理为次数资料。
凡是试验结果用次数表示的资料,皆称为次数资料。
次数资料的统计分析方法有二项分布的正态接近法和卡平方(χ2)测验法等。
本章主要介绍卡平方测验。
第一节卡平方(χ2)测验一、卡平方(χ2)概念为了便于理解,现结合一实例说明χ2统计量的意义。
菠菜雌雄株的性比为1:1,今观测200株菠菜,其中有92棵雌株,108棵雄株。
按1:1的性比计算,雌、雄株均应为100株。
以O表示实际观察次数,E表示理论次数,可将上述情况列成表8-1。
表8-1 菠菜雌雄株实际观测株数与理论株数的比较性别观测株数O理论株数EO-E(O-E)2/E雌92(O1) 100(E1) -8 0.64雄108(O2) 100(E2) 8 0.64合计200 200 0 1.28从表8-1看到,实际观察次数与理论次数存在一定的差异,这里雌、雄各相差8株。
这个差异是属于抽样误差,还是菠菜雌雄性比发生了实质性的变化?要回答这个问题,首先需要确定一个统计量用以表示实际观察次数与理论次数偏离的程度,然后判断这一偏离程度是否属于抽样误差,即进行显著性测验。
为了度量实际观察次数与理论次数偏离的程度,最简单的办法是求出实际观察次数与理论次数的差数。
从表8-1看出:O1-E1= 8,O 2-E 2=8,由于这两个差数之和为0, 显然不能用这两个差数之和来表示实际观察次数与理论次数的偏离程度。
为了避免正、负抵消,可将两个差数O 1-E 1、O 2-E 2平方后再相加,即计算∑-2)(E O ,其值越大,实际观察次数与理论次数相差亦越大,反之则越小。
但利用∑-2)(E O 表示实际观察次数与理论次数的偏离程度尚有不足。
例如某一组实际观察次数为505,理论次数为500,相差5;而另一组实际观察次数为26,理论次数为21,相差亦为5。
显然这两组实际观察次数与理论次数的偏离程度是不同的。
因为前者是相对于理论次数500相差5,后者是相对于理论次数21相差5。
为了弥补这一不足,可先将各差数平方除以相应的理论次数后再相加,并记之为χ2,即∑-=E E O 22)(χ (8-1) 也就是说,χ2是度量实际观察次数与理论次数偏离程度的一个统计量。
χ2越小,表明实际观察次数与理论次数越接近;χ2 =0,表示两者完全吻合;χ2越大,表示两者相差越大。
对于表8-1的资料,可计算得χ2=∑=+-=-28.11008100)8()(222E E O 但是,由于抽样误差的存在,χ2值究竟大到什么程度才算差异显著(不相符合),小到什么程度才算差异不显著(相符合)呢?这个问题需用χ2的显著性测验来解决,而χ2测验的依据则是χ2的抽样分布(χ2分布)。
二、卡平方(χ2)的分布理论研究证明,χ2的分布为正偏态分布,其分布特点为: 1. χ2分布没有负值,均在0~+∞之间,即在χ2=0的右边,为正偏态分布。
2. χ2的分布为连续性分布,而不是间断性的。
3. χ2分布曲线是一组曲线。
每一个不同的自由度都有一条相应的χ2分布曲线。
4. χ2分布的偏斜度随自由度ν不同而变化。
当ν=1时偏斜最厉害,ν>30时曲线接近正态分布,当ν→∞时,则为正态分布。
图8-1为几个不同自由度的χ2分布曲线。
附表列出不同自由度时χ2的一尾(右尾)概率表,可供次数资料的χ2测验之用。
三、卡平方(χ2)的连续性矫正χ2分布是连续性的,而次数资料则是间断性的。
由(8-1)式计算的χ2只是近似地服从连续型随机变量χ2分布。
在对次数资料进行χ2检验利用连续型随机变量χ2分布计算概率时,常常偏低,特别是当自由度ν=1时偏差较大。
Yates(1934)提出了一个矫正公式,矫正后的χ2值记为:2χc2χc =∑--E E O 2)5.0( (8-2)当自由度ν>1时,(8-1)式的χ2分布与连续型随机变量χ2分布相近似,这时,可不作连续性矫正。
第二节 适合性测验一、适合性测验的意义判断实际观察的属性类别分配是否符合已知属性类别分配理论或学说的假设测验称为适合性测验。
在适合性测验中,无效假设H 0:实际观察的属性类别分配符合已知属性类别分配的理论或学说;备择假设H A :实际观察的属性类别分配不符合已知属性类别分配的理论或学说。
并在无效假设H 0成立的条件下,按照已知属性类别分配的理论或学说计算各属性类别的理论次数。
因计算所得的各个属性类别理论次数的总和应等于各个属性类别实际观察次数的总和,即独立的理论次数的个数等于属性类别分类数减1。
也就是说,适合性测验的自由度等于属性类别分类数减1。
若属性类别分类数为k ,则适合性测验的自由度ν=k -1。
然后根据(8-1)或(8-2)计算出χ2或2χc 。
将计算所得的χ2或2χc 值与根据自由度ν=k -1查χ2值表(附表6)所得的临界χ2值:2050χ.、2010χ.比较:若χ2 (或2χc )<2050χ.,P >0.05,表明实际观察次数与理论次数差异不显著,可以认为实际观察的属性类别分配符合已知属性类别分配的理论或学说;若2050χ.≤χ2 (或2χc )<2010χ.,0.01<P ≤0.05,表明实际观察次数与理论次数差异显著,可以认为实际观察的属性类别分配不符合已知属性类别分配的理论或学说;若χ2 (或2χc )≥2010χ.,P ≤0.01,表明实际观察次数与理论次数差异极显著,可以认为实际观察的属性类别分配极显著地不符合已知属性类别分配的理论或学说。
二、适合性测验的方法下面结合实例说明适合性测验方法。
[例8.1]大豆花色一对等位基因的遗传研究,在F 2获得表8-2所列分离株数。
问这一资料的实际观察比例是否符合于孟德尔遗传规律中3:1的遗传比例?测验步骤如下:1.提出无效假设与备择假设H 0:大豆花色F 2分离符合3:1比例。
H A :不符合3:1比例。
2.选择计算公式 由于该资料只有k =2组,自由度ν=k -1=2-1=1,须使用公式(8-2)来计算2χc 。
3.计算理论株数 根据理论比例3:1求理论株数:紫花理论株数:E 1=289×3/4=216.75白花理论株数:E 2=289×1/4=72.25或 E 2=260-E 1=289-216.75=72.254.计算2χc表8-2 大豆花色一对等位基因基因遗传的适合性测验紫 色208 216.75 -8.75 0.3140 白 色81 72.25 +8.75 0.9420 总 和289 289 0 1.2560 2560.125.72)5.0|25.7281(|75.162)5.0|75.216208(|)5.0|(|χ2222=--+--=--=∑E E O c 5.查临界χ2值,作出统计推断 当自由度ν=1时,查附表6得2005χ.=3.84,计算的2χc <2005χ.,故P >0.05,不能否定H 0,表明实际观察次数与理论次数差异不显著,可以认为大豆花色这对性状符合孟德尔遗传分离定律3:1的理论比例。
[例8.2]两对等位基因遗传试验,如基因为独立分配,则F 2代的四种表现型在理论上应有9:3:3:1的比率。
有一水稻遗传试验,以稃尖有色非糯品种与稃尖无色糯性品种杂交,其F 2代得表8-3结果。
试问这两对性状是否符合孟德尔遗传规律中9:3:3:1的遗传比例?测验步骤:1.提出无效假设与备择假设H 0:实际观察次数之比符合9:3:3:1的分离理论比例。
H A :实际观察次数之比不符合9:3:3:1的分离理论比例。
2.选择计算公式 由于本例共有k =4组,自由度ν=k -1=4-1=3>1,故利用(8-1)式计算χ2。
3.计算理论次数 依据理论比例9:3:3:1计算理论次数:稃尖有色非糯稻的理论次数E 1:743×9/16=417.94稃尖有色糯稻的理论次数E 2:743×3/16=139.31稃尖无色非糯稻的理论次数E 3:743×3/16=139.31稃尖无色糯稻的理论次数E 4:743×1/16=46.44或 E 4=743-417.94-139.31-139.31=46.444.计算χ2表8-3 F 2代表现型的观察次数和理论次数类 型实际观察次数O 理论次数E O-E ()E E O 2-稃尖有色非糯491(O 1) 417.94(E 1) 73.06 12.772 稃尖有色糯稻76(O 2) 139.31(E 2) -63.31 28.771 稃尖无色非糯90(O 3) 139.31(E 3) -49.31 17.454 稃尖无色糯稻86(O 4) 46.44(E 4) 39.56 33.699 总 计 743 743 0 92.696 χ2=∑-E E O 2)(=12.772+28.771+17.454+33.699=92.6965.查临界χ2值(附表6),作出统计推断 当ν=3时,2005χ.=7.815,因χ2>2005χ.,P <0.05,所以应否定H 0 ,接受H A ,表明实际观察次数与理论次数差异显著,即该水稻稃尖和糯性性状在F 2的实际结果不符合9:3:3:1的理论比率。
这一情况表明,该两对等位基因并非独立遗传,而可能为连锁遗传。
实际资料多于两组的χ2值通式则为:χ2=n n m a i i -⎪⎪⎭⎫ ⎝⎛∑2 (8-3)上式的m i 为各项理论比率,a i 为其对应的观察次数。
如本例,亦可由(8-3)算得χ2=()()()()706.927437431618674316390743163767431694912222=-⎥⎦⎤⎢⎣⎡⨯+⨯+⨯+⨯前面的χ2=92.696,与此χ2=92.706略有差异,系前者有较大计算误差之故。
第三节独立性测验一、独立性测验的意义对于次数资料,除进行适合性测验外,有时需要分析两个变数是相互独立还是彼此相关,这是次数资料的一种相关研究。
例如,小麦种子灭菌与否和麦穗发病两个变数之间,若相互独立,表示种子灭菌和麦穗发病高低无关,灭菌处理对发病无影响;若不相互独立,则表示种子灭菌和麦穗发病高低有关,灭菌处理对发病有影响。
应用χ2进行独立性测验的无效假设是:H0:两个变数相互独立,对H A:两个变数彼此相关。
在计算χ2时,先将所得次数资料按照两个变数作两向分组,排列成相依表;然后,根据两个变数相互独立的假设,算出各个组的理论次数;再由(8-1)算得χ2值。