第四章 MATLAB与交直流调速系统仿真

基于MATLAB的直流调压调速控制系统的仿真引言本文将介绍如何利用MATLAB进行直流调压调速控制系统的仿真，并对系统的性能进行分析和优化。

我们将对直流调压调速控制系统的原理进行简要介绍，然后利用MATLAB进行仿真分析，最后对仿真结果进行评估和优化。

直流调压调速控制系统原理直流调压调速控制系统通常由直流电源、整流器、电动机、控制器和负载组成。

整流器将交流电源转换为直流电源，控制器通过对电动机的电流和电压进行调节，实现对电动机的调压调速控制，从而达到满足负载的要求。

MATLAB仿真分析在MATLAB中，对直流调压调速控制系统进行仿真分析，可以使用Simulink工具箱来模拟实际系统的行为。

Simulink提供了丰富的模块和函数，用户可以方便地构建控制系统的模型，并对系统的性能进行仿真和优化。

我们需要建立直流调压调速控制系统的模型，包括直流电源、整流器、电动机、控制器和负载。

控制器的设计是关键，它需要根据负载要求和环境条件对电动机进行调压调速控制。

在Simulink中，用户可以通过对模块的连接和参数的设定，快速构建控制系统的模型，并对系统的性能进行仿真。

接下来，我们需要对仿真结果进行分析，包括电动机的输出转速、输出转矩和功率等性能指标。

通过对这些性能指标的分析，可以评估控制系统的稳定性和效率，并对系统的参数进行优化。

仿真结果评估和优化在仿真过程中，我们可以对控制系统的参数进行调节和优化，以提高系统的稳定性和效率。

可以对控制器的参数进行调节，以实现对电动机的更精准的调压调速控制；也可以对整流器和负载的参数进行调节，以提高系统的整体性能。

还可以通过引入反馈控制和预测控制等先进的控制策略，对控制系统进行优化。

可以根据负载的变化和环境的变化，动态调整控制器的参数，实现对系统的实时优化。

我们需要对优化后的控制系统进行再次仿真分析，以评估优化效果。

通过对优化后的系统性能的评估，可以确定控制系统是否满足负载的要求，并产生良好的控制效果。

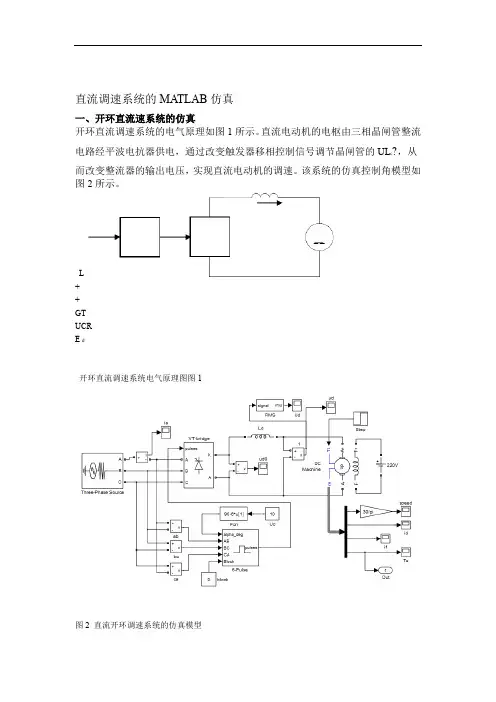
直流调速系统的MA TLAB仿真一、开环直流速系统的仿真开环直流调速系统的电气原理如图1所示。

直流电动机的电枢由三相晶闸管整流电路经平波电抗器供电，通过改变触发器移相控制信号调节晶闸管的U L c ，从而改变整流器的输出电压，实现直流电动机的调速。

该系统的仿真控制角模型如图2所示。

L++GTUCRE d--开环直流调速系统电气原理图图1图2 直流开环调速系统的仿真模型L?0，直为了减小整流器谐波对同步信号的影响，宜设三相交流电源电感s流电动机励磁由直流电源直接供电。

触发器（6-Pulse）的控制角（alpha_deg）由U 决定，移相特性的数学表达式为移相控制信号c???90?min U?90??c U cmax 1??。

在直流电动机的负载，所以，在本模型中取U?10V6??30?90U?ccmaxmin转矩输入端用Step模块设定加载时刻和加载转矩。

T L仿真算例1已知一台四极直流电动机额定参数为，，136AIU?220V?NN22。

励磁电压，励磁电，，220VminUR?0.2??1460rn?/m?22.5NGD?fNa流。

采用三相桥式整流电路，设整流器内阻。

平波电抗器??1.5A0.3RI?recf。

仿真该晶闸管-直流电动机开环调速系统，观察电动机在全压起动20mHL?d n、电磁转矩、电枢电流和起动后加额定负载时的电机转速及电枢电压的uTi ded变化情况。

220V?U N仿真步骤：1）绘制系统的仿真模型（图2）。

2）设置模块参数（表1）①供电电源电压U?RI220?0.3?136NNrec130(V)U???2?2.34?cos302.34cos?min②电动机参数励磁电阻：U220f)146.7(?R???f I1.5f励磁电感在恒定磁场控制时可取“0”。

电枢电阻：?0.2R?a电枢电感由下式估算：CU0.4?220N?19.1?L?19.1?0.0021(H)a2pnI2?2?1460?136NN L：电枢绕组和励磁绕组间的互感af U?RI220?0.2?136NNa?K?0.132(V?min/r)?e n1460N 2 6060K??0.132?K?1.26eTπ2π2K1.26T0.84(H)??L?af1.5I f电机转动惯量222.5GD2 )??0.57(kg?mJ?9.814?4g 额定负载转矩③模块参数名参数，直流电动机空载起动，5.0s3）设置仿真参数：仿真算法odel5s，仿真时间m171.4N??T 。

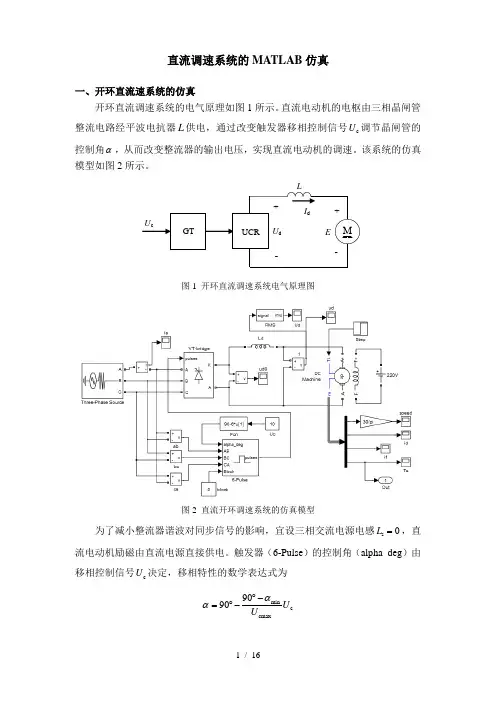
直流调速系统的MATLAB 仿真一、开环直流速系统的仿真开环直流调速系统的电气原理如图1所示。

直流电动机的电枢由三相晶闸管整流电路经平波电抗器L 供电，通过改变触发器移相控制信号c U 调节晶闸管的控制角α，从而改变整流器的输出电压，实现直流电动机的调速。

该系统的仿真模型如图2所示。

MU d+I dGTU cE +--UCR图1 开环直流调速系统电气原理图图2 直流开环调速系统的仿真模型为了减小整流器谐波对同步信号的影响，宜设三相交流电源电感s 0L =，直流电动机励磁由直流电源直接供电。

触发器（6-Pulse ）的控制角（alpha_deg ）由移相控制信号c U 决定，移相特性的数学表达式为minc cmax9090U U αα︒-=︒-在本模型中取min 30α=︒，cmax 10V U =，所以c 906U α=-。

在直流电动机的负载转矩输入端L T 用Step 模块设定加载时刻和加载转矩。

仿真算例1 已知一台四极直流电动机额定参数为N 220V U =，N 136A I =，N 1460r /min n =，a 0.2R =Ω，2222.5N m GD =⋅。

励磁电压f 220V U =，励磁电流f 1.5A I =。

采用三相桥式整流电路，设整流器内阻rec 0.3R =Ω。

平波电抗器d 20mH L =。

仿真该晶闸管-直流电动机开环调速系统，观察电动机在全压起动和起动后加额定负载时的电机转速n 、电磁转矩e T 、电枢电流d i 及电枢电压d u 的变化情况。

N 220V U =仿真步骤：1）绘制系统的仿真模型（图2）。

2）设置模块参数（表1） ① 供电电源电压N rec N 2min 2200.3136130(V)2.34cos 2.34cos30U R I U α++⨯==≈⨯︒② 电动机参数 励磁电阻：f f f 220146.7()1.5U R I ===Ω 励磁电感在恒定磁场控制时可取“0”。

基于MATLAB的直流调压调速控制系统的仿真1. 引言1.1 研究背景直流调压调速系统作为电力电子领域中的重要研究方向，其控制技术的研究一直备受关注。

随着工业自动化的发展和能源需求的增加，直流调压调速系统在工业控制和电力传输中发挥着重要作用。

传统的直流调压调速系统在控制精度、响应速度和稳定性方面存在一定的不足，因此需要不断改进和优化。

在这样的背景下，基于MATLAB的直流调压调速控制系统的仿真研究变得尤为重要。

利用MATLAB这一强大的工具，研究人员可以对系统进行建模、设计控制器、分析系统稳定性并进行仿真验证，从而实现对系统性能的优化和提升。

本文旨在通过对直流调压调速控制系统的建模、PID控制器设计与仿真、系统稳定性分析、参数优化与性能评价以及系统仿真结果分析等方面进行研究，进一步探讨如何通过MATLAB工具来实现直流调压调速系统的优化和控制。

希望通过本文的研究，能够为直流调压调速系统的控制技术研究提供一定的参考和借鉴，促进该领域的发展与进步。

1.2 研究目的直流调压调速控制系统是电气工程中常见的控制系统，在工业生产和实验研究中有着广泛的应用。

研究的目的在于通过MATLAB进行仿真，探究系统的建模、PID控制器设计、系统稳定性分析、参数优化以及性能评价等方面的问题。

通过深入研究直流调压调速控制系统的各种特性及其影响因素，可以更好地理解控制系统的工作原理和性能特点，为实际工程应用提供指导。

通过仿真实验，可以降低实验成本、提高实验效率，并能够在设计过程中进行多次调试和优化，从而得到更加理想的控制效果。

研究直流调压调速控制系统的仿真具有重要的现实意义和理论价值。

通过本研究的深入探讨，不仅可以加深对控制系统理论的理解，还可以为工程实践提供有益的借鉴和指导。

1.3 研究意义直流调压调速控制系统作为工业控制领域中的重要组成部分，其研究具有重要的理论价值和实际应用意义。

首先，在工业生产中，直流调压调速控制系统广泛应用于电动机、风电变流器、UPS电源等设备中，能够实现对电压和速度的精确控制，提高设备的运行效率和稳定性。

基于MATLAB的直流调压调速控制系统的仿真直流调压调速控制系统是一种常见的工业控制系统，广泛用于电力系统、电机驱动系统等领域。

MATLAB是一种功能强大的数学软件，可以用于建立系统的数学模型，进行仿真和控制算法的设计。

在直流调压调速控制系统中，主要包括两个部分：调压环节和调速环节。

调压环节用于控制直流电压的大小，而调速环节则用于控制直流电机的转速。

需要建立直流调压调速系统的数学模型。

以调压环节为例，可以根据直流调压系统的电路特性，建立其数学模型。

假设直流调压调速系统的输入电压为Vin，输出电压为Vout，输入电流为Iin，输出电流为Iout，则可以得到以下数学模型：Vout = K1 * Vin - K2 * IoutK1和K2分别为系统的增益参数。

接下来，需要设计调压环节的控制算法。

常见的控制算法包括比例控制、积分控制和PID控制。

假设调压环节的控制信号为U，设定电压为Vref，则可以得到以下控制算法：U = Kp * (Vref - Vout) + Ki * ∫(Vref - Vout)dt + Kd * d(Vref - Vout)/dtKp、Ki和Kd分别为比例、积分和微分参数。

然后，可以使用MATLAB进行系统仿真。

需要在MATLAB中定义系统的参数和控制算法。

然后，可以使用SIMULINK工具箱来建立系统的模型，连接各个模块，并设置输入电压和负载。

可以运行模型，观察系统的输出结果，评估系统的性能。

在仿真过程中，可以根据不同的需求和控制策略，调整系统的参数和控制算法，进行参数优化和性能改进。

基于MATLAB的直流调压调速控制系统的仿真可以帮助工程师和研究人员进行系统设计和性能评估，提高系统的稳定性和可靠性。

通过仿真还可以节省成本和时间，快速验证和优化控制算法。

基于MATLAB的直流调压调速控制系统的仿真一、直流调压调速控制系统的基本原理直流调压调速控制系统通常由电源模块、调速器、电流反馈回路、转速反馈回路以及电机等组成。

其基本工作原理是通过电源模块提供不同的电压和电流输入，调速器根据控制信号对电源模块进行控制，实现对电机的调速和调压。

电流反馈回路和转速反馈回路则可以实时监测电机的电流和转速，并将监测到的信号反馈给调速器，以实现闭环控制。

在实际应用中，一般会根据具体的需求，设计不同的调速、调压算法和控制策略，以实现系统的高性能和稳定性。

1. 模型建立我们需要建立直流调压调速控制系统的MATLAB仿真模型。

在Simulink中，我们可以按照实际系统的组成，分别建立电源模块、调速器、电流反馈回路、转速反馈回路和电机等部分的仿真模型。

在建立模型的过程中，我们需要考虑各个部分之间的耦合关系、传递函数以及控制算法和策略等因素，以建立一个真实可靠的仿真模型。

2. 参数设置在建立模型之后，我们需要对各个部分的参数进行设置。

这些参数包括电源模块的输出电压和电流、调速器的控制信号、电流反馈回路和转速反馈回路的传感器参数、电机的参数等。

在设置参数的过程中，我们需要根据实际系统的要求，进行合理的选择和调整，以保证仿真的准确性和有效性。

3. 仿真验证完成模型建立和参数设置之后，我们可以进行仿真验证。

在仿真过程中，我们可以输入不同的电压和电流信号，观察系统的输出电流和转速，并通过对比实际数据，验证仿真模型的准确性和有效性。

我们还可以对系统的性能和稳定性进行评估和优化，以提高系统的控制精度和响应速度。

4. 控制策略优化在仿真验证的基础上，我们还可以对系统的控制策略进行优化。

通过改变调速算法、调压策略和闭环控制方法等参数，在仿真环境中对系统的性能和稳定性进行评估和对比，以达到系统优化的目的。

结论通过MATLAB的Simulink工具，我们可以方便地建立直流调压调速控制系统的仿真模型，并对系统的性能和稳定性进行评估和优化。

一，转速反馈控制直流调速系统的matlab仿真1,基本原理：根据自动控制原理，将系统的被调节量作为反馈量引入系统，与给定量进行比较，用比较后的偏差值对系统进行控制，可以有效地抑制甚至消除扰动的影响，而维持被调节量很少变化或不变，这就是反馈控制的基本作用。

在负反馈基础上的“检查误差，用以纠正误差”这一原理组成的系统，其输出量反馈的传递途径构成一个闭环回路，因此被称作闭环控制系统。

在直流系统中，被调节量是转速，所构成的是转速反馈控制的直流调速系统。

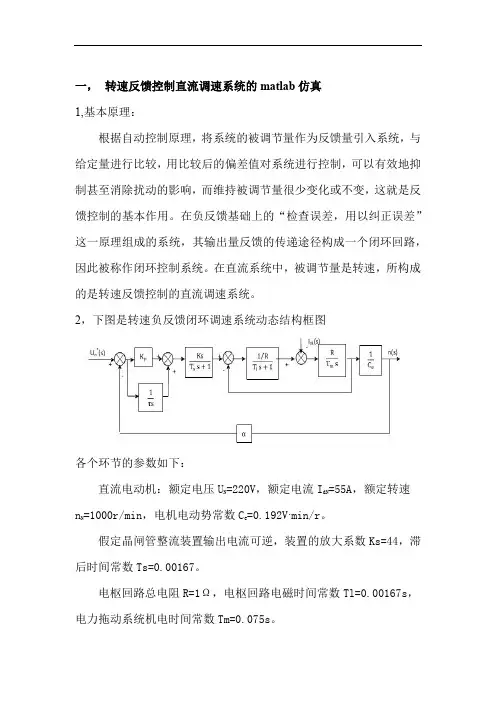
2，下图是转速负反馈闭环调速系统动态结构框图各个环节的参数如下：直流电动机：额定电压U N=220V，额定电流I dN=55A，额定转速n N=1000r/min，电机电动势常数C e=0.192V·min/r。

假定晶闸管整流装置输出电流可逆，装置的放大系数Ks=44，滞后时间常数Ts=0.00167。

电枢回路总电阻R=1Ω，电枢回路电磁时间常数Tl=0.00167s，电力拖动系统机电时间常数Tm=0.075s。

转速反馈系数α=0.01 V·min/r。

对应的额定电压U n*=10V。

在matlab的simulink里面的仿真框图如下其中PI调节器的值暂定为Kp=0.56，1/τ=11.43。

3,仿真模型的建立：进入matlab，单击命令窗口工具栏的simulink图标，打开simulink模块浏览器窗口，如下图所示：打开模型编辑器窗口，双击所需子模块库的图标，则可以打开它，用鼠标左键选中所需的子模块，拖入模型编辑窗口。

要改变模块的参数双击模块图案即可（各模块的参数图案）。

加法器模块对话框Gain模块对话框把各个模块连接起来并按照上面给定的电机参数修改各个模块相应的参数，可以得到如下的比例积分的无静差直流调速系统的仿真框图：4，仿真后的结果及其分析：其中输出scope1中可以看出超调和上升时间等。

改变PI调节器的参数，并在仿真的曲线中得到最大的超调级调整时间，相互间进行比较，如下表所示：参照以上表格中的数据分析可知，改变PI调节器的参数，可以得到快速响应的超调量不一样，调节时间不一样的响应曲线。

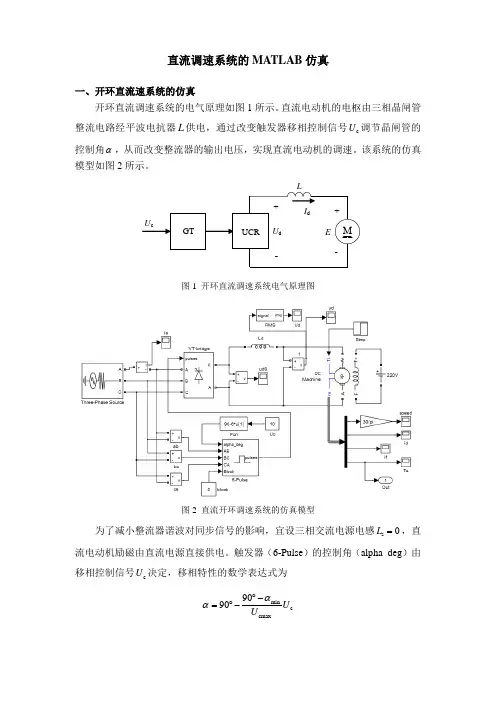
直流调速系统的MATLAB 仿真一、开环直流速系统的仿真开环直流调速系统的电气原理如图1所示。

直流电动机的电枢由三相晶闸管整流电路经平波电抗器L 供电，通过改变触发器移相控制信号c U 调节晶闸管的控制角α，从而改变整流器的输出电压，实现直流电动机的调速。

该系统的仿真模型如图2所示。

图1 开环直流调速系统电气原理图图2 直流开环调速系统的仿真模型为了减小整流器谐波对同步信号的影响，宜设三相交流电源电感s 0L =，直流电动机励磁由直流电源直接供电。

触发器（6-Pulse ）的控制角（alpha_deg ）由移相控制信号c U 决定，移相特性的数学表达式为minc cmax9090U U αα︒-=︒-在本模型中取min 30α=︒，cmax 10V U =，所以c 906U α=-。

在直流电动机的负载转矩输入端L T 用Step 模块设定加载时刻和加载转矩。

仿真算例1 已知一台四极直流电动机额定参数为N 220V U =，N 136A I =，N 1460r /min n =，a 0.2R =Ω，2222.5N m GD =⋅。

励磁电压f 220V U =，励磁电流f 1.5A I =。

采用三相桥式整流电路，设整流器内阻rec 0.3R =Ω。

平波电抗器d 20mH L =。

仿真该晶闸管-直流电动机开环调速系统，观察电动机在全压起动和起动后加额定负载时的电机转速n 、电磁转矩e T 、电枢电流d i 及电枢电压d u 的变化情况。

仿真步骤：1）绘制系统的仿真模型（图2）。

2）设置模块参数（表1） ① 供电电源电压N rec N 2min 2200.3136130(V)2.34cos 2.34cos30U R I U α++⨯==≈⨯︒② 电动机参数 励磁电阻：f f f 220146.7()1.5U R I ===Ω 励磁电感在恒定磁场控制时可取“0”。

电枢电阻：a 0.2R =Ω电枢电感由下式估算：N a N N 0.422019.119.10.0021(H)2221460136CU L pn I ⨯==⨯≈⨯⨯⨯电枢绕组和励磁绕组间的互感af L ：N a N e N 2200.21360.132(V min/r)1460U R I K n --⨯==≈⋅ T e 60600.132 1.262π2πK K ==⨯≈T af f 1.260.84(H)1.5K L I === 电机转动惯量2222.50.57(kg m )449.81GD J g ==≈⋅⨯③ 额定负载转矩L T N 1.26136171.4(N m)T K I ==⨯≈⋅表1 开环直流调速系统主要模型参数3）设置仿真参数：仿真算法odel5s ，仿真时间5.0s ，直流电动机空载起动，起动2.5s 后加额定负载L 171.4N m T =⋅。

一、单闭环（内容）1 开环直流调速系统的仿真2 单闭环有静差转速负反馈调速系统的建模与仿真3 单闭环无静差转速负反馈调速系统的建模与仿真4 单闭环电流截止转速负反馈调速系统的建模与仿真5 单闭环电压负反馈调速系统的建模与仿真6 单闭环电压负反馈和带电流正反馈调速系统的建模与仿真7 单闭环转速负反馈调速系统定量仿真8 双闭环直流调速系统定量仿真9 三闭环直流调速系统仿真10 α=β配合控制调速系统仿真11 逻辑无环流可逆直流调速系统仿真12 pwm直流调速系统仿真3 Simulink环境中的系统模型、仿真结果及分析3.1Matlab和Simulink简介3.2 Matlab建模与仿真3.3电流环的MATLAB计算及仿真3.3.1电流环校正前后给定阶跃响的MATLAB 计算及仿真3.3.2绘制单位阶跃扰动响应曲线并计算其性能指标3.3.3单位冲激信号扰动的响应曲线3.3.4电流环频域分析的MATLAB计算及仿真3.4转速环的MATLAB计算及仿真3.4.1转速环校正前后给定阶跃响应的MATLAB计算及仿真3.4.2绘制单位阶跃信号扰动响应曲线并计算其性能指标3.4.3单位冲激信号扰动的响应曲线3.4.4转速环频域分析的MATLAB计算及仿真目录摘要I1双闭环直流调速系统的工作原理1.1双闭环直流调速系统的介绍1.2双闭环直流调速系统的组成1.3双闭环直流调速系统的稳态结构图和静特性1.4双闭环直流调速系统的数学模型2系统设计方法及步骤2.1系统设计的一般原则2.2电流环设计2.2.1确定时间常数2.2.2选择电流调节器结构2.2.3选择电流调节器参数2.2.4校验近似条件2.3转速环设计2.3.1确定时间常数2.3.2选择转速调节器结构2.3.3选择转速调节器参数2.3.4校验近似条件3 Simulink环境中的系统模型、仿真结果及分析3.1Matlab和Simulink简介3.2 Matlab建模与仿真3.3电流环的MATLAB计算及仿真3.3.1电流环校正前后给定阶跃响的MATLAB 计算及仿真3.3.2绘制单位阶跃扰动响应曲线并计算其性能指标3.3.3单位冲激信号扰动的响应曲线3.3.4电流环频域分析的MATLAB计算及仿真3.4转速环的MATLAB计算及仿真3.4.1转速环校正前后给定阶跃响应的MATLAB计算及仿真3.4.2绘制单位阶跃信号扰动响应曲线并计算其性能指标3.4.3单位冲激信号扰动的响应曲线3.4.4转速环频域分析的MATLAB计算及仿真4V-M双闭环直流不可逆调速系统的电气原理总图5总结参考文献电机参数为：调速系统的基本数据如下:晶闸管三相桥式全控整流电路供电的双闭环直流调速系统,直流电动机:220V,136A,1460r/min,电枢电阻Ra=0.2Ω,允许过载倍数λ= 1.5;电枢回路总电阻:R= 0.5Ω,电枢回路总电感:L= 15mH,电动机轴上的总飞轮力矩:GD2= 22.5N·m2,晶闸管装置:放大系数Ks=40,电流反馈系数:β=0.05V/A,转速反馈系数:α=0.007Vmin/r,滤波时间常数:Toi=0.002s ,Ton=0.01s设计要求:(1)稳态指标:转速无静差;(2)动态指标:电流超调量σi≤5%,空载起动到额定转速的转速超调量σn≤10%。

基于MATLAB的直流调压调速控制系统的仿真一、引言直流调压调速控制系统是工业领域中常见的电力控制系统，其主要功能是对直流电动机进行调速和调压。

通过对电机的调速和调压，可以实现对生产过程中机械设备的精确控制，提高生产效率和质量。

对直流调压调速控制系统的研究和仿真具有重要的意义。

二、直流调压调速控制系统的基本原理和数学模型1. 直流电动机直流电动机是直流调压调速控制系统的关键部件，其工作原理是利用电磁感应原理实现电能与动能之间的转换。

直流电动机由定子、转子、电刷和电枢等部件组成，根据控制电流的大小和方向可以实现对电机的调速和调压。

直流调压调速控制系统可以使用数学模型描述其动态特性，其数学模型可以表示为以下方程：电动机转矩方程：\[T = K_{t} * Ia\]电动机电压方程：\[Va = Ri + L\frac{di}{dt} + Eb\]T表示电动机转矩，\(K_{t}\)为电动机转矩常数，Ia为电动机电流，Va为电动机电压，R为电动机电阻，L为电动机电感，\(di/dt\)为电动机电流的变化率，Eb为电动机的反电动势。

控制系统中的调速环节可以描述为：\[Eb = K_{e} * \Omega_m\]\(K_{e}\)为电动机转速常数，\(\Omega_m\)表示电动机的转速。

\(K_{c}\)为调压系数，Vr为调节电压。

以上方程描述了直流调压调速控制系统的基本动态特性，可以通过模拟仿真研究系统在不同工况下的调速和调压表现。

1. 模型参数设定首先需要确定直流电动机的参数，包括转矩常数\(K_{t}\)、转速常数\(K_{e}\)、电阻R、电感L等参数，以及控制系统的参数，包括调压系数\(K_{c}\)等参数。

2. 模型搭建利用MATLAB的Simulink工具箱进行模型搭建。

首先建立直流电动机的数学模型，包括转矩方程和电压方程。

然后建立控制系统的数学模型，包括调速环节和调压环节。

最后将直流电动机模型和控制系统模型进行组合，构建直流调压调速控制系统的整体仿真模型。

摘要随着电力拖动控制系统的发展，交流调速系统在动态响应，调速范围，稳态精度等各个方面的优良性能可以与直流调速系统相媲美，而且交流电动机拥有结构简单，维护方便等优点，交流调速系统已经成为了电动机调速的主要发展方向。

然而交流调速系统比直流调速系统复杂，所以采用计算机仿真的方法来分析交流调速系统是解决这一问题的一种有效工具。

传统的计算机仿真软件缺乏直观性和灵活性，而且操作起来并不方便，不容易实现仿真，而MATLAB软件拥有着直观、灵活、高效、易拓展等特点，而且在实时监控上有着很大的优势，又具有较强的开放性，可以在软件中编写自己的程序来拓展工具包，这是最受人们欢迎的地方。

所以本次设计采用MATLAB软件中的Simulink部分和SimPowerSystem部分进行交流调速系统的仿真，并且分析其特性。

关键字:MATLAB 交流调速系统Simulink 仿真ABSTRACTWith the development of electric drive control system, the excellent performance of AC speed regulation system in dynamic response, speed regulation range and steady-state accuracy can be compared with that of DC speed regulation system, and AC motor has the advantages of simple structure and convenient maintenance, so AC speed regulation system has become the main development direction of motor speed regulation. However, AC speed control system is more complex than DC speed control system, so using computer simulation method to analyze AC speed control system is an effective tool to solve this problem.The traditional computer simulation software is poor in intuition and flexibility, and it is inconvenient to operate and not easy to realize simulation. MATLAB software has the characteristics of intuition, flexibility, high efficiency and easy to expand, and it has great advantages in real-time monitoring and has strong openness, so it is the most popular place for people to develop toolkits by writing their own programs in the software. Therefore, thisdesign adopts Simulink part of MATLAB software to simulate the AC speed control system and analyze its characteristics.Key Words: Simulink Simulation MATLAB AC speed control system目录第一章绪论 (1)1.1 研究背景及意义 (1)1.2 交流调速系统国内外发展情况 (1)1.3 交流调速系统存在的问题 (2)第二章 MATLAB/Simulink仿真环境 (3)2.1 MATLAB的发展历程 (3)2.2 Simulink的简介 (3)2.3 MATLAB与Simulink的操作界面 (3)2.3.1 MATLAB与Simulink的操作界面 (3)2.3.2 Simulink的操作界面 (4)第三章转速闭环控制交流异步电动机调压调速系统仿真 (6)3.1基本原理 (6)3.2系统仿真模型和参数设置 (7)3.2.1系统仿真模型 (7)3.2.2主电路参数模型设置 (7)3.2.3控制电路模型参数设置 (8)3.2.4系统仿真参数设置 (9)3.3仿真结果分析 (9)第四章变频调速系统的仿真 (10)4.1 SPWM 内置波调速系统仿真 (10)4.1.1 基本原理 (10)4.1.2 系统仿真模型 (10)4.1.3 主电路模型参数设置 (10)4.1.4 控制电路模型参数 (10)4.1.5 系统仿真参数设置 (11)4.1.6 仿真结果分析 (11)4.2 SPWM外置波调速系统仿真 (11)4.2.1 系统仿真模型及参数设置 (11)4.2.2 仿真参数设置及仿真结果分析 (11)4.3 转速开环的交流异步电动机恒压频比控制调速系统 (12)4.3.1基本原理 (12)4.3.2系统仿真模型和参数设置 (12)4.3.3仿真结果分析 (13)4.4转速闭环转差频率控制的变压变频调速系统 (14)4.4.1基本原理 (14)4.4.2系统仿真模型与参数设置 (14)4.4.3仿真结果分析 (15)4.5异步电动机直接转矩控制调速系统 (15)4.5.1基本原理 (15)4.5.2系统仿真模型与参数设置 (16)4.5.3仿真结果分析 (20)4.6转速闭环、磁链闭环控制的异步电动机矢量控制调速系统 (20)4.6.1基本原理 (20)4.6.2系统仿真模型与参数设置 (20)4.6.3仿真结果的分析 (22)第五章总结........................... 错误！未定义书签。

4 MATLAB仿真应用计算机仿真技术对交直流调速系统进行仿真分析，可以加深我们对所有理论的理解，提高实践动手能力。

计算机仿真还是一种低成本的实验手段，近年来获得了广泛的应用。

目前，使用MATLAB对控制系统进行计算机仿真的主要方法是：以控制系统的传递函数为基础，使用MATLAB的Simulink工具箱对其进行计算机仿真研究。

本章就对PWM交流变频调速的MATLAB仿真作以研究。

4.1 Matlab软件简介MATLAB是矩阵实验室（Matrix Laboratory）的简称，是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分。

MATLAB和Mathematica、Maple并称为三大数学软件。

它在数学类科技应用软件中在数值计算方面首屈一指。

MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。

Matlab有以下诸多优势：（1）友好的工作平台和编程环境MATLAB由一系列工具组成。

这些工具方便用户使用MATLAB的函数和文件，其中许多工具采用的是图形用户界面。

包括MATLAB桌面和命令窗口、历史命令窗口、编辑器和调试器、路径搜索和用于用户浏览帮助、工作空间、文件的浏览器。

随着MATLAB的商业化以及软件本身的不断升级，MATLAB的用户界面也越来越精致，更加接近Windows的标准界面，人机交互性更强，操作更简单。

而且新版本的MATLAB提供了完整的联机查询、帮助系统，极大的方便了用户的使用。

简单的编程环境提供了比较完备的调试系统，程序不必经过编译就可以直接运行，而且能够及时地报告出现的错误及进行出错原因分析。

（2）简单易用的程序语言Matlab一个高级的矩阵/阵列语言，它包含控制语句、函数、数据结构、输入和输出和面向对象编程特点。