解简易方程 等式的性质

简易方程知识点梳理
简易方程是初中数学中的基础概念，下面是简易方程的知识点梳理：
1. 方程的定义
方程是含有未知量（通常用字母表示）和已知量（数或式子）的等式。

其中未知量是方程的主要研究对象。

2. 等式的性质
等式具有等价性、对称性、传递性、加法性、乘法性和反向性等性质。

3. 方程的解
方程的解就是能够使该方程成立的未知量的值。

解分有理数解、无理数解和方程无解等情况。

4. 解方程的方法
解方程的方法主要有平移法、加减消元法、倍加消元法、代入法、因式分解法、配方法等。

5. 一元一次方程
一元一次方程指只含有一个未知数，并且未知数的最高次数为1的方程。

形如ax+b=0 (a≠0)的方程为一元一次方程，其中a、b为常数，x为未知数。

6. 二元一次方程组
二元一次方程组由两个含有两个未知数的一次方程组成。

例如：ax+by=c和dx+ey=f，其中a、b、c、d、e、f为已知数。

7. 实际应用
简易方程是数学的基础，广泛应用于实际生活和工作中的计算、推理、判断等领域。

例如：在商业中应用于成本、收益的计算；在物理学中应用于速度、加速度的计算等。

以上是简易方程的知识点梳理，掌握好这些知识点对于初中学生来说非常重要，能够帮助他们更好地理解、掌握数学的基础知识。

简易方程知识点归纳一、字母表示数字母既可以表示数，也可以表示运算定律和公式1、表示数时，注意规范书写①字母和字母相乘，乘号可以简写为“·”或省略不写。

如a×b=a.b 或a×b=ab。

相同字母相乘可以简写为平方;如:a×a=a²②数字和字母相乘，可以省略乘号不写，数字必须写在前边。

如3×m=3m③含有加减除法的代数式，如果要带单位名称，代数式必须加上小括号。

2、字母表示运算定律加法交换律:a+b=b+a加法结合律:a+b+c=a+(b+c)减法的性质:a－b－c=a－(b+c) a－b－c=a－c－b乘法交换律:ab=ba乘法结合律:abc=a(cb)乘法分配律:a(b+c)=ab+ac除法的性质:a÷b÷c=a÷(bc) a÷b÷c=a÷c÷b3、字母表示公式:①长方形周长:C=2(a+b) 长方形面积:S=ab②正方形周长:C=4a 正方形面积:S=a²③行程问题路程=速度×时间:s=vt速度=路程÷时间:v=s÷t时间=路程÷速度:t=s÷v④工程问题工作总量=工作效率×工作时间c=at工作效率=工作总量÷工作时间a=c÷t工作时间=工作总量÷工作效率t=c÷a⑤总价单价和数量问题总价=单价×数量:c=ax单价=总价÷数量:a=c÷x数量=总价÷单价:x=c÷a二:解简易方程1、等式的性质1:等式两边加上或减去同一个数，左右两边仍然相等。

2、等式的性质2:等式两边乘同一个数，或除以同一个不为0的数，左右两边仍然相等。

3、含有未知数的等式叫做方程。

4、使方程左右两边相等的未知数的值，叫做方程的解。

5、求方程的解的过程叫做解方程。

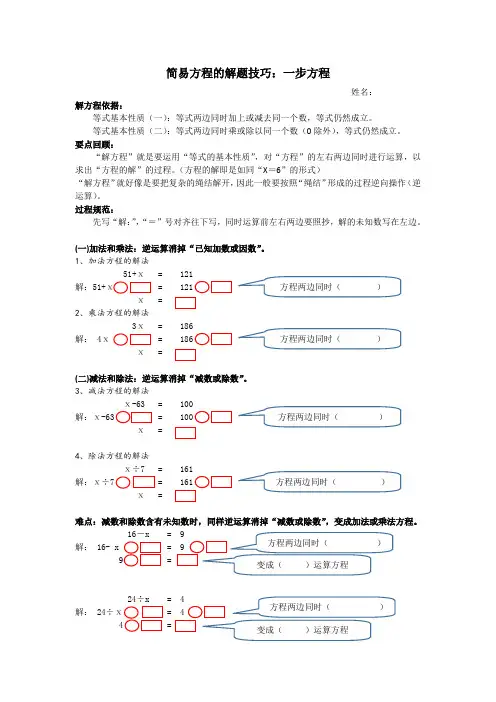
简易方程的解题技巧：一步方程姓名：解方程依据：等式基本性质（一）：等式两边同时加上或减去同一个数，等式仍然成立。

等式基本性质（二）：等式两边同时乘或除以同一个数（0除外），等式仍然成立。

要点回顾：“解方程”就是要运用“等式的基本性质”，对“方程”的左右两边同时进行运算，以求出“方程的解”的过程。

（方程的解即是如同“X ＝6”的形式）“解方程”就好像是要把复杂的绳结解开，因此一般要按照“绳结”形成的过程逆向操作（逆运算）。

过程规范：先写“解：”，“＝”号对齐往下写，同时运算前左右两边要照抄，解的未知数写在左边。

(一)加法和乘法：逆运算消掉“已知加数或因数”。

1、加法方程的解法51+ⅹ = 121解：51+ⅹ2、乘法方程的解法3ⅹ = 186解： 4ⅹⅹ(二)减法和除法：逆运算消掉“减数或除数”。

3、减法方程的解法ⅹ-63 = 100解：ⅹ ⅹ4、除法方程的解法ⅹ÷7 = 161解：ⅹ÷ ⅹ难点：减数和除数含有未知数时，同样逆运算消掉“减数或除数”，变成加法或乘法方程。

16－解：24÷x = 4 解： 24解一步方程练习X+3.2=6.4 X—7.9=2.6 1.5X=4.56 40.8＋x=57.3X÷0.92=1.57 x=63 x × 9=4.5 13+X=28.5x－6=19 x－3.3=8.9 x－25.8=95.4 x－54.3=100 x－77=275 x－77=144 x ÷7=9 x÷4.4=10 819÷x=78 x÷2.5=100 x÷3=33.3 17.6÷x=8 9－x=4.5 73.2－x=52.5 87－x=22 66－x=32.3 77－x=21.9 99－x=61.9 3.3÷x=0.3 8.8÷x=4.4。

第五单元 简易方程第 2 节 解简易方程【知识梳理】1.方程的意义。

含有未知数的等式就是方程。

注意：（1）方程一定是等式，而等式不一定是方程。

等式和方程的关系如下图所示：（2）方程必须具备的两个条件：① 必须是等式；②必须含有未知数。

2.等式的基本性质。

等式的性质1：等式两边加上或减去同一个数，左右两边仍然相等。

等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，左右两边仍然相等。

注意：因为除数不能为0，所以等式两边同时除以的数不能为0。

3.方程的解与解方程。

使方程左右两边相等的未知数的值，叫做方程的解；求方程的解的过程叫做解方程。

重点提示：“方程的解”中的“解”是名词，指使方程左右两边相等的未知数的值；“解方程”中的“解”是动词，指求方程的解的过程。

4.解形如b a =±x ，b ax =，c b =±ax 和()c b =±x a 的方程。

注意：①解方程的依据等式的性质。

②解方程的书写格式：在解方程之前必须先写“解”字，等号上、下要对齐。

5.检验。

把求得的未知数的值代入原方程，看方程左边的值是否等于方程右边的值，如果相等， 所求的未知数的值就是原方程的解；否则就不是。

依据方程的解的含义检验方程的解是否正确。

【诊断自测】一、判断：（1）5x+3是方程。

（）（2）方程是等式，等式是方程。

（）。

（3）方程的解就是解方程。

（）（4）x=0.5是方程4x=2的解。

（）二、下列式子中，哪些是等式？哪些是方程？（填序号）①6.5+3=9.5 ②0x+5 ③2x-50=2 ④4+2x=10⑤7-x>5 ⑥5+12x=65 ⑦9x=0 ⑧x÷12=6⑨9y等式：方程：三、选择。

（1）等式两边除以（）的数，左右两边仍然相等。

A.不为0B. 相同C.同一个不为0（2）x=1.5是方程（）的解。

A.18÷x=5.4+6.6B. (1.5+x)×4=7.5C.x+10.8+2.7=16四、解方程。

关于小学用等式的性质解简易方程的再认识【摘要】等式在数学中起着非常重要的作用，它是表达两个数或量相等的数学关系。

通过研究等式的性质，可以帮助小学生更好地解决简易方程，培养他们的逻辑思维能力。

在解简易方程的过程中，小学生需要掌握常见的方程类型和解方程的方法，同时还要能够将这些知识应用到实际问题中。

解方程在数学学习中是非常基础的，对于培养学生的数学素养至关重要。

等式的运用也不仅局限于数学领域，还可以在生活中解决各种实际问题。

通过学习等式的性质解简易方程不仅能够提升学生的数学水平，还可以帮助他们更好地应用数学知识解决现实生活中的难题。

【关键词】等式、性质、解方程、简易、小学生、逻辑思维能力、数学素养、实际问题、运用、基础。

1. 引言1.1 什么是等式等式是代数学中非常重要的概念，简单来说，等式是由相等关系连接的代数表达式。

在等式中，左边的表达式等于右边的表达式，表示两者相等。

等式通常由字母、数字和运算符号组成，通过运算符号的操作可以得出等式的解。

举个例子，我们可以看一个简单的等式：2x + 3 = 7。

在这个等式中，左边的表达式为2x + 3，右边的表达式为7。

通过解这个等式，我们可以得到x的值为2。

这就是等式的基本含义。

等式在数学中的作用是十分重要的，它不仅可以帮助我们理解代数运算的规律，还可以用来解决各种数学问题。

对于小学生来说，学习等式的性质和解简易方程可以培养他们的逻辑思维能力，提高他们的数学素养。

深入理解等式的概念和性质对数学学习起着至关重要的作用。

1.2 为什么要研究等式等式是数学中一个非常基础而又重要的概念，它是数学中的基本工具之一。

研究等式的性质和解简易方程的目的在于培养学生的逻辑思维能力。

通过学习等式的性质和解方程的方法，学生可以锻炼自己的推理和解决问题的能力，培养自己的逻辑思维。

在解方程的过程中，学生需要进行分析、推理和演绎，这些思维方式对于学生的日常生活和学习都具有重要的意义。

解方程是数学学习中的基础，对培养学生的数学素养至关重要。

第一单元：简易方程知识点1、在含有字母的式子里，字母中间的乘号可以记作“·”，也可以省略不写。

数与数之间的乘号不能省略。

a×a可以写作a·a (或2a) ，2a读作a的平方，表示两个a相乘。

2a表示a+a2、数字和字母相乘，省略乘号时要把数字写在前面。

（如b×4写作4b ）3、等式的性质：等式左右两边同时加、减、乘、除相同的数（0除外），等式依然成立。

方程两边同时加、减、乘、除一个不等于0的数，左右两边仍然相等。

4、方程和等式的关系：含有未知数的等式叫做方程，所有的方程都是等式，但等式不一定都是方程。

如2+3=5是等式，但不是方程。

此类题如乐园第1页，第一题。

注意：X=3此类也是方程。

5、解方程需要注意什么？（每天坚持练习）（1）一定要写‘解’字。

（2）等号要对齐。

（3）两边乘除相同数的时候，这个数不要为0.典型例子：3.8x-x=0.56 3.8-x=0.56 7x+3x+26=74 2x-4×2.5=3.66、方程的检验过程：方程左边=……=方程右边所以，X=…是方程的解。

7、列方程解应用题总结几种情况：（1）比字句。

（如课本20页第7题，根据比字句找出关系式，列方程）（2）找总量。

（如课本19页第3、4题，根据总量找关系式，列方程）（3）相遇问题（如课本21页第9题，根据总路程列方程）。

（4）根据公式列方程（如15页第3题，根据公式列方程）。

（5）根据不变量列方程。

（如：如果每个房间住6人，有20人没床位；如果每房间住8人，正好住满。

有多少房间？根据两种方案的不变量“总人数”列方程）。

请根据几种情况，找题练习。

注意：问题为两个未知量时，一般根据有关倍数的句子，写设。

方程的解是一个数值，如x=3，不加单位名称。

解方程是一个过程。

如30-3x=21，这类-x或÷x的方程的解法小学阶段没有学习，因此，列方程时，尽量不要列成此类。

人教版数学五上第五单元简易方程《等式的性质》教学设计及反教学内容：课本第55-56页教学目标：1、经历自主探索等式的基本性质的过程。

2、理解并能用语言描述等式的性质，能用等式的性质解决简单的问题。

3、积极参与数学活动，体验探索等式基本性质过程的挑战性和数学结论的确定性。

教学重点：在具体的情境中，理解等式的性质。

教学难点：理解等式的基本性质教学活动设计：一、导入新课：现在老师两只手中各拿了3支粉笔，两中手中粉笔支数的关系是怎样的？板书：3=3老师那手中的粉笔各拿下去一支，现在老师手中粉笔支数的关系又是怎样的？谁能把这个过程用一个式子表示出来呢？3－1=3=1二、新知学习（一）等式的基本性质一1、探究等式的两边同时加上或减去同一个数，等式仍然成立①天平演示：老师在天平的左盘放x克的物体，右边放50克的砝码，观察天平平衡，天平平衡说明了什么？（天平左右两边物体的质量相等），用式子表示x=50②在天平的左盘在放入20克的砝码，观察天平怎么样了？怎样表示？x+20>50③猜想要想使天平平衡应该怎样做？x+20=50+20④天平左盘放100克砝码，又边怎样放天平平衡？x+20+100=x+20+100⑤左边拿去20克，观察天平出现了什么现象？怎样才能使天平平衡？x+20+100—20=50+20+100—202、通过刚才的实验，对照这些等式你发现了什么？学生讨论3、全班交流：小结：等式的两边同时加上或减去同一个数，等式仍然成立。

4、练习：判断并说明理由①等式的两边同时加上或减去一个数等式仍然成立()②如果x=176,x+98=76—98()试做：根据等式的这个基本性质写出相关的等式：x=65x+()=65+()x—()=65—()(二)、探究等式的基本性质二1、出示：课件天平图,观察,写出式子x=105x=5X106x=6X102x=2X102、观察比较上面的两组式子,你发现了什么？(你是怎么知道的,对照式子说明理由)3、小结：等式的两边同时乘或除以同一个数(除数不能为0),等式仍然成立。

部编版五年级上册数学解简易方程，主要涉及以下知识点：
1.方程的意义：描述两个数学对象之间相等关系的一种数学工具。

2.方程的解：使方程左右两边相等的未知数的值。

3.等式的性质：等式两边加上（或减去）同一个数，结果仍然是等
式；等式两边乘（或除以）同一个数，结果仍然是等式。

4.解方程的方法：通过移项、合并同类项、化简等步骤，将方程化
为一元一次方程，然后求解得到未知数的值。

5.解方程的步骤：审题、设未知数、根据题意列方程、解方程、验
根、作答。

通过学习解简易方程，学生可以掌握基本的代数知识，为后续学习更复杂的数学问题打下基础。

1、左右两边相等的式子叫等式简易方程知识点。

举例：（自己举）方程：含有未知数的等式是方程。

举例：（自己举）2、方程一定是等式，但等式不一定是方程。

方程是特殊的等式。

等式和方程的关系用下图表示：3、等式的性质1：等式两边同时加上或减去同一个数，所得的结果仍然是等式。

等式的性质2：等式两边同时乘或除同一个不为0的数，所得的结果仍然是等式。

4、解方程的原理：天平平衡方程的解：使方程左右两边相等的未知数的值，叫做方程的解。

解方程：求方程的解的过程叫做解方程。

方程的解是一个数；解方程是一个计算过程。

5、解方程需要注意什么？（1）一定要写“解”字。

（2）等号要对齐。

（3）检验。

6、数量关系式：加法：和＝加数+加数一个加数＝和-另一个加数减法：差＝被减数-减数被减数＝差+减数减数＝被减数－差等式方程乘法：积＝因数×因数一个因数＝积÷另一个因数除法：商＝被除数÷除数被除数＝商×除数除数＝被除数÷商长方形的面积＝长×宽长方形的周长＝（长＋宽）×2正方形的面积＝边长×边长正方形的周长＝边长×4三角形的面积＝底×高÷2平行四边形的面积＝底×高梯形的面积＝（上底＋下底）×高÷2总价＝单价×数量路程＝速度×时间7、和倍问题，根据和写等量关系式；差倍问题，根据差写等量关系式。

解：设一倍数为X，几倍数就为几X。

8、行程问题注意点：要看清行驶的方向相遇问题①甲的路程＋乙的路程＝相距的路程②速度和×相遇时间＝相遇路程追及问题①快的路程－慢的路程＝相距的路程②速度差×追及时间＝路程差9、工作效率和×工作时间＝工作总量。