三年级下册数学试题-奥数练习题(1)(含答案)全国通用

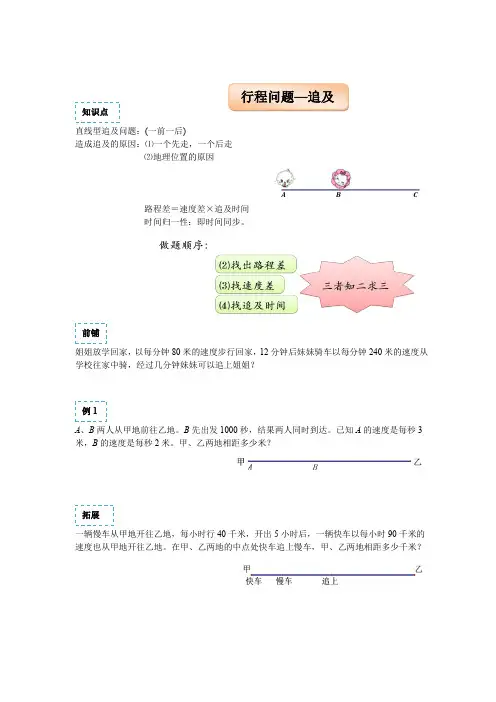
直线型追及问题：(一前一后)造成追及的原因：⑴一个先走，一个后走⑵地理位置的原因路程差＝速度差×追及时间时间归一性：即时间同步。

姐姐放学回家，以每分钟80米的速度步行回家，12分钟后妹妹骑车以每分钟240米的速度从学校往家中骑，经过几分钟妹妹可以追上姐姐？A、B两人从甲地前往乙地。

B先出发1000秒，结果两人同时到达。

已知A的速度是每秒3米，B的速度是每秒2米。

甲、乙两地相距多少米？一辆慢车从甲地开往乙地，每小时行40千米，开出5小时后，一辆快车以每小时90千米的速度也从甲地开往乙地。

在甲、乙两地的中点处快车追上慢车，甲、乙两地相距多少千米？拓展例1前铺知识点行程问题—追及甲、乙二人练习跑步，若甲让乙先跑10米，则甲跑5秒钟可追上乙；若甲让乙先跑2秒钟，则甲跑4秒钟就能追上乙。

问：甲、乙二人的速度各是多少？兄弟两人骑自行车同时从学校出发回家。

哥哥每小时行15千米，弟弟每小时行10千米。

出发半个小时后哥哥因事返回学校，到学校后又耽搁了1小时，然后动身去追弟弟。

当哥哥追上弟弟时，距学校多少千米？两人在环形跑道中同时同地同向而行1．两个人每追及一次，路程差增加一个周长；反之，两个人路程差每增加一周，必定追及一次。

2．两个人每追及一次，每次所需要的时间均相等，即每次增加t。

幸福村小学有一条200米长的环形跑道，冬冬和晶晶同时从起跑线起跑，冬冬每秒钟跑6米，晶晶每秒钟跑4米，问冬冬第2次追上晶晶时两人各跑了多少圈？在周长为400米的圆形跑道的一条直径的两端，甲、乙两人分别以每秒6米和每秒4米的速例5例4知识点例3例2度骑自行车同时同向出发(顺时针)沿圆周行驶，经过多长时间，甲第二次追上乙？测试题1．甲、乙两地相距240千米，一列慢车从甲地出发，每小时行60千米．同时一列快车从乙地出发，每小时行90千米。

两车同向行驶，快车在慢车后面，经过多少小时快车可以追上慢车？A．6 B．8 C．10 D．122．小红和小蓝练习跑步，若小红让小蓝先跑20米，则小红跑5秒钟就可追上小蓝；若小红让小蓝先跑4秒钟，则小红跑6秒钟就能追上小蓝、小红、小蓝二人的速度各是多少？A．10，6 B．6，10 C．6，8 D．8，63．王芳和李华放学后，一起步行去体校参加排球训练，王芳每分钟走110米，李华每分钟走70米，出发5分钟后，王芳返回学校取运动服，在学校又耽误了2分钟，然后追赶李华。

小学三年级下册奥数题100道附答案(完整版)1. 一条毛毛虫由幼虫长成成虫，每天长大一倍，30 天能长到20 厘米。

问长到5 厘米时要用多少天？答案：毛毛虫每天长大一倍，30 天长到20 厘米，那么29 天长到：20÷2 = 10（厘米），28 天长到：10÷2 = 5（厘米）。

所以长到5 厘米时要用28 天。

2. 小明和小红共有图书84 本，如果小明给小红14 本后，两人的图书本数相同。

小明和小红原来各有多少本图书？答案：两人图书总数不变，后来两人各有：84÷2 = 42（本）。

小明原来有：42 + 14 = 56（本），小红原来有：42 - 14 = 28（本）。

3. 一桶水，连桶重250 千克，用去一半水后，连桶还有145 千克。

桶里原有多少千克水？桶重多少千克？答案：一半水重：250 - 145 = 105（千克），桶里原有水：105×2 = 210（千克），桶重：250 - 210 = 40（千克）。

4. 果园里有梨树、桃树和苹果树共1200 棵，其中梨树的棵数是苹果树的3 倍，桃树的棵数是苹果树的4 倍。

求梨树、桃树和苹果树各有多少棵？答案：把苹果树的棵数看作1 份，梨树就是3 份，桃树就是4 份，一共是1 + 3 + 4 = 8 份。

苹果树有：1200÷8 = 150（棵），梨树有：150×3 = 450（棵），桃树有：150×4 = 600（棵）。

5. 某工厂三个车间共有180 人，第二车间人数是第一车间人数的3 倍多1 人，第三车间人数是第一车间人数的一半还少1 人。

三个车间各有多少人？答案：设第一车间有x 人，则第二车间有3x + 1 人，第三车间有0.5x - 1 人。

x + (3x + 1) + (0.5x - 1) = 1804.5x = 180x = 40第一车间有40 人，第二车间有3×40 + 1 = 121 人，第三车间有0.5×40 - 1 = 19 人。

三年级下册数学奥数题100道及答案1. 有4 个小朋友，每人分得3 个苹果，一共有多少个苹果？答案：4×3=12（个）解题思路：用人数乘以每人分得的苹果数可得苹果总数。

2. 小明每分钟跑80 米，5 分钟跑多少米？答案：80×5=400（米）解题思路：速度乘以时间等于路程。

3. 24 除以3 等于多少？答案：8解题思路：直接计算。

4. 一条绳子长15 米，剪去5 米，还剩多少米？答案：10 米解题思路：总长度减去剪去的长度。

5. 一个数加上3 等于10，这个数是多少？答案：7解题思路：10 减去3 可得。

6. 小红有15 颗糖，给了弟弟5 颗，她还剩几颗？答案：10解题思路：原有糖数减去给弟弟的数量。

7. 36 里面有几个9？答案：4解题思路：用36 除以9。

8. 长方形的长是8 厘米，宽是5 厘米，周长是多少？答案：（8+5）×2=26（厘米）解题思路：长方形周长等于（长+宽）×2。

9. 56 连续减7，减几次是0？答案：8解题思路：56 除以7 即可。

10. 把24 个苹果平均分成3 份，每份几个？答案：8解题思路：总数除以份数。

11. 18 朵花，每3 朵扎一束，可以扎几束？答案：6解题思路：花的总数除以每束的朵数。

12. 3 只鸭子5 天吃15 千克食物，1 只鸭子1 天吃多少千克食物？答案：1 千克解题思路：先算出3 只鸭子1 天吃的量，再算1 只鸭子1 天吃的量。

13. 小明有20 元，买一支笔用去8 元，还剩多少钱？答案：12 元解题思路：总钱数减去花去的钱。

14. 27 是9 的几倍？答案：3解题思路：27 除以9。

15. 一本书有30 页，每天看5 页，几天能看完？答案：6解题思路：总页数除以每天看的页数。

16. 一个正方形的边长是4 厘米，面积是多少？答案：16 平方厘米解题思路：正方形面积等于边长乘边长。

17. 45 里面有几个5？答案：9解题思路：45 除以5。

全国通用2022-2023学年三年级全册数学精选奥数题1、简单推理一、知识要点数学课上，老师布置了一道题：□＋△=28□=△＋△＋△□=（）△=（）要得出正确的结论，就要进行分析、推理。

学会了推理，能使你变得更聪明，头脑更灵活。

数学上有许多重大的发现和疑难问题的解决都离没有开推理。

解答这类推理题时，要求小朋友仔细观察，认真分析等式中几个图形之间的关系，寻找解题的突破口，然后再利用等量代换、消去等方法来进行解答。

二、精讲精练【例题1】下式中，□和△各代表几？□＋△=28□=△＋△＋△□=（）△=（）【思路导航】根据□＋△=28，我们可以得出□=28－△；由□=△＋△＋△得到28=△＋△＋△＋△，4个△等于28，一个△等于28÷4=7；由□=△＋△＋△可求出□=7＋7＋7=21。

典型练习1：1．☆＋○=18☆=○＋○☆=（）○=（）2．△＋○=25△=○＋○＋○＋○△=（）○=（）3．○＋□=36○=□＋□＋□＋□＋□○=（）□=（）【答案解析】1.12、6 2.20、5 3.30、6【例题2】下式中，□和△各代表几？□×△=36□÷△=4□=（）△=（）【思路导航】根据□÷△=4可知△为一份，□是这样的4份，即□=4△；又根据□×△=36，可以得到4△×△=36，即△×△=9，进一步得到△=3，□=4△=4×3=12。

典型练习21．○和□各表示几？○×□=16□÷○=4○=（）□=（）2．想想，填填。

○×△=20○=△＋△＋△＋△＋△○=（）△=（）3．□和○各代表几？□=○＋○＋○＋○○×□=16□=（）○=（）【答案解析】1.2、8 2.10、2 3.8、2【例题3】下式中，□和△各代表几？□＋□＋△=16□＋△＋△=14□=（）△=（）【思路导航】16里面有2个□，1个△；14里面有1个□，2个△，16减去14等于2，即□－△=2，那么如果把△换成了□，则16需要加上2，即□＋□＋□=16＋2，那么□=（16＋2）÷3=6，△=16－6×2=4。

树形图(有特殊要求的树形图、比赛进程问题)1.一个三位数，每一位上的数字都是1、2、3 中的一个，并且相邻的两个数字不同，一共有______个满足条件的三位数．2.一个三位数，每一位上的数字都是2、4、6 中的一个，并且相邻的两个数字不同，一共有______个满足条件的三位数．3.旦旦、雁雁和蒙蒙玩传球游戏，每次持球人要把球传给另外两人中的任何一人．先由旦旦拿球，第1次传球可以传给其他两人中的任何一人，经过 4 次传球之后，球又回到了旦旦手里．那么一共有________种不同的传球过程．4.旦旦、雁雁和蒙蒙玩传球游戏，每次持球人要把球传给另外两人中的任何一人．先由旦旦拿球，第1次传球可以传给其他两人中的任何一人，经过 4 次传球之后，球到了蒙蒙手里．那么一共有__________种不同的传球过程．5.一个三位数，百位数字比十位数字大，十位数字比个位数字大，个位数字不小于5，那么这样的三位数一共有__________个．6.一个三位数，个位数字比十位数字大，十位数字比百位数字大，并且都比 5 小．那么这样的三位数一共有__________个．7.阿呆、阿瓜、旦旦、雁雁四个人每个人写了一封信，把这4 封信放在一起，每个人拿一封信且不能拿自己写的信，那么一共有__________种不同的拿法．8.有4 本书排成一排，阿呆、阿瓜、旦旦、雁雁四个人选书，每人选1 本书．阿呆不要第 1 本书，阿瓜不要第2 本书，旦旦不要第3 本书，雁雁不要第 4 本书，那么一共有__________种不同的选法．9.旦旦和雁雁比赛乒乓球，约定三局两胜，如果最后旦旦获胜了，那么比赛的进程有__________种可能．10.文雯和蒙蒙比赛羽毛球，约定谁先赢两局就获胜，比赛就结束．如果最后文雯获胜了，那么比赛的进程有__________种可能．11.旦旦、雁雁和蒙蒙三个人在打牌（没有和局），一旦有人赢了2 局就获胜，牌局结束．最后旦旦赢了，那么打牌的进程有__________种不同的可能．12.阿呆、阿瓜和文雯三个人在打牌（没有和局），一旦有人赢了2 局就获胜，牌局结束．最后阿瓜赢了，那么打牌的进程有__________种不同的可能．13.小山羊、卡莉娅和小高三个人在打牌（没有和局），一旦有人赢了 2 局就获胜，牌局结束．最后小高赢了，那么有__________种不同的打牌进程．14.高高队和思思队进行足球比赛，高高队在比赛过程中从未让思思队比分领先过，最后以4 比3 取得胜利，那么比赛的进球顺序有__________ 种可能．15.高高队和思思队进行足球比赛，高高队在比赛过程中从未让思思队比分领先过，最后以 3 比2 取得胜利，那么比赛的进球顺序有__________种可能．答案：1.（12） 2.（12） 3.（6） 4.（5）5.（10）6.（4）7.（9）8.（9）9.（3）10.（3）11.（11）12.（11）13.（11）14.（14）15.（5）割圆术数学意义：“割圆术”，则是以“圆内接正多边形的面积”，来无限逼近“圆面积”。

巧填算符巧填算符，就是指在一些数之间的适当地方填上适当的运算符号（包括括号），从而使这些数和运算符号构成的算式成为一个等式。

在填算符的问题中，所填的算符包括:＋”“－”“×”“÷”“＝”“＞”“＜”“（）”“[ ]”“｛｝” 巧填算符常用的方法有：1．凑数法：先选出一个与结果比较接近的数，然后再对剩下的数进行适当的增加或减少，使算式成立。

我们把这种方法称为凑数法。

2．逆推法：是从算式中的最后一个数开始，由后往前，逐步求解，我们把这种方法称为逆推法。

逆推法思路比较固定，但是分析起来头绪繁多，因此适合于数比较少、结果比较小的添运算符号问题。

注：添运算符号问题的解都比较多，并不唯一。

如果没有特殊的要求，只要添出一种答案就可以了。

例1在5＋3×9－4＋8÷2＝66这个算式中添上两个小括号，使算式成立。

例2在下面算式的适当地方，添上运算符号＋，－，×，÷和( )，使等式成立。

9 8 7 6 5 4 3 2 1 ＝1000例3在八个8之间的适当地方，添上＋，－，×，÷运算符号，使算式成立。

8 8 8 8 8 8 8 8 ＝1000例4(第二届迎春杯决赛)试在15个8之间适当的位置填上适当的运算符号：＋、－、×、÷，使运算结果等于1986。

8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 ＝1986例5在□中填上“＋”、“－”、“×”、“÷”、“( )”使算式成立。

⑴5□5□5□5□5＝1⑵5□5□5□5□5＝2⑶5□5□5□5□5＝3⑷5□5□5□5□5＝4同学们一定都玩过扑克牌，但你会用扑克牌玩一种叫“24点”的游戏吗？其实就是－种添运算符号的游戏。

游戏规则是拿出四张牌，根据四张牌上的点数，运用加、减、乘、除四种运算中的任意几种进行计算，每张牌的点数都必须用：并且只能用一次，使最后的结果等于24。

一般地，如果完成一件事有k类方法，第一类方法中有m1种不同的做法，第二类方法中有m2种不同的做法，…，第k步有m k种不同的方法，则完成这件事共有N＝m1×m2×…×m k种不同的方法。

注：完成一件事的方法分成几类，每一类中的任何一种方法都能完成任务，这样的问题可以通过分类计数解决。

我们可以简记为：“加法分类，类类独立”。

分类时，首先要根据问题的特点确定一个适合于它的分类标准，然后在这个标准下进行分类；其次，分类时要注意满足两条基本原则：①完成这件事的任何一种方法必须属于某一类；②分别属于不同两类的两种方法是不同的方法。

只有满足这两条基本原则，才可以保证分类计数原理计算正确。

学校组织读书活动，要求每个同学读一本书，小明到图书馆借书时，图书馆有不同的外语书150 本，不同的科技书200本，不同的小说100本，那么小明借一本书可以有多少种不同的选法？一个口袋内装有3个小球，另一个口袋内装有8个小球，所有这些小球颜色各不相同，问：⑴任取一个小球，有多少种不同的取法？⑵从两个口袋内各取一个小球，有多少种不同的取法？如图，从甲地到乙地有三条路，从乙地到丁地有三条路，从甲地到丙地有两条路，从丙地到丁地有四条路，问：从甲地到丁地共有多少种走法？例4不限制数字的使用次数，用0到9这10个数字，可以组成多少个三位偶数？拓展用0到9这10个数字，可以组成多少个没有重复数字的三位偶数？例5某信号兵用红黄蓝3面旗从上到下在竖直的旗杆上表示信号，每次可以任挂1面，2面或3面，并且不同的顺序表示不同的信号，一共可以表示多少种不同的信号？例6七个相同的球，放入四个不同的盒子里，每个盒子至少放一个，不同的放法有几种？例7从19，20，21，…，97，98，99这81个数中，选取两个不同的数，使其和为偶数的选法总数是多少？测试题1．书架上有6本不同的画报，10本不同的科技书，请你每次从书架上取一本画报或者一本科技书，共有（）种不同的取法。

三年级下奥数试题及答案1. 计算题- 题目：计算下列算式的结果。

- (1) \( 35 \times 2 + 4 \)- (2) \( 72 \div 8 - 3 \)- (3) \( 48 - (12 \times 3) \)- 答案：- (1) \( 35 \times 2 + 4 = 70 + 4 = 74 \)- (2) \( 72 \div 8 - 3 = 9 - 3 = 6 \)- (3) \( 48 - (12 \times 3) = 48 - 36 = 12 \)2. 逻辑推理题- 题目：如果一个数的个位是3，十位是偶数，那么这个数可能是多少？- 答案：这个数可能是13, 23, 43, 53, 63, 73, 83, 93。

3. 图形题- 题目：观察下列图形序列，找出规律并完成序列。

- 序列：△, □, ○, △, □, ○, △, □, ○, ?- 答案：序列的规律是三角形、正方形、圆形循环出现。

所以下一个图形是○。

4. 应用题- 题目：小明有10个苹果，他给小华5个苹果，然后小华又给了小明3个苹果，最后小明有多少个苹果？- 答案：小明最初有10个苹果，给小华5个后剩下5个，小华给回3个后，小明有5 + 3 = 8个苹果。

5. 数列题- 题目：找出下列数列的规律并填写缺失的数字。

- 数列：2, 4, 8, 16, ?, 64- 答案：数列的规律是每个数字是前一个数字的两倍。

所以缺失的数字是32。

6. 空间想象题- 题目：如果一个立方体的每个面都涂有颜色，那么至少需要多少种颜色才能保证每个面至少有一种颜色？- 答案：至少需要3种颜色。

因为一个立方体有6个面，如果每种颜色涂两个面，那么需要3种颜色。

7. 时间计算题- 题目：如果现在是下午3点，那么5小时后是几点？- 答案：5小时后是晚上8点。

8. 速度与距离题- 题目：如果一辆车以每小时60公里的速度行驶，那么它需要多少时间才能行驶120公里？- 答案：时间 = 距离 / 速度 = 120公里 / 60公里/小时 = 2小时。

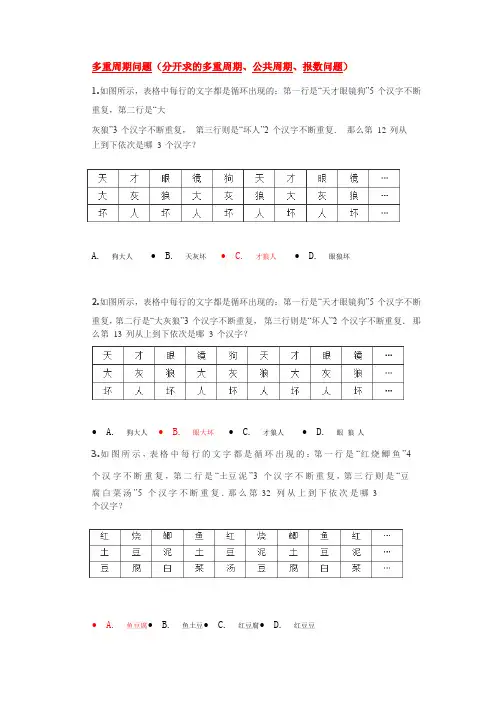
多重周期问题（分开求的多重周期、公共周期、报数问题）1.如图所示，表格中每行的文字都是循环出现的：第一行是“天才眼镜狗”5 个汉字不断重复，第二行是“大灰狼”3 个汉字不断重复，第三行则是“坏人”2个汉字不断重复．那么第12 列从上到下依次是哪3 个汉字？A. 狗大人•B. 天灰坏•C. 才狼人•D. 眼狼坏2.如图所示，表格中每行的文字都是循环出现的：第一行是“天才眼镜狗”5 个汉字不断重复，第二行是“大灰狼”3 个汉字不断重复，第三行则是“坏人”2 个汉字不断重复．那么第13 列从上到下依次是哪 3 个汉字？• A. 狗大人• B. 眼大坏• C. 才狼人• D. 眼狼人3.如图所示，表格中每行的文字都是循环出现的：第一行是“红烧鲫鱼”4个汉字不断重复，第二行是“土豆泥”3个汉字不断重复，第三行则是“豆腐白菜汤”5个汉字不断重复．那么第32 列从上到下依次是哪3个汉字？• A. 鱼豆腐• B. 鱼土豆• C. 红豆腐• D. 红豆豆4.用“疯、狂、原、始、人”5 个字，在一张方格纸中自左上到右下的斜行里按顺序循环填入．那么第80行80 列交叉处填入的字是__________．• A. 疯• B. 狂• C. 原• D. 始• E. 人5.观察下图中图形的规律，第100 个图形应该是下面A、B、C、D 四个图形中的哪一个？• A. • B.C. •D.6.如图所示，表格中每行的文字都是循环出现的：第一行是“小鸡炖蘑菇”5 个汉字不断重复，第二行是“土豆泥”3 个汉字不断重复．那么这两行的公共周期长度是__________．7.如图所示，表格中每行的文字都是循环出现的：第一行是“胡萝卜”3 个汉字不断重复，第二行是“兔子”2 个汉字不断重复．那么前95 列中“卜子”同一列中出现了__________次．8.如图所示，表格中每行的文字都是循环出现的：第一行是“火龙果”3 个汉字不断重复，第二行是“冰镇西瓜”4 个汉字不断重复．那么第4 次出现“龙瓜”在第__________列．9.观察下图中图形的规律，前121 个图形中出现了__________个黑色正方形．10.一排士兵，第一次从左到右1-3 报数，第二次从左到右1-4 报数，那么报数的公共周期长度是___．11.一排士兵，第一次从左到右1-2 报数，第二次从左到右1-5 报数，那么报数的公共周期长度是___．12.155 名士兵排成一横排，第一次从左到右1 至2 循环报数，第二次从左到右1 至5 循环报数．那么，两次都报1 的士兵有_________名．13.123 名士兵排成一横排，第一次从左到右1 至2 循环报数，第二次从左到右1至 3 循环报数．那么，两次分别报了1 和 3 的士兵有__________名．14.66 名士兵排成一横排，第一次从左到右1 至2 循环报数，第二次从右到左1至3 循环报数．那么，两次分别报了1 和 3 的士兵有__________名．15.120 名士兵排成一横排，第一次从左到右1 至3 循环报数，第二次从右到左1至4 循环报数．那么，两次分别报了1 和 4 的士兵有__________名．答案：1.（12） 2.（B） 3.（A） 4.（D）5.（D）6.（15）7.（15）8.（44）9.（20）10.（12）11.（10）12.（16）13.（21）14.（11）15.（10）。

移多补少求结果1. 阿呆和阿瓜有同样多的巧克力，阿呆给了阿瓜 3 颗巧克力，这时阿瓜比阿呆多_________颗巧克力．2. 阿呆和阿瓜有同样多的巧克力，阿呆给了阿瓜 2 颗巧克力，这时阿瓜比阿呆多_________颗巧克力．3. 阿瓜的苹果比阿呆的苹果多20 个，阿瓜给阿呆4 个苹果，这时阿瓜比阿呆多_________个苹果．4. 阿瓜的苹果比阿呆的苹果多10 个，阿瓜给阿呆 2 个苹果，这时阿瓜比阿呆多__________个苹果．5. 阿呆比阿瓜多10 颗巧克力，那么阿呆给阿瓜_________颗巧克力后，两人的巧克力数相等。

6. 阿呆比阿瓜多20 颗巧克力，那么阿呆给阿瓜_________颗巧克力后，两人的巧克力数相等7.阿瓜的积分卡比阿呆的积分卡多10 张，那么阿呆给阿瓜_________张积分卡后，阿瓜比阿呆多18张积分卡。

8. 2 个篮球的价钱可以买 6 个排球，6 个足球的价钱可以买 3 个篮球．买排球、足球、网球各 1 个的价钱可以买 1 个篮球．那么，买1 个篮球的价钱可以买_______个网球？9. 全部电灯5 小时要用40 度电，如果关掉其中一半的电灯，120 度电可以用_____小时．10. 2 只羊可换一头猪，5头猪可换1 匹马，2匹马可换_______ 只羊．11. 如果，，那么_______12. 如下图所示，5 个A 与3 个B 一样重，1 个B 与1 个A 和2 个C 一样重．1 个A 和1 个B 与______ 个C 一样重．13. 如图，观察图示规律，然后填空：（）（）（）14. 阿瓜给阿呆 4 个金币后，阿瓜比阿呆多 6 个金币，那么开始阿瓜比阿呆多__________个金币。

15. 阿瓜给阿呆 6 个金币后，阿瓜比阿呆多 4 个金币，那么开始阿瓜比阿呆多__________个金币。

16. 阿呆给阿瓜 4 张积分卡后，阿瓜比阿呆多13 张积分卡，那么原来阿瓜比阿呆多________张积分卡。

差倍（差倍问题、有暗差的差倍问题）1.旦旦的年龄比雁雁年龄的3 倍多4 岁, 旦旦比雁雁大24 岁．下列线段图正确的是__________。

A.B.C.2.雁雁和旦旦一起做仰卧起坐锻炼身体,一段时间后,雁雁做的个数比旦旦做的2 倍多 5 个,且雁雁比旦旦多做15 个．那么下列线段图正确的是__________。

A.B.C.3.某校三年级的男生比女生多45 人, 且男生比女生的3 倍少5 人．那么下列线段图正确的是_______。

A.B.C.4.某校三年级男生人数是女生人数的3 倍, 且男生比女生多30 人, 那么男生有__________人。

5.某校三年级男生人数是女生人数的4 倍, 且男生比女生多60 人, 那么女生有_________人。

6.某班级男生人数是女生人数的5 倍, 且男生比女生多20 人, 那么男生有__________人。

7.狼村里有一些狼和羊, 狼的只数比羊的2 倍多3 只, 且狼比羊多20 只．那么狼村里有羊_______只。

8.狼村里有一些狼和羊,狼的只数比羊的3 倍多2 只,且狼比羊多12 只．那么狼村里有羊________只。

9.狼村里有一些狼和羊, 狼的只数比羊的3 倍多5 只, 且狼比羊多17 只．那么狼村里有狼_______只。

10.松鼠妈妈和松鼠宝宝去釆松子, 一天下来, 妈妈釆的松子比宝宝的3 倍少2 个, 且妈妈釆的松子比宝宝的多10 个, 那么松鼠宝宝釆了_________个松子。

11.鼠妈妈带着鼠宝宝去挖土豆, 结果鼠妈妈比鼠宝宝多挖了8 个土豆, 且鼠妈妈挖的土豆比鼠宝宝的4 倍少1 个, 那么鼠妈妈挖了__________个土豆。

12.鼠妈妈带着鼠宝宝去挖土豆,结果鼠妈妈比鼠宝宝多挖了21 个土豆,且鼠妈妈挖的土豆比鼠宝宝的4 倍少3 个, 那么鼠宝宝挖了__________个土豆。

13.甲、乙两盒糖的个数一样多,现在甲盒中放入 2 颗糖,乙盒中放入12 颗糖,此时乙盒中的糖是甲盒中的 3倍．那么原来甲盒里有__________颗糖。

方阵问题【课前引入】学生排队，士兵列队，横着排叫做行，竖着排叫做列。

如果行数与列数都相等，则正好排成一个正方形，这种图形就叫方队，也叫做方阵。

方阵包括：空心方阵和实心方阵。

而实心方阵的每一层又可以单独看成一个空心方阵，因此空心方阵的规律对它也是适用的。

版块一例1小明养了一些花，他将这些花排成3行3列的方阵，后来小明又买了一些花，形成一个新的方阵，这样正好比原来的多2行2列，求小明后来买了多少盆花？拓展四年级一班同学参加了广播操比赛，排成每行8人，每列8人的方阵，问方阵中共有多少学生？如果去掉一行一列，还剩多少同学？例2同学们做操，小林站在左起第5列，右起第3列；从前数前面有4个同学，从后数后面有6个同学。

每行每列的人数同样多，做操的同学一共有多少人？拓展小美在一长方形的队伍里，她数了一下她左边有13人，右边有14人，前边有11人，后边有12人，请问你知道这队伍有多少人么？例3二年级舞蹈队为全校做健美操表演，组成一个正方形队列，后来由于表演的需要，又增加一行一列，增加的人数正好是17人，那么原来准备参加健美操表演的有多少人？拓展学生进行队列表演，排成了一个正方形队列，如果去掉一行一列，要去掉11人，问这个方阵共有多少人？版块二前铺最外层总数每层总数：(每边人数－1)×4(风车法)每边人数：每层总数÷4＋1(风车法)例4某校三年级学生排成一个方阵，最外一层的人数为36人，问方阵外层每边有多少人？这个方阵共有三年级学生多少人？前埔每向里一层：每边少2，每层少8(单数层最中心1个，第二层8个，是特例)前埔在一次团体操表演中，有一个空心方阵最外层有60人，最内层有36人，参加团体操表演的共多少人？例5将120个棋子摆成一个3层空心方阵，最内层每边有多少枚棋子？拓展人民公园有一实心方阵花坛，最外两层有32盆花，求这个花坛共有多少盆花？求总数＝(最外层每边－层数)×层数×4求最外层每边＝总数÷4÷层数＋层数例6李小姐想将原本8行8列的实心方阵花坛改成一个2层的空心方阵，求此空心方阵的最外层每边有多少盆花枚棋子？将一个最外层每边20枚棋子的2层空心方阵转换成一个6层空心方阵，求新的方阵最外层每边有多少枚棋子？版块三在一次运动会开幕式上，有一大一小2个方阵合并变换成一个10行10列的方阵，求原来这2个方阵各有多少人？测试题1．一群小猴排成整齐的队伍做操。

第十四讲逻辑推理在有些问题中，条件和结论中不出现任何数和数字，也不出现任何图形，因而，它既不是一个算术问题，也不是一个几何问题．也有这样的题目，表面看来是一个算术或几何问题，但在解决它们的过程中却很少用到算术或几何知识．所有这些问题的解决，需要我们深入地理解条件和结论，分析关键所在，找到突破口，由此入手，进行有根有据的推理，做出正确的判断，最终找到问题的答案．这类问题我们称它为逻辑推理．暑假精讲【例1】如图，请问数字1和2的对面是几？分析：由图知，1的对面不是4和6；也不可能是2和3，所以只能是5.同理2的对面是6.【例2】甲乙丙三人分别说了下面三句话，请你从他们所说的话判定谁说假话？甲说：“乙在说谎.”乙说：“丙在说谎.”丙说：“甲和乙都在说谎.”分析：假设甲没说谎，那么乙说谎，也就是丙没有说谎，这样丙所言“甲和乙都在说谎”属实，所以甲一定说谎.故乙说：“丙在说谎.”属实，所以丙也说谎，即甲和丙两人都说谎.【例3】编号是1，2，3，4的四位同学参加了学校的110米栏比赛，获得了全校的前四名.1号说：“3号比我先到终点.”得第三名的同学说：“1号不是第四名.”而另一位同学说：“我们的号码与我们所得的名次都不相同.”你能说出他们的名次吗？分析：得第三名的同学说：“1号不是第四名.”推知：1号是第一或二名，又1号说：“3号比我先到终点.”说明1号是第二名，3号是第一名. 而另一位同学说：“我们的号码与我们所得的名次都不相同.”所以4号是第三名，第四名是2号.【例4】李波、顾锋、刘英三位老师共同担负六年级某班的语文、数学、政治、体育、音乐和图画六门课的教学，每人教两门．已知：（1）顾锋最年轻；（2）李波喜欢与体育老师、数学老师交谈；（3）体育老师和图画老师都比政治老师年龄大；（4）顾锋、音乐老师、语文老师经常一起去游泳；（5）刘英与语文老师是邻居.问：各人分别教哪两门课程？分析：由（1）（3）（4）推知顾锋教数学和政治；由（2）推知刘英教体育；由（3）（5）推知李波教图画、语文．李波教语文、图画，顾锋教数学、政治，刘英教音乐、体育．【例5】四个小朋友宝宝、星星、强强和乐乐在院子里踢足球，一阵响声，惊动了正在读书的陆老师，陆老师跑出来查看，发现一块窗户玻璃被打破了．陆老师问：“是谁打破了玻璃？”宝宝说：“是星星无意打破的．”星星说：“是乐乐打破的．”乐乐说：“星星说谎．”强强说：“反正不是我打破的．”如果只有一个孩子说了实话，那么这个孩子是谁？是谁打破了玻璃？分析：因为星星和乐乐说的正好相反，所以必是一对一错，我们可以逐一假设检验．假设星星说得对，即玻璃窗是乐乐打破的，那么强强也说对了，这与“只有一个孩子说了实话”矛盾，所以星星说错了．假设乐乐说对了，按题意其他孩子就都说错了．由强强说错了，推知玻璃是强强打破的．宝宝、星星确实都说错了．符合题意．所以是强强打破了玻璃．【例6】小刚在纸条上写了一个四位数，让小明猜．小明问：“是603l吗?”小刚说：“猜对了1个数字，且位置正确．”小明问：“是5672吗?”小刚说：“猜对了2个数字，但位置都不正确．”小明问：“是4796吗?”小刚说：“猜对了4个数字，但位置都不正确．”根据以上信息，可以推断出小刚所写的四位数多少？分析：由两人的第3次问答可知小刚所写的四位数是由数字4，7，9，6组成的．因为数字6在603l中出现，所以据小刚的第1次回答知四位数的千位数字就是6．又数字7在5672和4796中均出现过，且小刚说其位置均不正确，所以7应该出现在个位．数字9在4796中出现，但它的位置也不正确，所以9只能在百位，进而4是十位数字．综上所述，所求的四位数是6947．【例7】甲、乙、丙每人有两个外号，人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家”、“大作家”和“歌唱家”称呼他们．此外：（1）数学博士夸跳高冠军跳得高；（2）跳高冠军和大作家常与甲一起去看电影；（3）短跑健将请小画家画贺年卡；（4）数学博士和小画家很要好；（5）乙向大作家借过书；（6）丙下象棋常赢乙和小画家．你知道甲、乙、丙各有哪两个外号吗？分析：由（2）知，甲不是跳高冠军和大作家；由（5）知，乙不是大作家；由（6）知，丙、乙都不是小画家．由此可得到下表：因为甲是小画家，所以由（3）（4）知甲不是短跑健将和数学博士，推知甲是歌唱家．因为丙是大作家，所以由（2）知丙不是跳高冠军，推知乙是跳高冠军．因为乙是跳高冠军，所以由（1）知乙不是数学博士．将上面的结论依次填入上表，便得到下表：所以，甲是小画家和歌唱家，乙是短跑健将和跳高冠军，丙是数学博士和大作家．【例8】学校新来了一位老师，五个学生分别听到如下的情况：（1）是一位姓王的中年女老师，教语文课；（2）是一位姓丁的中年男老师，教数学课；（3）是一位姓刘的青年男老师，教外语课；（4）是一位姓李的青年男老师，教数学课；（5）是一位姓王的老年男老师，教外语课．他们每人听到的四项情况中各有一项正确．问：真实情况如何？分析：姓刘的老年女老师，教数学．假设是男老师，由（2）（3）（5）知，他既不是青年、中年，也不是老年，矛盾，所以是女老师．再由（1）知，她不教语文，不是中年人．假设她教外语，由（3）（5）知她必是中年人，矛盾，所以她教数学．由（2）（4）知她是老年人，由（3）知她姓刘．【例9】甲乙丙丁四人进行羽毛球双打比赛，其中已知：①甲比乙年轻：②丁比他的两个对手年龄都大；③甲比他的伙伴年龄大：④甲与乙的年龄差距要比丙与丁的年龄差距要大一些．则甲的伙伴是谁？年龄最大的人是谁？分析：丙，丙．由条件①甲比乙年轻，可知甲的年龄小于乙的年龄；再由条件③甲比他的伙伴年龄大，可知甲的伙伴只能是丁或丙．而实际上丁不可能是甲的伙伴，否则甲、乙、丙3人的年龄顺序就为丁<甲<乙，这样丁就找不到两个对手都比他年轻，与条件②矛盾．因此，甲的伙伴只能是丙，故甲与丙搭档，而乙与丁搭档．根据上述的推理，我们可以得到甲、乙、丙三人的年龄大小顺序为：丙<甲<乙．再结合条件②，我们可以推断出甲、乙、丙、丁4人的年龄顺序应该是：丙<甲<乙<丁或丙<甲<丁<乙．实际上前一种情况是不可能的，否则甲、乙的年龄差距要比丁、丙的差距小，这与条件④不符，故4人的年龄顺序为丙<甲<丁<乙．年龄最大者为乙．【例10】在一次数学竞赛中，A，B，C，D，E五位同学分别得了前五名（没有并列同一名次的），关于各人的名次大家作出了下面的猜测：A说：“第二名是D，第三名是B．”B 说：“第二名是C，第四名是E．”C说：“第一名是E，第五名是A．”D说：“第三名是C，第四名是A．”E说：“第二名是B，第五名是D．”结果每人都只猜对了一半，他们的名次如何？分析：第1名是E，第2名是C，第3名是B，第4名是A，第5名是D．附加内容【附1】现有甲乙两个队比赛，甲队有A、B、C三名队员，乙队有X、Y、Z三名队员，从之前的比赛情况是：A能胜Y，Y能胜C，C能胜Z.但在第一轮比赛中他们都没有相遇，请问在第一轮比赛中谁与谁“过招”？分析：由题意知，C不与Y、Z相遇，则C只能与X相遇；Y不与A、C相遇，则Y只能与B相遇，所以A只能与Z相遇.【附2】在每四年一次的世界杯足球赛上，四支球队A、B、C、D，已知：A队两胜一负，B队两胜一和，C队医胜两负，请问D队成绩如何？分析：A、B、C、D一共需赛6场，而每场比赛只有胜、负或者平局两种情况.已知A、B、C三队共获5场胜利、1场平局，所以D除了一场平局外不可能再有胜局，所以D是两负一和.【附3】根据条件判断旅游团去了A、B、C、D、E中的哪几个地方？（1）如果去A，就必须去B；（2）D、E两地至少去一地；（3）B、C两地只能去一地；（4）C、E两地要去都去，要不去都不去；（5）若去D，则A、E两地必须去.分析：从（3）入手，分别假设去B或C：（3）若去B则不能去C，（4）也不能去E，（2）只能去D.（5）必须去A、E，与不能去E矛盾.所以不能去B.假设去C：（4）必去E，（2）需去D，（5）必须去A、E，（1）去A必须去B，与（3）B、C不能同去矛盾，所以不能去D.综上只能去C、E.大显身手1.甲乙丙三人中只有一人会开汽车.甲说：“我会开.”乙说：“我不会开.”丙说：“甲不会开.”三人中只有一人说真话.请问谁会开车？分析：如果甲说真话，那么乙也说真话，矛盾.如果乙说真话，那么甲说假话，丙说真话，矛盾.所以只能是丙说真话，只有乙会开车.2.甲乙丙三人参加完田径比赛的100米跑后，甲说：“我第一.”乙说：“我第二.”丙说：“我不是第一.”已知三人中有一人说假话.请问谁第一？谁第二？谁第三？分析：如果丙说的是假话，丙应该第一，那么甲说自己第一就矛盾.所以丙不可能说假话，那么丙肯定不是第一，显然乙不是第一，所以甲第一，乙说假话.所以甲第一、丙第二、乙第三.3.甲乙丙丁四人，乙的身高不是最高，但比甲、丁高，甲比丁高.请你按从高到矮排列.分析：乙不是最高，但比甲、丁高，甲乙也不可能是最高，所以丙是最高.乙比甲丁高，其次是乙，又已知甲比丁高，所以再次是甲，因此从高到矮是丙、乙、甲、丁.成长故事智者说：“如何才能在工作上获得100％的成功？”我们使用26个字母来玩一个游戏．A=1分，B＝2分，依此类推，Z=26分．有人说：“知识应该可以吧？”而KNOWLEDGE这个词加起来只有96分．又有人说：“辛劳的工作可以吗？”但HARDWORK这个词加起来也只有98分．那么大地怎么才能达到100％的成功呢？答案是：ATTITUDE（态度）．。

假设法解鸡兔同笼（头和腿和）1.例题1.鸡兔同笼共20 只，那么它们的腿和可能是下面哪个数？__________A. 38 条B. 43 条C. 76 条D. 88 条2.鸡兔同笼共30 只，那么它们的腿和可能是下面哪个数？__________A. 69 条B. 72 条C. 30 条D. 200 条3.鸡兔同笼共40 只，那么它们的腿和可能是下面哪个数？__________A. 150 条B. 40 条C. 70 条D. 200 条4.鸡和兔共20 只，鸡腿和兔腿共50 条，那么兔有__________只。

5.鸡和兔共25 只，鸡腿和兔腿共70 条，那么兔有__________只。

6.鸡和兔共30 只，鸡腿和兔腿共70 条，那么兔有__________只。

7.草原上有20 只三脚猫和四脚蛇在聚会，它们的脚和为72 只，那么四脚蛇有__________只。

8.草原上有30 只三脚猫和四脚蛇在聚会，它们的脚和为100 只，那么四脚蛇有__________只。

9.草原上有30 只独脚兽和三脚猫在聚会，它们的脚和为42 只，那么三脚猫有__________只。

10.50 名老师和同学参加聚餐，每名同学吃了2 个包子，每名老师吃了4 个包子，共吃了180 个包子．那么共有______名老师。

11.30 名老师和同学参加聚餐，每名同学吃了2 个包子，每名老师吃了4 个包子，共吃了68 个包子．那么共有__________名老师。

12.100 名老师和同学参加聚餐，每名同学吃了2 个包子，每名老师吃了4 个包子，共吃了280 个包子．那么共有__________名老师。

答案：1.（C） 2.（B） 3.（A） 4.（5）5.（10）6.（5）7.（12）8.（10）9.（6）10.（40）11.（4）12.（40）分组法解鸡兔同笼（头倍腿和、腿倍头和）1.鸡和兔一样多，腿和为30 条，那么鸡有__________只。

小学三年级数学下册奥数题训练1、从10000里面连续减25，减多少次差是0?【解析】10000÷25=400，所以减400次差是02、在一道没有余数的除法算式里，被除数(不为零)加上除数和商的积，得到的和，除以被除数，所得的商是多少?【解析】因为被除数÷除数=商，即被除数=除数×商所以[被除数+(除数×商)]÷被除数=1+1=23、明明和花花用同一个数做除法，明明用12去除，花花用15去除。

明明除得商是32余数是6，花花计算的结果应是多少?【解析】被除数=12×32+6=390花花计算的结果是：390÷15=264、三棵树上停着24只鸟。

如果从第一棵树上飞4只鸟到第二棵树上去，再从第二棵树飞5只鸟到第三树上去，那么三棵树上的小鸟的只数都相等，第二棵树上原有几只?【解析】三棵树上的小鸟的只数都相等时每棵树上的只数为24÷3=8只。

所以第二棵原有的只数为：8-4+5=9只。

25、两袋糖，一袋是84粒，一袋是20粒，每次从多的一袋里拿出8粒糖放到少的一袋里去，拿几次才能使两袋糖的粒数同样多。

【解析】一袋是84粒，一袋是20粒，多的比少的多了84-20=64粒;当两袋糖的粒数同样多时，拿动的粒数为64÷2=32粒，也就是每袋有20+32=52粒;每次拿出8粒一共需要的次数为：32÷8=4次6、小强、小清、小玲、小红四人中，小强不是最矮的，小红不是最高的，但比小强高，小玲不比大家高。

请按从高到矮的顺序，把名子写出来。

【解析】简单逻辑推理题，因为小强不是最矮的，小红不是最高的，但比小强高所以小强只能是第三高的，小红是第二高的;而小玲不比大家高，说明小玲最矮，此外就是小清最高;即从高到矮的顺序为：小清、小红、小强、小玲。

7、用0、6、7、8、9这五个数字组成各个数位上数字不相同的两位数共有多少个?【解析】两位数由个位和十位组成，而十位上一定不能为0，所以可能有6、7、8、9中的4种情况;而个位上除掉十位上的数字以外，还有4种可能。

三年级数学奥数题练习班级考号姓名总分（每道题都要写出解答过程）1、学校有808个同学，分乘6辆汽车去春游，第一辆车已经接走了128人，如果其余5辆车乘的人数相同，最后一辆车乘了几个同学?2、两块同样长的布，第一块用去32米，第二块用去20米，结果所余的米数第二块是第一块的3倍。

两块布原来各长多少米?3、箱里放着同样个数的铅笔盒，如果从每只里拿出60个，那么5只箱里剩下铅笔盒的个数的总和等于原来2只箱里个数的和。

原来每只箱里有多少个铅笔盒?4、3只猫3天吃了3只老鼠，照这样的效率，9只猫9天能吃( ) 只。

5、┖┴┴┴┴┴┴┴┴┴┚图中共有( )条线段。

6、一个正方形，被分成5个相等的长方形，每个长方形的周长是60厘米，正方形的周长是多少厘米7、有一串彩珠，按“2红3绿4黄”的顺序依次排列。

第600颗是( )颜色。

8、用一根绳子绕树三圈余30厘米，如果绕树四圈则差40厘米，树的周长有( )厘米，绳子长( )厘米。

9、一只蜗牛在12米深的井底向上爬，每小时爬上3米后要滑下2米，这只蜗牛要( )小时才能爬出井口。

10、锯一根10米长的木棒，每锯一段要2分钟。

如果把这根木棒锯成相等的5段，一共要( )分钟。

11、有10把不同的锁，开这10把锁的10把钥匙混在一起了，最多要试多少次，才能把这10把锁和钥匙全部配对。

12、7年前，妈妈年龄是儿子的6倍，儿子今年12岁，妈妈今年( )岁。

13、文具店有600本练习本，卖出一些后，还剩4包，每包25本，卖出多少本?14、同学们进行广播操比赛，全班正好排成相等的6行。

小红排在第二行，从头数，她站在第5个位置，从后数她站在第3个位置，这个班共有( )人15、40个梨分给3个班，分给一班20个，其余平均分给二班和三班，二班分到( )个。

16、三年级同学种树80颗，四、五年级种的棵树比三年级种的2倍多14棵，三个年级共种树多少棵?17、学校里组织兴趣小组，合唱队的人数是器乐队人数的3倍，舞蹈队的人数比器乐队少8人，舞蹈队有24人，合唱队有多少人?18、小强在计算除法时，把除数76写成67，结果得到的商是15还余5。

奥数综合练习题事物排列有次序，次序反复叫周期，先算共有几周期，余数表示是第几。

解答周期问题的关键是找规律，找出周期。

确定周期后，用总量除以周期，如果正好有整数个周期，结果就为周期里的最后一个；例1有一本书，每2页文字之间有5张插图，第一页为文字，第二页为插图，那么第100页是什么？前100页共多少张插图？例2观察下面的数列规律，说出2010在哪里？容斥原理主要运用包含，排除的思想，即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分，有时需要画文氏图，借助图形思考。

前埔有128位旅客，其中25人既不懂英语、又不懂法语，有98人懂英语，75人懂法语，请问：既懂英语、又懂法语的有多少人？例3在1至1000这1000个自然数中，能被5或11整除的自然数一共有多少个？例4甲、乙两地相距288公里，一辆汽车和一辆拖拉机同时从两地相对开出，经过4小时两车相遇，已知汽车的速度是拖拉机速度的2倍，相遇时，汽车比拖拉机多行多少公里？在行程问题中涉及到两个或两个以上物体运动的问题，其中最常见的是相遇问题和追及问题。

例5A、B两地相距480公里，两列火车同时从A地开往B地，快车每小时行60公里，慢车每小时行48公里，当快车到达B地时，慢车距B地还有多少公里？例6妹妹放学回家，以每分钟80米的速度从学校步行回家，6分钟后，哥哥骑自行车以每分钟200米的速度从学校回家，当妹妹到家时，哥哥正好追上妹妹，问哥哥经过多少分钟追上妹妹？例7甲、乙两辆车的速度差是每小时1公里(甲车的速度较快)，甲、乙两车同时从A、B两地相向而行，5小时后相遇，A、B间距离为45公里，求甲的速度？例8有一条圆形跑道长600米，小明和小林在同一地点同时出发，沿跑道背向而行。

小明每分钟前行90米，小林每分钟前行60米。

经过20分钟后，两人相遇了( )次测试题1．今年姐妹两人的年龄加起来是15岁，当姐姐和妹妹今年一样大时妹妹的年龄恰好是姐姐年龄的一半，今年姐姐几岁？2．悟空和八戒一共摘了190个桃子，悟空摘的个数比八戒的3倍还多10个，八戒和悟空各摘几个桃子？3．明明家的公寓每上一层楼就要登上21个台阶，到明明家要登上147个台阶，你知道他家住几楼吗？4．伦敦奥运会即将开幕，你能算出下面的算式中迎接奥运分别代表哪个数字吗？5．一个方阵花坛共有15层，最内层每边有20株花草，你知道整个花坛共有多少株花草吗？6．下图是一张北京到上海的列车时刻表，①从北京到济南火车运行了多长时间？②火车在济南站停靠多长时间？答案1．答案：通过线段图可知姐妹两人今年的年龄和15岁是5段，则一段是15÷5＝3(岁)妹妹＝3×2＝6(岁)姐姐＝3×3＝9(岁)答：姐姐今年9岁。

三年级下册数学竞赛试题奥数练习及解析｜通用版（含答案）1、南京长江大桥共分两层,上层是公路桥,下层是铁路桥。

铁路桥和公路桥共长11270米,铁路桥比公路桥长2270米,问南京长江大桥的公路和铁路桥各长多少米？分析：和差基本问题,和11270米,差2270米,大数=(和+差)/2,小数=(和-差)/2。

解：铁路桥长=(11270+2270)/2=6770米,公路桥长=(11270-2270)/2=4500米。

2、三个小组共有180人,一、二两个小组人数之和比第三小组多20人,第一小组比第二小组少2人,求第一小组的人数。

分析：先将一、二两个小组作为一个整体,这样就可以利用基本和差问题公式得出第一、二两个小组的人数和,然后对第一、二两个组再作一次和差基本问题计算,就可以得出第一小组的人数。

解：一、二两个小组人数之和=(180+20)/2=100人,第一小组的人数=(100-2)/2=49人。

3、甲、乙两筐苹果,甲筐比乙筐多19千克,从甲筐取出多少千克放入乙筐,就可以使乙筐中的苹果比甲筐的多3千克？分析：从甲筐取出放入乙筐,总数不变。

甲筐原来比乙筐多19千克,后来比乙筐少3千克,也即对19千克进行重分配,甲筐得到的比乙筐少3千克。

于是,问题就变成最基本的和差问题：和19千克,差3千克。

解：(19+3)/2=11千克,从甲筐取出11千克放入乙筐,就可以使乙筐中的苹果比甲筐的多3千克。

三年级奥数题：和差倍数问题（二）1、在一个减法算式里,被减数、减数与差的和等于120,而减数是差的3倍,那么差等于多少？分析：被减数=减数+差,所以,被减数和减数与差的和就各自等于被减数、减数与差的和的一半,即：被减数=减数+差=(被减数+减数+差)/2。

因此,减数与差的和= 120/2=60。

这样就是基本的和倍问题了。

小数=和/(倍数+1)解：减数与差的和=120/2=60,差=60/(3+1)=15。

2、已知两个数的商是4,而这两个数的差是39,那么这两个数中较小的一个是多少？分析：两个数的商是4,即大数是小数的4倍,因此,这是一个基本的差倍问题。

归一问题（单位量、倍比法）1. 1 只猫1 天吃3 条鱼, 如果每只猫每天吃同样多的鱼, 那么5 只猫3 天吃__________条鱼。

2. 1 只猫1 天吃4 条鱼, 如果每只猫每天吃同样多的鱼, 那么3 只猫4 天吃__________条鱼。

3. 4 只兔子3 天吃36 根胡萝卜, 如果每只兔子每天吃同样多的胡萝卜, 那么1 只兔子 1 天吃_______根胡萝卜。

4. 5 只兔子2 天吃20 根胡萝卜, 如果每只兔子每天吃同样多的胡萝卜, 那么 1 只兔子 1 天吃_______ 根胡萝卜。

5. 3 只猩猩4 天吃36 个香蕉, 如果每只猩猩每天吃同样多的香蕉, 那么5 只猩猩 3 天吃__________个香蕉。

6. 5 只猩猩3 天吃45 个香蕉, 如果每只猩猩每天吃同样多的香蕉, 那么4 只猩猩 2 天吃__________个香蕉。

7.有一定量的水可以供8 只大象喝30 天,如果每只大象每天喝同样多的水,那么这些水可以供____只大象喝 6 天。

8.有一定量的水可以供7 只大象喝40 天, 如果每只大象每天喝同样多的水, 那么这些水可以供______只大象喝28 天。

9.有一定量的水可以供5 只大象喝30 天,如果每只大象每天喝同样多的水,那么这些水可以供_____只大象喝10 天。

10.10 只猫10 天吃10 条鱼, 如果每只猫每天吃同样多的鱼, 那么20 只猫20 天吃________条鱼。

11. 3 只猫3 天吃2 条鱼, 如果每只猫每天吃同样多的鱼, 那么6 只猫9 天吃__________条鱼。

12. 5 只猫5 天吃5 条鱼, 如果每只猫每天吃同样多的鱼, 那么10 只猫15 天吃_________条鱼。

13.8 只兔子6 天吃36 根胡萝卜,如果每只兔子每天吃同样多的胡萝卜,那么 2 只兔子 2 天吃_____根胡萝卜。

14. 6 只兔子10 天吃20 根胡萝卜,如果每只兔子每天吃同样多的胡萝卜,那么 3 只兔子 2 天吃___2___根胡萝卜。