下载文档原格式
1、下图是一用于干涉原理进行测试的干涉场图像，要求判读条纹的间距，请给出图像处理的方案并说明每一步的作用及其对其它处理步骤可能产生的影响。
解：步骤与思路：○1.进行模糊处理，消除噪声○2.边缘检测，进行图像增强处理○3．二值化图像，再进行边缘检测，能够得到很清晰的边界。
○4.采用横向标号法，根据值为1像素在标号中的相邻位置可以确定间距I=imread('xz mjt.bmp');I1=medfilt2(I); %对图像中值滤波imshow(I1);[m,n]=size(I1);for i=1:mfor j=1:nif(I1(i,j)<100) %阈值为100I1(i,j)=255;elseI1(i,j)=0; %进行二值化endendendfigure;imshow(I1);Y1=zeros(1,25);y2=y1;c=y2;i=100;for j=1:1200if (I1(i,j)==255&&I1(i,j+1)==0)Y1=j+1;endif (I1(i,j)==0&&I1(i,j+1)==255)Y2=j;endendfor i=1:25c=Y2(i)-Y1(i)endc %找出每两个条纹之间的距离2. 现有8个待编码的符号m0,……,m7,它们的概率分别为0.11,0.02,0.08,0.04,0.39,0.05,0.06,0.25,利用哈夫曼编码求出这一组符号的编码并画出哈夫曼树。
3. 请以图像分割方法为主题，结合具体处理实例，采用期刊论文格式，撰写一篇小论文。
各种算子对图像进行边缘检测效果的研究图像分割是根据需要将图像划分为有意义的若干区域或部分的图像处理技术。
通过边缘检测在Matlab 中实现方法，及用四叉数分解函数进行区域分割的方法，掌握了Matlab 区域操作函数的使用和图像分析和理解的基本方法,并学到了'roberts','sobel','prewitt','canny','log'算子对图像进行边缘检测的不同效果。
数字图像处理1.图像工程的三个层次是指哪三个层次？各个层次对应的输入、输出对象分别是什么？①图像处理特点：输入是图像，输出也是图像，即图像之间进行的变换。
②图像分割特点：输入是图像，输出是数据。
③图像识别特点：以客观世界为中心，借助知识、经验等来把握整个客观世界。
“输入是数据，输出是理解。
2.常用的颜色模型有哪些（列举三种以上）？并分别说明颜色模型各分量代表的意义。
①RGB（红、绿、蓝）模型②CMY（青、品红、黄）模型③HSI（色调、饱和度、亮度）模型3.什么是图像的采样？什么是图像的量化？1．采样采样的实质就是要用多少点来描述一幅图像，采样结果质量的高低就是用前面所说的图像分辨率来衡量。
简单来讲，对二维空间上连续的图像在水平和垂直方向上等间距地分割成矩形网状结构，所形成的微小方格称为像素点。
一副图像就被采样成有限个像素点构成的集合。
例如：一副640*480分辨率的图像，表示这幅图像是由640*480＝307200个像素点组成。
2．量化量化是指要使用多大范围的数值来表示图像采样之后的每一个点。
量化的结果是图像能够容纳的颜色总数，它反映了采样的质量。
针对数字图像而言：采样决定了图像的空间分辨率，换句话说，空间分辨率是图像中可分辨的最小细节。
量化决定了图像的灰度级，即指在灰度级别中可分辨的最小变化。
数字图像处理（第三次课）调用图像格式转换函数实现彩色图像、灰度图像、二值图像、索引图像之间的转换。
图像的类型转换：对于索引图像进行滤波时，必须把它转换为RGB图像，否则对图像的下标进行滤波，得到的结果是毫无意义的;2.用MATLAB完成灰度图像直方图统计代码设计。
6789101112131415161718192021222324252627282930title('lady-lenna');if isrgb(a);b=rgb2gray(a);%RGB转换为灰度图像endsubplot(2,2,2);imshow(b);%显示图像title('ladygaga-lenna');[m,n]=size(a);%返回图像大小e=zeros(1,256);for k=0:255for i=1:mfor j=1:nif a(i,j)==ke(k+1)=e(k+1)+1;%灰度值相同的进行累加endendendendsubplot(2,2,4);bar(e);%画图像的灰度直方图title('灰度直方图');c=imrotate(a,20);%图像的旋转subplot(2,2,3);imshow(c);数字图像处理（第四次课）编写matlab函数，实现在医学图像中数字减影血管造影。
1.数字图像与连续图像相比具有哪些优点?连续图像f(x,y)与数字图像I(c,r)中各量的含义是什么?它们有何联系和区别? (To be compared with an analog image, what are the advantagesof a digital image? Let f(x,y) be an analog image, I(r, c) be a digital image, please giveexplanation and comparison for defined variables: f/I, x/r, and y/c)2.图像处理可分为哪三个阶段? 它们是如何划分的？各有什么特点? (We can divide image processing into 3 stages, what are they? how they are divided? What are their features?)答：低级处理---低层操作,强调图像之间的变换,是一个从图像到图像的过程;中级处理---中层操作,主要对图像中感兴趣的目标进行检测和测量,从而建立对图像的描述,是一个从图像到数值或符号的过程;高级处理---高层操作,研究图像中各目标的性质和相互联系,得出对图像内容含义的理解以及对原来客观场景的解释;3.试从结构和功能等角度分析人类视觉中最基本的几个要素是什么?什么是马赫带效应? 什么是同时对比度?它们反映了什么共同问题? (According to the structure and function of theeyes, what are the basic elements in human vision? What is the Mach Band Effect? What is Simultaneous Contrast? What common facts can we infer from both Mach Band Effect and Simultaneous Contrast?)答：人的视觉系统趋向于过高或过低估计不同亮度区域边界的现象称为“马赫带”效应;同时对比度指的是人的视觉系统对某个区域感觉到的亮度除了依赖于它本身的强度,还与背景有关. 马赫带效应和同时对比度现象表明人所感觉到的亮度并不是强度的简单函数.4.比较说明像素邻域、连接、通路以及连通基本概念的联系与区别。
研究生《数字图像处理》考试1. 编写程序完成不同滤波器的图像频域降噪和边缘增强的算法并进行比较，得出结论。
● 图像频域降噪的实验原理与算法分析：图像的能量大部分集中在幅度谱的低频和中频部分，而图像的边缘和噪声对应于高频部分，因此能降低高频成分幅度的滤波器就能减弱噪声的影响，由卷积定理，在频域实现低通滤波的数学表达式：),(),(),(v u F v u H v u G =1. 理想低通滤波器（ILPF ）0),(),(01),(D v u D D v u D v u H >≤⎩⎨⎧=2. 巴特沃斯低通滤波器（BLPF ） nD v u D v u H 20),()12(11),(⎥⎦⎤⎢⎣⎡-+=3. 指数型低通滤波器（ELPF ） 2),(0),(nD v u D ev u H ⎥⎦⎤⎢⎣⎡-=● 图像频域降噪的实验过程： 1. 理想低通滤波器程序I=imread('xpy.jpg'); f=double(I); g=fft2(f); g=fftshift(g); [M,N]=size(g); d0=100;m=fix(M/2);n=fix(N/2); for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2); if(d<=d0) h=1; else h=0; endresult(i,j)=h*g(i,j);endend>> result=ifftshift(result);>> J1=ifft2(result);>> J2=uint8(real(J1));>> imshow(J2)2.巴特沃斯低通滤波器程序I=imread('xpy.jpg');f=double(I);g=fft2(f);g=fftshift(g);[M,N]=size(g);nn=2;d0=30;m=fix(M/2);n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=1/(1+0.414*(d/d0)^(2*nn));result(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));imshow(J2)3.高斯低通滤波器程序I=imread('xpy.jpg');f=double(I);g=fft2(f);g=fftshift(g);[M,N]=size(g);d0=100;m=fix(M/2);n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=exp(-(d.^2)./(2*(d0^2)));result(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));imshow(J2)图像频域降噪的实验结果分析与讨论下面是理想低通滤波器、巴特沃斯低通滤波器、高斯低通滤波器的滤波效果分析与讨论。
新疆开放大学直属《数字与图像处理》2023春季学期数字与图像处理第2
次平时作业-100分
题1：下列哪一个不是数字图像处理的目的。
A.存储和传输
B.显示和打印
C.增强和恢复
D.可视化
正确答案：D
题2：下列算法中属于图象锐化处理的是：（）
A.低通滤波
B.加权平均法
C.高通滤波
D.中值滤波
正确答案：C
题3：下列算法中属于局部处理的是：（）
A.灰度线性变换
B.二值化
C.傅立叶变换
D.中值滤波
正确答案：D
题4：下列哪一项不是伪彩色图像增强的方法。
A.过滤法
B.密度切割法
C.灰度级-彩色变换
D.滤波法。
数字图像处理作业班级：Y100501姓名：**学号：*********一、编写程序完成不同滤波器的图像频域降噪和边缘增强的算法并进行比较，得出结论。
频域降噪。
对图像而言，噪声一般分布在高频区域，而图像真是信息主要集中在低频区，所以，图像降噪一般是利用低通滤波的方法来降噪。
边缘增强。
图像的边缘信息属于细节信息，主要由图像的高频部分决定，所以，边缘增强一般采取高通滤波，分离出高频部分后，再和原频谱进行融合操作，达到边缘增强，改善视觉效果，或者为进一步处理奠定基础的目的。
1频域降噪，主程序如下：I=imread('lena.bmp'); %读入原图像文件J=imnoise(I,'gaussian',0,0.02);%加入高斯白噪声A=ilpf(J,0.4);%理想低通滤波figure,subplot(222);imshow(J);title('加噪声后的图像');subplot(222);imshow(A);title('理想低通滤波');B=blpf(J,0.4,4);%巴特沃斯低通滤波subplot(223);imshow(B);title('巴特沃斯低通滤波');C=glpf(J,0.4);%高斯低通滤波subplot(224);imshow(C);title('高斯低通滤波');用到的滤波器函数的程序代码如下：function O=ilpf(J,p) %理想低通滤波，p是截止频率[f1,f2]=freqspace(size(J),'meshgrid');hd=ones(size(J));r=sqrt(f1.^2+f2.^2);hd(r>p)=0;y=fft2(double(J));y=fftshift(y);ya=y.*hd;ya=ifftshift(ya);ia=ifft2(ya);O=uint8(real(ia));function O=blpf(J,d,n) %巴特沃斯低通滤波器，d是截止频率，n是阶数[f1,f2]=freqspace(size(J),'meshgrid');hd=ones(size(J));r=f1.^2+f2.^2;for i=1:size(J,1)for j=1:size(J,2)t=r(i,j)/(d*d);hd(i,j)=1/(t^n+1);endendy=fft2(double(J));y=fftshift(y);ya=y.*hd;ya=ifftshift(ya);ia=ifft2(ya);O=uint8(real(ia));function O=glpf(J,D) %高斯滤波器，D是截止频率[f1,f2]=freqspace(size(J),'meshgrid');r=f1.^2+f2.^2;Hd=ones(size(J));for i=1:size(J,1)for j=1:size(J,2)t=r(i,j)/(D*D);Hd(i,j)=exp(-t);endendY=fft2(double(J));Y=fftshift(Y);Ya=Y.*Hd;Ya=ifftshift(Ya);ia=ifft2(Ya);O=uint8(real(ia));运行结果如图1所示。
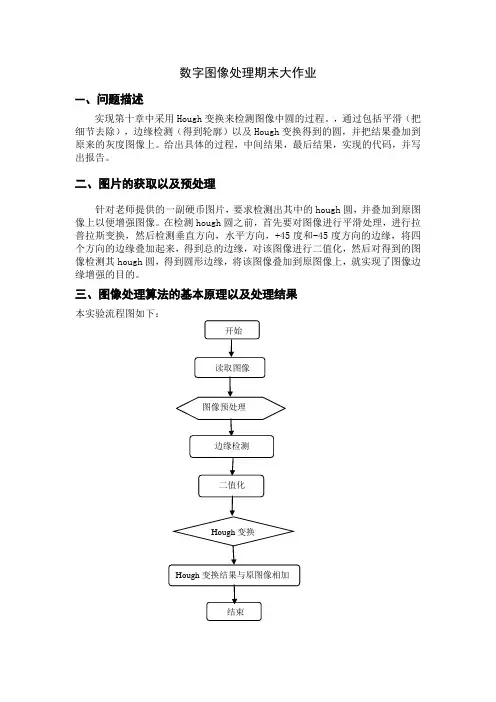
数字图像处理期末大作业一、问题描述实现第十章中采用Hough变换来检测图像中圆的过程。
，通过包括平滑（把细节去除），边缘检测（得到轮廓）以及Hough变换得到的圆，并把结果叠加到原来的灰度图像上。
给出具体的过程，中间结果，最后结果，实现的代码，并写出报告。
二、图片的获取以及预处理针对老师提供的一副硬币图片，要求检测出其中的hough圆，并叠加到原图像上以便增强图像。
在检测hough圆之前，首先要对图像进行平滑处理，进行拉普拉斯变换，然后检测垂直方向，水平方向，+45度和-45度方向的边缘，将四个方向的边缘叠加起来，得到总的边缘，对该图像进行二值化，然后对得到的图像检测其hough圆，得到圆形边缘，将该图像叠加到原图像上，就实现了图像边缘增强的目的。
三、图像处理算法的基本原理以及处理结果本实验流程图如下：1.读取图像图像处理的第一步就是对所采集的图像进行读入，本次实验的输入图像是一幅灰度图像，不需要将图像转换成为灰度图像，直接利用函数imread （）完成。
原图像如下所示：原图像2.图像预处理在图像预处理中，我们完成了两步工作，首先使用方差为1的高斯噪声对图像进行平滑，然后进行拉普拉斯变换，即)],(*)([2y x f r h ∇，222r 2e 21)(σσ-=πr h 为方差为2σ的高斯噪声，本实验中12=σ。
又),(*)]([)],(*)([22y x f r h y x f r h ∇=∇，其中2224222]2[)(σσσr er r h --=∇，将)(2r h ∇和),(y x f 分别进行傅里叶别换，将其逐点相乘，再进行傅里叶反变换，就得到了预处理后的图像。
3.边缘检测对水平，垂直，+45度，-45度方向进行边缘检测，本实验中我们采用了Prewitt 梯度算子，它用于检测水平方向，垂直方向，+45度方向和-45度方向的掩膜分别如下：水平掩膜 垂直掩膜 +45度掩膜 -45度掩膜使用这四个掩膜分别对上一步得到的图像逐点进行处理，就可以得到四个方向的边缘了（本实验中边缘的一个像素都不处理），再将它们加起来，就得到了总的边缘，实验结果如下：水平边缘垂直边缘-45度边缘总的边缘如下图所示：4.二值化对上图得到的图像进行二值化，这里我采用的是循环方式确定图像全局阈值，即首先以图像的平均值作为阈值，将图像分成两部分，分别求两部分的平均值，新的阈值为这两个平均值的均值，重复上述过程，直到两次阈值之差小于特定的值时停止，并以最后一次得到的阈值对图像进行二值化，本实验中我要求两次阈值之差小于0.5时停止，最后得到的全局阈值为 -102.1332，二值化后的图像如下所示：二值化后的图像5.Hough变换检测圆形边界Hough 变换的原理就是利用图像全局特征将边缘像素连接起来组成区域封闭边界，它将图像空间转换到参数空间，在参数空间对点进行描述，达到检测图像边缘的目的。
数字图像处理一、图像复原1、（1）matlab程序代码（使用电路板图片）a=imread('C:\Users\SUN\Desktop\a.tif'); %读图像b=imnoise(a,'gaussian',0,800/255^2); %加入0均值，方差800的噪声。
c=imnoise(b,'salt & pepper',0.1); % 在(a)的基础上，进一步加入椒盐噪声进一步污染图像（Pa=Pb=0.1的椒盐噪声）subplot(2,4,1),imshow(a) ,title('原始图像') %显示图片subplot(2,4,2),imshow(b) ,title('高斯噪声污染')subplot(2,4,3),imshow(c) ,title('继续被椒盐噪声污染')h=ones(5,5)/25; %算术均值滤波g1=imfilter(c,h);subplot(2,4,4),imshow(g1) ,title('算数均值滤波')%g2=power(exp(imfilter(log(double(c)),4*fspecial('average',2))),1/4); %几何均值滤波g2=exp(imfilter(log(double(c)),fspecial('average',1)));subplot(2,4,5),imshow(uint8(g2)) ,title('几何均值滤波')g3= medfilt2(c,[5,5]); %中值滤波subplot(2,4,6),imshow(g3) ,title('中值滤波')i=ones(5,5)/20;g4=imfilter(c,i);subplot(2,4,7),imshow(g4) ,title('修正后的α均值滤波')运行结果：（2）matlab程序代码（使用含有自己的图片）a=imread('C:\Users\SUN\Desktop\i.jpg'); %读图像a1=rgb2gray(a);b=imnoise(a1,'gaussian',0,800/255^2); %加入0均值，方差800的噪声。
1. Give a single intensity transformation function for spreading the intensities of an image so the lowest intensity is 0 and the highest is L -1. [为了扩展一幅图像的灰度，使其最低灰度为0、最高灰度为L -1，请给出一个单调的变换函数。
]Answer: Let f denote the original image. First subtract the minimum value of f denoted f min from f to yield a function whose minimum value is 0:1min g f f =-Next divide g 1 by its maximum value to yield a function in the range [0,1] and multiply the result by L 一1 to yield a function with values in the range [0, L 一1]1min 1min11()max()max()L L g g f f g f f --==--Keep in mind that f min is a scalar and f is an image.[让f 表示原始图像。
首先从图像函数f 中减掉f 的最小值f min , 然后生成一个新的函数g 1，它的最小值为0：1min g f f =-接下来让g 1的最大值除g 1得到另一新的函数，它的值域在[0,1]区间，然后再乘上L 一1，得到值域为[0, L 一1]的新函数。
请注意f min 是一个标量，而f 是一个图像。
2.Explain why the discrete histogram equalization technique does not,in general,yield a flat histogram. [请解释为什么离散直方图均衡化技术一般不能得到平坦的直方图。
]Answer: All that histogram equalization does is remap histogram components on the intensity scale. To obtain a uniform (flat) histogram would require in general that pixel intensities actually be redistributed so that there are L groups of n/L pixels with the same intensity, where L is the number of allowed discrete intensity levels and n=MN is the total number of pixels in the input image. The histogram equalization method has no provisions for this type of (artificial) intensity redistributionprocess.[直方图均衡化就是把直方图重新映射到灰度尺度上。
为了得到平坦的直方图，通常需要图像中像素的灰度值重新分配，这样会产生L个组，每个组中包含相同灰度值的像素的数量是n/L，其中L是允许的离散灰度值的个数，n=MN是输入图像中总的像素的个数。
而离散直方图的均衡化没有提供这样一个重新分配的过程。
]3.In a given application an averaging mask is applied to input image to reduce noise, and then a Laplacian mask is applied to enhance small details. Whould the result be the same if the order of these operations were reserved? [在给定的应用中，一个均值模板被用于输入图像以减少噪声，然后再用一个拉普拉斯模板来增强细节。
如果交换一下两个操作步骤的顺序，能否得到相同的结果？]Answer: The student should realize that both the Laplacian and the averaging process are linear operations, so it makes no difference which one is applied first.[学生应该认识到拉普拉斯和平均化的处理过程都是线性运算过程，所以无论先应用哪一个模板对结果是没有影响的。
]4. You saw in Fig. 2.18 that the Laplacian with a -8 in the center yields sharper results than the one with a -4 in the center. Explain the reason in detail. [在图2.18中所看到的中心系数为-8 的拉普拉斯模板所得到的结果，要比中心系数为-4的模板所得到的结果清晰一些。
请详细说明原因。
] Answer: The Laplacian mask with a -4 in the center performs an operation proportional to differentiation in the horizontal and vertical directions. Consider for a moment a 3 x 3 "Laplacian" mask with a -2 in the center and 1 above and below the center. All other elements are 0. This mask will perform differentiation in only one direction, and will ignore intensity transitions in the orthogonal direction. An image processed with such a mask will exhibit sharpening in only onedirection. A Laplacian mask with a -4 in the center and 1 in the vertical and horizontal directions will obviously produce an image with sharpening in both directions and in general will appear sharper than with the previous mask. Similarly, and mask with a -8 in the center and is in the horizontal, vertical, and diagonal directions will detect the same intensity changes as the mask with the -4 in the center but, in addition, it will also be able to detect changes along the diagonals, thus generally producing sharper-looking results.[中心系数为-4的拉普拉斯模板执行的是与水平和垂直方向的差分成比例的运算。
考虑一个中心系数为-2的拉普拉斯模板，2的上下都是1。
模板中其它所有的系数都是0。
这个模板只会在一个方向上（垂直方向）执行差分计算，并会忽略掉水平方向上灰度值的变化。
用这样的模板处理图像，只会在一个方向上展示出图像的锐化。
若采用中心系数为-4，上下左右的系数都为1的拉普拉斯模板对图像进行处理，则会在水平和垂直的两个方向上展示图像的锐化，并且锐化的效果比前一个模板的要好。
类似，若采用中心系数为-8，水平，垂直和对角线方向的系数都为1的模板对图像进行处理，与前一个模板一样，能检测到水平和垂直方向上的灰度值的变化，此外，它还能检测到对角线方向的灰度值的变化，所以看起来结果要更清晰一些。
]5.Write an expression for 2-D discrete convolution. [请写出一个2维离散卷积的表达式。
] 1100(,)(,)(,)(,)(0,1,...,1;0,1, (1)M N e e e e m n f x y g x y f m n g x m y n x M y N --==*=--=-=-∑∑(,)(,)e e f x y g x y 和分别是(,)(,)f x y g x y 和的周期化函数。
6.The two fourier spectra shown are of the same image. The spectrum on the left corresponds to the original image, and the spectrum on the right was obtained after the image was padded with zeros. Explain the significant increase in signal strength along the vertical and horizontal axes of thespectrum shown on the right. [同一幅图像的两个傅立叶频谱如图所示。
左边的频谱对应于原图像，右边的频谱图像使用0值填充后所得。
请解释右图所示的谱沿垂直轴和水平轴方向的信号强度显著增强的原因。
]Answer: Unless all borders on of an image are black, padding the image with 0 introduces significant discontinuities (edges) at one or more borders of the image. These can be strong horizontal and vertical edges. These sharp transitions in the spatial domain introduce high-frequency components along the vertical and horizontal axes of the spectrum.[除非图像中所有的边界都是黑色的，否则图像中填充0值会在一个或多个边界产生灰度值上的明显的不连续性，这样能够增强图像中水平和垂直的边缘。
