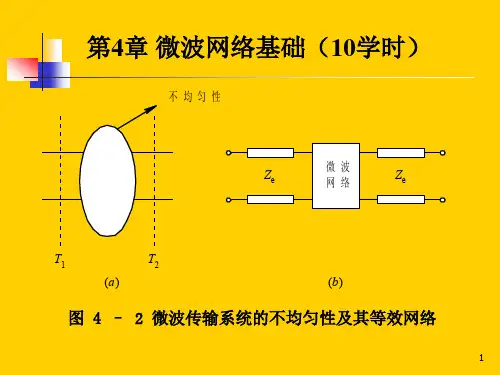
第4章 微波网络基础 4.5 习题【1】 为什么说微波网络方法是研究微波电路的重要手段？微波网络与低频网络相比较有哪些异同点？【2】 表征微波网络的参量有哪几种？分别说明它们的意义、特征及其相互间的关系。
【3】 二端口微波网络的主要工作特性参量有哪些？它们与网络参量有何关系？ 【4】 求图4-17 所示电路的归一化转移矩阵。
图4-17 习题4图其【解】同[例4-9］见教材PP95 求图4-9长度为θ的均匀传输线段的A 和S 。
图4-9 长度为θ的均匀传输线段【解】：从定义出发求参数，定义为：11121221212222U A U A I I A U A I =-⎧⎨=-⎩ 先确定A 矩阵。
当端口(2)开路（即20I =）时，2T 面为电压波腹点，令2m U U =，则()1cos 2j j m m U U e e U θθθ-=+=，且此时端口(1)的输入阻抗为10cot in Z jZ θ=-。
由A 矩阵的定义得： 21112cos I U A U θ=== ，2111212200/cos sin cot in m m I U Z U I A j U U jZ U Z θθθ=====- 此文档最近的更新时间为：2019-6-30 23:29:00当端口(2)短路（即20U =）时，2T 面为电压波节点，令22,22m mU U U U +-==-，则()1sin 2j j m m U U e e jU θθθ-=-=，且此时端口(1)的输入阻抗为10tan in Z jZ θ=。
由A 矩阵的定义得： 21120200sin sin m m U jU U A jZ I U Z θθ====- ，212220cos cos m mU I IA I I θθ====-也可以利用网络性质求1222,A A 。
由网络的对称性得：2211cos A A θ==再由网络可逆性得：211221202101cos 1sin sin /A A A jZ A j Z θθθ--===于是长度为θ的均匀传输线段的A 矩阵为00cos sin sin /cos jZ j Z θθθθ⎡⎤=⎢⎥⎣⎦A 如果两端口所接传输线的特性阻抗分别为01Z 和02Z ，则归一化A 矩阵为0jθθ⎡⎤⎢⎢=⎢⎢⎥⎢⎥⎣⎦A当01020Z Z Z ==时cos sin sin cos j j θθθθ⎡⎤=⎢⎥⎣⎦A【6】（返回）求图4-19所示π型网络的转移矩阵。
221I V图4-19 习题6图【解】（返回）计算的方法有两种：方法一：根据定义式计算； 方法二：如下，分解的思想。
思路：分解成如图所示的单元件单元电路，之后利用级联网络转移矩阵。
221I V221I V转移矩阵的关系式为：11121221212222U A U A I I A U A I =-=-根据电路理论，得出两个子电路的电压电流关系，并与定义式对比后得出两个子电路的转移矩阵Ａ1和A2分别为：122121212212110011U U I Z U U I I I YU I Z A A Y =-=⎧⎧⎨⎨=-=-⎩⎩⎡⎤⎡⎤⇒=⇒=⎢⎥⎢⎥⎣⎦⎣⎦总的电路为三个单元电路级联，所以总的转移矩阵为：211011011010111121total YZZ Z Z A YYY YZ YY Y Z YZ +⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+++⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦【7】求图4-20所示电路的Z 矩阵和Y 矩阵。
22V 1I 1V221I 1V图4-20 习题7图【解】（返回）221I 1V Z Z221I V Y Y(a)先根据定义计算形如上图电路的阻抗矩阵为：133323Z Z Z Z Z Z Z +⎡⎤=⎢⎥+⎣⎦将（a ）图与之对比，得（a ）图阻抗矩阵为：先根据定义计算形如上图电路的导纳矩阵为：：11111222211222I Y V Y V I Y V Y V =+=+213211101321123()()V Y Y Y I Y Y Y Y V Y Y Y =⋅+==+=++ 123122202123()V Y Y Y IY V Y Y Y =⋅+==++13112112012123231111V Y Y I Y Y Y Y V Y Y Y Y Y Y =+⋅==-⋅=-++++ 22122101123V I Y Y Y V Y Y Y =⋅==-++ 在(a)图中1321,,YY j C Y j Lωω===∞(b)将（b ）图与之对比，得（b ）图阻抗矩阵为：()113112213221122232321131112212122121LC j L j L C j L j C Y Y Y j L j L Y Y Y Y j C j Lj L Y Y Y Y Y j C j Lj L C ωωωωωωωωωωωωω--⎛⎫+ ⎪-+⎝⎭====++⎛⎫ ⎪⎝⎭====++---问题：Pozar4.7【8】求图4-21 所示电路的散射矩阵。
Z图4-21 习题8图【解】（返回） (a)[]00j a j e S e θθ--⎡⎤=⎢⎥⎢⎥⎣⎦(b)查表4-2知单个并联电容（导纳）构成网络的S 参数：222222y yy S y y y -⎡⎤⎢⎥++⎢⎥=-⎢⎥⎢⎥++⎣⎦其中0y j c Y ω=利用参考面移动对S 参数的影响，可得，其中S11=S22，S12=S21： []222222200222222222002222j j j j j b j j j j yy ee e e y y y y ye S y y y ye e ee yy y y θθθθθθθθθ-----------⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤-++++⎡⎤⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥+⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥++++⎣⎦⎣⎦矩阵相乘得：（0Y 其中为归一化特性导纳且001Y Z =）。
【10】用Z 、Y 、A 、S 参量分别表示可逆二端口微波网络和对称二端口微波网络的特点。
1．可逆网络（互易网络）1221Z Z = 或 1221Z Z = 1221Y Y = 或 1221Y Y =112212211A A A A -= 或 112212211A A A A -=1221S S =2．对称网络1122Z Z = 或 1122Z Z =1122Y Y = 或 1221Y Y = 1122S S = ，1122A A = (1122A A =) 。
【13】求图4-24所示电路中1T 与2T 参考面所确定网络的归一化转移参量矩阵和归一化散射参量矩阵。
图4-24 习题13图 【解】思路：把原电路分解成单元电路，并利用单元电路结果（表4-2）、参量矩阵转换及级联网络A 矩阵特点进行计算。
(a)详解：将(a)图分解成：Y p Y ⇒其中等效的并联归一化输入导纳为：2cot cot8p Y j l j j πλβλ=== 查表4-2知，单个并联导纳网络的归一化转移参量：13101A A y ⎡⎤==⎢⎥⎣⎦传输线的归一化转移参量：2cos sin sin cos j A j θθθθ⎡⎤=⎢⎥⎣⎦，4λ对应的θ为2π。
1231A A A A y=⨯⨯=⎢⎣利用表4-1的转换公式计算归一化散射参量矩阵：11221221det A A A A =-A11122122111111122122111221221211122122111221222111122122111221221112212222111221222det det 122jA A A A S S A A A A A A A A j S A A A A A A A A j S A A A A A A A A j A A A A S A A A A ⎧+--==⎪-+++⎪⎧+--=⎪⎪=⎪=⎪⎪+++⎨⎨+++=-+⎪⎪=⎪⎪+++-+-+=⎩⎪-+-+⎪=⎪+++⎩A A ()()()()122122122542225422251225j j j S j j S j j jS j ⎧-=⎪+⎪⎪--⎪==-+⎪⎨--⎪==⎪-+⎪-⎪==⎪-+⎩(b)中间段是短路短截线，00tan 4in in Z jZ l jZ l z jββπ===∴=查表4-2知：201A =⎢⎣123101A A A A y⎡⎤=⨯⨯=⎢⎥⎣⎦111221221111122122111221221112121112212211122122211112212211122122111221222211122122002det det 1220A A A A S A A A A A A A A S S S A A A A A A A A j S A A A A A A A A A A A A S A A A A⎧+--=⎪+++⎪⎧+--==⎪⎪=⎪=⎪⎪+++⎨⎨+++=⎪⎪=⎪⎪+++-+-+=⎩⎪-+-+⎪=⎪+++⎩A A 21220 S=00jj j S jS ⎧⎪=--⎡⎤⎪⎨⎢⎥-=-⎣⎦⎪⎪=⎩(c)第1和第3是短路短截线，0000tan 41in in in Z jZ l jZ l Y jZ jY y jββπ===∴==-=-查表4-2知：101y ⎡⎤⎢⎥⎣⎦ 代入得：13101A A j ⎡⎤==⎢⎥-⎣⎦123101A A A A y ⎡=⨯⨯=⎢⎣111221221111111221221112212212111221221112212221111221221112212211122122221112212242det det 12424A A A A S S A A A A A A A A j S A A A A A A A A j S A A A A A A A A j A A A A S A A A A ⎧+--==⎪+++⎪⎧+--=⎪⎪=⎪=⎪⎪+++⎨⎨+++=-⎪⎪=⎪⎪+++-+-+=⎩⎪-+-+⎪=⎪+++⎩A A 12212222425122422555 S=22412552522425j j j j j j S j j j j S j j j S j -+⎧=⎪-⎪⎪+-++⎡⎤==⎪⎢⎥-⎪⎢⎥⎨+-++⎢⎥⎪==⎢⎥⎪-⎣⎦⎪-+⎪==⎪-⎩【14】如图4-25所示二端口网络参考面2T 处接归一化负载阻抗L Z ，而11A 、12A 、21A 、22A为二端口网络的归一化转移参量，试证明参考面1T 处的输入阻抗为：【证明】回顾定义：11122121212222()()U A U A I I A U A I ⎧=+-⎪⎨=+-⎪⎩简记为： 1112111221222122A A A A A A A A ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦A A 有： 21112111222212122222121222()()()()in U A A U A U A I I Z I A U A I U A A I ++--===+-+- 因为：22L U Z I =-，代入上式即得：11122122L in L A Z A Z A Z A +=+【19】已知二端口网络的散射参量矩阵为：3/23/20.20.980.980.2j j j j e e e e ππππ⎡⎤=⎢⎥⎣⎦S 求二端口网络的插入相移θ、插入衰减(dB)L 、电压传输系数T 及输入驻波比ρ。
