Journal of Theoretics Volume 6-2, AprilMay 2004 Does the Speed of Light Have to be Constant

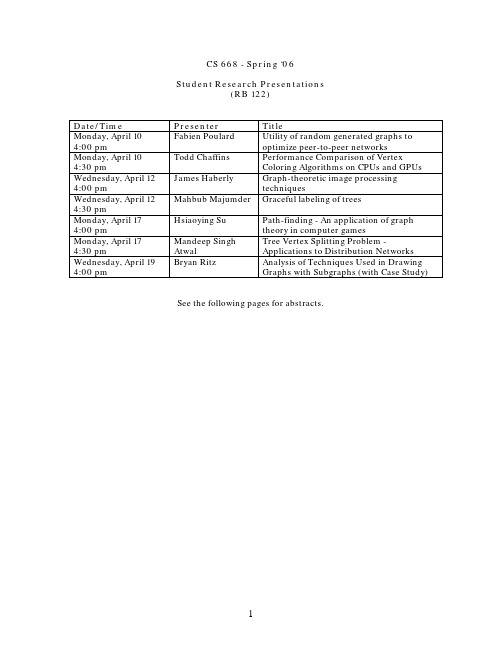
CS 668 - Spring ‘06Student Research Presentations(RB 122)Date/Time Presenter TitleMonday, April 10 4:00 pm Fabien Poulard Utility of random generated graphs tooptimize peer-to-peer networksMonday, April 10 4:30 pm Todd Chaffins Performance Comparison of VertexColoring Algorithms on CPUs and GPUsWednesday, April 12 4:00 pm James Haberly Graph-theoretic image processingtechniquesWednesday, April 124:30 pmMahbub Majumder Graceful labeling of treesMonday, April 17 4:00 pm Hsiaoying Su Path-finding - An application of graphtheory in computer gamesMonday, April 17 4:30 pm Mandeep SinghAtwalTree Vertex Splitting Problem -Applications to Distribution NetworksWednesday, April 19 4:00 pm Bryan Ritz Analysis of Techniques Used in DrawingGraphs with Subgraphs (with Case Study) See the following pages for abstracts.Monday, April 104:00 pmUtility of random generated graphs to optimize peer-to-peer networksFabien PoulardThe first peer-to-peer networks emerged with the Gnutella protocol in the early 2000, thanks to a team of developers at Nullsoft. When tested in a lab, the protocol was able to manage some hundreds nodes; but when released, it was quickly used by thousands of users, creating as much nodes and revealing the weaknesses of its conception. Since then the peer-to-peer has evolved and some others protocols have appeared, fixing partially the weaknesses of Gnutella. However, those protocols do not really implement a real peer-to-peer network, but a kind of topologically hybrid network sharing characteristics of the decentralized topology and some characteristics from other topologies (most likely hierarchy and centralized).As at the origins the peer-to-peer was developed to share music files (Nullsoft develops a widely used mp3 player product) “illegally”, there was no more research to extend the capabilities and exploit the peer-to-peer networks. However, nowadays, peer-to-peer is considered as a possible topology for a lot of networks, and especially for the mobile device applications. So, improving the algorithms at the origin of Gnutella becomes industrially interesting.Much progress has been achieved in the last few years, especially due to graph theory. The main issues to resolve are about preserving the connectivity of the graph when adding or removing a peer and in making the graph evolve towards an expander graph to optimize the exchanges between clients. However, the huge constraint is to make that happen with a minimum number of transactions considering that each manipulation of the network implies latencies and loss of packets that will have to be resent. Another issue is the fault tolerance, as each node can fail due to the extreme heterogeneity of the network, it must always be possible to find another path from one node to another.The different techniques I will try to cover during the presentation are based on the random transformation of regular graphs and the de Bruijn graphs. We will see how they can be applied to the original Gnutella to improve its efficiency without losing its decentralized characteristics.References• Peer-to-peer Networks based on Random Transformations of Connected Regular Undirected Graphs, P. Mahlmann, C. Schindelhauer, ACM July 2005• Graph-Theoretic Analysis of Structured Peer-to-Peer Systems : Routing Distances and Fault Resilience, D. Loguinov, J. Casas, X. Wang, IEEE/ACM Transactions on Networking • Distributed Construction of Random Expander Networks, C. Law, K. Siu, IEEE INFOCOM• The diameter of random massive graphs, L. Lu, Proceedings of the twelfth annual ACMSIAM symposium on Discrete algorithms• Generating Random Regular Graphs, J.H. Kim, V.H. Vu, Proceedings of the thirty-fifth annual ACM symposium on Theory of computing• On the Fundamental Tradeoffs Between Routing Table Size and Network Diameter in Peer-to-peer Networks, J. Xu, IEEE INFOCOMMonday, April 104:30 pmPerformance Comparison of Vertex Coloring Algorithms on CPUs and GPUsTodd ChaffinsCurrent high-end graphics processing units (GPUs) have evolved from dump co-processors with fixed functionality into highly capable stream processors. [Purcell, et al. 2002] In the ever-growing games industry there is a demand to be able to create more realistic graphics and effects. The current trend is to create these realistic graphics and effects through the use of graphics code known as shaders [Harris, et al. 2003]. Shaders are small pieces of code which determine how graphics are rendered on the screen. These shaders and their adoption in games require the graphics card manufacturers to create faster and more programmable GPUs. This pressure will continue and as such the speed and programmability of GPUs are set to continue to increase as time goes on. [Christen 2005]This increase in processing power and the parallel nature of GPUs has led to the adoption of the GPU for general purpose computations outside of the realm of graphics. While the GPU has made vaster architectural changes over recent years CPUs have also made advances. Aside from the common increases associated with CPUs (clock speed and cache), CPUs have moved to be more parallel with a dual-core architecture. With parallel vertex-coloring algorithms [Kale, et al. 1995] the question is raised as to which approach will yield the fastest results when performing vertex-coloring: CPU based, GPU based, or a hybrid CPU/GPU approach. This research seeks to implement, instrument, and measure the performance of these approaches in a quantitative manner and evaluate the economy of these approaches.References:[Purcell, et al. 2002] Purcell, T.J., Buck, I., Mark, W.R. and Hanrahan, P. Ray Tracing on Programmable Graphics Hardware. In Proceedings of SIGGRAPH 2002, ACM / ACM Press. 2002.[Christen 2005] Christen M.: Ray Tracing on GPU. Diploma thesis, University of Applied Sciences Basel, Switzerland, 2005.[Kale, et al. 1995] L. V. Kale, B. H. Richards, and T. D. Allen. Efficient parallel graph coloring with prioritization. In Lecture Notes in Computer Science, volume 1068, pages 190{208. Springer-Verlag, August 1995.[Harris, et al. 2003] Mark Harris, Greg James, Physically-Based Simulation on Graphics Hardware, GameDevelopers Conference, 2003.Wednesday, April 124:00 pmGraph-theoretic image processing techniquesJames HaberlyThe aim of my proposed topic would be to present an exposition on Graph Theoretic approaches and algorithms as they’re being researched for use in image processing and machine vision. Some example problems in the area of image processing and machine vision are; computational complexity, object recognition, object measurement, image segmentation, edge detection, noise detection and filtering, line, arc and other feature detection, image coding and compression.The project will be focused on presenting how graph theoretic algorithms with examples such as the Prim and Kruskal algorithms for minimum spanning trees, Dijkstra’s and Dial's shortest path and graph theoretic Euclidean distance mapping techniques are being examined for problem solving in the image processing and machine vision fields.I do not want to yet limit the scope of this proposal by proposing an exposition on any one paper or problem since I’m just beginning the research phase of the project. A couple specific areas that may become the main focus of the project are:1. Improvements in computational speed using graph-theoretic image processing techniques [1].2. Object recognition using a graph theoretical approach [2].The image processing and machine vision industry is a fast growing and exciting field. I’m looking forward to researching the topic further.References:[1] “Faster Graph-Theoretic Image Processing via Small-World and Quadtree Topologies” Leo Grady and Eric L. Schwartz Dept. of Imaging & Visualization, Siemens Corp. Res. Inc., Princeton, NJ, USA; This paper appears in: Computer Vision and Pattern Recognition, 2004. CVPR 2004. Proceedings of the 2004 IEEE Computer Society Conference on Publication Date: 27 June-2 July 2004Volume: 2, On page(s): II-360- II-365 Vol.2[2] "Color Invariant Object Recognition using Entropic Graphs" Jan C. van Gemert, Gertjan J. Burghouts, Frank J. Seinstra, Jan-Mark Geusebroek Intelligent Systems Lab Amsterdam, Informatics Institute, University of Amsterdam, Kruislaan 403, 1098 SJ Amsterdam, The Netherlands.[3] “Graph-Theoretical Methods in Computer Vision” Ali Shokoufandeh1 and Sven Dickinson2 G.B. Khosrovshahi et al. (Eds.): Theoretical Aspects of Computer Science, LNCS 2292, pp. 148–174, 2002.Wednesday, April 124:30 pmGraceful labeling of TreesMahbub MajumderA tree T with n vertices is said to be gracefully labeled if its vertices are labeled with the integers [1..n] such that the edges, when labeled with the difference between their endpoint vertex labels, are uniquely labeled with the integers [1..n-1]. If T can be gracefully labeled, it is called a “graceful tree”.The concept of graceful labeling of trees and graphs was introduced by Rosa (1967). The term “graceful labeling” was invented by Golomb (Golomb 1972). The Graceful Tree Conjecture states that all trees are graceful. There have been over 670 papers to date on various graph labeling methods and issues (Gallian 2005). So far, no proof of the truth or falsity of the conjecture has been found. Even though the conjecture is open, some partial results have been proved (Gallian 2005).My motivation in pursuing this project came from its nature and the study many people have put into it. My aim with this project work is to1.Find out current works and results.2.Study and understand the condition of gracefulness3.If possible, add some ideas in graceful LabelingReferences:Gallian J. A., A Dynamic Survey of Graph Labeling (2005), Electronic Journal of Combinatorics.Golomb S.W. How to number a graph. In R.C. Read, editor, Graph Theory and Computing, pages 23-37. Academic Press, 1972.Rosa A., On certain valuations of the vertices of a graph, Theory of Graphs (Internat. Symposium, Rome, July 1966), Gordon and Breach, N.Y. and Dunod Paris (1967) 349-355.Monday, April 174:00 pmPath-finding - An application of graph theory in computer gamesHsiaoying SuGraph theory is widely used in solving and presenting computer games. One of the most common applications is path-finding. Path-finding algorithms grant agents in the virtual world the ability to consciously find their own way around the land. They can also be used in real life to find driving directions, such as the service offered by many popular web sites. The project is going to focus on the game implementation.Path-finding algorithms are usually, but not only, used in computer games catalogued as role playing games (RPGs). Programmers build a virtual world for the games. The characters, or called autonomous agents, have certain level of artificial intelligence. The simplest way to present their intelligence is to find their own paths moving around the world without hitting a tree or going through a wall. The successful implementation of path-finding is important to the artificial intelligence performance of a game.According to the numbers of sources and destinations, path-finding algorithms can be roughly divided into three categories: single source, single pair, and all pairs. In single source algorithms, the path from one node to all the others is required. However, single pair algorithms take a specific source and destination. Only one path is required in response. The all pairs algorithm returns the shortest paths from every node to all other nodes.This project plans to explore different path-finding algorithms and their complexity. Furthermore, coding these algorithms in JEdit and practically experiment their efficiency. In single source algorithms, Dijkstra’s Algorithm and Bellman-Ford-Moore, which deals with negative arc-lengths graph, would be discussed. Then, the most popular algorithm A* (A star) would be presented to implement single-pair shortest path finding. To find out all-pairs shortest paths, the algorithms described above could be used in a naïve but inefficient way. The project then would seek out whether there exist more efficient algorithms to solve the problem.Path-finding related topics have been discussed on more application than research. However, there are still some interesting studies going on. One of a recent research is about solving incoherent behavior of multiple units in a cluttered environment. Another one is to discuss an open problem of emulating the rich complexity of real pedestrians in urban environment. The two papers are listed below as references.References•Kamphuis A., Overmars M. H.: Motion planning: Finding Paths for Coherent Groups using Clearance. In Eurographics/ACM SIGGRAPH Symposium on Computer Animation (2004).•Shao W., Terzopoulos D.: Artificial intelligence for animation: Autonomous pedestrians. In Eurographics/ACM SIGGRAPH Symposium on Computer Animation (2005).Monday, April 174:30 pmTree Vertex Splitting Problem - Applications to Distribution NetworksMandeep Singh AtwalIn an Ethernet network, the number of connections (taps) and their intervening distances are limiting factors [BN90]. Repeaters are used to regenerate the signal every 500 meters or so [BN90]. If these repeaters were not used, “standing waves” (additive reflections) would distort the signal and cause errors [BN90]. Because collision detection depends partly on timing, only five 500-meter segments and four repeaters can be placed in series before the propagation delay becomes longer than the maximum allowed time period for detecting a collision [BN90].Directed acyclic graphs (dags) or directed trees can be used to model such interconnection networks. Each edge of such a tree is labeled with a real number called its weight. Trees with edge weights are called weighted trees. Nodes or vertices in the tree correspond to receiving stations and edges correspond to transmission lines [HSR98]. Each edge weight corresponds to the delay in traversing that edge [HSR98]. However, as stated above, the network may not be able to tolerate losses in signal strength beyond a certain level.In places where the loss exceeds the tolerance level, repeaters have to be placed. Given a network and a loss tolerance level Tree Vertex Splitting Problem is to determine an optimal placement of repeaters.RESEARCH OBJECTIVESThe proposed research aims at the study of Tree Vertex Splitting Problem (TVSP). Designing the algorithms for TVSP and analyzing in terms of the computing time and space requirements. The most efficient algorithm can then possibly be implemented inC++/Java.However, it is not an objective to implement the algorithm for the proposed study. REFERENCES[BN90] Barry Nance, Network Programming in C, QUE Corporation 1990,ISBN: 0-88022-569-6, page # 23.[HSR98] Ellis Horowitz, Sartaj Sahni, Sanguthevar Rajasekaran, Fundamentals of Computer Algorithms, Galgotia Publications’ Pvt. Ltd. 1998,ISBN: 81-7515-257-5, page # 203.[PRS98] Doowon Paik, Sudhakar Reddy, Sartaj Sahni, Vertex Splitting In Dags And Application To Partial Scan Designs And Lossy Circuits, International Journal of Foundations of Computer Science, 1998.[ME93] Matthias Mayer, Fikret Ercal, Genetic Algorithms for Vertex Splitting in DAGs, Proceedings of the 5th International Conference on Genetic Algorithms, 1993, ISBN: 1-55860-299-2[SR96] Stephanie Forrest, Genetic Algorithms, ACM Computing Surveys, Vol. 28, No. 1, March 1996.Wednesday, April 194:00 pmAnalysis of Techniques Used in Drawing Graphs with Subgraphs(with Case Study)Bryan RitzIn the paper “Drawing Graphs Within Graphs” [5] by Paul Holleis, Thomas Zimmermann, and Daniel Gmach, the authors present methods for helping to reduce complexity of large and complicated graphs and subgraphs. The methods of finding an optimal layout of subgraphs and a summary graph, of the use of connection sets, and of the use of motifs are all combined into an approach for emphasizing subgraphs within graphs. This paper will attempt to evaluate the worthiness of these methods through examination of sources used in the paper and by applying the methods to a case study in the form of a complex graph (displayed using JEdit).References:1. F. J. Brandenburg. Graph clustering 1: Cycles of cliques. In Proceedings of the Graph Drawing 1997, volume 1353 of Lecture Notes in Computer Science, Berlin, Germany, 1997. Springer.2. G. Di Battista, P. Eades, R. Tamassia, and I. G. Tollis. Graph Drawing: Algorithms for the Visualization of Graphs. Prentice-Hall, Englewood Cliffs, N.J., 1999.3. T. M. J. Fruchterman and E. M. Reingold. Graph drawing by force-directed placement. Software-Practice and Experience, 21(11):1129-1164, 1991.4. T. Kamada and S. Kawai. An algorithm for drawing general undirected graphs. Information Processing Letters, 31(1):7-15, 1989.5. P. Holleis, T. Zimmermann, D. Gmach. Drawing Graphs Within Graphs. Journal of Graph Algorithms and Applications, 9(1):7-18, 2005.Case Study will use TouchGraph as applied to .1) Go to /TGGoogleBrowser.html2) Enter “” without the quotes in the text field and hit enter.。

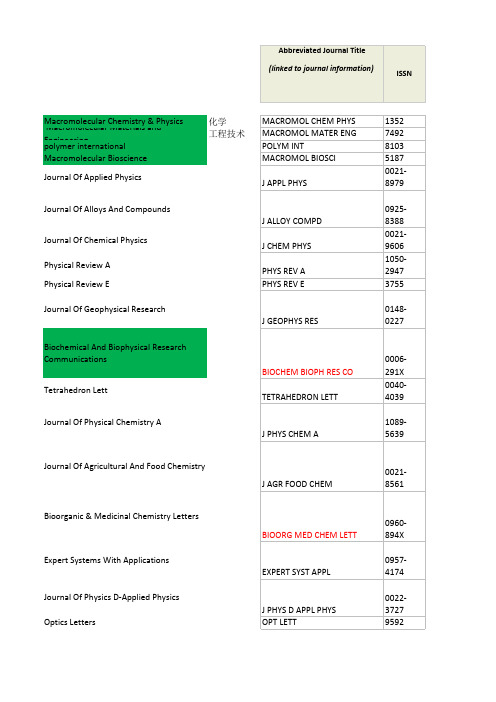
Abbreviated Journal Title (linked to journal information)Macromolecular Chemistry & Physics化学MACROMOL CHEM PHYS 1022-1352Macromolecular Materials and Engineering工程技术MACROMOL MATER ENG 1438-7492polymer international POLYM INT 0959-8103Macromolecular Bioscience MACROMOL BIOSCI 1616-5187Journal Of Applied Physics J APPL PHYS 0021-8979Journal Of Alloys And Compounds J ALLOY COMPD 0925-8388Journal Of Chemical Physics J CHEM PHYS 0021-9606Physical Review A PHYS REV A 1050-2947Physical Review E PHYS REV E 1539-3755Journal Of Geophysical Research J GEOPHYS RES 0148-0227Biochemical And Biophysical Research Communications BIOCHEM BIOPH RES CO 0006-291XTetrahedron LettTETRAHEDRON LETT 0040-4039Journal Of Physical Chemistry A J PHYS CHEM A 1089-5639Journal Of Agricultural And Food Chemistry J AGR FOOD CHEM 0021-8561Bioorganic & Medicinal Chemistry Letters BIOORG MED CHEM LETT 0960-894XExpert Systems With Applications EXPERT SYST APPL 0957-4174Journal Of Physics D-Applied Physics J PHYS D APPL PHYS 0022-3727Optics Letters OPT LETT 0146-9592Annals Of The New York Academy Of Sciences ANN NY ACAD SCI 0077-8923Chemical Physics Letters CHEM PHYS LETT 0009-2614Brain Research BRAIN RES 0006-8993Journal Of The Electrochemical Society J ELECTROCHEM SOC 0013-4651Desalination DESALINATION 0011-9164Bioorganic & Medicinal Chemistry BIOORGAN MED CHEM 0968-0896Physics Letters A PHYS LETT A 0375-9601Journal Of Colloid And Interface Science J COLLOID INTERF SCI 0021-9797Physics Of Plasmas PHYS PLASMAS 1070-664XWorld Journal Of Gastroenterology WORLD J GASTROENTERO 1007-9327EPL-EUROPHYS LETT 0295-5075Energy & Fuels ENERG FUEL 0887-0624Materials Chemistry And Physics MATER CHEM PHYS 0254-0584Inorganica Chimica Acta INORG CHIM ACTA 0020-1693Sensors And Actuators B-Chemical SENSOR ACTUAT B-CHEM 0925-4005European Journal Of Operational Research EUR J OPER RES 0377-2217European Journal Of Organic Chemistry EUR J ORG CHEM 1434-193XAdvances In Experimental Medicine And Biology ADV EXP MED BIOL 0065-2598Chemical Engineering Journal CHEM ENG J 1385-8947Journal Of Lightwave Technology J LIGHTWAVE TECHNOL 0733-8724Synlett SYNLETT 0936-5214Science Of The Total Environment SCI TOTAL ENVIRON 0048-9697Journal Of Dairy Science J DAIRY SCI 0022-0302Polyhedron POLYHEDRON 0277-5387ISSNScripta MaterSpineUrologySynthesis-StuttgartVirologyInternational Journal Of Pharmaceutics ElectrophoresisJournal Of Biomedical Materials Research Part ACatalysis CommunicationsLaryngoscopeJournal Of Biomedical Materials Research Part BBMC MicrobiologyExperimental Biology And Medicine International Journal Of Biological Macromolecules BiopolymersImpact5-Year Immediacy Cited Eigenfacto r TM ArticleInfluence T FactorImpact IndexHalf-lifeScore ScoreFactor101302.570 2.4780.382169.40.019720.7682039 1.742 1.9310.295 5.30.006990.5534555 2.137 2.0460.26319060.013380.58725443.108 3.630.6041344.10.011630.987115445 2.072 2.2780.36442718.40.322940.877JOURNAL OF APPLIED PHYSICS 26784 2.135 1.9730.4833338 4.90.073320.488JOURNAL OF ALLOYS AND COMP 175443 3.093 3.1770.7125460.29136 1.015JOURNAL OF CHEMICAL PHYSICS 84617 2.866 2.8950.75825378.40.23938 1.084PHYSICAL REVIEW A 70802 2.400 2.6030.5052456 6.70.24908 1.016PHYSICAL REVIEW E 144430 3.082 3.4750.67622569.80.34899 1.427JOURNAL OF GEOPHYSICAL RESE 75448 2.548 2.720.48219437.10.215310.905BIOCHEMICAL AND BIOPHYSICAL 75104 2.660 2.5060.62618748.90.124090.603TETRAHEDRON LETT46944 2.899 2.980.5851825 5.80.14390.882JOURNAL OF PHYSICAL CHEMIST 56340 2.469 3.0510.303158870.103820.669JOURNAL OF AGRICULTURAL AN 25857 2.650 2.5920.6021509 4.50.074330.578BIOORGANIC & MEDICINAL CHEM 5421 2.908 3.1620.394138530.009910.403EXPERT SYSTEMS WITH APPLICAT 21238 2.083 2.3050.4341363 5.70.079990.858JOURNAL OF PHYSICS D-APPLIED 36454 3.059 3.2990.5981308 6.40.13076 1.244OPTICS LETTERS 40422 2.670 2.5780.37611017.70.104970.866ANNALS OF THE NEW YORK ACAD 56231 2.291 2.4020.50510729.20.116620.793CHEMICAL PHYSICS LETTERS 56822 2.463 2.5510.40310510.095680.795BRAIN RESEARCH 41699 2.241 2.6660.4369330.077930.791JOURNAL OF THE ELECTROCHEM 11695 2.034 2.0510.16589950.026180.384DESALINATION17468 2.822 3.0460.554890 4.20.056180.7BIOORGANIC & MEDICINAL CHEM 26352 2.009 2.0130.3558797.60.071170.652PHYSICS LETTERS A 38208 3.019 3.1720.5178678.10.082440.852JOURNAL OF COLLOID AND INTER 17672 2.475 2.240.62865 5.50.068840.835PHYSICS OF PLASMAS 12740 2.0920.254863 3.60.05832WORLD JOURNAL OF GASTROEN16820 2.893 2.4630.79852 5.80.08934 1.3359498 2.319 2.5940.331826 4.90.024930.58ENERGY & FUELS 10486 2.015 2.2640.477819 5.10.03330.631MATERIALS CHEMISTRY AND PHY 16732 2.322 2.1990.5017827.60.02650.45INORGANICA CHIMICA ACTA 21794 3.083 3.2420.486777 5.30.052430.713SENSORS AND ACTUATORS B-CH 22478 2.093 2.5990.4177298.30.051270.801EUROPEAN JOURNAL OF OPERAT 14727 3.096 3.070.61689 4.50.052620.84EUROPEAN JOURNAL OF ORGAN 9103 2.020 1.3760.11268780.024480.493Advances in Experimental Medic 7707 2.816 2.9180.481680 4.30.023260.708CHEMICAL ENGINEERING JOURN 12227 2.185 2.5980.226660 6.30.041990.909JOURNAL OF LIGHTWAVE TECHN 16997 2.718 2.6160.523652 5.50.051550.719SYNLETT20059 2.905 3.3990.448648 6.50.053590.955SCIENCE OF THE TOTAL ENVIRON 25382 2.463 2.9420.4916359.80.03010.554JOURNAL OF DAIRY SCIENCE 133922.2072.2460.4286107.10.021740.429POLYHEDRONRankJCR DataEigenfactorTM Metrics Total CitesArticlesMaterials Rof Biomedical Materials R。

吕俊丽，任志龙，云月英，等. 基于模糊数学法的辣木籽杂粮面包配方优化及其品质分析[J]. 食品工业科技，2023，44（23）：167−174. doi: 10.13386/j.issn1002-0306.2023010105LÜ Junli, REN Zhilong, YUN Yueying, et al. Formulation Optimization and Quality Analysis of Moringa Seed Multigrain Bread Based on Fuzzy Mathematics[J]. Science and Technology of Food Industry, 2023, 44(23): 167−174. (in Chinese with English abstract). doi:10.13386/j.issn1002-0306.2023010105· 工艺技术 ·基于模糊数学法的辣木籽杂粮面包配方优化及其品质分析吕俊丽1, *，任志龙2，云月英1，郭　慧1（1.内蒙古科技大学生命科学与技术学院，内蒙古包头 014010；2.包头轻工职业技术学院食品生物与检测系，内蒙古包头 014035）摘　要：为了满足人们对营养食品的需求，本研究以面包为载体，运用模糊数学感官评价法，以感官评分为依据，通过单因素和正交试验对辣木籽杂粮面包配方进行优化，在此基础上，分析了辣木籽杂粮面包的理化特性和抑菌特性。

结果显示：辣木籽杂粮面包的因素影响顺序为：辣木籽添加量>薏米添加量>红豆添加量>红薯泥的添加量，辣木籽杂粮面包最佳配方为：牛奶34%，黄油7.5%，全蛋液40%，酵母添加量为0.8%，白糖添加量5.1%，辣木籽的添加量为2.6%，红薯泥的添加量为2.1%，红豆的添加量为1.6%，薏米的添加量为2.1%。

此配方下面包的模糊数学感官评分最高（86.35分），此时面包味道浓郁，松软适口，过氧化值、酸价、菌落总数均符合国家标准，蛋白质含量比普通面包高5.6 g/100 g 。

social rationality which can be used to guide an agent’s decisions making in realistic, multi-agent en-vironments, and this paper represents a preliminary step towards this goal. The robustness of the prin-ciple under varying constraints, will also be explored and this will lead to the development of socially bounded rational agents.5. References[1]S. Russell,Rationality and Intelligence, 14th International Joint Conference on ArtificialIntelligence, Montreal, Canada, August: pp 950-957, 1995.[2]J. Doyle,Rationality and its Roles in Reasoning,Computational Intelligence, Volume 8 No. 3,1992.[3]H. A. Simon,A Behavioural Model of Rational Choice,Quarterly journal of Economics, 69:pp99-118, 1955.[4]S. Russell and E. Wefald,Do the right thing,MIT Press, Cambridge Mass, 1991.[5] E.Horvitz,Reasoning Under Varying and Uncertain Resource Constraints,Proceedings of theSeventh National Conference on AI, Minneapolis,August:pp111-116,1988.[6] A.H. Bond and L. Gasser,Readings in DAI,Morgan Kauffman, San Mateo, California, 1988.[7]M. Huhns,Distributed Artificial Intelligence,Pittman, 1989.[8]R. Weihmayer and H. Velthuijsen,Applications of distributed AI and cooperative problemsolving to telecommunications,in J. Liebowitz and D. Prereau (eds), Ai Approahces to telecom-munications and network management, IOS Press, 1994.[9]H.V.D. Parunak,Applications of distribuited artificial intelligence in industry, in G.M.PO’Hare and N.R. Jennings (eds), Foundations of Distributed Artificial IntelligenceWiley:pp139-164, 1996.[10] C. Castelfranchi,Social Power: A Point Missed in Multi-Agent, DAI and HCI,DecentralizedA.I., Yves Demazeau & Jean-Pierre Muller eds., Elsevier Science Publishers,B.V (North Hol-land), 1990.[11]N.R. Jennings & J. Campos,Towards a Social Level Characterization of SociallyResponsible Agents,IEE Proceedings on Software Engineering: pp 11-25, 1997.[12] A. Newell,The Knowledge Level,Artificial intelligence, 18: pp87-127, 1982.[13] A. Shehory and S. Kraus,Task Allocation via Coalition formation amongautonomous agents,14th International Joint Conference on Artificial Intelligence, Montreal, Canada, August1995.[14]S. Ketchpel,Coalition Formation Amongst Autonomous Agents,in: Castelfranci Cristiano and Muller J-P (eds.), : From Reaction to Cognition, 5th European Workshop on Modelling Autonomous Agents in a Multi-Agent World, MAAMAW ‘93,Neuchatel, Switzerland, August 25-27, 1993., Selected papers, Lecture Notes in ArtificialIntelligence 957, Springer Verlag, Berling, Heidelberg, 1995, 73-88.together as a team is profitable or not [13], [14]. Along similar lines, an agent may wish to perform actions which are potentially helpful to the others who it is interacting with (be it for selfish or social motives). An example of this would be if an agent thought that by performing an action which was beneficial to others now, it may prompt others to favour (help) it in the future. It is therefore possible to further distinguish between the agent’s commitment to achieving benefit for the ‘society’ in general and the commitment to assisting those agents or groups with which it is currently interacting. Adding this consideration to the above equation we obtain:EU Ai (a) = w 1.EIU(a) + w 2.EPU(a) + w 3.ESU(a)where EPU is the E xpected P artners U tility (partners being those with whom the agent is currently interacting) and ESU is the benefit to the general society (this may be in terms of following social norms and conventions, or level of achievement of social goals):An agent may not necessarily interact with the same agents all of the time. Hence the notion of part-ners is a dynamic concept, with the agent likely to interact with different sets of agents to varying de-grees. From the previous equation, the utility to society is thus divided into utility of agents with whom the agent has some form of relationship (i.e. interacting and may be dependent in some way on each other) and the utility to the society in general (e.g. doing something for the common good). By making this distinction, agents can identify actions which are rational given the small community within the society that the agent is interacting with.In deliberating in this manner, an agent can exhibit more socially rational behaviour in terms of the small groups of agents which it finds itself interacting with on a regular basis. However, consideration of the wider social context can be seen as an extra bound on an agent in the same vein as the resource limitations mentioned in section one. It takes time and resources to calculate the utility an action af-fords to others. Resources which agents may not always have. In such cases, it would be advantageous to have a flexible control mechanism which, allows the agent to tailor the amount of social reasoning it performs to its current situation. Thus, in times of heavy resource constraints where it may be im-practical to take the effect of actions on others into consideration, the agent will make decisions based solely on individual benefits. In situations where it has more resources, it may be able to include the consideration of individual and partners utility for choosing action and in the most plentiful scenario,may use full social rationality. By having this flexibility the agent can manage its goal priorities (i.e individual and social goals) more efficiently and hence make its decision making more socially ra-tional as its resource bounds increase. Additionally, if the agent has the ability to learn from previous decision making successes and failures, there is the potential that it could converge towards finding the right balance, depending on the situation, between individual and societal needs.4. Conclusions and future aimsRationality is a desirable property of agents since it provides a means of assessing and attaining intel-ligent behaviour. Previous work on rationality has concentrated on the benefits gained from making a decision based on an individualistic, selfish perspective. Given the increasing use of the multi-agent paradigm in tackling complex problems, some other principle of rationality needs to be considered which would guide the agent’s actions within a multi-agent environment. Social rationality provides a principle by which agents make decisions which strike a balance between the needs of the system/society and those of the individual agent. However, such a theory needs to also take into consideration the fact that the agent is bounded and that being ‘social’ is a limitation as well other considerations such as time and computational power. The ultimate aim of this research is to define a principle ofEPU(a) =ΣA p ∈S EU Ap (a)and ESU(a) =ΣA s ∈{S-A P }EU As (a)agent, of figure 1, is faced with many decisions before taking action and we believe an adequately formulated principle of social rationality would assist at all its choice points. A preliminary attempt by Jennings and Campos [11] to define social rationality using individual and global benefits is as fol-lows:Principle of Social Rationality: If a member of a responsible society1 canperform an action whose joint benefit is greater than its joint loss, then itmay select that action.As with Newell’s rationality hypothesis of the knowledge level [12], this principle conveys, at an ab-stract level, a normative theory of decision making which takes into account the benefits accrued from actions to the society that the agent inhabits. Joint benefit is defined as the benefit provided to the in-dividual plus the benefit afforded to society as a result of an action. Similarly, joint loss is the indi-vidual plus societal loss of performing an action. Although this definition focuses the agent into choosing more beneficial actions from the societal viewpoint, it lacks concrete guidance in the choice of alternatives and the concept of maintaining a balance between individual and system needs. Thus, in order to be applied in real systems the definition needs to be expanded to show how the agent chooses between actions and how the situation that the agent finds itself in effects its decision.As stated previously, the decision theoretic concept of maximizing the utility of an action is an intu-itive and appealing way of conceptualizing decision making. It provides a way of evaluating a set of alternatives by considering the expected utility of each alternative in that set. Jennings and Campos’principle of social rationality, can be mapped onto a utility based definition in the following way. Consider a society of agents S = {A1, A2,..., A n}, and let B Ai be the benefit afforded to agent A i by the action a and B S the benefit afforded to the society. Similarly, let L Ai be the loss (or cost) the action produces for A i and L S the loss afforded to society. Hence the expected utility, EU Ai(a), of an action a to agent A i isEU Ai(a) = (B Ai - L Ai) + (B S- L S)≡EU(a) =f (EIU(a), ESU(a))where EIU is the E xpected I ndividual U tility, and is the standard decision theoretic notion of the ex-pected utility of an action2. ESU is the E xpected S ocietal U tility and is the expected benefit that an action a produces to the society. Function f shows the relationship of the two utilities from the agents’perspective and ultimately defines the characteristics of the agent. A social agent would use a function which places a greater weighting on the social utility of actions, while a self-interested agent would place more emphasis on the individual utility of actions.As a first approximation, f might be defined to be the weighted addition of the individual and societal utilities:EU Ai(a) = w1.EIU(a)+ w2.ESU(a)where w1 and w2 are in the range [0,1] and are theimportance the agent places on the respectiveutility functions.Given a relatively large society, an agent is likely to find itself interacting with various other individ-ual agents, and in some cases groups of agents, at different times. For example, if an agent does not have the necessary resources to carry out a task it may enlist the help of another agent, or agents, in the society to help it. Work on coalition formation investigates how agents calculate whether working1. A responsible society is defined as a system of autonomous agents which balance individual needs with thoseof the overall system when making decisions. This is equivalent to our social agent.2.EIU(a) =∑P(s, a)U(s). P(s,a) is the probability of reaching a state s after performing action a, and U(s) is theutility of that state to the agentsolving capability, an agent may need to obtain the assistance from other agents to help it achieve a goal. To do this, an agent may use its knowledge about how other agents are dependent on certain resources in order to influence others to adopt one or more of its goals [10]. An example scenario would be the case where there are two transporter agents, each responsible for the delivery of some goods. One agent has a truck full of its goods, which it cannot empty alone. A second agent needs an empty truck to transport its goods to its customer. Given that the second agent needs an empty truck,the first agent can suggest that the second help it unload its truck, and then use the truck to deliver its goods. In another situation of interdependence, an agent may decide to work together as a team with others, as a necessary or more profitable means of achieving individual or system goals. Figure 1. dis-plays the main decision making components and reasoning complexity of a social agent. Given the situation the agent finds itself in, it faces a number of choices which control its actions. Not only must the agent decide the benefit of combining forces with other agents to work more efficiently, but also it must determine if it acts alone how it can produce most benefit from its actions balancing individual and societal needs. Agents which merely follow the individual perspective of rationality only perform actions which bring themselves the most benefit. In multi-agent system research however, the design objective is to produce successful behaviour at both the individual and the system level.We believe rationality needs to be considered not only from the indi-viduals point of view, but also from the societal perspective. An agentadopting a selfish strategy may in-hibit the achievement of system/so-cial goals. For example if one agenthas sole control over a resourcewhich is required by others, then byselfishly using all of this resourceitself it can inhibit other agents achieving their goals and hence thesystem producing the desired be-haviour. It may even be the casethat decisions taken from a more social perspective actually producegreater benefit for the individualthan taking the individualistic pointof view. Decision making at a soci-etal level can thus be seen to becomposed of a multitude of factorsincluding current situation and in-dividual and global utility consid-erations. To produce a socially rational choice the agent needs to be able to determine the effect of its actions on others by estimating the benefit that a course of action would provide. In order to do this,the agent needs to know the goals and the preferences of the other agents in the society. Using this information, the agent can determine how desirable the outcome of its actions are to others and hence make decisions which are more socially acceptable.3. Towards social rationalityFor agents situated in a social context, it is clear that they require a fundamental decision making prin-ciple to help guide their behaviour in the same way that individual utility maximisation works for aso-cial agents. This principle should take into consideration both resource bounds (to be practical) and task and social interdependencies (to interact effectively). Such a principle of social rationality pro-vides the agent with a normative theory of decision making within a multi-agent context. The social situation assessment choice of strategy work individually work as a team all actions yourself “use” other agents coalition formation choice of team choice of structure/from current state of world from previous experience Figure 1: Flow of decision making in a socially rational agent how to attain goals choice of how to form team Problem strategySocially Rational Agents - Some Preliminary ThoughtsLisa M. Hogg and Nick R. JenningsDepartment of Electronic EngineeringQueen Mary & Westfield College, University of London.{L.M.Hogg, N.R.Jennings}@AbstractRationality relates to making the right decisions and producing successful behaviour. The notion ofbuilding rational agents is one of the main aims of research into artificial intelligence. The current pre-dominant approach is to develop agents which follow a decision theoretic notion of rationality in whichthe agent maximizes the expected utility of its actions. Although this is intuitively and formally appeal-ing, it lacks applicability in real systems where the agent is faced with resource limitations. Furthermore,this view fails to adequately cope with the case in which an agent is embedded within a system of inter-acting agents. In such an environment, the agent has the further consideration of the effects of its actionson other agents and the effect of their actions on itself. Therefore to operate effectively in such environ-ments the agents need a principle of social rationality. In this paper we outline our preliminary thoughtson devising such a principle and indicate how it helps the agent strike a balance between its individualneeds and the needs of the overall system.1. Theories of rationalityRationality is all about doing the ‘right’ thing, where right equates to performing successful actions [1]. Agent rationality is concerned with intelligent decision making as defined by the mapping of per-cepts into actions. Thus determining whether an agent is behaving rationally can only be ascertained by examining the information that it possesses and by evaluating the success of the actions that it per-forms based upon this information. The predominant theory of rational decision making in agents is that of the economic principle of maximizing the expected gain of actions [2]. Decision theoretic ra-tionality dictates that the agent should choose an action which will maximize the expected utility of performing that action given the probability of reaching a desired state in the world and the desirabil-ity of that state. However, this theory makes the assumption that the agent has both complete infor-mation and sufficient time to carry out the necessary reasoning. In reality, however, agents have limitations on their deliberation with regard to the resources they have available. Hence theories of decision making need to take such boundedness into consideration if the agents are to be applied in real systems. Recognising this shortcoming, work on bounded rationality [3], [4], [5] takes into con-sideration the fact that the agent is faced with resource limitations which affect its reasoning. Despite numerous attempts at overcoming the problems of resource bounds on reasoning, there is yet to emerge a definitive concept of bounded rationality which can be applied in real systems. In addition, most work on ideal and bounded rationality fails to recognize the importance of the fact that many systems are composed of several interacting agents and that the decisions that each agent makes have consequences on the others within the system. To this end, this work proposes an alternative view of rationality, which takes these factors into consideration. It also explores how resource limitations fur-ther affect the agents reasoning in this context.2. Shortcomings of individual rationality in multi-agent systemsThe successful combination of several autonomous, intelligent agents working together is the aim of research into multi-agent systems [6], [7]. Increasingly, the multi-agent paradigm is being used to build real, complex systems [8], [9]. Reasons for this include the inherent natural distribution of prob-lem components and the maturing of distributed computing technology. In such systems, the agents are interdependent, due to resource limitations and problem interdependencies, andl need to interact with one another in order to achieve their goals. For example, due to lack of knowledge or problem。