初一下数学证明经典例题及答案

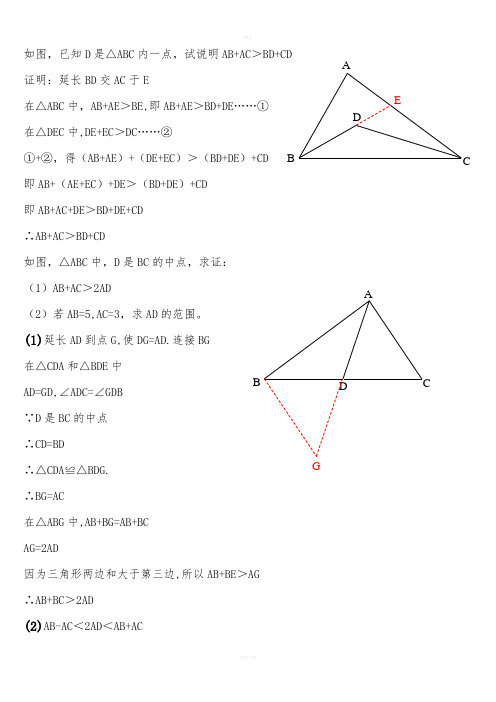
如图，已知D是△ABC内一点，试说明AB+AC＞BD+CD 证明：延长BD交AC于E在△ABC中，AB+AE＞BE,即AB+AE＞BD+DE……①在△DEC中,DE+EC＞DC……②①+②，得（AB+AE）+（DE+EC）＞（BD+DE）+CD 即AB+（AE+EC）+DE＞（BD+DE）+CD即AB+AC+DE＞BD+DE+CD∴AB+AC＞BD+CD如图，△ABC中，D是BC的中点，求证：（1）AB+AC＞2AD（2）若AB=5,AC=3，求AD的范围。

(1)延长AD到点G,使DG=AD.连接BG在△CDA和△BDE中AD=GD,∠ADC=∠GDB∵D是BC的中点∴CD=BD∴△CDA≌△BDG.∴BG=AC在△ABG中,AB+BG=AB+BCAG=2AD因为三角形两边和大于第三边,所以AB+BE＞AG ∴AB+BC＞2AD(2)AB-AC＜2AD＜AB+ACDC BAEAB CDG2＜2AD ＜8 1＜AD ＜4如图，AB=AD,AC=AE,∠BAD=∠CAE=90°，点F 为DE 的中点，求证：BC=2AF. 延长AF 到点G,使AF=DF.连接GD 在△AFE 和△DFG 中 AF=GF,∠AFE=∠DFG ∵点F 为DE 的中点 ∴DF=EF所以△AFE ≌△DFG. (SAS) GD=AE=AC;∠G=∠FAE.∴DG ∥AE.(内错角相等,两直线平行)则∠GDA+∠DAE=180°.(两直线平行,同旁内角互补） 又∵∠BAC+∠DAE=180°.∴∠GDA=∠BAC.(同角的补角相等). 又∵AD=AB.∴⊿ADG ≌⊿BAC(SAS) ∴AG=BC,即2AF=BC. ∴BC=2AF.如图，AD 是△ABC 的中线，点E 在BC 的延长线上，CE=AB, ∠BAC=∠BCA 求证：AE=2AD证明：在AD 的延长线上取点F,使AD ＝FD,连接CF ∵AD 是中线∴BD ＝CD,AD ＝FD,∠ADB ＝∠FDCECDBA∴△ABD≌△FCD （SAS）∴CF＝AB,∠B＝∠FCD∵∠ACF＝∠BCA+∠BCE,∠ACE＝∠BAC+∠B,∠BAC＝∠BCA∴∠ACF＝∠ACE∵CE＝AB∴CE＝CF∴△ACE≌△ACF （SAS）∴AE＝AF∵AF＝AD+FD＝2AD∴AE＝2AD如图，△ABC中，∠ABC=90°，AC=CE,BC=CD,∠ACE=∠BCD=90°，BC的延长线交DE于F。

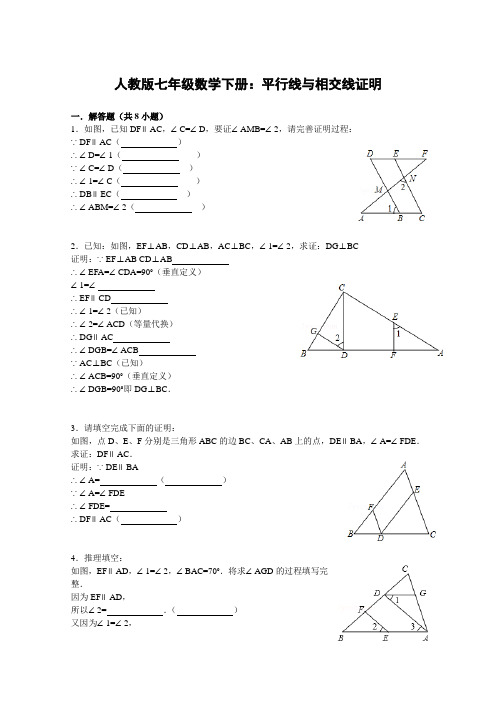
人教版七年级数学下册：平行线与相交线证明一．解答题（共8小题）1．如图，已知DF∥AC，∠C=∠D，要证∠AMB=∠2，请完善证明过程：∵DF∥AC（_________）∴∠D=∠1（_________）∵∠C=∠D（_________）∴∠1=∠C（_________）∴DB∥EC（_________）∴∠ABM=∠2（_________）2．已知：如图，EF⊥AB，CD⊥AB，AC⊥BC，∠1=∠2，求证：DG⊥BC证明：∵EF⊥AB CD⊥AB_________∴∠EFA=∠CDA=90°（垂直定义）∠1=∠_________∴EF∥CD_________∴∠1=∠2（已知）∴∠2=∠ACD（等量代换）∴DG∥AC_________∴∠DGB=∠ACB_________∵AC⊥BC（已知）∴∠ACB=90°（垂直定义）∴∠DGB=90°即DG⊥BC．3．请填空完成下面的证明：如图，点D、E、F分别是三角形ABC的边BC、CA、AB上的点，DE∥BA，∠A=∠FDE．求证：DF∥AC．证明：∵DE∥BA∴∠A=_________（_________）∵∠A=∠FDE∴∠FDE=_________∴DF∥AC（_________）4．推理填空：如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．因为EF∥AD，所以∠2=_________．（_________）又因为∠1=∠2，所以∠1=∠3．（_________）所以AB∥_________．（_________）所以∠BAC+_________=180°（_________）又因为∠BAC=70°，所以∠AGD=_________．5．如图：∠ABC=∠ACB，BD平分∠ABC，CE平分∠ACB，∠DBF=∠F，那么EC与DF平行吗？为什么？请完成下面的解题过程解：∵BD平分∠ABC，CE平分∠ACB （已知）∴∠DBC=∠_________，∠ECB=∠_________∵∠ABC=∠ACB （已知）∴∠_________=∠_________．∠_________=∠_________（已知）∴∠F=∠_________∴EF∥AD_________．6．补全下列推理过程：如图，EF∥AD，∠1=∠2，∠BAC=80°．求∠AGD的度数．因为EF∥AD （已知）所以∠2=_________（_________）又因为∠1=∠2 （已知）所以∠1=∠3（等量代换）所以AB∥_________（_________）所以∠BAC+_________=180°（两直线平行，同旁内角互补）因为∠BAC=80°（已知）所以∠AGD=_________（等量代换）7．完成下面的证明：（1）如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA．求证：∠FDE=∠A．证明：∵DE∥BA，∴∠FDE=_________（_________），∵DF∥CA，∴∠A=_________（_________），∴∠FDE=∠A；（2）如图2，AB和CD相交于点O，∠C=∠COA，∠D=∠BOD，求证：AC∥BD；证明：∵∠C=∠COA，∠D=∠BOD，∵∠COA=∠BOD（_________），∴∠C=_________，∴AC∥BD（_________）．参考答案与试题解析一．解答题（共8小题）1．如图，已知DF∥AC，∠C=∠D，要证∠AMB=∠2，请完善证明过程：∵DF∥AC（已知）∴∠D=∠1（两直线平行，内错角相等）∵∠C=∠D（已知）∴∠1=∠C（等量代换）∴DB∥EC（同位角相等，两直线平行）∴∠ABM=∠2（两直线平行，同位角相等）考点：平行线的判定与性质．专题：推理填空题．分析：先根据平行线的性质由DF∥AC得到∠D=∠1，再根据等量代换得到∠1=∠C，于是可根据平行线的判定方法得到DB∥EC，然后根据平行线的性质得到∠AMB=∠2．解答：证明：∵DF∥AC（已知），∴∠D=∠1（两直线平行，内错角相等），∵∠C=∠D（已知），∴∠1=∠C（等量代换），∴DB∥EC（同位角相等，两直线平行），∴∠AMB=∠2（两直线平行，同位角相等）．故答案为：已知，两直线平行，内错角相等，已知，等量代换，同位角相等，两直线平行，两直线平行，同位角相等．点评：本题考查了平行线的判定与性质：同位角相等，两直线平行；内错角相等，两直线平行；两直线平行，同位角相等；两直线平行，内错角相等．2．已知：如图，EF⊥AB，CD⊥AB，AC⊥BC，∠1=∠2，求证：DG⊥BC 证明：∵EF⊥AB CD⊥AB已知∴∠EFA=∠CDA=90°（垂直定义）∠1=∠ACD∴EF∥CD（两直线平行，同位角相等）∴∠1=∠2（已知）∴∠2=∠ACD（等量代换）∴DG∥AC（内错角相等，两直线平行）∴∠DGB=∠ACB（两直线平行，同位角相等）∵AC⊥BC（已知）∴∠ACB=90°（垂直定义）∴∠DGB=90°即DG⊥BC．考点：平行线的判定与性质；垂线．专题：推理填空题．分析：根据垂直定义求出∠EFA=∠CDA=90°，求出∠1=∠ACD，推出EF∥CD，根据平行线的性质得出∠2=∠ACD，推出DG∥AC，根据平行线的性质推出∠ACB=∠DGB即可．解答：证明：∵EF⊥AB，CD⊥AB（已知），∴∠EFA=∠CDA=90°（垂直定义），∴EF∥CD（同位角相等，两直线平行），∴∠1=∠ACD（两直线平行，同位角相等），∵∠1=∠2（已知），∴∠2=∠ACD（等量代换），∴DG∥AC（内错角相等，两直线平行），∴∠DGB=∠ACB（两直线平行，同位角相等），∵AC⊥CB，∴∠ACB=90°，∴∠DGB=90°，即DG⊥BC，故答案为：已知，ACD，（两直线平行，同位角相等），（内错角相等，两直线平行），（两直线平行，同位角相等）．点评：本题考查了平行线的判定和性质，三角形内角和定理，垂直定义的应用，主要考查学生的推理能力．3．请填空完成下面的证明：如图，点D、E、F分别是三角形ABC的边BC、CA、AB上的点，DE∥BA，∠A=∠FDE．求证：DF∥AC．证明：∵DE∥BA∴∠A=∠DEC（两直线平行，同位角相等）∵∠A=∠FDE∴∠FDE=∠DEC∴DF∥AC（内错角相等，两直线平行）考点：平行线的判定与性质．专题：推理填空题．分析：根据平行线的性质得出∠A=∠DEC，求出∠FDE=∠DEC，根据平行线的判定推出即可．解答：证明：∵DE∥BA，∴∠A=∠DEC（两直线平行，同位角相等），∵∠A=∠FDE（已知），∴∠FDE=∠DEC（等量代换），∴DF∥AC（内错角相等，两直线平行），故答案为：∠DEC，两直线平行，同位角相等；∠DEC，内错角相等，两直线平行．点评：本题考查了平行线的性质和判定的应用，注意：①两直线平行，同位角相等，②内错角相等，两直线平行．4．推理填空：如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．因为EF∥AD，所以∠2=∠3．（两直线平行，同位角相等）又因为∠1=∠2，所以∠1=∠3．（等量代换）所以AB∥DG．（内错角相等，两直线平行）所以∠BAC+∠AGD=180°（两直线平行，同旁内角互补）又因为∠BAC=70°，所以∠AGD=110°．考点：平行线的判定与性质．专题：推理填空题．分析：根据平行线的性质推出∠1=∠2=∠3，推出AB∥DG，根据平行线的性质得出∠BAC+∠DGA=180°，代入求出即可．解答：解：∵EF∥AD，∴∠2=∠3（两直线平行，同位角相等），∵∠1=∠2，∴∠1=∠3（等量代换），∴AB∥DG（内错角相等，两直线平行），∴∠BAC+∠DGA=180°（两直线平行，同旁内角互补），∵∠BAC=70°，∴∠AGD=110°，故答案为：∠3，两直线平行，同位角相等，等量代换，DG，内错角相等，两直线平行，∠AGD，两直线平行，同旁内角互补，110°．点评：本题考查了平行线的性质和判定的应用，注意：平行线的性质是①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．5．如图：∠ABC=∠ACB，BD平分∠ABC，CE平分∠ACB，∠DBF=∠F，那么EC与DF 平行吗？为什么？请完成下面的解题过程解：∵BD平分∠ABC，CE平分∠ACB （已知）∴∠DBC=∠ABC，∠ECB=∠ACB∵∠ABC=∠ACB （已知）∴∠DBC=∠ECB．∠F=∠DBF（已知）∴∠F=∠ECB∴EF∥AD（同位角相等，两直线平行）．考点：平行线的判定．专题：推理填空题．分析：利用角平分线的性质得出∠DBC=∠ABC，∠ECB=∠ACB，进而求出∠F=∠ECB，得出答案即可．解答：解：∵BD平分∠ABC，CE平分∠ACB（已知）∴∠DBC=∠ABC，∠ECB=∠ACB，∵∠ABC=∠ACB （已知）∴∠DBC=∠ECB．∵∠DBF=∠F，（已知）∴∠F=∠ECB，∴EF∥AD（同位角相等，两直线平行）．点评：此题主要考查了平行线的判定以及角平分线的性质，得出∠F=∠ECB是解题关键．6．补全下列推理过程：如图，EF∥AD，∠1=∠2，∠BAC=80°．求∠AGD的度数．因为EF∥AD （已知）所以∠2=∠3（两直线平行，同位角相等）又因为∠1=∠2 （已知）所以∠1=∠3（等量代换）所以AB∥DG（内错角相等，两直线平行）所以∠BAC+∠AGD=180°（两直线平行，同旁内角互补）因为∠BAC=80°（已知）所以∠AGD=100°（等量代换）考点：平行线的判定与性质．专题：推理填空题．分析：根据平行线性质推出∠2=∠3，推出∠1=∠3，根据平行线的判定推出AB∥DG，根据平行线的性质得出∠BAC+∠AGD=180°，代入求出即可．解答：解：∵EF∥AD，∴∠2=∠3（两直线平行，同位角相等），∵∠1=∠2，∴∠1=∠3，∴AB∥DG（内错角相等，两直线平行），∴∠BAC+∠AGD=180°，∵∠BAC=80°，∴∠AGD=100°，故答案为：∠3，两直线平行，同位角相等，DG，内错角相等，两直线平行，∠AGD，100°．点评：本题考查了平行线的性质和判定的应用，注意：平行线的性质是：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．7．完成下面的证明：（1）如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA．求证：∠FDE=∠A．证明：∵DE∥BA，∴∠FDE=∠BFD（两直线平行，内错角相等），∵DF∥CA，∴∠A=∠BFD（两直线平行，同位角相等），∴∠FDE=∠A；（2）如图2，AB和CD相交于点O，∠C=∠COA，∠D=∠BOD，求证：AC∥BD；证明：∵∠C=∠COA，∠D=∠BOD，∵∠COA=∠BOD（对顶角相等），∴∠C=∠D，∴AC∥BD（内错角相等，两直线平行）．考点：平行线的判定与性质．专题：推理填空题．分析：（1）根据平行线的性质得出∠FDE=∠BFD，∠A=∠BFD，推出即可；（2）根据对顶角相等和已知求出∠C=∠D，根据平行线的判定推出即可．解答：（1）证明：∵DE∥BA，∴∠FDE=∠BFD（两直线平行，内错角相等），∵DF∥CA，∴∠A=∠BFD（两直线平行，同位角相等），∴∠FDE=∠A，故答案为：∠BFD，两直线平行，内错角相等，∠BFD，两直线平行，同位角相等；（2）证明：∵∠C=∠COA，∠D=∠BOD，又∵∠COA=∠BOD（对顶角相等），∴∠C=∠D，∴AC∥BD（内错角相等，两直线平行），故答案为：对顶角相等，∠D，内错角相等，两直线平行．点评：本题考查了平行线的性质和判定的应用，注意：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然，题目比较好，难度适中．8．如图，在△ABC中，DE∥BC，连结DC，点F是边BC上一点，GF⊥AB，垂足为G，∠1=∠2，求证：CD⊥AB．考点：平行线的判定与性质；垂线．专题：证明题．分析：求出∠BGF=90°，根据平行线的性质和已知求出∠2=∠BCD，推出FG∥CD，根据平行线的性质得出∠CDB=∠BGF=90°即可．解答：证明：∵FG⊥AB，∴∠BGF=90°，∵DE∥BC，∴∠1=∠BCD，∵∠1=∠2，∴∠2=∠BCD，∴FG∥CD，∴∠CDB=∠BGF=90°，∴CD⊥AB．点评：本题考查了平行线的性质和判定，垂直的定义的应用，主要考查学生的推理能力．。

七年级下册数学证明题及参考答案初一下的数学不好学，因为迎来很多的证明题，这些的证明题的解法是怎样的呢？下面就是店铺给大家整理的初一下数学证明题内容，希望大家喜欢。

初一下数学证明题方法一如图，CE平分∠ACB且CE⊥BD，∠DAB =∠DBA，AC = 18，△CDB的周长是28。

求BD的长大家看我的步骤，我的步骤只做到这里就坐不下去了解：因为∠DAB =∠DBA(已知)所以AD=BD(等角对等边)因为CE平分∠ACB，CE⊥BD(已知)所以∠DCE= ∠BCE(角平分线的意义)∠BEC= ∠DEC=90度(垂直意义)在△ACE与△BCE中因为{ ∠DCE= ∠BCE(已求){CE=EC(公共边){ ∠BEC= ∠DEC(已求)所以△ACE≌ △BCE(A.S.A)所以BC=CD(全等三角形对应边相等)因为AC=18,即CD+AD=18所以CD+BD=18因为△CDB的周长是28，即CD+BD+BC=28所以BC=28-18=10所以CD=10所以BD=18-10=8初一下数学证明题方法二在△ABC中，已知∠CAB=60°，D，E分别是边AB，AC上的点，且∠AED=60°，ED+DB=CE，∠CDB=2∠CDE，则∠DCB= ()A.15°B.20°C.25 °D.30°这题实际上是一传统题的翻版，原题中条件为△ADE为等边三角形，C，B分别是AE，AD延长线的点，且EC=AB，求证;CD=CB，结论明确，本题增加了一个条件∠CDB=2∠CDE，把结论改为求值题，其它改动没有多大变化，很快就会知道△ADE为等边三角形，EC=AB，∠EDC=∠CDB/2=40°，但结论为求值题后使结论没有目标，实际上是故弄玄虚，习难学生，使分析没有方向，要是学生没做过原题要得出正确结论是不大可能的!但学生可做一下投机;地图作得尽量正确，用量角器测一下也可得正确的结论。

初一典型几何证明题1、已知： AB=4，AC=2，D是 BC中点， AD是整数，求 AD解：延长 AD到 E, 使 AD=DE∵D是 BC中点∴ BD=DC在△ ACD和△ BDE中AAD=DE∠BDE=∠ADC BD=DC∴△ ACD≌△ BDE ∴AC=BE=2∵在△ ABE中AB-BE＜AE＜ AB+BE ∵AB=4即4-2 ＜2AD＜ 4+2 1＜AD＜3∴AD=2B CD2、已知： BC=DE，∠ B=∠ E，∠ C=∠ D， F 是 CD中点，求证：∠ 1=∠ 2A12B EC F D证明：连接 BF 和 EF∵BC=ED,CF=DF,∠ BCF=∠EDF∴△ BCF≌△ EDF (S.A.S)∴BF=EF,∠ CBF=∠ DEF连接 BE在△ BEF中 ,BF=EF∴ ∠ EBF=∠ BEF。

∵ ∠ ABC=∠ AED。

∴ ∠ ABE=∠ AEB。

∴AB=AE。

在△ ABF和△ AEF中AB=AE,BF=EF,∠ABF=∠ ABE+∠ EBF=∠AEB+∠BEF=∠AEF∴△ ABF≌△ AEF。

∴ ∠ BAF=∠ EAF ( ∠1=∠ 2) 。

3、已知：∠ 1=∠2，CD=DE， EF//AB，求证： EF=ACA12FCDEB过C 作 CG∥EF 交 AD的延长线于点G CG∥EF，可得，∠ EFD＝ CGDDE＝DC∠FDE＝∠ GDC（对顶角）∴△ EFD≌△ CGDEF＝CG∠CGD＝∠ EFD又， EF∥AB∴，∠ EFD＝∠1∠1=∠2∴∠ CGD＝∠2∴△ AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC4、已知： AD平分∠ BAC，AC=AB+BD，求证：∠ B=2∠C证明：延长 AB取点 E，使 AE＝AC，连接 DE∵AD平分∠ BAC∴∠ EAD＝∠ CAD∵AE＝AC，AD＝ AD∴△ AED≌△ ACD （SAS）∴∠ E＝∠ C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠ BDE＝∠ E∵∠ ABC＝∠ E+∠BDE∴∠ ABC＝2∠E∴∠ ABC＝2∠C5、已知： AC平分∠ BAD，CE⊥ AB，∠ B+∠D=180°，求证： AE=AD+BE证明：在AE上取 F，使 EF＝EB，连接 CF∵CE⊥AB∴∠ CEB＝∠ CEF＝90°∵EB＝EF，CE＝ CE，∴△ CEB≌△ CEF∴∠ B＝∠ CFE∵∠ B＋∠ D＝180°，∠ CFE＋∠ CFA＝180°∴∠ D＝∠ CFA∵AC平分∠ BAD∴∠ DAC＝∠ FAC∵AC＝AC∴△ ADC≌△ AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝ AD＋BE6、如图，四边形 ABCD中， AB∥DC，BE、CE分别平分∠ ABC、∠BCD，且点 E 在 AD上。

初一典型几何证明题1、已知： AB=4，AC=2，D是BC中点， AD是整数，求AD解：延长A D到 E,使AD=DE∵D是 BC中点A ∴BD=DC在△ ACD和△ BDE中AD=DE∠BDE=∠ADC B CDBD=DC∴△ACD≌△ BDE∴AC=BE=2∵在△ ABE中AB-BE＜AE＜AB+BE∵AB=4即 4-2＜2AD＜4+21＜AD＜3∴AD=22、已知： BC=DE，∠B=∠E，∠ C=∠D，F 是 CD中点，求证：∠1=∠2A21B EC F D证明：连接BF和 EF∵BC=ED,CF=DF∠, BCF=∠EDF∴△BCF≌△ EDF 第1页共22 页∴BF=EF,∠CBF=∠DEFB E连接在△ BEF中,BF=EF∴∠EBF=∠BEF。

∵∠ABC=∠AED。

∴∠ABE=∠AEB。

∴AB=AE。

在△ ABF和△ AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴△ABF≌△ AEF。

∴∠BAF=∠EAF (∠1=∠2)。

3、已知：∠1=∠2，CD=D，E EF证明：连接EF ∵AB∥CD共22 页第9页∴∠B=∠C∴△BEM≌△CFM（ SAS）∵M是 BC中点∴CF=BE∴BM=CM在△BEM和△CFM中BE=CF∠B=∠CBM=CM7. 已知：如图所示，AB＝AD，BC＝DC，E、F 分别是DC、BC的中点，求证：AE＝AF。

证：连接AC DE=BF∵在△ ADC和△ABC中∴△ADE≌△ ABF（SAS）AD=AB ∴AE=AFDC=BCAC=AC∴△ADC≌△ ABC（SSS）D∴∠B=∠ DE∵E、F 分别是DC、BC的中点AC又∵ BC＝DCF∴DE=BFB∵在△ ADE和△ABF中AD=AB∠D=∠B8. 如图，在四边形ABCD中， E是AC上的一点，∠1=∠2，∠3=∠4，求证 : ∠5=∠6．证明：∵在△ADC和△ ABC中∴△DEC≌△ BEC（SAS）∠BAC=∠DAC ∴∠DEC=∠BEC∠BCA=∠DCAAC=AC∴△ADC≌△ ABC（AAS）D∵AB=AD，BC=CD在△ DEC与△ BEC中A12E5634CCE=CEB∠BCA=∠DCABC=CD9. 如图，在△ABC中， AD为∠ BAC的平分线，DE⊥AB于 E，DF⊥AC于 F。

[精选]初一下-三角形证明初一(含答案)–资料1. 引言初中数学的三角形证明是一个基础而重要的内容，它涉及到了三角形的性质和相关定理的证明。

掌握了三角形证明的方法和技巧，能够提高学生的逻辑思维能力和证明能力，并为日后的高中数学学习打下坚实的基础。

本文档精选了一些初一下学期的三角形证明题目，并提供了详细的解答和解题过程，旨在帮助初中学生更好地理解和掌握三角形证明的方法。

2. 题目与解答2.1 证明三角形的内角和为180度题目：证明任意三角形的内角和等于180度。

解答：我们知道，在直角三角形中，其中一个角是90度，而另外两个角的和等于90度。

因此，我们可以通过直角三角形来证明三角形的内角和等于180度。

假设有一个三角形ABC，其中$\\angle A$、$\\angle B$、$\\angle C$ 分别为三个内角。

我们可以通过画一条辅助线，将三角形ABC分割成两个直角三角形来证明。

具体的证明过程如下：1.在边AC上找一点D，在边BC上找一点E；2.链接点D和点B，连接点E和点A，得到线段BD和线段AE；3.由直角三角形的性质可知，$\\angle BDC =90^{\\circ}$，$\\angle AEC = 90^{\\circ}$；4.因为$\\angle ABC$是$\\angle BDC$和$\\angleAEC$的外角，所以 $\\angle ABC = \\angle BDC + \\angle AEC$；5.代入已知的角度，得到 $\\angle ABC = 90^{\\circ}+ 90^{\\circ} = 180^{\\circ}$。

因此，任意三角形的内角和等于180度得证。

2.2 证明等边三角形的三个内角均为60度题目：证明等边三角形的三个内角均为60度。

解答：等边三角形是指三条边的长度相等的三角形。

我们需要证明等边三角形的三个内角均为60度。

具体的证明过程如下：1.画一个等边三角形ABC，其中三条边的长度分别为AB、BC、CA；2.因为等边三角形的三条边的长度相等，所以AB =BC = CA；3.假设等边三角形的任意两个内角分别为$\\angle A$、$\\angle B$；4.因为AB = BC，所以它们所对的两个内角相等，即$\\angle A = \\angle B$；5.同理可以得到$\\angle B = \\angle C$；6.因此，$\\angle A = \\angle B = \\angle C$；7.代入已知的角度，得到 $\\angle A = \\angle B =\\angle C = 60^{\\circ}$。

初一典型几何证明题1、已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=22、 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23、4、 证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDFBC DF ADBC∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。

∴ ∠BAF=∠EAF (∠1=∠2)。

已知：∠1=∠2，CD=DE ，EFP 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-ABBA CDF2 1 EA在AC 上取点E ， 使AE ＝AB 。

∵AE ＝AB AP ＝AP ∠EAP ＝∠BAE ，∴△EAP ≌△BAP ∴PE ＝PB 。

PC ＜EC ＋PE∴PC ＜（AC －AE ）＋PB ∴PC －PB ＜AC －AB 。

8. 已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BE 证明：在AC 上取一点D ，使得角DBC=角C ∵∠ABC=3∠C∴∠ABD=∠ABC-∠DBC=3∠C-∠C=2∠C ； ∵∠ADB=∠C+∠DBC=2∠C; ∴AB=AD∴AC – AB =AC-AD=CD=BD在等腰三角形ABD 中，AE 是角BAD 的角平分线， ∴AE 垂直BD∵BE ⊥AE∴点E 一定在直线BD 上，在等腰三角形ABD 中，AB=AD ，AE 垂直BD ∴点E 也是BD 的中点 ∴BD=2BE ∵BD=CD=AC-AB ∴AC-AB=2BE9. 如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．P DACB解：延长AD 至BC于点E,∵BD=DC ∴△BDC是等腰三角形∴∠DBC=∠DCB又∵∠1=∠2 ∴∠DBC+∠1=∠DCB+∠2即∠ABC=∠ACB∴△ABC是等腰三角形∴AB=AC在△ABD和△ACD中AB=AC∠1=∠2BD=DC∴△ABD和△ACD是全等三角形（边角边）∴∠BAD=∠CAD∴AE是△ABC的中垂线∴AE⊥BC∴AD⊥BC10. 如图，OM平分∠POQ，MA⊥OP,MB⊥OQ，A、B为垂足，AB交OM于点N．求证：∠OAB=∠OBA证明：∵OM平分∠POQ∴∠POM＝∠QOM∵MA⊥OP，MB⊥OQ∴∠MAO ＝∠MBO ＝90 ∵OM ＝OM∴△AOM ≌△BOM （AAS ） ∴OA ＝OB ∵ON ＝ON∴△AON ≌△BON （SAS ） ∴∠OAB=∠OBA ，∠ONA=∠ONB ∵∠ONA+∠ONB ＝180 ∴∠ONA ＝∠ONB ＝90 ∴OM ⊥AB11. 如图，已知AD ∥BC ，∠PAB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ． 证明：在AB 上取F ，使AF ＝AD ，连接EF ∵AE 平分∠DAB ∴∠DAE=∠FAE 在⊿ADE 和⊿AFE 中AD ＝AF ∠DAE=∠FAE AE = AE∴⊿ADE ≌⊿AFE （SAS ） ∴∠ADE=∠AFE∵AB 如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ． （1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立若成立PEDCBA{{请给予证明；若不成立请说明理由．(1)证：∵DE ⊥AC 于E ，BF ⊥AC 于F ， ∴∠DEC=∠BFA=90°，DE ∥BF ， 在Rt △DEC 和Rt △BFA 中， ∵AF=CE ，AB=CD ， ∴Rt △DEC ≌Rt △BFA （HL ） ∴DE=BF ．在△DEM 和△BFM 中 ∠DEM=∠BFM ∠DME=∠BMF DE=BF∴△DEM ≌△BFM(AAS) ∴MB=MD ，ME=MF(2) 证：∵DE ⊥AC 于E ，BF ⊥AC 于F ， ∴∠DEC=∠BFA=90°，DE ∥BF ， 在Rt △DEC 和Rt △BFA 中， ∵AF=CE ，AB=CD ， ∴Rt △DEC ≌Rt △BFA （HL ） ∴DE=BF ．在△DEM 和△BFM 中 ∠DEM=∠BFM ∠DME=∠BMF DE=BF{{∴△DEM≌△BFM(AAS)∴MB=MD，ME=MF13如图，△ABC中，∠BAC=90度，AB=AC，BD是∠ABC的平分线，BD的延长线垂直于过C点的直线于E，直线CE交BA的延长线于F．求证：BD=2CE．证：∵∠CEB=∠CAB=90°∠ADB=∠CDE在△ABD中，∠ABD = 180°-∠CAB-∠ADB 在△CED中，∠DCE = 180°-∠CEB-∠CDE ∴∠ABD =∠DCE在△ABD和△ACF中∠DAB=∠CAFAB=AC∠ABD =∠DCF∴△ABD≌△ACF(ASA)∴BD=CF∵BD是∠ABC的平分线∴∠FBE =∠CBE在△FBE和△CBE中∠FBE =∠CBEBE=BE∠BEF =∠BEC∴△FBE≌△CBE(ASA)∴CE=FE CF=2CE∴BD=2CEFEDC BA{ {14. 如图：DF=CE，AD=BC，∠D=∠C。

证明题七年级下册一、相交线与平行线证明题。

1. 如图，已知直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，∠2 : ∠1 = 4:1，求∠AOF的度数。

证明：设∠1 = x，因为∠2:∠1 = 4:1，则∠2 = 4x。

因为OE平分∠BOD，所以∠DOE=∠1 = x。

又因为∠2+∠DOE = 180°（邻补角之和为180°），即4x + x=180°，5x = 180°，解得x = 36°。

所以∠COE=180° - ∠1=180° - 36° = 144°。

因为OF平分∠COE，所以∠COF=(1)/(2)∠COE=(1)/(2)×144° = 72°。

∠AOC = ∠1 = 36°（对顶角相等）所以∠AOF=∠AOC + ∠COF = 36°+72° = 108°。

2. 已知：如图，AB∥CD，∠1 = ∠2，求证：AM∥CN。

证明：因为AB∥CD，所以∠EAB = ∠ACD（两直线平行，同位角相等）。

又因为∠1 = ∠2，所以∠EAB - ∠1=∠ACD - ∠2，即∠MAC = ∠NCA。

所以AM∥CN（内错角相等，两直线平行）3. 如图，已知∠1 = ∠2，∠C = ∠D，求证：∠A = ∠F。

证明：因为∠1 = ∠2，∠1 = ∠3（对顶角相等），所以∠2 = ∠3。

所以DB∥EC（同位角相等，两直线平行）。

所以∠D = ∠4（两直线平行，同位角相等）。

又因为∠C = ∠D，所以∠C = ∠4。

所以DF∥AC（内错角相等，两直线平行）。

所以∠A = ∠F（两直线平行，内错角相等）二、三角形证明题。

4. 在△ABC中，AD是BC边上的中线，E是AD的中点，BE的延长线交AC于F。

求证：AF=(1)/(3)AC。

证明：过点D作DG∥BF交AC于G。