1.1 探索勾股定理 课件(北师大版上册)7
- 格式：ppt
- 大小：573.00 KB
- 文档页数：20
下载文档原格式
合集下载
北师大数学八上课件1.1《探索勾股定理》教学课件
我实践,我验证 方法一
证明： S= a b2
b S=S小正方形 S4直角三角形
c2 4 1 ab
a c
2
a b2 c2 4 1 ab
2b c
a2 b2 c2
a
灿若寒星
a
b c
c a
b
我实践,我验证 方法二
a bc
c a
b
S梯形
1 2
a
b
灿若寒星
我观察,我猜想
观察所得到的数据，你有什么发现？ SA+SB=SC
B 4b c5
a3 A
32+42=52 a2+b2=c2
猜想:两直角边a、b与斜边c 之间的关系？
灿若寒星
我实践,我验证
命题：如果直角三角形的两直角 边长分别为a、b，斜边长为c，那 么 a2+b2=c2.
c a
b 灿若寒星
灿若寒星
我会用,我挑战
1.求下列直角三角形中未知边的长:
比
一
5
比
看8
17
看
x
12
谁
x
算
得
快 ！
方法小结: 可用勾股定理建立方程.
灿若寒星
我自信,我挑战
已知:R△t△ABACB的C的两两边直为边角3为和边34和为，43，和4， 求:第三边c. 解：由于三角形的两边为3、4 所以它的第三边c的平方等于25 即：c=5
A
? 8
灿若寒星
B 24 E
C 10 D
灿若寒星
1. 课本4页，第１、２题； 2.查阅有关勾股定理的历史资料, 关注 验证勾股定理的方法.
北师大版八年级上册探索勾股定理课件
为股，斜边称为弦。“勾股定理
”因此而得名．（在西方文献中
股
又称为毕达哥拉斯定理）
练一练
求下列直角三角形中未知边的长:
8
17
x 解：由勾股定理可得：
82+ x2=172 即: x2=172-82
x=15
12 5
x 解:由勾股定理可得：
52+ 122= x2 即： x2=52+122
x=13
当堂练习 1.图中阴影部分是一个正方形，则此正方 形的面积为 36 cm² .
讲教授学新目知
标
勾股定理：
直角形三角形两条直角边的平方和等于斜边 的平方.
几何语言 表示：
Aቤተ መጻሕፍቲ ባይዱ
若在Rt△ABC中，∠C=90°
b
c
那么 a2+b2=c2
(AC2+BC2=AB2)
C
a
B
讲教授学新目知
标
勾股定理： 直角形三角形两条直角边的平方和等于斜边的平方.
我国古代把直角三角形中，较短
弦
的边称为勾，较长的直角边称之 勾
SA=16 SB=9 SC=?
方法一：补
C
补成大正方形，用大正方形的面积减去四个直角三 角形的面积.
方法三：拼
C
将几个小块拼成若干个小正方形，图中两块红色（或绿色） 可拼成一个小正方形.
方法二：割
C
分割为四个直角三角形和一个小正方形.
数学知识
图为2002年在我 国北京召开的世 界数学家大会的 会标。
（3）试试猜想SA，SB，SC的数量关系？
SA=16 SB=9 SC=25
猜想：SA+SB=SC
北师大版八年级数学上册1.1《探索勾股定理》课件
c=
。
2.在△ABC中，∠C=90°,若c=13，ቤተ መጻሕፍቲ ባይዱ=12，则
a=
。
3.若直角三角形中，有两边长是3和4，则第三
边长的平方为（ ）
A 25 B 14 C 7 D 7或25
二、提高训练
4．一个长为10 m为梯子斜靠在墙上，梯子的顶端距
地面的垂直高度为8m，梯子的顶端下滑2 m后，底端
滑动
m．
5．已知Rt△ABC中，∠C＝90°，若 a+b=14cm， c=10cm，则Rt△ABC的面积为（ ）
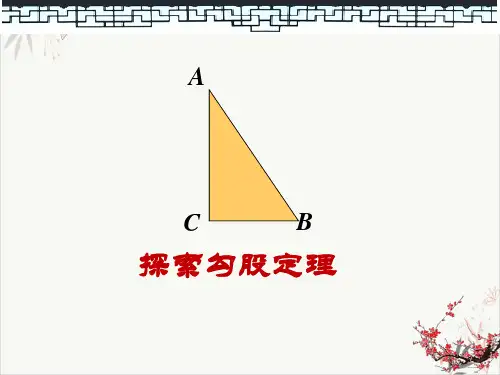
视察这三 个正方形
你发现图中三个正方形的面积之间 存在什么关系吗？
换个角度来看呢？
你发现了什么？
结论1 以等腰直角三角形两直角边为边长 的小正方形的面积的和，等于以斜边为边长的正 方形的面积.
分小组动手操作实践
用四张全等的等腰直角三角形纸片，拼成一个 正方形。（不能重叠，不能有间隙）
∵c2= 4×12 a2 ∴c2=2a2
（1）如果三角形的三边长分别为a,b,c，则 a2+b2=c2
( ×)
（2）如果直角三角形的三边长分别为a,b,c，则a2+b2=c2
( ×)
( 3) 如果直角三角形的三边长分别为a,b,c，且c为斜边，
则 a+b=c
( ×)
(4) 如果直角三角形的三边长分别为a,b,c，且c为斜边，
则 b2=c2-a2
2002年国际数 学家大会会标 ——弦图.
四、课堂小结 定理内容
重要的 思想方 法及数 学思想
勾股 定理
从特殊 到一般、 数形结 合思想
定理运用
五、布置作业
1．习题1.1. 2．阅读《读一读》——勾股世界.
北师大版八年级数学上册《探索勾股定理》课件(24张PPT)
勾是6， 62=36, 勾是5，
股是8， 82=64, 股是12，
弦一定是10；
102=100
62+82=102
弦一定是13，
52=25, 122=144, 132=169 52+122=132 等等. 是不是所有的直角三角形都有这个性质呢？世界上许
多数学家，先后用不同方法证明了这个结论. 我国把它称 为勾股定理.
正方形C的面积是__1_8__ 个单位面积.
（图中每个小方格代表1个单位面积）
C A
B
S正方形C 4 1 33 2
=18个单位面积
把正方形C分割成若干 个直角边为整数的三角 形来求
（图中每个小方格代表1个单位面积）
C A
B
S正方形C
1 2
62
=18个单位面积
把正方形C看成边长为 6的正方形面积的一半
第一章 勾股定理
1 探索勾股定理
1.经历探索勾股定理及验证勾股定理的过程，了解勾股 定理的探究方法及其内在联系. 2.掌握勾股定理，并能运用勾股定理解决一些实际问题.
这是1955年希腊为纪念一个数学学派发行的邮票.
P
C
A
Q
R B
如图，小方格的边长为1.
正方形P 正方形Q 正方形R 的面积 的面积 的面积
2
通过本课时的学习，需要我们掌握： 勾股定理： 直角三角形两直角边的平方和等于斜边的平方，即
a2 b2 c2
没有智慧的头脑，就像没有蜡烛的灯笼.
•不习惯读书进修的人，常会自满于现状，觉得再没有什么事情需要学习，于是他们不进则退。经验丰富的人读书用两只眼睛，一只眼睛看到纸面上的话，另 一眼睛看到纸的背面。2022年4月12日星期二2022/4/122022/4/122022/4/12 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/122022/4/122022/4/124/12/2022 •正确的略读可使人用很少的时间接触大量的文献，并挑选出有意义的部分。2022/4/122022/4/12April 12, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
探索勾股定理北师大版数学课件
4组织学生自主完成教 材中的P2页的第（3） 问。总结出直角三角 形的三边上的三个正 方形面积之间的关系 关系。A+B=C
ቤተ መጻሕፍቲ ባይዱ
1归纳出直角三角形 的三边上的三个正 方形面积之间的关 系关系。
2有条理的表达出来 所获的结论。
♣教师活动
5出示教材P3中的做一做 进一步巩固探究过程。 6 出示教材3页的议一议
指导并小结完成的情况。
巩固所学知识。
检查学生的掌握情况。 培养学生的动手操作 能力。
10引导学生对本节内 容作出总结。
组员之间互相补充切磋 得到本节 所学主要内容。
提高学生的归纳能 力和语言表达能力， 合作能力。
教学重点和难点
● ○ 重点
1 利用观察归纳猜想方法 :即由特殊到一般的探索 定理的过程. 2 体会数形结合的 思想. 3 掌握勾股定理的内容. 4 会利用勾股定理解决一些实际问题.
● ○ 难点
1勾股定理的发现
我国著名的数学家华罗庚教 授曾建议“发射”一种勾股 定理图形作为与“外星人” 联系的信号。
81
B
& 教学设计
♣教师活动
1 出示投影图文 p1，教师 介绍我国古代在勾股定理研 究方面的贡献，并结合课本 p5谈一谈，讲述我国是最早 了解勾股定理的国家之一， 介绍商高(三千多年前周期的 数学家)在勾股定理方面的贡 献.
☺ 学生活动
1了解勾股定理的重要 性. 2勾股定理悠久的历史, 以及古代人民的聪明 才智.
7出示勾股定理的内容
熟悉并记忆
并介绍勾股弦的含义。
♣教师活动
11 出示 错例辨析： 直角△ABC的两边为3和4，求第 三边 解：由于三角形的两边为3、4 所以它的第三边的c应满足=25 即：c=5
第1章第1课时 探索勾股定理PPT课件(北师大版)
2．(2018·山东滨州)在直角三角形中，若勾为 3，股
为 4，则弦为( A )
A．5
B．6
C．7
D．8
3．在一个直角三角形中，两直角边长分别为 3 和 4，
下列说法正确的是( C )
A．斜边长为 25
B．该三角形的周长为 25
C．斜边长为 5
D．该三角形的面积为 20
4．如图，在由边长均为 1 个单位长度的小正方形组 成的网格中，点 A，B 都是格点，则线段 AB 的长为( A )
1．下列说法正确的是( D ) A．若 a，b，c 是△ABC 的三边，则 a2＋b2＝c2 B．若 a，b，c 是 Rt△ABC 的三边，则 a2＋b2＝c2 C．若 a，b，c 是 Rt△ABC 的三边，∠A＝90°， 则 a2＋b2＝c2 D．若 a，b，c 是 Rt△ABC 的三边，∠C＝90°，则 a2＋b2＝c2
变式 3 飞机在空中水平飞行，某一时刻刚好飞到一 个男孩头顶上方 3 km 处，过了 20 s，飞机距离这个男孩 头顶 5 km(如图)．这一过程中飞机飞行的速度是每秒多 少千米？
解：在 Rt△ABC 中，BC2＝52－32＝16. 因为 BC＞0，所以 BC＝4(km)． 4÷20＝0.2(km/s)． 答：这一过程中飞机飞行的速度是每秒 0.2 千米．
A．5 C．7
B．6 D．25
5．已知在 Rt△ABC 中，∠C＝90°，∠A，∠B， ∠C 的对应边分别为 a，b，c.
(1)若 a＝3，b＝4，则 c＝____5____； (2)若 a＝40，b＝9，则 c＝___4_1____； (3)若 a＝6，c＝10，则 b＝____8____； (4)若 c＝25，b＝15，则 a＝___2_0____．
北师大版七年级上册第一章勾股定理1.1.2 探索勾股定理(共30张PPT)
勾股定理的
在1876年一个周末的傍晚，在美国首都华盛顿 的郊外，有一位中年人正在散步，欣赏黄昏的美 景……他走着走着，突然发现附近的一个小石凳上， 有两个小孩正在聚精会神地谈论着什么，时而大声 争论，时而小声探讨．由于好奇心驱使他循声向两 个小孩走去，想搞清楚两个小孩到底在干什么．只 见一个小男孩正俯着身子用树枝在地上画着一个直 角三角形……
b c
∴a2+b2=c2
方法二
2 (a+b) 大正方形的面积可以表示为 ；
也可以表示为c2 + 2ab. a a2+2ab+b2 = c2 +2ab b a b ∵ (a+b)2 = c2 + 2ab
a a
b
c
c
c
b c
∴a2+b2=c2
方法三 c b 大正方形的面积等于
a
c
2
大正方形面积 也可以表示为
1 4 ab (b a ) 2 2 2ab b 2 a 2 2ab a 2 b2 .
∴a2+b2=c2
方法四
b a c a2
c2
b2
∴ a 2 + b 2 = c2
方法五
④
c
③
⑤
b
a
① ②
∴ c2 = b2 + a2
方法六
a
b
S梯形
c c b
1 a b a b 2
2002 年 的 数 学 家 大 会 （ ICM-2002）在北京召开，这 届大会会标 的中央图案正是经 过艺术处理的弦图，这既标志 着中国古代的数学成就 ，又像 一只转动的风车，欢迎来自世 界各地的数学家们！
北师大版八年级数学上册1.1 第1课时 勾股定理的认识 课件(共23张PPT)
探究新知
1.在纸上画若干个直角三角形，分别测量它们的
三条边，看看三边长的平方之间有怎么样的关系？
c
a
b
直角三角形的两直角边的平方和等于斜边的平方，这就是
著名的“勾股定理”。
如果直角三角形的两条直角边为a、b，斜边为c，那么有
a2+b2=c2.
数学小知识
我国古代称直角三角形的较短的直角边为勾，较长的直角
求 的长.
解：因为 ⊥ ，
所以 ∠ = ∠ = 90∘ .
在 Rt △ 中， 2 = 2 − 2 = 102 − 82 = 36 ，
所以 = 6 .
设 = = ，则 = − 6 .
在 Rt △ 中， 2 = 2 + 2 ，
所以 △ =
1
2
1
2
⋅ = × 25 × 12 = 150 .
6. 如图，直线 上有三个正方形 ， ， .若 ， 的面积分别
为 5 和 11 ，则 的面积为( C )
A. 4
B. 6
C. 16
D. 55
7. 如图，在 △ 中， = ， = 10 ， ⊥ ，垂足为 ， = 8 .
（2） 已知 = 12 ， = 16 ，求 .
【解】在 Rt △ 中， ∠ = 90∘ ， = 12 ， = 16 ，
所以 2 = 2 + 2 = 122 + 162 = 400 .
所以 = 20 .
例2 如图，在 △ 中， ⊥ 于点 ，且 + = 32 ，
因为 ∠ = 90∘ ，所以 2 + 2 = 2 .
北师大版八年级数学上册第一章全部课件
总结
勾股定理的验证主要是通过拼图法利用面积的 关系完成的，拼图又常以补拼法和叠合法两种方式拼 图，补拼是要无重叠，叠合是要无空隙；而用面积法 验证的关键是要找到一些特殊图形(如直角三角形、 正方形、梯形)的面积之和等于整个图形的面积，从 而达到验证的目的．
（来自《点拨》）
知1－练
1 用四个边长均为a，b，c的直角三角板，拼成如
（来自《典中点》）
知2－导
知识点 2 勾股定理的应用
例2 我方侦察员小王在距离东西向公路400m处侦察，发现一 辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪，测得 汽车与他相距400m，10s后，汽车与他相距500m,你能 帮小王计算敌方汽车的速度吗？
分析：根据题意，可以画出右图， 其中点A表示小王所在位置， 点C、点B表示两个时刻敌方 汽车的位置.
弦 勾
股 图1
北师大版八年级数学上册
C A
B C
图2-1
A
B
图2-2
(图中每个小方格代表一个单位面积)
知1－导
(1)观察图2-1 正方形A中含有 9 个 小方格，即A的面积 是 9 个单位面积. 正方形B的面积是 9 个单位面积.
正方形C的面积是 18 个单位面积.
北师大版八年级数学上册
C A
B C
（来自《点拨》）
知1－讲
总结
勾股定理的验证主要是通过拼图法利用面积的 关系完成的，拼图又常以补拼法和叠合法两种方式拼 图，补拼是要无重叠，叠合是要无空隙；而用面积法 验证的关键是要找到一些特殊图形(如直角三角形、 正方形、梯形)的面积之和等于整个图形的面积，从 而达到验证的目的．
（来自《点拨》）
知1－讲
1 课堂讲解 2 课时流程
勾股定理的验证主要是通过拼图法利用面积的 关系完成的，拼图又常以补拼法和叠合法两种方式拼 图，补拼是要无重叠，叠合是要无空隙；而用面积法 验证的关键是要找到一些特殊图形(如直角三角形、 正方形、梯形)的面积之和等于整个图形的面积，从 而达到验证的目的．
（来自《点拨》）
知1－练
1 用四个边长均为a，b，c的直角三角板，拼成如
（来自《典中点》）
知2－导
知识点 2 勾股定理的应用
例2 我方侦察员小王在距离东西向公路400m处侦察，发现一 辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪，测得 汽车与他相距400m，10s后，汽车与他相距500m,你能 帮小王计算敌方汽车的速度吗？
分析：根据题意，可以画出右图， 其中点A表示小王所在位置， 点C、点B表示两个时刻敌方 汽车的位置.
弦 勾
股 图1
北师大版八年级数学上册
C A
B C
图2-1
A
B
图2-2
(图中每个小方格代表一个单位面积)
知1－导
(1)观察图2-1 正方形A中含有 9 个 小方格，即A的面积 是 9 个单位面积. 正方形B的面积是 9 个单位面积.
正方形C的面积是 18 个单位面积.
北师大版八年级数学上册
C A
B C
（来自《点拨》）
知1－讲
总结
勾股定理的验证主要是通过拼图法利用面积的 关系完成的，拼图又常以补拼法和叠合法两种方式拼 图，补拼是要无重叠，叠合是要无空隙；而用面积法 验证的关键是要找到一些特殊图形(如直角三角形、 正方形、梯形)的面积之和等于整个图形的面积，从 而达到验证的目的．
（来自《点拨》）
知1－讲
1 课堂讲解 2 课时流程
北师大版初中八年级数学上册 1.1.1 认识勾股定理 课件(共20张PPT)
( 55 ) 25
30
( 34)
95 61
( 42 ) 18
60
200 ( 350)
150
总结归纳
C A
B
SA+SB=SC
ac b
ac b
a2+b2=c2
a2+b2=c2
总结归纳
勾股定理
直角三角形两直角边的平方和等于斜边的 平方．如果a，b和c分别表示直角三角形的 两直角边和斜边，那么a2+b2=c2．
第一章 勾股定理
1.1 探索勾股定理
第1课时 认识勾股定理
导入新课
情境引入
如图，这是一幅美丽的图案，仔细观察，你能发 现这幅图中的奥秘吗？带着疑问我们来一起探索吧.
数学家毕达哥拉斯的故事
相传2005年前，毕达哥拉斯有一次在朋友家做客时，发现 朋友家的用砖铺成的地面…
毕达哥拉斯就从地面上这十分常见的图形中，发现了令世人震惊的定理：
方法一：割
方法二：补
方法三：拼
分割为四个直角三 角形和一个小正方 形.
补成大正方形，用大正 方形的面积减去四个直 角三角形的面积.
将几个小块拼成若干个小 正方形，图中两块红色 （或绿色）可拼成一个小 正方形.
填一填：观察右边两 幅图：完成下表（每 个小
A的面积 B的面积 C的面积
左图 4
9
13
右图 16
9
25
怎样计 算正方 形C的面 积呢？
分析表中数据，你发现了什么？
A的面积 B的面积 C的面积
左图 4
9
13
右图 16
9
25
C A
B
SA+SB=SC
结论：以直角三角形两 直角边为边长的小正方 形的面积的和，等于以 斜边为边长的正方形的 面积.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6m
课堂小结
通过本节课的学习你有何收获呢？
布置作业
（1）习题1.2 1 ，2，3题． （2）上网或查阅有关书籍，搜集至少1种 勾股定理的其它证法，至少1个勾股定理 的应用问题，一周后进行展评．
1 1
？
趣闻调查组报告
勾股定理的
在1876年一个周末的傍晚，在美国首都 华盛顿的郊外，有一位中年人正在散步，欣 赏黄昏的美景……他走着走着，突然发现附 近的一个小石凳上，有两个小孩正在聚精会 神地谈论着什么，时而大声争论，时而小声 探讨．由于好奇心驱使他循声向两个小孩走 去，想搞清楚两个小孩到底在干什么．只见 一个小男孩正俯着身子用树枝在地上画着一 个直角三角形……
a
验证方法一
a b b a
c c
a
c c a
b
b
图1 方法小结：我们利用拼图的方法，将 形的问题与数的问题结合起来，再进行整 式运算，从理论上验证了勾股定理． 你还能用图2进行验证吗？
1 2 c ab 4 (a b) 2 2 2 2 a b c
2 a) c 2
于是这位中年人不再散步，立即回家， 潜心探讨小男孩给他留下的难题．他经过 反复的思考与演算，终于弄清楚了其中的 道理，并给出了简洁的证明方法．
1876年4月1日，他在《新英格兰教育 日志》上发表了他对勾股定理的这一证 法．
1881年，这位中年人 —伽菲尔德就任 美国第二十任总统．后来，人们为了纪念 他对勾股定理直观、简捷、易懂、明了的 证明，就把这一证法称为“总统”证法．
第一章
勾股定理
1. 探索勾股定理（第2课时）
问题情境
1．上节课我们已经通过探索得到了 勾股定理，请问勾股定理的内容是什么？ 2．如何验证勾股定理呢 ？ 据不完全统计，验证的方法有 400多种，你想得到自己的方 法吗？
合作探究
小组活动：请你利用自己准备的四个全等的 直角三角形拼出以斜边为边长的正方形．
a b c
2 2 2
图2
延伸拓展
1.议一议:观察下图,用数格子的方法判 断图中三角形的三边长是否满足a2+b2=c2
2.一个直角三角形的斜边为20cm ,且两 直角边长度比为3:4，求两直角边的长。
Zxx、k
追溯历史
国内调查组报告 用图 2 验证勾股定理的方 法，据载最早是 三国时期数学 家赵爽在为《周髀算经》作注 时给出的，我国历史上将图 2 弦上的正方形称为弦图． 2002 年 的 数 学 家 大 会 （ICM-2002）在北京召开，这 届大会会标 的中央图案正是经 过艺术处理的弦图，这既标志 着中国古代的数学成就 ，又像 一只转动的风车，欢迎来自世 界各地的数学家们！
O
M
30km
N 40km
50km
P
Q
120km
2．如图，一个25 m长的梯子 AB ， 斜靠在一竖直的墙 AO 上，这时的 AO 距 离为 24 m ，如果梯子的顶端 A 沿墙下滑 4m，那么梯子底端B也外移4 m吗？
A C
O
B
D
3．如图，受台风麦莎影响，一棵 高18米的大树断裂，树的顶部落在离树 根底部6 m处，这棵树折断后有多高？
勾股定理与第一次数学危机
约公元前 500 年，毕达哥拉斯学派的
弟子希帕索斯 (Hippasus) 发现了一个惊人
的事实，一个正方形的对角线的长度是不 可公度的.按照毕达哥拉斯定理(勾股定理)， 若正方形边长是 1 ，则对角线的长不是一 个有理数，它不能表示成两个整数之比，
1 1
？
这一事实不但与毕氏学派的哲学信念大相
美国总统证法
D c C c a
b A
a
b
B
生 活 中 勾 股 定 理 的 应 用
例题： 飞机在空中水平飞行，某一时刻 刚好飞到一个男孩子头顶上方4000 m处， 过了20 s，飞机距离这个男孩子头顶5000m， 飞机每小时飞行多少千米？
C B
4km
A
拓展练习
1．如图是某沿江地区交通平面图， 为了加快经济发展，该地区拟修建一条 连接M，O，Q三城市的沿江高速，已 知沿江高速的建设成本是100万元/ km， 该沿江高速的造价预计是多少？
径庭，而且建立在任何线段都可公度基础 上的几何学面临被推翻的威胁，第一次数 学危机由此爆发． •
勾股定理与第一次数学危机
据说，毕达哥拉斯学派对希帕索 斯的发现十分惶恐、恼怒，为了保守 秘密，最后将希帕索斯投入大海．不 能表示成两个整数之比的数，15世纪 意大利著名画家达.芬奇称之为“无理 的数”，无理数的英文“irrational”原 义就是“不可比”．第一次数学危机 一直持续到19世纪实数的基础建立以 后才圆满解决．我们将在下一章学习 有关实数的知识 ．
zxxk
有不同的拼法吗？
拼图展示
图1
图2
自主探究
b
a
c b 1. 如图，你能表示大正方形 c 的面积吗？能用两种方法表 c 示吗？ c 2 ( a b ) （ 1） a b 1 2 （2） c 4 ab a 图1 b 2 1 2 2 2. (a b) 与 c 4 ab 有什么关系？为什么？ 2 你能验证勾股定理了吗？