2020成都一诊分析

2020年四川省成都市高考数学一诊试卷（理科）一、选择题：本大题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的．1.若复数z1与z2＝−3−i（i为虚数单位）在复平面内对应的点关于实轴对称，则z1＝（）A.−3iB.−3+iC.3+iD.3−i2.已知集合A＝{−1, 0, m}，B＝{1, 2}，若A∪B＝{−1, 0, 1, 2}，则实数m的值为（）A.−1或0B.0或1C.−1或2D.1或23.若sinθ=√5cosθ，则tan2θ＝（）A.−√53B.√53C.−√52D.√524.某校随机抽取100名同学进行“垃圾分类”的问卷测试，测试结果发现这l00名同学的得分都在[50, 100]内，按得分分成5组：[50, 60),[60, 70),[70, 80),[80, 90),[90, 100]，得到如图所示的频率分布直方图则这100名同学的得分的中位数为（）A.72.5B.75C.77.5D.805.设等差数列{a n}的前n项和为S n，且a n≠0，若a5＝3a3，则S9S5=()A.95B.59C.53D.2756.已知α，β是空间中两个不同的平面，m，n是空间中两条不同的直线，则下列说法正确的是（）A.若m // α，n // β，且α // β，则m // nB.若m // α，n // β，且α⊥β，则m // nC.若m⊥α，n // β，且α // β，则m⊥nD.若m⊥α，n // β且α⊥β，则m⊥n7.(x2+2)(x−1x)6的展开式的常数项为（）A.25B.−25C.5D.−58.将函数y＝sin(4x−π6)图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把所得图象向左平移π6个单位长度，得到函数f(x)的图象，则函数f(x)的解析式为（）A.f(x)=sin(2x+π6) B.f(x)=sin(2x−π3)C.f(x)=sin(8x+π6) D.f(x)=sin(8x−π3)9.已知抛物线y2＝4x的焦点为F，M，N是抛物线上两个不同的点．若|MF|+|NF|＝5，则线段MN的中点到y轴的距离为（）A.3B.32C.5 D.5210.已知a=212,b=313,c=ln32，则（）A.a>b>cB.a>c>bC.b>a>cD.b>c>a11.已知定义在R上的函数f(x)满足f(2−x)＝f(2+x)，当x≤2时，f(x)＝(x−1)e x−1．若关于x的方程f(x)−kx+2k−e+1＝0有三个不相等的实数根，则实数k的取值范围是（）A.(−2, 0)∪(0, 2)B.(−2, 0)∪(2, +∞)C.(−e, 0)∪(0, +∞)D.(−e, 0)∪(0, e)12.如图，在边长为2的正方形AP1P2P3中，线段BC的端点B，C分别在边P1P2，P2P3上滑动，且P2B＝P2C＝x．现将△AP1B，△AP3C分别沿AB，AC折起使点P 1，P 3重合，重合后记为点P ，得到三棱锥P −ABC ．现有以下结论： ①AP ⊥平面PBC ；②当B ，C 分别为P 1P 2，P 2P 3的中点时，三棱锥P −ABC 的外接球的表面积为6π；③x 的取值范围为(0, 4−2√2)； ④三棱锥P −ABC 体积的最大值为13． 则正确的结论的个数为（ ）A.1B.2C.3D.4二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡上．已知实数x ，y 满足约束条件{x +y −4≤0x −2y +2≥0y ≥0 ，则z ＝x +2y 的最大值为________．设正项等比数列{a n }满足a 4＝81，a 2+a 3＝36，则a n ＝________．已知平面向量a →，b →满足|a →|＝2，|b →|=√3，且b →⊥(a →−b →)，则向量a →与b →的夹角的大小为________．已知直线y ＝kx 与双曲线C:x 2a 2−y 2b 2=1(a >0, b >0)相交于不同的两点A ，B ，F 为双曲线C 的左焦点，且满足|AF|＝3|BF|，|OA|＝b （O 为坐标原点），则双曲线C 的离心率为________．三、解答题：本大题共5小题，共70分解答应写出文字说明、证明过程或演算步骤．bc．在△ABC中，角A，B，C的对边分别为a，b，c，且b2+c2−a2=4√23 (Ⅰ)求sinA的值；(Ⅱ)若△ABC的面积为√2，且√2sinB＝3sinC，求△ABC的周长某公司有l000名员工，其中男性员工400名，采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查，将计划在今年购买5G手机的员工称为“追光族”，计划在明年及明年以后才购买5G手机的员工称为“观望者”调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人．(Ⅰ)完成下列2×2列联表，并判断是否有95%的把握认为该公司员工属于“追光族”与“性别”有关；(Ⅱ)已知被抽取的这l00名员工中有10名是人事部的员工，这10名中有3名属于“追光族”现从这10名中随机抽取3名，记被抽取的3名中属于“追光族”的人数为随机变量X，求X的分布列及数学期望．附：K2=n(ad−bc)2，其中n＝a+b+c+d．(a+b)(c+d)(a+c)(b+d)如图，在四棱锥P−ABCD中，AP⊥平面PBC，底面ABCD为菱形，且∠ABC ＝60∘，E分别为BC的中点．(Ⅰ)证明：BC⊥平面PAE；(Ⅱ)若AB＝2．PA＝1，求平面ABP与平面CDP所成锐二面角的余弦值．已知函数f(x)＝(a−1)lnx+x+ax，a∈R．(Ⅰ)讨论函数f(x)的单调性；(Ⅱ)当a<−1时，证明∀x∈(1, +∞)，f(x)>−a−a2．已知椭圆C:x 22+y2＝1的右焦点为F，过点F的直线（不与x轴重合）与椭圆C相交于A，B两点，直线l:x＝2与x轴相交于点H，过点A作AD⊥l，垂足为D．(Ⅰ)求四边形OAHB（O为坐标原点）面积的取值范围；(Ⅱ)证明直线BD过定点E．并求出点E的坐标请考生在第22，23题中任选择一题作答，如果多做，则按所做的第一题记分，作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．[选修4-4：坐标系与参数方程]在平面直角坐标系xOy中，已知P是曲线C1:x2+(y−2)2＝4上的动点，将OP绕点O顺时针旋转90∘得到OQ，设点Q的轨迹为曲线C2以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．(Ⅰ)求曲线C1，C2的极坐标方程；(Ⅱ)在极坐标系中，点M(3, π2)，射线θ=π6(ρ≥0)与曲线C1，C2分别相交于异于极点O的A，B两点，求△MAB的面积．[选修45：不等式选讲]已知函数f(x)＝|x−3|．(Ⅰ)解不等式f(x)≥4−|2x+l|；(Ⅱ)若1m +4n=2(m>0, n>0)，求证：m+n≥|x+32|−f(x)．2020年四川省成都市高考数学一诊试卷（理科）一、选择题：本大题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的．1.若复数z1与z2＝−3−i（i为虚数单位）在复平面内对应的点关于实轴对称，则z1＝（）A.−3iB.−3+iC.3+iD.3−i【解答】∵复数z1与z2＝−3−i（i为虚数单位）在复平面内对应的点关于实轴对称，∴复数z1与z2＝−3−i（i为虚数单位）的实部相等，虚部互为相反数，则z1＝−3+i．2.已知集合A＝{−1, 0, m}，B＝{1, 2}，若A∪B＝{−1, 0, 1, 2}，则实数m的值为（）A.−1或0B.0或1C.−1或2D.1或2【解答】集合A＝{−1, 0, m}，B＝{1, 2}，A∪B＝{−1, 0, 1, 2}，因为A，B本身含有元素−1，0，1，2，所以根据元素的互异性，m≠−1，0即可，故m＝1或2，3.若sinθ=√5cosθ，则tan2θ＝（）A.−√53B.√53C.−√52D.√52【解答】若sinθ=√5cosθ，则tanθ=√5，则tan2θ=2tanθ1−tan2θ=−√52，4.某校随机抽取100名同学进行“垃圾分类”的问卷测试，测试结果发现这l00名同学的得分都在[50, 100]内，按得分分成5组：[50, 60),[60, 70),[70, 80),[80, 90),[90, 100]，得到如图所示的频率分布直方图则这100名同学的得分的中位数为（）A.72.5B.75C.77.5D.80【解答】由频率分布直方图得：[50, 70)的频率为：(0.010+0.030)×10＝0.4，[70, 80)的频率为：0.040×10＝0.4，∴这100名同学的得分的中位数为：70+0.5−0.40.4×10=72.(5)5.设等差数列{a n}的前n项和为S n，且a n≠0，若a5＝3a3，则S9S5=()A.95B.59C.53D.275【解答】依题意，S9S5=a1+a92×9a1+a52×5=9a55a3，又a5a3=3，∴S9S5=95×3=275，6.已知α，β是空间中两个不同的平面，m，n是空间中两条不同的直线，则下列说法正确的是（）A.若m // α，n // β，且α // β，则m // nB.若m // α，n // β，且α⊥β，则m // nC.若m⊥α，n // β，且α // β，则m⊥nD.若m⊥α，n // β且α⊥β，则m⊥n【解答】由m // α，n // β，且α // β，得m // n或m与n异面，故A错误；由m // α，n // β，且α⊥β，得m // n或m与n相交或m与n异面，故B错误；由m⊥α，α // β，得m⊥β，又n // β，则m⊥n，故C正确；由m⊥α，n // β且α⊥β，得m // n或m与n相交或m与n异面，故D错误．7.(x2+2)(x−1x)6的展开式的常数项为（）A.25B.−25C.5D.−5【解答】(x−1x )6的通项公式为T r+1=∁6r x6−r(−1x)r＝(−1)r∁6r x6−2r，r＝0，1，2， (6)则(x 2+2)(x −1x )6的展开式的常数项须6−2r ＝0或者6−2r ＝−2⇒r ＝3或者r ＝4：∴常数项为(−1)4∁64+2×(−1)3∁63=15−40＝−(25)8.将函数y ＝sin(4x −π6)图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把所得图象向左平移π6个单位长度，得到函数f(x)的图象，则函数f(x)的解析式为（ ） A.f(x)=sin(2x +π6) B.f(x)=sin(2x −π3) C.f(x)=sin(8x +π6) D.f(x)=sin(8x −π3)【解答】函数y ＝sin(4x −π6)图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到y ＝sin(2x −π6)的图象，再把所得图象向左平移π6个单位长度，得到函数f(x)＝sin(2x +π6)的图象， 9.已知抛物线y 2＝4x 的焦点为F ，M ，N 是抛物线上两个不同的点．若|MF|+|NF|＝5，则线段MN 的中点到y 轴的距离为（ ） A.3 B.32C.5D.52【解答】由抛物线方程得，准线方程为：x ＝−1， 设M(x, y)，N(x ′, y ′)，由抛物线的性质得，MF +NF ＝x +x ′+p ＝x +x ′+2＝5， 中点的横坐标为32，线段MN 的中点到y 轴的距离为：32， 10.已知a =212,b =313,c =ln 32，则（ ） A.a >b >c B.a >c >b C.b >a >c D.b >c >a【解答】∵a =√2=√86，b =√33=√96，∴1<a <b ． c ＝ln 32<(1) ∴c <a <b ．故选：C．11.已知定义在R上的函数f(x)满足f(2−x)＝f(2+x)，当x≤2时，f(x)＝(x−1)e x−1．若关于x的方程f(x)−kx+2k−e+1＝0有三个不相等的实数根，则实数k的取值范围是（）A.(−2, 0)∪(0, 2)B.(−2, 0)∪(2, +∞)C.(−e, 0)∪(0, +∞)D.(−e, 0)∪(0, e)【解答】②令f′(x)<0，解得x<0(1)③令f′(x)>0，解得0<x≤(2)∴f(x)在(−∞, 0)上单调递减，在(0, 2]上单调递增，在x＝0处取得极小值f(0)＝−(2)且f(1)＝−1；x→−∞，f(x)→(0)又∵函数f(x)在R上满足f(2−x)＝f(2+x)，∴函数f(x)的图象关于x＝2对称．∴函数y＝f(x)的大致图象如下：关于x的方程f(x)−kx+2k−e+1＝0可转化为f(x)＝k(x−2)+e−(1)而一次函数y＝k(x−2)+e−1很明显是恒过定点(2, e−1)．结合图象，当k＝0时，有两个交点，不符合题意，当k＝e时，有两个交点，其中一个是(1, −1)．此时y＝f(x)与y＝k(x−2)+e−1正好相切．∴当0<k<e时，有三个交点．同理可得当−e<k<0时，也有三个交点．实数k的取值范围为：(−e, 0)∪(0, e)．故选：D．12.如图，在边长为2的正方形AP1P2P3中，线段BC的端点B，C分别在边P1P2，P2P3上滑动，且P2B＝P2C＝x．现将△AP1B，△AP3C分别沿AB，AC折起使点P1，P3重合，重合后记为点P，得到三棱锥P−ABC．现有以下结论：①AP ⊥平面PBC ；②当B ，C 分别为P 1P 2，P 2P 3的中点时，三棱锥P −ABC 的外接球的表面积为6π；③x 的取值范围为(0, 4−2√2)； ④三棱锥P −ABC 体积的最大值为13． 则正确的结论的个数为（ ）A.1B.2C.3D.4【解答】当B ，C 分别为P 1P 2，P 2P 3的中点时，PB ＝PC ＝1，BC =√2， 所以PB 2+PC 2＝BC 2，又AP ⊥平面PBC ，所以PA ，PB ，PC 两两垂直，所以三棱锥P −ABC 的外接球与 以PA ，PB ，PC 为长宽高的长方体的外接球半径相等． 设半径为r ，所以(2r)2＝22+12+12＝6，S ＝4πr 2＝6π．即三棱锥P −ABC 的外接球的表面积为6π，②正确（1）因为P 2B ＝P 2C ＝x ，所以PB ＝PC ＝2−x ，而BC =√2x ，故2(2−x)>√2x ，解得x <4−2√2，③正确（2）因为△PBC 的面积为S =12×√2x ×√(2−x)2−(√22x)2=12√x 4−8x 3+8x 2 设f(x)＝x 4−8x 3+8x 2，f′(x)＝4x 3−24x 2+16x ＝4x(x 2−6x +4)当0<x <3−√5时，f′(x)>0，当3−√5<x <4−2√2时，f′(x)<0 f m ax ＝f(3−√5)>f(1)=12，所以S >12． V P−ABC ＝V A−PBC =13S ×2=23S >13，④错误． 故选：C ．二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡上．已知实数x ，y 满足约束条件{x +y −4≤0x −2y +2≥0y ≥0 ，则z ＝x +2y 的最大值为________． 【解答】作出实数x ，y 满足约束条件{x +y −4≤0x −2y +2≥0y ≥0 对应的平面区域如图：（阴影部分）由z ＝x +2y 得y =−12x +12z ， 平移直线y =−12x +12z ，由图象可知当直线y =−12x +12z 经过点A 时，直线y =−12x +12z 的截距最大， 此时z 最大． 由{x +y −4=0x −2y +2=0，解得A(2, 2)，代入目标函数z ＝x +2y 得z ＝2×2+2＝6设正项等比数列{a n }满足a 4＝81，a 2+a 3＝36，则a n ＝________． 【解答】依题意{a 1q 3=81a 1q +a 1q 2=36 ，解得{a 1=3q =3 ，∴a n =a 1⋅q n−1=3⋅3n−1＝3n ，已知平面向量a →，b →满足|a →|＝2，|b →|=√3，且b →⊥(a →−b →)，则向量a →与b →的夹角的大小为________． 【解答】∵平面向量a →，b →满足|a →|＝2，b →=√3，且b →⊥(a →−b →)， ∴b →⋅(a →−b →)=b ¯⋅a →−b →2=0，∴a →⋅b →=b →2． 设向量a →与b →的夹角的大小为θ，则2⋅√3⋅cosθ＝3， 求得cosθ=√32，故θ=π6，已知直线y ＝kx 与双曲线C:x 2a 2−y 2b 2=1(a >0, b >0)相交于不同的两点A ，B ，F 为双曲线C 的左焦点，且满足|AF|＝3|BF|，|OA|＝b （O 为坐标原点），则双曲线C 的离心率为________． 【解答】设|BF|＝m ，则|AF|＝3|BF|＝3m ， 取双曲线的右焦点F ′，连接AF ′，BF ′， 可得四边形AF ′BF 为平行四边形，可得|AF ′|＝|BF|＝m ，设A 在第一象限，可得3m −m ＝2a ，即m ＝a ， 由平行四边形的对角线的平方和等于四条边的平方和， 可得(2b)2+(2c)2＝2(a 2+9a 2)， 化为c 2＝3a 2，则e =ca =√3．三、解答题：本大题共5小题，共70分解答应写出文字说明、证明过程或演算步骤．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且b 2+c 2−a 2=4√23bc ． (Ⅰ)求sinA 的值；(Ⅱ)若△ABC 的面积为√2，且√2sinB ＝3sinC ，求△ABC 的周长 【解答】（1）∵b 2+c 2−a 2=4√23bc ， ∴由余弦定理可得2bccosA =4√23bc ， ∴cosA =2√23， ∴在△ABC 中，sinA =√1−cos 2A =13．（2）∵△ABC 的面积为√2，即12bcsinA =16bc =√2， ∴bc ＝6√2，又∵√2sinB＝3sinC，由正弦定理可得√2b＝3c，∴b＝3√2，c＝2，则a2＝b2+c2−2bccosA＝6，∴a=√6，∴△ABC的周长为2+3√2+√6．某公司有l000名员工，其中男性员工400名，采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查，将计划在今年购买5G手机的员工称为“追光族”，计划在明年及明年以后才购买5G手机的员工称为“观望者”调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人．(Ⅰ)完成下列2×2列联表，并判断是否有95%的把握认为该公司员工属于“追光族”与“性别”有关；(Ⅱ)已知被抽取的这l00名员工中有10名是人事部的员工，这10名中有3名属于“追光族”现从这10名中随机抽取3名，记被抽取的3名中属于“追光族”的人数为随机变量X，求X的分布列及数学期望．，其中n＝a+b+c+d．附：K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)【解答】（1）由题，2×2列联表如下：∵K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)=100×(20×20−40×20)240×60×60×40=259≈2.778<3.841，∴没有95%的把握认为该公司员工属于“追光族”与“性别”有关；（2）由题，随机变量X的所有可能的取值为0，1，2，3，P(X＝0)=C30C73C03=724，P(X＝1)=C31C72C103=2140，P(X＝2)=C32C71C103=740，P(X＝3)=C33C103=1120，∴X的分布列为：∴E(X)＝1×2140+2×740+3×1120=910．如图，在四棱锥P−ABCD中，AP⊥平面PBC，底面ABCD为菱形，且∠ABC ＝60∘，E分别为BC的中点．(Ⅰ)证明：BC⊥平面PAE；(Ⅱ)若AB＝2．PA＝1，求平面ABP与平面CDP所成锐二面角的余弦值．【解答】（1）如图，连接AC，因为底面ABCD为菱形，且∠ABC＝60∘，所以△ABC为正三角形，因为E为BC的中点，所以BC⊥AE，又因为AP⊥平面PBC，BC⊂平面PBC，所以BC⊥AP，因为AP∩AE＝A，AP，AE⊂平面PAE，所以BC⊥平面PAE；（2）因为AP⊥平面PBC，PB⊂平面PBC，所以AP⊥PB，又因为AB＝2，PA＝1，所以PB=√3，由(Ⅰ)得BC⊥PE，又因为E为BC中点，所以PB＝PC=√3，EC＝1，所以PE =√2，如图，过点P 作BC 的平行线PQ ，则PQ ，PE ，PA 两两互相垂直，以P 为坐标原点，PE →,PQ →,PA →的方向分别为xyz 轴的正方形，建立如图所示的空间直角坐标系Pxyz ，则P(0, 0, 0)，A(0, 0, 1)，B(√2, −1, 0)，C(√2, 1, 0)，D(0, 2, 1)， 设平面BAP 的一个法向量m →=(x, y, z)，又PA →=(0, 0, 1)，PB →=(√2, −1, 0)，由{m →⋅PA →=0m →⋅PB →=0，得√2x −y ＝0，z ＝0，令x ＝1，则m →=(1, √2, 0)， 设平面CDP 的一个法向量n →=(a, b, c)，又PC →=(√2, 1, 0)，PD →=(0, 2, 1)，由{m →⋅PC →=0m →⋅PD →=0，得√2a +b ＝0，2y +z ＝0，令a ＝1，则n →=(1, −√2, 2√2)， 所以cos <m →,n →>=√3⋅√11=−√3333， 即平面ABP 与平面CDP 所成锐二面角的余弦值为√3333．已知函数f(x)＝(a −1)lnx +x +ax ，a ∈R ． (Ⅰ)讨论函数f(x)的单调性；(Ⅱ)当a <−1时，证明∀x ∈(1, +∞)，f(x)>−a −a 2． 【解答】 （1）f′(x)=a−1x+1−ax 2=x 2+(a−1)x−ax 2=(x−1)(x+a)x 2，因为x >0，a ∈R ，所以当a ≥0时，x +a >0，所以函数在(0, 1)上单调递减，在(1, +∞)上单调递增；当−1<a <0时，0<−a <1，函数f(x)在(0, −a)上单调递增，在(−a, 1)上单调递减，在(1, +∞)上单调递增；当a ＝−1时，f′(x)=(x−1)2x 2≥0，函数f(x)在(0, +∞)上单调递增；当a <−1时，−a >1，函数f(x)在(0, 1)上单调递增，在(1, −a)上单调递减，在(−a, +∞)上单调递增；（2）当a <−1时，由(Ⅰ)得，函数f(x)在(1, −a)上单调递减，在(−a, +∞)上单调递增；函数f(x)在(1, +∞)上的最小值为f(−a)＝(a −1)ln(−a)−a −1， 欲证明不等式f(x)>−a −a 2成立，即证明−a −a 2<(a −1)ln(−a)−a −1，即证明a 2+(a −1)ln(−a)−1>0，因为a <−1，所以只需证明ln(−a)<−a −1， 令ℎ(x)＝lnx −x +1(x ≥1)，则ℎ′(x)=1x −1=−(x−1)x≤0，所以函数ℎ(x)在[1, +∞)上单调递减，则有ℎ(x)≤ℎ(1)＝0， 因为a <−1，所以−a >1，所以ℎ(−a)＝ln(−a)+a +1<0，即当a <−1时，ln(−a)<−a −1成立， 所以当a <−1时，任意x ∈(1, +∞)，f(x)>−a −a 2． 已知椭圆C:x 22+y 2＝1的右焦点为F ，过点F 的直线（不与x 轴重合）与椭圆C 相交于A ，B 两点，直线l:x ＝2与x 轴相交于点H ，过点A 作AD ⊥l ，垂足为D ．(Ⅰ)求四边形OAHB （O 为坐标原点）面积的取值范围； (Ⅱ)证明直线BD 过定点E ．并求出点E 的坐标 【解答】（1）由题意F(1, 0)，设直线AB 的方程：x ＝my +1，A(x 1, y 1)，B(x 2, y 2)，与抛物线联立(m 2+2)y 2+2my −1＝0，因为△＝4m 2+4(m 2+2)>0，y 1+y 2=−2m2+m 2，y 1y 2=−12+m 2，所以|y 1−y 2|=√(y 1−y 2)2−41yy 2=2√2√1+m 22+m 2， 所以四边形OAHB 的面积S =12|OH|⋅|y 1−y 2|＝|y 1−y 2|=2√2⋅√1+m 22+m 2，令t =√1+m 2≥1，S =2√2t1+t =2√2t+1t≤√2，当且仅当t ＝1时，即m ＝0时取等号，所以0<S ≤√2，所以四边形OAHB 的面积的取值范围为(0, √2,](2) B(x2, y2)，D(2, y1)，k BD=y1−y22−x2，所以直线BD的方程：y−y1=y1−y2 2−x2(x−2)，令y＝0，得x=x2y1−2y2y1−y2=my1y2+y1−2y2y1−y2由(Ⅰ)得，y1+y2=−2m2+m2，y1y2=−12+m2，所以y1+y2＝2my1y2，化简得x=12(y1+y2)+y1−2y2y1−y2=32(y1−y2)y1−y2=32，所以直线BD过定点E(32, 0)．请考生在第22，23题中任选择一题作答，如果多做，则按所做的第一题记分，作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．[选修4-4：坐标系与参数方程]在平面直角坐标系xOy中，已知P是曲线C1:x2+(y−2)2＝4上的动点，将OP绕点O顺时针旋转90∘得到OQ，设点Q的轨迹为曲线C2以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．(Ⅰ)求曲线C1，C2的极坐标方程；(Ⅱ)在极坐标系中，点M(3, π2)，射线θ=π6(ρ≥0)与曲线C1，C2分别相交于异于极点O的A，B两点，求△MAB的面积．【解答】（1）由题意，点Q的轨迹是以(2, 0)为圆心，以2为半径的圆，则曲线C2：(x−2)2+y2＝4，∵ρ2＝x2+y2，x＝ρcosθ，y＝ρsinθ，∴曲线C1的极坐标方程为ρ＝4sinθ，曲线C2的极坐标方程为ρ＝4cosθ；（2）在极坐标系中，设A，B的极径分别为ρ1，ρ2，∴|AB|＝|ρ1−ρ2|＝4|sinπ6−cosπ6|=2(√3−1)．又∵M(3, π2)到射线θ=π6(ρ≥0)的距离ℎ=3sinπ3=3√32．∴△MAB的面积S=12|AB|⋅ℎ=9−3√32．[选修45：不等式选讲]已知函数f(x)＝|x−3|．(Ⅰ)解不等式f(x)≥4−|2x+l|；(Ⅱ)若1m +4n=2(m>0, n>0)，求证：m+n≥|x+32|−f(x)．【解答】（I ）原不等式可化为：|x −3|≥4−|2x +1|，即|2x +1|+|x −3|≥4， 当x ≤−12时，不等式−2x −1−x +3≥4，解得x ≤−23，故x ≤−23； 当−12<x <3时，不等式2x +1−x +3≥4，解得x ≥0，故0≤x <3； 当x ≥3时，不等式2x +1+x −3≥4，解得x ≥0，故x ≥3； 综上，不等式的解集为(−∞, −23]∪[0, +∞)； (II)因为f(x)＝|x −3|，所以|x +32|−f(x)＝||x +32|−|x −3|≤|x +32−x +3|=92，当且仅当(x +32)(x +3)≥0，且|x +32|≥|x −3|时，取等号， 又1m +4n =2(m >0, n >0)，所以(m +n)(1m +4n )≥(1+2)2＝9，当且仅当m ＝2n 时，取得等号， 故m +n ≥92，所以m +n ≥|x +32|−f(x)成立．。

高考英语一诊试卷题号I II III IV V总分得分一、阅读理解（本大题共15小题，共30.0分）AThe Five Best Countries TO Move To For Retirement Retiring in a different country is gaming popularity．Below are five of the best countries to seek retirementCosta RicaMild climate，breathtaking landscapes and beaches draw retirees（退休人员）to Costa Rica ．The country readily welcomes immigrants and offers a simple residency process．With a monthly income of at least ﹩1，000 per month from Social Security or a similar source，people enjoy a high standard of living at a much lower cost than the U．S．MalaysiaRetirees who choose to make Malaysia home will appreciate its rich culture and attractive scenery．Moreover，the country offers modern facilities at modest prices．Immigrants enjoy convenience and comfort in their daily life．You will find low-cost rental units，delicious street food，and various shopping malls．MexicoBecause it's close to the U．S．，Mexico draws more than a million American retirees to its borders．Increasing immigrant communities enjoy seaside living and conversations with friendly．English speaking locals．Plus，legal residents over the age of 60 receive airline ，grocery，and restaurant discounts．PanamaGentle ocean wind takes the heat out of hot year-round temperatures，which has been the chief attraction to foreign retirees．Beautiful beaches and a booming economy also attract retirees to Panama．An income of ﹩2，000 per month covers modest living costs．Furthermore，the country offers discounts to retirees with a special visa．EcuadorLazy coastal towns，sun-shining hot spots，and nature-filled views wait for immigrants seeking a carefree lifestyle．Public transportation costs in Ecuador make owning a vehicle unnecessary．A bus ride only costs 25cents and taxi rides will run about ﹩3．1.What do Costa Rica and Malaysia have in common？______A. Convenient shopping．B. Relatively low living cost．C. Various cultural activities．D. Simple immigration procedures．2.Which country's location specially attracts retirees from the U．S．？______A. Malaysia's．B. Ecuador's．C. Panama's．D. Mexico's．3.What is the main reason for retirees to choose Panama？______A. Beautiful beaches．B. A booming economy．C. A pleasant climate．D. Discounts for retirees．BBack about 20 months ago I started college and just struggled with everything，such as classes and friends．I quickly became depressed and angry at myself for not being about to do better in school，in addition to lack of friends due to poor social and communication skills．This went on for months until my 19th birthday．My parents sent me a cake，which was a great cake．But I remember having this large cake and absolutely no one to share it with．I ended throwing out the cake after having one piece，with about 90% of it leftover．That night I was depressed that I decided to go outside to the freezing temperature of the winter and run．I put my earphones in，went outside and ran about 2 miles at 11 p．m．on my birthday．When I got back inside I was content．I was proud of what I was able to do．The next night did the same．I wasn't quick or fit but you know that I went outside and did something．The continued for about 2 months until I finally worked up the courage to go to the gym，where I started swimming again as I used to in high school．A month went by and I started lifting weights and continually running．Looking back I can see that exercise helped cure my depression but it didn't only do that．At the gym I met new friends and back at my dorm I grew confidence to go to the end of the hall seeing people playing Super Smash Brothers and ask if I could join．So go forward to present now．I exercise every day and look forward to that hour and a half I get daily to do what I love with people who love it as well．I hope this helps someone who may be or have been in a similar situation．4.What made the author decide to run at night？______A. His l9th birthday．B. His parents' cake．C. His loneliness．D. His friends．5.Which of the following best describes the author？______A. Traditional．B. Determined．C. Humorous．D. Generous．6.What is the biggest benefit of the author's running？______A. Regaining his confidence．B. Losing his weight．C. Playing with his brothers．D. Joining other activities．7.Why do you think the author wrote this passage？______A. To recall his life in college．B. To show his gratitude to his parents．C. To emphasize the importance of friendship．D. To share his experience of dealing with hardship．CImagine a cat that does not need someone to clean up after it keeps an older person company and helps them remember to take their medicine．That is the shared dream of the toy maker Hasbro and scientists at Brown University in Providence，Rhode Island．The researchers received a ﹩3-million-dollar award from the National Science Foundation for a special project ．They want to find ways to add artificial intelligence，or A．I．，to Hasbro's "Joy for All" robotic．The cat has already been for sale for two years．Though priced over 1000 dollars，it sold quite well．It was meant to act as a "companion" for older people．Now the project is aimed at developing additional abilities for the cat．Researchers at Brown's Humanity-Centered Robotics Initiative are working to decide which activities older adults may need the most．They hope to make the cat perform a small number of activities very well．Such activities include finding lost objects and reminding the person to take medicine or visit their doctor．They also want to keep the cost down to just a few hundred dollars．It is an idea that has appealed to Jeanne Elliott．Her 93-year-old mother Mary Derr lives withher in South Kingstown．Derr has dementia（痴呆）．The Joy for All cat that Elliott bought this year has become a true companion for Derr．The cat stays with Derr and keeps her calm while Elliott is at work．Elliott said a robotic cat that helps her mother to remember to take her medicine and be careful when she walks would be greater．The researchers are trying to learn how the improved cats will complete helpful activities and how they will communicate．They say that they do not want a talking cat，however．Instead they are trying to design a cat that can move its head in a special way to successfully communicate its message．In the end，they hope to create an exchange between the human and the cat in which the human feels the cat needs them．By doing so，the researchers hope they can even help prevent feelings of loneliness and sadness among elderly people．8.What's the purpose of the project？______A. To relieve the pain of the elderly．B. To promote the sales of a medicine．C. To invent a robotic cat for the elderly．D. To help make the robotic cat smarter．pared with the old model，the new robotic cat will be ______ ．A. smallerB. cheaperC. more talkativeD. more expensive10.What does Paragraph 3intend to tell us？______A. The cat gives much help to the elderly．B. The more functions of the cat，the better．C. There is no cure for dementia at present．D. Mary Derr would have died without the cat．11.What can we infer from the last paragraph？______A. A talking cat is quite popular among the elderly．B. Feelings of sadness among the elderly are unavoidable．C. Each family can afford such a cat in the future．D. The feeling of being needed is vital to the elderly．DSome of the best research on daily experience is rooted in rates of positive and negative interactions，which has proved that being blindly positive or negative can cause others to be frustrated or annoyed or to simply tune out．Over the last two decades，scientists have made remarkable predictions simply by watching people interact with one another and then scoring the conversations based on the rate of positive and negative interactions．Researchers have used the findings to predict everything from the likelihood that a couple will divorce to the chances of a work team with high customer satisfaction and productivity levels．More recent research helps explain why these brief exchanges matter so much．When you experience negative emotions as a result of criticism or rejection，for example，your body produces higher levels of the stress hormone，which shuts down much of your thinking and activates（激活）conflict and defense mechanisms（机制）．You assume that situations are worsethan they actually are．When you experience a positive interaction，it activates a very different response．Positive exchanges increase your body's production of oxytocin，a feel-good that increases your ability to communicate with，cooperate with and trust others．But the effects of a positive occurrence are less dramatic and lasting than they are for a negative one．We need at least three to five positive interactions to outweigh every one negative exchange．Bad moments simply outweigh good ones．Whether you're having a conversation，keep this simple short cut in mind：At least 80 percent of your conversations should be focused on what's going right．Workplaces，for example，often see this．During performance reviews，managers routinely spend 80 percent of their time on weaknesses and "areas for improvement"．They spend roughly 20 percent of the time on strengths and positive aspects．Any time you have discussions with a person or group，spend the vast majority of the time talking about what is working，and use the remaining time to address weaknesses．12.The underlined phrase "tune out" in Paragraph 1 probably means ______ ．A. stop listeningB. change mindC. sing aloudD. be crazy13.What will happen if you experience negative emotions？______A. The situations are sure to become worse．B. Much of your thinking will be prevented．C. You will feel an urge to improve and become better．D. You'll be motivated to resolve conflicts with people．14.From Paragraph 4，we can learn that ______ ．A. we need a positive feeling to beat one negative feelingB. positive interactions have greater effects than negative onesC. our conversation should center on what needs improvementD. the effect of negative feelings lasts longer than that of positive ones15.What is the best title for the passage？______A. Harmful NegativesB. More Positive InteractionsC. How to Be a Productive ManagerD. Less Time on Strengths二、阅读七选五（本大题共5小题，共10.0分）Many cosplay activities are being organized in China，making the subculture popular among some youths．Cosplay means costume play，in which participants wear costumes and fashion accessories （配饰）to represent a specific character．What's the reason why youths are interested in cosplay？(1) Cosplay participants often interact with each other to dress up as characters from animes （动漫），cartoons，comic books，films，TV programs and video games．Youths who love cosplay have their own sets of jokes，which "outsiders" rarely understand．(2)Cosplayers are almost always young，most of them under 25，and as they grow older，they tend to give up the practice．(3) Instead，they should treat such youngsters as normal youths，but at the same time warn them never to cross the social and moral boundaries．The cosplay subculture is a kind of performing arts．Cosplayers usually get the costumes in these ways．First，through some companies that make and sell packaged suits for cosplay．Second，through some individuals that make costumes and accessories．(4)With capital flowing into the AGC （二次元）industry，more specific and mature business models help the industry develop further．(5) Since then the domestic animation and game industry has been developing healthily with a stronger sense of using legal products．China's ACG industry is likely to see higher growth in 2019．A．And besides，by making them themselves．B．It's a way for youths to express virtual （虚拟的）love．C．Perhaps that's why people are prejudiced against them．D．Based on a research，2015 proved to be a turning point．E．The cosplay industry is expected to witness more success．F．Therefore，there is no need for parents to overreact to cosplay．G．So regulators should strictly monitor such events to prevent improper behaviors．16. A. A B. B C. C D. D E.E F.F G. G17. A. A B. B C. C D. D E.E F.F G. G18. A. A B. B C. C D. D E.E F.F G. G19. A. A B. B C. C D. D E.E F.F G. G20. A. A B. B C. C D. D E.E F.F G. G三、完形填空（本大题共20小题，共30.0分）My father lived a long life and was deeply loved by his wife，three children，eleven grandchildren and a large number of friends．He was smart and quick- headed．When I asked if he'd like to join me on Virgin Airlines，I remember him(21) replying："Why not？It's as close to heaven as I'll ever get"While he could always make us(22)，he was also quiet，considerate and full of wonderful (23) for us so that we could do better．When I was a child，I (24) myself to the change in Dad's loose drawer --- I didn't see it as stealing，but rather as just borrowing without a (25) to give back - and bought chocolate from our local corner shop．One day，while (26)the shop with my father，the shopkeeper questioned my (27) spending habits："'Now I don ' t want to get him into any (28)，Mr Branson，but I don' t know where young Richard is getting all his (29)from．He's becoming my best customer--- I (30) he isn't stealing it．"Dad (31)by looking her straight in the eyes and saying loudly，" Madam，how dare you (32)my son of stealing？"After we left the shop，my father never spoke a word about the(33)．However，his deliberate (34) for the rest of the day expressed everything．The way he (35)the situation taught me a hugely effective lesson．I learned that the power of the(36)words can be frighteningly influential．His (37)my honesty was more (38)than if he had scolded me．I also learned the power of (39) and second chances．And these lessons have (40)me a lot in both life and work．21. A. nervously B. deliberately C. sensitively D. humorously22. A. calm B. laugh C. benefit D. reflect23. A. advice B. patience C. expectation D. appreciation24. A. led B. sent C. helped D. attracted25. A. dream B. receipt C. way D. plan26. A. visiting B. discussing C. exploring D. progressing27. A. reasonable B. flexible C. usual D. common28. A. debt B. trouble C. honor D. change29. A. confidence B. pleasure C. pride D. money30. A. know B. hope C. admit D. remember31. A. responded B. exploded C. attacked D. comforted32. A. express B. inform C. accuse D. warn33. A. question B. incident C. trip D. shopkeeper34. A. absence B. sadness C. anger D. silence35. A. put up with B. kept away fromC. dealt withD. lived through36. A. unspoken B. proper C. meaningful D. enjoyable37. A. discovering B. losing C. defending D. exhibiting38. A. concerned B. powerful C. annoying D. frightening39. A. communication B. friendship C. blame D. forgiveness40. A. grasped B. benefited C. expressed D. surprised四、语法填空（本大题共1小题，共15.0分）41.Dujiangyan is the oldest man-made water system in the world，and a wonder in thedevelopment of Chinese science．(1) （build）over 2，200 years ago in what is now Sichuan Province in Southwest China，this amazing engineering (2) （achieve）is still used today．In ancient times，the region in which Dujiangyan now stands (3) （suffer）fromregular floods caused by overflow from the Minjiang River．(4) （help）the victims of the flooding，Li Bing，the region governor，together with his son，decided to finda solution．Li designed a series of channels built at different levels along Mount Yuleithat would take away the floodwater while leaving the river flowing naturally．(5) （good）still，the extra water could be directed to the dry Chengdu Plain，making (6) suitable for farming．Once the system was finished，no more floods occurred and the people were able to live(7) （peaceful）．Today，Dujiangyan is admired by scientists from around the worldbecause of one feature．Unlike modern dams (8) the water is blocked with a huge wall，Dujiangyan still lets water flow through the Minjiang River naturally，(9) （enable）ecosystem（生态系统）and fish populations to exist (10) harmony．五、书面表达（本大题共1小题，共25.0分）42.假设你是李华，你所在的城市成都为了提升国际形象，下个月将举行国际中文写作比赛．请你根据以下要点给曾在你班学习两年的美国同学 Tom 发封邮件，邀请他提供作品．1．主题：我眼中的成都2．截稿时间：2018 年 12 月 20 日3．字数：不限4．投稿邮箱 HYPERLINK "mailto：chengdu123@126．com" chengdu123@126．com 注意：1．词数：100 左右（开头和结尾已经给出，不计入总词数）．2．可以适当增加细节，以使行文连贯．Dear Tom，How is everything going？ You must be happy back with your family．Yours，Li Hua答案和解析1.【答案】【小题1】B【小题2】D【小题3】C【解析】（1）B．细节理解题．根据Costa Rica部分中的people enjoy a high standard of living at a much lower cost than the U． S．和Malaysia中的You will find low-cost rental units， delicious street food， and various shopping malls 可知Costa Rica和Malaysia的共同点是"生活费用相对较低"，故答案为B．（2）D．细节理解题．根据Mexico部分中的Because it's close to the U．S．，Mexico draws more than a million American retirees to its borders可知墨西哥特别吸引来自美国的退休人员，故答案为D．（3）C．细节理解题．根据Panama部分中的Gentle ocean wind takes the heat out of hot year-round temperatures，which has been the chief attraction to foreign retirees可知令人愉快的气候是吸引退休人员的主要理由，故答案为C．本文是一篇说明文，介绍了退休人员最愿意去的五个国家，分别是Costa Rica，Malaysia ，Mexico，Panama和Ecuador．做这类题材阅读理解时要求考生对文章通读一遍，做题时结合原文和题目有针对性的找出相关语句进行仔细分析，结合选项选出正确答案．推理判断题也是要在抓住关键句子的基础上合理的分析才能得出正确答案，切忌胡乱猜测，一定要做到有理有据．4.【答案】【小题1】C【小题2】B【小题3】A【小题4】D【解析】24．C．细节理解题．根据文章That night I was depressed that I decided to go outside to the freezing temperature of the wint er and run可知他的孤独使作者决定晚上跑步；故选C．25．B．细节理解题．根据文章So go forward to present now．I exercise every day and look forward to that hour and a half I get daily to do what I love with people who love it as well可知作者是一个有决心的人；故选B．26．A．细节理解题．根据文章At the gym I met new friends and back at my dorm I grew confidence to go to the end of the hall seeing people playing Super Smash Brothers and ask if I could join可知作者跑步最大的好处是恢复他的信心；故选A．27．D．推理判断题．根据文章I quickly became depressed and angry at myself for not being about to do better in school，in addition to lack of friends due to poor social and communication skills可知作者写这篇文章是为了分享他处理困难的经验；故选D．本文属于说明文阅读，作者通过这篇文章主要向我们描述了作者由于交际能力差患上了抑郁症，然而通过坚持每天跑步的方式不仅恢复了自信，病也好了．考察学生的细节理解和推理判断能力，做细节理解题时一定要找到文章中的原句，和题干进行比较，再做出正确的选择．在做推理判断题不要以个人的主观想象代替文章的事实，要根据文章事实进行合乎逻辑的推理判断．8.【答案】【小题1】D【小题2】B【小题3】A【小题4】D【解析】1．D．细节理解题．根据文章第二段内容，"Now the project is aimed at developing additional abilities for the cat"可知，这个项目的目的是为了让机器猫更聪明．故选D．2．B．细节理解题．根据文章第二段内容，"They also want to keep the cost down to just a few hundred dollars"可知，与旧的模型相比，新的机器猫会更便宜．故选B．3．A．细节理解题．根据文章第二段内容，"Researchers at Brown's Humanity-Centered Robotics Initiative are working to decide which activities older adults may need the most"可知，这种机器猫对老年人的生活有很大帮助．故选A．4．D．推理判断题．根据文章第四段内容，"In the end，they hope to create an exchange between the human and the cat in which the human feels the cat needs them．"可知，被需要的感觉对老年人是至关重要的．故选D．本文讲述了一种机器猫的研制，这种机器猫对老年人的生活有很大帮助．因为被需要的感觉对老年人是至关重要的．做这类题材阅读理解时要求考生对文章通读一遍，做题时结合原文和题目有针对性的找出相关语句进行仔细分析，结合选项选出正确答案．推理判断题也是要在抓住关键句子的基础上合理的分析才能得出正确答案，切忌胡乱猜测，一定要做到有理有据．12.【答案】【小题1】A【小题2】A【小题3】D【小题4】B【解析】1．A．词意猜测．根据文章第一段内容，Some of the best research on daily experience is rooted in rates of positive and negative intera ctions，which has proved that being blindly positive or negative can cause others to be frustrated or a nnoyed or to simply tune out．盲目的积极或消极会让别人感到沮丧或恼怒，或者干脆充耳不闻．所以该词的意思是"充耳不闻"．结合选项，故选A．2．A．细节理解．根据文章第三段内容，"You assume that situations are worse than they actually are．"可知，如果消极面对事情，那么情况会变得更加糟糕．故选A．3．D．细节理解．根据文章第四段内容，" But the effects of a positive occurrence are less dramatic and lasting than they are for a negative one"可知，负面情绪的影响比积极情绪持续的时间更长．故选D．4．B．主旨大意．根据文章第四段内容，"When you experience a positive interaction，it activates a very different response．Positive exchanges increase your body's production of oxytocin，a feel-good that increases your ability to communicate with，cooperate with and trust others"可知，本文讲述的是积极情绪的重要性，积极的心态能够提高办事效率，所以作者建议我们要以乐观的心态面对事物．故选B．本文讲述的是积极情绪的重要性，积极的心态能够提高办事效率，所以作者建议我们要以乐观的心态面对事物．如果消极面对事情，那么情况会变得更加糟糕．做这类题材阅读理解时要求考生对文章通读一遍，做题时结合原文和题目有针对性的找出相关语句进行仔细分析，结合选项选出正确答案．推理判断题也是要在抓住关键句子的基础上合理的分析才能得出正确答案，切忌胡乱猜测，一定要做到有理有据．16.【答案】【小题1】B【小题2】C【小题3】F【小题4】A【小题5】D【解析】36-40 BCFAD36．B。

2020年中考数学一诊试卷一、选择题1．如图所示，数轴的单位长度为1，且点B表示的数是2，那么点A表示的数是（）A．1B．0C．﹣1D．﹣22．如图所示的几何体是由六个相同的小正方体搭成，则该几何体的俯视图为（）A．B．C．D．3．2月14日下午，国务院联防联控机制就加大防控财税金融支持力度召开新闻发布会．会上，财政部应对疫情工作领导小组办公室主任、社会保障司司长符金陵透露，财政部建立了全国财政系统疫情防控经费的日报制度，实时跟踪各地方经费保障情况，截至2月13日各级财政共计支出了805.5亿元保障资金，其中805.5亿元用科学记数法表示正确的是（）A．0.8055×1011元B．8.055×1010元C．8.055×102元D．80.55×109元4．下列运算正确的是（）A．2m+n＝2mn B．3a2b﹣2b＝a2C．（﹣2m2n）3＝﹣8m6n3D．（n﹣2）2＝n2+45．如图，直线a∥b，将一块含30°角的直角三角尺按图中方式放置，其中点A和点B两点分别落在直线a和b上．若∠2＝50°，则∠1的度数为（）A．10°B．20°C．30°D．40°6．点（﹣3，1）关于y轴的对称点在反比例函数y＝的图象上，则实数k的值为（）A．3B．C．﹣3D．﹣7．下列关于分式方程+1＝的解的情况，判断正确的是（）A．x＝1.5B．x＝﹣0.5C．x＝0.5D．无解8．为全力抗战疫情，响应政府“停课不停学”号召，某市教育局发布关于疫情防控期间开展在线课程教学辅导答疑的通知：从2月10日开始，全市中小学按照教学计划，开展在线课程教学辅导和答疑，提高了同学们在线学习的质效．随机抽查了某中学九年级5名学生一周在线学习的时长分别为：17，18，19，20，21，（单位：时）则这5名学生一周在线学习时间的方差（单位：时2）为（）A．2B．19C．10D．9．如图，△ABC内接于⊙O，∠A＝60°，OM⊥BC于点M，若OM＝2，则的长为（）A．4πB．πC．πD．π10．已知抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣2，与x轴的一个交点坐标为（﹣4，0），其部分图象如图所示，下列结论：①当x＜0时，y随x增大而增大；②抛物线一定过原点；③方程ax2+bx+c＝0（a≠0）的解为x＝0或x＝﹣4；④当﹣4＜x＜0时，ax2+bx+c＞0；⑤a﹣b+c＜0．其中结论错误的个数有（）个A．1B．2C．3D．4二、填空题（每小题4分，共16分）11．代数式中，实数m的取值范围是．12．如图，菱形ABCD的周长是12，∠ABC＝120°，那么这个菱形的对角线BD的长是．13．已知点A（x1，y1），B（x2，y2）都在反比例函数y＝（k＜0）的图象上，且y1＜0＜y2，则x1与x2的大小关系是．14．如图，在△ABC中，AB＝BC，以点A为圆心，AC长为半径画弧，交BC于点C和点D，再分别以点C，D为圆心，大于CD长为半径画弧，两弧相交于点E，作射线AE 交BC于点M，若CM＝1，BD＝3，则sin B＝．三、解答题（本大题共小题，共54分，答题应写出文字说明、证明过程或演算步骤）15．（1）计算：（﹣π）0+2﹣2﹣2cos45°+|1﹣|．（2）解不等式组，并写出不等式组的整数解．16．先化简，再求值：÷（+m﹣3），其中m ＝﹣1．17．某社区为了加强社区居民对病毒防护知识的了解，通过微信群宣传病毒的防护知识，并鼓励社区居民在线参与作答《2020年病毒防治全国统一考试（全国卷）》试卷（满分100分），社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩，并对他们的成绩（单位：分）进行统计、分析，过程如下：收集数据甲小区：80 85 90 95 90 95 90 65 75 10090 70 95 90 80 80 90 95 60 100乙小区：60 80 95 80 90 65 80 85 85 10080 95 90 80 90 70 80 90 75 100整理数据成绩x（分）小区60≤x≤70 70＜x≤80 80＜x≤9090＜x≤100甲小区3476乙小区3764分析数据数据名称计量小区平均数中位数众数甲小区85.7590b乙小区83.5a80应用数据（1）填空：a＝b＝；（2）若乙小区共有1200人参与答卷，请估计乙小区成绩大于90分的人数；（3）社区管理人员看完统计数据，认为甲小区对病毒防护知识掌握更好，请你写出社区管理人员的理由；为了更好地宣传病毒防护知识，社区管理人员决定从甲、乙小区的4个满分试卷中随机抽取两份试卷对小区居民进行网络宣传讲解培训，请用列表格或画树状图的方法求出甲、乙小区各抽到一份满分试卷的概率．18．我国第一艘国产航空母舰山东舰2019年12月17日在海南三亚某军港交付海军，中国海军正式迈入双航母时代．如图，在一次海上巡航任务中，山东舰由西向东航行，到达A处时，测得小岛C位于它的北偏东54°方向，再航行一段距离到达B处，测得小岛C 位于它的北偏东30°方向，且与山东舰相距30海里．求山东舰从A到B航行了多少海里？（精确到0.1）参考数据：sin54°＝0.81，cos54°＝0.59，tan54°＝1.38，≈1.73．19．如图，在平面直角坐标系xOy中，一次函数y＝﹣x﹣5和y＝2x的图象相交于点A，反比例函数y＝的图象经过点A．（1）求反比例函数的解析式；（2）将直线y＝﹣x﹣5，沿y轴正方向向上平移m（m＞0）个单位长度得到的新直线l与反比例函数y＝（x＜0）的图象只有一个公共点，求新直线l的函数表达式．20．如图，AB是⊙O的直径，CD是⊙O的一条弦，＝，CO的延长线交⊙O于点E，交BD的延长线于点F，连接FA，且恰好FA∥CD，连接BE交CD于点P，延长BE 交FA于点G，连接DE．（1）求证：FA是⊙O的切线；（2）求证：点G是FA的中点；（3）当⊙O的半径为6时，求tan∠FBE的值．一、填空题（每小题4分，共20分）21．比较大小：（填“＞”“＜”或“＝”）．22．某商场为了吸引顾客，设立了一个可以自由转动的转盘（如图，转盘被等分成20个扇形，并规定：顾客每购买100元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域（如果指针正对分格线重转），那么顾客就可以分别获得价值相当于100元，50元，20元的购物券．则顾客每次转转盘的平均收益为元．23．已知关于x的方程x2﹣（3+2a）x+a2＝0的两个实数根为x1，x2，且x1x2﹣5＝x1+x2，则a的值为．24．如图，在平面直角坐标系xOy中，等边△OAB的面积为，边AB交y轴于点C，且AC＝2BC，反比例函数y＝（x＜0）的图象经过点A．则反比例函数的解析式为．25．在平面直角坐标系xOy中，直线l：y＝kx﹣1（k≠0）与直线x＝﹣k，y＝﹣k分别交于点A，B．直线x＝﹣k与y＝﹣k交于点C．记线段AB，BC，AC围成的区域（不含边界）为W；横，纵坐标都是整数的点叫做整点．（1）当k＝﹣2时，区域W内的整点个数为；（2）若区域W内没有整点，则k的取值范围是．二、解答题（本大题共3小题，共30分．其中26题8分，27题10分，28题12分）26．某网店专售一品牌牙膏，其成本为22元/支，销售中发现，该商品每天的销售量y（支）与销售单价x（元/支）之间存在如图所示的关系．（1）请求出y与x之间的函数关系式；（2）该品牌牙膏销售单价定为多少元时，每天销售利润最大？最大利润是多少元？（3）在武汉爆发“病毒”疫情期间，该网店店主决定从每天获得的利润中抽出100元捐赠给武汉，为了保证捐款后每天剩余的利润不低于350元，在抗“病毒”疫情期间，市场监督管理局加大了对线上、线下商品销售的执法力度，对商品售价超过成本价的20%的商家进行处罚，请你给该网店店主提供一个合理化的销售单价范围．27．如图，在正方形BCD中，E是AD边上一点，连接BE，过A作AF⊥BE于P，交CD 于F．（1）如图1，连接BF，当AE＝1，AD＝4时，求BF的长；（2）如图2，对角线AC，BD交于点O．连接OP，若DE＝2AE＝4，求OP的长；（3）如图3，对角线AC，BD交于点O．连接OP，DP，若DP⊥PO，试探索DP与BP 的数量关系，并说明理由．28．如图1所示，在平面直角坐标系xOy中，直线y＝x﹣4与x轴交于点A，与y轴交于点B，抛物线y＝x2+bx+c经过A，B两点，与x轴的另一交点为点C．（1）求抛物线的函数表达式；（2）点M为直线AB下方抛物线上一动点．①如图2所示，直线CM交线段AB于点N，求的最小值；②如图3所示，连接BM过点M作MD⊥AB于D，是否存在点M，使得△BMD中的某个角恰好等于∠CAB的2倍？若存在，求点M的坐标；若不存在，请说明理由．参考答案一、选择题（每小题3分，共30分．下列各小题给出的四个选项中，只有一个符合题目要求）1．如图所示，数轴的单位长度为1，且点B表示的数是2，那么点A表示的数是（）A．1B．0C．﹣1D．﹣2【分析】根据数轴的单位长度为1，点A在点B的左侧距离点B4个单位长度，直接计算即可．解：点A在点B的左侧距离点B4个单位长度，∴点A表示的数为：2﹣4＝﹣2，故选：D．2．如图所示的几何体是由六个相同的小正方体搭成，则该几何体的俯视图为（）A．B．C．D．【分析】根据从上边看得到的图形是俯视图，可得答案．解：从上边看第一列是两个小正方形，第二列上层是一个小正方形，第三列上层是一个小正方形，故选：C．3．2月14日下午，国务院联防联控机制就加大疫情防控财税金融支持力度召开新闻发布会．会上，财政部应对疫情工作领导小组办公室主任、社会保障司司长符金陵透露，财政部建立了全国财政系统疫情防控经费的日报制度，实时跟踪各地方经费保障情况，截至2月13日各级财政共计支出了805.5亿元保障资金，其中805.5亿元用科学记数法表示正确的是（）A．0.8055×1011元B．8.055×1010元C．8.055×102元D．80.55×109元【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n 的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．解：805.5亿元用科学记数法表示正确的是8.055×1010元．故选：B．4．下列运算正确的是（）A．2m+n＝2mn B．3a2b﹣2b＝a2C．（﹣2m2n）3＝﹣8m6n3D．（n﹣2）2＝n2+4【分析】直接利用合并同类项法则、积的乘方运算法则、完全平方公式计算得出答案．解：A、2m与n不是同类项，不能合并，原计算错误，故此选项不符合题意；B、3a2b与2b不是同类项，不能合并，原计算错误，故此选项不符合题意；C、（﹣2m2n）3＝﹣8m6n3，原计算正确，故此选项符合题意；D、（n﹣2）2＝n2﹣4n+4，原计算错误，故此选项不符合题意；故选：C．5．如图，直线a∥b，将一块含30°角的直角三角尺按图中方式放置，其中点A和点B两点分别落在直线a和b上．若∠2＝50°，则∠1的度数为（）A．10°B．20°C．30°D．40°【分析】根据平行线的性质即可得到结论．解：∵直线a∥b，∠2＝50°，∴∠1+90°+∠2+30°＝180°，即∠1+90°+50°+30°＝180°，解得∠1＝10°．故选：A．6．点（﹣3，1）关于y轴的对称点在反比例函数y＝的图象上，则实数k的值为（）A．3B．C．﹣3D．﹣【分析】先根据关于y轴对称的点的坐标特点求出点（﹣3，1）关于y轴的对称点的坐标，代入反比例函数y＝即可得出k的值．解：∵点（﹣3，1）关于y轴的对称点为（3，1），∴1＝，解得k＝3．故选：A．7．下列关于分式方程+1＝的解的情况，判断正确的是（）A．x＝1.5B．x＝﹣0.5C．x＝0.5D．无解【分析】根据分式方程的解法即可求出答案．解：∵＝，∴＝，∴（x﹣1）（2﹣4x）＝2x﹣1，∴4x2﹣4x+1＝0，∴（2x﹣1）2＝0，∴x＝，经检验，x＝不是原方程的解，故选：D．8．为全力抗战疫情，响应政府“停课不停学”号召，某市教育局发布关于疫情防控期间开展在线课程教学辅导答疑的通知：从2月10日开始，全市中小学按照教学计划，开展在线课程教学辅导和答疑，提高了同学们在线学习的质效．随机抽查了某中学九年级5名学生一周在线学习的时长分别为：17，18，19，20，21，（单位：时）则这5名学生一周在线学习时间的方差（单位：时2）为（）A．2B．19C．10D．【分析】根据平均数的计算公式先求出这组数据的平均数，再代入方差公式S2＝[（x1﹣）2+（x2﹣）2+…+（x n﹣）2]，进行计算即可得出答案．解：这组数据的平均数是：（17+18+19+20+21）＝19（时），则方差：S2＝[（17﹣19）2+（18﹣19）2+（19﹣19）2+（20﹣19）2+（21﹣19）2]＝2（时2）；故选：A．9．如图，△ABC内接于⊙O，∠A＝60°，OM⊥BC于点M，若OM＝2，则的长为（）A．4πB．πC．πD．π【分析】连接OB、OC，根据圆周角定理求出∠BOC，根据直角三角形的性质求出OB，根据弧长公式计算，得到答案．解：连接OB、OC，由圆周角定理得，∠BOC＝2∠A＝120°，∵OB＝OC，∴∠OBC＝（180°﹣120°）＝30°，∴OB＝2OM＝4，∴的长＝＝π，故选：C．10．已知抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣2，与x轴的一个交点坐标为（﹣4，0），其部分图象如图所示，下列结论：①当x＜0时，y随x增大而增大；②抛物线一定过原点；③方程ax2+bx+c＝0（a≠0）的解为x＝0或x＝﹣4；④当﹣4＜x＜0时，ax2+bx+c＞0；⑤a﹣b+c＜0．其中结论错误的个数有（）个A．1B．2C．3D．4【分析】①根据函数图象变化趋势进行解答；②根据对称轴，求出抛物线与x轴的另一个交点，便可判断；③根据抛物线与x轴的交点横坐标进行判断；④根据﹣4＜x＜0时，抛物线在x轴上方，进行判断；⑤根据当x＝﹣1时，y的函数值的位置进行判断．解：①由函数图象可知，当﹣2＜x＜0时，y随x增大而减小，则此小题结论错误；②∵对称轴为直线x＝﹣2，与x轴的一个交点坐标为（﹣4，0），∴另个交点为（0，0），即抛物线一定过原点，则此小题结论正确；③∵抛物线与x轴交于（﹣4，0）和（0，0），∴方程ax2+bx+c＝0（a≠0）的解为x＝0或x＝﹣4，则此小题结论正确；④由函数图象可知，当﹣4＜x＜0时，抛物线在x轴上方，即ax2+bx+c＞0，则此小题结论正确；⑤则函数图象可知，当x＝﹣1时，y＝a﹣b+c＞0，则此小题结论错误；故选：B．二、填空题（每小题4分，共16分）11．代数式中，实数m的取值范围是m≥﹣．【分析】二次根式的被开方数是非负数，即2m+1≥0．解：由题意，得2m+1≥0．解得m≥﹣．故答案是：m≥﹣．12．如图，菱形ABCD的周长是12，∠ABC＝120°，那么这个菱形的对角线BD的长是3．【分析】根据∠ABC＝120°，而AB＝AD，易证△BAD是等边三角形，从而可求BD 的长．解：∵四边形ABCD是菱形，BD是对角线，∴AB＝BC＝CD＝AD，AD∥BC，∵∠ABC＝120°，∴∠A＝60°，∴△BAD是等边三角形，∴AB＝BD＝AD，∵菱形ABCD的周长是12，∴AB＝3，∴BD＝3，故答案为：3．13．已知点A（x1，y1），B（x2，y2）都在反比例函数y＝（k＜0）的图象上，且y1＜0＜y2，则x1与x2的大小关系是x1＞x2．【分析】先判断出点A、B在第三象限，再根据反比例函数的增减性判断．解：∵k＜0，y1＜0＜y2，∴点A在第四象限，点B在第二象限，∴x1＞x2．故答案为x1＞x2．14．如图，在△ABC中，AB＝BC，以点A为圆心，AC长为半径画弧，交BC于点C和点D，再分别以点C，D为圆心，大于CD长为半径画弧，两弧相交于点E，作射线AE 交BC于点M，若CM＝1，BD＝3，则sin B＝．【分析】连接AD，利用等腰三角形的性质得出DM＝MC，进而利用直角三角形的解法解答即可．解：连接AD，由作图可知，AD＝AC，AM是∠DAC的角平分线，∴AM⊥DC，DM＝MC＝1，∵BD＝3，∴BM＝3+1＝4，AB＝3+2＝5＝BC，∴AM＝，∴sin B＝，故答案为：．三、解答题（本大题共小题，共54分，答题应写出文字说明、证明过程或演算步骤）15．（1）计算：（﹣π）0+2﹣2﹣2cos45°+|1﹣|．（2）解不等式组，并写出不等式组的整数解．【分析】（1）原式利用零指数幂法则，负指数幂的法则，特殊角的三角函数、绝对值的意义计算即可得到结果；（2）先求得两个不等式的解集，再在数轴上得出不等式组的整数解．解：（1）原式＝1+﹣2×+2﹣1＝1+﹣+2﹣1＝+；（2）解不等式①得x＞﹣1；解不等式②得x≤1；∴不等式组的解集为﹣1＜x≤1，∴不等式组的整数解为0，1．16．先化简，再求值：÷（+m﹣3），其中m＝﹣1．【分析】根据分式的加法和除法可以化简题目中的式子，然后将m的值代入化简后的式子即可解答本题．解：÷（+m﹣3）＝＝＝＝，当m＝﹣1时，原式＝＝．17．某社区为了加强社区居民对病毒防护知识的了解，通过微信群宣传病毒的防护知识，并鼓励社区居民在线参与作答《2020年病毒防治全国统一考试（全国卷）》试卷（满分100分），社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩，并对他们的成绩（单位：分）进行统计、分析，过程如下：收集数据甲小区：80 85 90 95 90 95 90 65 75 10090 70 95 90 80 80 90 95 60 100乙小区：60 80 95 80 90 65 80 85 85 10080 95 90 80 90 70 80 90 75 100整理数据成绩x（分）小区60≤x≤70 70＜x≤80 80＜x≤9090＜x≤100甲小区3476乙小区3764分析数据数据名称计量小区平均数中位数众数甲小区85.7590b乙小区83.5a80应用数据（1）填空：a＝82.5b＝90；（2）若乙小区共有1200人参与答卷，请估计乙小区成绩大于90分的人数；（3）社区管理人员看完统计数据，认为甲小区对病毒防护知识掌握更好，请你写出社区管理人员的理由；为了更好地宣传病毒防护知识，社区管理人员决定从甲、乙小区的4个满分试卷中随机抽取两份试卷对小区居民进行网络宣传讲解培训，请用列表格或画树状图的方法求出甲、乙小区各抽到一份满分试卷的概率．【分析】（1）根据中位数和众数的定义即可求得a、b的值；（2）用乙小区总人数乘以乙小区成绩大于90分的人数所占的百分比即可；（3）从平均数，中位数，众数三方面进行分析，得出甲小区的居民对病毒防护知识掌握更好些；根据题意画出树状图得出所有等情况数和甲、乙小区各抽到一份满分试卷的情况数，然后根据概率公式即可得出答案．解：（1）把乙小区的数据从小到大排列，则中位数a＝＝82.5；∵甲小区中90出现了6次，出现的次数最多，∴甲小区的众数b＝90；故答案为：82.5，90；（2）根据题意得：1200×＝240（人），答：乙小区成绩大于90分的人数为240人；（3）因为从试卷得分的平均数，中位数，众数来看都是甲小区的试卷分数大于乙小区的试卷分数，所以甲小区的居民对病毒防护知识掌握更好些；根据题意列表如下：甲1甲2乙1乙2甲1（甲2，甲1）（乙1，甲1）（乙2，甲1）甲2（甲1，甲2）（乙1，甲2）（乙2，甲2）乙1（甲1，乙1）（甲2，乙1）（乙2，乙1）乙2（甲1，乙2）（甲2，乙2）（乙1，乙2）由表可知共有12种等可能情况，其中满足条件的有8种，所以P（甲、乙小区各抽到一份满分试卷）＝＝．18．我国第一艘国产航空母舰山东舰2019年12月17日在海南三亚某军港交付海军，中国海军正式迈入双航母时代．如图，在一次海上巡航任务中，山东舰由西向东航行，到达A处时，测得小岛C位于它的北偏东54°方向，再航行一段距离到达B处，测得小岛C 位于它的北偏东30°方向，且与山东舰相距30海里．求山东舰从A到B航行了多少海里？（精确到0.1）参考数据：sin54°＝0.81，cos54°＝0.59，tan54°＝1.38，≈1.73．【分析】作CD⊥AB交其延长线于点D，由∠BCD＝30°，∠BDC＝90°，BC＝30知BD＝15，CD＝15，再由tan∠ACD＝求得AD＝CD tan∠ACD＝CD•tan45°≈35.81（海里），根据AB＝AD﹣BD求解可得答案．解：过C作CD⊥AB交其延长线于点D，由题可知∠BCD＝30°，∠ACD＝54°，在Rt△BCD中，∵∠BCD＝30°，∠BDC＝90°，BC＝30，∴BD＝15，CD＝15，在Rt△ACD中，∵∠ACD＝54°，∠BDC＝90°，CD＝15，tan∠ACD＝，∴AD＝CD tan∠ACD＝CD•tan45°≈1.38×15×1.73≈35.81（海里），∴AB＝AD﹣BD＝35.81﹣15＝20.81≈20.8（海里），答：山东舰从A到B航行约20.8海里．19．如图，在平面直角坐标系xOy中，一次函数y＝﹣x﹣5和y＝2x的图象相交于点A，反比例函数y＝的图象经过点A．（1）求反比例函数的解析式；（2）将直线y＝﹣x﹣5，沿y轴正方向向上平移m（m＞0）个单位长度得到的新直线l与反比例函数y＝（x＜0）的图象只有一个公共点，求新直线l的函数表达式．【分析】（1）两直线解析式联立组成方程组，解方程组求得A的坐标，然后根据待定系数法即可求得反比例函数的解析式；（2）据题意设直线l函数表达式为：y＝﹣﹣5+m，然后解，消去y整理得﹣2+（m﹣5）x﹣8＝0，根据题意有△＝（m﹣5）2﹣4×（﹣）×（﹣8）＝0，解得m＝1，即可求得新直线l的函数表达式．【解答】（1）解：将解析式联立得解之得，∴点A（﹣2，﹣4），∵反比例函数y＝的图象经过点A．∴﹣4＝，k＝8，∴反比例函数解析式为y＝；（2）据题意设直线l函数表达式为：y＝﹣﹣5+m，将解析式联立得，消去y得﹣﹣5+m＝，去分母得﹣2+（m﹣5）x﹣8＝0，据题意有△＝（m﹣5）2﹣4×（﹣）×（﹣8）＝0，解之得m＝1或9又反比例函数中x＜0，∴m＝1，∴新直线l函数表达式为：y＝﹣﹣4．20．如图，AB是⊙O的直径，CD是⊙O的一条弦，＝，CO的延长线交⊙O于点E，交BD的延长线于点F，连接FA，且恰好FA∥CD，连接BE交CD于点P，延长BE 交FA于点G，连接DE．（1）求证：FA是⊙O的切线；（2）求证：点G是FA的中点；（3）当⊙O的半径为6时，求tan∠FBE的值．【分析】（1）根据垂径定理得出AB⊥CD，根据FA∥CD求出FA⊥AB，根据切线的判定得出即可；（2）根据相似三角形的判定求出△GAB∽△GEA，△FEG∽△BFG，得出比例式，即可求出GF＝GA；（3）根据FA∥CD得出比例式＝＝，求出DP＝HP，求出DE＝BH，求出OH＝DE＝BE，求出OH和OH，解直角三角形求出即可．【解答】（1）证明：∵AB是⊙O的直径，CD是⊙O的一条弦，＝，∴AB⊥CD，又∵FA∥CD，∴FA⊥AB，∵OA过O，∴FA是⊙O的切线；（2）证明：连接AE，∵AB是⊙O的直径，∴AE⊥BG，又∵FA⊥AB，∴∠GEA＝∠BAG，又∵∠BGA＝∠EGA，∴△GAB∽△GEA，∴＝，∴GA2＝GB×EG，∵FA∥CD，∴∠C＝∠EFG，又∵∠C＝∠FBE，∴∠EFG＝∠FBE，又∵∠FGE＝∠BGF，∴△FEG∽△BFG，∴＝，∴GF2＝GB×GE，∴GF＝GA，∴G为AF的中点；（3）解：∵FA∥CD，∴＝＝，又∵GF＝GA，∴DP＝HP，又∵CE是⊙O的直径，D在圆上，∴CD⊥DE，又∵AB⊥CD于点H，EO＝OC，∴点H是CD的中点，AB∥DE，又∵DP＝HP，∴DE＝BH，又∵点O是CE中点，点H是CD的中点，∴OH＝DE＝BE，又∵⊙O的半径为6，∴OH＝2，CH＝＝＝4，∴tan∠FBE＝tan C＝＝＝．一、填空题（每小题4分，共20分）21．比较大小：＞（填“＞”“＜”或“＝”）．【分析】先通分得出，再估算出的范围，最后比较分子大小，即可得出答案．解：∵2＜＜3，∴8＜4＜9，∴3＜12﹣4＜4，∴＞．故答案是：＞．22．某商场为了吸引顾客，设立了一个可以自由转动的转盘（如图，转盘被等分成20个扇形，并规定：顾客每购买100元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域（如果指针正对分格线重转），那么顾客就可以分别获得价值相当于100元，50元，20元的购物券．则顾客每次转转盘的平均收益为14元．【分析】直接利用概率公式求解可得．解：100×+50×+20×＝14（元），故答案为：14．23．已知关于x的方程x2﹣（3+2a）x+a2＝0的两个实数根为x1，x2，且x1x2﹣5＝x1+x2，则a的值为4．【分析】先利用判别式的意义得到a≥﹣，再根据根与系数的关系得到x1+x2＝3+2a，x1x2＝a2，则利用x1x2﹣5＝x1+x2得到a2﹣5＝3+2a，然后解关于a的方程确定满足条件的a的值．解：根据题意得△＝（3+2a）2﹣4a2≥0，解得a≥﹣，∵x1+x2＝3+2a，x1x2＝a2，而x1x2﹣5＝x1+x2，∴a2﹣5＝3+2a，整理得a2﹣2a﹣8＝0，解得a1＝4，a2＝﹣2（舍去），∴a的值为4．故答案为4．24．如图，在平面直角坐标系xOy中，等边△OAB的面积为，边AB交y轴于点C，且AC＝2BC，反比例函数y＝（x＜0）的图象经过点A．则反比例函数的解析式为y ＝﹣．【分析】作OD⊥AB于D，AE⊥OC于E，根据三角形面积求得等边三角形的边长为，根据题意求得BC＝，AC＝，CD＝，根据勾股定理求得OC，然后证得△ACE∽△OCD，根据相似三角形的性质求得AE＝，CE＝，进而求得OE＝2，即可求得A（﹣，2），代入y＝（x＜0）求得k的值，得到反比例函数的解析式．解：作OD⊥AB于D，AE⊥OC于E，设等边三角形OAB的边长为a，∵等边△OAB中，∠OAB＝60°，∴OD＝OA＝a，BD＝a，∵等边△OAB的面积为，∴AB•OD＝，即＝，∴a＝，∵AC＝2BC，∴BC＝a＝，AC＝a＝，∴CD＝BD﹣BD＝﹣＝，∴OC＝＝＝，∵∠ACE＝∠OCD，∠AEC＝∠ODC＝90°，∴△ACE∽△OCD，∴＝＝，＝＝，∴AE＝，CE＝，∴OE＝OC﹣CE＝﹣＝2，∴A（﹣，2），∵反比例函数y＝（x＜0）的图象经过点A．∴k＝﹣×2＝﹣2，∴反比例函数的解析式为y＝﹣，故答案为y＝﹣25．在平面直角坐标系xOy中，直线l：y＝kx﹣1（k≠0）与直线x＝﹣k，y＝﹣k分别交于点A，B．直线x＝﹣k与y＝﹣k交于点C．记线段AB，BC，AC围成的区域（不含边界）为W；横，纵坐标都是整数的点叫做整点．（1）当k＝﹣2时，区域W内的整点个数为6；（2）若区域W内没有整点，则k的取值范围是0＜k≤1或k＝2．【分析】（1）将k＝﹣2代入解析式，求得A、B、C三点坐标，并作出图形，便可求得W区域内的整数点个数；（2）分三种情况解答：当k＜0时，区域内必含有坐标原点，故不符合题意；当0＜k≤1时，W内点的横坐标在k到0之间，无整点，进而得0＜k≤1时，W内无整点；当1＜k≤2时，W内可能存在的整数点横坐标只能为﹣1，此时边界上两点坐标为（﹣1，﹣k）和（﹣1，﹣k﹣1），当k不为整数时，其上必有整点，但k＝2时，只有两个边界点为整点，故W内无整点；当k＞2时，横坐标为﹣2的边界点为（﹣2，﹣k）和（﹣2，﹣2k﹣1），线段长度为k+1＞3，故必有整点．解：（1）直线l：y＝kx﹣1＝﹣2x﹣1，直线x＝﹣k＝2，y＝﹣k＝2，∴A（2，﹣5），B（﹣，2），C（2，2），在W区域内有6个整数点：（0，0），（0，1），（1，0），（1，1），（1，﹣1），（1，﹣2），故答案为6；（2）当k＜0时，则x＝﹣k＞0，y＝﹣k＞0，∴区域内必含有坐标原点，故不符合题意；当0＜k≤1时，W内点的横坐标在﹣1到0之间，不存在整点，故0＜k≤1时W内无整点；当1＜k≤2时，W内可能存在的整数点横坐标只能为﹣1，此时边界上两点坐标为M（﹣1，﹣k）和N（﹣1，﹣k﹣1），MN＝1，此时当k不为整数时，其上必有整点，但k＝2时，只有两个边界点为整点，故W内无整点；当k＞2时，横坐标为﹣2的边界点为（﹣2，﹣k）和（﹣2，﹣2k﹣1），线段长度为k+1＞3，故必有整点．综上所述：0＜k≤1或k＝2时，W内没有整点．故答案为：0＜k≤1或k＝2．二、解答题（本大题共3小题，共30分．其中26题8分，27题10分，28题12分）26．某网店专售一品牌牙膏，其成本为22元/支，销售中发现，该商品每天的销售量y（支）与销售单价x（元/支）之间存在如图所示的关系．（1）请求出y与x之间的函数关系式；（2）该品牌牙膏销售单价定为多少元时，每天销售利润最大？最大利润是多少元？（3）在武汉爆发“病毒”疫情期间，该网店店主决定从每天获得的利润中抽出100元捐赠给武汉，为了保证捐款后每天剩余的利润不低于350元，在抗“病毒”疫情期间，市场监督管理局加大了对线上、线下商品销售的执法力度，对商品售价超过成本价的20%的商家进行处罚，请你给该网店店主提供一个合理化的销售单价范围．【分析】（1）利用待定系数法求解可得；（2）设每天的利润为W元，根据“总利润＝每支利润×每天销售量”得出函数解析式，配方成顶点式后利用二次函数的性质求解可得；（3）根据题意列出方程﹣10x2+620x﹣8800﹣100＝350，解之求出x的值，再根据二次函数的性质得出25≤x≤37，结合x≤22×（1+20%）可得答案．解：（1）根据题意设y＝kx+b（k≠0），将（30，100）、（35，50）代入得，解得，∴y与x之间的关系式为y＝﹣10x+400；（2）设每天的利润为W元，则W＝（x﹣22）y＝（x﹣22）（﹣10x+400）＝﹣10x2+620x﹣8800＝﹣10（x﹣31）2+810，∴销售单价定为31元时，每天最大利润为810元．（3）﹣10x2+620x﹣8800﹣100＝350，解得x＝25或x＝37，结合图象和二次函数的特点得出25≤x≤37，又x≤22×（1+20%），综上可得25≤x≤26.4，∴按要求网店店主的销售单价范围为大于或等于25元且小于或等于26.4元．27．如图，在正方形BCD中，E是AD边上一点，连接BE，过A作AF⊥BE于P，交CD 于F．（1）如图1，连接BF，当AE＝1，AD＝4时，求BF的长；（2）如图2，对角线AC，BD交于点O．连接OP，若DE＝2AE＝4，求OP的长；（3）如图3，对角线AC，BD交于点O．连接OP，DP，若DP⊥PO，试探索DP与BP 的数量关系，并说明理由．【分析】（1）证明△ABE≌△DAF（ASA），推出DF＝AE＝2，求出CF利用勾股定理即可解决问题．（2）证明△OPB∽△EDB，可得＝解决问题．（3）证明△DEP∽△BOP，可得＝，再证明OB＝DE即可解决问题．【解答】（1）解：如图1中，∵正方形ABCD，∴∠DAB＝∠D＝∠C＝90°，AB＝BC＝DC＝AD＝4∵AF⊥BE于P，∴∠EBA+∠FAB＝90°，又∠DAF+FAB＝90°，∴∠EBA＝∠DAF，又∠DAB＝∠D，AB＝DA，∴△ABE≌△DAF（ASA），∴DF＝AE＝1，∵AD＝CD＝BC＝4，∴CF＝DC﹣DF＝3，在Rt△BFC中，BF＝＝＝5．（2）如图2中，∵正方形ABCD对角线AC，BD相交于点O，∴∠CAB＝∠ADB＝45°，∠AOB＝90°，∵AF⊥BE于P，∴∠APB＝∠AOB＝90°，∴A，P，O，B四点共圆，∴∠OPB＝∠OAB＝45°（也可由相似证得），∴∠OPB＝∠ADB，又∠OBP＝∠DBE，∴△OPB∽△EDB，可得＝，又DE＝2AE＝4，可得AD＝AB＝6，BD＝6，OB＝3，BE＝2，∴＝，∴OP＝．（3）结论：DP＝BP．理由如下：如图3中，连接EF．∵DP⊥OP，由（2）问可知∠APB＝∠AOB＝90°，∴A，P，O，B四点共圆，∴∠OPB＝∠OAB＝45°，∴∠DPE＝∠OPB＝45°，又A，P，O，B四点共圆有∠POA＝∠PBA，∴∠DEP＝∠DAB+∠PBA＝∠AOB+∠POA＝∠POB，又∠DPE＝∠OPB，∴△DEP∽△BOP，∴＝，∵AF⊥BE，∠EDF＝90°，∴∠EDF+∠EPF＝180°，∴D，E，P，F四点共圆，∴∠DFE＝∠DPE＝45°，∴∠DEF＝∠DFE＝45°，∵DE＝DF，又AE＝DF，于是AE＝DE＝AD，OB＝BD＝×AD＝DE，∴＝＝，∴DP＝BP．28．如图1所示，在平面直角坐标系xOy中，直线y＝x﹣4与x轴交于点A，与y轴交于点B，抛物线y＝x2+bx+c经过A，B两点，与x轴的另一交点为点C．（1）求抛物线的函数表达式；（2）点M为直线AB下方抛物线上一动点．①如图2所示，直线CM交线段AB于点N，求的最小值；②如图3所示，连接BM过点M作MD⊥AB于D，是否存在点M，使得△BMD中的某个角恰好等于∠CAB的2倍？若存在，求点M的坐标；若不存在，请说明理由．【分析】（1）求出点A、B的坐标，将A、B两点坐标代入y＝x2+bx+c，即可求解；。

四川省成都市2020届高三数学上学期第一次诊断性检测试题 理（含解析）本试卷分选择题和非选择题两部分，第1卷（选择题）1至2页，第11卷（非选择题）3至4页，共4页，满分150分，考试时间120分钟. 注意事项：1，答题前，务必将自己的姓名、考籍号填写在答题卡规定的位置上.2，答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号.3，答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上. 4，所有题目必须在答题卡上作答，在试题卷上答题无效. 5，考试结束后，只将答题卡交回.一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的1.若复数1z 与23z i =--（i 为虚数单位）在复平面内对应的点关于实轴对称，则1z =( ) A. 3i -- B. 3i -+ C. 3i + D. 3i -【答案】B 【解析】 【分析】由题意得复数z 1与23z i =--的实部相等，虚部互为相反数，则z 1可求．【详解】∵复数z 1与23z i =--（i 为虚数单位）在复平面内对应的点关于实轴对称， ∴复数z 1与23z i =--（i 为虚数单位）的实部相等，虚部互为相反数，则z 1＝3i -+． 故选：B ．【点睛】本题考查复数的代数表示法及其几何意义，属于基础题．2.已知集合{}1,0,A m =-，{}1,2B =，若{}1,0,1,2A B ⋃=-，则实数m 的值为( ) A. 1-或0 B. 0或1 C. 1-或2D. 1或2【答案】D 【解析】 【分析】根据集合并集的定义即可得到答案. 【详解】集合{}1,0,A m =-，{}1,2B =，且{}1,0,1,2A B ⋃=-，所以1m =或2m =.故选：D【点睛】本题主要考查集合并集的基本运算，属于基础题． 3.若sin 5cos(2)θπθ=-，则tan 2θ=( )A. 5-B.53C. 52-D.5 【答案】C 【解析】 【分析】由题意利用同角三角函数的基本关系、诱导公式，求得tan θ，再利用倍角公式求得tan 2θ的值． 【详解】sin 5cos(2)θπθ=-，∴sin 5cos θθ=，得tan 5θ=，222tan 255tan 21tan 15θθθ∴===---.故选：C【点睛】本题主要考查同角三角函数的基本关系、诱导公式，倍角公式的应用，属于基础题． 4.某校随机抽取100名同学进行“垃圾分类"的问卷测试，测试结果发现这100名同学的得分都在[50，100]内，按得分分成5组：[50，60），[60，70），[70，80），[80，90），[90，100]，得到如图所示的频率分布直方图，则这100名同学的得分的中位数为( )A. 72.5B. 75C. 77.5D. 80【答案】A 【解析】 【分析】根据频率分布直方图求得中位数即可.【详解】在频率分步直方图中，小正方形的面积表示这组数据的频率，∴中位数为：0.50.01100.0310701072.50.0410-⨯-⨯+⨯=⨯.故选：A【点评】本题考查频率分布直方图的相关知识，直方图中的各个矩形的面积代表了频率，所有各个矩形面积之和为1，也考查了中位数，属于基础题． 5.设等差数列{}n a 的前n 项和为n S ，且533a a =，则95S S =( ) A. 95 B.59 C. 53D. 275【答案】D 【解析】 【分析】将S 9，S 5转化为用a 5，a 3表达的算式即可得到结论.【详解】由等差数列{}n a 的前n 项和为n S ，∴95S S ＝19159252a a a a +⨯+⨯＝5395a a ，且533a a =，∴95S S ＝95×3＝275.故选：D ．【点睛】本题考查了等差数列的前n 项和，等差中项的性质，考查计算能力，属于基础题． 6.已知,αβ是空间中两个不同的平面，,m n 是空间中两条不同的直线，则下列说法正确的是( )A. 若//m α，//n β，且//αβ，则//m nB. 若//m α，//n β，且αβ⊥，则//m nC. 若m α⊥，//n β，且//αβ，则m n ⊥D. 若m α⊥，//n β，且αβ⊥，则m n ⊥ 【答案】C 【解析】 【分析】由空间中直线与直线、直线与平面及平面与平面位置关系逐一核对四个选项得答案． 【详解】由m ∥α，n ∥β，且α∥β，得m ∥n 或m 与n 异面，故A 错误； 由m ∥α，n ∥β，且α⊥β，得m ∥n 或m 与n 相交或m 与n 异面，故B 错误； 由m ⊥α，α∥β，得m ⊥β，又n ∥β，则m ⊥n ，故C 正确；由m ⊥α，n ∥β且α⊥β，得m ∥n 或m 与n 相交或m 与n 异面，故D 错误． 故选：C ．【点睛】本题考查命题的真假判断与应用，考查空间中直线与直线、直线与平面及平面与平面位置关系的判定与应用，考查空间想象能力与思维能力，属于中档题． 7.261(2)()x x x+-的展开式的常数项为( ) A. 25 B. 25-C. 5D. 5-【答案】B 【解析】 【分析】利用二项式定理的通项公式计算即可得出．【详解】61()x x -的展开式的通项公式为：T r +1＝r 6C （x ）6﹣r r1x ⎛⎫- ⎪⎝⎭=r 6C （x ）6﹣r()-r x -=r 6C ()1r -()6-2rx ．令6﹣2r ＝﹣2，或6﹣2r ＝0，分别解得r ＝4，或r ＝3．所以261(2)()x x x+-的展开式的常数项为()44611C ⨯-+2×()33611C ⨯-＝154025.-=-故选：B【点睛】本题考查了二项式定理的应用、方程思想方法，考查了推理能力与计算能力，属于基础题．8.将函数sin(4)6y x π=-图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把所得图象向左平移6π个单位长度，得到函数()f x 的图象，则函数()f x 的解析式为( ) A. ()sin(2)6f x x π=+ B. ()sin(2)3f x x π=-C. ()sin(8)6f x x π=+D. ()sin(8)3f x x π=-【答案】A 【解析】 【分析】利用函数的图象平移变换和伸缩变换的应用求出结果即可. 【详解】函数sin(4)6y x π=-图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到sin(2)6y x π=-的图象，再把所得图象向左平移6π个单位长度，得到函数f （x ）＝sin 2()sin(2)666y x x πππ⎡⎤=+-=+⎢⎥⎣⎦的图象.故选：A ．【点睛】本题考查了函数图象的平移和伸缩变换的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题．9.已知抛物线24y x =的焦点为F ，,M N 是抛物线上两个不同的点若5MF NF +=，则线段MN 的中点到y 轴的距离为( ) A. 3B.32C. 5D.52【答案】B 【解析】 分析】抛物线到焦点的距离转化为到准线的距离，可求出横坐标之和，进而求出中点的横坐标，求出结果即可.【详解】由抛物线方程24y x =，得其准线方程为：1x =-，设11(,)M x y ，22(,)N x y ，由抛物线的性质得，1211=5MF NF x x +=+++，MN ∴中点的横坐标为32， 线段MN 的中点到y 轴的距离为：32. 故选：B ．【点睛】本题考查了抛物线定义的应用，属于基础题． 10.已知122a =，133b =，3ln 2c =，则( ) A. a b c >> B. a c b >> C. b a c >> D. b c a >>【答案】C 【解析】 【分析】利用根式的运算性质、幂函数的单调性可得a ，b 的大小关系，利用对数函数的单调性即可得出c ＜1．【详解】∵122a ==＝，且133b ==＝，∴1a b <<，3lnln 12e <=．∴b a c >>． 故选：C ．【点睛】本题考查了根式的运算性质、幂函数的单调性、对数函数的单调性，属于基础题．11.已知定义在R 上的数()f x 满足112n n n b b -+-=，当2x ≤时()(1)1xf x x e =--.若关于x的方程()210f x kx k e -+-+=有三个不相等的实数根，则实数k 的取值范围是( ) A. (2,0)(2,)-+∞ B. (2,0)(0,2)-C. (,0)(,)e e -⋃+∞D. (,0)(0,)e e -⋃【答案】D 【解析】 【分析】根据f （2﹣x ）＝f （2+x ）可知函数f （x ）关于x ＝2对称，利用当2x ≤时()(1)1xf x x e =--，画出函数y ＝f （x ）的大致图象．由题意转化为y ＝k （x ﹣2）+e ﹣1与f （x ）有三个交点，直线恒过定点（2，e ﹣1），再根据数形结合法可得k 的取值范围． 【详解】由题意，当x ≤2时，f （x ）＝（x ﹣1）e x﹣1．f ′（x ）＝xe x．①令f ′（x ）＝0，解得x ＝0；②令f ′（x ）＜0，解得x ＜0；③令f ′（x ）＞0，解得0＜x ≤2．∴f （x ）在（﹣∞，0）上单调递减，在（0，2]上单调递增，在x ＝0处取得极小值f （0）＝﹣2．且f （1）＝﹣1；x →﹣∞，f （x ）→0．又∵函数f （x ）在R 上满足f （2﹣x ）＝f （2+x ），∴函数f （x ）的图象关于x ＝2对称． ∴函数y ＝f （x ）的大致图象如图所示：关于x 的方程f （x ）﹣kx +2k ﹣e +1＝0可转化为f （x ）＝k （x ﹣2）+e ﹣1．而一次函数y ＝k （x ﹣2）+e ﹣1很明显是恒过定点（2，e ﹣1）．结合图象，当k ＝0时，有两个交点，不符合题意，当k ＝e 时，有两个交点，其中一个是（1，﹣1）．此时y ＝f （x ）与y ＝k （x ﹣2）+e ﹣1正好相切．∴当0＜k ＜e 时，有三个交点．同理可得当﹣e ＜k ＜0时，也有三个交点． 实数k 的取值范围为：（﹣e ，0）∪（0，e ）． 故选：D ．【点睛】本题主要考查数形结合法的应用，利用导数分析函数的单调性并画出函数图象，再根据直线过定点而斜率变动分析出斜率的取值范围，属于中档题．12.如图，在边长为2的正方形123APP P 中，线段BC 的端点,B C 分别在边12PP 、23P P 上滑动，且22P B P C x ==，现将1APB ∆，3AP C ∆分别沿AB ，AC 折起使点13,P P 重合，重合后记为点P ，得到三被锥P ABC -.现有以下结论：①AP ⊥平面PBC ；②当,B C 分别为12PP 、23P P 的中点时，三棱锥P ABC -的外接球的表面积为6π； ③x 的取值范围为(0,42)-； ④三棱锥P ABC -体积的最大值为13. 则正确的结论的个数为( ) A. 1 B. 2C. 3D. 4【答案】C 【解析】 【分析】根据题意得,折叠成的三棱锥P ﹣ABC 的三条侧棱满足PA ⊥PB 、PA ⊥PC ，由线面垂直的判断定理得①正确；三棱锥P ﹣ABC 的外接球的直径等于以PA 、PB 、PC 为长、宽、高的长方体的对角线长，由此结合AP ＝2、BP ＝CP ＝1，得外接球的半径R 6P ﹣ABC 的外接球的体积，故②正确；由题意得(0,2)x ∈，2BC x =，312PC PB PB PC x ====-，在CPB ∆中，由边长关系得(0,422)-，故③正确；由等体积转化P ABC A PBC V V --=计算即可，故④错误.【详解】由题意得，折叠成的三棱锥P ﹣ABC 的三条侧棱满足PA ⊥PB 、PA ⊥PC ， 在①中，由PA ⊥PB ，PA ⊥PC ，且PB PC P =，所以AP ⊥平面PBC 成立，故①正确； 在②中，当,B C 分别为12PP 、23P P 的中点时，三棱锥P ﹣ABC 的三条侧棱两两垂直，三棱锥P ﹣ABC 的外接球直径等于以PA 、PB 、PC 为长、宽、高的长方体的对角线长，结合AP ＝2、BP ＝CP ＝1x =，得外接球的半径R 2246x x ++=，所以外接球的表面积为224462S Rπππ⎛==⨯=⎝⎭，故②正确；在③中，正方形123APP P的边长为2，所以(0,2)x∈，BC=，312PC PB PB PC x====-，在CPB∆中，由边长关系得2x-+2x->，解得(0,4x∈-，故③正确；在④中，正方形123APP P的边长为2，且22P B P C x==，则2PB PC x==-，所以()()222111sin223263 P ABC A PBCx V V CP BP CPB AP x---==⨯⨯⨯∠⨯≤⨯-⨯=在(0,4-上递减，无最大值，故④错误.故选：C【点睛】本题将正方形折叠成三棱锥，求三棱锥的外接球的表面积．着重考查了长方体的对角线长公式、等体积转化求三棱锥的体积最值等知识，属于中档题．二、填空题（本大题共4小题，每小题5分，共20分）13.已知实数,x y满足约束条件40220x yx yy+-≤⎧⎪-+≥⎨⎪≥⎩，则2z x y=+的最大值为_______.【答案】6【解析】【分析】作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z的最大值．【详解】作出实数x，y满足约束条件40220x yx yy+-≤⎧⎪-+≥⎨⎪≥⎩对应的平面区域如图：（阴影部分）由2z x y =+得y ＝﹣12x +12z ，平移直线y ＝﹣12x +12z ， 由图象可知当直线y ＝﹣12x +12z 经过点A 时，直线y ＝﹣12x +12z 的截距最大，此时z 最大．由40220x y x y +-=⎧⎨-+=⎩，解得A （2，2），代入目标函数z ＝x +2y 得z ＝2×2+2＝6.故答案：6．【点睛】本题主要考查线性规划的应用，利用图象平行求得目标函数的最大值和最小值，利用数形结合是解决线性规划问题中的基本方法，属于基础题．14.设正项等比数列{}n a 满足481a =，2336a a +=，则n a =_______. 【答案】3n 【解析】 【分析】将已知条件转化为基本量a 1，q 的方程组，解方程组得到a 1，q ，进而可以得到a n ． 【详解】在正项等比数列{}n a 中，481a =，2336a a +=，得312118136a q a q a q ⎧=⎨+=⎩，解得133a q =⎧⎨=⎩，∴a n ＝11n a q -⋅＝3•3n ﹣1＝3n . 故答案为：3n【点睛】本题考查了等比数列的通项公式，主要考查计算能力，属于基础题．15.已知平面向量a ，b 满足||2a =，||3b =，且()b a b ⊥-，则向量a 与b 的夹角的大小为_______. 【答案】6π【解析】 【分析】利用两个向量垂直的性质，两个向量的数量积的定义，求出向量a 与b 的夹角即可． 【详解】∵平面向量a ，b 满足||2a =，||3b =，且()b a b ⊥-，∴2()0b a b b a b ⋅-=⋅-=，∴2b a b ⋅=．设向量a 与b 的夹角的大小为θ，则，求得∵[]0,θπ∈ ，故θ＝6π. 故答案为：6π． 【点睛】本题主要考查两个向量垂直的性质，两个向量的数量积的定义，属于基础题．16.已知直线y kx =与双曲线2222:1(0,0)x y C a b a b-=>>相交于不同的两点,A B ，F 为双曲线C 的左焦点，且满足||3||AF BF =，||OA b =（O 为坐标原点），则双曲线C 的离心率为_______.【解析】 【分析】取双曲线的右焦点'F ，连接A 'F ，B 'F ，可得四边形A 'F BF 为平行四边形，运用双曲线的定义和平行四边形的对角线的平方和等于四条边的平方和，以及离心率公式可得所求值．【详解】设|BF |＝m ，则|||3||3AF BF m ==，取双曲线的右焦点'F ，连接A 'F ，B 'F ，可得四边形A 'F BF 为平行四边形，可得|A 'F |＝|BF |＝m ，设A 在第一象限，可得3m ﹣m ＝2a ，即m ＝a ，由平行四边形的对角线的平方和等于四条边的平方和，可得（2b ）2+（2c ）2＝2（a 2+9a 2），化为c 2＝3a 2，则e ＝ca【点睛】本题考查双曲线的定义、方程和性质，考查平行四边形的性质，以及化简运算能力，属于中档题．三、解答题（共70分.解答应写出文字说明、证明过程或演算步骤） 17.在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且22223b c a +-=. （1）求sin A 的值；（2）若ABC ∆223sin B C =，求ABC ∆的周长. 【答案】（1）13；（2）2632【解析】 【分析】（1）由已知条件结合余弦定理可求cos A 的值，进而根据同角三角函数基本关系式可求sin A 的值．（2）利用三角形的面积公式可求bc 2b ＝3c ，解得b ，c 的值，根据余弦定理可求a 的值，即可求解三角形的周长．【详解】（1）∵22223b c a +-=，∴由余弦定理可得2bc cos A 42bc ，∴cos A 22， ∴在△ABC 中，sin A 21cos A -＝13． （2）∵△ABC 2，即12bc sin A ＝16bc 2，∴bc ＝2， 2sin B ＝3sin C ，2b ＝3c ，∴b ＝2，c ＝2，则a 2＝b 2+c 2﹣2bc cos A ＝6，a∴=，所以周长为2a b c++=+.【点睛】本题主要考查了余弦定理，同角三角函数基本关系式，三角形的面积公式，正弦定理在解三角形中的综合应用，考查了计算能力和转化思想，属于中档题．18.某公司有1000名员工，其中男性员工400名，采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查，将计划在今年购买5G手机的员工称为“追光族"，计划在明年及明年以后才购买5G手机的员工称为“观望者”，调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.（1）完成下列22⨯列联表，并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关；（2）已知被抽取的这100名员工中有10名是人事部的员工，这10名中有3名属于“追光族”.现从这10名中随机抽取3名，记被抽取的3名中属于“追光族”的人数为随机变量X，求X 的分布列及数学期望.附22()()()()()n ad bcKa b c d a c b d-=++++，其中n a b c d=+++【答案】（1）表见解析，没有95%的把握认为该公司员工属于“追光族"与“性别"有关；（2）分布列见解析，()910E X = 【解析】 【分析】（1）根据题意，列出列联表，计算K 2，查表判断即可；（2）随机变量X 的所有可能取值为0，1，2，3，分布求出对应概率，列出分布列，求期望即可．【详解】（1）由题意得，2×2列联表如下：22100(20204020)25= 2.778406040609K ⨯⨯-⨯=≈⨯⨯⨯ 3.841<，故没有95%的把握认为该公司员工属于“追光族"与“性别"有关；（2）由题意得，随机变量X 的所有可能的取值为0，1，2，3，373107(0)24C P X C ===；123731021(1)40C C PX C ⋅===； 21373107(2)40C C P X C ⋅===； 333101(3)120C P X C ===.所以X 的分布列为P724 2140 740 112021719()123.404012010E X ∴=⨯+⨯+⨯= 【点睛】本题考查了独立性检验，考查了超几何分布，主要考查分析解决问题的能力和计算能力，属于中档题．19.如图，在四棱锥P ABCD - 中，AP ⊥平面PBC ，底面ABCD 为菱形，且60ABC ︒∠=，E 为BC 的中点.（1）证明：BC ⊥平面PAE ；（2）若2AB =，1PA =，求平面ABP 与平面CDP 所成锐二面角的余弦值. 【答案】（1）见解析；（233【解析】 【分析】（1）根据菱形基本性质得BC ⊥AE ，再由线面垂直得BC ⊥AP ，故BC ⊥平面PAE ；（2）以P 为坐标原点，,,PE PQ PA 的方向分别为x ，y ，z 轴建立空间直角坐标系，分别求出平面BAP 与平面CDP 的法向量计算即可.【详解】（1）连接AC ，因为底面ABCD 为菱形，且∠ABC ＝60°，所以△ABC 为正三角形， 因为E 为BC 的中点，所以BC ⊥AE ，又因为AP ⊥平面PBC ，BC ⊂平面PBC ， 所以BC ⊥AP ，因为AP ∩AE ＝A ，AP ，AE ⊂平面PAE ，所以BC ⊥平面PAE ；（2）因为AP ⊥平面PBC ，PB ⊂平面PBC ，所以AP ⊥PB ，又因为AB ＝2，PA ＝1，所以PB 3 由（1）得BC ⊥PE ，又因为E 为BC 中点，所以PB ＝PC 3EC ＝1，所以PE 2， 如图，过点P 作BC 的平行线PQ ，则PQ ，PE ，PA 两两互相垂直，以P 为坐标原点，,,PE PQ PA 的方向分别为x ，y ，z 轴建立如图所示的空间直角坐标系， 则P （0，0，0），A （0，0，1），B （2，﹣1，0），C （2，1，0），D （0，2，1）， 设平面BAP 的一个法向量m ＝（x ，y ，z ），又PA ＝（0，0，1），PB ＝（2，﹣1，0），由00m PA m PB ⎧⋅=⎨⋅=⎩，得2x ﹣y ＝0，z ＝0，令x ＝1，则m ＝（1，2，0），设平面CDP 的一个法向量n ＝（a ，b ，c ），又PC ＝（2，1，0），PD ＝（0，2，1），由00n PC n PD ⎧⋅=⎨⋅=⎩，得2a +b ＝0，2y +z ＝0，令a ＝1，则n ＝（1，﹣2，22）， 所以33cos ,311m n ==-⋅，即平面ABP 与平面CDP 所成锐二面角的余弦值为3333．【点睛】本题考查空间平面二面角问题，涉及证明线面垂直等知识点，建系是解决该类问题的常用方法，属于中档题． 20.已知函数()(1)ln af x a x x x=-++，.a R ∈ （1）讨论函数()f x 的单调性；（2）当1a <-时，证明：(1,)x ∀∈+∞，2().f x a a >-- 【答案】（1）答案不唯一，见解析；（2）见解析； 【解析】 【分析】（1）求出导数，讨论a 的取值范围，求出单调区间；（2）由（1）得函数函数()f x 在(1,)+∞内的最小值为()(1)ln()1f a a a a -=----，根据题意转化为2(1)ln()10a a a +--->在1a <-恒成立即可.【详解】（1）22221(1)(1)()()1a a x a x a x x a f x x x x x'-+---+=+-==,因为0,x a R >∈，当0a ≥时，0x a +>，函数()f x 在（0，1）内单调递减，在(1,)+∞内单调递增； 当10a -<<时，即01a <-<，函数()f x 在(0,)a -内单调递增，在(,1)a -内单调递减，在(1,)+∞内单调递增；当1a =-时，22(1)()0x f x x'-=，函数()f x 在(0,)+∞内单调递增； 当1a <-时，即1a ->，函数()f x 在（0，1）内单调递增，在(1,)a -内单调递减，在(,)a -+∞内单调递增；综上：当0a ≥时，()f x 在（0，1）内单调递减，在(1,)+∞内单调递增；当10a -<<时，()f x 在(0,)a -内单调递增，在(,1)a -内单调递减，在(1,)+∞内单调递增； 当1a =-时，()f x 在(0,)+∞内单调递增；当1a <-时，()f x 在（0，1）内单调递增，在(1,)a -内单调递减，在(,)a -+∞内单调递增. （2）当1a <-时，由（1）可得函数()f x 在(1,)a -内单调递减，在(,)a -+∞内单调递增，∴函数()f x 在(1,)+∞内的最小值为()(1)ln()1f a a a a -=----，要证：不等式2().f x a a >--成立， 即证：2(1)ln()1a a a a a --<----，即证：()2(1)ln()(1)1l 01n a a a a a a ⎡⎤+--=-++->⎣⎦-，1a <-，即证：()1ln 0a a ++-<， 令1(1)()ln 1(1),()10x h x x x x h x x x'--=-+≥=-=≤， 则函数()h x 在[1,)+∞内单调递减，()(1)0h x h ≤=，因1,1a a <-∴->，则()ln()10h a a a -=-++<，即当1a <-时，ln()1a a -<--成立 则当1a <-时，2(1,),()x f x a a ∀∈+∞>--成立.【点睛】本题考查利用导数求函数单调性，运用分类讨论思想是关键，涉及构造新函数求区间等问题，属于中档题．21.已知椭圆C :2212x y +=的右焦点为F ，过点F 的直线（不与x 轴重合）与椭圆C 相交于A ，B 两点，直线l ：2x =与x 轴相交于点H ，过点A 作AD l ⊥，垂足为D.（1）求四边形OAHB （O 为坐标原点）面积的取值范围； （2）证明直线BD 过定点E ，并求出点E 的坐标. 【答案】（1）；（2）证明见解析，3,02E ⎛⎫⎪⎝⎭【解析】 【分析】（1）由题意设直线AB 的方程，代入椭圆整理得纵坐标之和与之积，将四边形的面积分成2个三角形，根据底相同，列出关于面积的函数式，再结合均值不等式可得面积的取值范围； （2）由（1）得B ，D 的坐标，设直线BD 的方程，令纵坐标为零得横坐标是定值，即直线BD 过定点．【详解】（1）由题F （1,0），设直线AB ：()()11221(),,,,x my m R A x y B x y =+∈，联立22112x my x y =+⎧⎪⎨+=⎪⎩，消去x ，得()222210m y my ++-=， 因为()224420m m ∆=++>，12122221,22m y y y y m m +=-=-++， 则1z y y -=== 所以四边形OAHB的面积12121||2S OH y y y y =⋅-=-=，2,1,11t t S t t t=∴∴==++因为12t t+（当且仅当t=1即m =0时取等号），所以02S <，所以四边形OAHB 的面积取值范围为； （2）()()221,,2,B x y D y ，所以直线BD 的斜率1222y y k x -=-，所以直线BD 的方程为1212(2)2y y y y x x --=--，令y =0，可得212121212122,x y zy my y y y x y y y y -+-==--①由（1）可得121212122221,,222m y y y y y y my y m m +=-=-∴+=++ 化简①可得()()112121212123222z s y y y y y y x y y y y ++--===-- 则直线BD 过定点3,02E ⎛⎫⎪⎝⎭. 【点睛】本题考查了直线和椭圆的位置关系，四边形面积的取值范围，求直线的方程，证明直线过定点的等问题，考查运算能力，属于中档题．请考生在第22，23题中任选择一题作答，如果多做，则按所做的第一题记分，作答时，用2B 铅笔在答题卡上把所选题目对应的标号涂黑.22.在平面直角坐标系xOy 中，已知P 是曲线1C ：22(2)4x y +-=上的动点，将OP 绕点O 顺时针旋转90︒得到OQ ，设点Q 的轨迹为曲线2C .以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系.（1）求曲线1C ，2C 的极坐标方程； （2）在极坐标系中，点(3,)2M π，射线(0)6πθρ=≥与曲线1C ，2C 分别相交于异于极点O的,A B 两点，求MAB ∆的面积.【答案】（1）曲线1C ：4sin ρθ=，曲线2C ：4cos ρθ=；（2【解析】 【分析】（1）由题意，点Q 的轨迹是以（2，0）为圆心，以2为半径的圆，写出其普通方程，再结合ρ2＝x 2+y 2，x ＝ρcosθ，y ＝ρsinθ，可得曲线C 1，C 2的极坐标方程；（2）在极坐标系中，设A ，B 的极径分别为ρ1，ρ2，求得|AB |＝|ρ1﹣ρ2|，再求出M （3，2π）到射线()06πθρ=≥的距离h＝3sin 3π=，即可求得△MAB 的面积．【详解】（1）由题意，点Q 的轨迹是以（2，0）为圆心，以2为半径的圆，则曲线C 2：22(2)4x y -+=，∵ρ2＝x 2+y 2，x ＝ρcosθ，y ＝ρsinθ，∴曲线C 1的极坐标方程为ρ＝4sinθ，曲线C 2的极坐标方程为ρ＝4cosθ；（2）在极坐标系中，设A ，B 的极径分别为ρ1，ρ2，124sincos1).66AB ππρρ∴=-=-=又点(3,)2M π到射线(0)6πθρ=≥的距离为3sin32h π==MAB ∴∆的面积12S AB h =⋅= 【点睛】本题考查简单曲线的极坐标方程，考查参数方程化普通方程，考查计算能力，属于中档题．23.已知函数() 3.f x x =- （1）解不等式()421f x x ≥-+；（2）若142(0,0)m n m n+=>>，求证：3().2m n x f x +≥+-【答案】（1）2(,][0,)3-∞-⋃+∞；（2）见解析.【解析】 【分析】（1）原不等式可化为：|x ﹣3|≥4﹣|2x +1|，即|2x +1|+|x ﹣3|≥4，分段讨论求出即可；（2）由基本不等式得m n +的最小值92，转化为|x +32|﹣f （x ）≤92恒成立即可．【详解】（1）原不等式化为3421x x -≥-+，即213 4.x x ++-≥ ①12x ≤-时，不等式化为2134x x ---+≥，解得23x ≤-； ②132x -<<时，不等式化为2134x x +-+≥，解得0x ≥，03x ∴≤<；③3x ≥时，不等式化为2134x x ++-≥，解得2x ≥，3x ∴≥. 综上可得：原不等式解集为2(,][0,)3-∞-⋃+∞. （2）() 3.f x x =-3339()3(3)2222x f x x x x x ∴+-=+--≤+--=， 当且仅当3()(3)02x x +-≥且332x x +≥-时取等号.又142(0,0)m n m n +=>>，1141419()()(5)(52222n m m n m n m n m n ∴+=++=++≥+=， 当且仅当4n m m n=时取等号.∴3().2m n x f x +≥+- 【点睛】考查绝对值不等式的解法和绝对值不等式的性质，利用分类讨论的思想结合绝对值的性质和基本不等式的应用，属于中档题．。

四川省成都市2020届高中毕业班第一诊断性检测文科数学试题参考答案1．B 【分析】由题意得复数z 1与23z i =--的实部相等，虚部互为相反数，则z 1可求． 【解析】∵复数z 1与23z i =--（i 为虚数单位）在复平面内对应的点关于实轴对称，∴复数z 1与23z i =--（i 为虚数单位）的实部相等，虚部互为相反数，则z 1＝3i -+．故选：B ．2．D 【分析】因为{1,0,1,2}AB =-，A ，B 本身含有元素1-，0，1，2，根据元素的互异性1m ≠-，0，求出m 即可．【解析】解：集合{1A =-，0，}m ，{1B =，2}，{1,0,1,2}AB =-，因为A ，B 本身含有元素1-，0，1，2，所以根据元素的互异性，1m ≠-，0即可， 故1m =或2，故选：D ．3．C 【分析】根据sin θθ=得到tan θ=.【解析】sin tan θθθ=∴=22tan tan 21tan 42θθθ===---故选：C 4．D 【分析】直接利用全称命题的否定定义得到答案.【解析】命题p ：x R ∀∈，221x x -≥，则p ⌝为： 0x R ∃∈，02021x x -<故选：D5．A 【分析】根据频率分布直方图求得中位数即可.【解析】在频率分步直方图中，小正方形的面积表示这组数据的频率，∴中位数为：0.50.01100.0310701072.50.0410-⨯-⨯+⨯=⨯.故选：A6．D 【分析】将S 9，S 5转化为用a 5，a 3表达的算式即可得到结论.【解析】解：依题意，19951553992552a a S a a a S a +⨯==+⨯，又533a a =，∴95927355S S =⨯=，故选：D .7．C 【分析】由空间中直线与直线、直线与平面及平面与平面位置关系逐一核对四个选项得答案．【解析】由m ∥α，n ∥β，且α∥β，得m ∥n 或m 与n 异面，故A 错误；由m ∥α，n ∥β，且α⊥β，得m ∥n 或m 与n 相交或m 与n 异面，故B 错误； 由m ⊥α，α∥β，得m ⊥β，又n ∥β，则m ⊥n ，故C 正确；由m ⊥α，n ∥β且α⊥β，得m ∥n 或m 与n 相交或m 与n 异面，故D 错误．故选：C ． 8．A 【分析】利用函数的图象平移变换和伸缩变换的应用求出结果即可. 【解析】函数sin(4)6y x π=-图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到sin(2)6y x π=-的图象，再把所得图象向左平移6π个单位长度，得到函数f （x ）＝sin 2()sin(2)666y x x πππ⎡⎤=+-=+⎢⎥⎣⎦的图象.故选：A ．9．B 【分析】抛物线到焦点的距离转化为到准线的距离，可求出横坐标之和，进而求出中点的横坐标，求出结果即可.【解析】由抛物线方程24y x =，得其准线方程为：1x =-，设11(,)M x y ，22(,)N x y ，由抛物线的性质得，1211=5MF NF x x +=+++，MN ∴中点的横坐标为32， 线段MN 的中点到y 轴的距离为：32.故选：B ． 10．C 【分析】利用根式的运算性质、幂函数的单调性可得a ，b 的大小关系，利用对数函数的单调性即可得出c ＜1．【解析】∵122a ==，且133b =∴1a b <<，3lnln 12e <=．∴b a c >>．故选：C ． 11．B 【分析】设F '是右焦点，利用对称性，得3AF AF '=，由双曲线定义得,|3AF a AF a '==，然后利用AOF AOF π'∠+∠=可得出关于,,a b c 的关系式，从而求得离心率e ．【解析】设F '是右焦点，则BF AF '=，3AF BF =，即3AF AF '=，又22AF AF AF a ''-==，∴AF a '=，3AF a =，而,OA b OF c '==，∴OA AF '⊥，由AOF AOF π'∠+∠=得cos cos 0AOF AOF '∠+∠=，∴222902b c a bbc c+-+=，整理得3==c e a ．故选：B ．12．A 【分析】根据函数的单调性和对称性画出函数图像，()22y k x =-+过定点()2,2，计算直线和曲线相切的情况计算斜率得到答案. 【解析】当2x ≤时，()()()'1xxf x xe f x x e =∴=+函数在(),1-∞-上单调递减，在()1,2-上单调递增，且()11f e-=-()()22f x f x -=+，函数关于2x =对称，()22y k x =-+过定点()2,2如图所示，画出函数图像：当()22y k x =-+与()xf x xe =相切时，设切点为()00,x y则()000000022122x x y x e x e k x x --+===-- 根据对称性考虑2x =左边图像，根据图像验证知00x =是方程唯一解，此时1k = 故答案为()()1,00,1k ∈-⋃故选：A13．6【分析】作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z 的最大值．【解析】作出实数x ，y 满足约束条件402200x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩对应的平面区域如图：（阴影部分）由2z x y =+得y ＝﹣12x +12z ，平移直线y ＝﹣12x +12z ， 由图象可知当直线y ＝﹣12x +12z 经过点A 时，直线y ＝﹣12x +12z 的截距最大，此时z最大．由40220x y x y +-=⎧⎨-+=⎩，解得A （2，2），代入目标函数z ＝x +2y 得z ＝2×2+2＝6. 故答案为：6．14．3n 【分析】将已知条件转化为基本量a 1，q 的方程组，解方程组得到a 1，q ，进而可以得到a n ．【解析】在正项等比数列{}n a 中，481a =，2336a a +=，得312118136a q a q a q ⎧=⎨+=⎩，解得133a q =⎧⎨=⎩，∴a n ＝11n a q -⋅＝3•3n ﹣1＝3n . 故答案为：3n15．6π【分析】由题意利用两个向量垂直的性质，两个向量的数量积的定义，求出向量a 与b 的夹角的大小．【解析】解：平面向量a ，b 满足||2a =，||3b =，且()b a b ⊥-，∴2()0b a b b a b -=-=，∴2a b b =．设向量a 与b 的夹角的大小为θ，则23cos 3θ=， 求得[]cos 0,π2θθ=∈，故6πθ=，故答案为：6π． 16【分析】根据,,PAPB PC 两两垂直得到2R =得到答案.【解析】易知,,PA PB PC 两两垂直，2,1PA PB PC ===将三棱锥P ABC -放入对应的长方体内得到2R R ==343V R π==17．【分析】（1）由已知条件结合余弦定理可求cos A 的值，进而根据同角三角函数基本关系式可求sin A 的值．（2）利用三角形的面积公式可求bc 的值，b ＝3c ，解得b ，c 的值，根据余弦定理可求a 的值，即可求解三角形的周长． 【解析】（1）∵2223b c a +-=，∴由余弦定理可得2bc cosA bc ，∴cosA ＝，∴在△ABC 中，sin A ＝13．（2）∵△ABC ，即12bc sin A ＝16bc ，∴bc ＝，又sin B ＝3sin C ，b ＝3c ，∴b ＝，c ＝2，则a 2＝b 2+c 2﹣2bc cos A ＝6，a ∴=2abc ++=+18．【分析】（Ⅰ）完善列联表，计算2 2.778 3.841K ≈<得到结论.（Ⅱ）设人事部的这6名中的3名“追光族”分别为“a ，b ，c ”，3名“观望者”分别为“A ，B ，C ，列出所有情况计算得到答案.【解析】（Ⅰ）由题，22⨯列联表如下：∵()221002020204025 2.778 3.841406040609K ⨯-⨯==≈<⨯⨯⨯，∴没有95%的把握认为该公司员工属于“追光族”与“性別”有关.（Ⅱ）设人事部的这6名中的3名“追光族”分别为“a ，b ，c ”，3名“观望者”分别为“A ，B ，C ”.则从人事部的这6名中随机抽取3名的所有可能情况有“,,a b c ；,,a b A ；,,a b B ；,,a b C ；,,a c A ；,,a c B ；,,a c C ；,,b c A ；,,b c B ；,,b c C ；,,a A B ；,,a A C ；,,a B C ；,,b A B ；,,b A C ；,,b B C ；,,c A B ；,,c A C ；,,c B C ；,,A B C ”共20种.其中，抽取到的3名中恰有1名属于“追光族”的所有可能情况有“,,a A B ；,,a A C ；,,a B C ；,,b A B ；,,b A C ；,,b B C ；,,c A B ；,,c A C ；,,c B C ”共9种.∴抽取到的3名中恰有1名属于“追光族”的概率920P =.19．【分析】（Ⅰ）证明BC AE ⊥和BC AP ⊥得到BC ⊥平面PAE . （Ⅱ）根据相似得到PDQM 证明PD 平面QAF .【解析】（Ⅰ）如图，连接AC .∵底面ABCD 为菱形，且60ABC ∠=︒， ∴三角形ABC 为正三角形.∵E 为BC 的中点，∴BC AE ⊥.又∵AP ⊥平面PBC ，BC ⊂平面PBC ， ∴BC AP ⊥. ∵APAE A =，,AP AE ⊂平面PAE ，∴BC ⊥平面PAE .（Ⅱ）连接BD 交AF 于点M ，连接QM . ∵F 为CD 的中点，∴在底面ABCD 中，12DM DF MB AB ==，∴13DM DB =. ∴13PQ DM PB DB ==，∴在三角形BPD 中，//PD QM . 又∵QM ⊂平面QAF ，PD ⊄平面QAF ， ∴//PD 平面QAF .20．【分析】（1）求出2(1)()()x x a f x x -+'=，然后分0a ≥、10a -<<、1a =-、1a <-四种情况讨论即可；（2）当2a =时，令212()1h x lnx x x=-+-，利用导数求出()0max h x =即可证明. 【解析】（1）22221(1)(1)()()1a a x a x a x x a f x x x x x-+---+'=+-==， 因为0x >，a R ∈，所以当0a ≥时，0x a +>，函数()f x 在(0,1)上单调递减，在(1,)+∞上单调递增； 当10a -<<时，01a <-<，函数()f x 在(0,)a -上单调递增，在(,1)a -上单调递减，在(1,)+∞上单调递增；当1a =-时，22(1)()0x f x x-'=≥，函数()f x 在(0,)+∞上单调递增； 当1a <-时，1a ->，函数()f x 在(0,1)上单调递增，在(1,)a -上单调递减，在(,)a -+∞上单调递增.（2）当2a =时，2()f x lnx x x =++，则212()1f x x x'=+-，[]1,2x ∈， 所以2212()()1f x f x x lnx x x x-'--=-+-， 令212()1h x lnx x x =-+-，则22331144()x x h x x x x x +-'=+-=，令2()4u x x x =+-，因为函数()u x 在[1，2]上单调递增，u （1）0<，u （2）0>， 所以存在唯一的0(1,2)x ∈，使得0()0h x '=，因为当0(1,)x x ∈时，0()0h x '<，当0(x x ∈，2)时，00()h x '>， 所以函数()h x 在0(1,)x 上单调递减，在0(x ，2)上单调递增， 又因为h （1）0=，h （2）210ln =-<，所以()0max h x =， 即2()()f x f x x x-'≤+对任意的[1x ∈，2]都成立. 21．【分析】（Ⅰ）令直线AB ：()1x my m R =+∈，联立方程利用韦达定理得到12222m y y m +=-+，12212y y m =-+，22S m =+t =带入化简得到答案.（Ⅱ）直线BE 的方程为223322y y x x ⎛⎫=- ⎪⎝⎭-，令2x =得，221212D y y my =-.代入（Ⅰ）中式子化简得到答案.【解析】（Ⅰ）由题，()1,0F ，令直线AB ：()1x my m R =+∈，()11,A x y ，()22,B x y .联立22112x my x y =+⎧⎪⎨+=⎪⎩消去x ，得()222210m y my ++-=. ∵()224420m m ∆=++>，12222m y y m +=-+，12212y y m =-+，∴12y y -===∴四边形OAHB 的面积211212S OH y y y y =⋅-=-=t =，∴1t ≥，∴S t t==+∵12t t+≥（当且仅当1t =即0m =时取等号），∴0S <≤.∴四边形OAHB 面积的取值范围为(.（Ⅱ）∵()2,0H ，()1,0F ，∴3,02E ⎛⎫⎪⎝⎭. ∴直线BE 的斜率2232y k x =-，直线BE 的方程为223322y y x x ⎛⎫=- ⎪⎝⎭-. 令2x =得，221212D y y my =-.……①由（Ⅰ），12222m y y m +=-+，12212y y m =-+. ∴12122y y my y +=，1222111222y y y my y y +==+. 化简①，得22122111221112222D y y y y y my y ===-+-. ∴直线AD 与x 轴平行.22．【分析】（1）由题意，点Q 的轨迹是以（2，0）为圆心，以2为半径的圆，写出其普通方程，再结合ρ2＝x 2+y 2，x ＝ρcosθ，y ＝ρsinθ，可得曲线C 1，C 2的极坐标方程； （2）在极坐标系中，设A ，B 的极径分别为ρ1，ρ2，求得|AB |＝|ρ1﹣ρ2|，再求出M （3，2π）到射线()06πθρ=≥的距离h＝3sin 3π=，即可求得△MAB 的面积．【解析】（1）由题意，点Q 的轨迹是以（2，0）为圆心，以2为半径的圆，则曲线C 2：22(2)4x y -+=，∵ρ2＝x 2+y 2，x ＝ρcosθ，y ＝ρsinθ，∴曲线C 1的极坐标方程为ρ＝4sinθ，曲线C 2的极坐标方程为ρ＝4cosθ；（2）在极坐标系中，设A ，B 的极径分别为ρ1，ρ2，124sincos1).66AB ππρρ∴=-=-=又点(3,)2M π到射线(0)6πθρ=≥的距离为3sin32h π==MAB ∴∆的面积12S AB h =⋅= 23．【分析】（1）原不等式可化为：|x ﹣3|≥4﹣|2x +1|，即|2x +1|+|x ﹣3|≥4，分段讨论求出即可；（2）由基本不等式得m n +的最小值92，转化为|x +32|﹣f （x ）≤92恒成立即可．【解析】（1）原不等式化为3421x x -≥-+，即213 4.x x ++-≥ ①12x ≤-时，不等式化为2134x x ---+≥，解得23x ≤-；②132x -<<时，不等式化为2134x x +-+≥，解得0x ≥，03x ∴≤<； ③3x ≥时，不等式化为2134x x ++-≥，解得2x ≥，3x ∴≥. 综上可得：原不等式解集为2(,][0,)3-∞-⋃+∞.（2）() 3.f x x =-3339()3(3)2222x f x x x x x ∴+-=+--≤+--=， 当且仅当3()(3)02x x +-≥且332x x +≥-时取等号.又142(0,0)m n m n+=>>，1141419()()(5)(52222n m m n m n m n m n ∴+=++=++≥+=， 当且仅当4n mm n=时取等号.∴3().2m n x f x +≥+-。

成都市2020届高中毕业班第一次诊断性检测语文注意事项：1.答卷前，务必将自己的姓名、考籍号填写在答题卡规定的位置上。

2.答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3.答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上4.所有题目必须在答题卡上作答，在试题卷上答题无效。

5.考试结束后，只将答题卡交回。

一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1~3题。

家庭在西洋是一种界服分明的团体。

在英美，家庭包括他和他的妻以及未成年的孩子而在我们中国“家里的”可以指自己的太太一个人，“家门”可以指叔伯侄子一大批，“自家人”可以包罗任何要拉入自己的图子，表示亲热的人物这表示了我们的社会结构本身和西洋的不同，我们的格局不是一捆一捆扎清楚的柴，而是好像把一块石头丢在水面上所发生的一圈圈推出去的波纹，愈推愈远，愈推愈簿。

每个人都是他社会影响所推出去的圈子的中心。

被圈子的波纹所推及的就发生联系我们社会中最重要的亲属关系就是这种丢石头形成同心圆波纹的性质。

从生育和婚姻所结成的网络，可以一直推出去包括无穷的人。

这个网络像个蜘蛛的网，有一个中心，就是自己我们每个人都有这么一个以亲属关系布出去的网，但是没有一个网所平住的人是相同的。

以亲属关系所联系成的社会关系的每一个网络有个“己”作为中心，各个网络的中心都不同在乡土社会里，地缘关系也是如此。

每一家以自己的地位做中心，周围划出一个圈子，这个圈子是“街坊”。

可是这不是一个固定的团体，而是一个范围。

范围的大小也要依着中心的势力厚薄而定。

有势力的人家的街坊可以遍及全村，穷苦人家的街坊只是比邻的两三家。

中国传统结构中的差序格局具有这种伸縮能力。

中国人也特别对世态炎凉有感触，正因为这富于伸缩的社会圈子会因中心势力的变化而大小。

儒家最考究的是人伦。

“伦”重在分别，在《礼记·祭统》所讲的十伦，鬼神、君臣、父子、贵贱、亲疏、爵赏、夫妇、政事、长幼、上下，都是指差等。

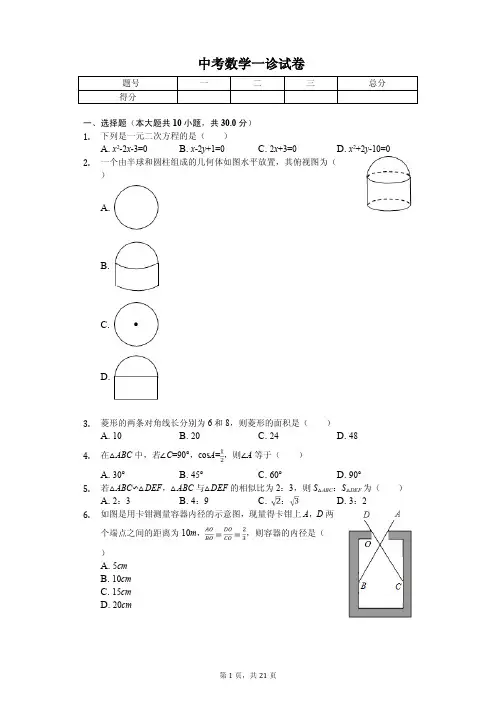
中考数学一诊试卷题号一二三总分得分一、选择题（本大题共10小题，共30.0分）1.下列是一元二次方程的是（ ）A. x2-2x-3=0B. x-2y+1=0C. 2x+3=0D. x2+2y-10=02.一个由半球和圆柱组成的几何体如图水平放置，其俯视图为（ ）A.B.C.D.3.菱形的两条对角线长分别为6和8，则菱形的面积是（ ）A. 10B. 20C. 24D. 484.在△ABC中，若∠C=90°，cos A=，则∠A等于（ ）A. 30°B. 45°C. 60°D. 90°5.若△ABC∽△DEF，△ABC与△DEF的相似比为2：3，则S△ABC：S△DEF为（ ）A.2：3 B. 4：9 C. ： D. 3：26.如图是用卡钳测量容器内径的示意图，现量得卡钳上A，D两个端点之间的距离为10m，，则容器的内径是（ ）A. 5cmB. 10cmC. 15cmD. 20cm7.如图，已知AB∥CD∥EF，BD：DF=2：5，那么下列结论正确的是（ ）A. AC：EC=2：5B. AB：CD=2：5C. CD：EF=2：5D. AC：AE=2：58.某超市一月份营业额为100万元，一月、二月、三月的营业额共500万元，如果平均每月增长率为x，则由题意可列方程（ ）A. 100（1+x）2=500B. 100+100•2x=500C. 100+100•3x=500D. 100[1+（1+x）+（1+x）2]=5009.在同一坐标系中，函数y=和y=kx+3（k≠0）的图象大致是（ ）A. B.C. D.10.如图，⊙O的半径OD垂直于弦AB，垂足为点C，连接AO并延长交⊙O于点E，连接BE，CE．若AB=8，CD=2，则△BCE的面积为（ ）A. 12B. 15C. 16D. 18二、填空题（本大题共9小题，共36.0分）11.若，则=______．12.抛物线y=x2-4x-4的顶点坐标是______．13.设A（x1，y1），B（x2，y2）是反比例函数y=-图象上的两点，若x1＜x2＜0，则y1与y2之间的关系是______．14.如图，在平行四边形ABCD中，按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB，AD于点M，N；②分别以M，N为圆心，以大于MN的长为半径作弧，两弧相交于点P；③作AP射线，交边CD于点Q．若QC=1，BC=3，则平行四边形ABCD周长为______15.设a、b是方程x2+x-2021=0的两个实数根，则（a-1）（b-1）的值为______．16.在一个不透明的袋中装有若干个红球，为了估计袋中红球的个数，小明在袋中放入3个黑球（每个球除颜色外其余都与红球相同），摇匀后每次随机从袋中摸出一个球，记下颜色后放回袋中，通过大量重复摸球试验后发现，摸到红球的频率稳定在0.85左右，则袋中红球约有______个．17.已知一列数a1，a2，…，a n（n为正整数）满足a1=1，a2==，…，a n=，请通过计算推算a2019=______，a n=______．（用含n的代数式表示）18.如图，点A在双曲线y=（k≠0）的第一象限的分支上，AB垂直x轴于点B，点C在x轴正半轴上，OC=2AB，点E在线段AC上，且AE=3EC，点D为OB的中点，连接CD，若△CDE的面积为1，则k的值为______．19.如图，矩形ABCD中，AB=3，BC=4，点E是A边上一点，且AE=，点F是边BC上的任意一点，把△BEF沿EF翻折，点B的对应点为G，连接AG，CG，则四边形AGCD的面积的最小值为______．三、解答题（本大题共9小题，共84.0分）20.（1）计算：（π-2）0-2cos30°-（2）解方程：x2-5x+4=0．21.已知：如图，M为平行四边形ABCD边AD的中点，且MB=MC．求证：四边形ABCD是矩形．22.小明在热气球A上看到正前方横跨河流两岸的大桥BC，并测得B，C两点的俯角分别为45°，35°．已知大桥BC与地面在同一水平面上，其长度为100m，请求出热气球离地面的高度．（结果保留整数）（参考数据：sin35°≈，cos35°≈，tan35°≈）23.今年猪肉价格受非洲猪瘟疫情影响，有较大幅度的上升，为了解某地区养殖户受非洲猪瘟疫情感染受灾情况，现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查（把调查结果分为四个等级：A级：非常严重；B级：严重；C级：一般；D 级：没有感染），并将调查结果绘制成如下两幅不完整的统计图．请根据统计图中的信息解决下列问题：（1）本次抽样调查的养殖户的总户数是______；把图2条形统计图补充完整．（2）若该地区建档的养殖户有1500户，求非常严重与严重的养殖户一共有多少户？（3）某调研单位想从5户建档养殖户（分别记为a，b，c，d，e）中随机选取两户，进一步跟踪监测病毒传播情况，请用列表或画树状图的方法求出选中养殖户e的概率．24.如图，在平面直角坐标系中，一次函数y=-x+m的图象与反比例函数y=（x＞0）的图象交于A、B两点，已知A（2，4）.（1）求一次函数和反比例函数的解析式；（2）求B点的坐标；（3）连接AO、BO，求△AOB的面积．25.如图，△ABC内接于⊙O，AB是直径，过点A作直线MN，且∠MAC=∠ABC．（1）求证：MN是⊙O的切线．（2）设D是弧AC的中点，连结BD交AC于点G，过点D作DE⊥AB于点E，交AC于点F．①求证：FD=FG．②若BC=3，AB=5，试求AE的长．26.为建设天府新区“公园城市”，实现城市生活垃圾减量化、资源化、无害化的目标．近日，成都市天府新区计划在各社区试点实施生活垃圾分类处理活动，取得市民积极响应．某创业公司发现这一商机，研发生产了一种新型家庭垃圾分类桶，并投入市场试营销售．已知该新型垃圾桶成本为每个40元，市场调查发现，该垃圾桶每件售价y（元）与每天的销售量为x（个）的关系如图．为推广新产品及考虑每件利润因素，公司计划每天的销售量不低于1000件且不高于2000件．（1）求每件销售单价y（元）与每天的销售量为x（个）的函数关系式；（2）设该公司日销售利润为W（元），求每天的最大销售利润是多少元？27.已知，在△ABC和△EFC中，∠ABC=∠EFC=90°，点E在△ABC内，且∠CAE+∠CBE=90°（1）如图1，当△ABC和△EFC均为等腰直角三角形时，连接BF，①求证：△CAE∽△CBF；②若BE=2，AE=4，求EF的长；（2）如图2，当△ABC和△EFC均为一般直角三角形时，若=k，BE=1，AE=3，CE=4，求k的值．28.已知，如图，抛物线y=ax2+bx+c（a≠0）的顶点为M（1，9），经过抛物线上的两点A（-3，-7）和B（3，m）的直线交抛物线的对称轴于点C．（1）求抛物线的解析式及点B的坐标．（2）在抛物线上A，M两点之间的部分（不包含A，M两点），是否存在点D，使得S△DAC=2S△DCM？若存在，求出点D的坐标；若不存在，请说明理由．（3）上下平移直线AB，设平移后的直线与抛物线交与A′，B′两点（A′在左边，B'在右边），且与y轴交与点P（0，n），若∠A′MB′=90°，求n的值．答案和解析1.【答案】A【解析】解：A、是一元二次方程，故此选项正确；B、是二元一次方程，故此选项错误；C、是一元一次方程，故此选项错误；D、是二元二次方程，故此选项错误；故选：A．根据一元二次方程的定义即可求出答案．此题主要考查了一元二次方程定义，判断一个方程是否是一元二次方程应注意抓住5个方面：“化简后”；“一个未知数”；“未知数的最高次数是2”；“二次项的系数不等于0”；“整式方程”．2.【答案】A【解析】解：这个几何体的俯视图为：故选：A．根据俯视图是指从几何体的上面观察得出的图形作答．本题考查了简单几何体的三视图，能理解三视图的定义是解此题的关键．3.【答案】C【解析】【分析】此题考查了菱形的性质．菱形的面积等于对角线积的一半是解此题的关键．由菱形的两条对角线的长分别是6和8，根据菱形的面积等于对角线积的一半，即可求得答案．【解答】解：∵菱形的两条对角线的长分别是6和8，∴这个菱形的面积是：×6×8=24．故选C．4.【答案】C【解析】解：∵△ABC中，∠C=90°，cos A=，∴∠A=60°．故选：C．根据∠A为△ABC的内角，且∠C=90°可知∠A为锐角，再根据cos A=即可求出∠A的度数．本题比较简单，考查的是直角三角形的性质及特殊角的三角函数值．5.【答案】B【解析】解：因为△ABC∽△DEF，所以△ABC与△DEF的面积比等于相似比的平方，所以S△ABC：S△DEF=（）2=，故选B．因为两相似三角形的面积比等于相似比的平方，所以．本题比较容易，考查了两个相似三角形面积比等于相似比的平方的性质．6.【答案】C【解析】解：连接AD、BC，∵，∠AOD=∠BOC，∴△AOD∽△BOC，∴==，∵A，D两个端点之间的距离为10m，∴BC=15m，故选：C．首先连接AD、BC，然后判定△AOD∽△BOC，根据相似三角形的性质可得==，进而可得答案．此题主要考查了相似三角形的应用，关键是掌握相似三角形的判定和性质．7.【答案】A【解析】解：∵AB∥CD∥EF，∴AC：EC=BD：DF=2：5，AC：AE=BD：BF=2：7．故选：A．根据平行线分线段成比例定理对各选项进行判断．本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．8.【答案】D【解析】解：设平均每月增长率为x，100[1+（1+x）+（1+x）2]=500．故选：D．如果平均每月增长率为x，根据某超市一月份营业额为100万元，一月、二月、三月的营业额共500万元，可列方程．本题考查理解题意的能力，分别求出一，二，三月份的，以总和为等量关系列出方程．9.【答案】C【解析】解：分两种情况讨论：①当k＞0时，y=kx+3与y轴的交点在正半轴，过一、二、三象限，y=的图象在第一、三象限；②当k＜0时，y=kx+3与y轴的交点在正半轴，过一、二、四象限，y=的图象在第二、四象限．故选C．根据一次函数和反比例函数的特点，k≠0，所以分k＞0和k＜0两种情况讨论．当两函数系数k取相同符号值，两函数图象共存于同一坐标系内的即为正确答案．本题主要考查了反比例函数的图象性质和一次函数的图象性质，关键是由k的取值确定函数所在的象限．10.【答案】A【解析】解：∵⊙O的半径OD垂直于弦AB，垂足为点C，AB=8，∴AC=BC=AB=4．设OA=r，则OC=r-2，在Rt△AOC中，∵AC2+OC2=OA2，即42+（r-2）2=r2，解得r=5，∴AE=10，∴BE===6，∴△BCE的面积=BC•BE=×4×6=12．故选：A．先根据垂径定理求出AC的长，再设OA=r，则OC=r-2，在Rt△AOC中利用勾股定理求出r的值，再求出BE的长，利用三角形的面积公式即可得出结论．本题考查的是圆周角定理，熟知直径所对的圆周角是直角是解答此题的关键．11.【答案】【解析】解：∵=，∴3（x+y）=5y，∴3x=2y，∴=．故答案为：．根据两内项之积等于两外项之积列式整理即可．本题考查了比例的性质，主要利用了两内项之积等于两外项之积的性质，需熟记．12.【答案】（2，-8）【解析】解：解法1：利用公式法y=ax2+bx+c的顶点坐标公式为（，），代入数值求得顶点坐标为（2，-8）；解法2：利用配方法y=x2-4x-4=x2-4x+4-8=（x-2）2-8，所以顶点的坐标是（2，-8）．故答案为：（2，-8）．本题可以运用配方法求顶点坐标，也可以根据顶点坐标公式求坐标．本题考查求抛物线的顶点坐标、对称轴的方法．13.【答案】y2＞y1＞0【解析】解：∵反比例函数y=-中，k=-2＜0，∴函数图象的两个分支位于二、四象限，且在每一象限内y随x的增大而增大，∵x1＜x2＜0，∴y2＞y1＞0．故答案为：y2＞y1＞0．先根据反比例函数的解析式判断出函数图象所在的象限，再根据x1＜x2＜0即可得出结论．本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．14.【答案】14【解析】解：∵由作图可知，AQ是∠DAB的平分线，∴∠DAQ=∠BAQ．∵四边形ABCD是平行四边形，∴CD∥AB，BC=AD=3，∠BAQ=∠DQA，∴∠DAQ=∠DQA，∴△AQD是等腰三角形，∴DQ=AD=3．∵QC=1，∴CD=DQ+CQ=3+1=4，∴平行四边形ABCD周长=2（DC+AD）=2×（4+3）=14．故答案为：14．根据角平分线的性质可知∠DAQ=∠BAQ，再由平行四边形的性质得出CD∥AB，BC=AD=3，∠BAQ=∠DQA，故可得出△AQD是等腰三角形，据此可得出DQ=AD，进而可得出平行四边形ABCD周长．本题考查的是复杂作图，解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．15.【答案】-2019【解析】解：∵a、b是方程x2+x-2021=0的两个实数根，∴a+b=-1，ab=-2021，∴（a-1）（b-1）=ab-（a+b）+1=-2021+1+1=-2019，故答案为：-2019．根据根与系数的关系得出a+b=-1，ab=-2021，再代入计算即可．本题主要考查根与系数的关系，熟练掌握根与系数的关系是解题的关键．16.【答案】17【解析】解：通过大量重复摸球试验后发现，摸到红球的频率稳定在0.85左右，口袋中有3个黑球，∵假设有x个红球，∴=0.85，解得：x=17，经检验x=17是分式方程的解，∴口袋中有红球约有17个．故答案为：17．根据口袋中有3个黑球，利用小球在总数中所占比例得出与实验比例应该相等求出即可．此题主要考查了用样本估计总体，根据已知得出小球在总数中所占比例得出与实验比例应该相等是解决问题的关键．17.【答案】【解析】解：根据题意得，a1=1=；a2=；a3==；…发现规律：∴a n=．∴a2019==．故答案为：，．根据题意先计算出前几个数，发现规律即可求解．本题考查了规律型-数字的变化类，解决本题的关键是写出前几个数之后，寻找规律，总结规律，运用规律．18.【答案】【解析】解：设A（a，b），∵OC=2AB，点D为OB的中点，∴C（2a，0），D（0，b），∵AE=3EC，△CDE的面积为1，∴S△ADC=4S△CDE=4，∵S梯形ABOC=S△ABD+S△OCD+S△ADC，∴（a+2a）•b=•a•b+•2a•b+4，∴ab=，∵点A在双曲线y=（k≠0）的图象上，∴k=．故答案为．设A（a，b），则C（2a，0），D（0，b），根据三角形面积公式，由AE=3EC得到S△ADC=4S△CDE=4，由于S梯形ABOC=S△ABD+S△OCD+S△ADC，则（a+2a）•b=•a•b+•2a•b+4，整理得ab=，然后根据反比例函数图象上点的坐标特征即可得到k=．本题考查了反比例函数系数k的几何意义：在反比例函数y=图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．也考查了反比例函数图象上点的坐标特征．19.【答案】【解析】解：如图，在矩形ABCD中，AB=3，BC=4，∠B=∠D=90°，连接AC，∴AC=5，∵AB=3，AE=，∴点F是边BC上的任意位置时，点G始终在AC的下方，设点G到AC的距离为h，S四边形AGCD=S△ACD+S△ACG=3×4+×5h，=6+h．要使四边形AGCD的面积的最小，即h最小．∵点G在以点E为圆心，BE为半径的圆上，且在矩形ABCD的内部．过点E作EH⊥AC，交圆E于点G，此时h最小．在Rt△ABC中，sin∠BAC==，在Rt△AEH中，AE=，sin∠BAC==，解得EH=AE=，EG=BE=AB-AE=3-，∴h=EH-EG=-（3-）=-3．∴S四边形AGCD=6+×（-3）=-=．故答案为：．根据矩形ABCD中，AB=3，BC=4，可得AC=5，由AE=可得点F是边BC上的任意位置时，点C始终在AC的下方，设点G到AC的距离为h，要使四边形AGCD的面积的最小，即h最小．所以点G在以点E为圆心，BE为半径的圆上，且在矩形ABCD的内部．过点E作EH⊥AC，交圆E于点G，此时h最小．根据锐角三角函数先求得h的值，再分别求得三角形ACD和三角形ACG的面积即可得结论．本题考查了翻折变换，解决本题的关键是确定满足条件的点G的位置，运用相似、锐角三角函数等知识解决问题．20.【答案】解：（1）原式=1-2×-4+-1=1--4+-1=-4；（2）分解因式得：（x-1）（x-4）=0，可得x-1=0或x-4=0，解得：x1=1，x2=4．【解析】（1）原式利用零指数幂法则，特殊角的三角函数值，算术平方根定义，以及绝对值的代数意义计算即可求出值；（2）方程利用因式分解法求出解即可．此题考查了解一元二次方程的解法，以及实数的运算，熟练掌握运算法则是解本题的关键．21.【答案】证明：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∴∠A+∠D=180°，在△ABM和△DCM中，，∴△ABM≌△DCM（SSS），∴∠A=∠D=90°，即可得出平行四边形ABCD是矩形．【解析】根据平行四边形的两组对边分别相等可知△ABM≌△DCM，可知∠A=∠D=90°，所以是矩形．此题主要考查了平行四边形的性质，矩形的判定，即有一个角是90度的平行四边形是矩形．22.【答案】解：作AD⊥BC交CB的延长线于D，设AD为x，由题意得，∠ABD=45°，∠ACD=35°，在Rt△ADB中，∠ABD=45°，∴DB=x，在Rt△ADC中，∠ACD=35°，∴tan∠ACD=，∴=，解得，x≈233m．【解析】本题考查的是解直角三角形的应用，理解仰角和俯角的概念、掌握锐角三角函数的概念是解题的关键，解答时，注意正确作出辅助线构造直角三角形．作AD⊥BC交CB的延长线于D，设AD为x，表示出DB和DC，根据正切的概念求出x 的值即可．23.【答案】60【解析】解：（1）21÷35%=60户，60-9-21-9=21户，故答案为：60，补全条形统计图如图所示：（2）1500×=750户，答：若该地区建档的养殖户有1500户中非常严重与严重的养殖户一共有750户；（3）用表格表示所有可能出现的情况如下：共有20种不同的情况，其中选中e的有8种，∴P（选中e）==，（1）从两个统计图可得，“B级”的有21户，占调查总户数的35%，可求出调查总户数；求出“C级”户数，即可补全条形统计图：（2）样本估计总体，样本中“严重”和“非常严重”占，估计总体1500户的是“严重”和“方程严重”的户数；（3）用列表法或树状图法列举出所有等可能出现的情况，从中找出符合条件的情况数，进而求出概率．考查扇形统计图、条形统计图的意义和制作方法，从统计图中获取数量及数量之间的关系是解决问题的关键，样本估计总体是统计中常用的方法．考查列表法或树状图法求等可能事件发生的概率，使用此方法一定注意每一种结果出现的可能性是均等的，即为等可能事件．24.【答案】解：（1）将A（2，4）代入y=-x+m与y=（x＞0）中得4=-2+m，4=，∴m=6，k=8，∴一次函数的解析式为y=-x+6，反比例函数的解析式为y=；（2）解方程组得或，∴B（4，2）；（3）设直线y=-x+6与x轴，y轴交于C，D点，易得D（0，6），∴OD=6，∴S△AOB=S△DOB-S△AOD=×6×4-×6×2=6．【解析】（1）由点A的坐标利用一次函数、反比例函数图象上点的坐标特征即可得出反比例函数解析式；（2）联立方程，解方程组即可求得；（3）求出直线与y轴的交点坐标后，即可求出S△AOD和S△BOD，继而求出△AOB的面积．本题考查了反比例函数与一次函数的交点问题、待定系数法求一次函数和反比例函数解析式以及三角形的面积，解题的关键是：根据点的坐标利用待定系数法求出函数解析式；利用分割图形求面积法求出△AOB的面积．25.【答案】（1）证明：∵AB是直径，∴∠ACB=90°，∴∠CAB+∠ABC=90°；∵∠MAC=∠ABC，∴∠MAC+∠CAB=90°，即MA⊥AB，∴MN是⊙O的切线；（2）①证明：∵D是弧AC的中点，∴∠DBC=∠ABD，∵AB是直径，∴∠CBG+∠CGB=90°，∵DE⊥AB，∴∠FDG+∠ABD=90°，∵∠DBC=∠ABD，∴∠FDG=∠CGB=∠FGD，∴FD=FG；②解：连接AD、CD，作DH⊥BC，交BC的延长线于H点．∵∠DBC=∠ABD，DH⊥BC，DE⊥AB，∴DE=DH，在Rt△BDE与Rt△BDH中，，∴Rt△BDE≌Rt△BDH（HL），∴BE=BH，∵D是弧AC的中点，∴AD=DC，在Rt△ADE与Rt△CDH中，，∴Rt△ADE≌Rt△CDH（HL）．∴AE=CH．∴BE=AB-AE=BC+CH=BH，即5-AE=3+AE，∴AE=1．【解析】（1）由AB为直径知∠ACB=90°，∠ABC+∠CAB=90°．由∠MAC=∠ABC可证得∠MAC+∠CAB=90°，则结论得证；（2）①证明∠BDE=∠DGF即可．∠BDE=90°-∠ABD；∠DGF=∠CGB=90°-∠CBD．因为D 是弧AC的中点，所以∠ABD=∠CBD．则问题得证；②连接AD、CD，作DH⊥BC，交BC的延长线于H点．证明Rt△ADE≌Rt△CDH，可得AE=CH．根据AB=BH可求出答案．本题是圆的综合题，考查了切线的判定，圆周角定理，全等三角形的判定与性质，等腰三角形的判定，正确作出辅助线来构造全等三角形是解题的关键．26.【答案】解：（1）设y与x的函数解析式为：y=kx+b（k≠0），∵函数图象过点（1500，55）和（2000，50），∴，∴，∴y与x的函数解析式为：y=-0.01x+70；（2）由题意得，w=（y-40）x=（-0.01x+70-40）x=-0.01x2+30x，即w=-0.01x2+30x，∵-0.01＜0，∴当x=时，，∵1000≤x≤2000，∴当每天销售1500件时，利润最大为22500元．∴每天的最大销售利润是22500元．【解析】（1）设y与x的函数解析式为：y=kx+b（k≠0），将函数图象上的两个点的坐标代入列出方程组，进行解答便可；（2）根据“利润=（售价-进价）×销售量“列出函数解析式，然后根据二次函数的性质，求出其最大值．本题是一次函数与二次函数的应用的综合题，主要考查了一次函数的实际应用，二次函数的实际应用，待定系数法求函数的解析式，求二次函数的最大值，关键是正确运用待定系数法和从实际问题中列出二次函数的解析式．27.【答案】解：（1）①∵△ABC和△CEF都是等腰直角三角形，∴∠ECF=∠ACB=45°，∴∠BCF=∠ACE，∵△ABC和△CEF都是等腰直角三角形，∴CE=CF，AC=CB，∴=，∴，∴△BCF∽△ACE；②由①知，△BCF∽△ACE，∴∠CBF=∠CAE，=，∴BF=AE=×4=2，∵∠CAE+∠CBE=90°，∴∠CBF+∠CBE=90°，即：∠EBF=90°，根据勾股定理得，EF===2；（2）如图（2），连接BF，在Rt△ABC中，tan∠ACB==k，同理，tan∠ECF=k，∴tan∠ACB=tan∠ECF，∴∠ACB=∠ECF，∴∠BCF=∠ACE，在Rt△ABC中，设BC=m，则AB=km，根据勾股定理得，AC==m；在Rt△CEF中，设CF=n，则EF=nk，同理，CE=n∴，=，∴，∵∠BCF=∠ACE，∴△BCF∽△ACE，∴∠CBF=∠CAE，∵∠CAE+∠CBE=90°，∴∠CBF+∠CBE=90°，即：∠EBF=90°，∵△BCF∽△ACE，∴，∴BF=AE=，∵CE=4，∴n=4，∴n=，∴EF=，在Rt△EBF中，根据勾股定理得，BE2+BF2=EF2，∴12+（）2=（）2，∴k=或k=-（舍），即：k的值为．【解析】（1）①先判断出∠BCF=∠ACE，再判断出，即可得出结论；②先判断出∠CBF=∠CAE，进而判断出∠EBF=90°，再求出BF=2，最后用勾股定理求解即可得出结论；（2）先判断出∠BCF=∠ACE，再判断出，进而判断出△BCF∽△ACE，进而表示出BF=，再表示出EF=，最后用勾股定理得，BE2+BF2=EF2，建立方程求解即可得出结论．此题是相似形综合题，主要考查了等腰直角三角形的性质，勾股定理，相似三角形的判定和性质，判断出∠EBF=90°是解本题的关键．28.【答案】解：（1）抛物线的表达式为：y=a（x-1）2+9，将点A的坐标代入上式并解得：a=-1，故抛物线的表达式为：y=-x2+2x+8，将点B坐标代入上式并解得：m=5，故点B（3，5）；（2）过点M、C、A分别作三条相互平移的平行线，分别交y轴于点G、H、N，直线l 与抛物线交于点D，设直线m的表达式为：y=kx+t，将点M的坐标代入上式并解得：t=9-k，故直线m的表达式为：y=kx+9-t，即点G（0，9-t），同理直线l的表达式为：y=kx+1-k，故点H（0，1-k），同理直线n的表达式为：y=kx+3k-7，故点N（3k-7），S△DAC=2S△DCM，则HN=2GH，即1-k-（3k-7）=2（9-k-1+k），解得：k=-2，故直线l的表达式为：y=-2x+3…②，联立①②并解得：x=5（舍去）或-1，故点D（-1，5）；（3）直线A′B′的表达式为：y=2x+n，设点A′、B′的坐标分别为：（x1，y1）、（x2，y2），将抛物线与直线A′B′的表达式联立并整理得：x2+n-8=0，故x1+x2=0，x1x2=n-8，y1+y2=2（x1+x2）+2n=2n，同理可得：y1y2=4n-32+n2，过点M作x轴的平行线交过点A′与y轴的平行线于点G，交过点B′与y轴的平行线于点H，∵∠A′MB′=90°，∴∠GMA′+∠GA′M=90°，∠GMA′+∠MHB′=90°，∴∠GA′M=∠HMB′，故tan∠GA′M=tan∠HMB′，即：，而x1+x2=0，x1x2=n-8，y1+y2=2n，y1y2=4n-32+n2，整理得：n2-13n+30=0，解得：n=3或10（舍去10），故n=3．【解析】（1）抛物线的表达式为：y=a（x-1）2+9，将点A的坐标代入上式并解得：a=-1，即可求解；（2）S△DAC=2S△DCM，则HN=2GH，即1-k-（3k-7）=2（9-k-1+k），即可求解；（3）∠GA′M=∠HMB′，故tan∠GA′M=tan∠HMB′，即：，而x1+x2=0，x1x2=n-8，y1+y2=2n，y1y2=4n-32+n2，即可求解．主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．第21页，共21页。

2020年四川省成都市武侯区中考数学一诊试卷一、选择题（本大題共10个小题，每小题3分，共30分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）1．（3分）在如下放置的立体图形中，其主视图与左视图不相同的是（）A．圆柱B．正方体C．圆柱D．球2．（3分）已知点P（3，2）在反比例函数y＝（k≠0）的图象上，则下列各点中在此反比例函数图象上的是（）A．（﹣3，﹣2）B．（3，﹣2）C．（﹣2，3）D．（2，﹣3）3．（3分）如图，在平面直角坐标系中，点A的坐标为（3，4），那么cosα的值是（）A．B．C．D．4．（3分）若关于x的一元二次方程（k+2）x2﹣2x﹣1＝0有实数根，则实数k的取值范围是（）A．k＞3B．k≥﹣3C．k＞﹣3且k≠﹣2D．k≥﹣3且k≠﹣2 5．（3分）如图，在△ABC中，D，E分别是AB和AC上的点，且DE∥BC，若AE＝1，CE ＝AD＝2，则AB的长是（）A．6B．5C．4D．26．（3分）下列说法正确的是（）A．对角线相等且互相垂直的四边形是正方形B．坡面的水平宽度与铅直高度的比称为坡度C．两个相似图形也是位似图形D．平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧7．（3分）如图，⊙O为△ABC的外接圆，∠BAC＝55°，则∠OBC的度数为（）A．25°B．35°C．55°D．70°8．（3分）在一个不透明的袋子里装有20个红球和若干个蓝球，这些球除颜色外都相同将袋子中的球搅拌均匀，每次从袋子里随机摸出一个球，记录下它的颜色后再放网袋子中，不断重复这一过程，发现摸到蓝球的频率稳定在0.6左右，请你估计袋子中装有蓝球的个数是（）A．12个B．20个C．30个D．35个9．（3分）在2020年元旦期间，某商场销售某种冰箱，每台进货价为2500元，调查发现：当销售价为2900元时，平均毎天能销售出8台；而当销售价每降低50元时，平均每天就能多售出4台，商场要想使这种冰箱的销售利润平均每天达到5000元，每台冰箱的定价应为多少元？设每台冰箱定价x元，根据题意，可列方程为（）A．（x﹣2500）（8+4×）＝5000B．（x﹣2500）（8+4×）＝5000C．（2900﹣x﹣2500）（8+4×）＝5000D．（2900﹣x）（8+4×）＝500010．（3分）已知二次函数y＝ax2+bx+c（其中a，b，c为常数）的图象如图所示，有以下结论：①abc＞0；②a+b+c＝0；③2a﹣b＝0；④关于x的一元二次方程ax2+bx+c＝0有两个不相等的实数根．其中正确结论的番号是（）A．①②④B．①③④C．①④D．③④二、填空题（本大题共4个小题，每小题4分，共16分，答案写在答题卡上）11．（4分）已知＝，则的值为．12．（4分）如图，在△ABC中，P为边AB上一点，且∠ACP＝∠B，若AP＝6，BP＝4，则AC的长为．13．（4分）已知关于x的元二次方程x2﹣2kx﹣8＝0的一个根是2，则此方程的另一个根是．14．（4分）如图，现将四根木条钉成的矩形框ABCD变形为平行四边形木框A'BCD′，且A′D′与CD相交于CD边的中点E，若AB＝4，则△ECD′的面积是．三、解答題（本大题共6个小题，共54分，解答过程写在答题卡上）15．（12分）（1）计算：﹣22+（π﹣3.14）0﹣|﹣4|﹣4sin60°（2）解方程：4x2+4x﹣3＝016．（6分）2019年9月10日是我国第35个教师节，某中学德育处发起了感恩小学恩师的活动，德育处要求每位同学从以下三种方式中选择一种方式表达感恩：A．信件感恩，B．信息感恩，C．当面感恩．为了解同学们选择以上三种感恩方式的情况，德育处随机对本校部分学生进行了调查，并根据调查结果绘制成了如下两幅不完整的统计图．根据图中信息解答下列问题：（1）扇形统计图中C部分所对应的扇形圆心角的度数为，并补全条形统计图；（2）本次调查在选择A方式的学生中有两名男生和两名女生来自于同一所小学，德育处打算从他们四个人中选择两位在主题升旗仪式上发言，请用画树状图或列表的方法求恰好选到一男一女的概率．17．（8分）2019年10月1日，中华人民共和国成立70周年，成都市天府广场举行了盛大的升旗仪式，我市部分学生有幸见证了这一激动人心的时刻，并在现场作了如下测量工作：身高1.8米的某同学（图中AE部分）在护旗手开始走正步的点A处测得旗杆顶部D 的仰角为22°，在护旗手结束走正步的点B处测得旗杆顶部D的仰角为45°，又测量得到A，B两点间的距离是30米，求旗杆DC的高度．（结果精确到0.1米；参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40．）18．（8分）如图，在正方形ABCD中，点E，F在对角线BD上，AE∥CF，连接AF，CE．（1）求证：△ABE≌△CDF；（2）试判断四边形AECF的形状，并说明理由．19．（10分）如图，在平面直角坐标系xOy中，次函数y＝﹣x+5的图象与反比例函数y＝（k＞0）的图象相交于A，B两点，与x轴相交于点C，连接OB，且△BOC的面积为．（1）求反比例函数的表达式；（2）将直线AB向下平移，若平移后的直线与反比例函数的图象只有一个交点，试说明直线AB向下平移了几个单位长度？20．（10分）如图，⊙O是△ABC的外接圆，AB为⊙O的直径，在△ABC外侧作∠CAD＝∠CAB，过点C作CD⊥AD于点D，交AB延长线于点P．（1）求证：PC是⊙O的切线；（2）若tan∠BCP＝，AD•BC＝4m2（m＞0），求⊙O的半径；（用含m的代数式表示）（3）如图2，在（2）的条件下，作弦CF平分∠ACB，交AB于点E，连接BF，且BF ＝5，求线段PE的长．一、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上B卷（共50分）21．（4分）已知方程x2﹣x﹣7＝0的两个实数根分别为m，n，则m2+n的值为．22．（4分）“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用数学语言可表述为：“如图，CD为⊙O的直径，弦AB⊥CD于E，CE＝1寸，AB＝10寸，求直径CD的长”．（1尺＝10寸）则CD＝．23．（4分）我们知道黄金比例是，利用这个比例，我们规定一种“黄金算法”即：a b＝a+b，比如12＝1+×2＝．若x（24）＝5，则x的值为．24．（4分）如图，点P为双曲线y＝（x＜0）上一动点，连接OP并延长到点A，使P A＝PO，过点A作x轴的垂线，垂足为B，交双曲线于点C．当AC＝AP时，连接PC，将△APC沿直线PC进行翻折，则翻折后的△A′PC与四边形BOPC的重叠部分（图中阴影部分）的面积是．25．（4分）如图，在矩形ABCD中，已知AB＝3，BC＝4，点P是边BC上一动点（点P 不与点B，C重合），连接AP，作点B关于直线AP的对称点M，连接MP，作∠MPC 的角平分线交边CD于点N．则线段MN的最小值为．二、解答题（本大题共3个小题，共30分，解答过程写在答题卡上）26．（8分）据报道，从2018年8月以来，“非洲猪瘟”给生猪养殖户带来了不可估量的损失．某养殖户为了预防“非洲猪瘟”的侵袭，每天对猪场进行药熏消毒，已知一瓶药物释放过程中，一个圈舍内每立方米空气中含药量y（毫克）与时间x（分钟）之间满足正比例函数关系；药物释放完后，y与x之间满足反比例函数关系，如图所示，结合图中提供的信息解答下列问题：（1）分别求当0≤x≤10和x＞10时，y与x之间满足的函数关系式；（2）据测定，当空气中每立方米的含药量不低于6毫克时，消毒才有效，那么这次熏药的有效消毒时间是多少分钟．27．（10分）如图，已知AC为正方形ABCD的对角线，点P是平面内不与点A，B重合的任意一点，连接AP，将线段AP绕点P顺时针旋转90°得到线段PE，连接AE，BP，CE．（1）求证：△APE∽△ABC；（2）当线段BP与CE相交时，设交点为M，求的值以及∠BMC的度数；（3）若正方形ABCD的边长为3，AP＝1，当点P，C，E在同一直线上时，求线段BP 的长．28．（12分）如图，在平面直角坐标系xOy中，抛物线y＝ax2+x+c与x轴交于A，B 两点（点A在点B的左侧），交y轴于点C，经过B，C两点的直线为y＝．（1）求抛物线的函数表达式；（2）点P为抛物线上的动点，过点P作x轴的垂线，交直线BC于点M，连接PC，若△PCM为直角三角形，求点P的坐标；（3）当P满足（2）的条件，且点P在直线BC上方的抛物线上时，如图2，将抛物线沿射线BC方向平移，平移后B，P两点的对应点分别为B′，P′，取AB的中点E，连接EB′，EP′，试探究EB'+EP'是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．2020年四川省成都市武侯区中考数学一诊试卷参考答案与试题解析一、选择题（本大題共10个小题，每小题3分，共30分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）1．（3分）在如下放置的立体图形中，其主视图与左视图不相同的是（）A．圆柱B．正方体C．圆柱D．球【分析】主视图、左视图是分别从物体正面、左面看，所得到的图形．【解答】解：A、圆锥的主视图和左视图均为全等的等腰三角形，不符合题意；B、正方体的主视图和左视图均为全等的正方形，不符合题意；C、主视图是长方形，左视图是圆，符合题意；D、球的主视图和左视图均为圆，不符合题意；故选：C．2．（3分）已知点P（3，2）在反比例函数y＝（k≠0）的图象上，则下列各点中在此反比例函数图象上的是（）A．（﹣3，﹣2）B．（3，﹣2）C．（﹣2，3）D．（2，﹣3）【分析】直接把点P（3，2）代入反比例函数y＝（k≠0）求出k的值，进而可得出结论．【解答】解：∵点P（3，2）在反比例函数y＝（k≠0）的图象上，∴k＝3×2＝6，A、∵﹣3×（﹣2）＝6，∴此点在该函数图象上，故本选项正确；B、∵3×（﹣2）＝﹣6，∴此点不在该函数图象上，故本选项错误；C、∵﹣2×3＝﹣6，∴此点不在该函数图象上，故本选项错误；D、∵2×（﹣3）＝﹣6，∴此点不在该函数图象上，故本选项错误．故选：A．3．（3分）如图，在平面直角坐标系中，点A的坐标为（3，4），那么cosα的值是（）A．B．C．D．【分析】作AB⊥x轴于B，先利用勾股定理计算出OA＝5，然后在Rt△AOB中利用余弦的定义求解即可．【解答】解：作AB⊥x轴于B，如图，∵点A的坐标为（3，4），∴OB＝3，AB＝4，∴OA＝＝5，在Rt△AOB中，cosα＝＝．故选：C．4．（3分）若关于x的一元二次方程（k+2）x2﹣2x﹣1＝0有实数根，则实数k的取值范围是（）A．k＞3B．k≥﹣3C．k＞﹣3且k≠﹣2D．k≥﹣3且k≠﹣2【分析】根据根的判别式即可求出答案．【解答】解：由题意可知：△＝4+4（k+2）≥0，∴解得：k≥﹣3，∵k+2≠0，∴k≥﹣3且k≠﹣2，故选：D．5．（3分）如图，在△ABC中，D，E分别是AB和AC上的点，且DE∥BC，若AE＝1，CE ＝AD＝2，则AB的长是（）A．6B．5C．4D．2【分析】根据平行线分线段成比例定理列出比例式，进行计算即可．【解答】解：∵DE∥BC，∴＝，∴＝，∴AB＝6，故选：A．6．（3分）下列说法正确的是（）A．对角线相等且互相垂直的四边形是正方形B．坡面的水平宽度与铅直高度的比称为坡度C．两个相似图形也是位似图形D．平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧【分析】直接利用位似图形的性质以及坡比的定义、垂径定理的推论分别分析得出答案．【解答】解：A、对角线相等且互相垂直的平行四边形是正方形，故此选项错误；B、坡面的铅直高度与水平宽度的比称为坡度，故此选项错误；C、两个相似图形不一定位似图形，故此选项错误；D、平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧，正确．故选：D．7．（3分）如图，⊙O为△ABC的外接圆，∠BAC＝55°，则∠OBC的度数为（）A．25°B．35°C．55°D．70°【分析】由⊙O为△ABC的外接圆，∠BAC＝55°，利用在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠BOC的度数，又由等腰三角形的性质与三角形内角和定理，即可求得∠OBC的度数．【解答】解：∵⊙O为△ABC的外接圆，∠BAC＝55°，∴∠BOC＝2∠BAC＝2×55°＝110°，∵OB＝OC，∴∠OBC＝＝＝35°．故选：B．8．（3分）在一个不透明的袋子里装有20个红球和若干个蓝球，这些球除颜色外都相同将袋子中的球搅拌均匀，每次从袋子里随机摸出一个球，记录下它的颜色后再放网袋子中，不断重复这一过程，发现摸到蓝球的频率稳定在0.6左右，请你估计袋子中装有蓝球的个数是（）A．12个B．20个C．30个D．35个【分析】根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．【解答】解：设袋中蓝球有x个，根据题意得：＝0.6，解得：x＝30，经检验：x＝30是分式方程的解，故袋中蓝球有30个．故选：C．9．（3分）在2020年元旦期间，某商场销售某种冰箱，每台进货价为2500元，调查发现：当销售价为2900元时，平均毎天能销售出8台；而当销售价每降低50元时，平均每天就能多售出4台，商场要想使这种冰箱的销售利润平均每天达到5000元，每台冰箱的定价应为多少元？设每台冰箱定价x元，根据题意，可列方程为（）A．（x﹣2500）（8+4×）＝5000B．（x﹣2500）（8+4×）＝5000C．（2900﹣x﹣2500）（8+4×）＝5000D．（2900﹣x）（8+4×）＝5000【分析】设每台冰箱的降低x元时，这种冰箱的销售利润平均每天达到5000元，根据题意列方程即可；【解答】解：设每台冰箱降价x元时，种冰箱的销售利润平均每天达到5000元，由题意得：（x﹣2500）（8+4×）＝5000，故选：B．10．（3分）已知二次函数y＝ax2+bx+c（其中a，b，c为常数）的图象如图所示，有以下结论：①abc＞0；②a+b+c＝0；③2a﹣b＝0；④关于x的一元二次方程ax2+bx+c＝0有两个不相等的实数根．其中正确结论的番号是（）A．①②④B．①③④C．①④D．③④【分析】根据二次函数图象的开口方向、对称轴位置、与x轴的交点坐标等知识，逐个判断即可．【解答】解：抛物线开口向上，a＞0，对称轴在y轴的右侧，a、b异号，因此b＜0，与y轴的交点在正半轴，因此c＜0，abc＞0，故结论①正确；当x＝1时，y＝a+b+c＜0，因此选项②是不正确的；对称轴为x＝1，即﹣＝1，也就是2a+b＝0，因此选项③不正确；抛物线与x轴有两个不同的交点，因此方程ax2+bx+c＝0有两个不相等的实数根．选项④正确；故选：C．二、填空题（本大题共4个小题，每小题4分，共16分，答案写在答题卡上）11．（4分）已知＝，则的值为．【分析】根据合比性质，可得答案．【解答】解：＝，则＝，故答案为：．12．（4分）如图，在△ABC中，P为边AB上一点，且∠ACP＝∠B，若AP＝6，BP＝4，则AC的长为2．【分析】通过证明△ACP∽△ABC，可得，即可求解．【解答】解：∵AP＝6，BP＝4，∴AB＝10，∵∠A＝∠A，∠ACP＝∠B，∴△ACP∽△ABC，∴，∴AC2＝6×10，∴AC＝2，故答案为：2．13．（4分）已知关于x的元二次方程x2﹣2kx﹣8＝0的一个根是2，则此方程的另一个根是﹣4．【分析】根据根与系数的关系即可求出答案．【解答】解：设该方程的另外一个根为x，由根与系数的关系可知：2x＝﹣8，∴x＝﹣4，故答案为：﹣414．（4分）如图，现将四根木条钉成的矩形框ABCD变形为平行四边形木框A'BCD′，且A′D′与CD相交于CD边的中点E，若AB＝4，则△ECD′的面积是2．【分析】作A'F⊥BC于F，则∠A'FB＝90°，根据题意得：平行四边形A′BCD′的面积＝BC•A'F＝BC•AB，A'F＝AB＝2，得出∠D'＝∠A'BC＝30°，得出BF＝A'F＝2，由矩形和平行四边形的性质得出BC＝AD＝A'D'，A'D'∥AD∥BC，CD⊥BC，得出CD⊥A'D'，得出A'F∥CD，证出四边形A'ECF是矩形，得出CE＝A'F＝2，A'E＝CF，证出DE＝BF＝2，即可得出答案．【解答】解：作A'F⊥BC于F，如图所示：则∠A'FB＝90°，根据题意得：平行四边形A′BCD′的面积＝BC•A'F＝BC•AB，∴A'F＝AB＝2，∴∠D'＝∠A'BC＝30°，∴BF＝A'F＝2，∵四边形ABCD是矩形，四边形A′BCD′是平行四边形，∴BC＝AD＝A'D'，A'D'∥AD∥BC，CD⊥BC，∴CD⊥A'D'，∴A'F∥CD，∴四边形A'ECF是矩形，∴CE＝A'F＝2，A'E＝CF，∴DE＝BF＝2，∴△ECD的面积＝DE×CE＝×2×2＝2；故答案为2．三、解答題（本大题共6个小题，共54分，解答过程写在答题卡上）15．（12分）（1）计算：﹣22+（π﹣3.14）0﹣|﹣4|﹣4sin60°（2）解方程：4x2+4x﹣3＝0【分析】（1）根据实数的混合运算顺序和运算法则计算可得；（2）利用因式分解法求解可得．【解答】解：（1）原式＝﹣4+1﹣（4﹣2）﹣4×＝﹣3﹣4+2﹣2＝﹣7；（2）∵4x2+4x﹣3＝0，∴（2x+3）（2x﹣1）＝0，则2x+3＝0或2x﹣1＝0，解得x＝﹣或x＝．16．（6分）2019年9月10日是我国第35个教师节，某中学德育处发起了感恩小学恩师的活动，德育处要求每位同学从以下三种方式中选择一种方式表达感恩：A．信件感恩，B．信息感恩，C．当面感恩．为了解同学们选择以上三种感恩方式的情况，德育处随机对本校部分学生进行了调查，并根据调查结果绘制成了如下两幅不完整的统计图．根据图中信息解答下列问题：（1）扇形统计图中C部分所对应的扇形圆心角的度数为120°，并补全条形统计图；（2）本次调查在选择A方式的学生中有两名男生和两名女生来自于同一所小学，德育处打算从他们四个人中选择两位在主题升旗仪式上发言，请用画树状图或列表的方法求恰好选到一男一女的概率．【分析】（1）由A类别人数及其所占百分比可得总人数，用360°乘以C部分人数所占比例可得；据此即可补全条形图；（2）分别用树状图和列表两种方法表示出所有等可能结果，从中找到恰好选到一男一女的概率结果数，利用概率公式计算可得．【解答】解：（1）被调查的总人数为15÷25%＝60（人），C类的总人数＝60﹣25﹣15＝20（人）所以扇形统计图中C部分所对应的扇形圆心角的度数为360°×＝120°，补全条形统计图如图所示：故答案为：120°；（2）画树状图如下：共有12种可能的结果，恰好选到一男一女的结果有8个，∴P（选到一男一女）＝＝．17．（8分）2019年10月1日，中华人民共和国成立70周年，成都市天府广场举行了盛大的升旗仪式，我市部分学生有幸见证了这一激动人心的时刻，并在现场作了如下测量工作：身高1.8米的某同学（图中AE部分）在护旗手开始走正步的点A处测得旗杆顶部D 的仰角为22°，在护旗手结束走正步的点B处测得旗杆顶部D的仰角为45°，又测量得到A，B两点间的距离是30米，求旗杆DC的高度．（结果精确到0.1米；参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40．）【分析】首先分析图形，根据题意构造直角三角形．本题涉及多个直角三角形，应利用其公共边构造边角关系，进而可求出答案．【解答】解：延长EF交CD于G，∵∠DEF＝22°，∠DFG＝45°，∴在Rt△DGF中，DG＝GF，在Rt△DGE中，tan22°＝，即EG＝≈2.5DG，∵2.5DG﹣DG＝30，解得DG＝20，则DC＝DG+CG＝20+1.8＝21.8（米）．答：旗杆DC的高度大约是21.8米．18．（8分）如图，在正方形ABCD中，点E，F在对角线BD上，AE∥CF，连接AF，CE．（1）求证：△ABE≌△CDF；（2）试判断四边形AECF的形状，并说明理由．【分析】（1）根据正方形的性质以及平行线的性质可得△ABE≌△CDF；（2）连接AC，与BD交于点O，由△ABE≌△CDF，得出BE＝DF，进而得出OE＝OF，根据对角线互相垂直且平分的四边形是菱形，可得四边形AECF是菱形．【解答】解：（1）证明：∵在正方形ABCD中，AB＝AD，∠ABE＝∠CDF＝45°，又∵AE∥CF，∴∠AEF＝∠CFE（两直线平行，内错角相等），∴∠AEB＝∠CFD（等角的补角相等），∴△ABE≌△CDF（AAS）；（2）四边形AECF是菱形．理由如下：如图，连接AC，与BD交于点O，∵△ABE≌△CDF，∴BE＝DF，又∵OB＝OD，∴OB﹣BE＝OD﹣DF，即OE＝OF，又∵AC⊥EF，OA＝OC，∴四边形AECF是菱形．19．（10分）如图，在平面直角坐标系xOy中，次函数y＝﹣x+5的图象与反比例函数y＝（k＞0）的图象相交于A，B两点，与x轴相交于点C，连接OB，且△BOC的面积为．（1）求反比例函数的表达式；（2）将直线AB向下平移，若平移后的直线与反比例函数的图象只有一个交点，试说明直线AB向下平移了几个单位长度？【分析】（1）由一次函数解析式求得C的坐标，根据三角形面积求得B的纵坐标，代入一次函数解析式求得B的坐标，然后根据待定系数法即可求得反比例函数的解析式；（2）由于将直线AB向下平移m（m＞0）个单位长度得直线解析式为y＝﹣x+5﹣m，则直线y＝﹣x+5﹣m与反比例函数有且只有一个公共点，即方程＝﹣x+5﹣m只有一组解，再根据判别式的意义得到关于m的方程，最后解方程求出m的值．【解答】解：（1）一次函数y＝﹣x+5中，令y＝0，解得x＝5，∴C（5，0），∴OC＝5，作BD⊥OC于D，∵△BOC的面积为，∴OC•BD＝，即BD＝，∴BD＝1，∴点B的纵坐标为1，代入y＝﹣x+5中，求得x＝4，∴B（4，1），∵反比例函数y＝（k＞0）的图象经过B点，∴k＝4×1＝4，∴反比例函数的解析式为y＝；（2）将直线AB向下平移m（m＞0）个单位长度得直线解析式为y＝﹣x+5﹣m，∵直线AB向下平移m（m＞0）个单位长度后与反比例函数的图象只有一个公共交点，∴＝﹣x+5﹣m，整理得x2+（m﹣5）x+4＝0，△＝（m﹣5）2﹣4×1×4＝0，解得m＝9或m＝1，即m的值为1或9．20．（10分）如图，⊙O是△ABC的外接圆，AB为⊙O的直径，在△ABC外侧作∠CAD＝∠CAB，过点C作CD⊥AD于点D，交AB延长线于点P．（1）求证：PC是⊙O的切线；（2）若tan∠BCP＝，AD•BC＝4m2（m＞0），求⊙O的半径；（用含m的代数式表示）（3）如图2，在（2）的条件下，作弦CF平分∠ACB，交AB于点E，连接BF，且BF ＝5，求线段PE的长．【分析】（1）连接OC，则OA＝OC，则∠OAC＝∠OCA＝α，而∠CAD＝∠CAB＝α，故∠DAC＝∠OCA＝α，即可求解；（2）证明△ADC∽△ABC，设圆的半径为R，则AC＝AB cosα＝2R×＝，CD＝AC sinα＝，故AD•BC＝AC•CD＝＝4m2，即可求解；（3）证明PC＝PE，BF＝5＝R，则R＝5，利用CO∥AD，则，即，即可求解．【解答】解：（1）如图1，连接OC，则OA＝OC，则∠OAC＝∠OCA＝α，而∠CAD＝∠CAB＝α，故∠DAC＝∠OCA＝α，∴AD∥CO，而CD⊥AD，∴CO⊥BD，故PC是⊙O的切线；（2）PC是⊙O的切线，则∠BCP＝∠CAB＝α，即tan，则sin，cos，∵∠DAC＝∠CAB＝α，∴△ADC∽△ABC，设圆的半径为R，则AC＝AB cosα＝2R×＝，CD＝AC sinα＝，故AD•BC＝AC•CD＝＝4m2，故R＝m；（3）连接OF、OC，CF平分∠ACB，则FO⊥AB，∵∠ECP＝90°﹣∠OCE，∠CEP＝90°﹣∠OFC，而∠OCE＝∠OFC，∴∠EPC＝∠CEP，∴PC＝PE，BF＝5＝R，则R＝5，AD＝AC cosα＝×＝8，同理CD＝4，∵CO∥AD，∴，即，解得：PC＝＝PE．一、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上B卷（共50分）21．（4分）已知方程x2﹣x﹣7＝0的两个实数根分别为m，n，则m2+n的值为8．【分析】根据根与系数的关系即可求出答案．【解答】解：由题意可知：m2﹣m﹣7＝0，∴m2＝m+7，∵m+n＝1，∴原式＝m+7+n＝8，故答案为：8．22．（4分）“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用数学语言可表述为：“如图，CD为⊙O的直径，弦AB⊥CD于E，CE＝1寸，AB＝10寸，求直径CD的长”．（1尺＝10寸）则CD＝26寸．【分析】根据垂径定理和勾股定理求解．【解答】解：连接OA，如图所示，设直径CD的长为2x，则半径OC＝x，∵CD为⊙O的直径，弦AB⊥CD于E，AB＝10寸，∴AE＝BE＝AB＝×10＝5寸，连接OA，则OA＝x寸，根据勾股定理得x2＝52+（x﹣1）2，解得x＝13，CD＝2x＝2×13＝26（寸）．故答案为：26寸．23．（4分）我们知道黄金比例是，利用这个比例，我们规定一种“黄金算法”即：a b＝a+b，比如12＝1+×2＝．若x（24）＝5，则x的值为．【分析】根据新定义得到24＝2，则x2＝x+5﹣，从而得到x+5﹣＝5，然后解一次方程即可．【解答】解：∵24＝2+×4＝2，∴x2＝x+×2＝x+5﹣∴x+5﹣＝5，∴x＝．故答案为．24．（4分）如图，点P为双曲线y＝（x＜0）上一动点，连接OP并延长到点A，使P A＝PO，过点A作x轴的垂线，垂足为B，交双曲线于点C．当AC＝AP时，连接PC，将△APC沿直线PC进行翻折，则翻折后的△A′PC与四边形BOPC的重叠部分（图中阴影部分）的面积是．【分析】连接OC，BP，根据折叠性质得四边形ACA'P为菱形，进而得A'C∥AO，A'P∥AB，由反比例函数的比例系数的几何意义和相似三角形的性质求出△OPD，△OAB，△BCE的面积，进而结合边的比例关系求出△ACP的面积，最后便可求得阴影部分面积．【解答】解：连接OC，BP，则，∴，∵AP＝AC，将△APC沿直线PC进行翻折得△A′PC，∴AP＝AC＝A'C＝A'P，∴四边形ACA'P为菱形，∴P A'∥AB，A'C∥OA，∵AB⊥x轴，∴P A'⊥x轴，∴＝4，∴，∴OB•BC＝OD•PD，∵AP＝OP，PD∥AB，∴OD＝BD，∴PD＝，OD＝OB，∵CE∥OA，∴∠CEB＝∠POD，∵∠CBE＝∠PDO＝90°，∴△BCE∽△DPO，∴，∵OB•BC＝OD•PD，OD＝OB，∴BC＝PD＝AB，∴，，∴，∴，∵DP∥AB，∴△OPD∽△OAB，∴，∴，∵OP＝AP，∴，∴，∴．25．（4分）如图，在矩形ABCD中，已知AB＝3，BC＝4，点P是边BC上一动点（点P 不与点B，C重合），连接AP，作点B关于直线AP的对称点M，连接MP，作∠MPC 的角平分线交边CD于点N．则线段MN的最小值为．【分析】连接AM、MN、AN，由MN+AM≥AN，得出MN≥AN﹣AM，即当A、M、N三点共线时，MN＝AN﹣AM，最小，由矩形的性质得出AB＝CD＝3，AD＝BC＝4，∠B＝∠C＝∠D＝90°，由点B关于直线AP的对称点为M，得出AP垂直平分BM，则AB＝AM，PB＝PM，由SSS证得△ABP≌△AMP，得出∠B＝∠PMA＝90°，则∠PMN＝∠C，由角平分线定义得出∠NPM＝∠NPC，由AAS证得△NPM≌△NPC（AAS），得出MN＝CN，设MN＝x，则DN＝CD﹣CN＝3﹣x，AN＝AM+MN＝3+x，在Rt△ADN中，由勾股定理得出方程即可得出结果．【解答】解：连接AM、MN、AN，如图1所示：∵MN+AM≥AN，∴MN≥AN﹣AM，当A、M、N三点共线时，MN＝AN﹣AM，最小，当A、M、N三点共线时，如图2所示：∵四边形ABCD是矩形，∴AB＝CD＝3，AD＝BC＝4，∠B＝∠C＝∠D＝90°，∵点B关于直线AP的对称点为M，∴AP垂直平分BM，∴AB＝AM，PB＝PM，在△ABP和△AMP中，，∴△ABP≌△AMP（SSS），∴∠B＝∠PMA＝90°，∴∠PMN＝∠C＝90°，∵PN是∠MPC的角平分线，∴∠NPM＝∠NPC，在△NPM和△NPC中，，∴△NPM≌△NPC（AAS），∴MN＝CN，设MN＝x，则DN＝CD﹣CN＝3﹣x，AN＝AM+MN＝3+x，在Rt△ADN中，42+（3﹣x）2＝（3+x）2，解得：x＝，∴线段MN的最小值为，故答案为：．二、解答题（本大题共3个小题，共30分，解答过程写在答题卡上）26．（8分）据报道，从2018年8月以来，“非洲猪瘟”给生猪养殖户带来了不可估量的损失．某养殖户为了预防“非洲猪瘟”的侵袭，每天对猪场进行药熏消毒，已知一瓶药物释放过程中，一个圈舍内每立方米空气中含药量y（毫克）与时间x（分钟）之间满足正比例函数关系；药物释放完后，y与x之间满足反比例函数关系，如图所示，结合图中提供的信息解答下列问题：（1）分别求当0≤x≤10和x＞10时，y与x之间满足的函数关系式；（2）据测定，当空气中每立方米的含药量不低于6毫克时，消毒才有效，那么这次熏药的有效消毒时间是多少分钟．【分析】（1）分别利用当0≤x≤10，设y与x之间满足的函数关系式为y＝kx，以及x＞10时，设y与x之间满足的函数关系式为y＝，分别得出函数关系式；（2）直接利用y≥6时得出x的取值范围即可．【解答】解：（1）当0≤x≤10，设y与x之间满足的函数关系式为y＝kx，∵过点（10，30），∴30＝10k，解得：k＝3，∴y＝3x（0≤x≤10），x＞10时，设y与x之间满足的函数关系式为y＝，∵过点（10，30），∴30＝，k＝300，∴y＝（x＞10）；（2）y＝3x（0≤x≤10）中，当y≥6时，x≥2，y＝（x＞10）中，当y≥6时，x≤50，∴2≤x≤50，∴这次熏药的有效消毒时间是：50﹣2＝48（分钟）答：这次熏药的有效消毒时间是48分钟．27．（10分）如图，已知AC为正方形ABCD的对角线，点P是平面内不与点A，B重合的任意一点，连接AP，将线段AP绕点P顺时针旋转90°得到线段PE，连接AE，BP，CE．（1）求证：△APE∽△ABC；（2）当线段BP与CE相交时，设交点为M，求的值以及∠BMC的度数；（3）若正方形ABCD的边长为3，AP＝1，当点P，C，E在同一直线上时，求线段BP 的长．【分析】（1）先求出∠APE＝∠ABC＝90°，∠P AE＝∠PEA＝∠ABC＝45°，即可得出结论；（2）由（1）知，△APE∽△ABC，得出，再判断出∠P AB＝∠EAC，进而判断出△P AB∽△EAC，即可得出结论；（3）先画出图形，利用勾股定理求出CP'，再分两种情况，求出CE和CE'，借助（2）的结论，即可得出结论．【解答】解：（1）∵AC是正方形ABCD的对角线，∴∠ABC＝90°，∠BAC＝∠BCA＝45°，由旋转知，P A＝PE，∠APE＝90°＝∠ABC，∴∠P AE＝∠PEA＝45°＝∠BAC，∴△APE∽△ABC；（2）在Rt△ABC中，AB＝CB，∴AC＝AB，由（1）知，△APE∽△ABC，∴，∵∠BAC＝∠P AE＝45°，∴∠P AB＝∠EAC，∴△P AB∽△EAC，∴＝＝，∵△P AB∽△EAC，∴∠ABP＝∠ACE，∴∠BCE+∠CBM＝∠BCE+∠ABP+∠ABC＝∠BCE+∠ACE+∠ABC＝∠ACB+∠ABC＝45°+90°＝135°，∴∠BMC＝180°﹣（∠BCE+∠CBM）＝45°；（3）如图，在Rt△ABC中，AB＝AC＝3，∴AC＝3，∵点P，C，E在同一条线上，且∠APE＝90°，∴CP＝＝，∴CE＝CP﹣PE＝﹣1或CE'＝CP'+P'E＝+1，由（2）知，＝，∴BP＝CE＝（﹣1）＝或BP'＝CE'＝；即：BP的长为或．28．（12分）如图，在平面直角坐标系xOy中，抛物线y＝ax2+x+c与x轴交于A，B 两点（点A在点B的左侧），交y轴于点C，经过B，C两点的直线为y＝．（1）求抛物线的函数表达式；（2）点P为抛物线上的动点，过点P作x轴的垂线，交直线BC于点M，连接PC，若△PCM为直角三角形，求点P的坐标；（3）当P满足（2）的条件，且点P在直线BC上方的抛物线上时，如图2，将抛物线沿射线BC方向平移，平移后B，P两点的对应点分别为B′，P′，取AB的中点E，连接EB′，EP′，试探究EB'+EP'是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．【分析】（1）y＝，过点B，C，则点B、C的坐标分别为：（3，0）、（0，），则c＝，将点B的坐标代入抛物线表达式，即可求解；（2）分∠PCM＝90°、∠CPM＝90°两种情况，分别求解即可；（3）作点E关于P′B′的对称点E′，将点E′沿P′B′方向平移2个单位得到点E″，连接E、E″交P′B′所在的直线于点B′，点B′沿P′B′方向平移2个单位得到点。

2020届四川省成都市高三下学期一诊考试数学（文）试卷★祝考试顺利★(解析版)第I 卷（选择题）一、选择题：本大题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数1z 与23z i =--（i 为虚数单位）在复平面内对应的点关于实轴对称,则1z =( )A. 3i --B. 3i -+C. 3i +D. 3i - 【答案】B【解析】由题意得复数z 1与23z i =--的实部相等,虚部互为相反数,则z 1可求．【详解】∵复数z 1与23z i =--（i 为虚数单位）在复平面内对应的点关于实轴对称, ∴复数z 1与23z i =--（i 为虚数单位）的实部相等,虚部互为相反数,则z 1＝3i -+．故选：B ．2.已知集合{}1,0,A m =-,{}1,2B =,若{}1,0,1,2A B ⋃=-,则实数m 的值为( )A. 1-或0B. 0或1C. 1-或2D. 1或2 【答案】D【解析】根据集合并集的定义即可得到答案. 【详解】集合{}1,0,A m =-,{}1,2B =,且{}1,0,1,2A B ⋃=-,所以1m =或2m =.故选：D3.若sin θθ=,则tan 2θ=（ ）A. C.【答案】C 【解析】根据sin5cosθθ=得到tan5θ=,再利用二倍角公式得到答案.【详解】sin5cos tan5θθθ=∴=,22tan255tan21tanθθθ===--故选：C4.已知命题p：x R∀∈,221x x-≥,则p⌝为（）A.x R∀∉,221x x-< B. 0x R∃∉,02021x x-<C. x R∀∈,221x x-< D. 0x R∃∈,02021x x-<【答案】D 【解析】直接利用全称命题的否定定义得到答案. 【详解】命题p：x R∀∈,221x x-≥,则p⌝为：0x R∃∈,02021x x-<故选：D5.某校随机抽取100名同学进行“垃圾分类"的问卷测试,测试结果发现这100名同学的得分都在[50,100]内,按得分分成5组：[50,60）,[60,70）,[70,80）,[80,90）,[90,100],得到如图所示的频率分布直方图,则这100名同学的得分的中位数为( )A. 72.5B. 75C. 77.5D. 80【答案】A【解析】根据频率分布直方图求得中位数即可.【详解】在频率分步直方图中,小正方形的面积表示这组数据的频率,∴中位数为：。

2020年四川省成都市青羊区中考数学一诊试卷A卷一．选择题（共10小题）1．（﹣2）×＝（）A．﹣2 B．1 C．﹣1 D．2．用配方法解一元二次方程x2+4x﹣3＝0时，原方程可变形为（）A．（x+2）2＝1 B．（x+2）2＝7 C．（x+2）2＝13 D．（x+2）2＝19 3．下列几何体的主视图是三角形的是（）A．B．C．D．4．一个盒子装有除颜色外其它均相同的2个红球和3个白球，现从中任取2个球，则取到的是一个红球、一个白球的概率为（）A．B．C．D．5．下列性质中，菱形具有而矩形不一定具有的是（）A．对角线相等B．对角线互相平分C．对角线互相垂直D．邻边互相垂直6．如图，在△ABC中，AC＝1，BC＝2，AB＝，则sin B的值是（）A．B．C．2 D．7．如图，A、B、C是半径为3的⊙O上的三点，已知∠C＝30°，则弦AB的长为（）A．3 B．6 C．3.5 D．1.58．若点A（﹣5，y1），B（﹣3，y2），C（2，y3）在反比例函数y＝的图象上，则y1，y2，y3的大小关系是（）A．y1＜y3＜y2B．y1＜y2＜y3C．y3＜y2＜y1D．y2＜y1＜y39．某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（）A．560（1+x）2＝315 B．560（1﹣x）2＝315C．560（1﹣2x）2＝315 D．560（1﹣x2）＝31510．如图，已知∠DAB＝∠CAE，那么添加下列一个条件后，仍然无法判定△ABC∽△ADE的是（）A．＝B．＝C．∠B＝∠D D．∠C＝∠AED 二．填空题11．在△ABC中，若∠C＝90°，cos∠A＝，则∠A等于．12．方程2x﹣4＝0的解也是关于x的方程x2+mx+2＝0的一个解，则m的值为．13．如图，在△ABC中，已知∠ACB＝130°，∠BAC＝20°，BC＝2，以点C为圆心，CB为半径的圆交AB于点D，则BD的长为．14．二次函数y＝ax2+bx+c的图象如图，则点（，）在第象限．三．解答题15．（1）计算：﹣4sin45°+（2019﹣π）0﹣32（2）解方程：（x+5）（x+1）＝2116．如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于E，交BA的延长线于点F．（1）求证：∠DCP＝∠DAP；（2）如果PE＝3，EF＝5，求线段PC的长．17．为了解市民对全市创卫工作的满意程度，某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计，将调查结果分为不满意，一般，满意，非常满意四类，回收、整理好全部问卷后，得到下列不完整的统计图．请结合图中信息，解决下列问题：（1）求此次调查中接受调查的人数．（2）求此次调查中结果为非常满意的人数．（3）兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访，已知4位市民中有2位来自甲区，另2位来自乙区，请用列表或用画树状图的方法求出选择的市民均来自甲区的概率．18．如图，一航船在A处测到北偏东60°的方向有一灯塔B，航船向东以每小时20海里的速度航行2小时到达C处，又测到灯塔B在北偏东15°的方向上．求此时航船与灯塔相距多少海里？（结果保留根号）19．如图，已知一次函数y1＝kx+b的图象与x轴相交于点A，与反比例函数y2＝相交于B （﹣1，5），C（，d）两点．（1）利用图中条件，求反比例和一次函数的解析式；（2）连接OB，OC，求△BOC的面积．20．如图，在Rt△ABC中，AB⊥BC，以AB为直径的圆交AC于点D，E是BC的中点，连接DE．（1）求证：DE是⊙O的切线；（2）设⊙O的半径为r，证明r2＝AD•OE；（3）若DE＝4，sin C＝，求AD之长．B卷一,填空题21．点P（a，b）是直线y＝x﹣2上一点，则代数式a2﹣2ab+b2﹣1的值为．22．有五张正面分别标有数﹣7，0，1，2，5的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将卡片上的数记为a，则使关于x的方程﹣2＝有正整数解的概率为．23．如图，直线AB交双曲线y＝于A、B两点，交x轴于点C，且B恰为线段AC的中点，连结OA．若S△OAC＝，则k的值为．24．在平面直角坐标系中，A（1，0），B（0，），过点B作直线BC∥x轴，点P是直线BC上的一个动点，以AP为边在AP右侧作Rt△APQ，使∠APQ＝90°，且AP：PQ＝1：，连结AB、BQ，则△ABQ周长的最小值为．25．如图，在矩形ABCD中，AB＝4，BC＝6，点E为对角线BD的中点，点F在CB的延长线上，且BF＝1，连接EF，过点E作EG⊥EF交BA的延长线于点G，连接GF并延长交DB的延长线于点H，则＝．26．某厂按用户需求生产一种产品，成本每件20万元，规定每件售价不低于成本，且不高于40万元．经市场调查，每年的销售量y（件）与每件售价x（万元）满足一次函数关系，部分数据如下表：售价x（万元/件）25 30 35销售量y（件）50 40 30 （1）求y与x之间的函数表达式；（2）设商品每年的总利润为W（万元），求W与x之间的函数表达式（利润＝收入﹣成本）；（3）试说明（2）中总利润W随售价x的变化而变化的情况，并指出售价为多少万元时获得最大利涧，最大利润是多少？27．（1）如图1，△ABC为等边三角形，点D、E分别为边AB、AC上的一点，将图形沿线段DE所在的直线翻折，使点A落在BC边上的点F处．求证：BF•CF＝BD•CE．（2）如图2，按图1的翻折方式，若等边△ABC的边长为4，当DF：EF＝3：2时，求sin ∠DFB的值；（3）如图3，在Rt△ABC中，∠A＝90°，∠ABC＝30°，AC＝2，点D是AB边上的中点，在BC的下方作射线BE，使得∠CBE＝30°，点P是射线BE上一个动点，当∠DPC ＝60°时，求BP的长；28．如图，一次函数y＝x+2的图象与坐标轴交于A、B两点，点C的坐标为（﹣1，0），二次函数y＝ax2+bx+c的图象经过A、B、C三点．（1）求二次函数的解析式；（2）如图1，已知点D（1，n）在抛物线上，作射线BD，点Q为线段AB上一点，过点Q 作QM⊥y轴于点M，作QN⊥BD于点M，过Q作QP∥y轴交抛物线于点P，当QM与QN的积最大时，求点P的坐标；（3）在（2）的条件下，连接AP，若点E为抛物线上一点，且满足∠APE＝∠ABO，求点E的坐标．参考答案与试题解析A卷一．选择题（共10小题）1．（﹣2）×＝（）A．﹣2 B．1 C．﹣1 D．【分析】根据有理数乘法的法则进行计算即可．【解答】解：（﹣2）×＝﹣1，故选：C．2．用配方法解一元二次方程x2+4x﹣3＝0时，原方程可变形为（）A．（x+2）2＝1 B．（x+2）2＝7 C．（x+2）2＝13 D．（x+2）2＝19 【分析】把方程两边加上7，然后把方程左边写成完全平方式即可．【解答】解：x2+4x＝3，x2+4x+4＝7，（x+2）2＝7．故选：B．3．下列几何体的主视图是三角形的是（）A．B．C．D．【分析】主视图是从物体正面看，所得到的图形．【解答】解：A、圆柱的主视图是矩形，故此选项错误；B、圆锥的主视图是三角形，故此选项正确；C、球的主视图是圆，故此选项错误；D、正方体的主视图是正方形，故此选项错误；故选：B．4．一个盒子装有除颜色外其它均相同的2个红球和3个白球，现从中任取2个球，则取到的是一个红球、一个白球的概率为（）A．B．C．D．【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与取到的是一个红球、一个白球的情况，再利用概率公式求解即可求得答案．【解答】解：画树状图得：∵共有20种等可能的结果，取到的是一个红球、一个白球的有12种情况，∴取到的是一个红球、一个白球的概率为：＝．故选：C．5．下列性质中，菱形具有而矩形不一定具有的是（）A．对角线相等B．对角线互相平分C．对角线互相垂直D．邻边互相垂直【分析】菱形的性质有：四边形相等，两组对边分别平行，对角相等，邻角互补，对角线互相垂直且平分，且每一组对角线平分一组对角．矩形的性质有：两组对边分别相等，两组对边分别平行，四个内角都是直角，对角线相等且平分．【解答】解：（A）对角线相等是矩形具有的性质，菱形不一定具有；（B）对角线互相平分是菱形和矩形共有的性质；（C）对角线互相垂直是菱形具有的性质，矩形不一定具有；（D）邻边互相垂直是矩形具有的性质，菱形不一定具有．故选：C．6．如图，在△ABC中，AC＝1，BC＝2，AB＝，则sin B的值是（）A．B．C．2 D．【分析】利用正弦函数的定义计算即可．【解答】解：∵在△ABC中，∠ACB＝90°，AC＝1，BC＝2，AB＝，∴sin B＝．故选：B．7．如图，A、B、C是半径为3的⊙O上的三点，已知∠C＝30°，则弦AB的长为（）A．3 B．6 C．3.5 D．1.5【分析】根据圆周角定理求出∠AOB，根据等边三角形的判定求出△AOB是等边三角形，再根据等边三角形的性质得出即可．【解答】解：∵∠C＝30°，∴根据圆周角定理得：∠AOB＝2∠C＝60°，∵OA＝OB＝3，∴△AOB是等边三角形，∴AB＝OA＝3，故选：A．8．若点A（﹣5，y1），B（﹣3，y2），C（2，y3）在反比例函数y＝的图象上，则y1，y2，y3的大小关系是（）A．y1＜y3＜y2B．y1＜y2＜y3C．y3＜y2＜y1D．y2＜y1＜y3【分析】直接利用反比例函数图象的分布，结合增减性得出答案．【解答】解：∵点A（﹣5，y1），B（﹣3，y2），C（2，y3）在反比例函数y＝的图象上，∴A，B点在第三象限，C点在第一象限，每个图象上y随x的增大减小，∴y3一定最大，y1＞y2，∴y2＜y1＜y3．故选：D．9．某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（）A．560（1+x）2＝315 B．560（1﹣x）2＝315C．560（1﹣2x）2＝315 D．560（1﹣x2）＝315【分析】设每次降价的百分率为x，根据降价后的价格＝降价前的价格（1﹣降价的百分率），则第一次降价后的价格是560（1﹣x），第二次后的价格是560（1﹣x）2，据此即可列方程求解．【解答】解：设每次降价的百分率为x，由题意得：560（1﹣x）2＝315，故选：B．10．如图，已知∠DAB＝∠CAE，那么添加下列一个条件后，仍然无法判定△ABC∽△ADE的是（）A．＝B．＝C．∠B＝∠D D．∠C＝∠AED 【分析】利用相似三角形的判定依次判断可求解；【解答】解：∵∠DAB＝∠CAE，∴∠DAE＝∠BAC，A、若，且∠DAE＝∠BAC，无法判定△ABC∽△ADE，故选项A符合题意；B、若，且∠DAE＝∠BAC，可判定△ABC∽△ADE，故选项B不符合题意；C、若∠B＝∠D，且∠DAE＝∠BAC，可判定△ABC∽△ADE，故选项C不符合题意；D、若∠C＝∠AED，且∠DAE＝∠BAC，可判定△ABC∽△ADE，故选项D不符合题意；故选：A．二．填空题11．在△ABC中，若∠C＝90°，cos∠A＝，则∠A等于60°．【分析】直接利用特殊角的三角函数值求出即可．【解答】解：∵在△ABC中，∠C＝90°，cos∠A＝，∴∠A＝60°，故答案为：60°．12．方程2x﹣4＝0的解也是关于x的方程x2+mx+2＝0的一个解，则m的值为﹣3 ．【分析】先求出方程2x﹣4＝0的解，再把x的值代入方程x2+mx+2＝0，求出m的值即可．【解答】解：2x﹣4＝0，解得：x＝2，把x＝2代入方程x2+mx+2＝0得：4+2m+2＝0，解得：m＝﹣3．故答案为：﹣3．13．如图，在△ABC中，已知∠ACB＝130°，∠BAC＝20°，BC＝2，以点C为圆心，CB为半径的圆交AB于点D，则BD的长为2．【分析】如图，作CE⊥AB于E，在Rt△BCE中利用30度性质即可求出BE，再根据垂径定理可以求出BD．【解答】解：如图，作CE⊥AB于E．∵∠B＝180°﹣∠A﹣∠ACB＝180°﹣20°﹣130°＝30°，在Rt△BCE中，∵∠CEB＝90°，∠B＝30°，BC＝2，∴CE＝BC＝1，BE＝CE＝，∵CE⊥BD，∴DE＝EB，∴BD＝2EB＝2．故答案为2．14．二次函数y＝ax2+bx+c的图象如图，则点（，）在第三象限．【分析】根据抛物线的开口向上可得：a＞0，根据抛物线的对称轴在y轴左边可得：a，b同号，所以b＞0．根据抛物线与y轴的交点在负半轴可得：c＜0．所以bc＜0，所以点（，）在第三象限．【解答】解：∵抛物线的开口向上，∴a＞0，∵对称轴在y轴左边，∴a，b同号，即b＞0，∵抛物线与y轴的交点在负半轴，∴c＜0，∴＜0，＜0，∴点（，）在第三象限．故答案是：三．三．解答题15．（1）计算：﹣4sin45°+（2019﹣π）0﹣32（2）解方程：（x+5）（x+1）＝21【分析】（1）根据实数的混合运算顺序和运算法则计算可得；（2）先整理成一般式，再利用因式分解法求解可得．【解答】解：（1）原式＝2﹣4×+1﹣9＝2﹣2﹣8＝﹣8；（2）方程整理，得：x2+6x﹣16＝0，∵（x﹣2）（x+8）＝0，∴x﹣2＝0或x+8＝0，解得x＝2或x＝﹣8．16．如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于E，交BA的延长线于点F．（1）求证：∠DCP＝∠DAP；（2）如果PE＝3，EF＝5，求线段PC的长．【分析】（1）由菱形的性质可得AD＝CD，∠ADB＝∠CDB，CD∥AB，由“SAS”可证△ADP ≌△CDP，可得结论；（2）通过证明△APE∽△FPA，可得，可求AP的长，即可求解．【解答】证明：（1）∵四边形ABCD是菱形，∴AD＝CD，∠ADB＝∠CDB，CD∥AB，∵AD＝CD，∠ADB＝∠CDB，且DP＝DP，∴△ADP≌△CDP（SAS）∴AP＝PC，∠DCP＝∠DAP；（2）∵CD∥AB，∴∠DCP＝∠F，且∠DCP＝∠DAP，∴∠F＝∠DAP，且∠APE＝∠APF，∴△APE∽△FPA，∴，∴，∴AP＝2，∴PC＝2．17．为了解市民对全市创卫工作的满意程度，某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计，将调查结果分为不满意，一般，满意，非常满意四类，回收、整理好全部问卷后，得到下列不完整的统计图．请结合图中信息，解决下列问题：（1）求此次调查中接受调查的人数．（2）求此次调查中结果为非常满意的人数．（3）兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访，已知4位市民中有2位来自甲区，另2位来自乙区，请用列表或用画树状图的方法求出选择的市民均来自甲区的概率．【分析】（1）由满意的有20人，占40%，即可求得此次调查中接受调查的人数．（2）由（1），即可求得此次调查中结果为非常满意的人数．（3）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与选择的市民均来自甲区的情况，再利用概率公式即可求得答案．【解答】解：（1）∵满意的有20人，占40%，∴此次调查中接受调查的人数：20÷40%＝50（人）；（2）此次调查中结果为非常满意的人数为：50﹣4﹣8﹣20＝18（人）；（3）画树状图得：∵共有12种等可能的结果，选择的市民均来自甲区的有2种情况，∴选择的市民均来自甲区的概率为：＝．18．如图，一航船在A处测到北偏东60°的方向有一灯塔B，航船向东以每小时20海里的速度航行2小时到达C处，又测到灯塔B在北偏东15°的方向上．求此时航船与灯塔相距多少海里？（结果保留根号）【分析】过C作CD⊥AB，垂足为D，在直角△ACD中，根据三角函数求得CD的长，再在直角△BCD中运用三角函数即可求解．【解答】解：作CD⊥AB，垂足为点D．根据题意可得∠BAC＝30°，∠ACB＝105°，∴∠B＝45°，∵AC＝20×2＝40（海里），∴DC＝AC•sin30°＝40×＝20（海里），∴BC＝DC÷sin45°＝20÷＝20（海里）．答：此时航船与灯塔相距20海里．19．如图，已知一次函数y1＝kx+b的图象与x轴相交于点A，与反比例函数y2＝相交于B （﹣1，5），C（，d）两点．（1）利用图中条件，求反比例和一次函数的解析式；（2）连接OB，OC，求△BOC的面积．【分析】（1）将点B的坐标代入反比例函数解析式求出c，从而得解，再将点C的坐标代入反比例函数解析式求出d，从而得到点C的坐标，然后利用待定系数法求一次函数解析式求解；（2）根据一次函数解析式求出点A的坐标，再根据S△BOC＝S△AOB+S△AOC列式计算即可得解．【解答】解：（1）将B（﹣1，5）代入y2＝得，＝5，解得c＝﹣5，所以，反比例函数解析式为y＝﹣，将点C（，d）代入y＝﹣得d＝﹣＝﹣2，所以，点C的坐标为（，﹣2），将点B（﹣1，5），C（，﹣2）代入一次函数y1＝kx+b得，，解得，所以，一次函数y1＝﹣2x+3；（2）令y＝0，则﹣2x+3＝0，解得x＝，所以，点A的坐标为（，0），所以，OA＝，S△BOC＝S△AOB+S△AOC，＝××5+××2，＝．20．如图，在Rt△ABC中，AB⊥BC，以AB为直径的圆交AC于点D，E是BC的中点，连接DE．（1）求证：DE是⊙O的切线；（2）设⊙O的半径为r，证明r2＝AD•OE；（3）若DE＝4，sin C＝，求AD之长．【分析】（1）连接OD、BD，根据圆周角定理求出∠BDA＝∠BDC＝90°，根据直角三角形的性质和等腰三角形的性质求出∠ECD＝∠EDC，∠EBD＝∠EDB即可．（2）连接OE，构造相似三角形△ADB∽△ODE，由该相似三角形的对应边成比例证得结论；（3）根据圆周角定理得到∠ADB＝∠BDC＝90°，根据直角三角形的性质得到BC＝8；然后由sin C＝求出AC的长，再根据切割线定理求出AD的长即可．【解答】（1）证明：连接OD、BD，∵AB为圆O的直径，∴∠BDA＝90°，∴∠BDC＝180°﹣90°＝90°，∵E为BC的中点，∴DE＝BC＝BE，∴∠EBD＝∠EDB，∵OD＝OB，∴∠OBD＝∠ODB，∵∠EBD+∠DBO＝90°，∴∠EDB+∠ODB＝90°，∴∠ODE＝90°，∴DE是圆O的切线．（2）证明：如图，连接BD．由（1）知，∠ODE＝∠ADB＝90°，BD⊥AC．∵E是BC的中点，O是AB的中点，∴OE是△ABC的中位线，∴OE∥AC，∴OE⊥BD．∴OE∥AC，∴∠1＝∠2．又∵∠1＝∠A，∴∠A＝∠2．即在△ADB与△ODE中，∠ADB＝∠ODE，∠A＝∠2，∴△ADB∽△ODE．∴＝，即＝．∴r2＝AD•OE；（3）∵AB为⊙O的直径，∴∠ADB＝∠BDC＝90°，∵点E为BC的中点，∴BC＝2DE＝8，∵sin C＝，∴设AB＝3x，AC＝5x，根据勾股定理得：（3x）2+82＝（5x）2，解得x＝2．则AC＝10．由切割线定理可知：82＝（10﹣AD）×10，解得，AD＝3.6．B卷21．点P（a，b）是直线y＝x﹣2上一点，则代数式a2﹣2ab+b2﹣1的值为 3 ．【分析】先把点（a，b）代入一次函数y＝x﹣2求出a﹣b的值，再代入代数式进行计算即可．【解答】解：∵点（a，b）在一次函数y＝x﹣2上，∴b＝a﹣2，即a﹣b＝2，∴原式＝（a﹣b）2﹣1＝22﹣1＝4﹣1＝3．故答案为：3．22．有五张正面分别标有数﹣7，0，1，2，5的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将卡片上的数记为a，则使关于x的方程﹣2＝有正整数解的概率为．【分析】易得分式方程的解，看所给5个数中，能使分式方程有整数解的情况数占总情况数的多少即可．【解答】解：﹣2＝，解得：x＝，∵分式方程的解为正整数，∴a+1＞0，又∵x≠1，∴a≠5，∴a＝0或a＝1或a＝2，∴使关于x的分式方程有正整数解的概率为．故答案为：．23．如图，直线AB交双曲线y＝于A、B两点，交x轴于点C，且B恰为线段AC的中点，连结OA．若S△OAC＝，则k的值为．【分析】设A点坐标为（a，），C点坐标为（b，0），根据线段中点坐标公式得到B点坐标为（，），利用反比例函数图象上点的坐标特征得到•＝k，得到b＝3a，然后根据三角形面积公式得到•3a•＝，于是可计算出k＝．【解答】解：设A点坐标为（a，），C点坐标为（b，0），∵B恰为线段AC的中点，∴B点坐标为（，），∵B点在反比例函数图象上，∴•＝k，∴b＝3a，∵S△OAC＝，∴b•＝，∴•3a•＝，∴k＝．故答案为．24．在平面直角坐标系中，A（1，0），B（0，），过点B作直线BC∥x轴，点P是直线BC上的一个动点，以AP为边在AP右侧作Rt△APQ，使∠APQ＝90°，且AP：PQ＝1：，连结AB、BQ，则△ABQ周长的最小值为2+2 ．【分析】设P（m，）．作AM⊥BC于M，QN⊥BC于N．利用新三角形的性质求出点Q的坐标推出，点Q的运动轨迹是直线y＝﹣x+5，作点A关于直线y＝﹣x+5的对称点A′，连接BA′交直线于Q′，连接AQ′，此时△ABQ′的周长最小．【解答】解：设P（m，）．作AM⊥BC于M，QN⊥BC于N．∵∠AMP＝∠APQ＝∠QNP＝90°，∴∠APM+∠NPQ＝90°，∠NPQ+∠PQN＝90°，∴∠APM＝∠PQN，∴△AMP∽△PNQ，∴＝＝＝，∴＝＝，∴PN＝3，NQ＝（m﹣1），∴Q（m+3，2﹣m），∴点Q的运动轨迹是y＝﹣x+5，作点A关于直线y＝﹣x+5的对称点A′，连接BA′交直线于Q′，连接AQ′，此时△ABQ′的周长最小．∵A′（7，2），B（0，），A（1，0），∴A′B＝＝2，AB＝＝2，∴△ABQ的周长的最小值＝AQ′+BQ′+AB＝A′Q′+BQ′+AB＝A′B+AB＝2+2，故答案为2+2．25．如图，在矩形ABCD中，AB＝4，BC＝6，点E为对角线BD的中点，点F在CB的延长线上，且BF＝1，连接EF，过点E作EG⊥EF交BA的延长线于点G，连接GF并延长交DB 的延长线于点H，则＝．【分析】过点E作EM⊥BC于点M，过点E作EN⊥AB于点N，则EM＝2，EN＝BM＝3，求出EF的长和GN的长，则GB的长可求出，证明△FEH∽△BGH，可得得出结论．【解答】解：过点E作EM⊥BC于点M，过点E作EN⊥AB于点N，∴四边形ENBM是矩形，∵E是BD的中点，∴EM＝＝2，EN＝BM＝＝3，∴MF＝BF+BM＝1+3＝4，∴＝＝2，∵EG⊥EF，∴∠GEF＝90°，∴∠EGB＝∠BFE，∴tan∠EGB＝tan∠BFE，∴，∴GN＝6，∴GB＝GN+BN＝6+2＝8∵∠GEF＝∠GBF＝90°∴G，E，B，F四点共圆，∴∠BGF＝∠BEF，∵∠EHF＝∠GHB，∴△FEH∽△BGH，∴，∴．故答案为：．26．某厂按用户需求生产一种产品，成本每件20万元，规定每件售价不低于成本，且不高于40万元．经市场调查，每年的销售量y（件）与每件售价x（万元）满足一次函数关系，部分数据如下表：售价x（万元/件）25 30 35销售量y（件）50 40 30 （1）求y与x之间的函数表达式；（2）设商品每年的总利润为W（万元），求W与x之间的函数表达式（利润＝收入﹣成本）；（3）试说明（2）中总利润W随售价x的变化而变化的情况，并指出售价为多少万元时获得最大利涧，最大利润是多少？【分析】（1）根据题意可以设出y与x之间的函数表达式，然后根据表格中的数据即可求得y与x之间的函数表达式；（2）根据题意可以写出W与x之间的函数表达式；（3）根据（2）中的函数解析式，将其化为顶点式，然后根据成本每千克20元，规定每千克售价不低于成本，且不高于40元，即可得到利润W随售价x的变化而变化的情况，以及售价为多少元时获得最大利润，最大利润是多少．【解答】解：（1）设y与x之间的函数解析式为y＝kx+b（k≠0），，解得，即y与x之间的函数表达式是y＝﹣2x+100；（2）由题意可得，W＝（x﹣20）（﹣2x+100）＝﹣2x2+140x﹣2000，即W与x之间的函数表达式是W＝﹣2x2+140x﹣2000；（3）∵W＝﹣2x2+140x﹣2000＝﹣2（x﹣35）2+450，20≤x≤40，∴当20≤x≤35时，W随x的增大而增大，当35≤x≤40时，W随x的增大而减小，当x＝35时，W取得最大值，此时W＝450，答：当20≤x≤35时，W随x的增大而增大，当35≤x≤40时，W随x的增大而减小，售价为35元时获得最大利润，最大利润是450元．27．（1）如图1，△ABC为等边三角形，点D、E分别为边AB、AC上的一点，将图形沿线段DE所在的直线翻折，使点A落在BC边上的点F处．求证：BF•CF＝BD•CE．（2）如图2，按图1的翻折方式，若等边△ABC的边长为4，当DF：EF＝3：2时，求sin ∠DFB的值；（3）如图3，在Rt△ABC中，∠A＝90°，∠ABC＝30°，AC＝2，点D是AB边上的中点，在BC的下方作射线BE，使得∠CBE＝30°，点P是射线BE上一个动点，当∠DPC ＝60°时，求BP的长；【分析】（1）先利用等式的性质判断出∠BDF＝∠CFE，进而得出△BDF∽△CFE，即可得出结论；（2）先表示出BH＝x，DH＝x，再由（1）△BDF∽△CFE，进而表示出CF＝2x，BF＝BC﹣CF＝4﹣2x，HF＝BF﹣BH＝4﹣2x﹣x＝4﹣x，再利用勾股定理建立方程求出x的值，即可得出结论．【解答】（1）证明：∵△ABC是等边三角形，∠A＝∠B＝∠C＝60°，∴∠BDF+∠BFD＝180°﹣∠B＝120°，由折叠知，∠DFE＝∠A＝60°，∴∠CFE+∠BFD＝120°，∴∠BDF＝∠CFE，∵∠B＝∠C＝60°，∴△BDF∽△CFE，∴，∴BF•CF＝BD•CE；（2）解：如图2，设BD＝3x（x＞0），则AD＝AB﹣BD＝4﹣3x，由折叠知，DF＝AD＝4﹣3x，过点D作DH⊥BC于H，∴∠DHB＝∠DHF＝90°，∵∠B＝60°，∴BH＝x，DH＝x，由（1）知，△BDF∽△CFE，∴＝，∵DF：EF＝3：2，∴＝，CF＝2x，∴BF＝BC﹣CF＝4﹣2x，∴HF＝BF﹣BH＝4﹣2x﹣x＝4﹣x，在Rt△DHF中，DH2+HF2＝DF2，∴（x）2+（4﹣x）2＝（4﹣3x）2，∴x＝0（舍）或x＝，∴DH＝，DF＝4﹣3×＝，∴sin∠DFB＝＝＝；（3）如图3，在Rt△ABC中，AC＝2，∠ABC＝30°，∴BC＝2AC＝4，AB＝AC＝6，∵点D是AB的中点，∴BD＝AB＝3，过点C作BC的垂线交BP的延长线于Q，∴∠BCQ＝90°，在Rt△BCQ中，∠CBE＝30°，∴CQ＝＝4，∴BQ＝2CQ＝8，∴∠BCQ＝90°，∵∠CBE＝30°，∴∠Q＝90°﹣∠CBE＝60°，∴∠DBP＝∠ABC+∠CBE＝60°＝∠Q，∴∠CPQ+∠PCQ＝120°，∵∠DPC＝60°，∴∠BPD+∠CPQ＝120°，∴∠BPD＝∠PCQ，∴△BDP∽△QPC，∴＝，∴，∴BP＝2或BP＝6．28．如图，一次函数y＝x+2的图象与坐标轴交于A、B两点，点C的坐标为（﹣1，0），二次函数y＝ax2+bx+c的图象经过A、B、C三点．（1）求二次函数的解析式；（2）如图1，已知点D（1，n）在抛物线上，作射线BD，点Q为线段AB上一点，过点Q 作QM⊥y轴于点M，作QN⊥BD于点M，过Q作QP∥y轴交抛物线于点P，当QM与QN的积最大时，求点P的坐标；（3）在（2）的条件下，连接AP，若点E为抛物线上一点，且满足∠APE＝∠ABO，求点E的坐标．【分析】（1）一次函数y＝x+2的图象与坐标轴交于A、B两点，则点A、B的坐标分别为：（0，2）、（4，0），即可求解；（2）即直线BD的倾斜角为45°，则∠QGN＝45°，QN＝QG，QM•QN＝m×（﹣m+4+m﹣2）＝（﹣m2+2m），即可求解；（3）分PE在AP下方、PE在AP上方两种情况，利用解直角三角形的方法，分别求解即可．【解答】解：（1）一次函数y＝x+2的图象与坐标轴交于A、B两点，则点A、B的坐标分别为：（0，2）、（4，0），则抛物线的表达式为：y＝a（x﹣4）（x+1）＝a（x2﹣3x﹣4），即﹣4a＝2，解得：a＝﹣，则抛物线的表达式为：y＝﹣x2+x+2…①；（2）点D（1，3），点B（4，0），则BD所在的函数表达式为：y＝﹣x+4；即直线BD的倾斜角为45°，则∠QGN＝45°，QN＝QG，设点Q（m，﹣m+2），则点G（m，﹣m+4），QM•QN＝m×（﹣m+4+m﹣2）＝（﹣m2+2m），当m＝2时，QM与QN的积最大，则点P（2，3）；（3）设：∠APE＝∠ABO＝∠α，则tan；①当PE在AP下方时，如图，由点A（0，2）、P（2，3）知，AP＝，设AP与y轴的夹角为β，则tanβ＝2，过点H作MH⊥PA交PA的延长线于点M，设：MA＝x，则MH＝2x，tan∠APH＝＝＝tanα＝，解得：x＝，则AH＝x＝，则点H（0，），由点H、P的坐标得，直线PH的表达式为：y＝x+…②，联立①②并解得：x＝2（舍去）或﹣，故点E（﹣，﹣）；②当PE在AP上方时，同理可得：点E（1，3）；综上，点E的坐标为：（﹣，﹣）或E（1，3）．。

2020年四川省成都市高新区中考数学一诊试卷一、选择题（本大题共10个小题，每小题3分，共30分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）1．下列图形既是轴对称图形又是中心对称图形的是（）A．等腰三角形B．等边三角形C．平行四边形D．圆2．一个口袋中有红球、白球共10个，这些球除颜色外都相同．将口袋中的球搅拌均匀，从中随机摸出一个球，记下颜色后再放回口袋中．不断重复这一过程，共摸了100次球，发现有70次摸到红球．请你估计这个口袋中红球的数量是（）A．4B．5C．6D．73．如图所示的四棱柱的主视图为（）A．B．C．D．4．已知a，b，c，d是成比例线段，其中a＝3cm，b＝2cm，c＝6cm，则d的长度为（）A．4cm B．5cm C．6cm D．9cm5．某学习小组利用三角形相似测量学校旗杆的高度．测得身高为1.6米小明同学在阳光下的影长为1米，此时测得旗杆的影长为9米．则学校旗杆的高度是（）A．9米B．14.4米C．16米D．13.4米6．已知反比例函数的图象经过点（2，3），那么下列各点在该函数图象上的是（）A．（﹣，3）B．（2，﹣）C．（9，）D．（4，2）7．如图，点A、B、C在⊙O上，△OAB为等边三角形，则∠ACB的度数是（）A．60°B．50°C．40°D．30°8．顺次连接任意四边形四边中点所得的四边形一定是（）A．平行四边形B．矩形C．菱形D．正方形9．二次函数y＝x2﹣2的图象是一条抛物线，下列关于该抛物线的说法正确的是（）A．抛物线开口向下B．当x＝0时，函数的最大值是﹣2C．抛物线的对称轴是直线x＝2D．抛物线与x轴有两个交点10．函数y＝与y＝kx﹣k（k≠0）在同一平面直角坐标系中的图象可能是（）A．B．C．D．二、填空题（本大题共4个小题，每小题4分，共16分，答案写在答题卡上）11．若2a＝3b，则a：b＝．12．二次函数y＝2（x﹣2）2﹣1的顶点坐标是．13．在△ABC中与△DEF中，已知＝＝＝，则三角形△ABC与△DEF的周长之比为．14．如图：分别以A、C为圆心，以大于AC的长为半径作弧，两条弧分别相交于点B、D，依次连接A，B，C，D和BD．若AB＝5，AC＝8，则BD＝．三、解答题（本大题共6个小题，共54分，解答过程写在答题卡上）15．（1）计算：（π﹣2019）0+2sin60°﹣+|1﹣|（2）解方程：x2﹣2x﹣3＝016．已知：如图，在▱ABCD中，BA＝BD，M，N分别是AD和BC的中点．求证：四边形BNDM是矩形．17．2018年，国家卫生健康委员会和国家教育部在全国开展了儿童青少年近视调查工作，调查数据显示，全国儿童青少年近视过半．某校初三学习小组为了解本校学生对自己视力保护的重视程度，随机在校内调查了部分学生，调查结果分为“非常重视”“重视”“比较重视”“不重视”四类，并将结果绘制成下面的两幅不完整的统计图：根据图中信息，解答下列问题：（1）求本次调查的学生总人数，并补全条形统计图；（2）该校共有学生1000人，请你估计该校对视力保护“非常重视”的学生人数；（3）对视力“非常重视”的4人有A1，A2两名男生，B1，B2两名女生，若从中随机抽取两人向全校作视力保护交流，请利用树状图或列表的方法，求恰好抽到一男一女的概率．18．如图，渔船跟踪鱼群由西向东航行，到达A处时，测得小岛C位于它的北偏东53°方向，再航行3km达到B处（AB＝3km），测得小岛C位于它的北偏东45°方向．小岛C 的周围8km内有暗礁，如果渔船不改变航向继续向东航行，请你通过计算说明渔船有无触礁的危险？（参考数据：sin53°≈，cos53°≈，tan53°≈）19．如图，在平面直角坐标系xOy中，一次函数y＝x﹣1与x轴交于点C，与反比例函数y ＝（k＞0）交于点A（2，m）和点B．（1）求反比例函数表达式及点B的坐标；（2）点P是x轴上的一点，若△PAB的面积是6，求点P的坐标．20．如图，在Rt△ABC中，∠ACB＝90°，以AC为直径作⊙O，点D在⊙O上，BD＝BC，DE⊥AC，垂足为点E，DE与⊙O和AB分别交于点M、F．连接BO、DO、AM．（1）证明：BD是⊙O的切线；（2）若tan∠AMD＝，AD＝2，求⊙O的半径长；（3）在（2）的条件下，求DF的长．B卷一、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）21．在同一直角坐标系中，正比例函数y＝k1x的图象与反比例函数的图象有公共点，则k1k20（填“＞”、“＝”或“＜”）．22．一元二次方程x2﹣3x﹣2＝0的两根分别是m、n，则m3﹣3m2+2n＝．23．如图，在菱形ABCD四个顶点的字母中，任取两个字母相互交换它们的位置，交换后能使字母A、B在同一条对角线上的概率是．24．如图，在平面直角坐标系xOy中，矩形OABC的边OA、OC分别在x轴和y轴上，OA ＝6，OC＝4，点Q是AB边上一个动点，过点Q的反比例函y＝（x＞0）与BC边交于点P．若将△PBQ沿PQ折叠，点B的对应点E恰好落在对角线AC上，则此时反比例函数的解析式是．25．已知矩形ABCD的长和宽分别是n和1，其中n是正整数，若存在另一个矩形A′B′C′D′，它的周长和面积分别是矩形ABCD周长和面积的一半，则满足条件的n的最小值是．二、解答题（本大题共3个小题，共30分，解答过程写在答题卡上）26．某商店购进一批单价为8元的商品，经调研发现，这种商品每天的销售量y（件）是关于销售单价x（元）的一次函数，其关系如表：x（元）1011121314y（件）10090807060（1）求y与x之间的关系式；（2）设商店每天销售利润为w（元），求出w与x之间的关系式，并求出每天销售单价定为多少时利润最大？27．如图，在△ABC与△EBD中，∠ABC＝∠EBD＝90°，AB＝6，BC＝3，EB＝2，BD ＝，射线AE与直线CD交于点P．（1）求证：△ABE∽△CBD；（2）若AB∥ED，求tan∠PAC的值；（3）若△EBD绕点B逆时针旋转一周，直接写出线段AP的最大值与最小值．28．在平面直角坐标系xOy中，抛物线y＝a（x﹣3）（x+1）与x轴交于A、B两点，与轴交于点C（0，﹣），连接AC、BC．（1）求抛物线的函数表达式；（2）抛物线的对称轴与x轴交于点D，连接CD，点E为第二象限抛物线上的一动点，EF∥BC，直线EF与抛物线交于点F，设直线EF的表达式为．①如图①，直线y＝kx+b与抛物线对称轴交于点G，若△DGF∽△BDC，求k、b的值；②如图②，直线y＝kx+b与y轴交于点M，与直线y＝x交于点H，若﹣＝，求b的值．2020年四川省成都市高新区中考数学一诊试卷参考答案与试题解析一、选择题（本大题共10个小题，每小题3分，共30分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）1．下列图形既是轴对称图形又是中心对称图形的是（）A．等腰三角形B．等边三角形C．平行四边形D．圆【解答】解：A、等腰三角形是轴对称图形，不是中心对称图形；B、等边三角形是轴对称图形，不是中心对称图形；C、平行四边形不是轴对称图形，是中心对称图形；D、圆是轴对称图形，是中心对称图形．故选：D．2．一个口袋中有红球、白球共10个，这些球除颜色外都相同．将口袋中的球搅拌均匀，从中随机摸出一个球，记下颜色后再放回口袋中．不断重复这一过程，共摸了100次球，发现有70次摸到红球．请你估计这个口袋中红球的数量是（）A．4B．5C．6D．7【解答】解：由题意可得，红球的概率为＝70%，则这个口袋中红球的个数：10×70%＝7（个），故选：D．3．如图所示的四棱柱的主视图为（）A．B．C．D．【解答】解：由图可得，几何体的主视图是：故选：B．4．已知a，b，c，d是成比例线段，其中a＝3cm，b＝2cm，c＝6cm，则d的长度为（）A．4cm B．5cm C．6cm D．9cm【解答】解：因为a，b，c，d是成比例线段，可得：d＝cm，故选：A．5．某学习小组利用三角形相似测量学校旗杆的高度．测得身高为1.6米小明同学在阳光下的影长为1米，此时测得旗杆的影长为9米．则学校旗杆的高度是（）A．9米B．14.4米C．16米D．13.4米【解答】解：∵同一时刻物高与影长成正比例．∴1.6：1＝旗杆的高度：9，∴旗杆的高度为：14.4米．故选：B．6．已知反比例函数的图象经过点（2，3），那么下列各点在该函数图象上的是（）A．（﹣，3）B．（2，﹣）C．（9，）D．（4，2）【解答】解：∵反比例函数的图象经过点（2，3），∴k＝2×3＝6．A、∵﹣×3＝﹣6≠6，∴此点不在函数图象上；B、∵2×（﹣）＝﹣6≠6，∴此点不在函数图象上；C、∵9×＝6，∴此点在函数图象上；D、∵4×2＝8≠6，∴此点不在函数图象上；故选：C．7．如图，点A、B、C在⊙O上，△OAB为等边三角形，则∠ACB的度数是（）A．60°B．50°C．40°D．30°【解答】解：∵△OAB为等边三角形，∴∠AOB＝60°，∴∠ACB＝∠AOB＝30°．故选：D．8．顺次连接任意四边形四边中点所得的四边形一定是（）A．平行四边形B．矩形C．菱形D．正方形【解答】解：连接BD，已知任意四边形ABCD，E、F、G、H分别是各边中点．∵在△ABD中，E、H是AB、AD中点，∴EH∥BD，EH＝BD．∵在△BCD中，G、F是DC、BC中点，∴GF∥BD，GF＝BD，∴EH＝GF，EH∥GF，∴四边形EFGH为平行四边形．故选：A．9．二次函数y＝x2﹣2的图象是一条抛物线，下列关于该抛物线的说法正确的是（）A．抛物线开口向下B．当x＝0时，函数的最大值是﹣2C．抛物线的对称轴是直线x＝2D．抛物线与x轴有两个交点【解答】解：A、a＝1＞0，则抛物线y＝x2﹣2的开口向上，故本选项错误，不符合题意；B、当x＝0时，函数的最小值是﹣2，故本选项错误，不符合题意；C、抛物线的对称轴为直线x＝0，故本选项错误，不符合题意；D、当y＝0时，x2﹣2＝0，此方程有两个不相等的实数解，即抛物线与x轴有两个交点，故本选项符合题意；故选：D．10．函数y＝与y＝kx﹣k（k≠0）在同一平面直角坐标系中的图象可能是（）A．B．C．D．【解答】解：A、∵由反比例函数的图象在二、四象限可知，k＜0，∴﹣k＞0，∴一次函数y＝kx﹣k的图象经过一、二、四象限，故本选项正确；B、∵由反比例函数的图象在二、四象限可知，k＜0，∴﹣k＞0，∴一次函数y＝kx﹣k的图象经过一、二、四象限，故本选项错误；C、∵由反比例函数的图象在一、三象限可知，k＞0，∴﹣k＜0，∴一次函数y＝kx﹣k的图象经过一、三、四象限，故本选项错误；D、∵由反比例函数的图象在一、三象限可知，k＞0，∴﹣k＜0，∴一次函数y＝kx﹣k的图象经过一、三、四象限，故本选项错误；故选：A．二、填空题（本大题共4个小题，每小题4分，共16分，答案写在答题卡上）11．若2a＝3b，则a：b＝3：2．【解答】解：∵2a＝3b，∴a：b＝3：2．故答案为：3：2．12．二次函数y＝2（x﹣2）2﹣1的顶点坐标是（2，﹣1）．【解答】解：二次函数y＝2（x﹣2）2﹣1的顶点坐标是（2，﹣1），故答案为：（2，﹣1）．13．在△ABC中与△DEF中，已知＝＝＝，则三角形△ABC与△DEF的周长之比为．【解答】解：∵＝＝＝∴△ABC∽△DEF∴△ABC与△DEF的相似比为∵△ABC与△DEF的周长之比等于△ABC与△DEF的相似比∴△ABC与△DEF的周长之比为故答案为：．14．如图：分别以A、C为圆心，以大于AC的长为半径作弧，两条弧分别相交于点B、D，依次连接A，B，C，D和BD．若AB＝5，AC＝8，则BD＝6．【解答】解：由作法得AB＝AD＝CB＝CD＝5，所以四边形ABCD为菱形；∵四边形ABCD为菱形，∴OA＝OC＝4，OB＝OD，AC⊥BD，在Rt△AOB中，OB＝＝3，∴BD＝2OB＝6．故答案为：6．三、解答题（本大题共6个小题，共54分，解答过程写在答题卡上）15．（1）计算：（π﹣2019）0+2sin60°﹣+|1﹣|（2）解方程：x2﹣2x﹣3＝0【解答】解：（1）原式＝1+2×﹣2+﹣1＝1+﹣2+﹣1＝0；（2）∵x2﹣2x﹣3＝0，∴（x﹣3）（x+1）＝0，则x﹣3＝0或x+1＝0，解得x＝3或x＝﹣1．16．已知：如图，在▱ABCD中，BA＝BD，M，N分别是AD和BC的中点．求证：四边形BNDM是矩形．【解答】证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，BA＝DC，∵BA＝BD，∴BA＝BD＝DC，∵M、N分别是AD和BC的中点，∴BM⊥AD，DM＝AD，BN＝BC，∴DM＝BN，又∵DM∥BN，∴四边形BMDN是平行四边形，∵BM⊥AD，∴∠BMD＝90°，∴四边形BMDN是矩形．17．2018年，国家卫生健康委员会和国家教育部在全国开展了儿童青少年近视调查工作，调查数据显示，全国儿童青少年近视过半．某校初三学习小组为了解本校学生对自己视力保护的重视程度，随机在校内调查了部分学生，调查结果分为“非常重视”“重视”“比较重视”“不重视”四类，并将结果绘制成下面的两幅不完整的统计图：根据图中信息，解答下列问题：（1）求本次调查的学生总人数，并补全条形统计图；（2）该校共有学生1000人，请你估计该校对视力保护“非常重视”的学生人数；（3）对视力“非常重视”的4人有A1，A2两名男生，B1，B2两名女生，若从中随机抽取两人向全校作视力保护交流，请利用树状图或列表的方法，求恰好抽到一男一女的概率．【解答】解：（1）本次调查的学生总人数有：16÷20%＝80（人）；重视的人数有：80﹣4﹣36﹣16＝24（人），补图如下：（2）根据题意得：1000×＝50（人），答：该校对视力保护“非常重视”的学生人有50人；（3）画树状图如下：共有12种可能的结果，恰好抽到一男一女的结果有8个，则P（恰好抽到一男一女的）＝＝．18．如图，渔船跟踪鱼群由西向东航行，到达A处时，测得小岛C位于它的北偏东53°方向，再航行3km达到B处（AB＝3km），测得小岛C位于它的北偏东45°方向．小岛C 的周围8km内有暗礁，如果渔船不改变航向继续向东航行，请你通过计算说明渔船有无触礁的危险？（参考数据：sin53°≈，cos53°≈，tan53°≈）【解答】解：过点C作CD⊥AB，垂足为点D，由题意可得：∠ACD＝53°，∠BCD＝∠CBD＝45°，故BD＝CD，设BD＝CD＝x，则AD＝3+x，在Rt△ACD中，tan∠ACD＝，则tan53°＝，故≈，解得：x≈9≥8，∴如果渔船不改变航向继续向东航行，渔船无触礁的危险．19．如图，在平面直角坐标系xOy中，一次函数y＝x﹣1与x轴交于点C，与反比例函数y ＝（k＞0）交于点A（2，m）和点B．（1）求反比例函数表达式及点B的坐标；（2）点P是x轴上的一点，若△PAB的面积是6，求点P的坐标．【解答】解：（1）把A（2，m）代入一次函数y＝x﹣1，得m＝2﹣1＝1，∴A（2，1），把A（2，1）代入反比例函数y＝（k＞0），得k＝2，∴反比例函数解析式为y＝，解方程组得，，∴B（﹣1，﹣2）；（2）设点P的坐标为（m，0），在y＝x﹣1中，令y＝0，得x＝1，∴点C的坐标为（1，0），∵S△PAB ＝S△PAC+S△PBC＝，∴|m﹣1|＝4，∴m＝5或﹣3，∴点P的坐标为（5，0）或（﹣3，0）．20．如图，在Rt△ABC中，∠ACB＝90°，以AC为直径作⊙O，点D在⊙O上，BD＝BC，DE⊥AC，垂足为点E，DE与⊙O和AB分别交于点M、F．连接BO、DO、AM．（1）证明：BD是⊙O的切线；（2）若tan∠AMD＝，AD＝2，求⊙O的半径长；（3）在（2）的条件下，求DF的长．【解答】解：（1）在△BDO和△BCO中，BD＝BC，OD＝OC，BO＝BO，故△BDO≌△BCO（SSS），∴∠BDO＝∠ABC＝90°，BD是⊙O的切线；（2）连接CD，则∠AMD＝∠ACD，AB是直径，故∠ADC＝90°，在Rt△ADC中，tan∠ACD＝tan∠AMD＝＝，∵AD＝2，∴CD＝4，故圆的半径为5；（3）在Rt△ADC中，DE⊥AC，则DE＝＝4，则AE＝2，由（1）知△BDO≌△BCO，∴∠BOC＝∠BOD＝∠DOC，∵∠DAE＝∠DOC，∴∠DAE＝∠BOC，∵ED⊥AC，∴∠AED＝∠OCB＝90°，∴△DAE∽△BOC，∴，即，解得：BC＝10，∴∠BAC＝∠ABC＝45°，∴∠FAE＝∠AFE＝45°，∴FE＝AE＝2，DF＝DE﹣EF＝2．B卷一、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）21．在同一直角坐标系中，正比例函数y＝k1x的图象与反比例函数的图象有公共点，则k1k2＞0（填“＞”、“＝”或“＜”）．【解答】解：∵正比例函数y＝k1x的图象与反比例函数的图象有公共点，∴k1、k2同号，∴k1k2＞0．22．一元二次方程x2﹣3x﹣2＝0的两根分别是m、n，则m3﹣3m2+2n＝6．【解答】解：由题意可知：m+n＝3，mn＝﹣2，m2＝3m+2，∴m3＝3m2+2m，∴原式＝3m2+2m﹣3m2+2n＝2（m+n）＝6，故答案为：6．23．如图，在菱形ABCD四个顶点的字母中，任取两个字母相互交换它们的位置，交换后能使字母A、B在同一条对角线上的概率是．【解答】解：共有AB互换，AC互换，BC互换，AD互换，CD互换，BD互换6种情况，符合条件的是BC互换，AD互换2种情况，所以交换后能使字母A、B在同一条对角线上的概率是＝；故答案为：．24．如图，在平面直角坐标系xOy中，矩形OABC的边OA、OC分别在x轴和y轴上，OA ＝6，OC＝4，点Q是AB边上一个动点，过点Q的反比例函y＝（x＞0）与BC边交于点P．若将△PBQ沿PQ折叠，点B的对应点E恰好落在对角线AC上，则此时反比例函数的解析式是y＝（x＞0）．【解答】解：∵四边形OABC是矩形，OA＝6，OC＝4，∴BC＝OA＝6，AB＝OC＝4，∴B（6，4），设P（，4），Q（6，），∴PC＝，AQ＝，∴PB＝6﹣，BQ＝4﹣，∴tan∠BQP＝＝＝，∵tan∠BAC＝＝＝，∴tan∠BQP＝tan∠BAC，∴∠BQP＝∠BAC，∴PQ∥AC，连接BE，∵将△PBQ沿PQ折叠，点B的对应点E恰好落在对角线AC上，∴BH＝EH，∴AQ＝BQ＝2，∴＝2，∴k＝12，∴反比例函数的解析式是y＝，故答案为：y＝．25．已知矩形ABCD的长和宽分别是n和1，其中n是正整数，若存在另一个矩形A′B′C′D′，它的周长和面积分别是矩形ABCD周长和面积的一半，则满足条件的n的最小值是6．【解答】解：设矩形A′B′C′D′的长和宽分别为x、y，则，由①得：y＝﹣x③，把③代入②得：x2﹣+＝0，b2﹣4ac＝﹣4×≥0，∴（n﹣3）2≥8，∵n是正整数，∴n的最小值是6，故答案为：6．二、解答题（本大题共3个小题，共30分，解答过程写在答题卡上）26．某商店购进一批单价为8元的商品，经调研发现，这种商品每天的销售量y（件）是关于销售单价x（元）的一次函数，其关系如表：x（元）1011121314y（件）10090807060（1）求y与x之间的关系式；（2）设商店每天销售利润为w（元），求出w与x之间的关系式，并求出每天销售单价定为多少时利润最大？【解答】解：（1）设y与x的一次函数是y＝kx+b，由表得：，解得：k＝﹣10，b＝200，∴y与x的一次函数是y＝﹣10x+200；（2）根据题意得：w＝（x﹣8）（﹣10x+200）＝﹣（x﹣14）2+360，∴w是关于x的二次函数，且二次项系数为﹣1＜0，∴当x＝14时，w去掉最大值360，∴当每天销售单价定为14元时利润最大．27．如图，在△ABC与△EBD中，∠ABC＝∠EBD＝90°，AB＝6，BC＝3，EB＝2，BD ＝，射线AE与直线CD交于点P．（1）求证：△ABE∽△CBD；（2）若AB∥ED，求tan∠PAC的值；（3）若△EBD绕点B逆时针旋转一周，直接写出线段AP的最大值与最小值．【解答】（1）证明：∵，∠ABC＝∠EBD＝90°，∴∠ABE＝∠CBD，∵AB＝6，BC＝3，EB＝2，BD＝，∴＝＝2，∴△ABE∽△CBD．（2）解：如图，设DE交BC于M．∵AB∥DE，∠ABC＝90°，∴∠DMB＝∠ABC＝∠DMC＝90°，在Rt△DEB中，∵∠EBD＝90°，BE＝2，BD＝，∴DE＝＝＝5，BM＝＝＝2，∴DM＝＝＝1，∴CM＝CD＝1，CD＝，∴∠CDM＝∠DCM＝45°，∵△ABE∽△CBD，∴＝＝2，∠CDB＝∠AEB，∴AE＝2，∵∠AEB+∠PEB＝180°，∴∠CDB+∠PEB＝180°，∵∠EBD＝90°，∴∠APC＝90°，∴PE＝PD＝DE＝，∴PC＝PD﹣CD＝MPA＝PE+AE＝，∴tan∠PAC＝＝．（3）由（2）可知当点P与C重合时，PA的值最大，最大值PA＝AC＝＝＝3，如图，当AE在AB的下方且与⊙B相切时，∠CAP的值最大，此时PA＝AC•cos∠CAP 的值最小，∵∠BEP＝∠DPE＝∠DBE＝90°，∴四边形BEPD是矩形，∴BD＝PE＝，∵AE＝＝＝4，∴PA的最小值为4﹣，28．在平面直角坐标系xOy中，抛物线y＝a（x﹣3）（x+1）与x轴交于A、B两点，与轴交于点C（0，﹣），连接AC、BC．（1）求抛物线的函数表达式；（2）抛物线的对称轴与x轴交于点D，连接CD，点E为第二象限抛物线上的一动点，EF∥BC，直线EF与抛物线交于点F，设直线EF的表达式为y＝kx+b．①如图①，直线y＝kx+b与抛物线对称轴交于点G，若△DGF∽△BDC，求k、b的值；②如图②，直线y＝kx+b与y轴交于点M，与直线y＝x交于点H，若﹣＝，求b的值．【解答】解：（1）将C（0，﹣）代入y＝a（x﹣3）（x+1），得﹣3a＝﹣，∴a＝，∴抛物线的函数表达式为y＝（x﹣3）（x+1）＝x2﹣x﹣；（2）①如图1，过点F作FN⊥DG，垂足为点N，在y＝（x﹣3）（x+1）中，令y＝0，得x1＝3，x2＝﹣1，∴B（3，0），设直线BC的解析式为y＝mx﹣，将点B（3，0）代入y＝mx﹣，得0＝3m﹣，∴m＝，∴直线BC的表达式为y＝x﹣，∵抛物线y＝（x﹣3）（x+1）的对称轴为x＝1，∴D（1，0），∴CD＝＝2，∴CD＝BD＝2，在Rt△COD中，tan∠ODC＝，∴∠ODC＝60°，∠CDB＝120°，∵△DGF∽△BDC，∴DG＝FG，∠DGF＝120°，设DG＝FG＝2m，在Rt△NGF中，∠NGF＝60°，FG＝2m，∴NG＝m，NF＝m，∴F（1+m，3m），将点F（1+m，3m）代入y＝（x﹣3）（x+1）中，得m1＝﹣（不合题意，舍去），m2＝，∴点F（5，4），∵EF∥BC，∴EF的表达式为y＝x+b，将点F（5，4），代入y＝x+b，得4＝×5+b，∴b＝，∴k＝1，b＝；②如图2，分别过点F、H、E作y轴的垂线，垂足分别为P、Q、S，联立，得点H（，），联立，得x2﹣3x﹣3﹣b＝0，设点E、F的横坐标分别为x1，x2，则，由ES∥HQ∥FP，可得△MHQ∽△MES，△MHQ∽△MFP，∴＝＝，＝＝，∵﹣＝，∴﹣＝1，∴﹣＝1，∴＝﹣1，∴b＝2．。

高考英语一诊试卷一、阅读理解（本大题共15小题，共30.0分）AQ1：When does the 2020 Virgin Money London Marathon take place？A：The 2020 Virgin Money London Marathon takes place on Sunday 26 April．Q2 ：I have moved．How do I let you know my change of address？A；Please email changeofaddress@londonmarathonevents．co．uk with your name，date of birth，telephone number，old address and your new address．Q3：I need a hotel in London for the weekend of the race - any advice？A：Virgin Money London Marathon hotel packages are available at Holiday Inn® and other IHG® hotels in and around London，and include a champion's breakfast and coach transfer to the Start Line so you arrive rested and ready to run your victory lap．Visit www．restandrun．holidayinn．com to find out more．Q4：I am a visually disabled runner．Where can I find out more about running with a guide？A：If you are a runner with a visual disability and would like to find out more about running with a guide，please contact disability@londonmarathonevents，co．uk．Q5：What time does the race start？A：Start times for the 2020 Virgin Money London Marathon are as follows；09：05 Elite Wheelchair Races09：10 World Para Athletics Marathon Championships Ambulant Athletes09：25 The Elite Women's Race10 ：10 The Elite Men's Race，British Athletics & England Athletics Marathon Championships and Mass RaceQ6：What time do I need to get to the Start？A：We suggest you get to your Start at least one hour before the race begins．This will allow time for you to use the facilities，warm up and take your position．Q7：Can I track a runner during the race？A：Yes．On Race Day，there will be a link to our tracking service on the home page of www．virginmoneylondonmarathon．com．The best way to track a runner is by using the runner's running number．If you do not have the running number，it is also possible to search for a runner by surname．1.Which address should you contact if you need to run with a guide？______A. www．restandrun．holidayinn．com．B. disability@londonrnarathonevents．co．uk．C. www．virginmoneylondonmarathon．com．D. changeofaddress@londonmarathoncvents．co．uk．2.If Ann attends the Elite Women's Race，what's the best time to get to the Start？______A. 08：20．B. 09：05．C. 09：10．D. 09：25．3.How can we track a runner during the race？______A. With the address．B. With the running number．C. With the first name．D. With the telephone number．BHan Tianheng picked up a carving knife at the age of 6 and never put it down．Today，the 79 year-old artist，one of China's most respected living masters of seal carving（印章雕刻），calligraphy and Chinese painting，still remembers the incident the first time he held a knife in his hand．"I cut my thumb badly and was horrified by the bloody sight，" he said，adding that his mother applied ashes because she couldn't afford to take him to a hospital．"The cut left a scar，which is still clear today．"An eye for an eye and blood for blood，the incident didn't set him back．Instead，it aroused his passion for the ancient art form．He was determined to pursue a path that would lead to a career in seal carving．Han said．The journey of art exploration was a little bumpy for the young man in his quest for excellence，and his seal works were harshly criticized by a famous old painter．Most would have crumbled under the criticism，not Han．It made him even more determined．After six months' hard work，he visited the painter again．"This time，he asked me to carve a seal for him．This was positive affirmation，" Han said．"Praise and criticism are what an artist should learn to handle all his life．Praise is candy and criticism is medicine．We can live without candy，but cannot live without medicine when ill．"Han rose to fame during the early 1960s famous for bird and insect seal art．Han's seals are an essential ending part on the paintings of a long list of well-established artists．"A seal for a good painting is．like the buttons for an haute couture（高档女子时装）．An experienced tailor always knows how to choose buttons that matches the whole style，" Han saidHis seals are full of variety - grand and solemn for Liu Haisu's paintings，light and vivid for Lu Yanshao's，graceful and gentle for Xie Zhiliu's．"A good seal carver should keep bis own style，and at the same time go well with the painting's style．" he said．4.What influence did the incident have on Han when he was six？______A. He got injured very seriously．B. He learned how to use a knife．C. It aroused his interest in seal carving．D. It helped him learn how hard life was．5.Which best describes Han's journey of art exploration？______A. Smooth and fruitful．B. Inspiring and lucky．C. Boring but worthwhile．D. Tough but rewarding．6.In Han's opinion，what do an experienced tailor and a good seal carver share？______A. The huge respect they earn．B. The flexibility they display at work．C. The targeted customers they serve．D. The efforts they have to make to succeed．7.In which section，of a newspaper does this text most probably appear？______A. Education．B. Events．C. Entertainment．D. People．C"Ma uka，ma uka ka ua ，Ma kai，ma kai ka ua．" So sing the children at a kindergarten on the Island of Hawaii．The song is much like "Rain，rain，go away" nursery rhyme，but it has an unusual power：it is one of the tools that have revived a near-dead language．The decline of Hawaiian was not，as is the case with most disappearing languages，a natural death caused by migration（迁徙）and mass media．In 1896，after American business interests ended the Hawaiian original political system，schools were banned from using it．By the late 20th century，apart from a couple of hundred people on one tiny island，English had replaced Hawaiian and only the old spoke it to each other．The civil-rights movement brought a revival of interest among the young，centred on the University of Hawaii at Hilo．Larry Kimura，a professor there，was not satisfied that the language should be only a subject at college：he and his students wanted to bring it back to life．The idea for how to do that came from a visiting Maori，who suggested．"language nests"，which had successfully revived New Zealand's native language．In 1985，when educating children in Hawaiian was still banned，Kauanoe Kamana and her husband Pila Wilson，both students of Kimura's，created the first Language nest" at Hilo．Neither was a native speaker，but both were determined，to bring up their children，as such．They gathered a small group of children，including their own son and daughter，and elderly native speakers．The movement grew：there are now 12 kindergartens and 23 schools involved．The number of children being educated in Hawaiian has risen from 1，877 in 2008 to 3.028 in 2018．Along with Japanese，Hawaiian is the non-English language most commonly spoken among children．8.What makes the decline of Hawaiian different from other disappearing languages？______A. The number of its users．B. The language features it bears．C. People's unwillingness to use it．D. The unfair treatment it received．9.What has been done to save Hawaiian？______A. More schools have been set up．B. More people are persuaded to stay．C. More children are exposed to Hawaiian．D. Government promotes the use of Hawaiian．10.How does the author feel about the present situation of Hawaiian？______A. Relieved．B. Curious．C. Anxious．D. Doubtful．11.What is the best title for the text？______A. The Revival of HawaiianB. The Future of Hawaiian．C. The History of HawaiianD. The Development of HawaiianDThis morning we're going to head off down into the wetland，into a very specific kind of wetland called the Prairie fen．You can find Nate Fuller counting butterflies．The Sarett Nature Center needs an accurate count of Mitchell's satyr butterflies to help preserve one of their last known habitats．They're very particular about the kind of habitat where they can live，which is part of what makes them so rare and amazing indicators for our water quality．Today，Sarett expert Ashley Cole-Wick with Michigan's Natural Features Inventory helps Fuller count．She says "When I first started working on the butterfly in 2013，we had 18 populations and this year in 2019，we have 10．" The Mitchell Seder went on the endangered species list in 1991．Initially it was thought that loss of wetlands contributed to their decline．Fuller says "It's not just habitat availability．Its groundwater and the amount in the quality of groundwater coming into these wetlands seem tobe a challenge for the butterfly．Nothing has all been sorted out exactly．" While the decline is likely a combination of factors．the fact that water quality might contribute is alarming because the wetlands are the headwaters for the Midwest's rivers and streams．A captive breeding （人工繁殖）program was started four years ago at the Toledo Zoo to help get to the bottom of the mystery．Today Director Ryan Walsh who heads the program says it's been，the only successful captive program．The caterpillars （毛毛虫）spend the winter in a special weather control room that help determine the Mitchell satyrs don't do well below 4.4 degrees Celsius，a temperature that prevents the Fen wetlands from the hard freezes which kill the insects．With that knowledge，the program produced 1300 new eggs this summer，a development that may go a long way toward restoring the population．And if all goes well，may one day the Mitchell satyr butterfly earn a ticket off Endangered Species List．12.What are the indicators for the water quality？______A. The habitats．B. The butterflies．C. The wetlands．D. The experts．13.What is the main idea of the third paragraph？______A. The importance of water quality．B. Actions taken to protect the butterflies．C. The reasons why the butterflies decline．D. The natural conditions for the butterflies．14.What does the underlined word " restoring" in Paragraph 4 most probably mean？______A. Preserving．B. Increasing．C. Recovering．D. Controlling．15.What can we learn about the butterfly？______A. It can easily be found．B. It is not endangered now．C. It will die above 4.4 degree Celsius．D. It can be bred by humans．二、阅读七选五（本大题共5小题，共10.0分）A grateful heart is a satisfied heart．A satisfied heart is a simple heart which leads to a simplified life．Gratitude opens the door to simplicity．But we live in a culture that addresses dissatisfaction．(1) ．Intentionally choose it．Gratitude will never be a result of your next purchase，success，or accomplishment．(2) And you will never find it in life until you intentionally decide to choose it．Count your blessings．A new day，a warm bed，a unique personality，or a special talent…(3) Gratitude quickly sets in when we begin to spend a quiet moment each day remembering them．This practice alone has the potential to change your heart and life immeasurably．(4) Almost hall the world live on less than ﹩2.50 a day．1.1 billion people have inadequateaccess to clean water．Let those facts sink in for just a moment and slowly allow gratitude and a desire to become part of the solution to take their place．Find gratitude in difficulty．(5) It can be more difficult during the trials of life：death，disease，or failure．The truth is that no one is exempt（豁免）from the sufferings．However good can be found even in the worst of times．Being grateful during those difficulties may get you through them．In daily life we must see it is not happiness that makes us grateful，but gratefulness that makes us happy．A．Ignore what you don't have．B．We can learn how to be grateful．C．Open your eyes to those with less．D．Gratitude is available in your heart right now．E．You have wonderful things in your life already．F．It's easy to be grateful when things are going well．G．How can we find gratitude in a world that seeks to destroy it？16. A. A B. B C. C D. D E.E F.F G. G17. A. A B. B C. C D. D E.E F.F G. G18. A. A B. B C. C D. D E.E F.F G. G19. A. A B. B C. C D. D E.E F.F G. G20. A. A B. B C. C D. D E.E F.F G. G三、完形填空（本大题共20小题，共30.0分）Jim McGee was an American Air Force pilot．One day after he retired，he found himself (21)and then was told by the doctor that his kidneys（肾）were gone．Jim，69，(22)started dialysis（化疗），which didn't work well．The doctor said the transplant （移植）was a long-shot alternative．However，after several months' searching，no suitable(23) was found．Jim was so (24)that，in early 2018，he even(25) not attending a reunion of some Air Force companions in Monterey，California．Finally，withShirley's(26)，he decided to go，and that turned out to be a life-changing (27)．In California，Jim (28) with six fellow airmen，including one he hadn't seen in nearly 50 years；Doug Coffman．Jim told them about his (29)．"I asked him what his blood type is，and it (30) to be mine，" says Doug．"I was immediately thinking，'Gosh．I might be able to (31)．'"．Doug，then 70，was healthy and energetic．(32)，when he told Shirley that he wanted to donate a kidney to her husband，she worried that he might be too(33)．But Doug really wanted to help and (34) to have a try．He sent his (35)records to where Jim was treated and soon，he was asked to lake a series of physical examinations．(36)，the result showed that he was a perfect match．The doctors gave him the OK to (37)，and the surgery was a success．"It's pretty amazing to be able to take a（n）(38) organ out of one person's body，put it in another person's body，and have it (39)，" Doug says．"And there's nothing (40) than helping another person live a better life．"21. A. depressed B. exhausted C. nervous D. upset22. A. immediately B. suddenly C. happily D. simply23. A. doctor B. hospital C. plan D. match24. A. stubborn B. angry C. discouraged D. confused25. A. suggested B. regretted C. forgot D. considered26. A. permission B. recommendationC. invitationD. encouragement27. A. support B. decision C. reunion D. success28. A. reunited B. cooperated C. connected D. discussed29. A. idea B. achievement C. situation D. ambition30. A. tends B. needs C. seems D. happens31. A. come B. help C. change D. participate32. A. Therefore B. Besides C. However D. Meanwhile33. A. old B. far C. thin D. kind34. A. refused B. determined C. hesitated D. promised35. A. medical B. military C. service D. consuming36. A. Hopefully B. Honestly C. Obviously D. Luckily37. A. remove B. operate C. donate D. return38. A. living B. precious C. extra D. special39. A. grow B. move C. pause D. work40. A. stranger B. finer C. funnier D. harder四、语法填空（本大题共1小题，共15.0分）41.For some in China，the aim of travel is to create 15-second videos．It's not about whereyou've been，but about where you're seen to have been．Situated on cliffs above a river．Hongyadong is a stilt-house complex in （1）______city of Chongqing．The bars，restaurants and golden neon lights （2）______（be）a popular draw since it was built in 2006．Last year the number of visitors increased （3）______（sharp）．The main reason，it see med，was Hongyadong's sudden popularity on a social-media app．Douyin，（4）______aim is not to produce a well-crafted video or beautifulphotograph，but simply （5）______（show）that you have also been to the popular places．The beauty of the （6）______（attract）is less important than the fact that people are flocking there to daka．A subculture has developed of young people who embrace daka as a lifestyle．So-calledDaka Zu-- "daka tribes"--can （7）______（find）roaming various scenic spots，（8）______（check）in at as many hot local ions as possible within a single day．The daka craze may have（9）______（practice）origins．China's young urbanprofessionals don't have so much free lime．Sometimes．they reed to work overtime．So they have to make the most of their（10）______（limit）leisure time．Douyin captures the mood with it's slogan："Make every second count．"五、书面表达（本大题共1小题，共25.0分）42.假如你是校汉服（Han costume）俱乐部主席李华．近期俱乐部将举办一场有外国交换生参加的汉服设计大赛．你将代表主办方在开幕式上发言．请根据以下要点写一篇发言稿：1．大赛目的；2．大赛规则；3．对选手的祝福．注意：1．词数100左右；2．可以适当增加细节，以使行文连贯．答案和解析1.【答案】【小题1】B 【小题2】A 【小题3】B【解析】1．B 细节理解题．根据Q4"If you are a runner with a visual disability and would like to find out more about running with a guide， please contact disability@londonmarathonevents， co． uk．A：如果您是一名视觉残疾的跑步者，想了解更多关于与导游一起跑步的信息，请联系残疾@londonmarathonvents，co．uk．"可知如果你需要和向导一起跑步，你应该联系残疾@londonmarathonvents，co．uk．故选B．2．A 细节理解题．根据Q5"09： 25 The Elite Women's Race09：25精英女子比赛"以及"A： We suggest you get to your Start at least one hour before the race begins． This will all ow time for you to use the facilities， warm up and take your position．A：我们建议你在比赛开始前至少一小时到达出发点，这样你就有时间使用设施，热身，保持姿势．"可知要在08： 20开始．故选A．3．B 细节理解题．根据最后一段"The best way to track a runner is by using the runner's running number．追踪跑步者的最好方法是使用跑步者的跑步号码．"可知想要在比赛中跟踪赛跑者要用跑步者的跑步号码．故选B本文是一篇对话，主要是关于2020 Virgin Money London Marathon的相关问题．1．直接信息题：直接信息题是指能够直接从原文中找到信息，选项在语言表达上与原文基本一致的题目．2．间接信息题：间接信息题是能够从原文中找到信息，但在语言表达上与原文有差异，做题时需要对原文信息进行转换．3．综合信息题：综合信息题是指这类题目所涉及的信息不是原文的某一句话，可能是原文的几句话，或者是散落在文章不同的地方，要求学生把原文所提供的信息综合起来分析，而不能断章取义．4.【答案】【小题1】C 【小题2】D 【小题3】B 【小题4】D【解析】CDBD1．C．细节理解题．根据第三段Instead， it aroused his passion for the ancient art form． He was determined to pursue a pat h that would lead to a career in seal carving． Han said．可知，这次事件并没有吓到他，反而激发了他对印章雕刻的爱，决心要追求这条艺术之路；故选C．2．D．细节理解题．根据第四段The journey of art exploration was a little bumpy for the young man in his quest for excellenc e， and his seal works were harshly criticized by a famous old painter．可知，他的艺术探索之旅比较崎岖，而且受到了著名老艺术家的批评，但是最终证明这一切都是值得的，所以他的艺术探索之路艰辛但是很值得；故选D．3．B．推理判断题．根据倒数第三段An experienced tailor always knows how to choose buttons that matches the whole style，" Han said可知，一个有经验的老裁缝一直都懂得如何的选取纽扣且匹配完美，由此可知，灵活性是关键；故选B．4．D．文章出处题．本文描述的就是一个热爱印章雕刻艺术的人的传奇经历，是属于人物专栏中的内容，所以应该是出自人物介绍板块；故选D．本文属于人物传记类的短文阅读．主要描述的就是一个热爱印章雕刻艺术的人的传奇经历，介绍了他走上印章雕刻艺术之路的起源以及追求艺术巅峰的崎岖经历．阅读理解考察学生的细节理解和推理判断能力，做细节理解题时一定要找到文章中的原句，和题干进行比较，再做出正确的选择．在做推理判断题不要以个人的主观想象代替文章的事实，要根据文章事实进行合乎逻辑的推理判断．8.【答案】【小题1】D 【小题2】C 【小题3】A 【小题4】A【解析】1．D．推理判断题．根据第二段的句子In 1896， after American business interests ended the Hawaiian original political system， s chools were banned from using it．可知，它受到的不公平待遇使夏威夷语的衰落不同于其他正在消失的语言．故选D．2．C．细节理解题．根据文章最后一段的句子number of children being educated in Hawaiian has risen from 1， 877 in 2008 to 3.028 in 20 18．可知，更多的孩子接触到夏威夷语言这样可以拯救夏威夷语．故选C．3．A．推理判断题．根据文章第一段的句子The song is much like "Rain， rain， go away" nursery rhyme， but it has an unusual power ： it is one of the tools that have revived a near-dead language．可知，笔者对夏威夷语言的现状感到欣慰．故选A．4．A．标题判断题，根据全文和第一段的but it has an unusual power： it is one of the tools that have revived a near-dead language．可知，文章主要介绍夏威夷语的复兴，The Revival of Hawaiian是合适的标题．故选A．本文介绍夏威夷语言一度将要灭绝，人们采取措施，让更多的孩子学习夏威夷语，使它得以恢复．做这类题材阅读理解时要求考生对文章通读一遍，做题时结合原文和题目有针对性的找出相关语句进行仔细分析，结合选项选出正确答案．推理判断题也是要在抓住关键句子的基础上合理的分析才能得出正确答案，切忌胡乱猜测，一定要做到有理有据．12.【答案】【小题1】B 【小题2】C 【小题3】C 【小题4】D【解析】1．B．推理判断题．根据第一段中的"They're very particular about the kind of habitat where they can live， which is part of what makes them so rare and amazing indicators for our water quality．"可知它们对它们能够生活的栖息地非常挑剔，这也是它们如此稀有和惊人的水质指标的一部分，因此答案选B．2．C．段落大意题．根据第三段中的"Initially it was thought that loss of wetlands contributed to their decline． "可知本段主要讲的是蝴蝶数量下降的原因，因此答案选C．3． C．猜测词义题．根据第四段中的"With that knowledge， the program produced 1300 new eggs this summer， a developmentthat may go a long way towardrestoring the population． And if all goes well， may one day the Mitchell satyr butterfly ear n a ticket off Endangered Species List．"可知有了这些知识，这个项目在今年夏天生产了1300个新的卵，这一发展可能对恢复种群有很大的帮助．如果一切顺利，也许有一天米切尔色狼蝴蝶可以获得一张罚单濒危物种名单，由此可知restoring意为"恢复"，因此答案选C．4．D．推理判断题．根据最后一段中的"A captive breeding （人工繁殖）program was started four years ago at the Toledo Zoo to help get to the bottom of the mystery ． Today Director Ryan Walsh who heads the program says it's been， the only successful ca ptive program．"可知人工繁育蝴蝶是可行的，由此判断答案选D．本文主要讲的是米切尔色狼蝴蝶的数量在下降，接下来分析了原因，最后指出可以通过人工繁育的方式使得米切尔色狼蝴蝶不会灭绝．阅读理解考察学生的细节理解和推理判断能力，做细节理解题时一定要找到文章中的原句，和题干进行比较，再做出正确的选择．在做推理判断题不要以个人的主观想象代替文章的事实，要根据文章事实进行合乎逻辑的推理判断．16.【答案】【小题1】G 【小题2】D 【小题3】E 【小题4】C 【小题5】F【解析】1．G．推理判断题．根据前文A satisfied heart is a simple heart which leads to a simplified life． Gratitude opens the door t o simplicity． But we live in a culture that addresses dissatisfaction．一颗满意的心是一颗简单的心，它导致了一种简化的生活．感恩打开了通往简单的大门．但我们生活在一种解决不满的文化中．可知在一个试图摧毁感恩的世界里，我们怎么能找到感恩呢；故选G 2．D．推理判断题．根据前文 Intentionally choose it． Gratitude will never be a result of your next purchase， success ， or accomplishment．有意选择．感恩永远不会是你下次购买的结果，成功或成就．可知感恩之心现在就在你心中；故选D．3．E．推理判断题．根据后文Gratitude quickly sets in when we begin to spend a quiet moment each day remembering the m．当我们每天开始花一个安静的时间来回忆他们时，感激很快就开始了．可知你的生活中已经有了美好的东西；故选E．4．C．推理判断题．根据后文Almost hall the world live on less than ﹩2.50 a day． 1.1 billion people have inadequate access to clean water．世界上几乎每天生活费不到2.5美元．11亿人无法获得足够的清洁水．可知睁开你的眼睛看那些少了的东西；故选C．5．F．推理判断题．根据后文It can be more difficult during the trials of life： death， disease， or failure．在生命：死亡，疾病，或失败的试验中，这可能更加困难．可知当一切顺利的时候，感恩是很容易的；故选F．本文属于说明文阅读，作者通过这篇文章主要向我们描述了一颗感恩的心就是一颗满足的心．一颗满足的心就是一颗通向简单生活的简单的心．感恩打开了通往简单的大门．但是我们生活在一种处理不满的文化中．七选五阅读是完成性阅读，和完形填空很类似，不同的是一个选词，一个选句子．解题时，要注意上下文语境，充分考虑信息词（选项中和空格前后句子中相同或相近七的词），选出最符合语境的句子．21.【答案】【小题1】B 【小题2】A 【小题3】D 【小题4】C 【小题5】D 【小题6】D 【小题7】B 【小题8】A 【小题9】C 【小题10】D 【小题11】B 【小题12】C 【小题13】A 【小题14】B 【小题15】A 【小题16】D 【小题17】C 【小题18】A 【小题19】D 【小题20】B【解析】1---5 BADCD 6--10 DBACD 11---15 BCABA 16---20 DCADB（1）B．考查形容词及句意理解．A．depressed 沮丧的；B．exhausted 筋疲力尽的；C．nervous 紧张的；D．upset 心烦意乱的．根据后文句子was told by the doctor that his kidneys（肾）were gone．可见是感觉不舒服，没有精神才看的医生，所以选B．（2）A．考查副词及句意理解．A．immediately 马上；B．suddenly突然；C．happily 高兴地；D．simply 简单地．应该是立刻进行了化疗，但是没有用，所以选A．（3）D．考查名词及句意理解．A．doctor医生；B．hospital 医院；C．plan 计划；D．match 匹配．找了几个月，但是没有合适的匹配的肾，所以选D．（4）C．考查形容词及句意理解．A．stubborn 固执的；B．angry生气的；C．discouraged 沮丧的；D．confused 困惑的．根据后文in early 2018， he even（5）D not attending a reunion of some Air Force companions in Monterey， California．他甚至没有考虑要参加在加州蒙特利举行的一些空军同伴的聚会．可见他非常地泄气，所以选C．（5）D．考查动词及句意理解．A．suggested建议；B．regretted后悔；C．forgot 忘记；D．considered 考虑．他甚至没有考虑要参加在加州蒙特利举行的一些空军同伴的聚会．可见他非常地泄气，所以选D．（6）D．考查名词及句意理解．A．permission允许；B．recommendation 建议；C．invitation；邀请D．encouragement 鼓励．在Shirley的鼓励下，他去了有了改变，所以选D．（7）B．考查名词及句意理解．A．support支持；B．decision决策；C．reunion 重聚；D．success 成功．根据后文的转机，可见生活随着决定而改变，所以选B．（8）A．考查动词及句意理解．A．reunited重聚；B．cooperated 合作；C．connected 连接；D．discussed 讨论．聚会的时候应该是和飞行员们重聚，所以选A．（9）C．考查名词及句意理解．A．idea想法；B．achievement成就；C．situation 处境；D．ambition 抱负．Jim和他们谈起了自己的身体状况，所以选C．（10）D．考查动词及句意理解．A．tends 趋向；B．needs 需要；C．seems似乎；D．happens 发生．根据语境询问了一下血型，碰巧与我的匹配，所以选D．（11）B．考查动词及句意理解．A．come过来；B．help 帮助；C．change 改变；D．participate参加．根据前文血型相配，也许我有可能给予帮助，所以选B．（12）C．考查副词及句意理解．A．Therefore因此；B．Besides况且；C．However 然而；D．Meanwhile 同时．根据后文句子she worried that he might be too（13），担心他太老了，两句应该是转折关系，所以选C．（13）A．考查形容词及句意理解．A．old老的；B．far 远的；C，thin 薄的；D．kind 好心的．根据前文70岁了，应该是担心太老了，所以选A．（14）B．考查动词及句意理解．A．refused拒绝；B．determined决心；C．hesitated 犹豫；D．promised 答应．但是Doug真的想帮助于是决定试一试，所以选B．（15）A．考查名词及句意理解．A．medical 医学；B．military军事；C．service 服务；D．consuming．消费．他很快将自己的医学报告发到了Jim治疗的地方，所以选A．（16）D．考查副词及句意理解．A．Hopefully 希望地；B．Honestly 诚实地；C．Obviously 显然地；D．Luckily 幸运地．根据后文句子the result showed that he was a perfect match．这是很幸运的事，所以选D．（17）C．考查动词及句意理解．A．remove 取出；B．operate手术；C．donate捐献；D．return 归还．医生认为捐赠很好，治疗很成功．所以选C．（18）A．考查形容词及句意理解．A．living 活着的；B．precious 珍贵的；C．extra 额外的；D．special 特别的．这里是肾移植，是活体器官，所以选A．（19）D．考查动词及句意理解．A．grow 成长；B．move C．pause D．work A．成长；B．移动；C．暂停；D．工作．让这个器官在另一个人的身体里工作，所以选D．（20）B．考查形容词及句意理解．A．stranger奇怪的；B．finer 更好；C．funnier 更有趣；D．harder 更难．没有什么比帮助别人过上更好的生活更好的了．所以选B．Jim在退休后发现肾有了毛病，需要做肾移植才能存活，最后他的老朋友和他的相匹配，给他捐了一个肾的故事．做完型填空首先要通读全文，了解大意．一篇完形填空的文章有许多空格，所以，必须先通读一至两遍，才能大概了解文章的内容．千万不要看一句，做一句．其次要逐句分析，前后一致．选择答案时，要考虑整个句子的内容，包括搭配、时态、语法等．答案全部填完后，再通读一遍文章，检查是否通顺流畅了，用词得当，意思正确．41.【答案】the【解析】1．the．考查冠词，此处用冠词表示特指"重庆"．2．have been．考查时态．句意：酒吧、餐厅和金色霓虹灯自2006年建成以来，一直备受欢迎，根据后面的since it was built in 2006可知此处要用现在完成时．3．sharply．考查副词．此处用副词修饰动词increased．4．whose．考查定语从句引导词．此处是一个定语从句，先行词是Douyin，且从句缺少定语，因此用whose来引导．5．to show．考查不定式．通过分析可知此处用不定式与前面的"not to produce a well-crafted video "共同作表语．6．attraction．考查名词．此处表示"这个景点的美"，因此用名词做主语．7．be found．考查语态．句意：所谓的打卡族--"打卡部落"，在各个景点都能找到，主语 So-called Daka Zu-- "daka tribes"与find之间是被动关系，因此要用被动语态．8．checking．考查非谓语动词．通过分析可知此处用非谓语动词作状语，check与句子主语 So-called Daka Zu-- "daka tribes"之间是主动关系，因此用现在分词．9．practical．考查形容词．句意：打卡热可能有实际的起源，此处用形容词修饰后面的名词origin．10．limited．考查形容词．句意：所以他们必须充分利用有限的闲暇时间，此处用形容词limited（有限的）修饰后面的leisure time．本文主要讲的是对一些中国人来说，旅游的目的是制作15秒的视频，不是你去过哪里，而是你被人看到去过哪里，并分析了其原因．考查语法填空．语法填空主要考查了用单词或短语的适当形式填空．做本题的关键是在理解短文的基础上，灵活运用所学的基础知识．本题考到的知识点有：固定的短语，词类的转换，名词的复数形式，副词以及祈使句的用法等．因此，这就需要在平时的学习中，牢固掌握各语言点及一些语法知识．42.【答案】Boys and Girls，I am president of Han costume Club．Recently，my club will hold a Han costume design competition，which will include foreign exchange students．【高分句型一】（话题）The purpose of the competition is to enrich our school life and promote Chinese traditional culture．（目的）Anyone interested in Han costume can take part in it．You should design a set of Han costume．Your composition should be handed in before 25th september．It willbe a great chance for the talented students to show their potential．Those who win the competition can get a medal as well as a reward of 1000 yuan．【高分句型二】（规则）I hope all the participants will achieve the success．（祝愿）Thanks for your listening．【解析】高分句型一：Recently，my club will hold a Han costume design competition，which will include foreign exchange students．译文：最近，我的俱乐部将举办一个汉族服装设计比赛，比赛将包括外国留学生．分析：which引导非限制性定语从句．高分句型二：Those who win the competition can get a medal as well as a reward of 1000 yuan．译文：赢得比赛的人可以获得奖牌和1000元的奖励．分析：who引导定语从句修饰those．这是一篇提纲类作文，我们需要用正确的英语把给出的要点表达出来．动笔前，一定要认真分析要点，理解要点要表达的含义，不能遗漏要点，跑题偏题．本作文中给出的要点比较具体，故需要准确表达．写作时注意准确运用时态，上下文意思连贯，符合逻辑关系，尽量使用自己熟悉的单词句式，同时也要注意使用高级词汇和高级句型使文章显得更有档次．特别注意在选择句式时要赋予变他化．平时除了加强词汇积累，写作联系以外，还可以适当记忆一些类似的范文，这样在考试中可以起到事半功倍的效果．。

2020年四川省成都市高考数学一诊试卷（理科）一、选择题（本题共12小题）1．若复数z1与z2＝﹣3﹣i（i为虚数单位）在复平面内对应的点关于实轴对称，则z1＝（）A．﹣3i B．﹣3+i C．3+i D．3﹣i2．已知集合A＝{﹣1，0，m}，B＝{1，2}，若A∪B＝{﹣1，0，1，2}，则实数m的值为（）A．﹣1或0 B．0或1 C．﹣1或2 D．1或23．若，则tan2θ＝（）A．﹣B．C．﹣D．4．某校随机抽取100名同学进行“垃圾分类”的问卷测试，测试结果发现这l00名同学的得分都在[50，100]内，按得分分成5组：[50，60），[60，70），[70，80），[80，90），[90，100]，得到如图所示的频率分布直方图则这100名同学的得分的中位数为（）A．72.5 B．75 C．77.5 D．805．设等差数列{a n}的前n项和为S n，且a n≠0，若a5＝3a3，则＝（）A．B．C．D．6．已知α，β是空间中两个不同的平面，m，n是空间中两条不同的直线，则下列说法正确的是（）A．若m∥α，n∥β，且α∥β，则m∥nB．若m∥α，n∥β，且α⊥β，则m∥nC．若m⊥α，n∥β，且α∥β，则m⊥nD．若m⊥α，n∥β且α⊥β，则m⊥n7．的展开式的常数项为（）A．25 B．﹣25 C．5 D．﹣58．将函数y＝sin（4x﹣）图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把所得图象向左平移个单位长度，得到函数f（x）的图象，则函数f（x）的解析式为（）A．B．C．D．9．已知抛物线y2＝4x的焦点为F，M，N是抛物线上两个不同的点．若|MF|+|NF|＝5，则线段MN的中点到y轴的距离为（）A．3 B．C．5 D．10．已知，则（）A．a＞b＞c B．a＞c＞b C．b＞a＞c D．b＞c＞a11．已知定义在R上的函数f（x）满足f（2﹣x）＝f（2+x），当x≤2时，f（x）＝（x ﹣1）e x﹣1．若关于x的方程f（x）﹣kx+2k﹣e+1＝0有三个不相等的实数根，则实数k 的取值范围是（）A．（﹣2，0）∪（0，2）B．（﹣2，0）∪（2，+∞）C．（﹣e，0）∪（0，+∞）D．（﹣e，0）∪（0，e）12．如图，在边长为2的正方形AP1P2P3中，线段BC的端点B，C分别在边P1P2，P2P3上滑动，且P2B＝P2C＝x．现将△AP1B，△AP3C分别沿AB，AC折起使点P1，P3重合，重合后记为点P，得到三棱锥P﹣ABC．现有以下结论：①AP⊥平面PBC；②当B，C分别为P1P2，P2P3的中点时，三棱锥P﹣ABC的外接球的表面积为6π；③x的取值范围为（0，4﹣2）；④三棱锥P﹣ABC体积的最大值为．则正确的结论的个数为（）A．1 B．2 C．3 D．4二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡上．13．已知实数x，y满足约束条件，则z＝x+2y的最大值为．14．设正项等比数列{a n}满足a4＝81，a2+a3＝36，则a n＝．15．已知平面向量，满足||＝2，||＝，且⊥（﹣），则向量与的夹角的大小为．16．已知直线y＝kx与双曲线C：（a＞0，b＞0）相交于不同的两点A，B，F 为双曲线C的左焦点，且满足|AF|＝3|BF|，|OA|＝b（O为坐标原点），则双曲线C的离心率为．三、解答题：本大题共5小题，共70分解答应写出文字说明、证明过程或演算步骤．17．在△ABC中，角A，B，C的对边分别为a，b，c，且．（Ⅰ）求sin A的值；（Ⅱ）若△ABC的面积为，且sin B＝3sin C，求△ABC的周长18．某公司有l000名员工，其中男性员工400名，采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查，将计划在今年购买5G手机的员工称为“追光族”，计划在明年及明年以后才购买5G手机的员工称为“观望者”调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人．（Ⅰ）完成下列2×2列联表，并判断是否有95%的把握认为该公司员工属于“追光族”与“性别”有关；（Ⅱ）已知被抽取的这l00名员工中有10名是人事部的员工，这10名中有3名属于“追光族”现从这10名中随机抽取3名，记被抽取的3名中属于“追光族”的人数为随机变量X，求X的分布列及数学期望．附：K2＝，其中n＝a+b+c+d．19．如图，在四棱锥P﹣ABCD中，AP⊥平面PBC，底面ABCD为菱形，且∠ABC＝60°，E分别为BC的中点．（Ⅰ）证明：BC⊥平面PAE；（Ⅱ）若AB＝2．PA＝1，求平面ABP与平面CDP所成锐二面角的余弦值．20．已知函数f（x）＝（a﹣1）lnx+x+，a∈R．（Ⅰ）讨论函数f（x）的单调性；（Ⅱ）当a＜﹣1时，证明∀x∈（1，+∞），f（x）＞﹣a﹣a2．21．已知椭圆C：+y2＝1的右焦点为F，过点F的直线（不与x轴重合）与椭圆C相交于A，B两点，直线l：x＝2与x轴相交于点H，过点A作AD⊥l，垂足为D．（Ⅰ）求四边形OAHB（O为坐标原点）面积的取值范围；（Ⅱ）证明直线BD过定点E．并求出点E的坐标请考生在第22，23题中任选择一题作答，如果多做，则按所做的第一题记分，作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，已知P是曲线C1：x2+（y﹣2）2＝4上的动点，将OP绕点O 顺时针旋转90°得到OQ，设点Q的轨迹为曲线C2以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．（Ⅰ）求曲线C1，C2的极坐标方程；（Ⅱ）在极坐标系中，点M（3，），射线≥0）与曲线C1，C2分别相交于异于极点O的A，B两点，求△MAB的面积．[选修45：不等式选讲]23．已知函数f（x）＝|x﹣3|．（Ⅰ）解不等式f（x）≥4﹣|2x+l|；（Ⅱ）若＝2（m＞0，n＞0），求证：m+n≥|x+|﹣f（x）．参考答案一、选择题：本大题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的．1．若复数z1与z2＝﹣3﹣i（i为虚数单位）在复平面内对应的点关于实轴对称，则z1＝（）A．﹣3i B．﹣3+i C．3+i D．3﹣i【分析】由已知可得复数z1与z2＝﹣3﹣i（i为虚数单位）的实部相等，虚部互为相反数，则z1可求．解：∵复数z1与z2＝﹣3﹣i（i为虚数单位）在复平面内对应的点关于实轴对称，∴复数z1与z2＝﹣3﹣i（i为虚数单位）的实部相等，虚部互为相反数，则z1＝﹣3+i．故选：B．2．已知集合A＝{﹣1，0，m}，B＝{1，2}，若A∪B＝{﹣1，0，1，2}，则实数m的值为（）A．﹣1或0 B．0或1 C．﹣1或2 D．1或2【分析】因为A∪B＝{﹣1，0，1，2}，A，B本身含有元素﹣1，0，1，2，根据元素的互异性m≠﹣1，0，求出m即可．解：集合A＝{﹣1，0，m}，B＝{1，2}，A∪B＝{﹣1，0，1，2}，因为A，B本身含有元素﹣1，0，1，2，所以根据元素的互异性，m≠﹣1，0即可，故m＝1或2，故选：D．3．若，则tan2θ＝（）A．﹣B．C．﹣D．【分析】由题意利用同角三角函数的基本关系，二倍角公式，求得要求式子的值．解：若，则 tanθ＝，则tan2θ＝＝﹣，故选：C．4．某校随机抽取100名同学进行“垃圾分类”的问卷测试，测试结果发现这l00名同学的得分都在[50，100]内，按得分分成5组：[50，60），[60，70），[70，80），[80，90），[90，100]，得到如图所示的频率分布直方图则这100名同学的得分的中位数为（）A．72.5 B．75 C．77.5 D．80【分析】由频率分布直方图求出[50，70）的频率为0.4，[70，80）的频率为0.4，由此能求出这100名同学的得分的中位数．解：由频率分布直方图得：[50，70）的频率为：（0.010+0.030）×10＝0.4，[70，80）的频率为：0.040×10＝0.4，∴这100名同学的得分的中位数为：70+＝72.5．故选：A．5．设等差数列{a n}的前n项和为S n，且a n≠0，若a5＝3a3，则＝（）A．B．C．D．【分析】将S9，S5转化为用a5，a3表达的算式即可得到结论．解：依题意，＝＝，又＝3，∴＝×3＝，故选：D．6．已知α，β是空间中两个不同的平面，m，n是空间中两条不同的直线，则下列说法正确的是（）A．若m∥α，n∥β，且α∥β，则m∥nB．若m∥α，n∥β，且α⊥β，则m∥nC．若m⊥α，n∥β，且α∥β，则m⊥nD．若m⊥α，n∥β且α⊥β，则m⊥n【分析】由考查空间中直线与直线、直线与平面及平面与平面位置关系逐一核对四个选项得答案．解：由m∥α，n∥β，且α∥β，得m∥n或m与n异面，故A错误；由m∥α，n∥β，且α⊥β，得m∥n或m与n相交或m与n异面，故B错误；由m⊥α，α∥β，得m⊥β，又n∥β，则m⊥n，故C正确；由m⊥α，n∥β且α⊥β，得m∥n或m与n相交或m与n异面，故D错误．故选：C．7．的展开式的常数项为（）A．25 B．﹣25 C．5 D．﹣5【分析】求出（x﹣）6的通项公式，考虑r＝3，r＝4时的系数，相加求和即可得到所求值．解：（x﹣）6的通项公式为T r+1＝x6﹣r（﹣）r＝（﹣1）r x6﹣2r，r＝0，1，2， (6)则（x2+2）（x﹣）6的展开式的常数项须6﹣2r＝0或者6﹣2r＝﹣2⇒r＝3或者r＝4：∴常数项为（﹣1）4+2×（﹣1）3＝15﹣40＝﹣25．故选：B．8．将函数y＝sin（4x﹣）图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把所得图象向左平移个单位长度，得到函数f（x）的图象，则函数f（x）的解析式为（）A．B．C．D．【分析】直接利用函数的图象的平移变换和伸缩变换的应用求出结果．解：函数y＝sin（4x﹣）图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到y＝sin（2x﹣）的图象，再把所得图象向左平移个单位长度，得到函数f（x）＝sin（2x+）的图象，故选：A．9．已知抛物线y2＝4x的焦点为F，M，N是抛物线上两个不同的点．若|MF|+|NF|＝5，则线段MN的中点到y轴的距离为（）A．3 B．C．5 D．【分析】抛物线到焦点的距离转化为到准线的距离，可求出横坐标之和，进而求出中点的横坐标，求出结果即可．解：由抛物线方程得，准线方程为：x＝﹣1，设M（x，y），N（x'，y'），由抛物线的性质得，MF+NF＝x+x'+p＝x+x'+2＝5，中点的横坐标为，线段MN的中点到y轴的距离为：，故选：B．10．已知，则（）A．a＞b＞c B．a＞c＞b C．b＞a＞c D．b＞c＞a【分析】利用根式的运算性质、幂函数的单调性可得a，b的大小关系，利用对数函数的单调性即可得出c＜1．解：∵a＝＝，b＝＝，∴1＜a＜b．c＝ln＜1．∴c＜a＜b．故选：C．11．已知定义在R上的函数f（x）满足f（2﹣x）＝f（2+x），当x≤2时，f（x）＝（x ﹣1）e x﹣1．若关于x的方程f（x）﹣kx+2k﹣e+1＝0有三个不相等的实数根，则实数k 的取值范围是（）A．（﹣2，0）∪（0，2）B．（﹣2，0）∪（2，+∞）C．（﹣e，0）∪（0，+∞）D．（﹣e，0）∪（0，e）【分析】本题根据题意先利用一阶导数分析当x≤2时，f（x）＝（x﹣1）e x﹣1．的函数单调性及图象，然后根据f（2﹣x）＝f（2+x）可知函数f（x）关于x＝2对称．即可画出函数y＝f（x）的大致图象．一次函数y＝k（x﹣2）+e﹣1．很明显是恒过定点（2，e﹣1）．则只要考查斜率k的变动情况，当k＝e时，y＝f（x）与y＝k（x﹣2）+e﹣1正好在（1，﹣1）处相切，再根据数形结合法可得k的取值范围，当x＞2时也同理可得．解：由题意，当x≤2时，f（x）＝（x﹣1）e x﹣1．f′（x）＝xe x．①令f′（x）＝0，解得x＝0；②令f′（x）＜0，解得x＜0；③令f′（x）＞0，解得0＜x≤2．∴f（x）在（﹣∞，0）上单调递减，在（0，2]上单调递增，在x＝0处取得极小值f（0）＝﹣2．且f（1）＝﹣1；x→﹣∞，f（x）→0．又∵函数f（x）在R上满足f（2﹣x）＝f（2+x），∴函数f（x）的图象关于x＝2对称．∴函数y＝f（x）的大致图象如下：关于x的方程f（x）﹣kx+2k﹣e+1＝0可转化为f（x）＝k（x﹣2）+e﹣1．而一次函数y＝k（x﹣2）+e﹣1很明显是恒过定点（2，e﹣1）．结合图象，当k＝0时，有两个交点，不符合题意，当k＝e时，有两个交点，其中一个是（1，﹣1）．此时y＝f（x）与y＝k（x﹣2）+e ﹣1正好相切．∴当0＜k＜e时，有三个交点．同理可得当﹣e＜k＜0时，也有三个交点．实数k的取值范围为：（﹣e，0）∪（0，e）．故选：D．12．如图，在边长为2的正方形AP1P2P3中，线段BC的端点B，C分别在边P1P2，P2P3上滑动，且P2B＝P2C＝x．现将△AP1B，△AP3C分别沿AB，AC折起使点P1，P3重合，重合后记为点P，得到三棱锥P﹣ABC．现有以下结论：①AP⊥平面PBC；②当B，C分别为P1P2，P2P3的中点时，三棱锥P﹣ABC的外接球的表面积为6π；③x的取值范围为（0，4﹣2）；④三棱锥P﹣ABC体积的最大值为．则正确的结论的个数为（）A．1 B．2 C．3 D．4【分析】根据折起形状的形成条件，分析各结论，即可判断真假．解：折起后，△CP3A≌△CPA，故AP⊥PC．同理，AP⊥PB，所以AP⊥平面PBC，①正确；当B，C分别为P1P2，P2P3的中点时，PB＝PC＝1，BC＝，所以PB2+PC2＝BC2，又AP⊥平面PBC，所以PA，PB，PC两两垂直，所以三棱锥P﹣ABC的外接球与以PA，PB，PC为长宽高的长方体的外接球半径相等．设半径为r，所以（2r）2＝22+12+12＝6，S＝4πr2＝6π．即三棱锥P﹣ABC的外接球的表面积为6π，②正确；因为P2B＝P2C＝x，所以PB＝PC＝2﹣x，而BC＝，故2（2﹣x）＞，解得x＜4﹣2，③正确；因为△PBC的面积为S＝＝设f（x）＝x4﹣8x3+8x2，f′（x）＝4x3﹣24x2+16x＝4x（x2﹣6x+4）当0＜x＜3﹣时，f′（x）＞0，当3﹣＜x＜4﹣2时，f′（x）＜0f max＝f（3﹣）＞f（1）＝，所以S＞．V P﹣ABC＝V A﹣PBC＝＞，④错误．故选：C．二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡上．13．已知实数x，y满足约束条件，则z＝x+2y的最大值为 6 ．【分析】作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z的最大值．解：作出实数x，y满足约束条件对应的平面区域如图：（阴影部分）由z＝x+2y得y＝﹣x+z，平移直线y＝﹣x+z，由图象可知当直线y＝﹣x+z经过点A时，直线y＝﹣x+z的截距最大，此时z最大．由，解得A（2，2），代入目标函数z＝x+2y得z＝2×2+2＝6故答案为：6．14．设正项等比数列{a n}满足a4＝81，a2+a3＝36，则a n＝3n．【分析】将已知条件转化为基本量a1，q的方程组，解方程组得到a1，q，进而可以得到a n．解：依题意，解得，∴a n＝＝3•3n﹣1＝3n，故答案为：3n．15．已知平面向量，满足||＝2，||＝，且⊥（﹣），则向量与的夹角的大小为．【分析】由题意利用两个向量垂直的性质，两个向量的数量积的定义，求出向量与的夹角的大小．解：∵平面向量，满足||＝2，＝，且⊥（﹣），∴•（﹣）＝•﹣＝0，∴＝．设向量与的夹角的大小为θ，则 2••cosθ＝3，求得 cosθ＝，故θ＝，故答案为：．16．已知直线y＝kx与双曲线C：（a＞0，b＞0）相交于不同的两点A，B，F 为双曲线C的左焦点，且满足|AF|＝3|BF|，|OA|＝b（O为坐标原点），则双曲线C的离心率为．【分析】取双曲线的右焦点F'，连接AF'，BF'，可得四边形AF'BF为平行四边形，运用双曲线的定义和平行四边形的对角线的平方和等于四条边的平方和，以及离心率公式可得所求值．解：设|BF|＝m，则|AF|＝3|BF|＝3m，取双曲线的右焦点F'，连接AF'，BF'，可得四边形AF'BF为平行四边形，可得|AF'|＝|BF|＝m，设A在第一象限，可得3m﹣m＝2a，即m＝a，由平行四边形的对角线的平方和等于四条边的平方和，可得（2b）2+（2c）2＝2（a2+9a2），化为c2＝3a2，则e＝＝．故答案为：．三、解答题：本大题共5小题，共70分解答应写出文字说明、证明过程或演算步骤．17．在△ABC中，角A，B，C的对边分别为a，b，c，且．（Ⅰ）求sin A的值；（Ⅱ）若△ABC的面积为，且sin B＝3sin C，求△ABC的周长【分析】（Ⅰ）由已知利用余弦定理可求cos A的值，进而根据同角三角函数基本关系式可求sin A的值．（Ⅱ）利用三角形的面积公式可求bc的值，由正弦定理化简已知等式可得b＝3c，解得b，c的值，根据余弦定理可求a的值，即可求解三角形的周长．解：（Ⅰ）∵，∴由余弦定理可得2bc cos A＝bc，∴cos A＝，∴在△ABC中，sin A＝＝．（Ⅱ）∵△ABC的面积为，即bc sin A＝bc＝，∴bc＝6，又∵sin B＝3sin C，由正弦定理可得b＝3c，∴b＝3，c＝2，则a2＝b2+c2﹣2bc cos A＝6，∴a＝，∴△ABC的周长为2+3+．18．某公司有l000名员工，其中男性员工400名，采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查，将计划在今年购买5G手机的员工称为“追光族”，计划在明年及明年以后才购买5G手机的员工称为“观望者”调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人．（Ⅰ）完成下列2×2列联表，并判断是否有95%的把握认为该公司员工属于“追光族”与“性别”有关；（Ⅱ）已知被抽取的这l00名员工中有10名是人事部的员工，这10名中有3名属于“追光族”现从这10名中随机抽取3名，记被抽取的3名中属于“追光族”的人数为随机变量X，求X的分布列及数学期望．附：K2＝，其中n＝a+b+c+d．【分析】（Ⅰ）根据题意，列出列联表，计算K2，查表判断即可；（Ⅱ）随机变量X的所有可能取值为0，1，2，3，分布求出对应概率，列出分布列，求期望即可．解：（Ⅰ）由题，2×2列联表如下：∵K2＝＝＝≈2.778＜3.841，∴没有95%的把握认为该公司员工属于“追光族”与“性别”有关；（Ⅱ）由题，随机变量X的所有可能的取值为0，1，2，3，P（X＝0）＝＝，P（X＝1）＝＝，P（X＝2）＝＝，P（X ＝3）＝＝，∴X的分布列为：∴E（X）＝1×+2×+3×＝．19．如图，在四棱锥P﹣ABCD中，AP⊥平面PBC，底面ABCD为菱形，且∠ABC＝60°，E分别为BC的中点．（Ⅰ）证明：BC⊥平面PAE；（Ⅱ）若AB＝2．PA＝1，求平面ABP与平面CDP所成锐二面角的余弦值．【分析】（Ⅰ）根据菱形基本性质得BC⊥AE，再由线面垂直得BC⊥AP，故BC⊥平面PAE；（Ⅱ）建立如图所示空间直角坐标系，分别求出两平面的法向量即可解：（Ⅰ）如图，连接AC，因为底面ABCD为菱形，且∠ABC＝60°，所以△ABC为正三角形，因为E为BC的中点，所以BC⊥AE，又因为AP⊥平面PBC，BC⊂平面PBC，所以BC⊥AP，因为AP∩AE＝A，AP，AE⊂平面PAE，所以BC⊥平面PAE；（Ⅱ）因为AP⊥平面PBC，PB⊂平面PBC，所以AP⊥PB，又因为AB＝2，PA＝1，所以PB＝，由（Ⅰ）得BC⊥PE，又因为E为BC中点，所以PB＝PC＝，EC＝1，所以PE＝，如图，过点P作BC的平行线PQ，则PQ，PE，PA两两互相垂直，以P为坐标原点，的方向分别为xyz轴的正方形，建立如图所示的空间直角坐标系Pxyz，则P（0，0，0），A（0，0，1），B（，﹣1，0），C（，1，0），D（0，2，1），设平面BAP的一个法向量＝（x，y，z），又＝（0，0，1），＝（，﹣1，0），由，得x﹣y＝0，z＝0，令x＝1，则＝（1，，0），设平面CDP的一个法向量＝（a，b，c），又＝（，1，0），＝（0，2，1），由，得a+b＝0，2y+z＝0，令a＝1，则＝（1，﹣，2），所以cos＜＞＝＝﹣，即平面ABP与平面CDP所成锐二面角的余弦值为．20．已知函数f（x）＝（a﹣1）lnx+x+，a∈R．（Ⅰ）讨论函数f（x）的单调性；（Ⅱ）当a＜﹣1时，证明∀x∈（1，+∞），f（x）＞﹣a﹣a2．【分析】（Ⅰ）先求出函数的导数，通过讨论a的范围，得到函数的单调区间；（Ⅱ）欲证明不等式f（x）＞﹣a﹣a2成立，即证明﹣a﹣a2＜（a﹣1）ln（﹣a）﹣a﹣1，设新函数h（x）＝lnx﹣x+1（x≥1），利用其单调性求出h（x）≤h（1）＝0，进而得证．解：（Ⅰ）f′（x）＝＝＝，因为x＞0，a∈R，所以当a≥0时，x+a＞0，所以函数在（0，1）上单调递减，在（1，+∞）上单调递增；当﹣1＜a＜0时，0＜﹣a＜1，函数f（x）在（0，﹣a）上单调递增，在（﹣a，1）上单调递减，在（1，+∞）上单调递增；当a＝﹣1时，f′（x）＝≥0，函数f（x）在（0，+∞）上单调递增；当a＜﹣1时，﹣a＞1，函数f（x）在（0，1）上单调递增，在（1，﹣a）上单调递减，在（﹣a，+∞）上单调递增；（Ⅱ）当a＜﹣1时，由（Ⅰ）得，函数f（x）在（1，﹣a）上单调递减，在（﹣a，+∞）上单调递增；函数f（x）在（1，+∞）上的最小值为f（﹣a）＝（a﹣1）ln（﹣a）﹣a﹣1，欲证明不等式f（x）＞﹣a﹣a2成立，即证明﹣a﹣a2＜（a﹣1）ln（﹣a）﹣a﹣1，即证明a2+（a﹣1）ln（﹣a）﹣1＞0，因为a＜﹣1，所以只需证明ln（﹣a）＜﹣a﹣1，令h（x）＝lnx﹣x+1（x≥1），则h′（x）＝＝≤0，所以函数h（x）在[1，+∞）上单调递减，则有h（x）≤h（1）＝0，因为a＜﹣1，所以﹣a＞1，所以h（﹣a）＝ln（﹣a）+a+1＜0，即当a＜﹣1时，ln（﹣a）＜﹣a﹣1成立，所以当a＜﹣1时，任意x∈（1，+∞），f（x）＞﹣a﹣a2．21．已知椭圆C：+y2＝1的右焦点为F，过点F的直线（不与x轴重合）与椭圆C相交于A，B两点，直线l：x＝2与x轴相交于点H，过点A作AD⊥l，垂足为D．（Ⅰ）求四边形OAHB（O为坐标原点）面积的取值范围；（Ⅱ）证明直线BD过定点E．并求出点E的坐标【分析】（Ⅰ）由题意设直线AB的方程，带入椭圆整理设而不求得出纵坐标之和与之积，将四边形的面积分成2个三角形，底相同与纵坐标之差的绝对值之积的二分之一，然后又均值不等式可得面积的取值范围；（Ⅱ）由（Ⅰ）得，B，D的坐标，设直线BD的方程，令纵坐标为零得横坐标是定值，即直线BD过定点．解：（Ⅰ）由题意F（1，0），设直线AB的方程：x＝my+1，A（x1，y1），B（x2，y2），与抛物线联立（m2+2）y2+2my﹣1＝0，因为△＝4m2+4（m2+2）＞0，y1+y2＝﹣，y1y2＝﹣，所以|y1﹣y2|＝＝，所以四边形OAHB的面积S＝|OH|•|y1﹣y2|＝|y1﹣y2|＝，令t＝≥1，S＝＝≤，当且仅当t＝1时，即m＝0时取等号，所以0，所以四边形OAHB的面积的取值范围为（0，，]（Ⅱ）B（x2，y2），D（2，y1），k BD＝，所以直线BD的方程：y﹣y1＝（x﹣2），令y＝0，得x＝＝由（Ⅰ）得，y1+y2＝﹣，y1y2＝﹣，所以y1+y2＝2my1y2，化简得x＝＝＝，所以直线BD过定点E（，0）．请考生在第22，23题中任选择一题作答，如果多做，则按所做的第一题记分，作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，已知P是曲线C1：x2+（y﹣2）2＝4上的动点，将OP绕点O 顺时针旋转90°得到OQ，设点Q的轨迹为曲线C2以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．（Ⅰ）求曲线C1，C2的极坐标方程；（Ⅱ）在极坐标系中，点M（3，），射线≥0）与曲线C1，C2分别相交于异于极点O的A，B两点，求△MAB的面积．【分析】（Ⅰ）由题意，点Q的轨迹是以（2，0）为圆心，以2为半径的圆，写出其普通方程，再结合ρ2＝x2+y2，x＝ρcosθ，y＝ρsinθ，可得曲线C1，C2的极坐标方程；（Ⅱ）在极坐标系中，设A，B的极径分别为ρ1，ρ2，求得|AB|＝|ρ1﹣ρ2|，再求出M （3，）到射线≥0）的距离h＝，代入三角形面积公式求△MAB的面积．解：（Ⅰ）由题意，点Q的轨迹是以（2，0）为圆心，以2为半径的圆，则曲线C2：（x﹣2）2+y2＝4，∵ρ2＝x2+y2，x＝ρcosθ，y＝ρsinθ，∴曲线C1的极坐标方程为ρ＝4sinθ，曲线C2的极坐标方程为ρ＝4cosθ；（Ⅱ）在极坐标系中，设A，B的极径分别为ρ1，ρ2，∴|AB|＝|ρ1﹣ρ2|＝4||＝．又∵M（3，）到射线≥0）的距离h＝．∴△MAB的面积S＝．[选修45：不等式选讲]23．已知函数f（x）＝|x﹣3|．（Ⅰ）解不等式f（x）≥4﹣|2x+l|；（Ⅱ）若＝2（m＞0，n＞0），求证：m+n≥|x+|﹣f（x）．【分析】（I）原不等式可化为：|x﹣3|≥4﹣|2x+1|，即|2x+1|+|x﹣3|≥4，分段讨论求出即可；（II）根据绝对值的性质求出|x+|﹣f（x）≤，m+n，证明即可．解：（I）原不等式可化为：|x﹣3|≥4﹣|2x+1|，即|2x+1|+|x﹣3|≥4，当x≤时，不等式﹣2x﹣1﹣x+3≥4，解得x，故x；当﹣＜x＜3时，不等式2x+1﹣x+3≥4，解得x≥0，故0≤x＜3；当x≥3时，不等式2x+1+x﹣3≥4，解得x≥0，故x≥3；综上，不等式的解集为（﹣∞，﹣]∪[0，+∞）；（II）因为f（x）＝|x﹣3|，所以|x+|﹣f（x）＝||x+|﹣|x﹣3|≤|x+﹣x+3|＝，当且仅当（x+）（x+3）≥0，且|x+|≥|x﹣3|时，取等号，又＝2（m＞0，n＞0），所以（m+n）（）≥（1+2）2＝9，当且仅当m＝2n时，取得等号，故m+n，所以m+n≥|x+|﹣f（x）成立．。

-2020年青羊区初三一诊语文卷1．下面加点字注音有误的一项为哪一项〔〕A．惊骇．〔hài〕调．和〔tiáo〕矫．揉造作〔jiǎo〕B．诓．骗〔kuāng〕中．伤〔zhòng〕歇．斯底里〔*iē〕C．濡．养〔rú〕坍．塌〔tān〕间．不容发〔jiàn〕D．桑梓．〔zǐ〕筵．席〔yán〕自吹自擂．〔1éi〕【答案】C【详解】C.间不容发〔jiàn〕——〔jiān〕。

应选C。

2．以下语句中书写正确的一项为哪一项〔〕A．然而圆规很不平，显出鄙夷的神色，仿佛嗤笑法国人不知道拿破仑，美国人不知道华盛顿似的……B．假设一个男人跟朋友和熟人见面时斌斌有礼，可是在家里对妻子儿女动不动就大发雷霆——那就可以肯定他不是一个有教养的人。

C．走出大门不多路，一脚揣在塘里，挣起来，头发都跌散了，两手黄泥，淋淋漓漓一身的水……D．它们在轰隆隆的雷声中，苍皇逃窜着。

【答案】A【详解】B."斌斌有礼〞应为"彬彬有礼〞；C．"揣〞应为"踹〞；D."苍皇"应为"仓皇〞。

应选A。

3．以下语句中加点的成语使用有误的一项为哪一项〔〕A．*些别有用心的组织或个人，为了混淆视听，对*些史实作断章取义．．．．的理解，甚至肆意篡改历史，他们的阴谋最终是不会得逞的。

B．华的妈妈看着来家访的教师，冲动地说："您能不顾疲劳，三顾茅庐．．．．，太令我感动了。

〞C．公园城市的建立，有力促进了城市良好生态格局的形成，它对宜居美丽城市形象的提升作用，也是不言而喻．．．．的。

D．人群中挤攘了一下，一个衣衫褴褛的流浪汉，重其事．．．地把一块钱放进了捐款箱。

【答案】B【详解】A.断章取义：指不顾全篇文章或谈话的容，孤立地取其中的一段或一句的意思。

指引用与原意不符。

与语境相合，使用正确。

B.三顾茅庐：比喻真心诚意，一再邀请。

2020年四川省成都市高考数学一诊考试（理科）试题一、选择题：本大题共12小题．每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若全集U=R，集合A={x|x2﹣x﹣2＞0}，则∁UA=（）A．（﹣1，2）B．（﹣2，1）C．[﹣1，2] D．[﹣2，1]2．命题“若a＞b，则a+c＞b+c”的否命题是（）A．若a≤b，则a+c≤b+c B．若a+c≤b+c，则a≤bC．若a+c＞b+c，则a＞b D．若a＞b，则a+c≤b+c3．执行如图所示的程序框图，如果输出的结果为0，那么输入的x为（）A．B．﹣1或1 C．﹣l D．l4．已知双曲线的左，右焦点分别为F1，F2，双曲线上一点P满足PF2⊥x轴，若|F1F2|=12，|PF2|=5，则该双曲线的离心率为（）A．B．C．D．35．已知α为第二象限角．且sin2α=﹣，则cosα﹣sinα的值为（）A．B．﹣C．D．﹣6．（x+1）5（x﹣2）的展开式中x2的系数为（）A．25 B．5 C．﹣15 D．﹣207．如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，则该四棱锥的外接球的表面积为（）A．136πB．34πC．25πD．18π8．将函数f（x）=sin2x+cos2x图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将图象上所有点向右平移个单位长度，得到函数g （x）的图象，则g（x）图象的一条对称轴方程是（）A．x=一 B．x=C．x= D．x=9．在直三棱柱ABC﹣A1BlC1中，平面α与棱AB，AC，A1C1，A1B1分别交于点E，F，G，H，且直线AA1∥平面α．有下列三个命题：①四边形EFGH是平行四边形；②平面α∥平面BCC1B1；③平面α⊥平面BCFE．其中正确的命题有（）A．①②B．②③C．①③D．①②③10．已知A，B是圆O：x2+y2=4上的两个动点，||=2，=﹣，若M是线段AB的中点，则•的值为（）A．3 B．2C．2 D．﹣311．已知函数f（x）是定义在R上的偶函数，且f（﹣x﹣1）=f（x﹣1），当x∈[﹣1，0]时，f（x）=﹣x3，则关于x的方程f（x）=|cosπx|在[﹣，]上的所有实数解之和为（）A．﹣7 B．﹣6 C．﹣3 D．﹣112．已知曲线C1：y2=tx（y＞0，t＞0）在点M（，2）处的切线与曲线C2：y=e x+1﹣1也相切，则tln的值为（）A．4e2B．8e C．2 D．8二、填空题：本大题共4小题，每小题5分，共20分．13．若复数z=（其中a∈R，i为虚数单位）的虚部为﹣1，则a= ．14．我国南北朝时代的数学家祖暅提出体积的计算原理（祖暅原理）：“幂势既同，则积不容异”．“势’’即是高，“幂”是面积．意思是：如果两等高的几何体在同高处截得两几何体的截面积恒等，那么这两个几何体的体积相等，类比祖暅原理，如图所示，在平面直角坐标系中，图1是一个形状不规则的封闭图形，图2是一个上底为l的梯形，且当实数t取[0，3]上的任意值时，直线y=t被图l和图2所截得的两线段长始终相等，则图l的面积为．15．若实数x，y满足约束条件，则的最小值为．16．已知△ABC中，AC=，BC=，△ABC的面积为，若线段BA的延长线上存在点D，使∠BDC=，则CD= ．三、解答题：本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（12分）已知数列{an }满足al=﹣2，an+1=2an+4．（I）证明数列{an+4}是等比数列；（Ⅱ）求数列{|an |}的前n项和Sn．18．（12分）云南省2016年高中数学学业水平考试的原始成绩采用百分制，发布成绩使用等级制，各登记划分标准为：85分及以上，记为A等，分数在[70，85）内，记为B等，分数在[60，70）内，记为C等，60分以下，记为D等，同时认定等级分别为A，B，C都为合格，等级为D为不合格．已知甲、乙两所学校学生的原始成绩均分布在[50，100]内，为了比较两校学生的成绩，分别抽取50名学生的原始成绩作为样本进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]分别作出甲校如图1所示样本频率分布直方图，乙校如图2所示样本中等级为C、D 的所有数据茎叶图．（1）求图中x的值，并根据样本数据比较甲乙两校的合格率；（2）在选取的样本中，从甲、乙两校C等级的学生中随机抽取3名学生进行调研，用X表示所抽取的3名学生中甲校的学生人数，求随机变量X的分布列和数学期望．19．（12分）如图1，在正方形ABCD中，点E，F分别是AB，BC的中点，BD与EF交于点H，G 为BD中点，点R在线段BH上，且=λ（λ＞0）．现将△AED，△CFD，△DEF分别沿DE，DF，EF折起，使点A，C重合于点B（该点记为P），如图2所示．（I）若λ=2，求证：GR⊥平面PEF；（Ⅱ）是否存在正实数λ，使得直线FR与平面DEF所成角的正弦值为？若存在，求出λ的值；若不存在，请说明理由．20．（12分）已知椭圆的右焦点为F，设直线l：x=5与x轴的交点为E，过点F 且斜率为k的直线l与椭圆交于A，B两点，M为线段EF的中点．1的倾斜角为，求△ABM的面积S的值；（I）若直线l1（Ⅱ）过点B作直线BN⊥l于点N，证明：A，M，N三点共线．21．（12分）已知函数f（x）=xln（x+1）+（﹣a）x+2﹣a，a∈R．（I）当x＞0时，求函数g（x）=f（x）+ln（x+1）+x的单调区间；（Ⅱ）当a∈Z时，若存在x≥0，使不等式f（x）＜0成立，求a的最小值．请考生在第（22）、（23）题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．（10分）在平面直角坐标系xOy中，倾斜角为α（α≠）的直线l的参数方程为（t为参数）．以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程是ρcos2θ﹣4sinθ=0．（I）写出直线l的普通方程和曲线C的直角坐标方程；（Ⅱ）已知点P（1，0）．若点M的极坐标为（1，），直线l经过点M且与曲线C相交于A，B两点，设线段AB的中点为Q，求|PQ|的值．[选修4-5：不等式选讲]23．已知函数f（x）=x+1+|3﹣x|，x≥﹣1．（I）求不等式f（x）≤6的解集；（Ⅱ）若f（x）的最小值为n，正数a，b满足2nab=a+2b，求2a+b的最小值．2020年四川省成都市高考数学一诊考试（理科）试题参考答案一、选择题：本大题共12小题．每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．A=（）1．若全集U=R，集合A={x|x2﹣x﹣2＞0}，则∁UA．（﹣1，2）B．（﹣2，1）C．[﹣1，2] D．[﹣2，1]【分析】求出集合A，利用补集的定义进行求解即可．【解答】解：A={x|x2﹣x﹣2＞0}={x|x＞2或x＜﹣1}，A={x|﹣1≤x≤2}，则∁U故选：C【点评】本题主要考查集合的基本运算，比较基础．2．命题“若a＞b，则a+c＞b+c”的否命题是（）A．若a≤b，则a+c≤b+c B．若a+c≤b+c，则a≤bC．若a+c＞b+c，则a＞b D．若a＞b，则a+c≤b+c【分析】根据命题“若p，则q”的否命题是“若￢p，则￢q”．【解答】解：命题“若a＞b，则a+c＞b+c”的否命题是“若a≤b，则a+c≤b+c”．故选：A．【点评】本题考查了命题与它的否命题的应用问题，是基础题．3．执行如图所示的程序框图，如果输出的结果为0，那么输入的x为（）A．B．﹣1或1 C．﹣l D．l【分析】根据题意，模拟程序框图的运行过程，根据输出的结果为0，得出输入的x．【解答】解：根据题意，模拟程序框图的运行过程，x≤0，y=﹣x2+1=0，∴x=﹣1，x＞0，y=3x+2=0，无解，故选：C．【点评】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，即可得出正确的答案，属于基础题．4．已知双曲线的左，右焦点分别为F1，F2，双曲线上一点P满足PF2⊥x轴，若|F1F2|=12，|PF2|=5，则该双曲线的离心率为（）A．B．C．D．3【分析】双曲线上一点P满足PF2⊥x轴，若|F1F2|=12，|PF2|=5，可得|PF1|=13，利用双曲线的定义求出a，即可求出双曲线的离心率．【解答】解：∵双曲线上一点P满足PF2⊥x轴，若|F1F2|=12，|PF2|=5，∴|PF1|=13，∴2a=|PF1|﹣|PF2|=8，∴a=4，∵c=6，∴e==，故选C．【点评】本题考查双曲线的定义与性质，考查学生的计算能力，比较基础．5．已知α为第二象限角．且sin2α=﹣，则cosα﹣sinα的值为（）A．B．﹣C．D．﹣【分析】由α的范围和三角函数值的符号判断出cosα﹣sinα的符号，由条件、平方关系、二倍角的正弦函数求出cosα﹣sinα的值．【解答】解：∵α为第二象限角，∴cosα﹣sinα＜0，∵sin2α=﹣，∴cosα﹣sinα=﹣===，故选B．【点评】本题考查二倍角的正弦函数，平方关系，以及三角函数值的符号，属于基础题．6．（x+1）5（x﹣2）的展开式中x2的系数为（）A．25 B．5 C．﹣15 D．﹣20【分析】利用二项式定理的展开式即可得出．【解答】解：（x+1）5（x﹣2）=（x﹣2）的展开式中x2的系数=﹣2=﹣15．故选：C．【点评】本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．7．如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，则该四棱锥的外接球的表面积为（）A．136πB．34πC．25πD．18π【分析】由四棱锥的三视图知该四棱锥是四棱锥P﹣ABCD，其中ABCD是边长为3的正方形，PA⊥面ABCD，且PA=4，从而该四棱锥的外接球就是以AB，AC，AP为棱的长方体的外接球，由此能求出该四棱锥的外接球的表面积．【解答】解：由四棱锥的三视图知该四棱锥是如图所示的四棱锥P﹣ABCD，其中ABCD是边长为3的正方形，PA⊥面ABCD，且PA=4，∴该四棱锥的外接球就是以AB，AD，AP为棱的长方体的外接球，∴该四棱锥的外接球的半径R==，∴该四棱锥的外接球的表面积S=4πR2=4π×=34π．故选：B．【点评】本题考查球的表面积的求法，是中档题，解题时要认真审题，注意球、四棱锥、几何体的三视图的性质及构造法的合理应用．8．将函数f（x）=sin2x+cos2x图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将图象上所有点向右平移个单位长度，得到函数g （x）的图象，则g（x）图象的一条对称轴方程是（）A．x=一 B．x=C．x= D．x=【分析】利用函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，求得g（x）图象的一条对称轴方程．【解答】解：将函数f（x）=sin2x+cos2x=2（sin2x+cos2x）=2sin（2x+）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），可得y=2sin（x+）的图象；再将图象上所有点向右平移个单位长度，得到函数g （x）=2sin（x﹣+）=2sin（x+）的图象的图象的图象，令x+=kπ+，求得x=kπ+，k∈Z．令k=0，可得g（x）图象的一条对称轴方程是x=，故选：D．【点评】本题主要考查函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，属于基础题．9．在直三棱柱ABC﹣A1BlC1中，平面α与棱AB，AC，A1C1，A1B1分别交于点E，F，G，H，且直线AA1∥平面α．有下列三个命题：①四边形EFGH是平行四边形；②平面α∥平面BCC1B1；③平面α⊥平面BCFE．其中正确的命题有（）A．①②B．②③C．①③D．①②③【分析】在①中，由AA1EH GF，知四边形EFGH是平行四边形；在②中，平面α与平面BCC1B1平行或相交；在③中，EH⊥平面BCEF，从而平面α⊥平面BCFE．【解答】解：如图，∵在直三棱柱ABC﹣A1BlC1中，平面α与棱AB，AC，A1C1，A1B1分别交于点E，F，G，H，且直线AA1∥平面α．∴AA1EH GF，∴四边形EFGH是平行四边形，故①正确；∵EF与BC不一定平行，∴平面α与平面BCC1B1平行或相交，故②错误；∵AA1EH GF，且AA1⊥平面BCEF，∴EH⊥平面BCEF，∵EH⊂平面α，∴平面α⊥平面BCFE，故③正确．故选：C．【点评】本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．10．已知A，B是圆O：x2+y2=4上的两个动点，||=2，=﹣，若M是线段AB的中点，则•的值为（）A．3 B．2C．2 D．﹣3【分析】由A，B是圆O：x2+y2=4上的两个动点，||=2，得到与的夹角为，再根据向量的几何意义和向量的数量积公式计算即可．【解答】解：A，B是圆O：x2+y2=4上的两个动点，||=2，∴与的夹角为，∴•=||•||•cos=2×2×=2，∵M是线段AB的中点，∴=（+），∵=﹣，∴•=（+）•（﹣）=（5||2+3••﹣2||2）=（20+6﹣8）=3，故选：A【点评】本题考查了圆的有关性质以及向量的几何意义和向量的数量积公式，属于中档题．11．已知函数f（x）是定义在R上的偶函数，且f（﹣x﹣1）=f（x﹣1），当x∈[﹣1，0]时，f（x）=﹣x3，则关于x的方程f（x）=|cosπx|在[﹣，]上的所有实数解之和为（）A．﹣7 B．﹣6 C．﹣3 D．﹣1【分析】由f（x）是偶函数说明函数图象关于y轴对称，由f（﹣x﹣1）=f（x﹣1），得到x=﹣1是函数的对称轴，画出函数f（x）的图象，只要找出函数f（x）的图象与y=|cosπx|在[﹣，]上内交点的情况，根据对称性即可求出答案．【解答】解：∵函数f（x）是定义在R上的偶函数，f（﹣x﹣1）=f（x﹣1），∴x=﹣1是函数的对称轴，分别画出y=f（x）与y=|cosπx|在[﹣，]上图象，交点依次为x1，x2，x3，x4，x5，x6，x7，∴x1+x7=﹣2，x2+x6=﹣2，x3+x5=﹣2，x4=﹣1，∴x1+x2+x3+x4+x5+x6+x7=﹣2×3﹣1=﹣7，故选：A【点评】本题考查了函数与方程的综合应用以及函数图象的对称性与奇偶性等知识点，数形结合是解决本题的关键，属中档题12．已知曲线C1：y2=tx（y＞0，t＞0）在点M（，2）处的切线与曲线C2：y=e x+1﹣1也相切，则tln的值为（）A．4e2B．8e C．2 D．8【分析】利用曲线C1：y2=tx（y＞0，t＞0）在点M（，2）处的切线与曲线C2：y=e x+1﹣1也相切，求出t的值，则tln的值可求．【解答】解：曲线C1：y2=tx（y＞0，t＞0），y′=•t，x=，y′=，∴切线方程为y﹣2=（x﹣）设切点为（m，n），则曲线C2：y=e x+1﹣1，y′=e x+1，e m+1=，∴m=ln﹣1，n=﹣1，代入﹣1﹣2=（ln﹣1﹣），解得t=4，∴tln=4lne2=8．故选D．【点评】本题考查导数的几何意义的应用，解题时要认真审题，仔细解答，注意等价转化思想的合理运用．二、填空题：本大题共4小题，每小题5分，共20分．13．若复数z=（其中a∈R，i为虚数单位）的虚部为﹣1，则a= ﹣2 ．【分析】利用复数的运算法则、虚部的定义即可得出．【解答】解：复数z===+i的虚部为﹣1，则=﹣1，解得a=﹣2．故答案为：﹣2．【点评】本题考查了复数的运算法则、虚部的定义，考查了推理能力与计算能力，属于基础题．14．我国南北朝时代的数学家祖暅提出体积的计算原理（祖暅原理）：“幂势既同，则积不容异”．“势’’即是高，“幂”是面积．意思是：如果两等高的几何体在同高处截得两几何体的截面积恒等，那么这两个几何体的体积相等，类比祖暅原理，如图所示，在平面直角坐标系中，图1是一个形状不规则的封闭图形，图2是一个上底为l的梯形，且当实数t取[0，3]上的任意值时，直线y=t被图l和图2所截得的两线段长始终相等，则图l的面积为．【分析】根据祖暅原理，可得图1的面积=梯形的面积，即可得出结论．【解答】解：根据祖暅原理，可得图1的面积=梯形的面积==．故答案为．【点评】此题考查了梯形的面积公式，还考查了学生空间的想象能力及计算技能．15．若实数x，y满足约束条件，则的最小值为．【分析】由约束条件作出可行域，的几何意义是（x，y）与（0，1）连线的斜率，数形结合得到的最小值．【解答】解：由约束条件，作出可行域如图，的几何意义是（x，y）与（0，1）连线的斜率联立，解得A（1，），∴的最小值为=﹣．故答案为：﹣．【点评】本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．16．已知△ABC中，AC=，BC=，△ABC的面积为，若线段BA的延长线上存在点D，使∠BDC=，则CD= ．【分析】由已知利用三角形面积公式可求sin∠ACB=，从而可求∠ACB=，在△ABC中，由余弦定理可得AB，进而可求∠B，在△BCD中，由正弦定理可得CD的值．【解答】解：∵AC=，BC=，△ABC的面积为=AC•BC•sin∠ACB=sin∠ACB，∴sin∠ACB=，∴∠ACB=，或，∵若∠ACB=，∠BDC=＜∠BAC，可得：∠BAC+∠ACB＞+＞π，与三角形内角和定理矛盾，∴∠ACB=，∴在△ABC 中，由余弦定理可得：AB===，∴∠B=，∴在△BCD 中，由正弦定理可得：CD===．故答案为：．【点评】本题主要考查了三角形面积公式，余弦定理，正弦定理在解三角形中的应用，考查了转化思想和数形结合思想，求∠ACB 的值是解题的关键，属于中档题．三、解答题：本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（12分）已知数列{a n }满足a l =﹣2，a n+1=2a n +4． （I ）证明数列{a n +4}是等比数列； （Ⅱ）求数列{|a n |}的前n 项和S n ．【分析】（I ）数列{a n }满足a l =﹣2，a n+1=2a n +4，a n+1+4=2（a n +4），即可得出．（II ）由（I ）可得：a n +4=2n ，可得a n =2n ﹣4，当n=1时，a 1=﹣2；n ≥2时，a n ≥0，可得n ≥2时，S n =﹣a 1+a 2+a 3+…+a n ．【解答】（I ）证明：∵数列{a n }满足a l =﹣2，a n+1=2a n +4，∴a n+1+4=2（a n +4），∴数列{a n +4}是等比数列，公比与首项为2．（II ）解：由（I ）可得：a n +4=2n ，∴a n =2n ﹣4，∴当n=1时，a 1=﹣2；n ≥2时，a n ≥0， ∴n ≥2时，S n =﹣a 1+a 2+a 3+…+a n =2+（22﹣4）+（23﹣4）+…+（2n ﹣4） =﹣4（n ﹣1）=2n+1﹣4n+2．n=1时也成立．∴S n =2n+1﹣4n+2．n ∈N *．【点评】本题考查了等比数列的通项公式与求和公式、分组求和方法，考查了推理能力与计算能力，属于中档题．18．（12分）（2017•云南一模）云南省2016年高中数学学业水平考试的原始成绩采用百分制，发布成绩使用等级制，各登记划分标准为：85分及以上，记为A等，分数在[70，85）内，记为B等，分数在[60，70）内，记为C等，60分以下，记为D等，同时认定等级分别为A，B，C都为合格，等级为D为不合格．已知甲、乙两所学校学生的原始成绩均分布在[50，100]内，为了比较两校学生的成绩，分别抽取50名学生的原始成绩作为样本进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]分别作出甲校如图1所示样本频率分布直方图，乙校如图2所示样本中等级为C、D 的所有数据茎叶图．（1）求图中x的值，并根据样本数据比较甲乙两校的合格率；（2）在选取的样本中，从甲、乙两校C等级的学生中随机抽取3名学生进行调研，用X表示所抽取的3名学生中甲校的学生人数，求随机变量X的分布列和数学期望．【分析】（1）利用频率分布直方图的性质可得x，进而定点甲校的合格率．由茎叶图可得乙校的合格率．（2）甲乙两校的C等级的学生数分别为：0.012×10×50=6，4人．X=0，1，2，3．利用P（X=k）=，即可得出．【解答】解：（1）由频率分布直方图可得：（x+0.012+0.056+0.018+0.010）×10=1，解得x=0.004．=（1﹣0.004）×10=0.96=96%，甲校的合格率P1乙校的合格率P==96%．2可得：甲乙两校的合格率相同，都为96%．（2）甲乙两校的C等级的学生数分别为：0.012×10×50=6，4人．X=0，1，2，3．则P（X=k）=，P（X=0）==，P（X=1）==，P（X=2）==，P（X=3）==．∴X的分布列为：X 0 1 2 3PE（X）=0+1×+2×+3×=．【点评】本题主要考查了超几何分布列的性质及其数学期望、频率分布直方图的性质、茎叶图的性质等基础知识，考查了推理能力与计算能力，属于中档题．19．（12分）如图1，在正方形ABCD中，点E，F分别是AB，BC的中点，BD与EF交于点H，G 为BD中点，点R在线段BH上，且=λ（λ＞0）．现将△AED，△CFD，△DEF分别沿DE，DF，EF折起，使点A，C重合于点B（该点记为P），如图2所示．（I）若λ=2，求证：GR⊥平面PEF；（Ⅱ）是否存在正实数λ，使得直线FR与平面DEF所成角的正弦值为？若存在，求出λ的值；若不存在，请说明理由．【分析】（I）若λ=2，证明PD⊥平面PEF，GR∥PD，即可证明：GR⊥平面PEF；（Ⅱ）建立如图所示的坐标系，求出平面DEF的一个法向量，利用直线FR与平面DEF所成角的正弦值为，建立方程，即可得出结论．【解答】（I）证明：由题意，PE，PF，PD三条直线两两垂直，∴PD⊥平面PEF，图1中，EF∥AC，∴GB=2GH，∵G为BD中点，∴DG=2GH．图2中，∵=2，∴△PDH中，GR∥PD，∴GR⊥平面PEF；（Ⅱ）解：由题意，建立如图所示的坐标系，设PD=4，则P（0，0，0），F（2，0，0），E（0，2，0），D（0，0，4），∴H（1，1，0），∵=λ，∴R（，，0），∴=（，﹣，0），∵=（2，﹣2，0），=（0，2，﹣4），设平面DEF的一个法向量为=（x，y，z），则，取=（2，2，1），∵直线FR与平面DEF所成角的正弦值为，∴=，∴λ=，∴存在正实数λ=，使得直线FR与平面DEF所成角的正弦值为．【点评】本题考查了线面垂直的判定，线面角的计算，考查向量方法的运用，属于中档题．20．（12分）已知椭圆的右焦点为F，设直线l：x=5与x轴的交点为E，过点F 与椭圆交于A，B两点，M为线段EF的中点．且斜率为k的直线l1（I）若直线l的倾斜角为，求△ABM的面积S的值；1（Ⅱ）过点B作直线BN⊥l于点N，证明：A，M，N三点共线．【分析】（I ）由题意，直线l 1的x=y+1，代入椭圆方程，由韦达定理，弦长公式即可求得△ABM 的面积S 的值；（Ⅱ）直线y=k （x ﹣1），代入椭圆方程，由韦达定理，利用直线的斜率公式，即可求得k AM =k MN ，A ，M ，N 三点共线．【解答】解：（I ）由题意可知：右焦点F （1，0），E （5，0），M （3，0）， 设A （x 1，y 1），B （x 2，y 2）， 由直线l 1的倾斜角为，则k=1，直线l 1的方程y=x ﹣1，即x=y+1， 则，整理得：9x 2+8﹣16=0．则y 1+y 2=﹣，y 1y 2=﹣，△ABM 的面积S ，S=•丨FM 丨•丨y 1﹣y 2丨=丨y 1﹣y 2丨==，∴△ABM 的面积S 的值；（Ⅱ）证明：设直线l 1的方程为y=k （x ﹣1）， 则，整理得：（4+5k 2）x 2﹣10k 2x+5k 2﹣20=0．则x 1+x 2=，x 1x 2=，直线BN ⊥l 于点N ，则N （5，y 2）， 由k AM =，k MN =，而y 2（3﹣x 1）﹣2（﹣y 1）=k （x 2﹣1）（3﹣x 1）+2k （x 1﹣1）=﹣k[x 1x 2﹣3（x 1+x 2）+5]， =﹣k （﹣3×+5），=0， ∴k AM =k MN ，∴A ，M ，N 三点共线．【点评】本题考查椭圆的标准方程，直线与椭圆的位置关系，韦达定理，弦长公式，考查直线的斜率公式，考查计算能力，属于中档题．21．（12分）已知函数f（x）=xln（x+1）+（﹣a）x+2﹣a，a∈R．（I）当x＞0时，求函数g（x）=f（x）+ln（x+1）+x的单调区间；（Ⅱ）当a∈Z时，若存在x≥0，使不等式f（x）＜0成立，求a的最小值．【分析】（Ⅰ）求出函数g（x）的导数，通过讨论a的范围求出函数的单调区间即可；（Ⅱ）问题等价于a＞，令h（x）=，x≥0，唯一转化为求出a＞h（x），根据函数的单调性求出h（x）的最小值，从而求出a的最小值min即可．【解答】解：（Ⅰ）∵g（x）=（x+1）ln（x+1）+（1﹣a）x+2﹣a，（x＞0），∴g′（x）=ln（x+1）+2﹣a，当2﹣a≥0即a≤2时，g′（x）＞0对x∈（0，+∞）恒成立，此时，g（x）在（0，+∞）递增，无递减区间，当2﹣a＜0即a＞2时，由g′（x）＞0，得x＞e a﹣2﹣1，由g′（x）＜0，得0＜x＜e a﹣2﹣1，此时，g（x）在（0，e a﹣2﹣1）递减，在（e a﹣2﹣1，+∞）递增，综上，a≤2时，g（x）在（0，+∞）递增，无递减区间；a＞2时，g（x）在（0，e a﹣2﹣1）递减，在（e a﹣2﹣1，+∞）递增，（Ⅱ）由f（x）＜0，得（x+1）a＞xln（x+1）+x+2，当x≥0时，上式等价于a＞，令h（x）=，x≥0，，由题意，存在x≥0，使得f（x）＜0成立，则只需a＞h（x）min∵h′（x）=，令u （x ）=ln （x+1）+x ﹣，显然u （x ）在[0，+∞）递增，而u （0）=﹣＜0，u （1）=ln2﹣＞0，故存在x 0∈（0，1），使得u （x 0）=0，即ln （x 0+1）=﹣x 0，又当x 0∈[0，x 0）时，h ′（x ）＜0，h （x ）递减，当x ∈[x 0，+∞）时，h ′（x ）＞0，h （x ）递增，故x=x 0时，h （x ）有极小值（也是最小值），故h （x ）min =，故a ≥=，x 0∈（0，1），而2＜＜3，故a 的最小整数值是3．【点评】本题考查了函数的单调性、最值问题，考查导数的应用以及分类讨论思想，考查转化思想，是一道综合题．请考生在第（22）、（23）题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．（10分）在平面直角坐标系xOy 中，倾斜角为α（α≠）的直线l 的参数方程为（t 为参数）．以坐标原点为极点，以x 轴的正半轴为极轴，建立极坐标系，曲线C 的极坐标方程是ρcos 2θ﹣4sin θ=0．（I ）写出直线l 的普通方程和曲线C 的直角坐标方程；（Ⅱ）已知点P （1，0）．若点M 的极坐标为（1，），直线l 经过点M 且与曲线C 相交于A ，B 两点，设线段AB 的中点为Q ，求|PQ|的值．【分析】（Ⅰ）直线l 的参数方程消去参数t ，能求出直线l 的普通方程；由曲线C 的极坐标方程能求出曲线C 的直角坐标方程．（Ⅱ）求出点M的直角坐标为（0，1），从而直线l的倾斜角为，由此能求出直线l 的参数方程，代入x2=4y，得，由此利用韦达定理和两点间距离公式能求出|PQ|．【解答】解：（Ⅰ）∵直线l的参数方程为（t为参数）．∴直线l的普通方程为y=tanα•（x﹣1），由曲线C的极坐标方程是ρcos2θ﹣4sinθ=0，得ρ2cos2θ﹣4ρsinθ=0，∴x2﹣4y=0，∴曲线C的直角坐标方程为x2=4y．（Ⅱ）∵点M的极坐标为（1，），∴点M的直角坐标为（0，1），∴tanα=﹣1，直线l的倾斜角为，∴直线l的参数方程为，代入x2=4y，得，设A，B两点对应的参数为t1，t2，∵Q为线段AB的中点，∴点Q对应的参数值为，又P（1，0），则|PQ|=||=3．【点评】本题考查曲线的直角坐标方程的求法，考查弦长的求法及应用，考查两点间距离公式的求法，是中档题，解题时要认真审题，注意参数方程、直角坐标方程、极坐标方程互化公式的合理运用．[选修4-5：不等式选讲]23．已知函数f（x）=x+1+|3﹣x|，x≥﹣1．（I）求不等式f（x）≤6的解集；（Ⅱ）若f（x）的最小值为n，正数a，b满足2nab=a+2b，求2a+b的最小值．【分析】（Ⅰ）根据题意，由绝对值的性质可以将f（x）≤6转化可得或，解可得x的范围，即可得答案；（Ⅱ）根据题意，由函数f（x）的解析式分析可得f（x）的最小值为4，即n=4；进而可得正数a，b满足8ab=a+2b，即+=8，将2a+b变形可得2a+b=（++5），由基本不等式的性质可得2a+b的最小值，即可得答案．【解答】解：（Ⅰ）根据题意，函数f（x）=x+1+|3﹣x|，x≥﹣1．若f（x）≤6，则有或，解可得﹣1≤x≤4，故原不等式的解集为{x|﹣1≤x≤4}；（Ⅱ）函数f（x）=x+1+|3﹣x|=，分析可得f（x）的最小值为4，即n=4；则正数a，b满足8ab=a+2b，即+=8，2a+b=（+）（2a+b）=（++5）≥（5+2）=；即2a+b的最小值为．【点评】本题考查绝对值不等式的解法，涉及基本不等式的性质与应用，关键是正确求出函数f（x）的最小值。

2020成都一诊解析几何试题赏析
法三:点 A 在以 PF 为直径的圆上,联立圆和抛物线的方程可得 A 点坐标。

【点评】法一是解析几何基本方程,法二涉及垂直,可以借助焦半径公式优化,法三看到了动点的轨迹。

参考《解析几何的系统性突破》的赠书《解析几何高观点·新视野》
【点评1】在《解析几何高观点·新视野》中把面积问题作为基本问题,给出了常见的六种题型及处理方式,其中第四种就是借助“边相同,高相同,角相同”把面积之比化为长度之比,借助作坐标轴的垂线把长度之比化为坐标之比。

此题正是这一思想的体现。

反过来,第五种借助线段的长度关系对所求面积进行转化。

【点评2】此题具有一定的综合性,对运算提出了较高要求,在《解析几何高观点·新视野》中,给出了解析几何常用的两种运算模式和解题表,然后给出了 21 种突破运算的方案。