戴维宁等效电路

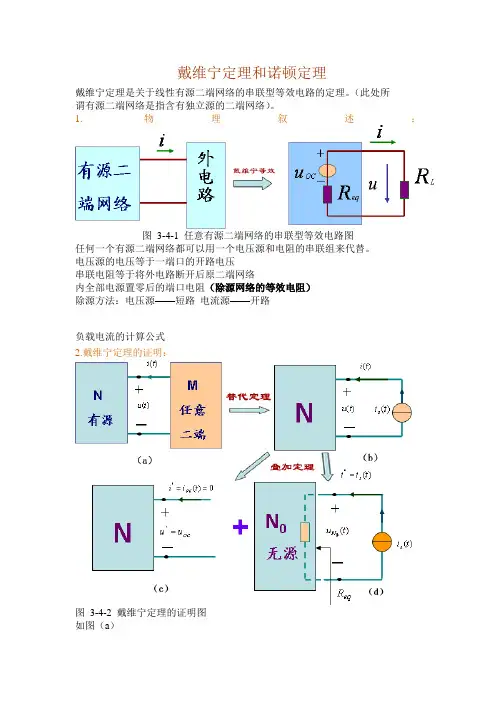
戴维宁定理和诺顿定理戴维宁定理是关于线性有源二端网络的串联型等效电路的定理。

（此处所谓有源二端网络是指含有独立源的二端网络）。

1. 物理叙述：图3-4-1 任意有源二端网络的串联型等效电路图任何一个有源二端网络都可以用一个电压源和电阻的串联组来代替。

电压源的电压等于一端口的开路电压串联电阻等于将外电路断开后原二端网络内全部电源置零后的端口电阻（除源网络的等效电阻）除源方法：电压源——短路电流源——开路负载电流的计算公式2.戴维宁定理的证明：图3-4-2 戴维宁定理的证明图如图（a）(1) 按替代定理用一个电流源代替任意二端网络M ，此电流源的电流(t)等于被代替的二端网络M 的端口电流，二者的参考方向也相同，如图（b）(2) 根据叠加定理，线性有源二端网络的端口电压和端口电流可以看成是两个分量叠加的结果：一个分量是当该网络内部所有独立源共同作用时在网络端口处产生的电压和电流，如图（c），另一个分量是当该网络外部的电流源单独作用时在同一端口处产生的电压和电流，如图（d）。

图（d）中无源网络的等效电阻为，网络可以用一个阻值为的等效电阻元件来代替，则有。

根据叠加定理可以确定原线性有源二端网络的端口电压为根据这个关系可以构造出原线性有源二端网络N的等效电路如图（e）(图中恢复了原任意二端网络M)由此说明有源二端网络可用电压源与电阻的串联组合等效代替：电压=有源二端网络的开路电压电阻=除源网络的等效电阻（除独立源）图3-4-3原线性有源二端网络N的等效电路图3．作用：在有些情况下只需计算一个复杂电路中某一支路（或某一部分）的电流。

我们可以把这个支路（部分）划出，而把其余部分看成是一个有源二端网络，这个有源二端网络对于此支路仅相当于一个供给电流的电源。

只要将这个网络用电压源于电阻的串联组合成电流源与电阻的并联组合等效代替就可以使问题简单化。

4.求解戴维宁定理的关键：1）、求开路电压：几乎用到解复杂电路的各种方法2）、等效电阻：当网络含受控源时方法：①外施电压法、电流②短路电流法例3-4-1诺顿定理是关于线性有源二端网络的并联型等效电路的定理。

实验二戴维宁和诺顿等效电路
一.实验目的
(1)熟练运用电路仿真软件，熟练运用电压表电流表以及功率表的运用。

（2）熟练运用戴维宁定理，掌握含受控源电路的戴维宁定理的运行。

（3）利用电路仿真软件验证戴维宁定理的正确性，深刻认识等效电路的变换
二.实验原理
实验原理：一个线性含源一端口电阻网络，对外电路来说，可以用一个电压源和电阻的串联组合来代替。

此电压源的电压等于含源一端口的开路电压Uoc，串联电阻等一一端口内部的全部独立电源置零后的等效电阻Req
二.实验步骤
1.分别从电源库、元件库和指示部件库中调用所需电源、电阻和电压表、电流,如图将电压表接至a，b两端，确定电压表属性中Mode为DC。

打开仿真，记下电压表数据为21.904V
2.如图将电流表接至a，b两端，确定电流表属性中Mode为DC。

打开仿真，记下电流表数据为0.968A。

四.仿真结果
戴维南和诺顿等效电路如图
五.分析现象
不难看出ab两端的开路电压和短路电流的仿真电路结果与理论结果相同。

即戴维宁定理是正确的
六.实验收获
深刻了解戴维宁等效电路的转变方法。

熟练运用Multisim仿真电路分析戴维宁等效电路。

在仿真电路分析中，接地还是不能忘记，电压源和电流源测量的也是直流电。

戴维宁等效电路受控源处理1. 引言大家好，今天咱们聊聊一个看似复杂但其实充满趣味的话题——戴维宁等效电路，尤其是它的受控源处理。

你可能会想：“这是什么鬼？听起来像是个无聊的数学公式。

”别急，咱们慢慢来，保证让你听得津津有味。

想象一下，我们要把电路变得简单明了，就像把一杯浓稠的牛奶稀释成清爽的奶昔，简单好喝又易于消化！2. 什么是戴维宁等效电路？2.1 戴维宁定理的背景首先，咱们得知道，戴维宁等效电路是用来简化复杂电路的一种方法。

这就像给你一盘复杂的菜，结果你只想吃简单的米饭配点儿菜，省事又好吃。

简单来说，戴维宁定理告诉我们，任何线性电路都能被一个电压源和一个电阻的组合替代。

听起来是不是很神奇？对了，这里说的线性电路，就像是一条笔直的路，不会突然拐弯，变化也很规律。

2.2 受控源的神秘面纱再说说受控源。

哇，这听起来就像是个高大上的名词，其实它并不复杂。

受控源就是那种其输出量（电压或电流）依赖于电路中其他参数的源。

想象一下，你在逗猫，猫咪的反应就决定了你继续逗还是停下来。

就是这么简单！而在戴维宁等效电路中，我们就得把这些受控源好好处理一下，才能让电路看起来更加清晰。

3. 受控源的处理技巧3.1 替换受控源接下来，咱们聊聊如何替换这些受控源。

通常，你会把受控源转化为电压源或电流源。

这听起来很复杂，但其实你只需要按部就班，就像做菜一样。

首先，你得明确受控源的“控制”变量是什么。

比如说，如果你有一个电流源，它的输出电流依赖于某个电压，那你就要把这个电压替换进来。

记住，换了“调料”，菜的味道就会变得不一样哦！3.2 求解等效电路一旦你把受控源替换好，接下来就得求解等效电路了。

这就像做一个拼图，你得把各个部分拼在一起，才能看到完整的画面。

利用基尔霍夫定律，咱们可以轻松求出电压和电流，最终得到一个美丽的等效电路。

这一步可不能马虎哦，不然拼图就会错位，最后只能让人干着急。

4. 实际应用与小结4.1 戴维宁等效电路的实际应用说到这里，很多人可能会问：“这有什么用？”其实，戴维宁等效电路在实际工程中用得可多了！无论是电力系统分析，还是电子设备设计，咱们都能见到它的身影。

戴维宁定理实验报告一、实验目的1、验证戴维宁定理的正确性，加深对该定理的理解。

2、掌握测量有源二端网络等效参数的一般方法。

3、学习使用电路实验仪器，如直流稳压电源、万用表等。

二、实验原理戴维宁定理指出：任何一个线性有源二端网络，对外电路来说，可以用一个电压源和一个电阻的串联组合来等效替代。

其中，电压源的电动势等于有源二端网络的开路电压＄U_{OC}＄，电阻等于有源二端网络除源（即理想电压源短路，理想电流源开路）后的等效电阻＄R_{0}＄。

三、实验设备1、直流稳压电源 1 台2、直流数字电压表 1 台3、直流数字电流表 1 台4、万用表 1 只5、电阻箱 1 个6、实验电路板 1 块7、连接导线若干四、实验内容与步骤1、测量有源二端网络的开路电压＄U_{OC}＄按图 1 所示连接电路，将负载电阻＄R_{L}＄开路，用直流数字电压表测量有源二端网络的开路电压＄U_{OC}＄，记录测量值。

！图 1 测量开路电压(此处应插入图 1)2、测量有源二端网络的短路电流＄I_{SC}＄将图 1 中的电路短路，用直流数字电流表测量有源二端网络的短路电流＄I_{SC}＄，记录测量值。

3、计算有源二端网络的等效内阻＄R_{0}＄根据公式＄R_{0} ＝＼frac{U_{OC}｝｛I_{SC}｝＄，计算有源二端网络的等效内阻＄R_{0}＄。

4、测量有源二端网络的外特性按图 2 所示连接电路，改变负载电阻＄R_{L}＄的值，测量不同负载电阻下的电流＄I$ 和电压＄U$ ，记录测量数据。

！图 2 测量外特性(此处应插入图 2)5、构建戴维宁等效电路根据测量得到的开路电压＄U_{OC}＄和等效内阻＄R_{0}＄，构建戴维宁等效电路，如图 3 所示。

！图 3 戴维宁等效电路(此处应插入图 3)6、测量戴维宁等效电路的外特性改变负载电阻＄R_{L}＄的值，测量戴维宁等效电路的电流＄I'＄和电压＄U'＄，记录测量数据。

戴维宁定理和诺顿定理的等效条件
戴维宁定理和诺顿定理都是电路分析中常用的定理，用来简化复杂的电路。

本文将介绍它们的等效条件。

一、基本概念
在介绍定理的等效条件前，先简要介绍一下它们的基本概念：
1.戴维宁定理
戴维宁定理指出，任意一个线性电路都可以用一个等效的电压源和电阻表示，这个等效的电阻叫做戴维宁等效电阻。

2.诺顿定理
二、等效条件
（1）在两个端口之间的电压是恒定的。

（2）只有被替代的电路单元上的电阻值与被替代的电路单元之间的两个端口所连接的剩余部分有关。

（3）被替代的电路单元的电流可以确定，这个电流等于电路两个端口之间的电压除以电路单元的电阻。

这里需要解释一下“被替代的电路单元”和“剩余部分”的概念。

被替代的电路单元指的是电路中的某一部分，它可以是一个电阻、一个电容、一个电感、一个电流源或者一个电压源等等。

剩余部分指的是被替代的电路单元所在的电路剩余部分，也就是除了被替代的电路单元以外的所有电路单元。

需要注意的是，在戴维宁定理和诺顿定理中，所谓的电路单元并不一定是一个电阻，它可以是任何一个元件，只要它们是线性的，而且符合定理的基本要求即可。

三、总结
戴维宁定理和诺顿定理是电路分析中非常重要的定理，它们的等效条件也是分析电路中等效电路的基础。

当需要分析一个复杂的电路时，可以使用这两个定理来简化电路，从而得到更简单的等效电路。

戴维宁等效电阻三种求法以《戴维宁等效电阻三种求法》为标题，探讨以下内容：一、戴维宁等效电阻介绍在现实世界中，电子设备中往往包含有许多变数电阻，这些变数电阻不可能完全地确定，因此需要计算出一个电路中的戴维宁等效电阻值来模拟具体的实际环境。

戴维宁等效电阻是一种通过电阻元件的加减来表示电路中变数电阻的等效电阻值，它是用来代替电路中实际变数电阻，以便简化电路设计。

二、三种计算戴维宁等效电阻的方法1）梯形积分法：这种方法是基于体积积分法，它可以求出变数电路中电阻的等效电阻，通过将变数电阻分割成多个梯形，然后根据电路的拓扑结构，分别用梯形的漏功率求出每个变数电阻的等效电阻值，最终求出流过整个变数电阻的电流，从而得出每个变数电阻的等效电阻值。

2）迭代求解法：这种方法基于迭代技术，在求解过程中，首先根据变数电路的拓扑结构，分别求出每个变数电阻的等效电阻值，然后根据拓扑结构，迭代求出变数电阻的总体等效电阻值，最终得出的结果便是整个电路的等效电阻值。

3）增量分析法：这种方法即通过增量分析的技术，来求解变数电路中的等效电阻值，具体的运算步骤是：首先把变数电路拆分为几个电子元件，然后根据拓扑结构求出每个电子元件的等效电阻值，最后将这些等效电阻值相加，即可得出变数电路的等效电阻值。

三、等效电阻求法的比较从上述介绍可知，梯形积分法、迭代求解法和增量分析法都可以用来求取变数电路中的等效电阻，它们各有优缺点，但从总体上看，增量分析法和迭代求解法比较简单易行，而梯形积分法比较复杂，但使用结果更加准确。

四、结论从上述介绍可知，戴维宁等效电阻是一种用来代替电路中实际变数电阻，以便简化电路设计的等效电阻值，而梯形积分法、迭代求解法和增量分析法都可以用来求取变数电路中的等效电阻，它们各有优缺点，增量分析法和迭代求解法比较简单易行，而梯形积分法比较复杂，但使用结果更加准确。

因此，正确的选择与利用这三种求解戴维宁等效电阻的方法，可以帮助我们更好地解决电路问题，节省时间和成本。

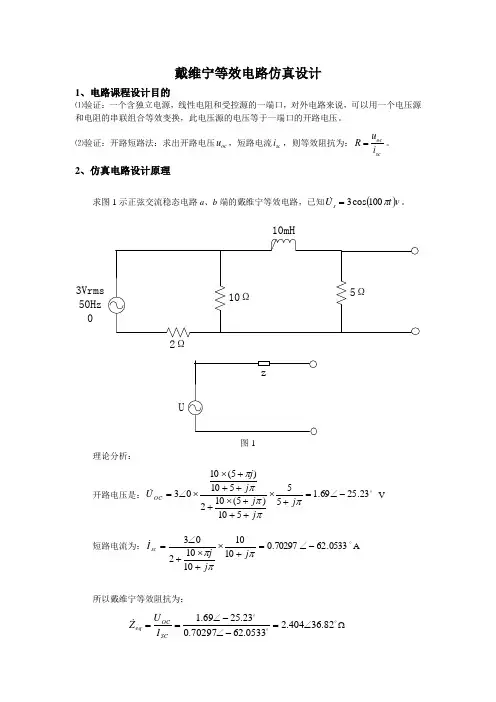
戴维宁等效电路仿真设计1、电路课程设计目的⑴验证：一个含独立电源，线性电阻和受控源的一端口，对外电路来说，可以用一个电压源和电阻的串联组合等效变换，此电压源的电压等于一端口的开路电压。

⑵验证：开路短路法：求出开路电压oc u ，短路电流sc i ，则等效阻抗为：scoci u R =。

2、仿真电路设计原理求图1示正弦交流稳态电路a 、b 端的戴维宁等效电路，已知()v t U sπ100cos 3= 。

3Vrms50Hz 010mHU图1理论分析：开路电压是： 23.2569.155510)5(102510)5(1003-∠=+⨯+++⨯++++⨯⨯∠=πππππj j j j j U OCV短路电流为： 0533.6270297.010101010203-∠=+⨯+⨯+∠=πππj j j I scA所以戴维宁等效阻抗为：82.36404.20533.6270297.023.2569.1∠=-∠-∠==SC OC eqI U Z Ω3、电路设计内容与步骤如图2所示，设计仿真电路。

V13 Vrms 50 Hz 0°R110ΩR25ΩL110mHV23 Vrms 50 Hz 0°R310ΩR45ΩL210mHXMM1XMM2R50.0001ΩXSC1A BExt Trig++__+_R62ΩR72Ω图2 EWB仿真电路分别测量开路电压和短路电流有效值及观察它们的波形图3 开路电压与短路电流波形图4 测量开路电压与短路电流的相位差角通过仿真测出的开路电压和短路电路有效值分别为： 696.1=OC U V ；702951.0=sc I A开路电压和短路电流有效值之比得到戴维宁等效阻抗的模为：Ω===413.2702951.0696.1sc OC eq I U Z 因为示波器只能观察电压波形，为了观察短路电流波形，在短路线上接一微小电阻Ω=0001.0R ；观察其两端电压波形即相当于观察短路电流波形。

戴维宁等效定理
戴维宁等效定理（Thevenin's theorem）是电路分析中的一个重要定理，它可以用来简化复杂电路的分析和计算。

根据戴维宁等效定理，一个由电阻、电源和其他被连接在一起的元件组成的线性电路，在两个端口之间可以用一个等效的电源和等效的串联电阻来替代。

这个等效电源称为戴维宁电压源，其电压为戴维宁电压，等效串联电阻称为戴维宁电阻。

戴维宁等效定理的基本思想是将复杂的电路简化为等效的简单电路，使得分析和计算更为方便。

具体而言，戴维宁等效定理可以通过以下几个步骤来应用：
1.确定感兴趣的两个端口。

通常，我们会选择容易进行分析
的端口。

2.将电路切断，形成感兴趣的两个端口之间的电路。

3.计算戴维宁电压源的电压和戴维宁电阻。

为了计算戴维宁
电压源的电压，可以将感兴趣的两个端口开路，然后测量
电压。

为了计算戴维宁电阻，可以将所有电源置为零，然
后通过感兴趣的两个端口注入一个测试电流，测量其中的
电压降。

4.构建等效电路。

用计算得到的戴维宁电压源以及戴维宁电
阻来替代原始电路中的感兴趣的两个端口。

通过应用戴维宁等效定理，我们可以将复杂的电路简化为等效的简单电路。

这个简化后的等效电路在分析和计算时更加方便，
可以帮助我们更好地理解电路的行为和性质。

一计算戴维宁等效电路戴维宁等效电路是指把一个复杂的电路用简单的元件替代，以便于分析和计算。

在电子工程中，特别是在模拟电路设计中，戴维宁等效电路被广泛应用。

戴维宁等效电路通过使用电阻、电容和电感等元件，将复杂的电路简化为一个等效的电路。

这个等效电路在输出端口上具有相同的电压-电流特性，但是更容易分析和计算。

计算戴维宁等效电路的过程通常包括以下几个步骤：1.确定主要部分：首先，需要确定电路中的主要组成部分。

这些部分通常是会对电路的行为产生显著影响的元件。

例如，对于一个包含多个二极管和电阻的电路，我们可能只对其中的一些二极管和电阻感兴趣。

2.简化元件模型：一旦确定了主要部分，我们需要将它们简化为等效的电路元件。

这些等效元件可以是电阻、电容或电感。

简化的目标是保持等效电路在输出端口上具有相同的电压-电流特性。

例如，一个二极管可以被简化为一个恒定的电压源和一个电阻。

3.组合等效元件：接下来，我们需要将简化后的等效元件组合成一个整体的等效电路。

这可以通过串联和并联等简单电路连接方式实现。

通过这样的组合，我们可以获得尽可能简单的等效电路。

4.验证等效电路：最后，我们需要验证所得等效电路是否与原始电路在输出端口上有着相同的行为。

这可以通过对等效电路进行数学计算、模拟仿真或实际测量来实现。

如果等效电路的行为与原始电路相匹配，那么我们就得到了一个有效的戴维宁等效电路。

需要注意的是，计算戴维宁等效电路的过程是一个近似的过程。

特别地，戴维宁等效电路只在一定的频率范围内有效，而且需要对元件进行适当的选择和简化。

因此，在进行戴维宁等效电路计算时，我们需要权衡精确性和计算复杂性之间的关系，并根据实际情况进行适当的调整。

戴维宁等效电路的计算在电子工程中具有重要的意义。

它能够帮助工程师更好地理解和分析复杂的电路行为，从而实现电路的设计、调试和优化。

对于一些特定的电路部分，例如滤波器、放大器等，戴维宁等效电路的计算可以提供更深入的洞察力，加速设计过程，节省时间和成本。