高中物理竞赛解题方法:等效法
- 格式:doc
- 大小:3.16 MB
- 文档页数:12

巧妙使用等效思维解答高中物理试题等效思维是高中物理解题中一种非常重要的思维方式,它允许我们将复杂的物理问题简化为更易于处理的形式,或者将未知的问题转化为已知的问题来求解。
以下是一些巧妙使用等效思维解答高中物理试题的方法和示例:1. 等效替代法原理:在某些情况下,一个复杂的物理系统或过程可以被另一个更简单但效果相同的系统或过程所替代。
示例:在力学中,当分析多个力的共同作用时,可以使用力的合成与分解来等效替代。
例如,一个物体同时受到两个大小相等、方向相反的力的作用,这两个力的合力为零,可以等效为物体不受外力作用。
2. 等效电路法原理:在电路分析中,复杂的电路可以通过变换和简化,等效为简单的电路模型,从而方便求解。
示例:在求解复杂电路中的电流、电压或功率时,可以通过串并联电路的等效变换,将电路简化为简单的串并联组合,然后利用欧姆定律、基尔霍夫定律等求解。
3. 等效重力场法原理:在解决非惯性系中的物理问题时,可以引入一个等效的重力场,使得问题在惯性系中求解。
示例:在加速上升的电梯中,物体受到的支持力大于其重力,可以等效为物体在一个重力加速度更大的重力场中静止不动。
这样,就可以利用牛顿第二定律等惯性系中的规律来求解。
4. 等效过程法原理:在某些情况下,一个复杂的物理过程可以等效为一系列简单过程的组合。
示例:在求解变加速直线运动的位移时,如果加速度随时间变化,可以将其等效为多个匀变速直线运动的组合,然后分别求解每个阶段的位移并累加。
5. 等效质量法原理:在解决涉及多个物体相互作用的问题时,可以将多个物体看作一个整体,引入等效质量来简化问题。
示例:在连接体问题中,如果两个物体通过轻绳或轻杆相连,且加速度相同,可以将它们看作一个整体,引入等效质量(等于两物体质量之和),然后利用牛顿第二定律求解整体的加速度和受力情况。
应用技巧识别等效条件:在解题过程中,首先要识别出哪些条件或过程可以等效替代。
建立等效模型:根据等效条件建立等效模型,将复杂问题简化为简单问题。

高中物理中的等效替代法物理学是研究物质运动的最基本、最普遍的规律及物质的构成、物质间相互作用的一门科学。
物理学在长期的发展过程中,形成了一整套思维方法,这些方法不仅对物理学的发展起了重要的作用,而且对其他相关学科的发展以至社会思潮和社会生活也产生了一定的影响。
自然界物质的运动、构成及其相互作用是极其复杂的,但它们之间存在着各种各样的等同性,为了认识复杂的物理事物的规律,我们往往从事物的等同效果出发,将其转化为简单的、易于研究的物理事物,这种方法称为等效替代法。
按等同效果形式的不同,可将其分为模型等效替代、过程等效替代、作用等效替代和本质等效替代等。
一、模型等效替代在物理学研究问题的过程中,我们常常用简单的、易于研究的模型来代替复杂的物理原形,这种方法称为模型等效替代法。
它既包括对各种理想模型的具体应用,也包括利用各种实物模型来模仿、再现原形的某些特征、状态和本质。
这种方法并不是对客观存在的物理对象进行研究,而是借助于对模型的研究,达到认识原形的目的。
用模型来替代原形的方法是通过抽象、概括等思维过程形成的理想模型,如质点、重心、理想气体、点电荷等,都是在一定条件下、一定的精度范围内对实际客体的一种等效替代。
下面以重心为例说明这个问题。
学生对重力似乎很熟悉,以为很简单。
但仔细一想,不那么简单,物体有无数个微小的组成部分,实际上每个部分都要受到微小的重力,这些微小重力的作用点都各不相同。
若是这样来研究重力,复杂得无从下手。
物理学的研究方法,就是设想把无数个微小的重力用一个等效的重力来替代,重心就是这个等效重力的作用点。
当然,随着条件和要求精度的变化,这些模型也要随之变化,从而用更能反映实际客体属性的模型来替代。
模型等效替代的另一种形式是用实物模型来代替实际客体,通过对实物模型的研究来认识其原形的本质属性及其规律性。
在物理教学中,经常制成发电机模型、内燃机模型、电动机模型等来模拟实际发电机、内燃机、电动机的工作过程,从而使学生更好地理解其工作原理。


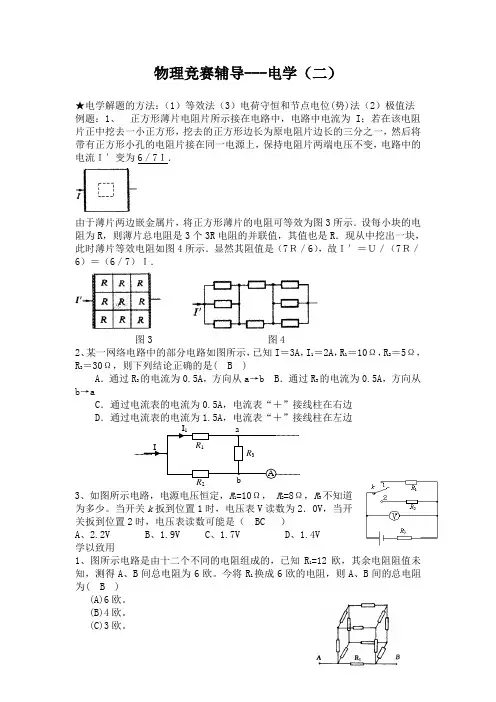
物理竞赛辅导---电学(二)★电学解题的方法:(1)等效法(3)电荷守恒和节点电位(势)法(2)极值法 例题:1、正方形薄片电阻片所示接在电路中,电路中电流为I ;若在该电阻片正中挖去一小正方形,挖去的正方形边长为原电阻片边长的三分之一,然后将带有正方形小孔的电阻片接在同一电源上,保持电阻片两端电压不变,电路中的电流I′变为6/7I.由于薄片两边嵌金属片,将正方形薄片的电阻可等效为图3所示.设每小块的电阻为R ,则薄片总电阻是3个3R 电阻的并联值,其值也是R .现从中挖出一块,此时薄片等效电阻如图4所示.显然其阻值是(7R/6),故I′=U/(7R/6)=(6/7)I.图3 图42、某一网络电路中的部分电路如图所示,已知I =3A ,I 1=2A ,R 1=10Ω,R 2=5Ω,R 3=30Ω,则下列结论正确的是( B )A .通过R 3的电流为0.5A ,方向从a →bB .通过R 3的电流为0.5A ,方向从b →aC .通过电流表的电流为0.5A ,电流表“+”接线柱在右边D .通过电流表的电流为1.5A ,电流表“+”接线柱在左边3、如图所示电路,电源电压恒定,R 1=10Ω, R 2=8Ω,R 3不知道为多少。
当开关k 扳到位置1时,电压表V 读数为2.0V ,当开关扳到位置2时,电压表读数可能是( BC )A 、2.2VB 、1.9VC 、1.7VD 、1.4V 学以致用1、图所示电路是由十二个不同的电阻组成的,已知R 1=12欧,其余电阻阻值未知,测得A 、B 间总电阻为6欧。
今将R 1换成6欧的电阻,则A 、B 间的总电阻为( B ) (A)6欧。
(B)4欧。
(C)3欧。
a R 1 AR 2 R 3b II 1(D)2欧。
2、把一根电阻为R的均匀电阻丝弯折成一个等边三角形abc(如图所示),d为底边ab的中点,如cd间的电阻R1为9欧,则ab间的电阻R2的阻值应该是( C )A.36欧B.12欧C.8欧D.4欧3、如图所示电路中,电源电压保持不变。




高考物理解题方法:等效法1500字高考物理解题方法:等效法物理是高考中的重要科目之一,也是许多考生难以攻克的一门科目。
在高考中,物理题目的解答方式多种多样,但其中一种常用且有效的方法是等效法。
等效法是将一个物理问题转化为一个相对简单且容易解答的等效问题,通过解答等效问题来得出原问题的答案。
本文将从原理、基本步骤以及实例解析三个方面对等效法进行详细介绍。
一、原理物理问题的等效法的原理基于以下两个假设:1. 物理定律和规律是普适的,不受具体条件的影响。
这意味着,相同的物理定律可以适用于不同的物理情境。
2. 物理现象可以用数学模型来描述和解析。
等效法通过建立适当的数学模型,将实际问题抽象成数学问题,从而简化问题的求解过程。
基于以上原理,等效法的核心思想是,通过将复杂的问题转化为简化的等效问题,利用数学方法解答等效问题,从而得出原问题的答案。
二、基本步骤等效法的解题过程可以分为以下几个基本步骤:1. 抽象:将实际问题抽象成数学模型,即将问题中的实际物理量用符号表示,并确定问题中所牵涉到的物理定律和规律。
2. 变换:通过适当的等效变换,将原始问题转化为一个等效问题。
在变换过程中,可以利用一些已知条件或者性质来简化问题。
3. 求解:通过求解等效问题,得出等效问题的答案。
4. 反变换:将等效问题的答案通过逆变换转化为原问题的答案。
三、实例解析下面通过一个具体的例子来说明等效法的解题过程。
例题:一个边长为L的正方形绕其对角线转动,求转动过程中动能的最大值。
解析:1. 抽象:设正方形的质量为m,角速度为ω,根据角动量守恒定律,可以得到Lω=const。
2. 变换:将问题转化为一个等效问题,即将正方形的转动转化为质点的移动。
考虑到正方形绕对角线转动时,质心沿着对角线方向运动。
因此,可以将问题等效为质点在对角线方向上的匀速直线运动。
3. 求解:根据匀速直线运动的动能公式,动能K=1/2mv²,其中v是质点的速度。


《高中奥林匹克物理竞赛解题方法》一、隔离法方法简介隔离法就是从整个系统中将某一局部物体隔离出来,然后单独分析被隔离局部的受力情况和运动情况,从而把复杂的问题转化为简单的一个个小问题求解。
隔离法在求解物理问题时,是一种非常重要的方法,学好隔离法,对分析物理现象、物理规律大有益处。
赛题精讲例1:两个质量一样的物体1和2紧靠在一起放在光滑水平桌面上,如图2—1所示,如果它们分别受到水平推力F 1和F 2作用,且F 1>F 2, 如此物体1施于物体2的作用力的大小为〔 〕A .F 1B .F 2C .12F F 2+D .12F F 2- 解析:要求物体1和2之间的作用力,必须把其中一个隔离出来分析。
先以整体为研究对象,根据牛顿第二定律:F 1-F 2=2ma ①再以物体2为研究对象,有N -F 2=ma ②解①、②两式可得N =12F F 2+,所以应选C 例2:如图2—2在光滑的水平桌面上放一物体A ,A 上再放一物体B ,A 、B 间有摩擦。
施加一水平力F 于B ,使它相对于桌面向右运动,这时物体A 相对于桌面〔 〕A .向左动B .向右动C .不动D .运动,但运动方向不能判断解析:A 的运动有两种可能,可根据隔离法分析设AB 一起运动,如此:a =A BF m m + AB 之间的最大静摩擦力:f m = μm B g以A 为研究对象:假设f m ≥m A a ,即:μ≥A B B A m m (m m )g +F 时,AB 一起向右运动。
假设μ<A B B A m m (m m )g+ F ,如此A 向右运动,但比B 要慢,所以应选B例3:如图2—3所示,物块A 、B 的质量分别为m 1、m 2,A 、B 间的摩擦因数为μ1,A 与地面之间的摩擦因数为μ2,在水平力F 的推动下,要使A 、B 一起运动而B 不至下滑,力F 至少为多大?解析: B 受到A 向前的压力N ,要想B 不下滑,需满足的临界条件是:μ1N=m 2g 。
等效法处理带电物体在电场中的多种运动一.应用技巧1.“等效重力场”模型解法综述将一个过程或事物变换成另一个规律相同的过程和或事物进行分析和研究就是等效法.中学物理中常见的等效变换有组合等效法(如几个串、并联电阻器的总电阻);叠加等效法(如矢量的合成与分解);整体等效法(如将平抛运动等效为一个匀速直线运动和一个自由落体运动);过程等效法(如将热传递改变物体的内能等效为做功改变物体的内能)“等效重力场”建立方法--概念的全面类比为了方便后续处理方法的迁移,必须首先搞清“等效重力场”中的部分概念与复合之前的相关概念之间关系.具体对应如下:等效重力场重力场、电场叠加而成的复合场等效重力重力、电场力的合力等效重力加速度等效重力与物体质量的比值等效“最低点”物体自由时能处于稳定平衡状态的位置等效“最高点”物体圆周运动时与等效“最低点”关于圆心对称的位置等效重力势能等效重力大小与物体沿等效重力场方向“高度”的乘积2.模型分类1“等效重力场”中的直线运动例:如图所示,在离坡底为L的山坡上的C点树直固定一根直杆,杆高也是L.杆上端A到坡底B之间有一光滑细绳,一个带电量为q、质量为m的物体穿心于绳上,整个系统处在水平向右的匀强电场中,已知细线与竖直方向的夹角θ=30º.若物体从A点由静止开始沿绳无摩擦的滑下,设细绳始终没有发生形变,求物体在细绳上滑行的时间.(g=10m/s2,sin37º=0.6,cos37º=0.8)因细绳始终没有发生形变,故知在垂直绳的方向上没有压力存在,即带电小球受到的重力和电场力的合力方向沿绳的方向.建立“等效重力场”如图所示“等效重力场”的“等效重力加速度”,方向:与竖直方向的夹角30°,大小:g =gcos30°带电小球沿绳做初速度为零,加速度为g 的匀加速运动S AB=2L cos30°①S AB=12g t2②由①②两式解得t=3L g2“等效重力场”中的抛体类运动例:如图所示,在电场强度为E的水平匀强电场中,以初速度为v0竖直向上发射一个质量为m、带电量为+q的带电小球,求小球在运动过程中具有的最小速度.建立等效重力场如图所示,等效重力加速度g设g 与竖直方向的夹角为θ,则g =g cosθ其中arcsinθ=qE (qE)2+(mg)2则小球在“等效重力场”中做斜抛运动v x=v0sinθv y=v0cosθ当小球在y轴方向的速度减小到零,即v y=0时,两者的合速度即为运动过程中的最小速度v min=v x=v0sinθ=v0qE (mg)2+(qE)23“等效重力场”中的单摆类模型例:如图所示,在沿水平方向的匀强电场中有一固定点O,用一根长度L=0.4m的绝缘细绳把质量为m= 0.10kg、带有正电荷的金属小球悬挂在O点,小球静止在B点时细绳与竖直方向的夹角为θ=37º.现将小球拉至位置A使细线水平后由静止释放:建立“等效重力场”如图所示,“等效重力加速度”g ,方向:与竖直方向的夹角30°,大小:g =gcos37°=1.25g由A、C点分别做绳OB的垂线,交点分别为A'、C',由动能定理得带电小球从A点运动到C点等效重力做功mg (LOA −LOC)=mg L(cosθ−sinθ)=12mv2C代入数值得v C≈1.4m/s当带电小球摆到B点时,绳上的拉力最大,设该时小球的速度为v B,绳上的拉力为F,则mg (L−L sinθ)=12mv2B①F−mg =m v2BL②联立①②两式子得F=2.25N4“等效重力场”中的圆周运动类模型例:如图所示,绝缘光滑轨道AB部分为倾角为30°的斜面,AC部分为竖直平面上半径为R的圆轨道,斜面与圆轨道相切.整个装置处于场强为E、方向水平向右的匀强电场中.现有一质量为m的带正电,电量为q=3mg3E小球,要使小球能安全通过圆轨道,在O点的初速度应为多大?运动特点:小球先在斜面上运动,受重力、电场力、支持力,然后在圆轨道上运动,受到重力、电场力,轨道作用力,且要求能安全通过圆轨道.对应联想:在重力场中,小球先在水平面上运动,重力不作功,后在圆轨道上运动的模型:过山车.等效分析:如图所示,对小球受电场力和重力,将电场力与重力合成视为等效重力mg ,大小mg =(qE)2+(mg)2=23mg3,tgθ=qEmg=33,得θ=30°,于是重效重力方向为垂直斜面向下,得到小球在斜面上运动,等效重力不做功,小球运动可类比为重力场中过山车模型.规律应用:分析重力中过山车运动,要过圆轨道存在一个最高点,在最高点满足重力当好提供向心力,只要过最高点点就能安全通过圆轨道.如果将斜面顺时针转过300,就成了如图3-3所示的过山车模型,最高点应为等效重力方向上直径对应的点B,则B点应满足“重力”当好提供向心力即:mg =mv2B R假设以最小初速度v0运动,小球在斜面上作匀速直线运动,进入圆轨道后只有重力作功,则根据动能定理:−mg 2R=12mv2B−12mv20解得:v0=103gR3二、实战应用(应用技巧解题,提供解析仅供参考)1如图所示,平行板电容器上极板MN与下极板PQ水平放置,一带电液滴从下极板P点射入,恰好沿直线从上极板N点射出。
四、等效法方法简介在一些物理问题中,一个过程的发展、一个状态的确定,往往是由多个因素决定的,在这一决定中,若某些因素所起的作用和另一些因素所起的作用相同,则前一些因素与后一些因素是等效的,它们便可以互相代替,而对过程的发展或状态的确定,最后结果并不影响,这种以等效为前提而使某些因素互相代替来研究问题的方法就是等效法.等效思维的实质是在效果相同的情况下,将较为复杂的实际问题变换为简单的熟悉问题,以便突出主要因素,抓住它的本质,找出其中规律.因此应用等效法时往往是用较简单的因素代替较复杂的因素,以使问题得到简化而便于求解.赛题精讲例1:如图4—1所示,水平面上,有两个竖直的光滑墙壁A 和B ,相距为d ,一个小球以初速度v 0从两墙之间的O 点斜向上抛出,与A 和B 各发生一次弹性碰撞后,正好落回抛出点,求小球的抛射角θ.解析:将弹性小球在两墙之间的反弹运动,可等效为一个完整的斜抛运动(见图).所以可用解斜抛运动的方法求解. 由题意得:gv v tv dsin2coscos2000可解得抛射角202arcsin21vgd 例2:质点由A 向B 做直线运动,A 、B 间的距离为L ,已知质点在A 点的速度为v 0,加速度为a ,如果将L 分成相等的n 段,质点每通过L/n 的距离加速度均增加a /n ,求质点到达B时的速度.解析从A 到B 的整个运动过程中,由于加速度均匀增加,故此运动是非匀变速直线运动,而非匀变速直线运动,不能用匀变速直线运动公式求解,但若能将此运动用匀变速直线运动等效代替,则此运动就可以求解.因加速度随通过的距离均匀增加,则此运动中的平均加速度为na n n a an n a n aa a a a 2)13(232)1(2末初平由匀变速运动的导出公式得2022vvLa B平解得naLn vv B )13(20例3一只老鼠从老鼠洞沿直线爬出,已知爬出速度v 的大小与距老鼠洞中心的距离s 成反比,当老鼠到达距老鼠洞中心距离s 1=1m 的A 点时,速度大小为s cm v /201,问当老鼠到达距老鼠洞中心s 2=2m 的B 点时,其速度大小?2v 老鼠从A 点到达B 点所用的时间t=?解析我们知道当汽车以恒定功率行驶时,其速度v 与牵引力F 成反比,即,v =P/F ,由此可把老鼠的运动等效为在外力以恒定的功率牵引下的弹簧的运动.由此分析,可写出kxP FP v当11,v v s x 时将其代入上式求解,得2211s v P s v P k所以老鼠到达B 点时的速度scm v s s v /1020211212再根据外力做的功等于此等效弹簧弹性势能的增加,21222121ksksPt 代入有关量可得)(21212211s s s v PPt由此可解得sv s s s t5.72.012122)(22112122此题也可以用图像法、类比法求解.例4 如图4—2所示,半径为r 的铅球内有一半径为2r 的球形空腔,其表面与球面相切,铅球的质量为M.在铅球和空腔的中心连线上,距离铅球中心L 处有一质量为m 的小球(可以看成质点),求铅球对小球的引力.解析因为铅球内部有一空腔,不能把它等效成位于球心的质点. 我们设想在铅球的空腔内填充一个密度与铅球相同的小铅球△M ,然后在对于小球m 对称的另一侧位置放另一个相同的小铅球△M ,这样加入的两个小铅球对小球m 的引力可以抵消,就这样将空腔铅球变成实心铅球,而结果是等效的.带空腔的铅球对m 的引力等效于实心铅球与另一侧△M 对m 的引力之和. 设空腔铅球对m 的引力为F ,实心铅球与△M 对m 的引力分别为F 1、F 2. 则F=F 1-F 2 ①经计算可知:M M 71,所以22178)(LGmM LM Mm GF ②222)2(7)2(r L GmMr L Mm GF ③将②、③代入①式,解得空腔铅球对小球的引力为图4—2])2(7178[2221r LLGmM F F F例5 如图4-3所示,小球长为L 的光滑斜面顶端自由下滑,滑到底端时与挡板碰撞并反向弹回,若每次与挡板碰撞后的速度大小为碰撞前速度大小的54,求小球从开始下滑到最终停止于斜面下端时,小球总共通过的路程.解析小球与挡板碰撞后的速度小于碰撞前的速度,说明碰撞过程中损失能量,每次反弹距离都不及上次大,小球一步一步接近挡板,最终停在挡板处. 我们可以分别计算每次碰撞垢上升的距离L 1、L 2、……、L n ,则小球总共通过的路程为L L L L sn )(221,然后用等比数列求和公式求出结果,但是这种解法很麻烦.我们假设小球与挡板碰撞不损失能量,其原来损失的能量看做小球运动过程中克服阻力做功而消耗掉,最终结果是相同的,而阻力在整个运动过程中都有,就可以利用摩擦力做功求出路程.设第一次碰撞前后小球的速度分别为v 、1v ,碰撞后反弹的距离为L 1,则sin21sin 211212mgL mvmgL mv其中222111)54(,54vv L L v v 所以碰撞中损失的动能为)25161(2121212212mv mvmvE k根据等效性有kE L L f )(1解得等效摩擦力sin419mg f通过这个结果可以看出等效摩擦力与下滑的长度无关,所以在以后的运动过程中,等效摩擦力都相同. 以整个运动为研究过程,有sinmgL s f 解出小球总共通过的总路程为.941L s此题也可以通过递推法求解,读者可试试.例6 如图4—4所示,用两根等长的轻质细线悬挂一个小球,设L 和已知,当小球垂直于纸面做简谐运动时,其周期为.解析此题是一个双线摆,而我们知道单摆的周期,若将又线摆摆长等效为单摆摆长,则双线摆的周期就可以求出来了.图4—3图4—4将双线摆摆长等效为单摆摆长sinL L ,则此双线摆的周期为gl g L T /sin 2/2例8 如图4—5所示,由一根长为L 的刚性轻杆和杆端的小球组成的单摆做振幅很小的自由振动. 如果杆上的中点固定另一个相同的小球,使单摆变成一个异形复摆,求该复摆的振动周期.解析复摆这一物理模型属于大学普通物理学的内容,中学阶段限于知识的局限,不能直接求解. 如能进行等效操作,将其转化成中学生熟悉的单摆模型,则求解周期将变得简捷易行.设想有一摆长为L 0的辅助单摆,与原复摆等周期,两摆分别从摆角处从静止开始摆动,摆动到与竖直方向夹角为时,具有相同的角速度,对两摆分别应用机械能守恒定律,于是得22)2(21)(21)cos (cos21)cos (cos lm l m mgmgl 对单摆,得200)(21)cos (cosl m mgl 联立两式求解,得ll 650故原复摆的周期为.65220gl gl T 例9 粗细均匀的U 形管内装有某种液体,开始静止在水平面上,如图4—6所示,已知:L=10cm ,当此U 形管以4m/s 2的加速度水平向右运动时,求两竖直管内液面的高度差.(g=10m/s 2)解析当U 形管向右加速运动时,可把液体当做放在等效重力场中,g 的方向是等效重力场的竖直方向,这时两边的液面应与等效重力场的水平方向平行,即与g 方向垂直.设g 的方向与g 的方向之间夹角为,则4.0tanga 由图4—6可知液面与水平方向的夹角为,所以,.04.044.010tan m cm L h 例10 光滑绝缘的圆形轨道竖直放置,半径为R ,在其最低点A 处放一质量为m 的带电小球,整个空间存在匀强电场,使小球受到电场力的大小为m g 33,方向水平向右,现给小球一个水平向右的初速度0v ,使小球沿轨道向上运动,若小球刚好能做完整的圆周运动,求0v .解析小球同时受到重力和电场力作用,这时也可以认为小球处在等效重力场中.图4—5图4—6小球受到的等效重力为mg mg mg G332)33()(22等效重力加速度gmG g332与竖直方向的夹角30,如图4—7甲所示.所以B 点为等效重力场中轨道的最高点,如图4—7,由题意,小球刚好能做完整的圆周运动,小球运动到B 点时的速度Rg v B在等效重力场中应用机械能守恒定律22021)cos (21BmvR R g m mv将g 、B v 分别代入上式,解得给小球的初速度为gRv )13(20例11 空间某一体积为V 的区域内的平均电场强度(E )的定义为ni ini ii nn n V V E V V V V E V E V E E11212211如图4—8所示,今有一半径为a 原来不带电的金属球,现使它处于电量为q 的点电荷的电场中,点电荷位于金属球外,与球心的距离为R ,试计算金属球表面的感应电荷所产生的电场在此球内的平均电场强度.解析金属球表面的感应电荷产生的球内电场,由静电平衡知识可知等于电量为q 的点电荷在金属球内产生的电场,其大小相等,方向相反,因此求金属球表面的感应电荷产生的电场,相当于求点电荷q 在金属球内产生的电场.由平均电场强度公式得n i ni i ii ni iii ni ini ii VV r kq VV E V E VV V E E1121111设金属球均匀带电,带电量为q ,其密度为Vq ,则有ni ni ii iir q k r V k E11221图4—7图4—7甲图4—8ni ii r q k 12为带电球体在q 所在点产生的场强,因而有2Rkq E,方向从O 指向q.例11 质量为m 的小球带电量为Q ,在场强为E 的水平匀强电场中获得竖直向上的初速度为0v . 若忽略空气阻力和重力加速度g 随高度的变化,求小球在运动过程中的最小速度.解析若把电场力E q 和重力mg 合成一个力,则小球相当于只受一个力的作用,由于小球运动的初速度与其所受的合外力之间成一钝角,因此可以把小球的运动看成在等效重力G (即为合外力)作用下的斜抛运动,而做斜抛运动的物体在其速度方向与G 垂直时的速度为最小,也就是斜抛运动的最高点,由此可见用这种等效法可以较快求得结果.电场力和重力的合力方向如图4—9所示,由图所示的几何关系可知Eqmg tan小球从O 点抛出时,在y 方向上做匀减速直线运动,在x 轴方向上做匀速直线运动. 当在y 轴方向上的速度为零时,小球只具有x 轴方向上的速度,此时小球的速度为最小值,所以220min )()(cosEq mg Eqv v v 此题也可以用矢量三角形求极值的方法求解,读者可自行解决.例12 如图4—10所示,R 1、R 2、R 3为定值电阻,但阻值未知,R x 为电阻箱.当R x 为101x R 时,通过它的电流18;121x x x R R A I 为当时,通过它的电流.6.02A I x 则当A I x 1.03时,求电阻.3x R 解析电源电动势、内电阻r 、电阻R 1、R 2、R 3均未知,按题目给的电路模型列式求解,显然方程数少于未知量数,于是可采取变换电路结构的方法.将图4—10所示的虚线框内电路看成新的电源,则等效电路如图4—10甲所示,电源的电动势为,内电阻为r . 根据电学知识,新电路不改变R x 和I x 的对应关系,有),(11r R I x x ①),(22r R I x x ②图4—9 图4—10图4—10甲)(33r R I x x ③由①、②两式,得2,12rV ,代入③式,可得1183x R 例13 如图4—11所示的甲、乙两个电阻电路具有这样的特性:对于任意阻值的R AB 、R BC 和R CA ,相应的电阻R a 、R b 和R c 可确定. 因此在对应点A 和a ,B 和b 、C 和c 的电位是相同的,并且,流入对应点(例如A 和a )的电流也相同,利用这些条件证明:CABCABCAAB aR R R R R R ,并证明对R b 和R c 也有类似的结果,利用上面的结果求图4—11甲中P 和Q 两点之间的电阻.解析图4—11中甲、乙两种电路的接法分别叫三角形接法和星形接法,只有这两种电路任意两对应点之间的总电阻部分都相等,两个电路可以互相等效,对应点A 、a 、B 、b 和C 、c 将具有相同的电势.由R a b =R AB ,R ac =R AC ,R bc =R BC ,对a b 间,有CABCABBCAB CA AB BCACABba R R R R R R R R R R R R 1)11(①同样,a c 间和bc 间,也有CABCABCABC CA AB BCABCA ca R R R R R R R R R R R R 1)11(②CABCABCABC BC AB CA AB BCc b R R R R R R R R R R R R 1)11(③将①+②-③得:CABCABCAAB aR R R R R R 再通过①-②+③和③+②-①,并整理,就得到R b 和R C 的表达式.CABCABACBC cCABCABBCAB bR R R R R R R R R R R R 图4—11下面利用以上结果求图4—12乙中P 和Q 两点之间的电阻. 用星形接法代替三角形接法,可得图4—12乙所示电路,PRQS 回路是一个平衡的惠斯登电桥,所以在RS 之间无电流,因此它与图4—12丙所示电路是等效的. 因此PQ 之间的总电阻R PQ 可通过这三个并联电阻求和得到.4)61181361(1PQR 例14 如图4—13所示,放在磁感应强度B=0.6T 的匀强磁场中的长方形金属线框a bcd ,框平面与磁感应强度方向垂直,其中a b 和bc 各是一段粗细均匀的电阻丝R ab =5Ω,R bc =3Ω,线框其余部分电阻忽略不计.现让导体EF 搁置在a b 、cd 边上,其有效长度L=0.5m ,且与a b 垂直,阻值R EF =1Ω,并使其从金属框ad 端以恒定的速度V=10m/s 向右滑动,当EF滑过ab 长的4/5距离时,问流过a E 端的电流多大?解析 EF 向右运动时,产生感应电动势,当EF 滑过a b 长的54时,电路图可等效为如图4—13甲所示的电路.根据题设可以求出EF 产生的感应电动势,VBLV 3)105.06.0(3,1,4bcEb aE R R R 此时电源内阻为导体EF 的电阻,1EFR r,则电路中的总电阻为3)()(bc EbaEbc Eb aE R R R R R R rR 电路中的总电流为.1A RI∴通过a E 的电流为AI aE5.0例15 有一薄平凹透镜,凹面半径为0.5m ,玻璃的折射率为 1.5,且在平面上镀一层反射层,如图4—14所示,在此系统的左侧主轴上放一物S ,S 距系统 1.5m ,问S 成像于何处?解析本题可等效为物点S 先经薄平凹透镜成像,其像为平面镜的物,平面镜对物成像又为薄平凹透镜成像的物,根据图4—13图4—13甲图4—144—12甲4—12乙4—12丙成像规律,逐次求出最终像的位置.根据以上分析,首先考虑物S 经平凹透镜的成像S ,根据公式11111f P P 其中)(1)15.01)(15.1()11)(1(1121m R Rn f 故有mP P 6.015.11111成像在左侧,为虚像,该虚像再经平凹透镜成像S 后,其像距为mP P P 6.0122成像在右侧,为虚像,该虚像再经平凹透镜成像S ,有)(11,6.0,11112333m fm P P fP P 其中故m P P 375.016.01133成虚像于系统右侧0.375m 处此题还可用假设法求解.针对训练1.半径为R 的金属球与大地相连,距球心L 处有一带电量为+q 的点电荷如图4—15所示. 求(1)球上感应电荷的总电量;(2)q 受到的库仑力. 2.如图4—16所示,设99,40,10,5,80,40654321R R R R R R 20,10187R R ,求AB 之间的电阻.图4—153.电路如图4—17所示,35431R R R R 时,12R ,求AB 间的等效电阻.4.有9个电阻联成如图4—18电路,图中数字的单位是,求PQ 两点间的等效电阻.5.如图4—19所示电路,求AB 两点间的等效电阻.6.如图4—20所示,由5个电阻联成的网络,试求AB 两点间的等效电阻.7.由7个阻值均为r 的电阻组成的网络元如图4—21甲所示.由这种网络元彼此连接形成的无限梯形网络如图4—21乙所示.试求P 、Q 两点之间的等效电阻.8.图4—22表示一交流电的电流随时间而变化的图像,此交流电流有效值是()A .A 25B.A 5 C.A 25.3 D.A5.39.磁流体发电机的示意图如图4—23所示,横截面为距形的管道长为L ,宽为a ,高为b ,上下两个侧面是绝缘体,相距为a 的两个侧面是电阻可忽略的导体,此两导体侧面与负载电阻R L 相连.整个管道放在一个匀强磁场中,磁感应强度的大小为B ,方向垂直于上下侧图4—19图4—20图4—21甲图4—21乙图4—22图4—23图4—24面向上. 现有电离气体(正、负带电粒子)持续稳定的流经管道,为了使问题简化,设横截面上各点流速相同. 已知流速与电离气体所受的压力成正比;且无论有无磁场存在时,都维持管道两端电离气体的压强差皆为p. 设无磁场存在时电离气体的流速为0v . 求有磁场存在时流体发电机的电动势的大小. 已知电离气体的平均电阻率为.10.一匀质细导线圆环,总电阻为R ,半径为a ,圆环内充满方向垂直于环面的匀强磁场,磁场以速率K 均匀地随时间增强,环上的A 、D 、C 三点位置对称. 电流计G 连接A 、C两点,如图4—24所示,若电流计内阻为R G ,求通过电流计的电流大小.11.固定在匀强磁场中的正方形导线框a bcd ,各边长为L 1,其中a b 是一端电阻为R 的均匀电阻丝,其余三边均为电阻可忽略的铜线,磁场的磁感应强度为B ,方向垂直纸面向里,现有一与a b 段的材料、粗细、长度都相同的电阻丝PQ 架在导线框上,如图4—25所示,以恒定的速度v 从a d 滑向bc ,当PQ 滑过1/3L的距离时,通过a P 段电阻丝的电流是多大?方向如何?12.如图4—26所示,一根长的薄导体平板沿x 轴放置,板面位于水平位置,板的宽度为L ,电阻可忽略不计,aebcfd 是圆弧形均匀导线,其电阻为3R ,圆弧所在的平面与x 轴垂直,圆弧的两端a 和d 与导体板的两个侧面相接解,并可在其上滑动. 圆弧a e=eb=cf=fd=(1/8)圆周长,圆弧bc=(1/4)圆周长,一内阻R g =nR 的体积很小的电压表位于圆弧的圆心O 处,电压表的两端分别用电阻可以忽略的直导线与b 和c 点相连,整个装置处在磁感应强度为B 、方向竖直向上的匀强磁场中. 当导体板不动而圆弧导线与电压表一起以恒定的速度v 沿x 轴方向平移运动时(1)求电压表的读数;(2)求e 点与f 点的电势差(U e -R f ).13.如图4—27所示,长为2πa 、电阻为r 的均匀细导线首尾相接形成一个半径为a 的圆.现将电阻为R 的电压表,以及电阻可以忽略的导线,按图a 和图 b所示的方式分别与圆的两点相连接. 这两点之间的弧线所对圆心角为θ.若在垂直圆平面的方向上有均匀变化图4—25图4—26图4—27的匀强磁场,已知磁感应强度的变化率为k ,试问在图a 、b 两种情形中,电压表的读数各为多少?14.一平凸透镜焦距为f ,其平面上镀了银,现在其凸面一侧距它2f 处,垂直于主轴主置一高为H 的物,其下端位于透镜的主轴上如图4—28所示.(1)用作图法画出物经镀银透镜所成的像,并标明该像是虚、是实;(2)用计算法求出此像的位置和大小.15.如图4—29所示,折射率n=1.5的全反射棱镜上方6cm 处放置一物体AB ,棱镜直角边长为6cm ,棱镜右侧10cm 处放置一焦距f 1=10cm 的凸透镜,透镜右侧15cm 处再放置一焦距f 2=10cm 的凹透镜,求该光学系统成像的位置和放大率.图28 图29答案:1.2222)(,R Lq KRL q LR 2.11120 3.37 4.4 5.5.0 6.4.17.1.32r 8.C 9.Lb R aBL aBv p p10 10.RqR K a G23211.Rv BL 1161 a 向P12.(1)RnR Bav nR 232(2)Bav nn )223122( 13.0,2224)2(sin 2Rr k a 14.(1)图略(2)距光心H f 31,32 15.凹透镜的右侧10cm 处,放大率为 2。
高中物理解题方法:等效法技巧及典型例题归纳大全(学习)
Hello,大家好,洪老师今天给大家推荐这个高中物理解题方法之:等效法技巧及典型例题归纳大全!
其实曹冲称象用的方法就是等效法。
这种思维方法的实质,就是在效果相同的前提下,利用等效法将一个陌生复杂的物理问题变换成熟悉简单的理想物理问题,建立研究问题的简化模型来揭示问题的本质特征和规律。
使问题化繁为简,由难变易,从而达到解决问题的目的。
常用的等效法有状态的等效、过程的等效、条件的等效和对象的等效,下面分别举例说明。
高中物理常用解题方法总共有21种,均有一套word版,如需word版的资料来打印,请发送085给洪老师。
不会私信的很简单的方式:点洪老师的头像,然后会看到底下有个“洪粉必看”的菜单按钮,里面会有个内容提示的。
等效法!。
高中物理解题方法专题指导方法专题二:等效法解题一.方法介绍等效法是科学研究中常用的思维方法之一,它是从事物的等同效果这一基本点出发的,它可以把复杂的物理现象、物理过程转化为较为简单的物理现象、物理过程来进行研究和处理,其目的是通过转换思维活动的作用对象来降低思维活动的难度,它也是物理学研究的一种重要方法.用等效法研究问题时,并非指事物的各个方面效果都相同,而是强调某一方面的效果.因此一定要明确不同事物在什么条件、什么范围、什么方面等效.在中学物理中,我们通常可以把所遇到的等效分为:物理量等效、物理过程等效、物理模型等效等. 二.典例分析1.物理量等效在高中物理中,小到等效劲度系数、合力与分力、合速度与分速度、总电阻与分电阻等;大到等效势能、等效场、矢量的合成与分解等,都涉及到物理量的等效.如果能将物理量等效观点应用到具体问题中去,可以使我们对物理问题的分析和解答变得更为简捷. 例l .如图所示,ABCD 为表示竖立放在场强为E=104V/m 的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD 部分是半径为R 的半圆环,轨道的水平部分与半圆环相切A 为水平轨道的一点,而且.2.0m R AB ==把一质量m=100g 、带电q=10-4C 的小球,放在水平轨道的A 点上面由静止开始被释放后,在轨道的内侧运动。
(g=10m/s 2)求:(1)它到达C 点时的速度是多大? (2)它到达C 点时对轨道压力是多大? (3)小球所能获得的最大动能是多少? 2.物理过程等效对于有些复杂的物理过程,我们可以用一种或几种简单的物理过程来替代,这样能够简化、转换、分解复杂问题,能够更加明确研究对象的物理本质,以利于问题的顺利解决.高中物理中我们经常遇到此类问题,如运动学中的逆向思维、电荷在电场和磁场中的匀速圆周运动、平均值和有效值等.例2.如图所示,在竖直平面内,放置一个半径R 很大的圆形光滑轨道,0为其最低点.在0点附近P 处放一质量为m 的滑块,求由静止开始滑至0点时所需的最短时间.例3.矩形裸导线框长边的长度为2l ,短边的长度为l ,在两个短边上均接有阻值为R 的电阻,其余部分电阻均不计.导线框的位置如图所示,线框内的磁场方向及分布情况如图,大小为0cos 2x B B l π⎛⎫= ⎪⎝⎭.一电阻为R 的光滑导体棒AB 与短边平行且与长边始终接触良好.起初导体棒处于x =0处,从t =0时刻起,导体棒AB 在沿x 方向的外力F 的作用下做速度为v 的匀速运动.试求:(1)导体棒AB 从x =0运动到x =2l 的过程中外力F 随时间t变化的规律;(2)导体棒AB 从x =0运动到x =2l 的过程中整个回路产生的热量. 3.物理模型等效物理模型等效在物理学习中应用十分广泛,特别是力学中的很多模型可以直接应用到电磁学中去,如卫星模型、人船模型、子弹射木块模型、碰撞模型、弹簧振子模型等.实际上,我们在学习新知识时,经常将新的问题与熟知的物理模型进行等效处理.例4.如图所示,R 1、R 2、R 3为定值电阻,但阻值未知,R x 为电阻箱.当R x 为R x1=10 Ω时,通过它的电流I x1=l A ;当R x 为R x2=18 Ω时,通过它的电流I x2=0.6A .则当I x3=0.l A 时,求电阻R x3.例5.如图所示,倾角为θ=300,宽度L =1 m 的足够长的U 形平行光滑金属导轨固定在磁感应强度B =1 T 、范围足够大的匀强磁场中,磁场方向垂直导轨平面斜向上,用平行于导轨且功率恒为6 w 的牵引力牵引一根质量m =0.2 kg ,电阻R =1 Ω放在导轨上的金属棒ab 由静止沿导轨向上移动,当金属棒ab 移动2.8 m 时获得稳定速度,在此过程中金属棒产生的热量为5.8 J(不计导轨电阻及一切摩擦,g 取10 m /s 2),求:(1)金属棒达到的稳定速度是多大?(2)金属棒从静止达到稳定速度所需时间是多少?三.强化训练( ) 1. 如图所示,一面积为S 的单匝矩形线圈处于一个交变的磁场中,磁感应强度的变化规律为t B B ωsin 0=。
四、等效法方法简介在一些物理问题中,一个过程的发展、一个状态的确定,往往是由多个因素决定的,在这一决定中,若某些因素所起的作用和另一些因素所起的作用相同,则前一些因素与后一些因素是等效的,它们便可以互相代替,而对过程的发展或状态的确定,最后结果并不影响,这种以等效为前提而使某些因素互相代替来研究问题的方法就是等效法.等效思维的实质是在效果相同的情况下,将较为复杂的实际问题变换为简单的熟悉问题,以便突出主要因素,抓住它的本质,找出其中规律.因此应用等效法时往往是用较简单的因素代替较复杂的因素,以使问题得到简化而便于求解.赛题精讲例1:如图4—1所示,水平面上,有两个竖直的光滑 墙壁A 和B ,相距为d ,一个小球以初速度v 0从两墙 之间的O 点斜向上抛出,与A 和B 各发生一次弹性 碰撞后,正好落回抛出点,求小球的抛射角θ. 解析:将弹性小球在两墙之间的反弹运动,可等效为 一个完整的斜抛运动(见图).所以可用解斜抛运动的 方法求解.由题意得:gv v t v d θθθsin 2cos cos 2000⋅=⋅= 可解得抛射角 202arcsin 21v gd =θ 例2:质点由A 向B 做直线运动,A 、B 间的距离为L ,已知质点在A 点的速度为v 0,加速度为a ,如果将L 分成相等的n 段,质点每通过L/n 的距离加速度均增加a /n ,求质点到达B 时的速度.解析 从A 到B 的整个运动过程中,由于加速度均匀增加,故此运动是非匀变速直线运动,而非匀变速直线运动,不能用匀变速直线运动公式求解,但若能将此运动用匀变速直线运动等效代替,则此运动就可以求解.因加速度随通过的距离均匀增加,则此运动中的平均加速度为na n n a an n an a a a a a 2)13(232)1(2-=-=-++=+=末初平 由匀变速运动的导出公式得222v v L a B -=平 解得 naLn v v B )13(20-+=例3一只老鼠从老鼠洞沿直线爬出,已知爬出速度v 的大小与距老鼠洞中心的距离s 成反比,当老鼠到达距老鼠洞中心距离s 1=1m 的A 点时,速度大小为s cm v /201=,问当老鼠到达距老鼠洞中心s 2=2m 的B 点时,其速度大小?2=v 老鼠从A 点到达B 点所用的时间t=? 解析 我们知道当汽车以恒定功率行驶时,其速度v 与牵引力F 成反比,即,v =P/F ,由此可把老鼠的运动等效为在外力以恒定的功率牵引下的弹簧的运动.由此分析,可写出kxP F P v == 当11,v v s x ==时 将其代入上式求解,得2211s v Ps v P k ==所以老鼠到达B 点时的速度s cm v s s v /1020211212=⨯==再根据外力做的功等于此等效弹簧弹性势能的增加,21222121ks ks Pt -= 代入有关量可得)(21212211s s s v P Pt -⋅=由此可解得s v s s s t 5.72.012122)(22112122=⨯⨯-=-=此题也可以用图像法、类比法求解.例4 如图4—2所示,半径为r 的铅球内有一半径为2r的 球形空腔,其表面与球面相切,铅球的质量为M.在铅球和空腔的中心连线上,距离铅球中心L 处有一质量为m 的小球(可以看成质点),求铅球对小球的引力.解析 因为铅球内部有一空腔,不能把它等效成位于球心的质点. 我们设想在铅球的空腔内填充一个密度与铅球相同的小铅球△M ,然后在对于小球m 对称的另一侧位置放另一个相同的小铅球△M ,这样加入的两个小铅球对小球m 的引力可以抵消,就这样将空腔铅球变成实心铅球,而结果是等效的.带空腔的铅球对m 的引力等效于实心铅球与另一侧△M 对m 的引力之和. 设空腔铅球对m 的引力为F ,实心铅球与△M 对m 的引力分别为F 1、F 2. 则F=F 1-F 2 ①经计算可知:M M 71=∆,所以 22178)(L GmM L M M m G F =∆+= ② 222)2(7)2(r L GmMr L M m G F -=-∆= ③将②、③代入①式,解得空腔铅球对小球的引力为图4—2])2(7178[2221r L L GmM F F F --=-=例5 如图4-3所示,小球长为L 的光滑斜面顶端自由下滑,滑到底端时与挡板碰撞并反向弹回,若每次与挡板碰撞后的速度大小为碰撞前速度大小的54,求小球从开始下滑到最终停止于斜面下端时,小球总共通过的路程.解析 小球与挡板碰撞后的速度小于碰撞前的速度,说明碰撞过程中损失能量,每次反弹距离都不及上次大,小球一步一步接近挡板,最终停在挡板处. 我们可以分别计算每次碰撞垢上升的距离L 1、L 2、……、L n ,则小球总共通过的路程为L L L L s n ++++=)(221 ,然后用等比数列求和公式求出结果,但是这种解法很麻烦.我们假设小球与挡板碰撞不损失能量,其原来损失的能量看做小球运动过程中克服阻力做功而消耗掉,最终结果是相同的,而阻力在整个运动过程中都有,就可以利用摩擦力做功求出路程.设第一次碰撞前后小球的速度分别为v 、1v ,碰撞后反弹的距离为L 1,则θθsin 21sin 211212mgL mv mgL mv == 其中222111)54(,54===v v L L v v 所以碰撞中损失的动能为)25161(2121212212-=-=∆mv mv mv E k 根据等效性有k E L L f ∆=+)(1 解得等效摩擦力θsin 419mg f = 通过这个结果可以看出等效摩擦力与下滑的长度无关,所以在以后的运动过程中,等效摩擦力都相同. 以整个运动为研究过程,有θsin ⋅=⋅mgL s f解出小球总共通过的总路程为.941L s =此题也可以通过递推法求解,读者可试试.例6 如图4—4所示,用两根等长的轻质细线悬挂一个小球,设L 和α已知,当小球垂直于纸面做简谐运动时,其周期为 . 解析 此题是一个双线摆,而我们知道单摆的周期,若将又线摆摆长等效为单摆摆长,则双线摆的周期就可以求出来了.图4—3 图4—4将双线摆摆长等效为单摆摆长αsin L L =',则此双线摆的周期为g l g L T /sin 2/2αππ='='例8 如图4—5所示,由一根长为L 的刚性轻杆和杆端的小球组成的单摆做振幅很小的自由振动. 如果杆上的中点固定另一个相同的小球,使单摆变成一个异形复摆,求该复摆的振动周期.解析 复摆这一物理模型属于大学普通物理学的内容,中学阶段限于知识的局限,不能直接求解. 如能进行等效操作,将其转化成中学生熟悉的单摆模型,则求解周期将变得简捷易行.设想有一摆长为L 0的辅助单摆,与原复摆等周期,两摆分别从摆角α处从静止开始摆动,摆动到与竖直方向夹角为β时,具有相同的角速度ω,对两摆分别应用机械能守恒定律,于是得22)2(21)(21)cos (cos 21)cos (cos l m l m mg mgl ωωαβαβ+=-+-对单摆,得 200)(21)cos (cos l m mgl ωαβ=-联立两式求解,得l l 650=故原复摆的周期为.65220gl g l T ππ== 例9 粗细均匀的U 形管内装有某种液体,开始静止在水平面上,如图4—6所示,已知:L=10cm ,当此U 形管以4m/s 2的加速度水平向右运动时,求两竖直管内液面的高度差.(g=10m/s 2)解析 当U 形管向右加速运动时,可把液体当做放在等效重力场中,g '的方向是等效重力场的竖直方向,这时两边的液面应与等效重力场的水平方向平行,即与g '方向垂直.设g '的方向与g 的方向之间夹角为α,则4.0tan ==gaα 由图4—6可知液面与水平方向的夹角为α, 所以,.04.044.010tan m cm L h ==⨯=⋅=∆α 例10 光滑绝缘的圆形轨道竖直放置,半径为R ,在其最低点A 处放一质量为m 的带电小球,整个空间存在匀强电场,使小球受到电场力的大小为m g 33,方向水平向右,现给小球一个水平向右的初速度0v ,使小球沿轨道向上运动,若小球刚好能做完整的圆周运动,求0v .解析 小球同时受到重力和电场力作用,这时也可以认为小球处在等效重力场中.图4— 5图4—6小球受到的等效重力为mg mg mg G 332)33()(22=+=' 等效重力加速度g m G g 332='=' 与竖直方向的夹角︒=30θ,如图4—7甲所示.所以B 点为等效重力场中轨道的最高点,如图4—7,由题意,小球刚好能做完整的圆周运动,小球运动到B 点时的速度R g v B '=在等效重力场中应用机械能守恒定律22021)cos (21B mv R R g m mv ++'=θ 将g '、B v 分别代入上式,解得给小球的初速度为gR v )13(20+=例11 空间某一体积为V 的区域内的平均电场强度(E )的定义为∑∑==∆=∆++∆+∆∆++∆+∆=ni ini ii nn n VVE V V V V E V E V E E 11212211如图4—8所示,今有一半径为a 原来不带电的金属球,现 使它处于电量为q 的点电荷的电场中,点电荷位于金属球外, 与球心的距离为R ,试计算金属球表面的感应电荷所产生的电 场在此球内的平均电场强度.解析 金属球表面的感应电荷产生的球内电场,由静电平衡知识可知等于电量为q 的点电荷在金属球内产生的电场,其大小相等,方向相反,因此求金属球表面的感应电荷产生的电场,相当于求点电荷q 在金属球内产生的电场.由平均电场强度公式得∑∑∑∑∑=====∆=∆=∆=∆∆=ni ni ii i ni i i i ni ini ii V V r kq V V E V E VVVE E 1121111 设金属球均匀带电,带电量为q ,其密度为Vq=ρ,则有 ∑∑==∆=∆=ni ni iii i r q k r V k E 11221ρ图4—7图4—7甲图4—8∑=∆ni ii r q k 12为带电球体在q 所在点产生的场强,因而有2R kqE =,方向从O 指向q. 例11 质量为m 的小球带电量为Q ,在场强为E 的水平匀强电场中获得竖直向上的初速度为0v . 若忽略空气阻力和重力加速度g 随高度的变化,求小球在运动过程中的最小速度.解析 若把电场力E q 和重力mg 合成一个力,则小球相当于只受一个力的作用,由于小球运动的初速度与其所受的合外力之间成一钝角,因此可以把小球的运动看成在等效重力G '(即为合外力)作用下的斜抛运动,而做斜抛运动的物体在其速度方向与G '垂直时的速度为最小,也就是斜抛运动的最高点,由此可见用这种等效法可以较快求得结果.电场力和重力的合力方向如图4—9所示, 由图所示的几何关系可知Eqm g=θtan 小球从O 点抛出时,在y 方向上做匀减速直线运动,在x 轴方向上做匀速直线运动. 当在y 轴方向上的速度为零时,小球只具有x 轴方向上的速度,此时小球的速度为最小值,所以2200min )()(cos Eq mg Eqv v v +==θ此题也可以用矢量三角形求极值的方法求解,读者可自行解决. 例12 如图4—10所示,R 1、R 2、R 3为定值电阻,但阻值未 知,R x 为电阻箱.当R x 为Ω=101x R 时,通过它的电流Ω==18;121x x x R R A I 为当时,通过它的电流.6.02A I x =则当A I x 1.03=时,求电阻.3x R解析 电源电动势ε、内电阻r 、电阻R 1、R 2、R 3均未知, 按题目给的电路模型列式求解,显然方程数少于未知量数,于 是可采取变换电路结构的方法.将图4—10所示的虚线框内电路看成新的电源,则等效电 路如图4—10甲所示,电源的电动势为ε',内电阻为r '. 根据 电学知识,新电路不改变R x 和I x 的对应关系,有),(11r R I x x '+='ε ① ),(22r R I x x '+=='ε ②图4—9图4—10图4—10甲)(33r R I x x '+='ε ③由①、②两式,得Ω='='2,12r V ε, 代入③式,可得Ω=1183x R例13 如图4—11所示的甲、乙两个电阻电路具有这样的特性:对于任意阻值的R AB 、R BC 和R CA ,相应的电阻R a 、R b 和R c 可确定. 因此在对应点A 和a ,B 和b 、C 和c 的电位是相同的,并且,流入对应点(例如A 和a )的电流也相同,利用这些条件 证明:CABC ABCAAB a R R R R R R ++=,并证明对R b 和R c 也有类似的结果,利用上面的结果求图4—11甲中P 和Q 两点之间的电阻.解析 图4—11中甲、乙两种电路的接法分别叫三角形接法和星形接法,只有这两种电路任意两对应点之间的总电阻部分都相等,两个电路可以互相等效,对应点A 、a 、B 、b 和C 、c 将具有相同的电势.由R a b =R AB ,R ac =R AC ,R bc =R BC ,对a b 间,有CA BC AB BC AB CAAB BC AC AB b a R R R R R R R R R R R R +++=++=+-1)11(① 同样,a c 间和bc 间,也有CA BC AB CA BC CAAB BC AB CA c a R R R R R R R R R R R R +++=++=+-1)11(② CABC AB CA BC BCAB CA AB BC c b R R R R R R R R R R R R +++=++=+-1)11(③ 将①+②-③得:CABC ABCAAB a R R R R R R ++=再通过①-②+③和③+②-①,并整理,就得到R b 和R C 的表达式.CABC AB ACBC c CABC ABBCAB b R R R R R R R R R R R R ++=++=图4—11下面利用以上结果求图4—12乙中P 和Q 两点之间的电阻. 用星形接法代替三角形接法,可得图4—12乙所示电路,PRQS 回路是一个平衡的惠斯登电桥,所以在RS 之间无电流,因此它与图4—12丙所示电路是等效的. 因此PQ 之间的总电阻R PQ 可通过这三个并联电阻求和得到.Ω=++=-4)61181361(1PQR 例14 如图4—13所示,放在磁感应强度B=0.6T 的匀强磁场中的长方形金属线框a bcd ,框平面与磁感应强度方向垂直,其中ab 和bc 各是一段粗细均匀的电阻丝R ab =5Ω,R bc =3Ω,线框其余部分电阻忽略不计.现让导体EF 搁置在a b 、cd 边上,其有效长度L=0.5m ,且与a b 垂直,阻值R EF =1Ω,并使其从金属框ad 端以恒定的速度V=10m/s 向右滑动,当EF 滑过ab 长的4/5距离时,问流过a E 端的电流多大?解析 EF 向右运动时,产生感应电动势ε,当EF 滑过a b 长的54时,电路图可等效为如图4—13甲所示的电路.根据题设可以求出EF 产生的感应电动势ε,V BLV 3)105.06.0(=⨯⨯==ε Ω=Ω=Ω=3,1,4bc Eb aE R R R此时电源内阻为导体EF 的电阻,Ω==1EF R r ,则电路中的总电阻为Ω=+++⋅+=3)()(bc Eb aE bc Eb aE R R R R R R r R电路中的总电流为.1A RI ==ε∴通过a E 的电流为A I aE 5.0=例15 有一薄平凹透镜,凹面半径为0.5m ,玻璃的折射 率为1.5,且在平面上镀一层反射层,如图4—14所示,在此 系统的左侧主轴上放一物S ,S 距系统1.5m ,问S 成像于何处?解析 本题可等效为物点S 先经薄平凹透镜成像,其像为 平面镜的物,平面镜对物成像又为薄平凹透镜成像的物,根据图4—13图4—13甲图4—144—12甲 4—12乙 4—12丙成像规律,逐次求出最终像的位置.根据以上分析,首先考虑物S 经平凹透镜的成像S ', 根据公式11111f P P =+' 其中)(1)15.01)(15.1()11)(1(1121--=∞---=--=m R R n f 故有m P P 6.015.11111-='-=+'成像在左侧,为虚像,该虚像再经平凹透镜成像S ''后,其像距为m P P P 6.0122='-=-='成像在右侧,为虚像,该虚像再经平凹透镜成像S ''',有)(11,6.0,11112333--=='=='+m fm P P f P P 其中 故m P P 375.016.01133-='-=+'成虚像于系统右侧0.375m 处此题还可用假设法求解.针对训练1.半径为R 的金属球与大地相连,距球心L 处有一带 电量为+q 的点电荷如图4—15所示. 求(1)球上感应电荷的总电量; (2)q 受到的库仑力. 2.如图4—16所示,设Ω=Ω=Ω=Ω=Ω=Ω=99,40,10,5,80,40654321R R R R R R Ω=Ω=20,10187R R ,求AB 之间的电阻.图4—15 图4—16图4—17图4—183.电路如图4—17所示,Ω====35431R R R R 时,Ω=12R ,求AB 间的等效电阻.4.有9个电阻联成如图4—18电路,图中数字的单位是Ω,求PQ 两点间的等效电阻. 5.如图4—19所示电路,求AB 两点间的等效电阻.6.如图4—20所示,由5个电阻联成的网络,试求AB 两点间的等效电阻.7.由7个阻值均为r 的电阻组成的网络元如图4—21甲所示.由这种网络元彼此连接形成的无限梯形网络如图4—21乙所示.试求P 、Q 两点之间的等效电阻.8.图4—22表示一交流电的电流随时间而变化的图像,此交流电流有效值是( ) A .A 25 B .A 5 C .A 25.3 D .A 5.39.磁流体发电机的示意图如图4—23所示,横截面为距形的管道长为L ,宽为a ,高为b ,上下两个侧面是绝缘体,相距为a 的两个侧面是电阻可忽略的导体,此两导体侧面与负载电阻R L 相连.整个管道放在一个匀强磁场中,磁感应强度的大小为B ,方向垂直于上下侧图4—19图4—20图4—21甲图4—21乙图4—22图4—23图4—24面向上. 现有电离气体(正、负带电粒子)持续稳定的流经管道,为了使问题简化,设横截面上各点流速相同. 已知流速与电离气体所受的压力成正比;且无论有无磁场存在时,都维持管道两端电离气体的压强差皆为p. 设无磁场存在时电离气体的流速为0v . 求有磁场存在时流体发电机的电动势的大小ε. 已知电离气体的平均电阻率为ρ.10.一匀质细导线圆环,总电阻为R ,半径为a ,圆环内充满方向垂直于环面的匀强磁场,磁场以速率K 均匀地随时间增强,环上的A 、D 、C 三点位置对称. 电流计G 连接A 、C 两点,如图4—24所示,若电流计内阻为R G ,求通过电流计的电流大小.11.固定在匀强磁场中的正方形导线框a bcd ,各边长为L 1,其中a b 是一端电阻为R 的均匀电阻丝,其余三边均为电阻可忽略的铜线,磁场的磁感应强度为B ,方向垂直纸面向里,现有一与a b 段的材料、粗细、长度都相同的电阻丝PQ 架在导线框上,如图4—25所示,以恒定的速度v 从a d 滑向bc ,当PQ 滑过1/3L的距离时,通过a P 段电阻丝的电流是多大?方向如何?12.如图4—26所示,一根长的薄导体平板沿x 轴放置,板面位于水平位置,板的宽度为L ,电阻可忽略不计,aebcfd 是圆弧形均匀导线,其电阻为3R ,圆弧所在的平面与x 轴垂直,圆弧的两端a 和d 与导体板的两个侧面相接解,并可在其上滑动. 圆弧a e=eb=cf=fd=(1/8)圆周长,圆弧bc=(1/4)圆周长,一内阻R g =nR 的体积很小的电压表位于圆弧的圆心O 处,电压表的两端分别用电阻可以忽略的直导线与b 和c 点相连,整个装置处在磁感应强度为B 、方向竖直向上的匀强磁场中. 当导体板不动而圆弧导线与电压表一起以恒定的速度v 沿x 轴方向平移运动时(1)求电压表的读数;(2)求e 点与f 点的电势差(U e -R f ).13.如图4—27所示,长为2πa 、电阻为r 的均匀细导线首尾相接形成一个半径为a 的圆.现将电阻为R 的电压表,以及电阻可以忽略的导线,按图a 和图b所示的方式分别与圆的两点相连接. 这两点之间的弧线所对圆心角为θ.若在垂直圆平面的方向上有均匀变化图4—25 图4—26 图4—27的匀强磁场,已知磁感应强度的变化率为k ,试问在图a 、b 两种情形中,电压表的读数各为多少?14.一平凸透镜焦距为f ,其平面上镀了银,现在其凸面一侧距它2f 处,垂直于主轴主置一高为H 的物,其下端位于透镜的主轴上如图4—28所示.(1)用作图法画出物经镀银透镜所成的像,并标明该像是虚、是实;(2)用计算法求出此像的位置和大小.15.如图4—29所示,折射率n=1.5的全反射棱镜上方6cm 处放置一物体AB ,棱镜直角边长为6cm ,棱镜右侧10cm 处放置一焦距f 1=10cm 的凸透镜,透镜右侧15cm 处再放置一焦距f 2=10cm 的凹透镜,求该光学系统成像的位置和放大率.图28 图29答案:1.2222)(,R L q KRL q L R -- 2.Ω11120 3.Ω37 4.Ω4 5.Ω5.0 6.Ω4.1 7.1.32r 8.C 9.Lb R a BL a Bv p p10++ρ 10.RqR K a G 232+π 11.R v BL 1161 a 向P 12.(1)R nR Bav nR 232+ (2)Bav n n )223122(+++- 13.0,2224)2(sin 2πθπθθπ+-Rr k a 14.(1)图略 (2)距光心H f 31,32 15.凹透镜的右侧10cm 处,放大率为2。