计量经济学经济模型分析

共计
表 2.1.1 某社区家庭每月收入与消费支出统计表 每月家庭可支配收入X（元）
800 1100 1400 1700 2000 2300 2600 2900 3200 3500 561 638 869 1023 1254 1408 1650 1969 2090 2299 594 748 913 1100 1309 1452 1738 1991 2134 2321 627 814 924 1144 1364 1551 1749 2046 2178 2530 638 847 979 1155 1397 1595 1804 2068 2266 2629
称i为观察值Yi围绕它旳期望值E(Y|Xi)旳离差
（deviation），是一种不可观察旳随机变量，又称 为随机干扰项（stochastic disturbance）或随机误 差项（stochastic error）。
例2.1中，个别家庭旳消费支出为：
(*)
即，给定收入水平Xi ,个别家庭旳支出可表达为两部分之和: （1）该收入水平下全部家庭旳平均消费支出E(Y|Xi)，称为 系统性（systematic）或拟定性（deterministic)部分。
注意： 这里将样本回归线看成总体回归线旳近似替代
则
样本回归函数旳随机形式/样本回归模型：
一样地，样本回归函数也有如下旳随机形式：
Yi Yˆi ˆ i ˆ0 ˆ1 X i ei
式中， ei 称为（样本）残差（或剩余）项（residual），代表
了其他影响Yi 的随机因素的集合，可看成是 i 的估计量ˆ i 。
相应旳函数：
E(Y | X i ) f ( X i )
称为（双变量）总体回归函数（population regression function, PRF）。

计量经济学分析模型摘要改革开放以来，我国经济呈迅速而稳定的增长趋势，由于分配机制和收入水平的变化，城镇居民生活水平在达到稳定小康之后，消费结构和消费水平都出现了一些新的特点。

本文旨在对近几年，我国城镇年人均收入变动对年人均各种消费变动的影响进行实证分析。

首先，我们综合了几种关于收入和消费的主要理论观点；本文根据相关的数据统计数据，运用一定的计量经济学的研究方法，进而我们建立了理论模型。

然后，收集了相关的数据，利用EVIEWS软件对计量模型进行了参数估计和检验，并加以修正。

最后，我们对所得的分析结果和影响消费的一些因素作了经济意义的分析，并相应提出一些政策建议。

并找到影响居民消费的主要因素。

关键词：居民消费；城镇居民；回归；Eviews目录摘要 (II)前言 (1)1 问题的提出 (2)2 经济理论陈述 (3)2.1西方经济学中有关理论假说 (3)2.2有关消费结构对居民消费影响的理论 (4)3 相关数据收集 (6)4 计量经济模型的建立 (9)5 模型的求解和检验 (10)5.1计量经济的检验 (10)5.1.1模型的回归分析 (10)5.1.2拟合优度检验： (11)5.1.3 F检验 (11)5.1.4 T检验 (12)5.2 计量修正模型检验： (12)5.2.1 Y与的一元回归 (13)5.2.2拟合优度的检验 (13)5.2.3 F检验 (14)5.2.4 T检验： (15)5.3经济意义的分析: (15)6 政策建议 (16)结论 (17)参考文献 (19)城镇居民消费模型分析前言近年来，改革开放的影响不断加大，人民的物质文化生活水平日益提高，消费水平和消费结构都有了一定的调整，随着城镇化程度的提高，城镇居民消费在整个国民经济中的地位日益重要，因此，对其进行计量经济分析的十分有必要的。

本文旨在对近15年我国城镇年人均收入变动对年人均各种消费变动的影响进行实证分析。

人均收入和消费支出的有关数据进行了计量经济的检验,通过两者之间的动态关系研究发现,居民人均收入与消费支出有长期的均衡关系,据此建立了居民人均收入和消费支出之间的长期均衡模型。

计量经济学分析模型摘要改革开放以来，我国经济呈迅速而稳定的增长趋势，由于分配机制和收入水平的变化，城镇居民生活水平在达到稳定小康之后，消费结构和消费水平都出现了一些新的特点。

本文旨在对近几年，我国城镇年人均收入变动对年人均各种消费变动的影响进行实证分析。

首先，我们综合了几种关于收入和消费的主要理论观点；本文根据相关的数据统计数据，运用一定的计量经济学的研究方法，进而我们建立了理论模型。

然后，收集了相关的数据，利用EVIEWS软件对计量模型进行了参数估计和检验，并加以修正。

最后，我们对所得的分析结果和影响消费的一些因素作了经济意义的分析，并相应提出一些政策建议。

并找到影响居民消费的主要因素。

关键词：居民消费；城镇居民；回归；Eviews目录摘要 (II)前言 (1)1 问题的提出 (2)2 经济理论陈述 (3)2.1西方经济学中有关理论假说 (3)2.2有关消费结构对居民消费影响的理论 (4)3 相关数据收集 (6)4 计量经济模型的建立 (9)5 模型的求解和检验 (10)5.1计量经济的检验 (10)5.1.1模型的回归分析 (10)5.1.2拟合优度检验： (11)5.1.3 F检验 (11)5.1.4 T检验 (12)5.2 计量修正模型检验： (12)5.2.1 Y与的一元回归 (13)5.2.2拟合优度的检验 (13)5.2.3 F检验 (14)5.2.4 T检验： (15)5.3经济意义的分析: (15)6 政策建议 (16)结论 (17)参考文献 (19)城镇居民消费模型分析前言近年来，改革开放的影响不断加大，人民的物质文化生活水平日益提高，消费水平和消费结构都有了一定的调整，随着城镇化程度的提高，城镇居民消费在整个国民经济中的地位日益重要，因此，对其进行计量经济分析的十分有必要的。

本文旨在对近15年我国城镇年人均收入变动对年人均各种消费变动的影响进行实证分析。

人均收入和消费支出的有关数据进行了计量经济的检验,通过两者之间的动态关系研究发现,居民人均收入与消费支出有长期的均衡关系,据此建立了居民人均收入和消费支出之间的长期均衡模型。

计量经济学模型应用分析计量经济学是一门以数据为基础，运用数学、统计学和经济学等相关学科分析和解释经济现象的学科。

在实践中，计量经济学主要通过建立各种经济模型来分析和预测现实经济问题。

在本文中，我们将探讨计量经济学模型的应用分析。

一、单因素模型单因素模型是一种简单的计量经济学模型，其特点是只考虑一个因素对经济变量的影响。

例如，研究公路通行费对公路使用量的影响，或者研究利率对消费者支出的影响。

在这种模型中，经济变量（因变量）被解释为一个单独的影响因素（自变量）的函数。

通常，单因素模型采用线性回归来描述变量之间的关系。

回归模型的基本形式为：Y= a + bX + ε其中，Y是因变量（例如，需求或价格），X是自变量（例如，收入或成本），a和b是常数，ε是误差项（通常性质是随机的）。

a反映了Y在X=0时的值，b反映了Y随X的变化。

单因素模型在经济学实践中应用广泛。

例如，研究收入水平对消费支出的影响，研究通货膨胀率对股票价格的影响，以及研究贸易政策对贸易流量的影响。

单因素模型提供了一个可靠的方法来评估影响因素对因变量的影响程度。

二、多重线性回归模型多重线性回归模型是一种计量经济学模型，它允许解释因变量在多个自变量（或因素）下的变化。

该模型的形式为：Y= a + b1X1 + b2X2 +......+ bnXn + ε在此模型中，Y是因变量，X1、X2、...、Xn是自变量（或因素），a、b1、b2等是回归系数，ε是观测误差。

回归系数反映了因变量与自变量之间的关系。

具体而言，回归系数越大，自变量对因变量的影响越大。

多重线性回归模型具有广泛的应用范围。

例如，它可以用于研究成本对价格的影响，对劳动力市场的影响以及对经济增长的影响。

此外，多重线性回归模型还可以用于评估因素之间的相互作用，这是单因素模型无法实现的。

三、时间序列模型时间序列模型是一种专门用于描述和预测时间序列数据的计量经济学模型。

时间序列数据是指按时间顺序收集的数据。

影响我国人均GDP的变量因素分析摘要人均国内生产总值，也称作“人均GDP"，是衡量经济发展状况的重要指标，，它是人们了解和把握一个国家或地区的宏观经济运行状况的有效工具。

是衡量各国人民生活水平的一个标准，为了更加客观的衡量，经常与购买力平价结合。

文章从从城市化率、城镇居民家庭可支配收入、政府支出以及城镇居民消费水平四个方面作为出发点，通过往年的数据发展来观察它们对于人均GDP的影响，从而对我国目前的经济发展提供一些建议。

笔者认为，在提高城镇居民可支配收入、城市化率以及政府支出的基础上，更要调节好我国目前贫富差距过大的问题，这样才能保持经济的稳定发展。

关键词：人均GDP；城市化率；城镇居民可支配收入；城府支出引言一国的经济乃立国之本，而经济发展是以GDP增长为前提的。

影响人均GDP 的因素看似众多，究竟哪些因素对人均GDP的增长起关键性的影响作用呢？由此引出了本小组的研究课题——对我国人均GDP影响因素的计量分析。

随着2009年中国GDP赶超日本，成为世界排名第二，无疑吸引了国内外的目光。

然而，在如此大的总量之下，中国的人均GDP却一直在世界100名左右徘徊。

“国服民穷”的现状一直是我们的问题。

经我们数据搜寻，在人均GDP的增长过程中，城市化率、城镇居民家庭人均可支配收入、城市政府支出以及城镇居民消费水平都有了显著的上升。

同时，我们知道GDP的构成取决于消费、投资、政府支出。

因此，我们把城市化率、城镇居民人均可支配收入、城市政府支出、城镇居民消费水平这四个指标作为反映了人均GDP的自变量，认为这四个变量是影响人均GDP的关键性因素。

本实验主要选取1979—2009年的统计数据。

一、人均GDP的基本概念及特点1、人均GDP的基本概念和经济意义（1）人均GDP的基本概念人均国内生产总值（Real GDP per capita），也称作“人均GDP"，常作为发展经济学中衡量经济发展状况的指标，是重要的宏观经济指标之一，它是人们了解和把握一个国家或地区的宏观经济运行状况的有效工具。

计量经济学回归分析模型计量经济学是经济学中的一个分支，通过运用数理统计和经济理论的工具，研究经济现象。

其中回归分析模型是计量经济学中最为常见的分析方法之一、回归分析模型主要用于确定自变量与因变量之间的关系，并通过统计推断来解释这种关系。

回归分析模型中的关系可以是线性的，也可以是非线性的。

线性回归模型是回归分析中最为常见和基础的模型。

它可以表示为:Y=β0+β1X1+β2X2+...+βkXk+ε其中，Y代表因变量，X1,X2,...,Xk代表自变量，β0,β1,β2,...,βk代表回归系数，ε代表随机误差项。

回归模型的核心是确定回归系数。

通过最小二乘法估计回归系数，使得预测值与实际观测值之间的差异最小化。

最小二乘法通过使得误差的平方和最小化来估计回归系数。

通过对数据进行拟合，我们可以得到回归系数的估计值。

回归分析模型的应用范围非常广泛。

它可以用于解释和预测经济现象，比如价格与需求的关系、生产力与劳动力的关系等。

此外，回归分析模型还可以用于政策评估和决策制定。

通过分析回归系数的显著性，可以判断自变量对因变量的影响程度，并进行政策建议和决策制定。

在实施回归分析模型时，有几个重要的假设需要满足。

首先，线性回归模型要求因变量和自变量之间存在线性关系。

其次，回归模型要求自变量之间不存在多重共线性，即自变量之间没有高度相关性。

此外，回归模型要求误差项具有同方差性和独立性。

在解释回归分析模型的结果时，可以通过回归系数的显著性来判断自变量对因变量的影响程度。

显著性水平一般为0.05或0.01，如果回归系数的p值小于显著性水平，则说明该自变量对因变量具有显著影响。

此外，还可以通过确定系数R^2来评估模型的拟合程度。

R^2可以解释因变量变异的百分比，值越接近1，说明模型的拟合程度越好。

总之，回归分析模型是计量经济学中非常重要的工具之一、它通过分析自变量和因变量之间的关系，能够解释经济现象和预测未来走势。

在应用回归分析模型时，需要满足一定的假设条件，并通过回归系数和拟合优度来解释结果。

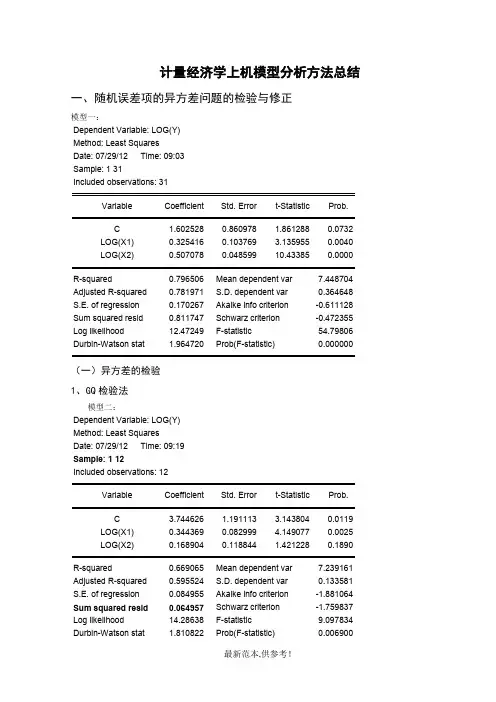
计量经济学上机模型分析方法总结一、随机误差项的异方差问题的检验与修正模型一：Dependent Variable: LOG(Y)Method: Least SquaresDate: 07/29/12 Time: 09:03Sample: 1 31Included observations: 31Variable Coefficient Std. Error t-Statistic Prob.C 1.602528 0.860978 1.861288 0.0732LOG(X1) 0.325416 0.103769 3.135955 0.0040LOG(X2) 0.507078 0.048599 10.43385 0.0000R-squared 0.796506 Mean dependent var 7.448704 Adjusted R-squared 0.781971 S.D. dependent var 0.364648 S.E. of regression 0.170267 Akaike info criterion -0.611128 Sum squared resid 0.811747 Schwarz criterion -0.472355 Log likelihood 12.47249 F-statistic 54.79806 Durbin-Watson stat 1.964720 Prob(F-statistic) 0.000000（一）异方差的检验1、GQ检验法模型二：Dependent Variable: LOG(Y)Method: Least SquaresDate: 07/29/12 Time: 09:19Sample: 1 12Included observations: 12Variable Coefficient Std. Error t-Statistic Prob.C 3.744626 1.191113 3.143804 0.0119LOG(X1) 0.344369 0.082999 4.149077 0.0025LOG(X2) 0.168904 0.118844 1.421228 0.1890R-squared 0.669065 Mean dependent var 7.239161 Adjusted R-squared 0.595524 S.D. dependent var 0.133581 S.E. of regression 0.084955 Akaike info criterion -1.881064 Sum squared resid 0.064957 Schwarz criterion -1.759837 Log likelihood 14.28638 F-statistic 9.097834 Durbin-Watson stat 1.810822 Prob(F-statistic) 0.006900模型三：Dependent Variable: LOG(Y)Method: Least SquaresDate: 07/29/12 Time: 09:20Sample: 20 31Included observations: 12Variable Coefficient Std. Error t-Statistic Prob.C -0.353381 1.607461 -0.219838 0.8309LOG(X1) 0.210898 0.158220 1.332942 0.2153LOG(X2) 0.856522 0.108601 7.886856 0.0000R-squared 0.878402 Mean dependent var 7.769851Adjusted R-squared 0.851381 S.D. dependent var 0.390363S.E. of regression 0.150490 Akaike info criterion -0.737527Sum squared resid 0.203824 Schwarz criterion -0.616301Log likelihood 7.425163 F-statistic 32.50732Durbin-Watson stat 2.123203 Prob(F-statistic) 0.000076进行模型二和模型三两次回归，目的仅是得到出去中间7个样本点以后前后各12个样本点的残差平方和RSS1和RSS2，然后用较大的RSS除以较小的RSS即可求出F统计量值进行显著性检验。

城镇居民家庭人均可支配收入及城市政府支出驱动经济增长的计量分析：1979~2009一．问题的提出2010年上海世界博览会已经圆满落下帷幕，在“城市让生活更美好”的主题下，这场持续184天的盛会向世界呈现了中国城市化进程中所取得的成就。

所谓城市化，就是指随着社会生产力的发展，人类的生产和生活有农村向城市转化的过程，表现为城市数量的增加和规模的扩大，城市消费、投资持续增加，进而改变经济发展的空间方向和基本方式。

二．模型设定统计表明，改革开放以来，特别是进入21世纪之后，在中国的城市化进程中，城市化率、城镇居民家庭人均可支配收入、城市政府支出以及城镇居民消费水平都有了显著的上升，因此，我们把这四个指标作为反映城市化的变量。

根据GDP 的取决于消费、投资、政府支出的基本原理，这四个变量应该可以很好的解揭示城市化对经济的驱动作用。

本实验主要选取1979~2009年的以下数据：1.城市化率：该指标主要反映的是城市人口规模。

2.经济增长：大多数的研究采用的是以人均GDP表示经济增长，也有使用单位资本GDP 来体现的，我们采用了前者。

3.城镇居民家庭人均可支配收入：4.城市政府支出：这里较为理想的指标是城镇人均政府支出，限于数据的可获得性，我们采用的是人均政府消费支出作为替代。

这是因为，政府消费支出多集中于城镇级别的政府，而农村基层行政部门消费支出比重较低。

5．城镇居民消费水平：这里采用城镇人均消费水平，而不是全社会人均消费水平以便能更好的反映出城市消费对经济增长的拉动作用。

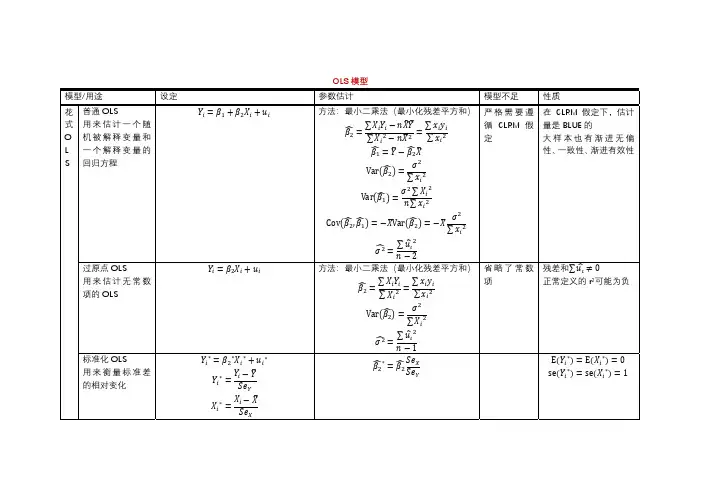
模型形式的设计：Y=β1+β2X1+β3X2+β4X3+β5X4+μ其中，Y:人均GDPX1：城市化率X2：城镇居民家庭人均可支配收入X3：城市政府支出X4：城镇居民消费水平三．数据的搜集本实验获取的是1979~2009年的数据，如下表：年份人均GDP 城市化率城镇居民家庭人均可支配收入政府支出城镇居民消费水平1978 381 17.92 343.4 1122.09 405 1979 419 18.96 405.0 1281.79 425 1980 463 19.39 477.6 1228.83 489 1981 492 20.16 500.4 1138.41 521 1982 528 21.13 535.3 1229.98 536 1983 583 21.62 564.6 1409.52 558 1984 695 23.01 652.1 1701.02 618 1985 858 23.71 739.1 2004.25 765 1986 963 24.52 900.9 2204.91 872 1987 1112 25.32 1002.1 2262.18 998 1988 1366 25.81 1180.2 2491.21 1311 1989 1519 26.21 1373.9 2823.78 1466 1990 1644 26.41 1510.2 3083.59 1596 1991 1893 26.94 1700.6 3386.62 1840 1992 2311 27.46 2026.6 3742.20 2262 1993 2998 27.99 2577.4 4642.30 2924 1994 4044 28.51 3496.2 5792.62 3852 1995 5046 29.04 4283.0 6823.72 4931 1996 5846 30.48 4838.9 7937.55 5532 1997 6420 31.91 5160.3 9233.56 5823 1998 6796 33.35 5425.1 10798.18 6109 1999 7159 34.78 5854.0 13187.67 6405 2000 7858 36.22 6280.0 15886.50 6850 2001 8622 37.66 6859.6 18902.58 7113 2002 9398 39.09 7702.8 22053.15 7387 2003 10542 40.53 8472.2 24649.95 7901 2004 12336 41.76 9421.6 28486.89 8679 2005 14185 42.99 10493.0 33930.28 9410 2006 16500 43.90 11759.5 40422.73 10423 2007 20169 44.94 13785.8 49781.35 11904 2008 23708 45.68 15780.8 62592.66 13526 2009 25575 46.59 17174.7 76299.93四．模型的估计与调整（一）．散点图020000400006000080000100002000030000Y（二）.OLS 回归结果：Dependent Variable: Y Method: Least Squares Date: 06/19/11 Time: 23:27 Sample(adjusted): 1979 2008Included observations: 30 after adjusting endpointsVariable Coefficient Std. Error t-Statistic Prob. C 1675.936 502.4538 3.335504 0.0027 X1 -85.42903 23.51347 -3.633196 0.0013 X2 0.694786 0.332357 2.090482 0.0469 X3 0.161081 0.034738 4.636982 0.0001 X40.3637490.2269861.6025140.1216R-squared0.998932 Mean dependent var 5882.433 Adjusted R-squared 0.998761 S.D. dependent var 6258.838 S.E. of regression 220.3462 Akaike info criterion 13.77929 Sum squared resid 1213812. Schwarz criterion 14.01282 Log likelihood -201.6893 F-statistic 5843.189Y=1675.936-85.42903X1+0.694786X2+0.161081X3+0.363749X4由此可见：该模型的R^2=0.998932，Adjusted R-squared=0.998761可决系数很高，F检验值为5843.189,明显显著。

1


E








需要

0








E
对变形后的模型做 OLS 估计即可








1

先忽略异方差做普通的 OLS，得到 ，然
后用 代替 来回归变形之后的模型



可以减小异方差
做平常的 OLS，然后在认为有异方差的情
况下，用 代替 ，进而得到一致估计量
∗

⇔


∗



∗ ∗




∗


方法：OLS 使得∑ ∗ 最小

∗
∑ ∑
∑ ∑

Var
∗
∑ ∑
∑
1

∑
∑ ∑
∑
性质
未知
E

E




1







对数法
怀特稳健
标准误
内
生
性



1

1

1

′


∑ 1
Var

∑

可线性化的模型
模型/用途
可
线
性
化
的
模
型
双对数
不变弹性模型
线性-对数
衡量增长率
设定

经济计量学模型建立与实证分析经济计量学是以数理统计学和经济理论为基础，运用统计方法和经济理论建立数学模型，对经济现象进行分析和预测的学科。

经济计量学模型的建立和实证分析对于经济学研究的发展和经济政策的制定具有重要意义。

本文将介绍经济计量学模型的建立和实证分析的基本步骤，并讨论其在实际应用中的一些注意事项。

一、经济计量学模型的建立1. 定义变量：经济计量学模型的第一步是明确研究的目标和所涉及的变量。

变量可以是经济体系中的各种经济指标，如GDP、通胀率、失业率等，也可以是影响经济现象的各种因素，如利率、汇率、政府支出等。

2. 确定函数关系：在建立经济计量模型时，需要确定各个变量之间的函数关系。

这可以通过理论基础和经验判断来确定，也可以通过回归分析等统计方法来估计。

3. 模型的形式化表示：确定各个变量之间的函数关系后，需要将模型形式化表示出来。

通常情况下，经济计量模型可以用数学方程或者等式来表示。

4. 确定参数：经济计量模型中的参数是指与模型中的变量相关的未知量。

确定参数的方法通常是通过经验估计或者进行统计分析得到。

二、经济计量模型的实证分析1. 数据的收集与准备：进行经济计量模型的实证分析之前，需要收集所需的数据，并对数据进行清洗和处理。

这包括数据的选择、整理、缺失值处理等。

2. 模型的估计与诊断：在进行实证分析时，需要选择适当的统计方法进行模型的估计和诊断。

常用的估计方法有最小二乘法、广义矩估计法等。

3. 实证结果的解释与评价：在获得经济计量模型的估计结果后，需要对结果进行解释和评价。

这包括对模型的拟合程度、参数的显著性、经济意义等进行评估。

4. 模型的预测与政策分析：通过经济计量模型的实证分析，可以进行经济现象的预测和政策的评估。

这有助于决策者制定合理的经济政策和预测未来经济发展趋势。

三、经济计量模型建立与实证分析的注意事项1. 数据的质量：经济计量模型的实证分析结果很大程度上取决于所使用的数据。

计量经济学的模型
计量经济学是一门运用数学、统计学和经济学理论来分析经济数据的学科。

它的核心是建立经济变量之间的数学模型，并利用实际数据进行估计和验证。

计量经济学模型通常由一组方程式组成，这些方程式描述了经济变量之间的关系。

其中，最常见的模型是线性回归模型，它假设因变量与自变量之间存在线性关系。

在建立计量经济学模型时，需要考虑许多因素，例如变量的选择、数据的收集和处理、模型的假设和限制等。

为了确保模型的可靠性和有效性，需要进行一系列的统计检验和诊断，例如拟合优度检验、异方差性检验、自相关检验等。

计量经济学模型可以用于预测经济变量的未来走势、评估政策的效果、检验经济理论的正确性等。

它在宏观经济、金融市场、产业经济等领域都有广泛的应用。

总之，计量经济学是一门重要的经济学分支，它通过建立数学模型来分析经济数据，为政策制定和经济决策提供了科学依据。

计量经济学经济数据分析和经济模型的要点计量经济学是经济学的一个重要领域，它通过运用统计学和数学方法，对经济数据进行定量分析，以揭示经济现象背后的规律性关系，并建立经济模型来解释和预测经济行为。

在本文中，我们将重点介绍计量经济学中经济数据分析和经济模型的要点。

一、经济数据分析经济数据是计量经济学的基础，它描述了经济现象以及经济变量之间的相互关系。

在经济数据分析中，我们需要掌握以下几个重要的要点：1. 数据收集：经济数据的来源多种多样，可以通过问卷调查、统计局数据、企业报表等方式进行收集。

在进行数据收集时，我们需要确保数据的准确性和全面性，避免数据的偏倚和遗漏。

2. 数据质量检验：在进行数据分析之前，我们需要对数据进行质量检验。

主要包括数据的完整性、一致性、合理性等方面的检查，以确保数据的可靠性。

3. 数据描述统计：数据描述统计是对数据进行初步的分析和概括，主要包括数据的中心位置、分散程度、分布形态等方面的统计指标。

常用的描述统计指标包括均值、方差、标准差等。

4. 数据可视化：数据可视化是将经济数据以图表的形式展现出来，以便更直观地理解和分析数据。

常用的数据可视化工具包括散点图、折线图、柱状图等。

二、经济模型经济模型是计量经济学的核心内容，它用数学语言描述经济行为和经济变量之间的关系。

在建立经济模型时，我们需要注意以下几个要点：1. 假设的设定：经济模型基于一定的假设前提，这些假设用于简化现实情况，并突出研究重点。

在建立模型时，我们需要合理设定假设，并对其进行合理性检验。

2. 变量选择：在经济模型中，我们需要选择具有经济意义的变量进行建模。

变量的选择应该考虑到其与研究主题的相关性和可测度。

3. 变量间关系的确定：在建立经济模型时，我们需要确定变量之间的关系形式。

常用的函数形式包括线性关系、非线性关系、概率分布等。

4. 模型参数的估计：经济模型的参数估计是计量经济学的核心内容之一。

常用的估计方法包括最小二乘法、极大似然法等。

计量经济学简单模型分析计量经济学是经济学领域中的一个重要分支，它借助数学和统计学的方法，通过建立模型来描述、解释和预测经济现象。

简单模型分析是计量经济学的基础，本文将介绍如何进行计量经济学简单模型分析。

首先，进行计量经济学简单模型分析需要明确研究问题和目标。

确定研究问题需要考虑实际背景和理论依据，确定模型的目标是为了回答研究问题。

其次，需要收集相关数据，包括时间序列数据、横截面数据等。

在收集数据时，需要注意数据的准确性、完整性和可比较性。

接下来，需要选择合适的模型。

简单线性回归模型是计量经济学中最简单的模型之一，适用于单一自变量和因变量的分析。

简单线性回归模型的数学形式为：y = β0 + β1x + ε，其中y是因变量，x是自变量，β0和β1是模型的参数，ε是误差项。

建立模型后，需要进行模型的估计和检验。

普通最小二乘法（OLS）是估计简单线性回归模型最常用的方法，它通过最小化残差平方和来估计模型的参数。

模型的检验包括拟合优度检验、统计检验和计量经济学检验等。

拟合优度检验用于评估模型对数据的拟合程度，统计检验用于检验模型的假设条件是否成立，计量经济学检验用于评估模型的可靠性、稳定性和预测能力。

最后，需要对模型进行分析和解释。

模型的参数估计值是解释模型的关键，β1表示自变量x每增加一个单位时因变量y的平均增加量。

需要分析模型的假设条件是否成立，以及模型的预测能力。

如果模型存在不足之处，需要进行相应的调整和改进。

总之，计量经济学简单模型分析是经济学研究的重要基础。

通过简单模型分析，我们可以描述、解释和预测经济现象，为经济决策提供科学依据。

随着数据科学和机器学习的发展，计量经济学的方法和技术将不断得到完善和创新，为经济学研究提供更加精确和实用的工具。

计量经济学did模型计量经济学DID模型引言计量经济学是经济学中的一个重要分支，通过运用统计学和数学方法来解决经济问题。

DID模型（Difference-in-Differences）是计量经济学中一种常用的分析方法，用于评估政策或其他干预措施对某一特定群体或地区的影响。

本文将介绍DID模型的基本原理、应用领域以及一些相关的注意事项。

一、DID模型的基本原理DID模型是一种自然实验设计，通过比较两个群体或地区在政策干预前后的差异，来评估政策对实验组的影响。

其中，实验组是受到政策干预的群体或地区，对照组是没有受到政策干预的群体或地区。

通过比较实验组和对照组在政策干预前后的差异，可以得出政策对实验组的效应。

DID模型的基本原理可以通过以下公式表示：Y_it = α + β*T_i + γ*D_t + δ*(T_i*D_t) + ε_it其中，Y_it表示观测单位i在时间t的结果变量；T_i表示观测单位i 是否受到政策干预的虚拟变量（Treatment）；D_t表示时间t是否为政策干预的虚拟变量（Difference）；α、β、γ、δ分别表示常数项和各个系数；ε_it表示误差项。

二、DID模型的应用领域DID模型在计量经济学中有广泛的应用领域。

以下列举了一些常见的应用案例：1. 教育政策评估：DID模型可以用于评估教育政策对学生学业成绩的影响。

通过比较政策实施前后不同学校或学生群体的学业成绩差异，可以评估教育政策的效果。

2. 劳动力市场研究：DID模型可以用于研究最低工资政策对就业率的影响。

通过比较实施最低工资政策的地区和没有实施最低工资政策的地区的就业率变化，可以评估最低工资政策的效果。

3. 医疗政策评估：DID模型可以用于评估医疗政策对健康指标的影响。

通过比较实施医疗政策的地区和没有实施医疗政策的地区的健康指标变化，可以评估医疗政策的效果。

4. 环境政策研究：DID模型可以用于研究环境政策对环境污染的影响。

计量经济学4种常用模型计量经济学是经济学的一个重要分支，主要研究经济现象的数量关系及其解释。

在计量经济学中，常用的模型有四种，分别是线性回归模型、时间序列模型、面板数据模型和离散选择模型。

下面将对这四种模型进行详细介绍。

第一种模型是线性回归模型，也是计量经济学中最常用的模型之一。

线性回归模型是通过建立自变量与因变量之间的线性关系来解释经济现象的模型。

在线性回归模型中，自变量通常包括经济学理论认为与因变量相关的变量，通过最小二乘法估计模型参数，得到经济现象的解释。

线性回归模型的优点是简单易懂，计算方便，但其前提是自变量与因变量之间存在线性关系。

第二种模型是时间序列模型，它主要用于分析时间序列数据的模型。

时间序列模型假设经济现象的变化是随时间演变的，通过分析时间序列的趋势、周期性和随机性，可以对经济现象进行预测和解释。

时间序列模型的常用方法包括自回归移动平均模型（ARMA）、自回归条件异方差模型（ARCH）等。

时间序列模型的优点是能够捕捉到时间的动态变化，但其局限性是对数据的要求较高，需要足够的时间序列观测样本。

第三种模型是面板数据模型，也称为横截面时间序列数据模型。

面板数据模型是将横截面数据和时间序列数据结合起来进行分析的模型。

面板数据模型可以同时考虑个体间的差异和时间的变化，因此能够更全面地解释经济现象。

面板数据模型的常用方法包括固定效应模型、随机效应模型等。

面板数据模型的优点是能够控制个体间的异质性，但其需要对个体间的相关性进行假设。

第四种模型是离散选择模型，它主要用于分析离散选择行为的模型。

离散选择模型假设个体在面临多种选择时，会根据一定的规则进行选择，通过建立选择概率与个体特征之间的关系，可以预测和解释个体的选择行为。

离散选择模型的常用方法包括二项Logit模型、多项Logit模型等。

离散选择模型的优点是能够分析个体的选择行为，但其局限性是对选择行为的假设较强。

综上所述，计量经济学中常用的模型有线性回归模型、时间序列模型、面板数据模型和离散选择模型。

计量经济学模型在财务分析中的应用研究随着社会经济的快速发展，以及金融市场的不断变化，财务分析成为企业决策过程中不可或缺的重要工具。

计量经济学模型是一种研究经济现象的数学方法，可以帮助分析人员建立合理的财务分析模型，以便更全面、准确地评估公司的财务状况、获得预测性的决策结果。

本文旨在探讨计量经济学模型在财务分析中的应用研究。

一、计量经济学模型在财务分析中的基本概念计量经济学模型是一种经济学方法，旨在利用数学和统计数据对经济现象进行建模和预测。

计量经济学模型通常包括一个数学方程或一组方程，用于捕捉一组经济变量之间的关系。

计量经济模型在财务分析中的应用通常涉及到两个主要分析领域：时间序列分析和横截面分析。

时间序列分析通常涉及从过去的数据中推断未来的表现趋势。

这种技术通常用于分析多项财务指标，如收入、利润、现金流和股票价格等，以确定公司未来的发展趋势。

通常使用具有时间维度的计量经济学模型，例如ARIMA、ARCH/GARCH等模型。

横截面分析通常涉及比较两个或更多不同公司的财务表现。

这种技术通常用于确定公司的相对绩效，以便在不同公司之间进行比较。

在这种情况下，使用具有多个相关因素的计量经济学模型，如回归模型、多元方程模型等。

二、计量经济学模型在财务分析中的应用案例研究在实践中，许多财务分析专家和经济学家都使用计量经济学模型来研究财务分析问题，并获得更全面、准确的分析结果。

以下是一些计量经济学模型在财务分析中的应用案例研究：1.时间序列分析一家公司希望通过分析其过去的财务表现来预测其未来表现。

该公司的研究人员采用ARIMA模型来分析公司的收入和利润数据。

研究人员发现，公司的收入和利润数据存在季节性波动。

因此，他们使用ARIMA模型来预测未来的季节性变化，并根据预测结果对公司进行投资决策。

2.横截面分析在一个跨国公司中，一个部门负责人想知道为什么在同一行业中，该公司的一些业务表现不如其他公司。

为此，他们采用了一个多元回归模型来分析许多潜在因素对业务绩效的影响。

○51位获奖者中8位直接因为对计量经济学发展的贡献而获 奖
1969 R. Frish J. Tinbergen 1973 W. Leotief 1980 L. R. Klein 1984 R. Stone 1989 T. Haavelmo 2000 J. J. Heckman D. L. McFadden ○16位担任过世界计量经济学会会长 ○ 30位左右在获奖成果中应用了计量经济学 ○“二战以后的经济学是计量经济学的时代”-Samuelson ○“计量经济学的讲授已经成为经济学课程表中最有权威 的济活动中各因素之间的理论关系， 用确定性的数学方程描述。例如，生产函数可描述为： Q Aet K L 公式描述了技术、资本、劳动与产出量之间 的理论关系，认为这种关系是准确实现的。利用数理经济 模型，可以分析经济活动中各种因素之间的互相影响，为 控制经济活动提供理论指导。但是，数理经济模型并没有 揭示因素之间的定量关系，在上式中，参数是未知的。
解释：如何正确地选择解释变量
• 首先，需要正确理解和把握所研究的经济现象中暗含的经济学理论和 经济行为规律。这是正确选择解释变量的基础 – 例如，在上述生产问题中，已经明确指出属于供给不足的情况， 那么，影响产出量的因素就应该在投人要素方面，而在当前，一 般的投人要素主要是技术、资本与劳动 – 如果属于需求不足的情况，那么影响产出量的因素就应该在需求 方面，而不在投入要素方面。这时，如果研究的对象是消费品生 产，应该选择居民收人等变量作为解释变量；如果研究的对象是 生产资料生产，应该选择固定资产投资总额等变量作为解释变量。
• 经济计量模型由系统或方程组成，方程由 变量和系数组成。其中，系统也是由方程 组成。
怎样看待计量经济模型？
• 广义地说，一切包括经济、数学、统计三 者的模型；