下载文档原格式
审 定日 期 2004.01标 检审 核校 对描 校编 制 吴 强描 打30000吨级散货船详 细 设 计舵系计算书JH403-230-01js上海佳豪船舶工程有限公司标记数量修改单号签 字 日 期总面积 m 2 0.6875 共 页 11 第 页1 会 签旧底图登记号 底图登记号1、概述本船为单甲板、双底层、艉机型、单机、单桨、单舵船。
航行在国内沿海港口。
本船装载货物以煤炭为主，兼运铁矿石谷物等散货。
2、计算依据本计算书是根据“2001钢质海船入级与建造规范”第2分册第3章第一节的有关要求进行计算的。
3、船舶的主要尺度及要素：总长L0a 178.00m垂线间长Lbp 170.80m型宽B 27.60m型深D 13.90m设计吃水d 9.60m服务航速v 13.5m4、舵的要素计算型式：半平衡半悬挂舵舵数量：1只4.1舵面积：A=A1+A2=25.26m2A1= A11+ A1ƒ==15.482m2A2= A22+ A2 ƒ==9.78m2ą1——系数0.33(正车)，0.66（倒车）ą2——系数0.25(正车)，0.55（倒车）A1ƒ=5.318 m2 A11=10.16 m2 A2 ƒ=1.425 m2 A2 2=8.357 m2正车：F=132×1.27×1.1×1.0×25.26×13.52=848.93KN 倒车：F=132×1.27×0.8×1.0×25.26×6.752=154.35KN 4.3舵杆扭矩T=F ·R NM式中：F —舵力 正车 F=848.93KN 倒车 F=154.35KNR —臂矩 m R=c 1(α1－β1)A A 1+ c 2(α2－β2)AA2 (m) 式中：A 1=15.482 m 2 A 2=9.78 m 2 c 1=78.32432.1614.2=+ c 2=22h A =2158.2815.2+＝2.49β1=11A f A =482.15318.5=0.343 β2=22A f A =78.9425.1=0.146 正车时:R=3.78×(0.33－0.343)×235.25482.15+2.49×(0.25－0.146)×235.25753.9 =－0.03+0.1=0.07 m 又在正车时 R>A 101（A 1c 1+ A 2c 2）=26.25101⨯×(15.483×3.78+9.753×2.49)=0.328取R=0.328m 倒车时：R=3.78×（0.66-0.343）×235.25482.15+2.49×(0.55-0.146) ×235.25753.9 =0.735+0.389=1.124m∴正车时舵杆扭矩：T=F ·R=848.93×0.328=278.45KN.m 倒车时舵杆扭矩：T=F ·R=154.35×1.124=173.1 KN.m考虑船在风浪中及航行中受到的附加扭矩和舵系的摩擦扭矩。
舵系的直接计算法
唐宁生
【期刊名称】《船舶》
【年(卷),期】2004(000)003
【摘要】本文给出了按船级社规定的模型计算舵和舵杆中的弯矩和剪力的公式.舵和舵杆被视为阶梯式变断面梁,且尾框底骨或挂舵臂处的支点被视为弹性支座.文中详细讨论了四种静不定结构的舵.
【总页数】6页(P49-53,57)
【作者】唐宁生
【作者单位】708研究所,上海,200011
【正文语种】中文
【中图分类】U664.36
【相关文献】
1.基于全船有限元建模直接计算法的3800TEU集装箱船总体强度分析 [J], 张小芳;施涛;郑莎莎
2.基于ABAQUS的海冰单元开发及冰载荷直接计算法 [J], 龚榆峰;张正艺;刘敬喜;董问;解德
3.|sinx|原函数的直接计算法 [J], 朱家桢;顾燕华;刘春平
4.舵系直接计算法设计 [J], 田野;张文斌;王平;于博;杨营;张光涛
5.基于ABAQUS的破损船舶静稳性曲线直接计算法研究 [J], 令波;张正艺;解德因版权原因，仅展示原文概要，查看原文内容请购买。
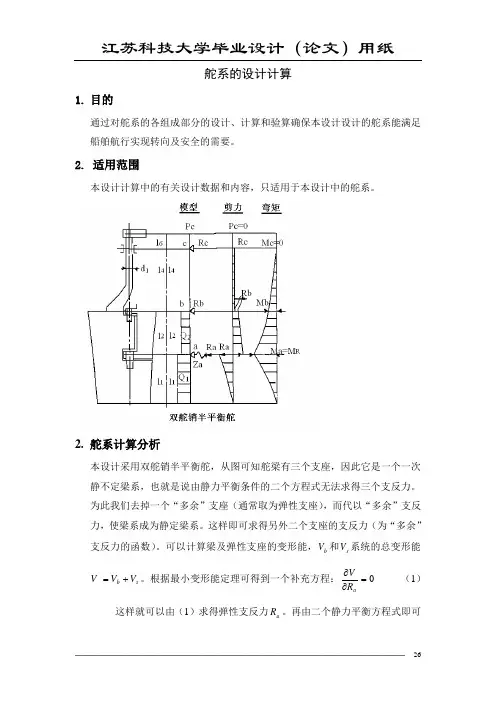
舵系的设计计算1. 目的通过对舵系的各组成部分的设计、计算和验算确保本设计设计的舵系能满足船舶航行实现转向及安全的需要。
2. 适用范围本设计计算中的有关设计数据和内容，只适用于本设计中的舵系。
2. 舵系计算分析本设计采用双舵销半平衡舵，从图可知舵梁有三个支座，因此它是一个一次静不定梁系，也就是说由静力平衡条件的二个方程式无法求得三个支反力。
为此我们去掉一个“多余”支座（通常取为弹性支座），而代以“多余”支反力，使梁系成为静定梁系。
这样即可求得另外二个支座的支反力（为“多余”支反力的函数）。
可以计算梁及弹性支座的变形能，b V 和s V 系统的总变形能s b V V V +=。
根据最小变形能定理可得到一个补充方程：0=∂∂aR V（1） 这样就可以由（1）求得弹性支反力a R 。
再由二个静力平衡方程式即可求得另二个支反力b R 和c R 。
接着就可按材料力学的方法作出断面剪力和弯矩图了。
因为 ⎰=lz b d z EI z M V 02)(2)(所以 ⎰∂∂⋅=∂∂l z aa bd R z M z EI z M R V 0)()()(。
又因梁是由几个不同断面的梁段组成，所以又可写成：zi ni l b d EIizi M V ∑⎰==1212)(， ∑⎰=∂∂⋅=∂∂n i l z aa bi d R zi M EIi zi M R V 10)()(弹性支座a 的支座变形能aas Z R V 221=，所以aaa s Z R R V =∂∂ （1） 式可写为：aa zi a ni l Z Rd R zi M EIi zi M +∂∂⋅∑⎰=)()(11（1a ） 式中 )(z M ,)(zi M —距原点z 处的断面变矩)(z M 和第i 段梁的距第i 段梁原点zi 断面弯矩)(zi M ；)(z I ,Ii —距原点z 处的断面惯性距)(z I 和第i 段梁段数；a Z —弹性支座a 的支座弹簧常数。
舵系设计分析作者：孙程程来源：《硅谷》2014年第02期摘要随着船型开发工作的进行，舵系设计越来越引起设计人员的重视。
但是由于我们在这方面积累的数据、经验不多，使我们在设计的过程中遇到很多问题。
因此通过查阅资料、规范，汇总出现在造船界常用的十种类型的舵系布置，并且针对十种类型的舵系布置分别建立了数学模型。
关键词舵系布置；数学模型；受力分析；弹性系数中图分类号：U664.36 文献标识码：A 文章编号：1671-7597（2014）02-0106-021 计算符号说明L：舵叶的高度（m）；l10，l20，l30，l40：舵系系统中各个单元的长度（m）；l50：舵踵的长度（m）；J10，J20，J30，J40：舵系系统中各个单元相对于x轴的惯性距（cm4）；J50：舵踵相对于Z轴的惯性距（cm4）；CR：作用在舵叶上的舵力（N）；CR1，CR1：作用在舵叶单元上的舵力（N）；E：弹性模数（N/m2）E=2.06×1011 N/m2；G：剪力弹性模数（N/m2）G=7.85×1010 N/m2。
2 不同舵系布置的数学模型及受力分析类型一：作用在舵叶上单位长度的舵力（单位：N/m）：（1）舵系结构的受力情况：1）舵杆上的最大的弯距（N/m）：MB=0。
2）各支点处的支反力（N）：FA1=FA2=FA3=CR/3，FA4=0。
3）对于流线型的舵叶，作用的舵叶上的弯距（N.m）：MR=CRl/24。
类型二：作用在舵叶单位长度上的舵力PR10和PR20（N/m）：对于弹性支点处的弹簧系数Zp按照公式（6）进行计算。
类型三：作用在舵叶单位长度上的舵力PR（N/m）：作用在舵系结构上的力：1）舵杆上的最大的弯距（N/m）：MB=02）各支点处的支反力（N）：FA1= FA2= CR/2 FA3=0。
类型四：作用在舵叶单位长度上的舵力PR（N/m）：对于弹性支点处的弹簧系数Zc按照公式（5）进行计算。
