直方图的均衡化

图像处理中直方图均衡化的使用教程图像处理中的直方图均衡化是一种常用的增强图像对比度的方法。

通过对图像的像素值进行重新分布，直方图均衡化可以使图像中的明暗区域更具有对比度，从而提高图像的质量和清晰度。

本文将介绍直方图均衡化的原理、应用场景以及具体的步骤。

1. 直方图均衡化的原理直方图均衡化的原理基于对图像的灰度级进行重新分布。

它通过将原始图像的像素值映射到新的像素值上，使得直方图在整个灰度范围内得到均匀分布。

这样就能够增强图像中的低对比度区域，提高图像的视觉效果。

2. 直方图均衡化的应用场景直方图均衡化在图像处理领域有着广泛的应用。

下面列举了一些常见的应用场景：- 增强图像的对比度：直方图均衡化可以使得图像中的亮度值更加均匀分布，提高图像的对比度，使得图像变得更加清晰。

- 增强图像的细节：直方图均衡化通过增强图像中的低对比度区域，可以使得细节更加显著，提高图像的可视化效果。

- 降低图像的噪声：直方图均衡化可以将图像中的噪声分布均匀化，从而减少噪声对图像质量的影响。

3. 直方图均衡化的步骤下面是使用直方图均衡化对图像进行处理的具体步骤：步骤 1: 将彩色图像转换为灰度图像如果原始图像是彩色图像，我们需要将其转换为灰度图像。

这是因为直方图均衡化是针对灰度级进行处理的。

步骤 2: 计算原始图像的像素值分布使用图像处理工具，计算原始图像中每个像素值的出现频率。

这样可以得到一个直方图，该直方图显示了原始图像中像素值的分布情况。

步骤 3: 计算累积分布函数通过对原始图像的直方图进行累积求和，得到一个累积分布函数。

该函数显示了每个像素值的累积出现频率。

步骤 4: 计算新的像素值根据累积分布函数，计算每个像素值的新的映射像素值。

这个计算公式可以根据具体的图像处理工具而有所不同。

步骤 5: 创建均衡化后的图像使用新的像素值替换原始图像中的像素值，将得到的图像称为均衡化后的图像。

4. 注意事项在使用直方图均衡化时，需要考虑以下几个注意事项：- 直方图均衡化可能会改变图像的整体亮度。

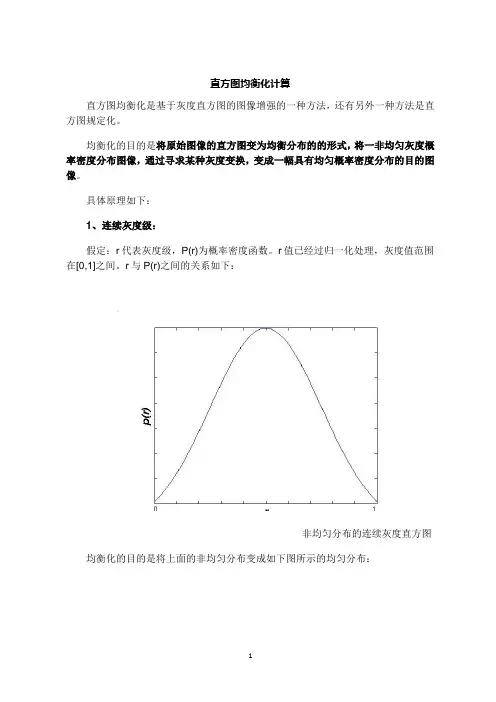
直方图均衡化计算直方图均衡化是基于灰度直方图的图像增强的一种方法，还有另外一种方法是直方图规定化。

均衡化的目的是将原始图像的直方图变为均衡分布的的形式，将一非均匀灰度概率密度分布图像，通过寻求某种灰度变换，变成一幅具有均匀概率密度分布的目的图像。

具体原理如下：1、连续灰度级：假定：r代表灰度级，P(r)为概率密度函数。

r值已经过归一化处理，灰度值范围在[0,1]之间。

r与P(r)之间的关系如下：非均匀分布的连续灰度直方图均衡化的目的是将上面的非均匀分布变成如下图所示的均匀分布：均匀分布的连续灰度直方图我们接下来要做的是要找到一种变换S=T(r)使直方图变平直，为使变换后的灰度仍保持从黑到白的单一变化顺序，且变换范围与原先一致，以避免整体变亮或变暗，需要有如下规定：（1）在0 <= r <= 1中，T(r)是单调递增函数，且0 <= T(r) <= 1；（2）反变换r=(s)，(s)也为单调递增函数，且0 <= s <= 1。

直方图均衡化变换公式推导图示因为灰度变换不影响像素的位置分布，而且也不会增减像素数目，所以有如下的推导公式：2、离散灰度级：设一幅图像的像素总数为n，分为L个灰度级，其中：：表示第K个灰度级出现的个数。

：第K个灰度级出现的概率。

（0<=<=1, k=0,1,2,...,L-1），公式如下：计算的基本步骤如下：（1）求出图像中所包含的灰度级,一般都经过归一化处理，范围在[0,1]之间，也可以定在[0,L-1]之间。

（2）统计各灰度级的像素数目（k=0,1,2,...,L-1）。

（3）计算图像直方图。

（4）计算变换函数，即：（5）用变换函数计算映射后输出的灰度级。

（6）统计映射后新的灰度级的像素数目。

（7）计算输出图像的直方图。

根据上面推导出来的公式以及计算步骤，我们可以结合栗子来加深理解~~~eg：设图像有64*64=4096的像素，有8个灰度级，灰度分布如下所示：由上图我们知道该图像的，和，下一步我们要做的就是通过变换函数求，即：依次可求得，，，，。

直方图均衡化原理直方图均衡化是一种用于增强图像对比度的经典方法，它通过重新分布图像的像素值来实现增强图像的对比度和亮度。

在本文中，我们将介绍直方图均衡化的原理，包括其基本概念、算法步骤和应用场景。

直方图均衡化的基本概念是通过重新分布图像的像素值，使得原始图像的像素值分布更加均匀，从而增强图像的对比度和亮度。

这种方法的核心思想是将原始图像的灰度直方图进行变换，使得变换后的直方图更加平坦，从而实现对比度的增强。

直方图均衡化的算法步骤可以简单概括为以下几步，首先，计算原始图像的灰度直方图，即统计图像中每个像素值的出现次数；然后，根据原始图像的灰度直方图计算累积分布函数（CDF），用于描述像素值的累积分布情况；接着，根据CDF对原始图像的像素值进行映射，得到变换后的图像；最后，根据映射后的像素值重新构建图像，实现对比度增强。

直方图均衡化的应用场景非常广泛，包括但不限于医学图像处理、遥感图像处理、数字摄影等领域。

在医学图像处理中，直方图均衡化可以帮助医生更清晰地观察病灶，提高诊断准确性；在遥感图像处理中，直方图均衡化可以增强图像的细节信息，提高图像的可视化效果；在数字摄影中，直方图均衡化可以改善照片的曝光不足或曝光过度的问题，提高照片的质量。

总之，直方图均衡化作为一种经典的图像增强方法，具有重要的理论意义和实际应用价值。

通过重新分布图像的像素值，直方图均衡化可以有效地增强图像的对比度和亮度，提高图像的质量和可视化效果。

在实际应用中，我们可以根据具体的需求选择合适的直方图均衡化算法，从而实现对图像的有效增强和优化。

希望本文对直方图均衡化的原理有所了解，对读者有所帮助。

如果您对直方图均衡化还有其他疑问或者需要进一步的了解，欢迎继续阅读相关的文献资料或者咨询相关领域的专业人士。

感谢您的阅读！。

直方图均衡化的原理和作用直方图均衡化是一种常见的图像处理技术，用于增强图像的对比度和视觉效果。

它的原理是通过重新分布图像的灰度级别，使得图像中的像素灰度值分布更加均匀，从而改善图像的视觉效果。

在进行直方图均衡化时，首先需要获取图像的灰度直方图，然后根据灰度直方图的累积概率密度函数对图像的像素进行重新分配。

直方图均衡化的作用主要体现在以下几个方面：1. 增强图像的对比度：直方图均衡化可以有效地增强图像的对比度，使得图像中不同区域的灰度级别更加明显，从而使得图像的细节更加清晰。

2. 提高图像的视觉效果：通过直方图均衡化，图像的灰度级别分布更加均匀，可以使得图像看起来更加自然和真实，同时增强了图像的视觉效果，使得观看者更容易理解和分析图像内容。

3. 抑制背景噪声：在图像处理中，背景噪声往往会影响图像的清晰度和质量。

通过直方图均衡化可以有效地抑制背景噪声，使得图像更加清晰和易于分析。

4. 增强图像的细节：直方图均衡化可以增强图像的细节，使得图像中的纹理和结构更加清晰和突出，同时也能够凸显出图像中的一些微弱的特征。

直方图均衡化的原理是基于图像的灰度级别分布的重新分配，其具体操作过程如下：1. 获取图像的灰度直方图：首先需要对图像进行灰度化处理，然后统计不同灰度级别的像素点数量，从而得到图像的灰度直方图。

2. 计算灰度直方图的累积概率密度函数：根据图像的灰度直方图，可以计算出每个灰度级别对应的累积概率密度函数，即将原始的灰度级别映射到新的灰度级别上。

3. 根据累积概率密度函数对像素进行重新分配：根据计算得到的累积概率密度函数，可以将图像中的每个像素的灰度级别重新映射到新的灰度级别上，从而得到均衡化后的图像。

通过以上操作，可以实现直方图均衡化，从而改善图像的对比度和视觉效果。

需要注意的是，直方图均衡化可能会增强图像中的噪声和细小的纹理，因此在实际应用中需要结合具体的图像特性进行调整，以达到最佳的效果。

总之，直方图均衡化是一种有效的图像处理技术，通过重新分配图像的灰度级别，可以增强图像的对比度，改善图像的视觉效果，并抑制背景噪声，使得图像更加清晰和易于分析。

实验1.直方图均衡化程序的原理及步骤直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某灰度区间变成在全部灰度范围内的均匀分布。

直方图均衡化的原理：直方图均衡化是把原图像的直方图通过灰度变换函数修正为灰度均匀分布的直方图,然后按均衡直方图修正原图像,其变换函数取决于图像灰度直方图的累积分布函数。

概括地说,就是把一已知灰度概率分布的图像,经过一种变换,使之演变成一幅具有均匀概率分布的新图像。

当图像的直方图为一均匀分布时,图像的信息熵最大,此时图像包含的信息量最大,图像看起来更清晰。

灰度直方图用各灰度值出现的相对频数(该灰度级的像素数与图像总像素数之比)表示。

直方图表示数字图像中每一灰度级与其出现频数的的统计关系，用横坐标表示灰度级，纵坐标表示频数。

直方图就能给出该图像的概貌性描述，例如图像的灰度范围、每个灰度级的频数和灰度的分布、整幅图像的亮度和平均明暗对比度等，由此可得出进一步处理的重要依据。

计算每个灰度级出现的概率为：P r (r k )＝N k /N k=0，1，2,…,L-1上式中， P r (r k )表示第k 个灰度级出现的概率，N k 为第 k 个灰度级出现的频数，N 为图像像素总数,L 为图像中可能的灰度级总数。

由此可得直方图均衡化变换函数,即图像的灰度累积分布函数Sk 为:1,...,2,1,0)()(00-====∑∑==L k r P r T s kj NN k j j r k k j 上式中, S k 为归一化灰度级。

这个变换映射称做直方图均衡化或直方图线性化。

直方图均衡化过程如下:（1） 输出原图像；（2） 根据公式P r (r k )＝n k /m*n （ k=0，1，2,…,L-1）计算对应灰度级出现的概率，绘制原图像的直方图。

（3） 计算原图象的灰度级累积分布函数：sk=Σp r (r k )；（4） 取整Sk=round((S1*256)+0.5);将Sk 归一到相近的灰度级，绘制均衡化后的直方图。

直⽅图均衡化（histogramequalization）⼀. 原理直⽅图均衡化是想要将聚集在某⼀区间内分布的灰度值，变为均匀的在所有区间内分布。

为了达到这⼀⽬的，我们需要找出⼀个函数T，将r（原图像灰度）映射到s（新图像灰度）上。

同时，由于不想将图像反转，我们需要保证函数单调不减（若需要逆运算，则要严格单调递增）s=T(r)设p r(r)为r的概率分布函数，p s(s)为s的概率分布函数，则两者关系如下p s(s)=p r(r)|dr ds|也就是说，T(r)这个函数现在要满⾜条件：单调递增值域范围为[0,L-1]p s(s)为⼀个常函数（表⽰每⼀个灰度值的概率都相等）现在给出⼀个函数（⾄于为什么是这个函数，我也不知道啊，哪位看官可以帮忙推导⼀下QAQ）：s=T(r)=(L−1)∫r0p r(w)dw我们将逐步证明，以上三点成⽴由于此函数为积分所得，因此函数单调递增由于p r(r)为概率密度函数，因此，积分区间为[0,1]，乘以常数，区间为[0,L-1]推导过程：ds=dT(r)=d((L−1)∫r0p r(w)dw)=(L−1)p r(r)drp s(s)=p r(r)|drds|=pr(r)|1(L−1)p r(r)|=1L−1此时p s(s)为⼀个均匀密度函数，符合对于离散值，计数每个不⼤于r的概率和，就是这个r对应的ss k=T(r k)=(L−1)k∑j=0p r(r j)⼆. 代码img = imread("14.jpeg");r = img(:,:,1);g = img(:,:,2);b = img(:,:,3);p = stat(r);map = cal(p);img_equa = my_hist_equation(r,map); % 画图%原图subplot(331)imshow(r);title('原图');subplot(332)imhist(r);title('原图直⽅图');%⾃⼰的直⽅图均衡化图subplot(334)imshow(img_equa);title('my直⽅图均衡化图');subplot(335)imhist(img_equa);title('my直⽅图均衡化直⽅图'); subplot(336)plot((0:255)/255,map/255);title('my函数');%标准的直⽅图均衡化图[std_img,T] = histeq(r);subplot(337)imshow(std_img);title('标准直⽅图均衡化图');subplot(338)imhist(std_img);title('标准直⽅图均衡化图直⽅图'); subplot(339)plot((0:255)/255,T);Processing math: 100%title('std函数');figureplot((0:255)/255,map/255);figureplot((0:255)/255,T);%计算图像的分布function p=stat(img)[r,c] = size(img);p = linspace(0,0,256);for i=1:1:rfor j=1:1:cp(img(i,j)+1)= p(img(i,j)+1)+1;endendp = p/(r*c);end%计算r与s的对应关系，矩阵坐标为r，值为s(动态规划) function s=cal(probality)s=probality;l = length(probality);for i=2:ls(i) = s(i-1)+s(i);ends = round(s*255);end%将图⽚根据映射函数，映射function img_equa=my_hist_equation(img,map)[r,c] = size(img);img_equa = zeros(r,c);for i=1:rfor j=1:cimg_equa(i,j) = map(img(i,j)+1);endendimg_equa = uint8(img_equa);end放⼤我的映射函数图⽚为：matlab⾃建的映射函数为：对⽐两个映射函数可以看出来，⾃⼰实现的为⽐较连续的，⽽matlab⾃建的为阶段性的。

直⽅图均衡化今天学习了下直⽅图均衡化的原理。

先来看看维基百科上的⼀个例⼦： 从这张未经处理的灰度图可以看出，其灰度集中在⾮常⼩的⼀个范围内。

这就导致了图⽚的强弱对⽐不强烈。

直⽅图均衡化的⽬的，就是使得灰度分布尽可能平均地“填满”整个灰度空间（0~255），就是做到直⽅图的上界是⼀条平⾏于X轴的直线（理想化）。

有了这个⽬标之后，开始推导。

这个推导过程从连续函数出发。

第⼀步：建⽴⼀个从灰度r到s的映射s=T(r)第⼆步：将均衡化后的直⽅图的分布H B 表⽰成原图灰度分布H A 的函数 --> H B(s)=H A(r)/T(r)，原理见下。

第三步：理想化的灰度分母应为常数，得T(r)=k*H A(r)，不妨另：k=C/A o .（A o为所有像素数）第四步：两边同时积分(0->L)，由密度函数的归⼀化条件得 : s=T(L)=C，因为s取值也是0->L，所以C=L。

第五步：把连续函数写成离散形式以适应计算机的处理。

（写出来⼤概就是这样，⾃⼰也能理解，但是总是感觉怪怪的） 可以看出，直⽅图均衡化只是将直⽅图进⾏了伸缩变换，或者说是⼀个搬移。

将变化律低的部分挤压，将变化率⾼的部分拉伸，得到⼀个两边变化陡峭中间平滑的灰度分布（单峰的话就很明显）。

可以看看维基百科上直⽅图均衡化之后的例⼦： 通过观察可以发现，由于中间部分灰度被拉伸了，灰度的取值变得不是很“连续”。

这个就是直⽅图均衡化的⼀个缺点吧。

（其实是离散的问题）———————————————————————————————————————————————————————————————————————————————闲着⽆聊搞了个最简单的直⽅图均衡化⼩程序，⼤家可以⾃⼰拿去试⼀下。

接下来的计划是做⾃适应直⽅图均衡化和对⽐对限制的直⽅图均衡化。

代码：#include <iostream>#include <string>#include <io.h>#include <opencv2/opencv.hpp>#include<math.h>#include<cv.h>using namespace std;using namespace cv;void main(int argc, char** argv){//变量定义//图⽚类IplImage *src , *dst;IplImage *histframesrc , *histframedst;CvSize size;//直⽅图类CvHistogram *histo_src , *histo_dst;int scale;float histmin,histmax;int bins=256;float range[]={0,255};float *ranges[]={range};//杂家int i,j,k,m,n; //循环变量……⽽已float s_r[256]; //S(r)映射函数//---------------------------------------------------------------src=cvLoadImage("11.jpg",0); //图⽚变量初始化cvShowImage("src",src);size=cvGetSize(src);dst=cvCreateImage(size,8,1);histo_src=cvCreateHist(1,&bins,CV_HIST_ARRAY,ranges); //直⽅图初始化histo_dst=cvCreateHist(1,&bins,CV_HIST_ARRAY,ranges);cvCalcHist(&src,histo_src,0,0); //计算直⽅图cvNormalizeHist(histo_src,1); //归⼀//累加，求S(r)映射s_r[0]=cvQueryHistValue_1D(histo_src,0);for(i=1;i<=255;i++){s_r[i]=s_r[i-1]+cvQueryHistValue_1D(histo_src,i);}//当然要把是S(r)归⼀到255啦for(i=0;i<=255;i++){s_r[i]=cvRound(s_r[i]*255);}//遍历图像并由sr关系进⾏直⽅图均衡化啦CvScalar s;for(m=0;m<size.height;m++){for(n=0;n<size.width;n++){s=cvGet2D(src,m,n);i=s.val[0];i=s_r[i];s.val[0]=i;cvSet2D(dst,m,n,s);}}//计算dst直⽅图cvCalcHist(&dst,histo_dst,0,0);cvNormalizeHist(histo_dst,1);//SHOWOFF⼀下啦cvShowImage("dst",dst);scale=1;//画出src和dst的直⽅图histframesrc=cvCreateImage( cvSize(bins*scale,256),8,1);histframedst=cvCreateImage( cvSize(bins*scale,256),8,1);//src的cvGetMinMaxHistValue(histo_src , &histmin , &histmax , 0 , 0 );for(int i = 0; i < bins; i++){/** 获得直⽅图中的统计次数，计算显⽰在图像中的⾼度 */float bin_val = cvGetReal1D(histo_src->bins,i);bin_val=bin_val*255/histmax;s.val[0]=cvRound(bin_val);cvRectangle(histframesrc,cvPoint(i*scale,256),cvPoint((i+1)*scale,256-bin_val),s,-1,8,0); }cvShowImage("src's hisogram",histframesrc);//dst的cvGetMinMaxHistValue(histo_dst , &histmin , &histmax , 0 , 0 );for(int i = 0; i < bins; i++){/** 获得直⽅图中的统计次数，计算显⽰在图像中的⾼度 */float bin_val = cvGetReal1D(histo_dst->bins,i);bin_val=bin_val*255/histmax;cout<<bin_val<<"\t";s.val[0]=cvRound(bin_val);cvRectangle(histframedst,cvPoint(i*scale,256),cvPoint((i+1)*scale,256-bin_val),s,-1,8,0); }cvShowImage("dst's hisogram",histframedst);//输出sr试⼀下for(i=0;i<=255;i++)cout<<s_r[i]<<"\n";for(;;)if(cvWaitKey(0)==27)break;}结果：（直⽅图变得平缓了但是中间部分变得稀疏了）。

简述直方图均衡化的基本原理。

直方图均衡化是图像处理领域广泛使用的一种技术，它主要用来平衡图像中各个亮度区域。

它可以改善图像的质量，提高图像的局部对比度，而且，这种技术很简单，易于实现。

1.什么是直方图均衡化直方图均衡化是一种用于改善图像质量的算法，能够提高图像的局部对比度和细节，这也是为什么会有这么大的流行度的原因之一。

按照其基本思想，直方图均衡化的目的是改善图像中暗部和亮部的区分度，使其直方图更平坦，从而改善图像的局部对比度。

2.直方图均衡化的原理直方图均衡化是基于直方图概率分布转换（HDPT）实现的，它使原本呈现出偏好的直方图（例如不均衡或不清晰）变得更加均匀。

具体来说，直方图均衡化通过对图像的每个像素的亮度值进行重新映射，以实现直方图的均衡化。

首先，计算出每个像素的累积直方图（CDH），并将其映射到（0，255）的范围内。

然后，将每个像素的亮度值重新映射为与 CDH应的亮度值，从而实现直方图的均衡化。

3.方图均衡化的优势直方图均衡化具有很多优点，下面列举其中几点：（1）改善图像质量：直方图均衡化可以提高图像的局部对比度，可以改善图像的质量；（2）易于实现：直方图均衡化算法非常简单，它只需要更改图像的像素值，而不需要昂贵的计算资源；（3）对不同亮度区域均衡：直方图均衡化可以使不同亮度区域之间的光照差异更加均衡，从而提高图像的整体质量；（4）减少图像噪声：由于直方图均衡化可以改变图像中各个亮度区域之间的差异，因此可以减少图像噪声的影响，从而提高图像质量。

4.直方图均衡化的应用直方图均衡化主要用于图像处理，有助于改善图像的质量，尤其是失真或模糊的图像。

此外，它还可以用于多媒体处理，如视频传输，视频压缩，图像压缩等，以提高这些多媒体文件的质量。

此外，直方图均衡化还可以用于计算机视觉，机器学习等领域。

以上是关于直方图均衡化的基本原理和其相关应用的简单介绍。

随着技术的进步，直方图均衡化将会得到更加深入的研究，以提高图像处理技术的效率和质量。

直方图均衡化目录1设计方案及功能描述 (1)2实现步骤 (3)3部分主要程序代码 (3)4运行结果 (7)5总结心得 (9)1设计方案及功能描述1.1 直方图均衡化图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。

直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。

直方图拉伸是通过对比度拉伸对直方图进行调整，从而“扩大”前景和背景灰度的差别，以达到增强对比度的目的，这种方法可以利用线性或非线性的方法来实现;直方图均衡化则通过使用累积函数对灰度值进行“调整”以实现对比度的增强。

直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。

直方图均衡化就是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同。

直方图均衡化就是把给定图像的直方图分布改变成“均匀”分布直方图分布。

直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。

这种方法通常用来增加许多图像的局部对比度，尤其是当图像的有用数据的对比度相当接近的时候。

通过这种方法，亮度可以更好地在直方图上分布。

这样就可以用于增强局部的对比度而不影响整体的对比度，直方图均衡化通过有效地扩展常用的亮度来实现这种功能。

这种方法对于背景和前景都太亮或者太暗的图像非常有用，这种方法尤其是可以带来X光图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。

这种方法的一个主要优势是它是一个相当直观的技术并且是可逆操作，如果已知均衡化函数，那么就可以恢复原始的直方图，并且计算量也不大。

这种方法的一个缺点是它对处理的数据不加选择，它可能会增加背景杂讯的对比度并且降低有用信号的对比度。

直方图均衡化的基本思想是把原始图的直方图变换为均匀分布的形式，这样就增加了象素灰度值的动态范围从而可达到增强图像整体对比度的效果。

设原始图像在(x，y)处的灰度为f，而改变后的图像为g，则对图像增强的方法可表述为将在(x，y)处的灰度f映射为g。

直方图均衡化方法
直方图均衡化是一种用来增强图像对比度的技术，它通过重新分布图像像素的灰度级来拉伸图像的动态范围。

下面介绍一种基本的直方图均衡化方法：
1. 计算原始图像的灰度直方图：统计每个灰度级出现的像素数量。

2. 计算原始图像的累积分布函数（CDF）：将每个灰度级的像素数量加到前一个灰度级的像素数量上，得到一个累积的像素数量曲线。

3. 计算均衡化后的累积分布函数：将CDF映射到新的像素值范围上，通常是0到255。

4. 计算均衡化后的灰度级映射表：将均衡化后的CDF映射到0到255的范围上。

5. 根据映射表，对原始图像的每个像素进行像素值替换：将原始像素值替换为对应的均衡化后的像素值。

6. 输出均衡化后的图像。

通过这个方法，直方图均衡化可以使得图像的像素值更均匀地分布在整个灰度级范围内，从而增强图像的对比度。

直方图均衡化计算公式直方图均衡化(色调均化)“图像(Image)>调整(Adjust)”菜单的功能色调均化(Equalize)Photoshop菜单：图像>调整>色调均化公式：（公式中Sk表示均衡化后的灰度值，∑表示总与，nj是原图中某个灰度色阶j 的像素数量，j的范围是0~k，N是图像像素总数。

）“色调均化”命令重新分布图像中像素的亮度值，以便它们更均匀地呈现所有范围的亮度级。

使用此命令时，Photoshop尝试对图像进行直方图均衡化(Histogram Equalization)，即在整个灰度范围中均匀分布每个色阶的灰度值。

当扫描的图像显得比原稿暗，而您想平衡这些值以产生较亮的图像时，能够使用“色调均化”命令。

配合使用“色调均化”命令与“直方图”命令，能够看到亮度的前后比较。

使用“色调均化”命令：1. 选择菜单图像>调整>色调均化。

2. 假如已选择一个图像区域，在弹出的对话框中选择要均化的内容，然后点按“好”。

•“仅色调均化所选区域”只均匀地分布选区的像素。

•“基于所选区域色调均化整个图像”基于选区中的像素均匀分布所有图像的像素。

原理直方图均衡化是一种灰度变换算法，因此我们重点研究灰度图像的直方图均衡化。

绝对的均匀图A是一个黑白灰均匀渐变，0~255的每一个色阶的灰度数量都是相同的。

图B 的是图A的像素打乱了顺序随机分布的，每种灰度的数量都与图A的相同，因而它的直方图也与图A的相同。

图A与图B的直方图。

每种灰度数量是相同的，直方图呈一个黑色矩形。

近似的均匀关于通常的图像，由于每种灰度的像素数量并不相同，我们没办法把每种灰度的分量调得像图A、B那么均匀，但是能够做到近似的均匀。

也就是说，把直方图横向平均分成几份之后，使每一份的像素数量大致相等。

下面是一幅图片的直方图，共有19200个像素，从左到右平均分成三份。

均衡化之后，每份的像素数量都在6400左右。

手工调整方法我们拍摄或者扫描的照片往往会由于光线太强或者太弱，使图像对比度减弱，细节分辨不清。