计算机原理(岳乡成)补码加减法运算(公开课)
- 格式:ppt
- 大小:113.50 KB
- 文档页数:9
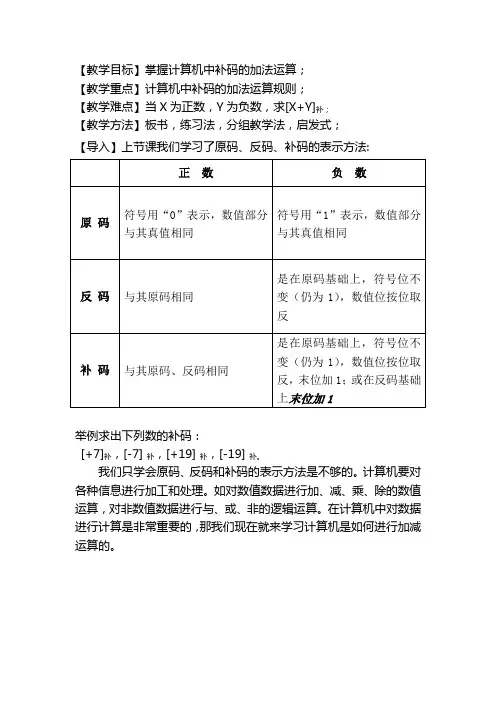
【教学目标】掌握计算机中补码的加法运算;【教学重点】计算机中补码的加法运算规则;【教学难点】当X为正数,Y为负数,求[X+Y]补;【教学方法】板书,练习法,分组教学法,启发式;【导入】上节课我们学习了原码、反码、补码的表示方法:举例求出下列数的补码:[+7]补,[-7]补,[+19]补,[-19]补。
我们只学会原码、反码和补码的表示方法是不够的。
计算机要对各种信息进行加工和处理。
如对数值数据进行加、减、乘、除的数值运算,对非数值数据进行与、或、非的逻辑运算。
在计算机中对数据进行计算是非常重要的,那我们现在就来学习计算机是如何进行加减运算的。
【新课讲授】3.1.1 定点补码的加法运算在计算机中,凡是带符号数一律用补码表示,运算结果自然也是补码。
若结果的符号为“0”表示正数,得到的补码即原码,数值部分前加上“+”号即为真值;若结果的符号为“1”表示负数,得到的是补码,这时如要求真值,需对结果的补码再求补码,变成原码,在数值部分前加上负号才为真值。
补码加法的运算规则为: 即:两数补码的和等于两数和的补码。
想一想 为什么两数补码的和等于两数和的补码?现根据X 、Y 的符号及绝对值的大小分三种情况予以证明 ①X 、Y 均为正数,则其和也为正数,那么 [X]补+[Y] 补=X+Y=[X+Y]补 (mod2n )a 、|X|≥|Y|,则其和在[0,2n-1)之间②X 为正数,Y 为负数b 、|X|≤|Y|,则其和在[-2n-1,0)之间 那么:a 、[X]补+[Y] 补= X+2n +Y= 2n +X+Y= X+Y= [X+Y]补 (mod2n ) b 、[X]补+[Y] 补= X+2n +Y= 2n +X+Y= [X+Y]补 (mod2n ) 例3.1已知X=+0010011B ,Y=-0000111B ,求[X+Y]补 例3.2已知X=+0000111B ,Y=-0010011B ,求[X+Y]补练一练 已知X=+1000010B (+66),Y=-0110011B (-51),求[X+Y]补已知X=+0110011B (+51),Y=-1000010B (-66),求[X+Y]补[][][]补补补Y X Y X +=+③X为负数,Y也为负数,则其和也为负数,那么[X]补+[Y]补= 2n+X+2n+Y= 2n+2n+X+Y= 2n+X+Y= [X+Y]补(mod2n)例3.3已知X=-0011001B,Y=-0000110B,求[X+Y]补综上所述,-2n-1≤X≤2n-1, -2n-1≤Y≤2n-1,且 -2n-1≤X+Y≤2n-1时,下列补码运算公式成立:[X]补+[Y]补= [X+Y]补(mod2n)【教学重点】计算机中补码的减法运算规则。





计算机组成原理--运算⽅法:加减乘除补码加减法补码加法公式:[x+y]补=[x]补+[y]补补码减法:为了将减法转变为加法,需证明公式: [x-y]补=[x]补+[-y]补(证明)为了求得同时[-y]补,需要证明[-y]补=[y]补+2^-n(意义是[-y]补等于[y]补取反,末位加1)溢出检测溢出的检测可能产⽣溢出的情况两正数加,变负数,上溢(⼤于机器所能表⽰的最⼤数)两负数加,变正数,下溢(⼩于机器所能表⽰的最⼩数)定点原码乘法定点乘法原理n位乘n位积可能为2n位.乘积的最后是所有部分积之和,有n个数相加,⽽FA只有两个输⼊端,机器⼀次只能进⾏两个数的相加,不能进⾏多个数据的加法。
⼿⼯计算中,乘数的每⼀位是0还是1都可直接看见,⽽在计算机中,采⽤放乘数的寄存器的每⼀位直接决定本次相加数是被乘数还是0是很不⽅便的,若采⽤该寄存器的最低⼀位来执⾏这种判断就简便了。
计算机中执⾏乘法时,积的符号位由被乘数和乘数的符号位通过⼀个半加器(即异或门)实现。
数值部分的运算规则是:从最低位Y0开始,当乘数Yi为1时,将上次部分积加上被乘数的绝对值,然后右移⼀位,得到新的部分积;当Yi为0时,则写下全0。
然后再对乘数Y的⾼⼀位进⾏类似乘法运算。
重复“加—右移”操作N次,可得到最后的乘积。
R0存放部分积,R2存放被乘数,R1存放乘数R0清零,R2存放被乘数,R1存放乘数。
乘法开始时,“启动”信号时控制CX置1,于是开启时序脉冲T,当乘数寄存器R1最末位为“1“时,部分积Z和被乘数X在加法器中相加,其结果输出⾄R0的输⼊端。
⼀旦控制脉冲T到来,控制信号LDR0使部分积右移1位,与此同时,乘数寄存其R1也在控制信号LDR1作⽤下右移⼀位,且计数器I记数⼀次;将步骤三重复执⾏N次当计数器I=n时,计数器I的溢出信号使控制触法器CX置0,关闭时序脉冲T,乘法宣告结束原码算法存在的缺点:⼀是符号位需要单独运算,最后给运算结构以正确的符号;⼆是对于采⽤补码存储的机器,从存储器中取出的是操作数的补码,需先将其转换成原码,这样很不⽅便,⽽且影响速度。




补码的运算原理补码是一种用来表示有符号数的编码方式。
在计算机中,补码常常用于进行数值运算,因为它能够简化减法运算,并且可以将加法和减法运算统一起来。
补码的运算原理基于两个重要的概念:补码的表示范围和补码的加减法规则。
对于一个n位的补码,其表示的范围为$-2^{n-1}$到$2^{n-1}-1$。
这是由于补码中最高位是符号位,如果它为1,则表示负数,否则为正数。
对于补码的加减法规则,需要根据补码的特性来进行运算。
对于两个补码的加法,只需要将它们相加,并检查最高位是否进位即可。
例如,对于两个4位二进制补码1101和1010的加法,可以按照以下步骤进行:1. 将两个数相加:1101+1010=101112. 检查最高位是否进位:最高位为1,因此表示结果为负数,需要进行补码转换。
将结果的每一位取反,再加上1,即可得到补码结果。
因此,10111的补码为0101。
对于补码的减法,可以将减数取反后再加上1,得到的结果就是减数的补码。
然后将被减数与减数的补码相加,即可得到补码结果。
例如,对于两个4位二进制补码1101和1010的减法,可以按照以下步骤进行:1. 将减数取反并加1得到其补码:1010的补码为0110。
2. 将被减数1101与减数的补码0110相加:1101+0110=100113. 检查最高位是否进位:最高位为1,因此表示结果为负数,需要进行补码转换。
将结果的每一位取反,再加上1,即可得到补码结果。
因此,10011的补码为0111。
补码的运算原理可以帮助我们理解计算机中的数值运算,并且能够帮助我们在编写程序时进行正确的运算。
