动态几何中的面积问题精品PPT课件

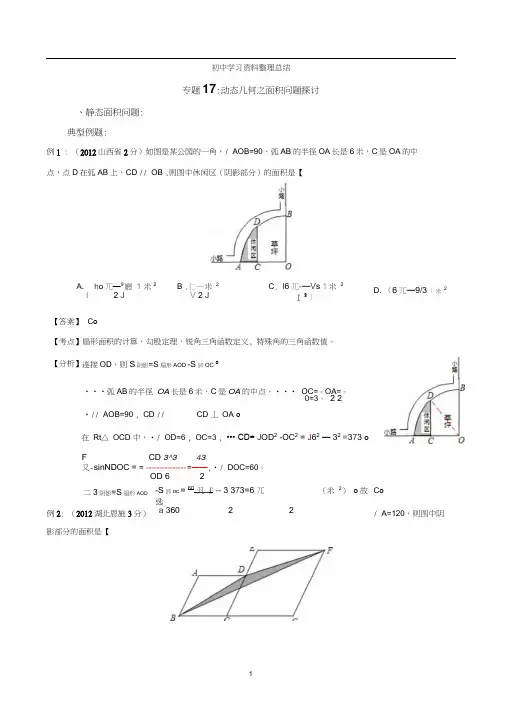
初中学习资料整理总结专题17:动态几何之面积问题探讨、静态面积问题: 典型例题:例1 : （2012山西省2分）如图是某公园的一角，/ AOB=90，弧AB 的半径OA 长是6米，C 是OA 的中 点，点D 在弧AB 上，CD // OB ,则图中休闲区（阴影部分）的面积是【影部分的面积是【A. h o 兀—9廳 1 米2 B .仁—米 2I2 J V 2 JC . I 6兀-—V s 1米 2I 2丿D . （6兀—9/3 ）米 2【答案】 C o【考点】 扇形面积的计算，勾股定理，锐角三角函数定义, 特殊角的三角函数值。

【分析】 连接OD ，则S 阴影=S 扇形AOD -S 卸OC o•••弧AB 的半径 OA 长是6米，C 是OA 的中点，••• OC= - OA= -0=3。

2 2 •// AOB=90 , CD //CD 丄 OA o在 Rt △ OCD 中，•/ OD=6 , OC=3 , ••• CD= J OD 2 -OC 2 = J 62 — 32 =373 oF CD 3^3 43 又-sinNDOC = = --------------- =——,•/ DOC=60。

OD 62-S 卸oc = 60 汎 £ -- 3 373=6 兀 （米 2） o 故选a 360 2 2 如图，菱形ABCD 和菱形ECGF 的边长分别为2和3,二3阴影=S 扇形AODC o例2: （2012湖北恩施3分） / A=120，则图中阴【答案】如图，过点 A 作AD 丄OC 于点D ，过点B 作BE 丄OC 于点E,设 A ( X A , y A ) , B ( X B ,y B ), C (c?0)。

•/ AB : BC=(m 一 I) : 1(m>l)，二 AC : BC=m : 1。

又•••△ ADC sA B EC ，二 AD : BE=DC : EC= AC : BC=m : 1。

抛物线中动态几何图形面积问题（一）
以抛物线为背景考察动态几何图形面积问题是中考压轴或数学学科竞赛当中常常出现的问题，本文结合教学实践以三角形为例说说常用的几种处理方式，与大家分享交流.
方法1：采用割补法，补的方法不唯一，不在阐述.下面说说割的办法（水平宽与铅锤高乘积的一半）.
方法2：本题也可以先采用平移法确定动点的位置，用几何办法解决问题.
方法3：用点到直线距离公式，公式可以补充给学生,满足各层次（尤其是优尖生）学生需求！
方法4：采用行列式计算平面图形（任意凹多边形）面积，可以补充给学生，在考试压轴题或是数学学科竞赛当中遇到复杂动态几何图
形时，上述几种方法又不好表面积时，可以考虑采用行列式的办法.公式如下：
行列式方法解答如下:
实践教学告诉我，优尖生多掌握一些方法，在遇到压轴大题与竞赛当中的动态多边形面积问题更能从容面对.如有阐述不当之处，请各位提出意见！。

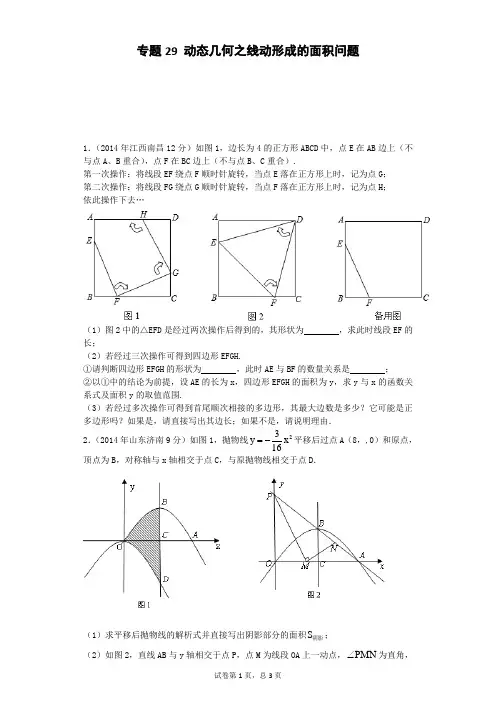
专题29 动态几何之线动形成的面积问题1．（2014年江西南昌12分）如图1，边长为4的正方形ABCD 中，点E 在AB 边上（不与点A 、B 重合），点F 在BC 边上（不与点B 、C 重合）.第一次操作：将线段EF 绕点F 顺时针旋转，当点E 落在正方形上时，记为点G ； 第二次操作：将线段FG 绕点G 顺时针旋转，当点F 落在正方形上时，记为点H ； 依此操作下去…（1）图2中的△EFD 是经过两次操作后得到的，其形状为 ，求此时线段EF 的长；（2）若经过三次操作可得到四边形EFGH.①请判断四边形EFGH 的形状为 ，此时AE 与BF 的数量关系是 ； ②以①中的结论为前提，设AE 的长为x ，四边形EFGH 的面积为y ，求y 与x 的函数关系式及面积y 的取值范围.（3）若经过多次操作可得到首尾顺次相接的多边形，其最大边数是多少？它可能是正多边形吗？如果是，请直接写出其边长；如果不是，请说明理由．2．（2014年山东济南9分）如图1，抛物线23y x 16=-平移后过点A （8，,0）和原点，顶点为B ，对称轴与x 轴相交于点C ，与原抛物线相交于点D ．（1）求平移后抛物线的解析式并直接写出阴影部分的面积S 影阴；（2）如图2，直线AB 与y 轴相交于点P ，点M 为线段OA 上一动点，PMN ∠为直角，边MN 与AP 相交于点N ，设OM t =，试探求：①t 为何值时，△MAN 为等腰三角形？②t 为何值时，线段PN 的长度最小，最小长度是多少？3．（2014年四川凉山12分）如图①，在平面直角坐标中，点A 的坐标为（1，﹣2），点B 的坐标为（3，﹣1），二次函数y=﹣x 2的图象为l 1．（1）平移抛物线l 1，使平移后的抛物线经过点A ，但不过点B ． ①满足此条件的函数解析式有 个．②写出向下平移且经点A 的解析式 ．（2）平移抛物线l 1，使平移后的抛物线经过A ，B 两点，所得的抛物线l 2，如图②，求抛物线l 2的函数解析式及顶点C 的坐标，并求△ABC 的面积．（3）在y 轴上是否存在点P ，使S △ABC =S △ABP ？若存在，求出点P 的坐标；若不存在，请说明理由．4．（2014年四川攀枝花12分）如图，抛物线2y ax 8ax 12a =-+（a ＞0）与x 轴交于A 、B 两点（A 在B 的左侧），与y 轴交于点C ，点D 的坐标为（﹣6，0），且∠ACD=90°．（1）请直接写出A 、B 两点的坐标；（2）求抛物线的解析式；（3）抛物线的对称轴上是否存在点P ，使得△PAC 的周长最小？若存在，求出点P 的坐标及周长的最小值；若不存在，说明理由；（4）平行于y 轴的直线m 从点D 出发沿x 轴向右平行移动，到点A 停止．设直线m 与折线DCA 的交点为G ，与x 轴的交点为H （t ，0）．记△ACD 在直线m 左侧部分的面积为s ，求s 关于t 的函数关系式及自变量t 的取值范围．5．（2014年山西省13分）综合与探究：如图，在平面直角坐标系xOy 中，四边形OABC 是平行四边形，A 、C 两点的坐标分别为（4，0），（﹣2，3），抛物线W 经过O 、A 、C 三点，D 是抛物线W 的顶点．（1）求抛物线W的解析式及顶点D的坐标；（2）将抛物线W和Y OABC一起先向右平移4个单位后，再向下平移m（0＜m＜3）个单位，得到抛物线W′和Y O′A′B′C′，在向下平移的过程中，设Y O′A′B′C′与Y OABC的重叠部分的面积为S，试探究：当m为何值时S有最大值，并求出S的最大值；（3）在（2）的条件下，当S取最大值时，设此时抛物线W′的顶点为F，若点M是x 轴上的动点，点N时抛物线W′上的动点，试判断是否存在这样的点M和点N，使得以D、F、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．6．（2014年陕西省10分）已知抛物线C：y=﹣x2+bx+c经过A（﹣3，0）和B（0，3）两点，将这条抛物线的顶点记为M，它的对称轴与x轴的交点记为N．（1）求抛物线C的表达式；（2）求点M的坐标；（3）将抛物线C平移到C′，抛物线C′的顶点记为M′，它的对称轴与x轴的交点记为N′．如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形，那么应将抛物线C怎样平移？为什么？评卷人得分六、新添加的题型参考答案 1．（1）等边三角形.EF=()2x 24438642=-+=-.（2）①①四边形EFGH 为正方形；AE=BF.②222y 2x 8x 162(x 4x 4)82(x 2)8=-+=-++=-+，y 的取值范围是8＜y ＜16.（3）经过多次操作可得到首尾顺次相接的多边形，其最大边数是8，它可能为正多边形，边长为424-．【解析】（1）根据正方形的性质，证明旋转后得到的两个直角三角形全等，得出AE 和FC 相等，再用勾股定理列出方程即可.（2）①根据旋转的性质可判定四边形EFGH 是正方形，得出AE=BF ；②根据正方形的面积公式，找出AE 长与正方形面积之间的等量关系式.（3）经过多次操作可得到首尾顺次相接的多边形，其最大边数是8，它可能为正多边形，边长为424-．如答图2所示，粗线部分是由线段EF 经过7次操作所形成的正八边形．设边长EF=FG=x ，则BF=CG=2x 2， BC=BF+FG+CG=22x x x 422++=，解得：x=424-．解：（1）等边三角形.∵四边形ABCD 是正方形，∴AD=CD=BC=AB ，∠A=∠B=∠C=90°.∵ED=FD ，∴△ADE ≌△CDF(HL). ∴AE=CF ，BE=BF.∴△BEF 是等腰直角三角形.设BE 的长为x ，则2x ，AE=4x -，∵在Ｒt △AED 中，222AE AD DE +=，DE=EF ，∴())2224 x 42x -+=，解得12x 443,x 443=-+=-- (不合题意，舍去). ∴2x 24438642=-+=-.（2）①四边形EFGH 为正方形；AE=BF.②∵AE=x ，∴BE=4x -.∵在Ｒt △BED 中，222EF BF BE =+，AE=BF ，∴()222222y EF 4x x 168x x x 2x 8x 16==-+=-++=-+.∵点E 不与点A 、B 重合，点F 不与点B 、C 重合，∴0＜x ＜4.∵222y 2x 8x 162(x 4x 4)82(x 2)8=-+=-++=-+，∴当x=2时有最小值8，当x=0或4时，有最大值16.∴y 的取值范围是8＜y ＜16.（3）经过多次操作可得到首尾顺次相接的多边形，其最大边数是8，它可能为正多边形，边长为424-．考点：1.线动旋转问题；2.正方形的判定和性质；3.等边三角形的判定和性质；4.全等三角形的判定和性质；5.勾股定理；6.二次函数的应用．2．（1）233y x x 162=-+ 12 （2）①9t 2=时，△MAN 为等腰三角形. ②故当t ＝3时，PN 取最小值为152． 【解析】（1）根据平移的性质，应用待定系数法即可求出平移后抛物线的解析式；如答图1，过点D 作DE ⊥y 轴于点E ，由()22333y x x x 4316216=-+=--+得顶点B （4，3），则阴影部分的面积等于矩形OCDE 的面积S 影阴=OC ×CB ＝12.（2）①分MN＝AN，AM＝AN，MN＝MA三种情况情况即可.②应用反证法求解即可.解：（1）∵抛物线23y x16=-平移后过原点，∴设平移后抛物线的解析式23y x bx16=-+.将点A（8，,0）代入，得30648b16=-⋅+，解得3b2=.∴平移后抛物线的解析式233y x x162=-+.S影阴＝12.（2）由A（8，,0），B（4，3）可求得直线AB的解析式为3y x64=-+，如答图2，过点N作NQ⊥x轴于点Q，①当MN＝AN时，N点的横坐标为8t2-，纵坐标为243t8-，由△NQM∽△MOP得NQ MQOM OP=,∴243t8t82t6--=，解得9t,82=（舍去）.当AM＝AN时，AN＝8t-,由△ANQ∽△APO得()()348tNQ8t,AQ8t,MQ555-=-=-=，由△NQM∽△MOP得NQ MQOM OP=，∴()38t8t55t6--=，解得：t＝12（舍去）.当MN＝MA时，MNA MAN45∠=∠<︒，∴AMN∠是钝角，显然不成立.综上所述，9t2=时，△MAN为等腰三角形.②如答图2，作PN的中点T，连接TM，则TM＝PT＝21PＮ，当TM垂直于x轴且M为OQ中点时PN最小，此时t＝3，证明如下：假设t＝3时M记为M0，T记为T0，若M不在M0处，即M在M0左侧或右侧，若T在T0左侧或者T在T0处，则TM一定大于00T M而PT却小于PT，这与TM＝PT矛盾，故T在T0右侧，则PT大于PT,相应PN也会增大，故若M不在M0处时 PN大于M0处的PN的值，故当t＝3时，MQ＝3,3NQ=2,根据勾股定理可求出PM＝35与MN352,15PN=2．故当t＝3时，PN取最小值为152．考点：1．二次函数综合题；2．单动点和线动平移问题；3．待定系数法的应用；4．曲线上点的坐标与方程的关系；5．等腰三角形的性质；6．相似三角形的判定和性质；7．直角三角形斜边上中线的性质；8．勾股定理；9．转换思想、分类思想和反证法的应用．3．（1）①无数；②y=﹣x2﹣1.（2）S△ABC=S梯形ABED﹣S梯形BCFE﹣S梯形ACFD=15 16．（3）所求点P的坐标为（0，5516-）或（0，2516-）.【解析】（1）①根据实际情况可以直接写出结果.②设平移以后的二次函数解析式是：y=﹣x2+c，把（1，﹣2）代入即可求得c=﹣1，从而得到函数的解析式：y=﹣x2﹣1.（2）利用待定系数法即可求得函数的解析式；化为顶点式得到点C 的坐标，过点A、B、C 三点分别作x轴的垂线，垂足分别为D、EE、F，求得△ABC的面积.（3）分当点P位于点G的下方和上方，两种情况进行讨论求解．解：（1）①无数；②y=﹣x2﹣1.（2）设l2的解析式是y=x2+bx+c，∵l2经过点A（1，﹣2）和B（3，﹣1），∴1b c 293b c 1-++=-⎧⎨-++=-⎩，解得：9b 211c 2⎧=⎪⎪⎨⎪=-⎪⎩. ∴l 2的解析式是：2911y x x 22=-+-. ∵2291197y x x x 22416⎛⎫=-+-=--- ⎪⎝⎭， ∴顶点C 的坐标是97,416⎛⎫- ⎪⎝⎭ ． 如答图1，过点A 、B 、C 三点分别作x 轴的垂线，垂足分别为D 、E 、F ，则AD=2，CF=716，BE=1，DE=2，DF=54，FE=34． ∴S △ABC =S 梯形ABED ﹣S 梯形BCFE ﹣S 梯形ACFD =1516． （3）存在. 如答图2，3，延长BA 交y 轴于点G ，设直线AB 的解析式为y mx n =+，则m n 23m n 1+=-⎧⎨+=-⎩，解得1m 25n 2⎧=⎪⎪⎨⎪=-⎪⎩. ∴直线AB 的解析式为15y x 22=-. ∴点G 的坐标为（0，52-）. 设点P 的坐标为（0，h ），①当点P 位于点G 的下方时，如答图2，PG=5h 2--，连接AP 、BP ， 则S △ABP =S △BPG ﹣S △APG =()155h 31h 222⎛⎫---=-- ⎪⎝⎭.又∵S△ABC=S△ABP=1516，得h=5516-.∴点P的坐标为（0，5516-）．②当点P位于点G的上方时，如答图3，PG=5h2+，同上可得h=2516-，点P的坐标为（0，2516-）．综上所述，所求点P的坐标为（0，5516-）或（0，2516-）.考点：1.二次函数综合题；2.线动平移问题；3.待定系数法的应用；4.曲线上点的坐标与方程的关系；5.二次函数的性质；6.三角形和梯形面积；7.分类思想、转换思想和方程思想的应用.4．（1）A（2，0），B（6，0）．（2）2343y23=-+（3）存在满足条件的点P，点P坐标为（423，△PAC周长的最小值为443+（4）s关于t的函数关系式为S))22323t636t0323t630t2⎧++-≤≤⎪=⎪++≤⎪⎩＜．【解析】（1）抛物线的解析式为：2y ax8ax12a=-+（a＞0），令y=0，即2ax8ax12a0-+=，解得x1=2，x2=6，∴A（2，0），B（6，0）．（2）由∠ACD=90°可知△ACD为直角三角形，利用勾股定理，列出方程求出a的值，进而求出抛物线的解析式.（3）△PAC的周长=AC+PA+PC，AC为定值，则当PA+PC取得最小值时，△PAC的周长最小．设点C关于对称轴的对称点为C′，连接AC′与对称轴交于点P，由轴对称的性质可知点P即为所求.（4）直线m运动过程中，有两种情形，需要分类讨论并计算，避免漏解．解：（1）A（2，0），B（6，0）．（2）抛物线的解析式为：2y ax8ax12a=-+（a＞0），令x=0，得y=12a，∴C（0，12a），OC=12a．在Rt△COD中，由勾股定理得：()222222CD OC OD12a6144a36=+=+=+；在Rt△COD中，由勾股定理得：()222222AC OC OA12a2144a4=+=+=+；在Rt△COD中，由勾股定理得：DC2+AC2=AD2，即：()()222144a36144a48+++=，解得：a=36或a=36-（舍去）.∴抛物线的解析式为：2343y x x2363=-+．（3）存在．对称轴为直线：433x4326-=-=⋅．由（2）知C（0，23），则点C关于对称轴x=4的对称点为C′（8，23），如答图1，连接AC′，与对称轴交于点P，则点P为所求．此时△PAC周长最小，最小值为AC+AC′．设直线AC′的解析式为y=kx+b，则有：2k b08k b23+=⎧⎪⎨+=⎪⎩3k23b⎧=⎪⎪⎨⎪=⎪⎩.∴直线AC′的解析式为323y=．当x=4时，23y=P（423．过点C′作C′E⊥x轴于点E，则C′E=23，AE=6，在Rt△AC′E中，由勾股定理得：()22AC23643'=+=在Rt△AOC中，由勾股定理得：()22AC2234=+=．∴AC+AC′=443+∴存在满足条件的点P ，点P 坐标为（4，233），△PAC 周长的最小值为443+． （4）①当﹣6≤t≤0时，如答图2．∵直线m 平行于y 轴，∴△DGH ∽△DCO. ∴GH DH OC OD =，即GH 6t 623+=. ∴()3GH 6t 3=+ ∴()()DGH 113S S DH GH 6t 6t 223∆==⋅=+⋅+ 23t 23t 636=++. ②当0＜t≤2时，如答图3．∵直线m 平行于y 轴，∴△AGH ∽△ACO.∴GH AH OC OA =2t 223-=， ∴GH 3t 23=-+∴S=S △COD +S 梯形OCGH()11OD OC GH OC OH 22=⋅++⋅ (21136233t 2323t 23t 6322=⨯⨯+-++⋅=++∴s 关于t 的函数关系式为S ()()223t 23t 636t 063t 23t 630t 22⎧++-≤≤⎪⎪=⎪-++≤⎪⎩＜．考点：1.二次函数综合题；2.轴对称的应用（最短线路问题）；3.线动平移问题；4.勾股定理；5.待定系数法的应用；6.曲线上点的坐标与方程的关系；7.相似三角形的判定和性质；8.由实际问题列函数关系式；9.分类思想的应用．5．解：（1）设抛物线W 的解析式为y=ax 2+bx+c ，∵抛物线W 经过O （0，0）、A （4，0）、C （﹣2，3）三点，∴c 016a 4b c 04a 2b c 3=⎧⎪++=⎨⎪-+=⎩，解得：1a 4b 1c 0⎧=⎪⎪=-⎨⎪=⎪⎩．∴抛物线W 的解析式为21y x x 4=-． ∵()2211y x x x 2144=-=--，∴顶点D 的坐标为（2，﹣1）． （2）由Y OABC 得，CB ∥OA ，CB=OA=4．又∵C 点坐标为（﹣2，3），∴B 点的坐标为（2，3）．如答图1，过点B 作BE ⊥x 轴于点E ，由平移可知，点C′在BE 上，且BC′=m．∴BE=3，OE=2.∴EA=OA ﹣OE=2．∵C′B′∥x 轴，∴△BC′G∽△BEA. ∴BC C G BE EA ''=，即m C G 32'=.∴C′G=2m 3． 由平移知，Y O′A′B′C′与Y OABC 的重叠部分四边形C′HAG 是平行四边形．∴()22233S C G C E m 3m m 3322⎛⎫='⋅'=⋅-=--+ ⎪⎝⎭. ∴当m=32时，S 有最大值为32．（3）存在．点M 的坐标分别为（0，0），（4，0），（6，0），（14，0）．【解析】（1）利用待定系数法求出抛物线的解析式，化为顶点式求出顶点D 的坐标.（2）由平移性质，可知重叠部分为一平行四边形．如答图1，作辅助线，利用相似比例式求出平行四边形的边长和高，从而求得其面积的表达式；然后利用二次函数的性质求出最值. （3）在（2）的条件下，抛物线W 向右平移4个单位，再向下平移32个单位，得到抛物线W′， ∵D （2，﹣1），∴F （6，52-）.∴抛物线W′的解析式为：()215y x 642=--． 设M （t ，0），以D 、F 、M 、N 为顶点的四边形是平行四边形，分点N 在x 轴上方、下方两种情况讨论： ①若点N 在x 轴下方，如答题2所示：过点D 作DP ∥y 轴，过点F 作FP ⊥DP 于点P ，∵D （2，﹣1），F （6，52-），∴DP=32，FP=4. 过点N 作DQ ⊥x 轴于点Q ，由四边形FDMN 为平行四边形，易证△DFP ≌△NMQ ，∴MQ=FP=4，NQ=DP=32.∴N （4+t ，﹣32）. 将点N 坐标代入抛物线W′的解析式()215y x 642=--，得：()2153t 2422--=-， 解得：t=0或t=4，∴点M 的坐标为（0，0）或（4，0）.②若点N 在x 轴上方，（请自行作图）与①同理，得N （4﹣t ，32） 将点N 坐标代入抛物线W′的解析式()215y x 642=--，得：()2153t 10422--=， 解得：t=6或t=14，∴点M 的坐标为（6，0）或（14，0）．综上所述，存在这样的点M 和点N ，点M 的坐标分别为（0，0），（4，0），（6，0），（14，0）．考点：1.二次函数综合题；2.线动平移、面动平移和双动点问题；3.待定系数法的应用；4.曲线上点的坐标与方程的关系；5.二次函数的性质；6.相似三角形的判定和性质；7.平行四边形的判定和性质；8.分类思想的应用．6．（1）2y x 2x 3=--+（2）M （﹣1，4）．（3）上述的四种平移，均可得到符合条件的抛物线C′．【解析】（1）直接把A （﹣3，0）和B （0，3）两点代入抛物线y=﹣x 2+bx+c ，求出b ，c 的值即可．（2）把（1）中抛物线的解析式化为顶点式可得出其顶点坐标．（3）根据平行四边形的定义，可知有四种情形符合条件，如解答图所示．需要分类讨论．解：（1）∵抛物线y=﹣x 2+bx+c 经过A （﹣3，0）和B （0，3）两点，∴93b c 0c 3--+=⎧⎨=⎩，解得b 2c 3=-⎧⎨=⎩．∴此抛物线的解析式为：2y x 2x 3=--+．（2）∵()22y x 2x 3x 14=--+=-++，∴M （﹣1，4）．（3）由题意，以点M 、N 、M′、N′为顶点的平行四边形的边MN 的对边只能是M′N′， ∴MN ∥M′N′且MN=M′N′．∴MN•NN′=16．∴NN′=4．i ）当M 、N 、M′、N′为顶点的平行四边形是▱MN N′M′时，将抛物线C 向左或向右平移4个单位可得符合条件的抛物线C′；ii ）当M 、N 、M′、N′为顶点的平行四边形是▱MNM′N′时，将抛物线C 先向左或向右平移4个单位，再向下平移8个单位，可得符合条件的抛物线C′．∴上述的四种平移，均可得到符合条件的抛物线C′．考点：1.二次函数图象与平移变换；2.曲线上点的坐标与方程的关系；3.二次函数的性质；4.平行四边形的性质；5.分类思想的应用．。