最新北师大版五年级数学下册长方体(一)专题

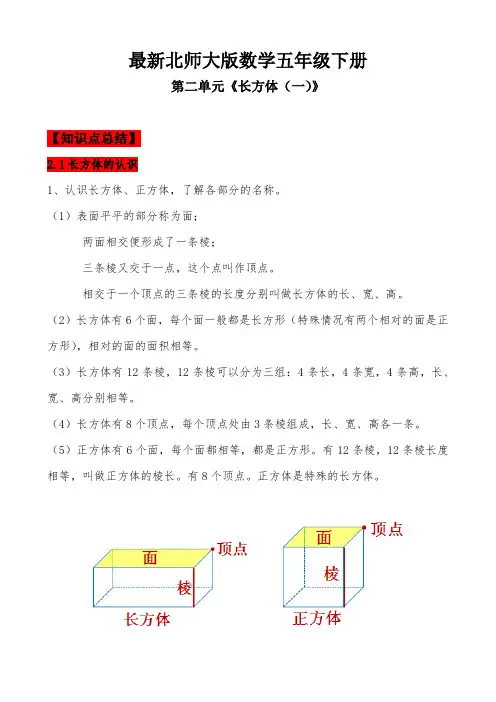
最新北师大版数学五年级下册第二单元《长方体（一）》【知识点总结】2.1长方体的认识1、认识长方体、正方体，了解各部分的名称。

（1）表面平平的部分称为面；两面相交便形成了一条棱；三条棱又交于一点，这个点叫作顶点。

相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。

（2）长方体有6个面，每个面一般都是长方形（特殊情况有两个相对的面是正方形），相对的面的面积相等。

（3）长方体有12条棱，12条棱可以分为三组：4条长，4条宽，4条高，长、宽、高分别相等。

（4）长方体有8个顶点，每个顶点处由3条棱组成，长、宽、高各一条。

（5）正方体有6个面，每个面都相等，都是正方形。

有12条棱，12条棱长度相等，叫做正方体的棱长。

有8个顶点。

正方体是特殊的长方体。

2、长方体、正方体各自的特点。

3、长方体的棱长总和=（长+宽+高）×4，或者是长×4+宽×4+高×4正方体的棱长总和=棱长×122.2展开与折叠正方体的展开图，一共11种。

第一类，中间四连方，两侧各一个，共六种。

第二类，中间三连方，两侧各有一、二个，共三种。

第三类，中间二连方，两侧各有二个，只有一种。

第四类，两排各三个，只有一种。

注意：“田”字型与“凹”字型的是错误的。

2.3长方体的表面积1、表面积的意义：是指六个面的面积之和。

2、长方体表面积的计算方法：长方体上面（或下面）的面积＝长×宽长方体前面（或后面）的面积＝长×高长方体左面（或右面）的面积＝宽×高长方体的表面积＝长×宽×2＋长×高×2 +宽×高×2，用字母表示为：S长 = a×b×2+ a×h×2 +b×h×2或者，长方体的表面积＝（长×宽＋长×高 +宽×高）×2，用字母表示为：S长 = （a×b+ a×h +b×h）×23、正方体表面积的计算方法：正方体每个面的面积＝棱长×棱长。

第二单元长方体（一）-五年级数学下册易错点汇总及优选易错题B卷本单元知识点易错汇总：1.长方体的6个面有时不都是长方形。

2.长方体的长发生变化，这个长方体的左面和右面的大小不变。

3.在长方体中，同一方向的4条棱互相平行。

4.长方体的高=棱长总和÷4-（长+宽）。

5.判断图形折叠后能否围成正方体，除了要具备6个相同的正方形外，还要考虑折叠时6个面是否重复。

6.正方体的棱长扩大到原来的n倍，表面积就扩大到原来的n2倍。

7.用几个相同的正方体拼成一个长方体后，有几个接合处，表面积就减少（接合处的个数×2）个面的面积。

8.在实际生活中，并不是所有的长方体形状的物体都有6个面，如长方体形状的鱼缸、游泳池等只有5个面，长方体形状的烟囱、通风管等只有4个面。

9.相同个数的小正方体摆放的方式不同，露在外面的面的个数一般也不同。

（时间：60分钟，总分：100分）一．选择题（满分16分，每小题2分）1．下图中不可能围成正方体的是()A．B．C．D．2．一个正方体的6个面分别写着1、2、3、4、5、6六个数字，下图是从三个不同角度所看到的图形，这个正方体正确的展开图是()A．B．C．D．3．图中能表示长方体和正方体关系的是()A．B．C．D．4．下面()可以折叠成正方体A．B．C．D．5．一个长方体只有两个相对的面是正方形，这个长方体有()条棱长度相等．A．4B．6C．8D．126．把一个棱长为1米的正方体切成两个完全相同的长方体，表面积将增加多少平方米？( )A．0.5B．1C．27．一个长26cm、宽18cm，高0.6cm的长方体物体，它可能是()A．黑板擦B．橡皮C．数学书8．装修工人把三块玻璃拼在一起装饰墙面，求三块玻璃的总面积，下列等式成立的是() A．535254(555)324⨯+⨯+⨯=++⨯⨯⨯B．535254(324)5⨯+⨯+⨯=++⨯C．5352545324⨯+⨯+⨯=⨯⨯⨯D．535254(555)(324)⨯+⨯+⨯=++⨯++二．填空题（满分16分，每小题2分）9．在一个长方体中，相交于同一顶点的三条棱长之和是30厘米，则这个长方体的棱长总和是厘米．10．将五本长15厘米，宽10厘米，厚4厘米的新华字典包在一起，至少需要平方厘米的包装纸。

五年级数学下册典型例题系列之第二单元长方体（一）的表面积提高部分（原卷版）编者的话：《五年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的，该系列主要包含典型例题和专项练习两大部分。

典型例题部分是按照单元顺序进行编辑，主要分为计算和应用两大部分，其优点在于考题典型，考点丰富，变式多样。

专项练习部分是从常考题和期末真题中选取对应练习，其优点在于选题经典，题型多样，题量适中。

本专题是第二单元长方体（一）的表面积提高部分。

本部分内容考察长方体和正方体的表面积的增减变化及不规则立体图形的表面积，考点和题型难度稍大，建议作为本章核心内容选择性进行讲解，一共划分为十个考点，欢迎使用。

【考点一】正方体表面积的增减变化：切片问题。

【方法点拨】1.表面积的增减变化问题主要有三种，一种是切片问题，表面积会相应增加，一种是拼接问题，表面积会相应减少，一种是高的变化引起的表面积变化。

2.切片问题，即切一刀多两个切面，沿着不同的方向切，多出的表面积一般是不一样的，但正方体比较特殊，它的表面积的增减变化都是都是正方形在进行变化，相对比较简单。

3.刀数×2=切面个数。

【典型例题】把一个棱长是2cm的正方体切成两个完全一样的长方体后，表面积比原来增加了（）平方厘米，每个小长方体的表面积是（）平方厘米。

【对应练习1】一个正方体的棱长是4厘米，把它切成两个完全相同的长方体后，表面积增大（）平方厘米，每个长方体的表面积是（）平方厘米，两个长方体的表面积和是（）平方厘米。

【对应练习2】把一个棱长是5分米的正方体木块锯成两个完全一样的长方体，表面积比原来增加了（）平方分米，每个小长方体的表面积是（）平方分米。

【对应练习3】一个正方体的表面积是20平方厘米，将它切成8个一样大小的小正方体，每个小正方体的表面积是多少平方厘米？【对应练习4】一个正方体形状的木块，棱长为1m，沿着水平方向将它锯成3片，每片又按任意尺寸锯成4条，每条再按任意尺寸锯成5小块，共得到大大小小的长方体60块，如图所示。

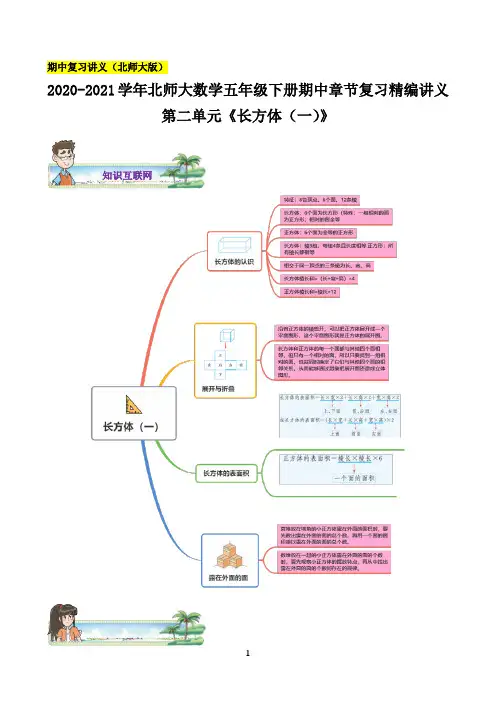
期中复习讲义（北师大版）2020-2021学年北师大数学五年级下册期中章节复习精编讲义第二单元《长方体（一）》知识互联网知识导航知识点一：长方体的认识1 长方体和正方体的各部分名称：在长方体或正方体中，围成的长方形或正方形叫作长方体或正方体的面；面和面相交的边叫作棱；棱和棱相交的点叫作顶点。

2 长方体和正方体的特征3 长方体和正方体的异同点4 长方体和正方体的关系：正方体可以看成是长、宽、高都相等的特殊的长方体5 长方体和正方体特征的应用：判断所给图形能否组成长方体，可以根据长方体的特征一组一组地进行寻找，看看能否找到3组相对应的面。

知识点二：展开与折叠1 正方体展开图的特点（1）沿着正方体的棱剪开，可以把正方体展开成一个平面图形，这个平面图形就是正方体的展开图。

在展开图中，正方体的6个面是相连的，相对的面完全隔开。

（2）将展开图沿虚线（折痕）向内折，能重新折叠成正方体。

（3）正方体的展开图是由6个大小、形状完全相同的正方形组成的组合图形。

（4）正方体的展开图，可分四个类型错误!“一四一”型：中间四个正方形相连，两侧各一个错误!“二三一”型：中间三个正方形相连，两侧分别是两个和一个错误!“二二二”型：中间两个正方形相连，两侧各两个错误!“三三”型：两侧各三个2 长方体展开图的特点：长方体相对的面大小、形状完全相同，并且相对的面完全隔开；长方体上、下两个面的面积相等，长和宽分别是长方体的长和宽；前、后两个面的面积相等，长和宽分别是长方体的长和高；左、右两个面的面积相等，长和宽分别是长方体的宽和高。

3长方体和正方体与展开图之间的对应关系（1）长方体和正方体的每一个面都与其他四个面相邻，但只有一个相对的面，所以只要找到一组相对的面，也就同时确定了它们与其他四个面的相邻关系，从而能够通过想象把展开图还原成立体图形。

（2）判断一个图形折叠后相对应的面，可以根据长方体、正方体展开图的特点，先确定一个面为下面，再想象折叠的过程，从而找出相对的面，也可以用实物折一折，直观地找一找。

小学数学长方体（一）练习题一．选择题（共25小题）1．如图所示的立方体，如果把它展开，可以是下列图形中的（）A．B．C．D．2．一个立方体的六个面上分别标上了数1点、2点、3点、4点、5点、6点，下图是从三个不同角度观察到的情况．“3点”这一面相对的面是（）A．2点B．4点C．6点或4点3．一个长方体的底是面积为3平方米的正方形，它的侧面展开图正好是一个正方形，这个长方体的侧面积是（）平方米．A．18B．48C．544．有一个长方体，它有一组相对的面是正方形，其余4个面的面积（）A．不一定相等B．一定不相等C．一定相等D．无法确定5．一个长方体长6dm，宽5dm，高3dm，这个长方体的棱长总和是（）A．14dm B．28dm C．56dm D．50dm6．正方体棱长扩大2倍，它的底面积扩大（）倍．A．2B．4C．87．下面图形不是正方体展开图的是（）A．B．C．D．8．把一个棱长为4厘米的正方体，分割成两个长方体，这两个长方体表面积总和是（）平方厘米．A．64B．128C．80D．969．如图能围成正方体的是（）A．B．C．D．10．要把7本长20厘米，宽10厘米，高1厘米的数学课本包装在一起，下面组合方法最节省包装纸的是（）A．B．C．11．一个长方体的底面是面积为4平方米的正方形，它的侧面展开图正好也是一个正方形，这个长方体的侧面积是（）平方米．A．16B．64C．48D．2412．把6个棱长为2厘米的正方体排成一排拼成一个长方体，这个长方体的表面积是（）平方厘米．A．96B．26C．50D．10413．从由8个棱长是1厘米的小正方体拼成的大正方体中拿去1个小正方体（如图），这时它的表面积是（）平方厘米。

A．24B．18C．2814．如图是一个长方体的展开图，围成长方体时，点A将与点（）重合。

A．G B．B C．C D．E15．用相同的方式包装两个大小不同的正方体礼盒（打结处不计），大礼盒的棱长是小礼盒棱长的2倍，包装大礼盒与小礼盒用去彩带的长度比、用去包装纸的面积比分别是（）A．2：1；8：1B．4：1；6：1C．2：1；4：116．一个长方体的底面周长是20厘米，左面面积是20平方厘米，前面面积是30平方厘米，则下面面积是（）平方厘米。

北师大版五年级下册数学第二单元长方体（一）应用题训练1．赵叔叔用60cm长的铁丝正好做成了一个正方体框架，在这个正方体框架的表面糊上一层彩纸，至少需要多少平方厘米的彩纸？2．一个长方体的食品盒，长9cm，宽5cm，高4cm，如果围它贴一圈商标纸（上、下面不贴），这张商标纸的面积至少需要多少cm2？3．一个长方体木箱，长10dm，宽8dm，高6dm，做这个木箱至少需要木板多少dm24．妈妈给奶奶买了一件母亲节礼物，她用丝带把礼物按照如图的方法捆扎，打结处需要45厘米的丝带。

捆扎这个礼物一共需要多少厘米的丝带？5．有一种通风管的横截面周长是100厘米的正方形，每节通风管的长度是2米，做25节这样的通风管至少需要多少平方米铁皮？6．一间教室长12米，宽8米，高4米，黑板及门窗面积为26平方米，要粉刷四壁和顶棚（黑板、门窗和地面不刷），一共要粉刷多大面积？若每平方米用涂料0.25千克，一共需要涂料多少千克？7．学校计划对各班教室的天花板和四壁重新进行粉刷。

五（1）班教室的长、宽、高分别是8米、6米、3.5米，门窗和黑板的面积一共是16平方米。

五（1）班教室需要粉刷多少平方米？8．一个长方体罐头盒，长6厘米，宽8厘米，高8厘米。

在它的四周贴上一圈商标纸（接头处不计），这张商标纸的面积至少有多少平方厘米？9．将8个棱长为2厘米的小正方体礼盒包装成一个大礼盒，包装纸至少要多少平方厘米？（先想一想，画出草图，再解答）10．用棱长1厘米的小正方体木块拼成一个大正方体模型。

（1）至少用多少块小正方体木块？（2）拼成的大正方体模型表面积是多少平方厘米？11．一个新建的游泳池长50m，宽25m，深2.5m。

现要在游泳池的四周和底面贴上瓷砖，一共需要贴多少平方米的瓷砖？12．一个长方体玻璃鱼缸（无盖），长9dm，宽6dm，高7dm，做一个这样的鱼缸需要多大面积的玻璃？13．一个长方体的棱长和是124cm，高是8cm，宽是5cm，这个长方体的长是多少厘米？14．一个长方体的棱长总和是40厘米，其中长是5厘米，宽是3厘米，高是多少厘米？15．一个长方体形状的露天水池，长20米，宽10米，深4米，如果在这个水池的四周和底面铺上边长是2分米的正方形瓷砖，至少需要多少块瓷砖？16．一种长方体铁皮通风管长3米，管口是边长为4厘米的正方形，做100根这样的通风管，至少需要多少平方米的铁皮？17．饼干盒的长和宽都是10cm，高是15cm，要在盒子的四周贴上商标，印制1000张这样的商标，至少需要纸多少平方米？18．粉刷一间教室，从里面量，教室长6.5米，宽5.6米，高3米。