下载文档原格式
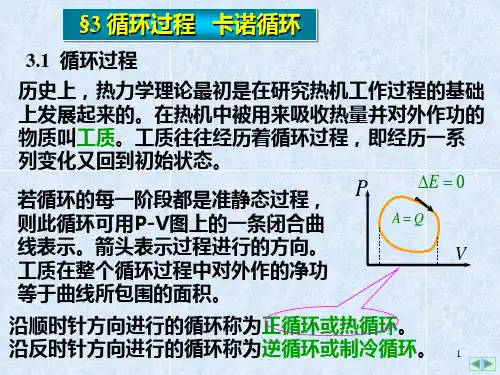
卡诺循环的四个过程公式卡诺循环是一种理想热机循环，以理论上最高效率进行工作。
它由两个等温过程和两个绝热过程组成，以下将详细介绍卡诺循环的四个过程公式。
一、等温膨胀过程公式在卡诺循环中的第一个过程是等温膨胀过程。
在这个过程中，工作物质与高温热源接触并吸收热量，同时保持温度不变。
根据热力学定律，等温膨胀过程的功率和热量之间的关系可以用以下公式表示：Q1 = W12其中，Q1是从高温热源吸收到的热量，W12是在等温膨胀过程中由该热量产生的功。
二、绝热膨胀过程公式在卡诺循环中的第二个过程是绝热膨胀过程。
在这个过程中，工作物质与绝热墙隔离，不受外界热量交换的影响，但可以对外做功。
根据绝热过程的能量守恒定律，绝热膨胀过程的功率和初始末态温度之间的关系可以用以下公式表示：T2 * S2 = T1 * S1其中，T1是等温膨胀过程初始的温度，T2是绝热膨胀过程末态的温度，S1和S2分别是初始和末态时的熵。
三、等温压缩过程公式在卡诺循环中的第三个过程是等温压缩过程。
在这个过程中，工作物质与低温热源接触并释放热量，同时保持温度不变。
根据热力学定律，等温压缩过程的功率和热量之间的关系可以用以下公式表示：Q2 = W34其中，Q2是向低温热源释放的热量，W34是在等温压缩过程中由该热量产生的功。
四、绝热压缩过程公式在卡诺循环中的第四个过程是绝热压缩过程。
在这个过程中，工作物质与绝热墙隔离，不受外界热量交换的影响，但可以对外做功。
根据绝热过程的能量守恒定律，绝热压缩过程的功率和初始末态温度之间的关系可以用以下公式表示：T4 * S4 = T3 * S3其中，T3是等温压缩过程初始的温度，T4是绝热压缩过程末态的温度，S3和S4分别是初始和末态时的熵。
综上所述，卡诺循环的四个过程（等温膨胀、绝热膨胀、等温压缩、绝热压缩）在热力学定律和绝热过程能量守恒定律的基础上，可以用一系列公式来表示各个过程中的功率和热量之间的关系。
这些公式提供了研究和分析卡诺循环的重要工具，帮助我们理解和应用卡诺循环的原理和性质。
卡诺循环的四个过程公式卡诺循环是热机中最理想的循环之一，它由四个过程组成，分别是绝热压缩、等温膨胀、绝热膨胀和等温压缩。
在这篇文章中，我们将详细介绍卡诺循环的四个过程公式，并对每个公式进行解释和应用。
1. 绝热压缩过程公式绝热压缩过程是卡诺循环中的第一个过程，此时气体被绝热墙隔离，并通过外界对其进行压缩，使其体积减小。
绝热压缩过程的公式如下：$$PV^γ = 常数$$其中，P代表气体的压力，V代表气体的体积，γ代表绝热指数或比热容比。
绝热指数是气体的性质参数，取决于气体的分子构成和结构，对于理想气体，γ为常数，通常取1.4。
2. 等温膨胀过程公式等温膨胀过程是卡诺循环的第二个过程，此时气体与热源接触，通过吸热使其膨胀。
等温膨胀过程的公式如下：$$PV = 常数$$在等温膨胀过程中，气体的压力和体积成反比，即当压力增加时，体积减小，反之亦成立。
由于与热源保持等温接触，气体内能的增加和外界对气体所做的功在这个过程中相互平衡。
3. 绝热膨胀过程公式绝热膨胀过程是卡诺循环的第三个过程，此时气体再次与绝热墙隔离，并通过外界膨胀，使其体积增大。
绝热膨胀过程的公式与绝热压缩过程相同：$$PV^γ = 常数$$在绝热膨胀过程中，气体的压力和体积呈指数关系，即当压力增加时，体积也随之增加，反之亦成立。
4. 等温压缩过程公式等温压缩过程是卡诺循环的第四个过程，此时气体再次与热源接触，通过放热使其压缩。
等温压缩过程的公式与等温膨胀过程相同：$$PV = 常数$$在等温压缩过程中，气体的压力和体积成正比，即当压力增加时，体积也随之减小，反之亦成立。
由于与热源保持等温接触，气体内能的减少和外界对气体所做的功在这个过程中相互平衡。
总结卡诺循环的四个过程公式分别是绝热压缩过程公式($PV^γ = 常数$)，等温膨胀过程公式 ($PV = 常数$)，绝热膨胀过程公式($PV^γ = 常数$)和等温压缩过程公式 ($PV = 常数$)。
卡诺循环的四个过程公式卡诺循环是热力学领域的一个重要概念，用于描述热机的理论效率。
卡诺循环包含四个过程，分别是绝热膨胀、等温膨胀、绝热压缩和等温压缩。
在这篇文章中，我们将探讨这四个过程，并提供相应的数学公式来描述它们。
1. 绝热膨胀在卡诺循环的第一个过程中，气体在绝热条件下进行膨胀。
在绝热膨胀过程中，热机从外部不接触任何热源或热池，也没有热量传递给外部环境。
这意味着绝热膨胀过程中没有热量转移，只有功对外界做功。
绝热膨胀的过程可以用以下公式表示：\[ Q = 0 \]其中，Q表示热量转移。
2. 等温膨胀在卡诺循环的第二个过程中，气体在恒定温度下进行膨胀，也称为等温过程。
在等温膨胀过程中，气体与外界保持热平衡，温度不变，从高温热源吸热并对外界做功。
等温膨胀的过程可以用以下公式表示：\[ \frac{Q}{T_H} = -W \]其中，Q表示从高温热源吸收的热量，TH表示高温热源的温度，W表示对外界做的功。
3. 绝热压缩在卡诺循环的第三个过程中，气体在绝热条件下进行压缩。
在绝热压缩过程中，热机从外部不接触任何热源或热池，也没有热量传递给外部环境。
这意味着绝热压缩过程中没有热量转移，只有外界对热机做功。
绝热压缩的过程可以用以下公式表示：\[ Q = 0 \]其中，Q表示热量转移。
4. 等温压缩在卡诺循环的第四个过程中，气体在恒定温度下进行压缩，也称为等温过程。
在等温压缩过程中，气体与外界保持热平衡，温度不变，将热量传递给低温热源。
等温压缩的过程可以用以下公式表示：\[ \frac{Q}{T_L} = W \]其中，Q表示向低温热源释放的热量，TL表示低温热源的温度，W 表示对热机做的功。
综上所述，卡诺循环的四个过程公式为绝热膨胀过程中的\(Q=0\)，等温膨胀过程中的\(\frac{Q}{T_H}=-W\)，绝热压缩过程中的\(Q=0\)，等温压缩过程中的\(\frac{Q}{T_L}=W\)。
这些公式描述了卡诺循环中各个过程中的热量转移和对外界的功，是热力学研究中的重要工具。
卡诺循环的四个过程公式卡诺循环是热力学中一个重要的循环过程，用来描述热机的理想工作原理。
它由四个过程组成，分别是绝热膨胀、等温膨胀、绝热压缩和等温压缩。
下面将详细介绍卡诺循环的四个过程和相应的公式。
1. 绝热膨胀（ADIABATIC EXPANSION）绝热膨胀过程是指在不与外界交换热量的情况下，系统从高温状况下膨胀至低温状态。
这一过程中系统不进行热传导和热交换，只进行功的转换。
根据理想气体状态方程PV^γ = 常数（γ为比热容比），绝热过程的理想气体功公式为：W_ad = (P_1V_1 - P_2V_2)/(γ - 1)其中， W_ad 表示绝热过程所做的功, P_1 和 V_1 表示初始状态下的压力和体积，P_2 和 V_2 表示终态下的压力和体积。
2. 等温膨胀（ISOCHORIC EXPANSION）等温膨胀过程是指在恒温条件下，系统从高温状态膨胀至低温状态。
这一过程中系统与外界交换热量，但不进行功的转换。
根据理想气体状态方程 PV = nRT，等温过程中热量 Q 的转移公式为：Q = nRΔTln(V_2/V_1)其中， Q 表示等温过程中的热量转移量， n 表示气体的摩尔数， R 表示理想气体常数，ΔT 表示温度差， V_1 和 V_2 表示初始状态下的体积和终态下的体积。
3. 绝热压缩（ADIABATIC COMPRESSION）绝热压缩过程是指在不与外界交换热量的情况下，系统从低温状态进行压缩至高温状态。
与绝热膨胀相似，绝热压缩过程中也不进行热传导和热交换，只进行功的转换。
绝热过程的理想气体功公式与绝热膨胀过程相同。
W_ad = (P_2V_2 - P_1V_1)/(γ - 1)其中， W_ad 表示绝热过程所做的功, P_1 和 V_1 表示初始状态下的压力和体积，P_2 和 V_2 表示终态下的压力和体积。
4. 等温压缩（ISOCHORIC COMPRESSION）等温压缩过程是指在恒温条件下，系统从低温状态压缩至高温状态。
卡诺循环的四个过程公式卡诺循环是热力学中的一个理想循环模型，用来描述热机的性能。
它由四个过程组成，分别是等温膨胀、绝热膨胀、等温压缩和绝热压缩。
每个过程都有对应的公式，下面将逐一介绍。
1. 等温膨胀过程等温膨胀是指在热机中，工作物质与热源保持恒温接触的过程。
根据理想气体状态方程，等温膨胀的关系式为：PV = 常数。
其中，P表示系统的压力，V表示系统的体积。
2. 绝热膨胀过程绝热膨胀是指在热机中，工作物质没有与外界交换热量的过程。
根据绝热过程的特性，绝热膨胀的关系式为：PV^γ = 常数。
其中，γ表示气体的绝热指数，取决于工作物质的性质。
3. 等温压缩过程等温压缩是指在热机中，工作物质与冷源保持恒温接触的过程。
与等温膨胀类似，等温压缩的关系式也为：PV = 常数。
4. 绝热压缩过程绝热压缩是指在热机中，工作物质没有与外界交换热量的压缩过程。
根据绝热过程的特性，绝热压缩的关系式为：PV^γ = 常数。
卡诺循环通过这四个过程的组合，将热量转化为机械功，达到最高效率。
它是热动力学中的理想模型，用于评估真实热机的性能。
卡诺循环的效率由以下公式给出：η = (T1 - T2) / T1其中，η表示卡诺循环的效率，T1表示高温热源的温度，T2表示低温热源的温度。
这个公式表明，在给定热源温度的情况下，卡诺循环的效率仅取决于两个热源之间的温差。
需要注意的是，卡诺循环是一个理想模型，不考虑摩擦、传热损失等实际因素，因此其效率是无法达到的上限。
总结：卡诺循环的四个过程公式如下：1. 等温膨胀过程：PV = 常数2. 绝热膨胀过程：PV^γ = 常数3. 等温压缩过程：PV = 常数4. 绝热压缩过程：PV^γ = 常数卡诺循环通过这四个过程的组合，实现了最高效率的热机工作。
其效率仅取决于两个热源之间的温差。
需要注意的是，卡诺循环是一个理想模型，不考虑实际因素，因此其效率是无法达到的上限。
卡诺循环的四个过程公式卡诺循环是热力学中的一个重要概念，它描述了理想热机的工作原理。
卡诺循环包括四个过程，分别是等温膨胀过程、绝热膨胀过程、等温压缩过程和绝热压缩过程。
本文将详细介绍卡诺循环的四个过程，并给出每个过程的数学公式。
一、等温膨胀过程等温膨胀是卡诺循环的第一个过程，也是一个重要的步骤。
在等温膨胀过程中，系统与热源接触并吸热，温度保持不变。
这个过程可以用以下公式表示：Q1 = nRTln(V2/V1)其中，Q1代表系统从热源吸收的热量，n代表物质的摩尔数，R代表气体常数，T代表热源的温度，V1和V2分别代表起始和终止状态下的体积。
二、绝热膨胀过程绝热膨胀是卡诺循环的第二个过程，也是影响循环效率的重要步骤。
在绝热膨胀过程中，系统与外界不进行能量交换，即没有热量传入或传出。
根据热力学第一定律，绝热过程中气体的内能保持不变。
这个过程可以用以下公式表示：W1 = C_v(T1 - T2)其中，W1代表系统所做的功，C_v代表比热容，T1和T2分别代表起始和终止状态下的温度。
三、等温压缩过程等温压缩是卡诺循环的第三个过程，与等温膨胀过程相反，系统从工作物质中释放热量并传递给冷源。
这个过程可以用以下公式表示：Q2 = nRTln(V3/V4)其中，Q2代表系统向冷源释放的热量，n代表物质的摩尔数，R代表气体常数，T代表冷源的温度，V3和V4分别代表起始和终止状态下的体积。
四、绝热压缩过程绝热压缩是卡诺循环的最后一个过程，与绝热膨胀过程相反，系统不与外界交换能量。
这个过程可以用以下公式表示：W2 = C_v(T4 - T3)其中，W2代表系统所做的功，C_v代表比热容，T4和T3分别代表起始和终止状态下的温度。
以上就是卡诺循环的四个过程公式。
通过以上公式，我们可以计算出每个过程中的热量变化和做功情况，进而分析循环的性能和效率。
卡诺循环作为理想热机，为热力学的发展做出了重要贡献，也为实际热机的设计和优化提供了理论基础。
