高等光学答案最终PDF版

10.4如图，以光线射入镜面间并反射n 次，最后沿入射时的光路返回，试写出i θ与α间的关系表达式。

解：最后的反射之后，其对另一镜的入射角应为0。

最后（第n 次）的反射角为αθ=n ，第n-1次的反射角为αθ21=-n 。

相邻的两次反射间，有关系式，απθπθ-=-+-2/)2/(1m m ，即αθθ+=-m m 1。

则ααθαθθn n m n m =+-=+-=)1()1(1。

10.5证明：当一条光线通过平板玻璃时，出射光线方向不变，只产生侧向平移。

当入射角1i 很小时，位移t i nn x 11-=∆。

其中，n 为玻璃的折射率，t 为玻璃板的厚度。

证：如图，由于上下两面平行，且两侧折射率相等，所以在下表面的入射角等于上表面的折射角，下表面的折射角等于上表面的入射角。

出射光线保持平行。

2212121221cos /)sin cos cos (sin )sin()cos /()sin(i i i i i t i i i t i i AB BC x -=-=-==∆)cos sin cos (sin 2111i n i i i t -=，在小角度时，有11sin i i ≈，211)2(1cos i i -≈，222)2(1cos i i -≈则)1(])2(1)2(1[)cos sin cos (sin 1222112111-≈---≈-n n ti i in n ti i n i i i t ，即t i n n x 11-=∆ 10.19cm nvf R v u R v u 5.22,2,,211===+∞==+ 10.23 n=210.32 题目有误 9cm 改为9m1.3, 在玻璃中z 方向上传播的单色平面波的波函数为)]}65.0(10[exp{10),(152czt i t P E -⨯-=π 式中c 为真空中的光速，时间以s 为单位，电场强度以V/m 为单位，距离以m 为单位，试求：（1）光波的振幅和时间频率；（2）玻璃的折射率；（3）z 方向的空间频率；（4）在xz 平面内与x 轴成450角方向上的空间频率。

1.4在光学中场量()t r E , 和()t r H ,的表达方法有许多种，分别推倒采用以下三种表达方式时平均光强的计算公式。

（1）设场量表示为()()t j e r E t r E ω-= 0,，()()tj e r H t r H ω-= 0,（2）设场量表示为()()..21,0c c e r E t r E t j +=-ω ，()()..21,0c c e r H t r H t j +=-ω（3）设场量表示为()()..,0c c e r E t r E t j +=-ω ，()()..,0c c e r H t r H t j +=-ω解：（1）电场强度和磁场强度乘积的大小为：()()()()()00002200000000011R e ,R e ,221 =41 =R e 2j t j t j tj t j tj t E r t H r t E e E e H e H e E H e E H E H E H eE ωωωωωω-*-*-****-⎡⎤⎡⎤=+∙+⎣⎦⎣⎦+++ ()()2000R e j t H e E H ω-*⎡⎤+⎣⎦ S E H =⨯在上式中出现了两个场量相乘的情况，所以()001R e 2I S E H *==⨯（2）(),E r t 和(),H r t均以实数表示，有()()()()()()()()000020000,,1111 222211 R e R e 22j t j t j t j t j tS E r t H r t E r e E r e H r e H r e E H e E H ωωωωω-*-*-*=⨯⎡⎤⎡⎤=+⨯+⎢⎥⎢⎥⎣⎦⎣⎦=⨯+⨯取时间平均值得()001R e 2I S E H *==⨯（3）(),E r t 和(),H r t均以实数表示，有()()()()()()()()000020000,, 2R e 2R e j t j t j t j t j t S E r t H r t E r e E r e H r e H r e E H e E H ωωωωω-*-*-*=⨯⎡⎤⎡⎤=+⨯+⎣⎦⎣⎦=⨯+⨯取时间平均值得()002R eI S E H*==⨯1.7 设一个偏振态与下列偏振态正交：()⎥⎦⎤⎢⎣⎡=-θθδθδsincos,jeJ（1）求该偏振态的琼斯矩阵表示。

1 1 0 1 1 1 = 2 − 1 2 0 − j− j
这正是一个偏振方向与 x 轴成 − 45 角的线偏振光， 它能够通过透光轴与 x 轴成 − 45 角的偏 振器。
2
tan θ o no = tan θ e n e
5-3（1）一右旋圆偏振光在通过 1/2 波片以后变成一个左旋圆偏振光，求此 1/2 波片的ቤተ መጻሕፍቲ ባይዱ 斯矩阵表示。
（2）快轴沿 x 方向的 1/4 波片，其琼斯矩阵为 1 0 ，一线偏振光的偏振方向与 x 轴的 0 j
交角为 45 ，求此线偏振光经过上述 1/4 波片后的偏振态。若入射至上述 1/4 波片的光 是一左旋圆偏振光，结果又如何？ （3） 用快轴沿 y 轴的 1/4 波片和透光轴与 x 轴成-45 角的偏振器组合在一起, 就构成了 一个只让入射的右旋圆偏振光通过的装置，试证明这一结论。 解： （1）由讲义第一章中表 1-2，入射的右旋圆偏振光电矢量的列矩阵为 E i =
2016高等光学第5次作业答案
解： （5.2 节）
解：D 与 E 之间的夹角等于 S 与 k 之间的夹角。推导参考 5.2.4 节
最后的结果为
解：
证明：参考 5.4.2 节 o 光折射满足折射定律
n o sin θ o = n1 sin θ1 (θ1为入射角) tan θ o = n1 / no sin θ1 1 − ( n1 / no sin θ1 )
因此有
1 1 1 J 11 = 2 J 21 2 j
1 0 J = 0 − 1
它是一个快轴沿 x 轴或 y 轴的 1 2 波片。
E tx 1 1 0 1 1 1 （2） = = 2 0 j 1 2 j E ty

3.3. 空间相干性和时间相干性指的是什么？如何量度？光源的角宽度和相干孔径角是如何定义的？证明相干长度 Lc = λ2/∆λ。

答：空间相干性是指光场中不同两点在同一时刻的相干程度。

时间相干性是指同一点在不同时刻的相干程度。

空间相干性的度量是采用相干面积进行度量。

时间相干性是采用相干时间或相干长度进行度量。

光源的角宽度定义为0a d λ=，d0是使得条纹可见的光源最大宽度。

相干孔径角定义为22c pλθ=。

证明：多色光源的干涉场分布的条纹可见度有：sin()22kl K kl ∆=∆ 当2klπ∆=条纹不可见，此时有： 2122l k λλπλλλ==∆∆∆证毕。

3.12.(1)当把一单色点光源放在一会聚透镜物空间焦点上, 观察屏与透镜空间焦面重合, 则观察到夫琅和费圆孔衍射图样。

现在将光源换为圆状准单色初级光源, 圆中心在光轴上, 圆面垂直于光轴, 要想仍获得夫琅和费圆孔衍射图样, 对光源大小。

频宽以及透镜直径应有什么限制? 答：这里可以认为光源在透镜前表面的场的相干性决定了衍射图样。

首先光源的频宽应该保证准单色有νν∆，光源宽度应保证相干面积大于透镜宽度，有L fd aλ<，dL 为透镜直径，a 为光源直径，f 是透镜焦距。

(2)在衍射计实验中, 光源不是单色点光源, 但仍引用夫琅和费圆孔衍射的结果,即取I Q I Q J u uu a ()()()()(()),sin 121222===πλφ根据(1)的结果, 试说明为什么可以如此处理?答：只要光源足够小，保证了其在屏处的相干面积大，同时圆孔本身面积远小于相干面积，加上光源准单色条件，即可认为屏幕上两孔光场依然具有足够的相干性，因此可以用夫琅和费圆孔衍射的结果。

3.1.已知太阳的表观角直径为0.5。

平均有效波长为6000A, 求阳光的相干面积。

解：由L zd aλ=，根据角直径定义，有2tan(0.25)0.00873az=≈ 因此可得相干线度为：68.7um ，相干面积4723um 2. 3.9.阻尼振子的辐射场中某点复扰动为V t A t t i t t t ()exp(/)exp()=--><⎧⎨⎩10200φπν式中t 1是自发辐射寿命。

第十七章光的干涉一. 选择题1.在真空中波长为的单色光，在折射率为n的均匀透明介质中从月沿某一路径传播到氏若儿万两点的相位差为3 ,则路径初的长度为：（D ）A. 1・ 5B. 1. onC. 3D. 1.5 /n解: △卩=二-nil = 3/r所以d= 1.52/n本题答案为D。

2.在杨氏双缝实验中, 若两缝之间的距离稍为加大，英他条件不变，则干涉条纹将(A)A. 变密B.变稀C.不变D.消失解：条纹间距= 所以/增大，Ar变小。

干涉条纹将变密。

本题答案为A。

3.在空气中做双缝干涉实验，屏幕E上的P处是明条纹。

若将缝S：盖住，并在S,、S：连线的垂直平分而上放一平面反射镜氐其它条件不变（如图），则此时（B ）A.P处仍为明条纹B.P处为暗条纹C.P处位于明、暗条纹之间D.屏幕E上无干涉条纹解对于屏幕E上方的P点，从S,直接入射到屏幕E上和从出发5经平而反射镜M 反射后再入射到屏幕上的光相位差在均比原来增，因此原来是明条纹的将变为暗条纹,而原来的暗条纹将变为明条纹。

故本题答案为B。

4.在薄膜干涉实验中，观察到反射光的等倾干涉条纹的中心是亮斑，则此时透射光的等倾干涉条纹中心是（B ）A.亮斑B.暗斑C.可能是亮斑，也可能是暗斑D.无法确泄解：反射光和透射光的等倾干涉条纹互补。

本题答案为&5.一束波长为的单色光由空气垂宜入射到折射率为刀的透明薄膜上，透明薄膜放在空气中，要使反射光得到干涉加强，则薄膜最小的厚度为（B ）A. /4B. / （4n）C・ /2 D・/ （2n）6.在折射率为m =1.60的玻璃表而上涂以折射率沪1.38的MgF：透明薄膜，可以减少光的反射。

当波长为500. Onm的单色光垂直入射时，为了实现最小反射，此透明薄膜的最小厚度为（C )A. 5. OnmB. 30. OnmC. 90.6nmD. 250. Onm解：增透膜e min = A/4n = 90.6 nm本题答案为C。

高等光学教程参考答案高等光学教程参考答案光学是一门研究光的传播和性质的学科，涉及到光的产生、传播、干涉、衍射、偏振等多个方面。

在高等光学教程中，学生需要掌握各种光学理论和实验技巧。

下面将为大家提供一些参考答案，希望能够帮助大家更好地理解和掌握光学知识。

1. 什么是光的干涉？光的干涉是指两束或多束光波相互叠加而产生的干涉现象。

干涉可以分为两种类型：构造干涉和干涉条纹。

构造干涉是指两束光波在空间中相遇并叠加形成明暗交替的干涉图案。

干涉条纹是指两束光波在光屏上产生的明暗条纹，用以描述光波的相位差。

2. 什么是光的衍射？光的衍射是指光波通过一个有限孔径或障碍物时，光波的传播方向发生偏离并呈现出一定的分布规律。

衍射现象是光的波动性质的重要体现。

光的衍射可以通过菲涅尔衍射和菲拉格衍射来进行描述和分析。

3. 什么是光的偏振？光的偏振是指光波中的电场矢量沿特定方向振动的现象。

偏振光是指只沿一个方向振动的光。

光的偏振可以通过偏振片来实现，偏振片可以选择性地通过或阻挡某个方向的光振动。

4. 什么是光的折射？光的折射是指光波从一种介质传播到另一种介质时，光波传播方向的改变现象。

光的折射遵循斯涅尔定律，即入射光线和折射光线的折射角和入射角之间的正弦比等于两种介质的折射率之比。

5. 什么是光的反射？光的反射是指光波从一个介质传播到同一介质中另一个方向上的现象。

光的反射遵循反射定律，即入射角等于反射角。

6. 什么是光的散射？光的散射是指光波与物质微粒或表面不规则结构相互作用而改变传播方向的现象。

散射可以分为弹性散射和非弹性散射。

弹性散射是指光波与物质微粒发生碰撞后，光波的能量和频率不发生改变。

非弹性散射是指光波与物质微粒发生碰撞后，光波的能量和频率发生改变。

7. 什么是光的吸收？光的吸收是指光波被物质吸收而转化为其他形式的能量，如热能。

光的吸收取决于物质的性质和光波的频率。

8. 什么是光的色散？光的色散是指光波在不同介质中传播时，不同频率的光波传播速度不同的现象。

⾼等光学教程-第4章参考答案第四章标量衍射理论基础4.1证明（4-21）式所⽰的索末菲辐射条件成⽴。

证明：球⾯2S 是中⼼位于1S ⾯上的发散球⾯波的波⾯，假定2S ⾯上的光场分布表⽰为 rjkr )exp(=U 式中r 表⽰产⽣发散球⾯波的点光源到球⾯2S 上任意⼀点的距离。

1exp()cos()cos(,)r jkr jk n r n r r r===-U U U n,r n r 当∞→R 时，有∞→r ，所以这时有1),cos(≈r n2)exp()exp(1rjkr jk r jkr r jk jk n -?-??? ??-=-??U U U 当∞→R 时，上式分母中的r 可⽤R 来代替，于是 2exp()1lim lim lim (cos sin )R R R jkr R jk R kr j kr n R R →∞→∞→∞-=-=-+U U lim 0jkrR e R →∞=-= ?4.2 参考图4-8，考虑在瑞利—索末菲理论中采⽤下式所表⽰的格林函数，即010110101exp()exp()()jkr jkr P r r +=+G %%(1) 证明+G 的法线⽅向的导数在孔径平⾯上为零。

(2) 利⽤这个格林函数，求出⽤孔径上的任意扰动来表⽰0()p U 的表达式，要得到这个结果必须⽤什么样的边界条件。

(3) 利⽤(2)的结果，求出当孔径被从2P 点发散的球⾯波照明时0()p U 的表达式证明: 下⾯是教材中图4-8（1）)(1P +G 由两项迭加⽽成，它们分别表⽰从互为镜像的点0P 和0~P 发出的两个初相位相同的单位振幅的球⾯波。

孔径平⾯1S 上任⼀点1P 的+G 值为010101010101010101~)~exp(~1)~,cos()exp(1),cos(r r r r n r n G jk jk r jkr r jk n ???? ??-+???? ??-=??+ （P4.2-2）对于互为镜像点的0P 和0~P 来说，有)~,cos(),cos(0101r n r n -= 0101~r r = （P4.2-3）将以上关系式代⼊（P4.2-2）式，得到0n+=G （P4.2-4）（2）根据（4-22）式，观察点0P 的光扰动可以⽤整个平⾯1S 上的光扰动U 和它的法向导数来表⽰-=1d 41)(0S s n n P G U G U U π（P4.2-5）由0101~r r =，得01011)exp(2)(r jkr P =+G （P4.2-6）将上式和（P4.2-4）式⼀同代⼊（P4.2-5）式，得到==+11d )exp(21d 41)(01010S S s r jkr n s G n P U U U ππ（P4.2-7）为了将上式所表⽰的结果进⼀步简化，根据孔径∑上的场去计算0P 点的复振幅分布)(0P U ，只需要规定如下两个边界条件：（a ）在孔径∑上，场分布的法向导数n U ?与不存在衍射屏时的值完全相同。

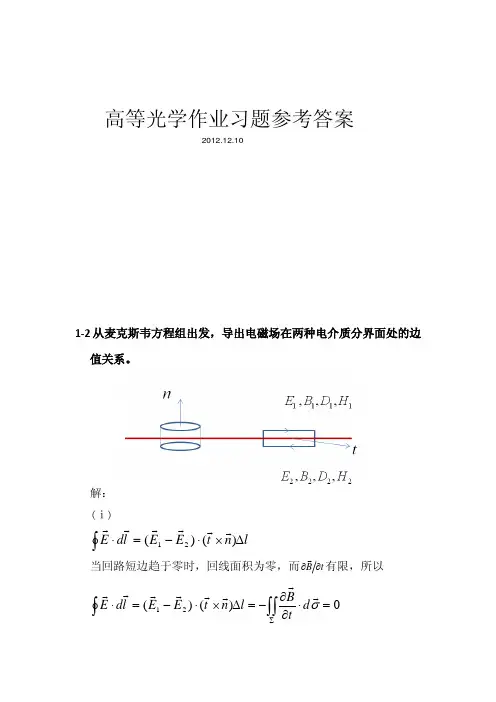
1-2 从麦克斯韦方程组出发，导出电磁场在两种电介质分界面处的边值关系。

解：(ⅰ)ln t E E l d E ∆×⋅−=⋅∫)()(21当回路短边趋于零时，回线面积为零，而t B ∂∂有限，所以0)()(21=⋅∂∂−=∆×⋅−=⋅∫∫∫Σσd t B l n t E E l d E高等光学作业习题参考答案2012.12.10即l E E n t ∆−⋅×)()(21l E E n t ∆−×⋅=))((210=得0)(21=−×E E n，即t t E E 21=(ⅱ)l t d t DJ l n t H H l d H ∆⋅=⋅∂∂+=∆×⋅−=⋅∫∫∫Σασ)()()(21t H H n t n t H H⋅=−×⋅=×⋅−α))(()()(2121当没有电流分布时0=α，得,0)(21=−×H H n即t t H H 21=(ⅲ)s n D D ds n D d D ∆⋅−=⋅=⋅∫∫)(21σ当不存在自由电荷时，0=sρ，积分0=∫∫∫Ωdv s ρ，所以0)(21=∆⋅−s n D D，即n n D D 21=(ⅳ)0)(21=∆⋅−=⋅=⋅∫∫s n B B ds n B d Bσ即n n B B 21=1-5 已知电场E 和磁场H 在直角坐标中的分量分别为：)cos(t kz A E x ω−=；);sin(wt kz B E y −=0=z E )sin(t kz B H x ωε−−=；)cos(t kz A H y ωε−=；0=z H试求电磁场的能量密度w 和玻印亭矢量S 。

解：HB E D µε==,电磁场能量密度)(21B H D E w ⋅+⋅=)(2122H E µε+= )]()([21222222z y x z y x H H H E E E +++++=µε )](sin )(cos [2)1(2222t kz B t kz A ωωµε−+−+=玻印亭矢量H E S ×=zyxz y xH H H E E E z y x =z H E H E y H E H E x H E H E x y y x z x x z y z z y)()()(−+−+−=z H E H E x y y x)(−=z t kz B t kz A))]((sin ))((cos [2222ωεωε−+−=1-6 设某一无限大介质中，,0,0==σρε、µ只是空间坐标的函数，试从麦克斯韦方程和物质方程出发证明：{}0)](ln [)()(ln 22=∇⋅∇+×∇×∇++∇εµεµωE E E E证明：)(),(r rµµεε==H B E Dµε==,E E E D⋅∇+⋅∇=⋅∇=⋅∇εεε由麦克斯韦方程 0=⋅∇D得 (ln )EE E εεε∇⋅∇⋅=−=−∇⋅取麦克斯韦方程组微分式第一式的旋度，)()(B tE ×∇∂∂−=×∇×∇其中，E E E 2)()(∇−⋅∇∇=×∇×∇2[(ln )]E E ε=−∇∇⋅−∇)()(H tB t µ×∇∂∂−=×∇∂∂− )(H H t×∇+×∇∂∂−=µµ)(µµµB t Dt×∇+∂∂∂∂= t B tE ∂∂×∇+∂∂= )(ln 22µεµ)()(ln 22E t E×∇×∇−∂∂=µεµ)()(B tE ×∇∂∂−=×∇×∇即222(ln )()[(ln )]0E E E E t εµµε∂∇−+∇×∇×+∇∇⋅=∂若ti e E E ω0 =，则22(ln )()[(ln )]0E E E E εµωµε∇++∇×∇×+∇∇⋅=1-7 从麦克斯韦方程组出发导出电磁场在有色散的非均匀介质中所满足的亥姆霍兹方程。

第五章 部分相干光理论5.1 证明解析信号的实部u 和虚部u 之间互为希尔伯特变换，即它们之间有下面的关系()t u t r ()()t i ()()⎰∞∞--=ξξξπd )(P.V.1)()()(t u t u r i ， ⎰∞∞---=ξξξπd )(.P.V 1)()()(tu t u i r证明：（1）由(5-10)式，解析函数的实部()()0()2Re ()exp(2)d r r u t j t νπνν∞⎡=-⎢⎣⎦⎰U ⎤⎥t （5.1-11）而，比较以上两式，可见有关系式)](Re[)()(t t u r u = （5.1-13）⎰∞-=0)(d )2exp()(2)(νπννt j t r U u 上式可表示为 （5.1-18）⎰∞∞--+=νπνννd )2exp()()sgn 1()()(t j t r U u 又因为 ()()exp(2)d t j νπνν∞-∞=-⎰u U所以有 ()()(1sgn )()r νν=+U νU )r （5.1-19）对上式两边取傅里叶逆变换11()1()()11((){()}{()}{(sgn )()}(){sgn )}{()}r r r t u t ννννν-----==+=+*u U U U U F F F F F ν上式中 1{sgn }jtνπ-=-F 再利用卷积定义⎰⎰∞∞---=*=*ηξηξηξd d ),(),(y x f g f g g f 令 t j f π-= ， )()(t j t f -=-ξπξ ， ， )()(t u g r =)()()(ξξr u g =所以 ⎰∞∞--+=ξξξπd )(..)()()()(t u V P jt ut r r u （5.1-22）可见 ⎰∞∞--=ξξξπd )(..1)()()(t u V P t ur i（2）参考教材中（5.1-10）式的推导过程，对于解析函数的虚部有下式成立（P5.1-1）⎥⎥⎦⎤⎢⎢⎣⎡-=⎰∞)()(d )2exp()(Re 2)(νπννt j t ui i U)](Re[)()(t j t u i u -= （P5.1-2）比较（P5.1-1）和（P5.1-2）式，得到⎰∞-=-0)(d )2exp()(2)(νπννt j t j i U u所以⎰∞-=0)(d )2exp()(2)(νπννt j j t i U u )()sgn 1()()(νννi j U U +=对上式两边取傅里叶逆变换得)}(){sgn )}({)}({)()(1)(11ννννi i j j t U U U u ---+==F F F)()}({}{sgn )()(11t ju j i i +*=--ννU F F )(d )(..1)()(t ju tu V P i i +--=⎰∞∞-ξξξπ所以 ⎰∞∞---=ξξξπd )(..1)()()(t u V P t ui r5.2 考察用宽带光作杨氏干涉实验(1) 证明观察屏上的入射光场可表示为⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=c r t P t c r t P t t Q 222111,d d ,d d ),(u K u K u 其中 iii i i i i i cr A s cr πθπθ2)(d 2)(k k K ≅=⎰⎰个针孔第 2,1=i 而为第个针孔的面积。

w 2π × 3 ×104 V= = = g k 2π × 3 ×10
2.5 Solved：
3 ×103
这题的题目应该出错了。如果不是出错的话，那么空间频率太大了， 导致 z 分量会很大， 计算会很麻烦。 因此， 应该将复振幅的公式改为：
3 × E ( x, y ) = exp i 2 10 π ( x + 1.5 y )
= λ
1 = fs
3 = 102 + 102 + 102 30
→
1
6.相位速度：相速度公式的推导可得：
常数 对于等相面，我们有： wt − k r =
0 ，于是我们得出： 两边取全微分，有： wdt − k d r =
→
Vp =
dr w = dt k
→
这里的 w 代表时间圆频率，k 代表总波数。故由题目可得：
2.13 Solved：
由于光波的群速度与 n，w，V p 都有关系，这里只要根据题目给出的 已知，选取合适的公式以简化计算就行了。题目不止一种解法，而且 选用的公式不同，得出的答案也会不同，都是正确的，但可能有的答 案比较复杂。以下只给出最简单的答案。 （1）对于给出折射率 n 的变化公式，由于题目说明是正常的色散介 质，所以可使用简化的群速度公式：
c 出发，变形可得： n c n = k w
两边对 w 取一阶导数（k 与 w 有关 ）：
dn c c dk = −k 2 + dw w w dw
c dw V p = ，得出： 利用 Vg = n dk 和
dn n c 1 = − + dw w w Vg
整理公式，最后可得：
Vg =
c n + w dn dw

(A1-1)
U1 U2 U U1 U2 U1 U2 v v t t t t t
2U t2
v2
2U 1 2
v2
2U 2 2
(A1-2)
将(A1-1)、(A1-2)式代入波动方程的左边，显见
1.4 在光学中场量 E (r , t ) 和 H (r , t ) 的表示方法有许多种， 分别推导采用以下三种表示方法时 平均光强的计算公式。 (1) 设场量表示为 E (r , t ) E 0 (r )e j t ， H (r , t ) H 0 (r )e j t (2) 设场量表示为 E (r , t )
高等光学教程第1章参考答案高等光学教程课后答案高等光学教程答案高等光学教程季家镕高等光学教程高等光学赵建林答案高等光学高等光学仿真高等光学仿真pdf高等光学赵建林
第一章 光的基本电磁理论
1.1 在非均匀介质中，介电系数 ( r ) 是空间位置的函数，波动方程有下面的形式
2 E (r )
设 令 则有
f1 f2 ( r U ) ( r f1 ) ( r f 2 ) f1 r f2 r r r r r r f1 f 2 U1 U1 U 2 U 2 r r
2 (rU ) r2

f1 f 2 U 1 1 U 1 2U 1 U 2 1 U 2 2U 2 2 2 r r r r 2 r r 2
对照第一章表 1-3，它是一个快轴沿 x 轴或 y 轴的 1 2 波片。
（2）
1
Etx 1 1 0 1 1 1 E 出射光为一左旋圆偏振光 2 j 2 0 j 1 ty

������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
表示介质中光线与法线的夹角） ㊂ 介质中的速度） ㊂ （３） 实验证明：ｎ ＝
ｃ （ ｃ 表示光在真空中的速度， ｖ 表示光在 ｖ
ｉ，折射角为 ｒ，由折射定律有ｓｉｎ ｉ ＝ （ 光密介质与光疏介质是相对 两种介质相比较，折射率较大的介质叫光密介质， 折射率较 （２） 光照射到两种介质的界面上时，光线全部被反射回原介 ①光线由光密介质射向光疏介质㊂ ②入射角大于或等于临界角㊂
（１） 定义：光从真空射入某种介质发生折射时， 入射角的正
２． 折射率
线在端面 ＡＢ 上的入射角应满足的条件； 长时间㊂
（ ⅰ） 为使光线能从玻璃丝的 ＡＢ 端面传播到另一端面，求光 （ ⅱ） 求光线从玻璃丝的 ＡＢ 端面传播到另一端面所需的最 解析㊀ （ ⅰ） 设光线在端面 ＡＢ 上 Ｃ 点 （ 见图 ） 的入射角为 ①
考点二㊀ 光的干涉㊁衍射㊁偏振
㊀ ㊀ １． 光的干涉
区域的光被减弱，并且光被加强和减弱的区域互相间隔， 这种现 象称为光的干涉现象㊂ 列光的振动情况完全相同， 则在光屏上距双缝的路程差为光波 波长整数倍的地方光被加强，将出现亮条纹； 光屏上距双缝的路 程差为光波半波长的奇数倍的地方光被减弱，将出现暗条纹㊂ 计算表明相邻两条亮条纹 （ 或暗条纹 ） 间的距离 Δｘ ＝ （１） 双缝干涉：在用单色光做双缝干涉实验时， 若双缝处两

2016高等光学第4次作业答案4-8一对称型带状波导，宽度和厚度分别为a 和b ，导光层的折射率为n ，覆盖层和衬底的折射率为n 0.证明：波导的基模传输条件为a=b 。

解：薄膜波导在x 向有限，y 方向无限大；带状波导，在x 和y 向都有限，宽度为a 和b （类似于矩形波导，参考图（4.1.1））。

x 方向受限的波导稳定传输的条件为（4.2.8）0122a cos ++2i n k m θδδπ=Y 方向受限的波导稳定传输条件为'''0122b cos ++2i n k n θδδπ=基模传输，''112'112===,0mn δδδθθδ==，，， 故a=b 。

4-9 一阶跃型光纤的纤芯和包层的折射率分别为1 1.55n =,2 1.50n =,求光纤在空气中的数值孔径和最大入射孔径角0θ.若将该光纤放入水中(设水的折射率为1.33),问光纤的数值孔径是否会改变?如果改变,则改变量是多少?解:光纤的数值孔径大小与纤芯折射率,及纤芯－包层折射率差有关,表达式为:.所以将该光纤放入水中,其数值孔径不会改变. 最大入射孔径角0θ==023≈4-10 一阶跃型光纤的纤芯和包层的折射率分别为n1=1.52，n2=1.51，现欲使该光纤单模传输，问工作波长分别为λλ00=11.222222和λλ00=00.882222时，光纤的最大芯径应该是多少？解：单模光纤的归一化截止频率（查阅光纤相关资料）0V=k 2.4048≤a λ≤max max =1.2m a =2.64m =0.8m a =1.76mλµµλµµ，，。

高等光学教程--第三章参考答案第三章光学薄膜的基本知识3.1 证明在TM 波入射的情况下单层膜的特征矩阵为=22sin cos sin cos j q jq ββββ⎛⎫- ⎪⎪⎪-⎝⎭M式中=2q 220cos /θμεn，其它参数及图示参考§3.1节中图3-2。

图p3-1解答: 模仿教材§3-1中推导TE 波入射情况下求特征矩阵所用的方法。

在界面I 处： 2II 2I 1I 1I I cos cos cos cos θθθθrt r i E E E E E '-=-= (p3.1-1) II I I I I rt r i H H H H H '+=+= (p3.1-2) 由非磁性介质中E 和的关系式H E s H ⨯=n 0με (p3.1-2)式化为 )()(II I 20I I 100I rt r i E E n E E n H '+=-=μεμε (p3.1-3) 在界面II 处： 3II 2II 2II II cos cos cos θθθt r i E E E E =-= (p3.1-4)II II II II t r i H H H H =+= (p3.1-5)由(p3.1-3)式，(p3.1-5)式化为II 30II II 200II )(t r i E n E E n H μεμε=+=(p3.1-6) 两个界面上的电矢量有关系式II tI II II j i j r r E E eE E eββ-⎧=⎪⎨'=⎪⎩ (p3.1-7)(p3.1-8)由(p3.1-7)和(p3.1-8)两式，(p3.1-4)、(p3.1-6)两式化为II tI 2I 2II2tI I cos cos (p3.1-9)(p3.1-10)()j j r j j r E E e E e H E e E e ββββθθ--'⎧=-⎪⎨'=+⎪⎩由(p3.1-9)和(p3.1-10)两式解出tI 2II 2II cos E E θ⎫=⎪⎪⎭H + (p3.1-11) 和 βθμεμεθj re n E n H E --='220II 20II 2II cos 2cos (p3.1-12)将(p3.1-11)、(p3.1-12)式代入(p3.1-1)式，并令有 II 2II 1sin cos H q j E E ββ-=(p3.1-13) 22q =用同样的方法得到II II 2I cos sin H E jq H ββ+-= (p3.1-14)由(p3.1-13)和(p3.1-14)式⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡II II 22I I cos sin sin cos H E jq q jH E ββββ ⎥⎥⎦⎤⎢⎢⎣⎡--=ββββcos sin sin cos 22I jq q j M∴式中 2202cos θμεn q =3.2 如图p3-2所示，有一单层介质膜，入射光由折射率为的介质经过界面I 、单层膜及界面II 后进入折射率为 的衬底，入射光在界面I 和界面II 一次反射的振幅反射率分别为和，一次透射的振幅透射率分别为和。

U（x, y）
1
m e e
j
z L2
j 2x L
m e e
j
z L2
j 2x L
1
[1
me
j
z L2
cos( 2x )]
24
42Leabharlann L在泰伯距离 z / L2 2 n 处，可以观察到物体的像；在 z / L2 （ 2 n 1） 处观察
题： t(x, y)
1 2
[1
cos(2fx0
)]
透镜焦距
20 讲题目：一.物理与数学基础：平面波与球面波；空间频率；波的叠加；空间频率的丢失/ 卷积的物理意义/成像系统的原理；抽样定理；二.标量衍射的基本理论：衍射与干涉；近场与 远场衍射；透过率函数；三.傅里叶光学的基本分析方法：“透镜的傅里叶变换作用”；衍射 的分析法；衍射的仿真；四.光学信息处理的基本理论和方法：阿贝成像原理；4f 系统；全息； 五。傅里叶光学在信息处理的应用：CTF;OTF;非相干与相干成像；六.应用实例:叠层成像/光学 加密。第 1 章给出了必要的数学基础。 指出了从空间域和频率域讨论系统的两种基本方法。 前者着眼于系统脉冲响应，后者着眼于系统的频率响应即传递函数。在后续各章中，正是按这
度看，函数被矩形函数限制范围后，成为 ,新的函数不再是限带函数，抽样时会发生频谱混
叠，可以得出同样的解释。
2.如果用很窄的矩形脉冲阵列对函数抽样（物理上并不可能在一些严格的点上抽样一个函数）
即式中，为每个脉冲在方向的宽度。若抽样间隔合适，说明能否由 还原函数。解：用很窄的
矩形脉冲阵列对函数进行抽样，例如当采用 CCD 采集图像，每个像素都有一定的尺寸大小。这
l 2F
当θ取 0 时要求光栅频率不大于系统截

≈ 0.409
cm
课 后 答 案 网
∆
y
2
=
180 0.022
×
2000
×10−8
≈
0.573
cm
r
y= j 0λ
又∵
d ， j=2
∆y =
r j 0 (λ
−λ ) = 2×
180
× (7000 − 5000) ×10−8
∴
d2
1
0.022
≈0.327 cm
or:
∆y = 2∆ y − 2∆ y ≈ 0.328
课 后 答 案 网
故; 应向前移动 0.25m，或向后移动 0.25m 2-5. 解 ：（ 1）
（2） 由题意知，该屏对于所参考的点只让偶数半波 带透光，故：
（3）
2-6. 解：
课 后 答 案 网
当移去波带片使用透镜后，透镜对所有光波的相
位延迟一样，所以 一致的，即：
=
× ≈ 4260 A
1.332 −12 × sin 2 30o 4
or : δ = 2h
n2
− n2 sin 2 i
λ +
2
1
12
2h n2 − n2 sin 2 i = (2 j − 1) λ
2
1
1
2
2 j −1 λ
h=
取j = 2, 合题意
n2 − n2 sin 2 i 4
2
1
1
课 后 答 案 网
（3）
2-18. 解： （1）
课 后 答 案 网
（2）
219. 解：
课 后 答 案 网
2-20.证：设单缝衍射的振幅为 aθ ,三缝衍射的总振幅为 Aθ ，则 Aθx ＝ aθ （１＋

第二章 干涉理论基础和干涉仪2.1用迈克耳逊干涉仪进行精密测长，光源波长为633nm ，其谱线宽度为104-nm ，光电接收元件的灵敏度可达1/10个条纹，问这台仪器测长精度是多少？一次测长量程是多少？ 解答：设测长精度为l δ，则l δ由探测器接受灵敏度10λδ=N 所决定，N l δδ=2∴ m 032.02μδδ≈=Nl （32nm ）一次测长量程M l 由相干长度c l 所决定，c M l l =2∴ m l l c M221212≈∆==λλ2.2 雨过天晴，马路边上的积水上有油膜，太阳光照射过去，当油膜较薄时呈现出彩色，解释为什么油膜较厚时彩色消失。

解答：太阳光是一多色光，相干长度较小。

当油膜较厚时光经上下两界面反射时的光程差超过了入射光的相干长度，因而干涉条纹消失。

2.3计算下列光的相干长度(1)高压汞灯的绿线，546.15nm nm λλ=∆=(2)HeNe 激光器发出的光，6331nm MHz λν=∆=解答：计算相干长度（1） m 6.592μλλ≈∆=c L（2） 300m c cL ν=≈∆2.4在杨氏双缝实验中（1）若以一单色线光源照明，设线光源平行于狭缝，光在通过狭缝以后光强之比为1:2，求产生的干涉条纹可见度。

（2）若以直径为0.1mm 的一段钨丝作为杨氏干涉实验的光源，为使横向相干宽度大于1mm ，双缝必须与灯丝相距多远？设λ=550nm解答：（1） δcos 2220000I I I I I ⋅++= V ∴=（2）由(2-104)式 dbP λ=0 λdP b =∴ 182.0>b M2.5图p2-5所示的杨氏干涉实验中扩展光源宽度为p ，光源波长为5893A ，针孔P 1、P 2大小相同，相距为d ，Z 0=1m ， Z 1=1m（1）当两孔P 1、P 2相距d=2mm 时，计算光源的宽度由p =0增大到0.1mm 时观察屏上可见度变化范围。

（2）设p=0.2mm ，Z 0、Z 1不变，改变P 1P 2之间的孔距d ，当可见度第一次为0时 d=? （3）仍设p=0.2mm ，若d=3mm ， 01Z m =.求0∑面上z 轴附近的可见度函数。