同济大学土木工程钢结构基本原理第5章详解
- 格式:pdf
- 大小:963.14 KB
- 文档页数:44


第五章 轴心受力构件5.1 验算由2635L ⨯组成的水平放置的轴心拉杆的强度和长细比。
轴心拉力的设计值为270KN ,只承受静力作用,计算长度为3m 。
杆端有一排直径为20mm 的孔眼,钢材为Q235钢。
如截面尺寸不够,应改用什么角钢?注:计算时忽略连接偏心和杆件自重的影响。
解:查型钢表2635L ⨯角钢,221.94, 2.82,215/,6.142x y i cm i cm f N mm A cm ====⨯ 确定危险截面如图1—1截面净截面面积2(6.1420.5)210.28n A cm =-⨯⨯=验算强度: 322227010262.65/215/10.2810n N N mm f N mm A ⨯==>=⨯ (说明截面尺寸不够) 验算长细比:[]0300154.63501.94x x l i λλ===<= 所以,刚度满足要求需用净截面面积322701012.56215n N A cm f ⨯≥== 改用2755L ⨯角钢,22.32,3.29,7.412x y i cm i cm A cm ===⨯此时净截面面积22(7.4120.5)212.8212.56n A cm cm =-⨯⨯=> (满足强度要求)[]030091.183503.29y y l i λλ===<= (满足刚度要求) 5.2 一块—400×20的钢板用两块拼接板—400×12进行拼接。
螺栓孔径为22mm ,排列如图5.30所示。
钢板轴心受拉,N =135KN (设计值)。
钢材为Q235钢,解答下列问题:(1)钢板1-1截面的强度够否? (2)是否还需要验算2—2截面的强度?假定N 力在13个螺栓中平均分配,2—2截面应如何验算?(3)拼接板的强度够否? 解:(1)验算钢板1—1截面的强度:A n =40×2-3×2.2×2=66.8cm 2(2)2-2截面虽受力较小,但截面消弱较多,尚应进行验算。




5.1 影响轴心受压稳定极限承载力的初始缺陷有哪些?在钢结构设计中应如何考虑?5.2 某车间工作平台柱高2.6m,轴心受压,两端铰接.材料用I16,Q235钢,钢材的强度设计值2215/d f N mm =.求轴心受压稳定系数ϕ及其稳定临界荷载.如改用Q345钢2310/d f N mm =,则各为多少?解答:查P335附表3-6,知I16截面特性,26.57, 1.89,26.11x y i cm i cm A cm === 柱子两端较接, 1.0x y μμ== 故柱子长细比为 1.0260039.665.7x x xli μλ⨯===,2600 1.0137.618.9y y y l i μλ⨯===因为x y λλ<,故对于Q235钢相对长细比为137.61.48λπ=== 钢柱轧制, /0.8b h ≤.对y 轴查P106表5-4(a)知为不b 类截面。
故由式5-34b得()223212ϕααλλλ⎡=++⎢⎣ ()2210.9650.300 1.48 1.482 1.48⎡=+⨯+⎢⎣⨯ 0.354=(或计算137.6λ=,再由附表4-4查得0.354ϕ=)故得到稳定临界荷载为20.35426.1110215198.7crd d N Af kN ϕ==⨯⨯⨯=当改用Q365钢时,同理可求得 1.792λ=。
由式5-34b 计算得0.257ϕ= (或由166.7λ=,查表得0.257ϕ=)故稳定临界荷载为20.25726.1110310208.0crd d N Af kN ϕ==⨯⨯⨯=5.3 图5-25所示为一轴心受压构件,两端铰接,截面形式为十字形.设在弹塑性范围内/E G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为Q235.5.4 截面由钢板组成的轴心受压构件,其局部稳定计算公式是按什么准则进行推导得出的.5.5 两端铰接的轴心受压柱,高10m,截面为三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值2205/d f N mm =,承受轴心压力设计值3000kN (包括自重).如采用图5-26所示的两种截面,计算两种情况下柱是否安全.图5-26 题5.5解答:截面特性计算: 对a)截面:32394112(5002020500260)8500 1.436101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 3384112205005008 4.167101212y I mm =⨯⨯⨯+⨯⨯=⨯ 2250020500824000A mm =⨯⨯+⨯=244.6x i mm ==131.8y i mm==对b)截面:32384112(4002540025212.5)104009.575101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 33841122540040010 2.667101212y I mm =⨯⨯⨯+⨯⨯=⨯ 24002524001024000A mm =⨯⨯+⨯=199.7x i mm ==105.4y i mm==整体稳定系数的计算:钢柱两端铰接,计算长度10000ox oy l l mm == 对a)截面: 1000040.88244.6ox x x l i λ=== 1000075.87131.8ox y y l i λ=== 对b)截面: 1000050.08199.7kx x x l i λ=== 1000094.88105.4ox y y l i λ=== 根据题意,查P106表5-4(a),知钢柱对x 轴为b 类截面,对y 轴为c 类截面.对a)截面:对x 轴:40.880.440x λπ===()223212x x x x ϕααλλλ⎡=++⎢⎣()2210.9650.30.440.4420.44⎡=⨯+⨯+-⎢⨯⎣0.895=(或计算40.88λ=,再由附表4-4查得0.896xϕ)对y 轴:25.870.816y λπ===()223212y y y y ϕααλλλ⎡=++⎢⎣()2210.9060.5950.8160.81620.816⎡=⨯+⨯+⎢⨯⎣0.604=(或计算75.87λ=,再由附表4-5查得0.604yϕ)故取该柱的整体稳定系数为0.604ϕ=对b)截面,同理可求得0.852x ϕ=,0.489y ϕ=,故取该柱截面整体稳定系数为0.489ϕ= 整体稳定验算:对a)截面 0.604240002052971.68 3000 crd d N Af kN kN ϕ==⨯⨯=<不满足。
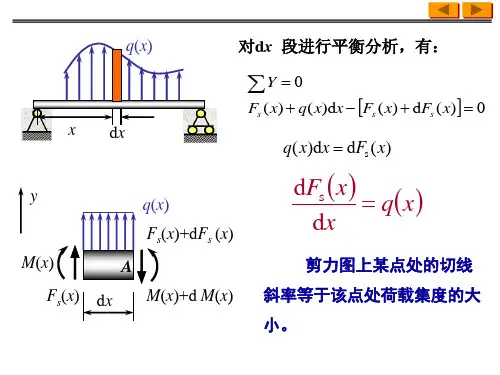
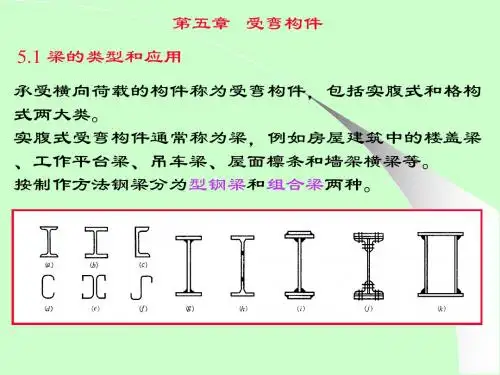


第五章 受弯构件 §5-1 概 述1、定义:主要承受横向荷载作用的构件,即通常所讲的梁。
2、类型按使用功能,可分为工作平台梁、吊车梁、楼盖梁、墙梁及檩条等;按支承情况,可分为简支梁、连续梁、伸臂梁和框架梁等;按荷载作用情况,可分为单向弯曲梁和双向弯曲梁;按截面形式有型钢梁和组合梁;实腹式和格构式。
图5-1 受弯构件的截面形式3、受弯构件——梁的内力:一般,仅考虑其弯矩和剪力;对于框架梁,需同时考虑M 、V 和N 作用。
※ 关键词受弯构件——member in bending梁——beam单向受弯构件——one-way member in bending双向受弯构件——two-way member in bending§5-2 受弯构件的强度一、抗弯强度1、梁在弯矩作用下,当M 逐渐增加时,截面弯曲应力的发展可分为三个阶段,见图5-2所示。
(1)弹性工作阶段弯矩较小时,梁截面受拉边缘σ<y f ,梁处于弹性工作阶段,弯曲应力呈三角形分布。
弹性极限弯矩为:n y e W f M ⋅=(截面受拉边缘的σ=y f )。
(2)弹塑性工作阶段弯矩继续增大,截面边缘部分进入塑性,中间部分仍处于弹性工作状态。
(3)塑性工作阶段当弯矩再继续增加,截面的塑性区发展至全截面,形成塑性铰,梁产生相对转动,pn y p W f M ⋅=。
图5-2 梁受弯时各阶段的应力分布情况问:取那个阶段作为设计或计算的模型?答《规范》中按弹性阶段或弹塑性阶段设计或计算。
塑性发展深度,通过塑性发展系数——γ来衡量。
截面形状系数:n pn e p F W W M M ==γ2、抗弯强度 • 单向受弯: fW M nx x x ≤⋅γ•双向受弯: fW M W M ny y y nx x x ≤⋅+⋅γγ 其中:x γ、y γ——截面塑性发展系数,一般情况按表6.1取值;• 若y f t b 23513>时,取x γ=y γ=1.0;• 若直接承受动力荷载作用时,取x γ=y γ=1.0。
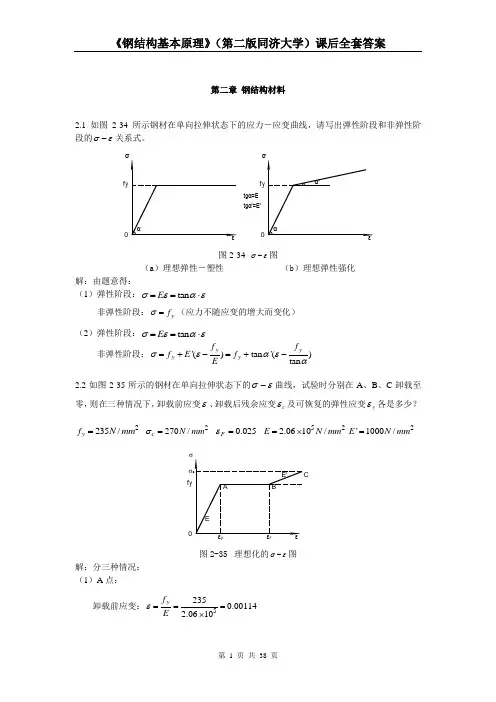
第二章 钢结构材料2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f 0f 0tgα=E 图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:由题意得:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f 0σF图2-35 理想化的σε-图解:分三种情况: (1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点: 卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
轴心受压构件L. Euler(1707-1783)§1 概 述受压构件:桁架/网架杆件、支撑、两端铰接柱等 截面的分类:P96-971 双轴对称截面2 单轴对称截面3 无对称轴截面破坏类型:强度破坏:截面有较大削弱处/非常粗短的构件 整体失稳:弯曲失稳、扭转失稳、弯扭失稳局部失稳:构件中板件失稳§2 轴心受压构件的强度强度承载力N u = An f y An —— 净截面面积(截面面积最小处) f y —— 屈服应力工程设计公式N ≤ An fd , fd = f y / γ R 或 fd = f y / Kσ=N An≤fdP97-98P98-109§3 轴心受压实腹构件的整体稳定补充§3.1 理想压杆和实际压杆的整体稳定压杆为什么会失稳?微小扰动: θkθ ⋅ 2θ < Pl sinθ ≈ Plθ⇒kθ<1 2Pl不稳定kθ ⋅ 2θ = Pl sinθ ≈ Plθ⇒kθ=1 2Pl临界kθ ⋅ 2θ > Pl sinθ ≈ Plθ⇒kθ>1 2Pl稳定kθ转动刚度: Mθ = Kθ扭簧 Mθ = kθ ⋅ 2θ ⇒ KE = 2kθ 弹性刚度l轴力 Mθ = −Pl ⋅θ ⇒ Kσ = −Pl 几何刚度K = KE + Kθ = 2kθ − PlK<0 不稳定 K=0 临界 K>0 稳定弹性刚度为正,几何刚度可正可负。
P受拉会如何?kθθPP98-100§3.1 理想压杆和实际压杆的整体稳定欧拉临界力EIv′′ + Nv = 0NE=π 2EA λ2 ,考虑非弹性时的临界力σE=π 2E λ2NE=π2 Etλ2A,σE= π 2 Et λ2Et 材料的切线模量σ cr弹性实际压杆的整体稳定 f y几何缺陷的影响非弹性力学缺陷的影响L. Euler(1707-1783)σ cr f y1.0理想压杆 λ 实际压杆 λ补充§3.2理想压杆弯曲失稳变形特性的力学本质截面内剪力的产生: 截面变形产生切向力V欧拉屈曲:不考虑截面形状 实际构件:需考虑截面形状考虑截面形状:剪力中心xx0x y0xyyyxxyx0 yx0形心 剪力中心y0形心处剪力对不同截面的变形特性:双轴对称截面:弯曲变形单轴对称截面:弯曲变形,弯扭变形无对称轴截面:弯扭变形vNV = N v′PP100§3.3 理想压杆弹性失稳的平衡方程N1 理想压杆的假定: 杆件轴线(截面形心的连线)为直线 轴力作用线与杆件轴线重合2 弹性失稳的平衡方程: 变形包括弯曲变形和扭转变形 变形后位置时的平衡方程 小变形绕 x 轴的弯曲变形EI x v IV + Nv '' − Nx0θ '' = 0绕 y 轴的弯曲变形x0,y0 剪力中心坐标EI yu IV + Nu '' − Ny0θ '' = 0N绕 z 轴的扭转变形EI ωθ IV − GI tθ '' − Nx0v '' + Ny0u '' + (Nr02 − R )θ ′′ = 03 自由扭转与约束扭转P156-159EI ωθ IV − GI tθ ′′ − Nx0v′′ + Ny0u′′ + (Nr02 − R )θ ′′ = 0自由扭转:圣文南扭转构件端部截面纵向纤维不受约束M k = GI tθ ′约束扭转:一工字形截面悬臂梁受端部扭矩作用发生扭转 θu = 0.5hθ u '' = 0.5hθ '' M y = −EI yu '' = −0.5EI y hθ ''Vy = dM / dz = −0.5EI y hθ '''M ω = Vy h = −0.5EI y h 2θ '''u记 I ω = 0.5I y h 2 = b3tf h 2 / 24M ω = −EI ωθ '''θhtf bM ω 翘曲扭矩瓦格纳(Wagner)扭矩I ω 扇性惯性矩M T = M ω + M k = GI tθ ′ − EIωθ ′′′P100-102§3.4 双轴对称截面理想压杆的临界力双轴对称截面:x0 = y0 = 0EI x v IV + Nv '' = 0 EI yu IV + Nu '' = 03个微分方程独立EI ωθ IV − GI tθ ′′ + (Nr02 − R )θ ′′ = 0NEx = π 2EI x / λ2ox = π 2EA(I x / A) / λ2ox = π 2EA / λ2x 绕x轴弯曲N Ey = π 2 EI y / λ2oy = π 2 EA / λ2y绕y轴弯曲NEθ = (π 2EIω / λ2oθ + GIt + R) / r02 = π 2EA / λθ2绕z轴扭转对应3种失稳模态:绕两主轴的弯曲和绕轴心的扭转 λθ = 控制压杆的承载力的失稳模态l0θ Iω + l02θ ⋅ GIt + R Ar02 π 2 EAr02一般的双轴对称截面(工字、H型),弯曲屈曲临界 (扭转长细比)力小于扭转屈曲临界力,但十字形截面有可能相反。
弯曲变形和扭转变形的计算长度系数失稳临界应力 σ E = NE / A = π 2E / λ2P102-103§3.5 单轴对称截面理想压杆的临界力设 x 轴为对称轴,y0=0。
基本方程之一解耦EI x v IV + Nv '' − Nx0θ '' = 0EI xvIV + Nv'' − Nx0θ '' = 0 弯扭失稳EI yu IV + Nu '' − Ny0θ '' = 0EI yu IV + Nu'' = 0弯曲失稳EI ωθ IV − GI tθ '' − Nx0v '' + Ny0u '' + (Nr02 − R )θ ′′ = 0EIωθ IV − (GIt − Nr02 + R)θ '' − Nx0v'' = 0 弯扭失稳整体失稳两种模态:绕非对称轴的弯曲失稳、弯扭失稳临界力弯曲失稳 NEy = π 2 EA / λ2y 独立方程 弯扭失稳 NEω = π 2EA / λω2 联立方程:p.108弯扭失稳换算长细比λω2=1 2(λ2x+ λθ2 ) +1 2(λ2x+λθ2)−4⎜⎜⎝⎛1 −x02 r02⎟⎟⎠⎞λ2xλθ2P103-104§3.6 弯曲失稳的极限承载力1 按边缘纤维屈服准则计算弯曲平衡方程 EIx(v − vo)'' + Nv = 0 假定初弯曲 vo = vomsin(π ⋅ z / λ) 最大挠度 vm = vom /(1− N / NE)边缘纤维屈服 N A+ NΔm Wx = fyPerry公式σcr=N A=fy+ (1+ε0 )σEx2−⎡ ⎢⎣fy+ (1+ε0 )σEx2⎤2 ⎥⎦−f yσ Ex轴心受压构件稳定系数 ϕNw v vovm vomϕ= σcrfy=1 2⎪⎨⎧1 ⎪⎩+1λ2(1+ε0) −⎢⎣⎡1+1λ2(1+ε0)⎥⎦⎤2−4λ2⎪⎫ ⎬ ⎪⎭N《冷弯薄壁型钢结构技术规范》初偏心率 ε0 按规范取值P104-107§3.6 弯曲失稳的极限承载力2 按稳定极限承载力理论计算:柱子曲线 轴心受压构件达到弯曲失稳时的压力NEϕ= σ cr/fy轴心受压构件 稳定系数影响因素:截面,材料,残余应力,初弯曲扭转,初偏心等等Np1.0弹塑性修正λeλ理想压杆临界力缺陷影响λ实际轴心压杆的柱子曲线P104-107§3.6 弯曲失稳的极限承载力3 按稳定极限承载力理论计算:多条柱子曲线《钢结构设计规范》的柱子曲线4条稳定系数曲线 依截面形式、失稳方向、 板件厚度、制造加工方式确定稳定系数确定方法公式法由相对长细比λ = λ fy按公式(5.34)计算πEp.105查表法 截面分类→计算长细比→查表p.371-374ϕ = σ cr / f ya1.0bcd柱子曲线λ(轴心压杆稳定系数)P104-107§3.7 轴心受压构件整体稳定工程计算方法计算公式N ≤ N u = σ cr A = (σ cr / f y ) Af y = ϕ Af yN ≤ ϕAfd或NϕA≤fd注意点 整体稳定计算时采用毛截面面积采用相应设计规范的轴压构件稳定系数计算步骤 确定轴力设计值 计算构件两主轴方向的长细比, 换算长细比 确定轴压构件稳定系数(公式或查表) 稳定校核P118-129§4 轴心受压实腹构件的局部稳定P118-129§4.1 构件中受压板件的屈曲受压翼缘的屈曲受压腹板的屈曲P118-119§4.2 弹性薄板受压时的失稳平衡方程理想轴心受压薄板板件平直且厚度相等 薄板:厚宽比为10-1数量级Nx b yx轴压均匀分布且作用板的中面att受压薄板的弹性失稳平衡方程w(Karman大变形理论)D(∂4w ∂x 4+2∂4w ∂x 2∂y 4+∂∂4yw4 )+Nx∂2w ∂x 2=0wD = Et 3单位板宽抗弯刚度12(1 −ν 2 )Nx单位板宽上的轴压力P118-119§4.3 四边简支条件下的临界应力边界条件:边界上挠度、弯矩为零解的假定:双重三角级数(满足简支边界条件)解的结果:N xcr=π 2Db2(mb a+n2a)2 mbm、n:失稳时沿长度和宽度方向的半波数(P119 图5-14)临界力(n=1)N xcr=kπ 2Db2k = (mb + a )2 稳定系数与 a mb 失稳模态临界应力σ xcr=N xcr t=kπ12(12E−μ2)⎜⎛ ⎝t b⎟⎞2 ⎠与宽厚比平方成正比P120-121§4.4 其他边界条件下的临界应力临界应力σ xcr=k12π(12E−μ2)⋅⎜⎝⎛t b⎟⎠⎞2k 板的稳定系数不同边界约束条件下的板的稳定系数四边简支:k=4如H型截面中的腹板三边简支与压力平行的一边卷边:k=1.35冷弯薄壁型钢中带卷边的翼缘三边简支与压力平行的一边自由:k=0.45+(b/a)2≈0.45如H型截面中的翼缘P121-122§4.5 影响临界应力的其他因素1 板组间的相互影响引入板组约束系数σ xcr=kπ12(12E−μ2)⋅t2 b2σ xcr=χ⋅kπ12(12E−μ2)⋅t2 b2(也可采用计入板间相互影响的稳定系数见表5-6)2 考虑板件弹塑性的影响σ xcr=k12π(12E−μ2)⋅t2 b2σ xcr =ψt⋅k⋅12π(12E−μ2)⋅t2 b2ψ t = Et / E§4.6 板件屈曲后性能P123-124屈曲后强度的概念σ板件σ cr压杆v wbe/2 be/2屈曲后强度的工程计算: 有效宽度概念P125-126§4.7 轴压构件板件局部稳定的设计原则1 允许利用屈曲后强度—容忍发生局部弹性失稳工程计算方法:经验公式be b=(1 − 0.22 / λe ) / λeλe = σ e / σ cr = 1.05(b / t) σ e / kE计算有效宽度和有效截 面,用有效截面计算截 面强度和整体稳定利用屈曲后强度可采用薄壁宽敞截面:增大构件弹性抗弯刚度 提高构件整体稳定性局部屈曲时应力较小:截面极限强度降低 无法利用材料塑性P126-129§4.7 轴压构件板件局部稳定的设计原则2 不允许出现局部失稳时σ cr ≥ f 其中 f : 强度控制时 f y整体稳定控制时 φ f y整体稳定控制时:ψtχkπ 2E 12(1 −υ 2 )⎜⎝⎛t b⎟⎞2 ⎠≥ϕ⋅fy1b t≤⎢⎢⎣⎡12(1ψ−tχkπ 2 υ 2 )ϕE ⋅fy⎤ ⎥ ⎥⎦2板件宽厚比限值p.127表5-7各项工程做法:用宽厚比限值代替局部稳定计算P109-118§5 轴心受压格构式构件的整体 稳定和局部稳定§5.1 格构式构件的概念Page109格构式构件轴压构件两主轴方向等稳定性格构式构件的类型肢杆:材料—型钢或组合焊接截面 肢数—双肢、三肢、四肢缀材:缀条—形成三角形区格 缀板—形成四边形区格实轴:穿过肢杆腹板的轴 虚轴:穿过缀材的轴格构式构件的稳定承载极限绕实轴的整体稳定:同实腹式 绕虚轴的整体稳定:缀材的剪切变形 单肢截面板件的局部稳定:同实腹式 单肢自身的稳定 缀材的稳定a a a0虚轴 肢杆 1 xyy 实轴1x c缀材Page110§5.2 考虑剪切变形的平衡方程剪切变形的理由NV考虑剪切变形影响的平衡方程Vv = v1 + v2v1'' = − M x / EI x = − Nv / EI xdv 2 dz=γ= γ 1V= γ 1Nv '→ v2'' = γ 1Nv ''N其中 γ 1 ——单位剪力作用下剪切角变形v '' = v1'' + v2'' = − Nv / EI x + γ 1Nv ''→ v'' +Nv=0EI x (1 − γ 1N )v平衡方程的解N cr=π 2 EI x (1 − γ 1N cr )λ2→N cr=λ2xπ 2 EA + π 2 EA γ 1NPage111-112§5.3 格构式构件绕虚轴的稳定承载力稳定承载力的表达式N cr=λ2xπ 2 EA + π 2 EA γ 1=π 2 EA λ20 x虚轴 肢杆 1 xyλ0x = λ2x + π 2 EA γ 1 --〉换算长细比剪切变形降低了构件 → λ0x ≥ λx 抗弯刚度,从而降低了弯曲稳定临界力1x cy 实轴 缀材a a a0 a0γ1与缀条缀板的尺寸及布 置位置等有关双肢缀条构件 表5-5双肢缀板构件λ0x = λ0x =λ2x + 27 A / A1x λ2x + λ12λx -按柱肢截面计算的长细比A1x -斜缀条毛截面面积和λ1 -单肢对最小刚度轴1-1的长细比(计算长度)Page129-133§5.4 缀条式轴心压杆的局部稳定a a受压板件的局部稳定与实腹式构件相同Nt单肢稳定V1λ1=a i1≤0 .7 λ max缀条稳定V max=Af d 85f y 剪力的实用公式 235Nt=V1n ⋅ cos α=Vmax2n ⋅ cos αNtϕ ⋅ At≤γ0⋅fd虚轴 1xyVmax 1xcy 实轴Page133-135§5.5 缀板式轴心压杆中的局部稳定受压板件的局部稳定与实腹式构件相同虚轴 1x单肢的稳定yλ1 ≤ min{ 40, 0.5λmax }1x缀板的稳定c缀板式构件:多层刚架,反弯点:中点缀板承受内力T= V1a cM=V1a 2Vmax , V1 计算方法同缀条式构件缀板局部稳定: tb≥c 40V1 / 2TV1 / 2缀板强度:σ=M W≤fdτ= 1.5 T bt b≤f vday 实轴Page135§6 轴心受压构件的刚度长细比限值:参考有关规范 钢结构设计规范: λmax ≤ [λ ][λ ] 为150~200Page轴心受压构件计算内容小结强度计算整体稳定计算实腹式:弯曲失稳/弯扭失稳/扭转失稳 Perry公式/柱子曲线格构式:缀条式/缀板式,实轴/虚轴局部稳定计算板件宽厚比限值 板件的有效宽度和有效截面计算 格构式:单肢与缀材刚度计算压杆整体失稳和局部失稳几何缺陷对压杆稳定的影响初始挠曲、初始扭转、初始偏心 对稳定承载力的影响例:双轴对称截面对强轴有初挠曲 v0 弯曲平衡方程Nv vo Δm ΔoEI x v '' + Nv = 0EI x (v − v0 )'' + Nv = 0设 vo = Δo sin(π ⋅ z / λ)解 v = Δm sin(π ⋅ z / λ)NE其中 Δm = Δo /(1 − N / N E )N = (1 − Δo / Δm )N E < N EN NN = (1 − Δo / Δm )N E Δm残余应力对压杆稳定的影响残余应力分布及峰值大小对稳定承载力的影响σ r+ σ r-σ无残余应力fyΔσ 2 < f yfp有残余应力NN ExNE*xv轧制H型钢的 残余应力分布σ max− = f yε残余应力使得截面部分区 域提前屈服,从而削弱了 构件刚度,导致稳定承载 力下降。