九年级数学三角函数的计算(201911整理)
- 格式:pptx
- 大小:222.05 KB
- 文档页数:13
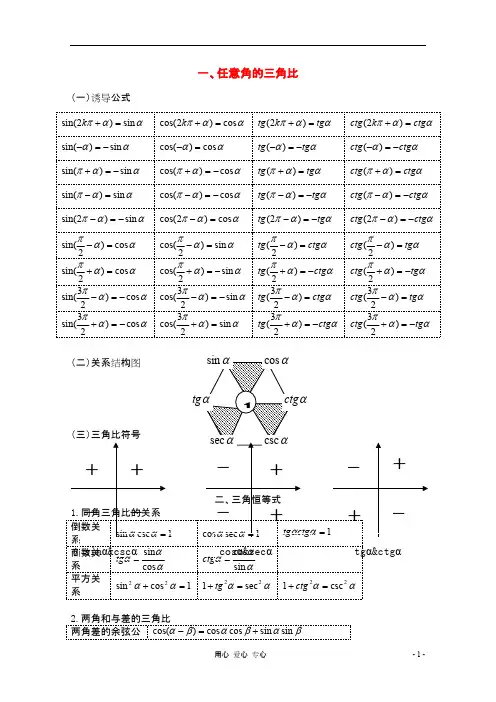

2019中考数学三角函数公式汇总锐角三角函数公式sin =的对边 / 斜边cos =的邻边 / 斜边tan =的对边 / 的邻边cot =的邻边 / 的对边倍角公式Sin2A=2SinA?CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注:SinA^2 是sinA的平方 sin2(A) )三倍角公式sin3=4sinsin(/3+)sin(/3-)cos3=4coscos(/3+)cos(/3-)tan3a = tan a tan(/3+a) tan(/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina辅助角公式Asin+Bcos=(A^2+B^2)^(1/2)sin(+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsin+Bcos=(A^2+B^2)^(1/2)cos(-t),tant=A/B 降幂公式sin^2()=(1-cos(2))/2=versin(2)/2cos^2()=(1+cos(2))/2=covers(2)/2tan^2()=(1-cos(2))/(1+cos(2))推导公式tan+cot=2/sin2tan-cot=-2cot21+cos2=2cos^21-cos2=2sin^21+sin=(sin/2+cos/2)^2=2sina(1-sina)+(1-2sina)sina=3sina-4sinacos3a=cos(2a+a)=cos2acosa-sin2asina=(2cosa-1)cosa-2(1-sina)cosa=4cosa-3cosasin3a=3sina-4sina=4sina(3/4-sina)=4sina[(3/2)-sina]=4sina(sin60-sina)=4sina(sin60+sina)(sin60-sina)=4sina*2sin[(60+a)/2]cos[(60-a)/2]*2sin[(60-a)/2]co s[(60-a)/2]=4sinasin(60+a)sin(60-a)cos3a=4cosa-3cosa=4cosa(cosa-3/4)=4cosa[cosa-(3/2)]=4cosa(cosa-cos30)=4cosa(cosa+cos30)(cosa-cos30)=4cosa*2cos[(a+30)/2]cos[(a-30)/2]*{-2sin[(a+30)/2] sin[(a-30)/2]}=-4cosasin(a+30)sin(a-30)=-4cosasin[90-(60-a)]sin[-90+(60+a)]=-4cosacos(60-a)[-cos(60+a)]=4cosacos(60-a)cos(60+a)上述两式相比可得tan3a=tanatan(60-a)tan(60+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(++)=sincoscos+cossincos+coscossin-sinsinsin cos(++)=coscoscos-cossinsin-sincossin-sinsincos tan(++)=(tan+tan+tan-tantantan)/(1-tantan-tantan-ta ntan)两角和差cos(+)=coscos-sinsincos(-)=coscos+sinsinsin()=sincoscossintan(+)=(tan+tan)/(1-tantan)tan(-)=(tan-tan)/(1+tantan)和差化积。


(完整)初中常用三角函数公式初中常用三角函数公式
三角函数是数学中常见的概念,它们在初中阶段的数学研究中起着重要的作用。
以下是一些常用的三角函数公式:
1. 正弦函数公式:
- 正弦函数的定义:在直角三角形中,对于一个锐角角度A,正弦函数的值等于对边与斜边的比值,可以表示为sin(A) = 对边/斜边。
2. 余弦函数公式:
- 余弦函数的定义:在直角三角形中,对于一个锐角角度A,余弦函数的值等于邻边与斜边的比值,可以表示为cos(A) = 邻边/斜边。
3. 正切函数公式:
- 正切函数的定义:在直角三角形中,对于一个锐角角度A,正切函数的值等于对边与邻边的比值,可以表示为tan(A) = 对边/邻边。
4. 余切函数公式:
- 余切函数的定义:在直角三角形中,对于一个锐角角度A,余切函数的值等于邻边与对边的比值,可以表示为cot(A) = 邻边/对边。
5. 正割函数公式:
- 正割函数的定义:在直角三角形中,对于一个锐角角度A,正割函数的值等于斜边与邻边的比值,可以表示为sec(A) = 斜边/邻边。
6. 余割函数公式:
- 余割函数的定义:在直角三角形中,对于一个锐角角度A,余割函数的值等于斜边与对边的比值,可以表示为csc(A) = 斜边/对边。
这些公式是初中数学中常用的三角函数公式,它们可以用来解决与三角函数相关的各种问题。
熟练掌握这些公式并灵活运用,有助于提高数学解题能力和理解几何概念的能力。

初中三角函数公式大全初中阶段主要学习的三角函数公式有正弦定理、余弦定理、正切定理以及诱导公式等。
下面将分别介绍这些公式。
一、正弦定理正弦定理是用来求解三角形的边长和角度的重要公式。
设三角形ABC的边长分别为a、b 和c,对应的角度分别为A、B和C,则正弦定理可以表示为:a/sinA = b/sinB = c/sinC根据正弦定理,如果我们已知两个角和它们对应的两条边的长度,可以通过公式求解第三条边的长度;如果我们已知一个角和它对应的两条边的长度,可以通过公式求解另外两个角的大小。
二、余弦定理余弦定理是在已知三角形的两边和夹角情况下,求解第三边的长度的重要公式。
设三角形ABC的边长分别为a、b和c,对应的角度分别为A、B和C,则余弦定理可以表示为:c² = a² + b² - 2abcosC根据余弦定理,如果我们已知三角形的两边和它们之间的夹角,可以通过公式求解第三边的长度;如果我们已知三角形的三个边长,可以通过公式求解任意一个角的大小。
三、正切定理正切定理是在已知三角形的两边和夹角情况下,求解切线斜率的重要公式。
设三角形ABC 的边长分别为a、b和c,对应的角度分别为A、B和C,则正切定理可以表示为:tanA = a/b根据正切定理,如果我们已知三角形的两边和它们之间的夹角,可以通过公式求解切线斜率;如果我们已知切线斜率和其中一条边的长度,可以通过公式求解夹角的大小。
四、诱导公式诱导公式是将不常用的角度转换为常用角度的公式,常用的诱导公式如下:sin(π-x) = sinxcos(π-x) = -cosxtan(π-x) = -tanxsin(π+x) = -sinxcos(π+x) = -cosxtan(π+x) = tanxsin(2π-x) = -sinxcos(2π-x) = cosxtan(2π-x) = -tanx其中,x为任意角度。
这些公式可以帮助我们在解决三角函数问题时进行角度的转化,简化计算过程。

初三数学三角函数值计算方法三角函数是初中数学中的一个重要概念,它在解决三角形和圆的相关问题中起着重要作用。
在计算三角函数值时,我们需要掌握一些常用的方法和公式。
本文将介绍初三数学中常用的三角函数值计算方法,帮助学生更好地理解和应用三角函数。
1. 正弦函数(sin)正弦函数是三角函数中最基本的函数之一。
计算正弦函数值的方法如下:- 对于已知角度的情况,可以查找三角函数表或使用计算器来求解。
例如,sin30°=0.5,sin45°=√2/2。
- 对于不常见角度的情况,可以利用三角函数的周期性进行换算。
例如,sin150°=sin(150°-180°)=-sin30°=-0.5,sin210°=sin(210°+180°)=sin30°=0.5。
- 对于任意角度的情况,可以利用正弦函数与余弦函数之间的关系进行计算。
例如,sin(180°-x)=sinx,sin(360°-x)=-sinx。
2. 余弦函数(cos)余弦函数也是三角函数中常用的函数之一。
计算余弦函数值的方法如下:- 对于已知角度的情况,可以查找三角函数表或使用计算器来求解。
例如,cos60°=0.5,cos90°=0。
- 对于不常见角度的情况,可以利用三角函数的周期性进行换算。
例如,cos210°=cos(210°-180°)=-cos30°=-√3/2,cos300°=cos(300°+180°)=cos120°=-0.5。
- 对于任意角度的情况,可以利用余弦函数与正弦函数之间的关系进行计算。
例如,cos(180°-x)=-cosx,cos(360°-x)=cosx。
3. 正切函数(tan)正切函数是三角函数中比较特殊的一个函数,计算正切函数值的方法如下:- 对于已知角度的情况,可以查找三角函数表或使用计算器来求解。



2019年中考数学必考:三角函数的公式总汇,家长:总结的太到位了三角函数的公式总汇:三角函数的公式关于初中三角函数公式,在考试中用的最多的就是特殊三角度数的特殊值。
如:sin30°=1/2sin45°=√2/2sin60°=√3/2cos30°=√3/2cos45°=√2/2cos60°=1/2tan30°=√3/3tan45°=1tan60°=√3[1]cot30°=√3cot45°=1cot60°=√3/3其次就是两角和公式,这是在初中数学考试中问答题中容易用到的三角函数公式。
两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)除了以上常考的初中三角函数公示之外,还有半角公式和和差化积公式也在选择题中用到。
所以同学们还是要好好掌握。
半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)t an(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosBtanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB- ctgA+ctgBsin(A+B)/sinAsinB初中三角函数的公式(二)锐角三角函数公式sin α=∠α的对边 / 斜边cos α=∠α的邻边 / 斜边tan α=∠α的对边/ ∠α的邻边cot α=∠α的邻边/ ∠α的对边倍角公式Sin2A=2SinA.CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1 tan2A=(2tanA)/(1-tanA^2)(注:SinA^2 是sinA的平方 sin2(A) )三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina辅助角公式Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B 降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2=2sina(1-sin2a)+(1-2sin2a)sina=3sina-4sin3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos2a-1)cosa-2(1-sin2a)cosa=4cos3a-3cosasin3a=3sina-4sin3a=4sina(3/4-sin2a)=4sina[(√3/2)2-sin2a]=4sina(sin260°-sin2a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos3a-3cosa=4cosa(cos2a-3/4)=4cosa[cos2a-(√3/2)2]=4cosa(cos2a-cos230°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)两角和差cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2]sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2诱导公式sin(-α) = -sinαcos(-α) = cosαtan (—a)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+tan^(α/2)]cosα=[1-tan^(α/2)]/1+tan^(α/2)]tanα=2tan(α/2)/[1-tan^(α/2)]其它公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC(9)sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+si n[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+c os[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0本人每天都为大家带来中考,高考一些重要知识点,每天不定时分享,各位考生以及家长及时关注,想要电子版的家长私信问小编要就可以了。
(完整版)初中三角函数公式表一、三角函数的基本定义在初中数学中,三角函数主要涉及正弦函数(sin)、余弦函数(cos)和正切函数(tan)。
这些函数与直角三角形的三边长度有着密切的关系。
1. 正弦函数(sin):正弦函数表示直角三角形中,对应于一个锐角的斜边与斜边与邻边之比。
公式为:sin(θ) = 对边 / 斜边。
2. 余弦函数(cos):余弦函数表示直角三角形中,对应于一个锐角的邻边与斜边之比。
公式为:cos(θ) = 邻边 / 斜边。
3. 正切函数(tan):正切函数表示直角三角形中,对应于一个锐角的斜边与邻边之比。
公式为:tan(θ) = 对边 / 邻边。
二、三角函数的相互关系1. 正弦函数和余弦函数的关系:sin(θ) = cos(90° θ),cos(θ) = sin(90° θ)。
2. 正切函数和余弦函数的关系:tan(θ) = sin(θ) / cos(θ)。
3. 正切函数和正弦函数的关系:tan(θ) = sin(θ) / cos(θ)。
三、三角函数的特殊值1. 0°:sin(0°) = 0,cos(0°) = 1,tan(0°) = 0。
2. 30°:sin(30°) = 1/2,cos(30°) = √3/2,tan(30°) =1/√3。
3. 45°:sin(45°) = √2/2,cos(45°) = √2/2,tan(45°)= 1。
4. 60°:sin(60°) = √3/2,cos(60°) = 1/2,tan(60°) = √3。
5. 90°:sin(90°) = 1,cos(90°) = 0,tan(90°) 无定义。
四、三角函数的周期性三角函数具有周期性,即函数值在一定的周期内会重复出现。
初三数学三角函数值的计算方法三角函数是数学中重要的概念之一,在初三数学学习中也占据了重要的地位。
计算三角函数值是初三数学的基础内容之一,本文将介绍三角函数值的计算方法。
一、正弦函数的计算方法正弦函数的计算是初三数学中最基础的内容,可以通过已知角度的正弦值表来计算。
以下是一些常见角度的正弦值表:角度 0° 30° 45° 60° 90°正弦值0 1/2 √2/2 √3/2 1例如,已知一个角度为45°,我们可以通过查表直接得出其正弦值为√2/2。
二、余弦函数的计算方法余弦函数的计算方法与正弦函数类似,也可以通过已知角度的余弦值表来计算。
以下是一些常见角度的余弦值表:角度 0° 30° 45° 60° 90°余弦值1 √3/2 √2/2 1/2 0例如,已知一个角度为60°,我们可以通过查表直接得出其余弦值为1/2。
三、正切函数的计算方法正切函数的计算方法稍微复杂一些,一般需要通过已知角度的正切值表来计算。
以下是一些常见角度的正切值表:角度 0° 30° 45° 60° 90°正切值0 √3/3 1 √3 不存在需要注意的是,正切函数在90°角时值不存在。
例如,已知一个角度为30°,我们可以通过查表直接得出其正切值为√3/3。
四、其他角度的计算方法对于非常见角度的计算,我们可以利用三角函数的性质通过已知角度的三角函数值来计算。
例如,已知一个角度为75°,我们可以利用正弦函数和余弦函数的性质来计算。
首先,我们可以将75°拆分为30°和45°两个常见角度的和,即75°=45°+30°。
然后,利用正弦函数和余弦函数的和角公式,可以得出正弦函数和余弦函数的关系式 sin(a + b) = sin(a)cos(b) + cos(a)sin(b)。
初三数学三角函数值计算方法详解三角函数是数学中常见的一类函数,它们的计算与应用广泛存在于数学的各个领域中。
对于初三学生来说,掌握三角函数值的计算方法是非常重要的,因为它是进一步学习和应用三角函数的基础。
本文将详细介绍初三数学中三角函数值的计算方法。
1. 正弦函数的计算方法正弦函数(简写为sin)常用于描述角度和边长之间的关系。
要计算一个角度的正弦值,需要按照以下步骤进行:a. 将角度转换为弧度:首先,将角度转换为弧度,用弧度与度之间的换算公式:弧度 = 度* π / 180。
这就是说,角度的弧度值等于角度值乘以圆周率π再除以180。
b. 计算正弦值:经过弧度转换后,使用计算器或查表等方式,找到对应角度的正弦值。
注意,正弦函数的值是一个介于-1和1之间的实数。
2. 余弦函数的计算方法余弦函数(简写为cos)也常用于描述角度和边长之间的关系。
要计算一个角度的余弦值,需要进行以下步骤:a. 将角度转换为弧度:与计算正弦值时的步骤相同,首先将角度转换为弧度。
同样地,用弧度与度之间的换算公式:弧度 = 度* π / 180。
b. 计算余弦值:经过弧度转换后,使用计算器或查表等方式,找到对应角度的余弦值。
和正弦函数一样,余弦函数的值也是介于-1和1之间的实数。
3. 正切函数的计算方法正切函数(简写为tan)常用于描述角度和边长之间的关系。
要计算一个角度的正切值,需要进行以下步骤:a. 将角度转换为弧度:同样地,将角度转换为弧度,使用换算公式:弧度 = 度* π / 180。
b. 计算正切值:经过弧度转换后,使用计算器或查表等方式,找到对应角度的正切值。
正切函数的值可以是任何实数。
4. 切比雪夫扩展函数的计算方法除了正弦函数、余弦函数和正切函数,还有其他类型的三角函数,其中切比雪夫扩展函数(简写为sec、cosec、cot)是常见的。
计算这些函数的值需要按照以下步骤进行:a. 先计算对应的余弦值、正弦值或正切值;b. 根据之前得到的值,求取其倒数来得到相应的切比雪夫扩展函数值。
2019中考数学三角函数公式集合数学是被很多人称之拦路虎的一门科目 ,同学们在掌握数学知识点方面还很欠缺 ,为此下文为大家整理了2019中考数学三角函数公式希望能够帮助到大家。
公式一:设α为任意角 ,终边相同的角的同一三角函数的值相等k是整数sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotαsec(2kπ+α)=secαcsc(2kπ+α)=cscα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsec(π+α)=-secαcsc(π+α)=-cscα公式三:任意角α与 -α的三角函数值之间的关系sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsec(-α)=secαcsc(-α)=-cscα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsec(π-α)=-secαcsc(π-α)=cscα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsec(2π-α)=secαcsc(2π-α)=-cscα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系sin(π/2+α)=cosαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsec(π/2+α)=-cscαcsc(π/2+α)=secαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsec(π/2-α)=cscαcsc(π/2-α)=secαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsec(3π/2+α)=cscαcsc(3π/2+α)=-secαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsec(3π/2-α)=-cscα为大家推荐的2019中考数学三角函数公式的内容 ,还满意吗?。