离散数学(2.5谓词演算的等价式与蕴含式)

格式：ppt
大小：81.00 KB
文档页数：8

下载文档原格式

离散数学-2-5谓词演算的等价式与蕴含式-PPT课件

姓。

(y)(x)A(x,y) 表示对于乙村所有的人，甲村都有人和他同姓。 (x)(y)A(x,y) 表示存在一个甲村的人，乙村所有人和他同姓。
上述四种语句，表达的情况各不相同，故全称量词与存在量词的次序，不能随意更换。
17
七、多个量词的使用
如下一蕴含式中不同量词间的次序是不可随意交换的。
15
七、多个量词的使用
例设 A(x,y)表示x和y同姓,论域x是甲村的人,y是
乙村的人 (x)(y)A(x,y): 甲村和乙村所有的人都同姓 ( y)(x)A(x,y)：乙村和甲村所有的人都同姓。显然上述俩语句的含义相同。故 (x)(y)A(x,y) (y)(x)A(x,y）
同理有：
(x)(y)A(x,y)：甲村与乙村有人同姓。 (y)(x)A(x,y)：乙村与甲村有人都同姓。故 (x)(y)A(x,y) (y)(x)A(x,y)
16
七、多个量词的使用
但是

(x)(y)A(x,y) 表示对于甲村所有的人，乙村都有人和他同姓。 (y)(x)A(x,y) 表示存在一个乙村的人，甲村所有的人和他同

1. 2. 3. 4.
(x)(A(x)B) (x)A(x)B (x)(A(x)B) (x)A(x)B (x)(A(x)B) (x)A(x)B (x)(A(x)B) (x)A(x)B
因为B中不出现约束变元 x,所以它属于或不属于量词作用域均有相同意义。
9
四．量词作用域的扩张与收缩
从1-4式还可推得如下几个式子：

5. 6. 7. 8.
((x)A(x)B)) (x)(A(x)B) ((x)A(x)B)) (x)(A(x)B) (B(x)A(x)) (x)(BA(x)) (B(x)A(x)) (x)(BA(x))

离散数学第2章谓词逻辑

命题“凡人要死。”符号化为：(x)F (x) ⑵ 令G(x)：x是研究生。命题“有的人是研究生。”符号化为：(x)G(x)
在命题函数前加上量词(x)和(x)分别叫做个体变元x 被全称量化和存在量化。一般地说，命题函数不是命题，如果对命题函数中所有命题变元进行全称量化或存在量化，该函数就变成了命题。这一结论在例2.3中得到验证。
为假。 ⑵ 如果5大于3，则2大于6。解：设G(x,y)： x大于y a：5，b：3，c：2，d：6 该命题符号化为：G(a,b)→G(c,d) G(a,b)表示5大于3，它是真命题。G(c,d)表示2大于6，
ห้องสมุดไป่ตู้这是个假命题。所以G(a,b)→G(c,d)为假。
(3) 2 是无理数, 而 3 是有理数解：设F(x): x是无理数, G(x): x是有理数符号化为 F( 2) G( 3) 真值为 0 (4) 如果2>3，则3<4 解：设 F(x,y): x>y, G(x,y): x<y, 符号化为 F(2,3)G(3,4) 真值为1
谓词：刻划个体性质或个体之间相互关系的模式叫做谓词。谓词常用大写英文字母表示，叫做谓词标识符。
例如可以用F，G，H表示上面三个命题中谓词： F：„是优秀共产党员。 G：„比„高。 H：„坐在„和„的中间。
第2章谓词逻辑
一元谓词：与一个个体相关联的谓词。如上例中的F。二元谓词：与两个个体相关联的谓词。如上例中的G。三元谓词：与三个个体相关联的谓词。如上例中的H。
返回章目录
第2章谓词逻辑
课外作业
• 教材P59-60页: 练习题（需要做在练习本上）（1）（2） a)、c) 、d)、e)、 f)、i)、k)、l)
返回章目录

离散数学谓词逻辑

例1 给定解释I1如下：
(1)个体域为自然数集合N； (2)N中的特定元素a=0；（3）F(x,y):x大于或等于y. 在解释I1下,求下列各式的真值： (1)(∀x)F(x,a)；(2)(∀x∃y)F(x,y) 解在解释I1下,公式分别解释为： (1)任何自然数都大于或等于零, 为真命题.
(2)对任一自然数x,都存在一自然数y使得x≥y, 为真命题.
4
例子
［例2-1.1］张明是位大学生。解：设S(x)：x是大学生,c：张明, 一元谓词：表则原句的谓词形式为S(c)。示客体性质［例2-1.2］我坐在张三和李四中间。解：设S(x,y,z)：x坐在y和z之间,i：我,z：张三,l：李四, 多元谓词：表示客体间关系则原句的谓词形式为S(i,z,l)。
★从以上两命题的符号化可以看出,同一命题在不同个体域下符号化的形式可能不同。
11
这里,M(x)称为特性谓词。应该注意的是,全称量词和存在量词符号化时,引入特性谓词时的形式是不同的。用全称量词符号化时,特性谓词作为条件式的前件；用存在量词符号化时则作为合取式的一项。
12
对于任一给定的实数x,都存在着一个实数y,使得 x+y=0。如果取个体域为实数集合 ∀ x ∃ y H(x, y ) 然而 ∃ y ∀ x H(x, y )：存在着一个少数y,对于任一实数x,使得x+y=0
3
谓词的表示
客体词有两种：客体常元和客体变元。客体常元表示具体的或特定的客体,一般用小写字母 a、b、c等表示；表示抽象的或泛指的客体的词称为客体变元,常用小写字母x、y、z等表示。谓词,通常用大写的字母A、B、C等表示。
谓词填式：单独一个谓词不是完整的命题, 把谓词字母后填以客体所得的式子。

2-5谓词演算的等价式

F(x)→G(y)⇔¬ ⇔¬F(x)∨G(y) ⇔¬ ∨
2-5.2 量词与联结词¬之间的关系量词与联结词¬ (quantifier)
定理：量词否定等价式（定理：量词否定等价式（P67）） (1)¬ (∀x)P(x) ⇔(∃x)¬P(x) ¬ ∀ ∃ ¬ (2) ¬ (∃x)P(x) ⇔(∀x)¬P(x) ∃ ∀ ¬ 可以在有限个体域中得到证明。可以在有限个体域中得到证明。
2-5. 3 量词作用域扩张与收缩
定理：量词作用域扩张与收缩等价式定理：量词作用域扩张与收缩等价式(P68) (1) (∀x)(A(x)∨B) ⇔ ((∀x)A(x)∨B) ∀ ∨ ∀ ∨ (∀x)(A(x)∧B) ⇔ ((∀x)A(x)∧B) ∀ ∧ ∀ ∧ (∃x)(A(x)∨B) ⇔ ((∃x)A(x)∨B) ∃ ∨ ∃ ∨ (∃x)(A(x)∧B) ⇔ ((∃x)A(x)∧B) ∃ ∧ ∃ ∧ 说明: 中不含x的出现说明 B中不含的出现中不含
例1: (∀x)(F(x)∨G(y)) ⇔ (∀x)F(x)∨G(y) ∀ ∨ ∀ ∨ 例2: (∀x)(∀y)(F(x)∧G(y)) ∀ ∀ ∧ ⇔(∀x)(F(x)∧(∀y)G(y)) ∀ ∧∀ ⇔ (∀x)F(x)∧(∀y)G(y) ∀ ∧∀ 例3: (∃x)(F(x)∨G(y)) ⇔ (∃x)F(x)∨G(y) ∃ ∨ ∃ ∨ 例4: (∀x)(∃y)(F(x)∧G(y)) ∀ ∃ ∧ ⇔(∀x)(F(x)∧(∃y)G(y)) ∀ ∧∃ ⇔(∀x)F(x)∧(∃y)G(y) ∀ ∧∃
2-5谓词演算的等价式谓词演算的等价式
定义2：谓词逻辑有效永真永真)式定义：谓词逻辑有效(永真式 (tautology)：：给定任意谓词公式wff A，其个体域为，给定任意谓词公式，其个体域为E，对于A的所有赋值的所有赋值，都为真，对于的所有赋值，wff A都为真，则称都为真则称wff A 上是有效在E上是有效（永真）式。上是有效（永真）命题逻辑永真式（重言式）: 命题逻辑永真式（重言式）给定一个命题公式，给定一个命题公式，若无论对分量作怎样的指派，其对应的真值永为T，的指派，其对应的真值永为，则称命题公式为重言式或永真公式。为重言式或永真公式。

天津理工大学《离散数学》教学教案(第二章)

47
《离散数学》教学教案
全称量词和存在量词统称为量词。可以用个体、谓词和量词将命题符号化，并且可以刻划命题的内在结构以及命题之间的关系。因此，引进个体、谓词和量词后，用形式符号表示命题的功能得到加强，表达意思更加全面、确切。例 2.1.4 符号化下列命题。（1）所有的人是要呼吸的。（2）任何整数或是正的或是负的。（3）有些人是聪明的。（4）有的人早饭吃面包。解（1） x( M ( x) H ( x)) ，其中 M ( x) ： x 是人。 H ( x) ： x 要呼吸的。
需要指出的是，在谓词演算的原子公式中不能出现命题联结词和量词。定义 2.2.1 谓词演算的合式公式定义如下：（1）原子谓词公式是合式公式。（2）若 A 是合式公式，则 A 也是合式公式。（3）若 A 和 B 是合式公式，则 A B ， A B ， A B 与 A B 是合式公式。（4）若 A 是合式公式， x 是 A 中出现的任何变元，则 xA 和 xA 都是合式公式。（5）只有经过有限次地应用规则（1）、（2）、（3）、（4）所得到的公式是合式公式。谓词演算的合式公式，简称为谓词公式(Predicate Formula)。由定义可知，命题公式也是谓词公式，因此命题逻辑包含在谓词逻辑中。谓词公式中的某些括号也可以省略，其规定与命题公式相同，但量词后若有括号则不能省略。
P Q R 并不是永真式，所以借助命题演算的推理理论不能证明其为重言式。
45
《离散数学》教学教案
为了克服命题逻辑的局限性，我们有必要对原子命题的结构作进一步的细分，划分出个体词、谓词和量词，研究它们的形式结构和逻辑关系、正确的推理形式和规则，这就是谓词逻辑的基本内容。

离散数学串讲

第一章命题逻辑1.1 命题及其表示方法1.2 联结词1.3 命题公式与翻译1.4 真值表与等价公式1.5 重言式与蕴含式1.6 其它联结词1.7 对偶与范式1.8 推理理论1.1 命题及其表示方法命题：具有确定真值的陈述句命题的类型（原子命题和复合命题）命题语句的形式（陈述句）命题的表示（一个命题标识符（比如P）表示确定的命题）1.2 联结词1. 否定⌝2.合取∧（TT T）3. 析取∨（FF F）4. 条件→(TF F)5. 双条件↔(同T异F)1.3 命题公式与翻译命题公式●所谓命题的符号化就是把一个用文字叙述的句子相应地写成由命题标识符、联结词和括号表示的合式公式。

●符号化应该注意下列事项:•①确定给定句子是否为命题。

•②句子中连词是否为命题联结词。

•③要正确地表示原子命题和适当选择命题联结词。

命题符号化的重要性●命题符号化是很重要的，一定要掌握好，在命题推理中最先遇到的就是符号化一个问题，解决不好，等于说推理的首要前提没有了。

1.4 真值表与等价公式真值表的构造方法1) 找出公式中所含的全体命题变元P1, P2, …, Pn, (若无下角标就按字典顺序排列), 列出2n个赋值. 赋值从00…0开始, 然后按二进制加法依次写出各赋值, 直到11…1为止.(2) 按从低到高的顺序写出公式的各个层次.(3) 对应各个赋值计算出各层次的真值, 直到最后计算出公式的真值.等价公式等价式的判别方法•真值表法•等价演算法基本等价式(1)对合律（双重否定）：⌝⌝P⇔P(2)幂等律：P∧P⇔P，P∨P⇔P(3)结合律：(P∧Q)∧R⇔P∧(Q∧R)，(P∨Q)∨R⇔P∨(Q∨R)(4)交换律：P∧Q⇔Q∧P，P∨Q⇔Q∨P(5)分配律：P∧(Q∨R)⇔(P∧Q)∨(P∧R)，P∨(Q∧R)⇔(P∨Q)∧(P∨R)(6)德·摩根律：⌝ (P∧Q) ⌝⇔P∨⌝Q，⌝ (P∨Q) ⌝⇔P∧⌝Q(7)吸收律：P∧(P∨Q)⇔P，P∨(P∧Q)⇔P(8)同一律：P∧T⇔P，P∨F⇔P(9)零律：P∧F⇔F，P∨T⇔T(10)否定律：P∧⌝P⇔F，P∨⌝P⇔T(11) 条件式转化律：P→Q⌝⇔P∨Q，P→Q⌝⇔Q→⌝P(12) 双条件式转化律：P↔Q ⇔(P→Q)∧(Q→P) ⇔(P∧Q)∨(⌝P∧⌝Q)⌝ (P↔Q) ⇔P⌝↔Q ⌝⇔P↔Q(13) 输出律(CP规则)：P→(Q→R) ⇔(P∧Q)→R1.5 重言式与蕴含式●定义1-5.1 给定一命题公式，若无论对分量作怎样的指派，其对应的真值永为真，则称该命题公式为重言式或永真公式。

第三讲谓词演算的等价式与蕴涵式

2.3 量词作用域的扩张与收缩 (x) (A(x) ∨B) (x) A(x)∨B 析取和 (x) (A(x) ∧B) (x) A(x)∧B 合取 (x) (A(x) ∨B) (x) A(x)∨B (x) (A(x) ∧B) (x) A(x)∧B (x)(A(x)B) (x)A(x)B 注意：B不会是 B(x), 可以是B(y)
谓词公式为不可满足的谓词公式为可满足的
2. 等价式与蕴 (x)(P(x) ∨Q(x)) (x) P(x) (y)Q(y) (x) P(x) ∨ (y)Q(y)
2.2 量词与联接词之间的关系 (x) P(x) (x) P(x) (x) P(x) (x) P(x) (1)没有不犯错误的人。设论域：我们班学生 P(x)：x今天来上课
第3讲：谓词演算的等价式与蕴涵式
1. 概念 • • • • • 谓词公式中常含客体变元和命题变在共同个体域 E上的两个谓词公式A 元，用确定的客体取代客体变元，和 B，若对A、B上的任一组变元进对谓词公式赋值用确定的命题取代命题变元，称为行赋值，所得命题的真值都相同，对谓词公式赋值。则称谓词公式 A、B等价。谓词公式等价 A在E上所有赋谓词公式A在个体域E上是有效的值都为T 所有赋值都为F 至少有一种赋值为T
(x) (A(x) B) (x) A(x) B 条件式 (x)(A(x) B) (x) A(x) B (x)(B A(x) ) B (x) A(x) (x) (B A(x) ) B (x) A(x)
设B为假，A(x)在论域中有真有假，则： (x) (A(x) B) 为假 (x) A(x) B 为真
?
见书P68证明
2.4 量词的分配律 (x) (A(x) ∧B(x)) (x) A(x)∧ (x) B(x) (x) (A(x) ∨B(x)) (x) A(x) ∨ (x)B(x) 设论域：我们班学生 A(x)：x聪明 B(x)：x勤奋 2.5 量词与联结词之间的一些蕴涵式 ( x) (A(x) ∧B(x)) ( x) A(x)∧ (x) B(x) (x) A(x) ∨(x)B(x) (x) (A(x) ∨B(x)) 设客体域：整数集合，A(x) : x是偶数， B(x): x是奇数。 ( x) (A(x) ∧B(x)) 有些整数既是奇数又是偶数。

离散数学(2.3谓词公式与翻译)

离散数学(Discrete Mathematics)
1
第二章谓词逻辑（Predicate Logic）
2.1谓词的概念与表示(Predicate and its expression) 2.2命题函数与量词(Propositional functions & Quantifiers) 2.3谓词公式与翻译(Predicate formulae) 2.4变元的约束(Bound of variable) 2.5谓词演算的等价式与蕴含式(Equivalences &
implications of predicate calculus)
2.6前束范式(Prenex normal form)
2.7谓词演算的推理理论(Inference theory of predicate calculus)
2
第二章谓词逻辑（Predicate Logic）
2.3谓词公式与翻译(Predicate formulae)
5
第二章谓词逻辑（Predicate Logic）
2.2命题函数与量词(Propositional functions &
Quantifiers)
• 例2：在谓词逻辑中将下列命题符号化. （1）所有运动员都钦佩某些教练. （2）有些运动员不钦佩教练. 设：L(x):x是运动员 J(y):y是教练 A(x,y):x钦佩y (1) (x)(L(x) （y)(J(y)∧A(x,y)))
(Q(δ,0)∧(Q(δ , x a)Q(ε,
f ( x) f ()a ) ). ))
8
第二章谓词逻辑（Predicate Logic）
2.2命题函数与量词(Propositional functions &

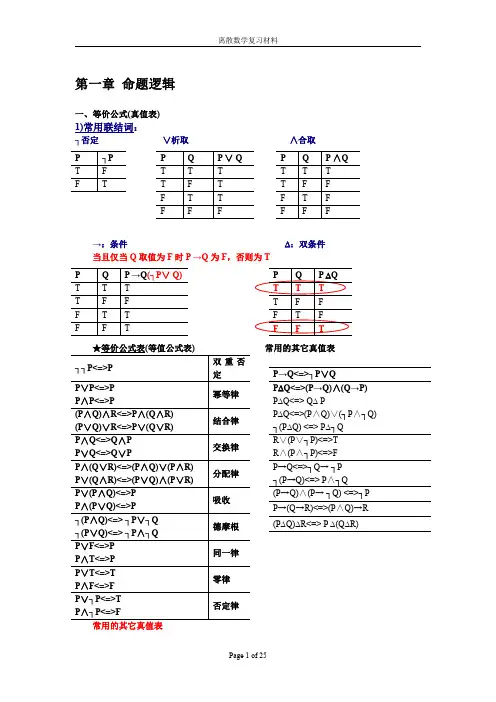
离散数学部分概念和公式总结(精简版)

第一章命题逻辑一、等价公式(真值表)1)常用联结词：┐否定∨析取∧合取→：条件∆：双条件当且仅当Q 取值为F 时P →Q 为F ，否则为T ★等价公式表(等值公式表)常用的其它真值表┐┐P<=>P 双重否定P ∨P<=>P P ∧P<=>P幂等律(P ∧Q)∧R<=>P ∧(Q ∧R)(P ∨Q)∨R<=>P ∨(Q ∨R)结合律P ∧Q<=>Q ∧P P ∨Q<=>Q ∨P交换律P ∧(Q ∨R)<=>(P ∧Q)∨(P ∧R)P ∨(Q ∧R)<=>(P ∨Q)∧(P ∨R)分配律P ∨(P ∧Q)<=>P P ∧(P ∨Q)<=>P 吸收┐(P ∧Q)<=>┐P ∨┐Q ┐(P ∨Q)<=>┐P ∧┐Q 德摩根P ∨F<=>P P ∧T<=>P 同一律P ∨T<=>T P ∧F<=>F 零律P ∨┐P<=>T P ∧┐P<=>F否定律常用的其它真值表P ┐P T F FTP Q P ∨Q T T T T F T F T T FFFP Q P ∧Q T T T T F F F T F F FFP Q P →Q (┐P ∨Q)T T T T F F F T T FFTP→Q<=>┐P ∨Q P ∆Q<=>(P→Q)∧(Q→P)P ∆Q<=>Q ∆PP ∆Q<=>(P ∧Q)∨(┐P ∧┐Q)┐(P ∆Q)<=>P ∆┐Q R ∨(P ∨┐P)<=>T R ∧(P ∧┐P)<=>F P→Q<=>┐Q→┐P ┐(P→Q)<=>P ∧┐Q (P→Q)∧(P→┐Q)<=>┐P P→(Q→R)<=>(P ∧Q)→R (P ∆Q)∆R<=>P ∆(Q ∆R)命题公式的类型：(1)若A在它的各种赋值下均取值为真，则称A为重言式或永真式。

离散数学_谓词逻辑

(3) 当个体域为全体整数的集合时：令P(x): x是正的。N(x): x是负的。则（3）符号化为（x）(P(x)∨N(x)) 当个体域为全总个体域时：令I(x): x是整数。则（3）符号化为（x）(I(x)(P(x)∨N(x))).
全称量词的一些重要性质：设P是任意的命题，F(x)与A(x,y)均为谓词，则有：
【例】设 P 表示命题：张辉是工人。 Q 表示命题：李明是工人。仅仅从命题符号 P 和 Q 看不出张辉和李明都是工人这一特性。【例】 x=3 ? x+y=z ? f(x)=0 ?
第二章谓词逻辑（Predicate Logic）
2.1 谓词的概念与表示(Predicate and Its Expression)
2.1 谓词的概念与表示(Predicate and Its Expression) 谓词：用来刻划个体的性质或个体之间的相互关系的词。例如在下面命题中：（1）张明是个劳动模范。（2）李华是个劳动模范。刻划客体的性质（3）王红是个大学生。（4）小李比小赵高2cm。（5）点a在b与c之间。刻划客体之间的相互关系（6）阿杜与阿寺同岁。（7） x与y具有关系L。 “是个劳动模范”、“是个大学生”、“…比…高2cm”、 “… 在…与…之间”、“…与…具有关系L”都是谓词。
2.1 谓词的概念与表示(Predicate and Its Expression)

（2）当个体域为人类集合时：令G(x): x活百岁以上。则（2）符号化为（ x）G(x) 当个体域为全总个体域时：令M(x): x是人。则（2）符号化为（x） (M(x) ∧ G(x))
存在量词的一些重要性质：设P是任意的命题，F(x)与A(x,y)均为谓词，则有：

离散数学第2章谓词逻辑

2-2 命题函数与量词
这里有一些人，Exist x,用反写 — 存在变量词，用于表示个体域中的某些客体（1）（x）（N（x） P（x））
（2）（x）（M（x） R（x））（3）（x）（M（x） E（x））全称量词与存在量词统称为量词，每个由量词确定的表达式，都与个体域有关，如：（x）（M（x） H（x）） M（x）是用于限定H（x）中的个体域， M (x）称为特性谓词，限定客体变元变化范围的谓词当限定范围为M（x）中时，可简写为：（x）（H（x））此命题对于论域为人类时，是正确的，而对于自然数则是FALSE，因为我们是讨论带有量词的命题函数时，必须确定其个体域，把特性谓词写出来。并且，为了方便，我们将所有命题函数的个体域全都统一，使用全总个体域。对变化范围用特性谓词加以限制。一般地，对全称量词，将特性谓词作为前提条件，命题通常写成条件式，对存在量词，常将之作为合取项。
定义：H是n元谓词，a1,a2,a3……an是n个客体，H(a1,a2……an)所代表的式子是一个命题，称为谓词填式。（当ai是客体时，A(a1…an) 才是命题。）
3 除了谓词，我们今后还要用到函数这一概念例：老张是小张的父亲。小张的父亲=老张
f:….的父亲； a:小张； b:老张；则b=f(a)
所以 (x)(M (x) F(x))也就是(x)(M (x) F(x))
(5)肖阳的爸爸到北京去了。 “…到…去了”是谓词。F(x,y): x到y去了。a:肖阳, f(x):x的爸爸， b:北京所以F(f(a),b) (6)谢世平和他的父亲及祖父三人一起去看演出。
F(x,y,z): x,y和z一起去看演出
H(1,c) H(c,1) :张三、李四一样高
例3：P(x): x是大学生 x的个体域：某大学中某班 P(x)永真 x的个体域：某中学中某班 P(x)永假 x的个体域：某剧场中观众 P(x)有真有假

谓词演算的等价式和蕴含式

（9） x(H ( x ) S ( x )) （10）H (a ) S (a )
B xA( x ) x( B A( x ))
xP( x ) xQ( x ) x( P ( x ) Q( x ))
x( P( x ) Q( x )) xP( x ) xQ( x )
xA( x ) xB( x ) x( A( x ) B( x ))
x( A( x ) B) xA( x ) B
x( A( x ) B) xA( x ) B
xA( x ) B x( A( x ) B)
xA( x ) B x( A( x ) B)
B xA( x ) x( B A( x ))
x (H ( x ) S ( x )) x ( H ( x ) C ( x )) x (C ( x ) E ( x )) xE ( x )
xS( x )
证明：（1）xE ( x ) （2） E (a ) （3）x(C ( x ) E ( x )) （4） C (a ) E (a ) （5） C (a ) （6）x( H ( x ) C ( x )) （7） H (a ) C (a )
I15
I16
例2-15用谓词演算的等价式和蕴含式证明（1）x( P ( x ) Q( x )) xP( x ) xQ( x ) （2） xy( P( x ) Q( y )) xP( x ) yQ( y ) （3） x( P( x ) Q( x )) xP( x ) xQ( x ) 证明(1)： x( P( x ) Q( x ))
如果论域D中的任意一个个体c，都能使A(c)成立，则由该规则可得结论成立。注意，此时的个体c不是论域中某一特定的个体，而是泛指论域中所有的个体。

自考离散数学第2章

域E，若对 A和B的任一组变元进行赋值，所得命题的真值相同，则称谓词公式A和B在E上是等价的，并记作 A B
定义2.3.2 给定任意谓词公式WffA，其个体域为E，对于A的所有赋值
WffA都为真，则称WffA在E上有效的（或永真的）
定义2.3.3 一个谓词公式WffA，如果在所有赋值下都为假，则称WffA
P
（2）H(s)→M(s)
（3）H(s) （4）M(s)
US(1)
P T(2)(3)I
2.5 谓词演算的推理理论
例：专业委员会成员都是教授，并且是计算机设计师，有些成员是资
深专家，所以有的成员是计算机设计师，且是资深专家。请用谓词推理理论证明上述推理。
证：设个体域为全总个体域。 M(x):x 是专业委员会成员； H(x):x 是教授； G(x):x 是计算机设计师；
2.3 谓词演算的等价式与蕴含式
表2.3.1
2.3 谓词演算的等价式与蕴含式
2.3 谓词演算的等价式与蕴含式
2.3 谓词演算的等价式与蕴含式
2.4 前束范式
定义2.4.1 一个公式，如果量词均在全式的开头，它们的作用域，延伸
到整个公式的末尾，则该公式叫做前束范式。
定理2.4.1 任意一个谓词公式均和一个前束范式等价。
2.3 谓词演算的等价式与蕴含式
例：寻求下式的真值。
(x)(P Q( x)) R(a) ，其中P:2>1,Q(x):x≦3，R(x):x>5,a=5，
且论域{-2,3,6}
2.3 谓词演算的等价式与蕴含式
2.3 谓词演算的等价式与蕴含式
定义2.3.1 给定任何两个谓词公式 WffA和WffB，设它们有共同的个体

离散数学

第一章命题逻辑1.1 命题及其表示方法1.2 联结词1.3 命题公式与翻译1.4 真值表与等价公式1.5 重言式与蕴含式1.6 其它联结词1.7 对偶与范式1.8 推理理论1.1 命题及其表示方法命题：具有确定真值的陈述句命题的类型（原子命题和复合命题）命题的表示（一个命题标识符（比如P）表示确定的命题）重点：如何判断语句是否为命题。

1.2 联结词否定⌝合取∧析取∨条件→双条件↔重点：五种联结词的含义、真值表1.3 命题公式与翻译命题公式符号化：所谓命题的符号化就是把一个用文字叙述的句子相应地写成由命题标识符、联结词和括号表示的合式公式。

命题符号化的重要性命题符号化是很重要的，一定要掌握好，在命题推理中最先遇到的就是符号化一个问题，解决不好，等于说推理的首要前提没有了。

重点：命题的符号化符号化应该注意下列事项:①确定给定句子是否为命题。

②句子中连词是否为命题联结词。

③要正确地表示原子命题和适当选择命题联结词。

1.4 真值表与等价公式真值表的构造方法(1) 找出公式中所含的全体命题变元P1, P2, …, Pn, (若无下角标就按字典顺序排列), 列出2n个赋值. 赋值从00…0开始, 然后按二进制加法依次写出各赋值, 直到11…1为止.(2) 按从低到高的顺序写出公式的各个层次.(3) 对应各个赋值计算出各层次的真值, 直到最后计算出公式的真值.等价关系的含义等价式的判别方法•真值表法•等价演算法基本等价式（必须掌握）(1)对合律（双重否定）：⌝⌝P⇔P(2)幂等律：P∧P⇔P，P∨P⇔P(3)结合律：(P∧Q)∧R⇔P∧(Q∧R)，(P∨Q)∨R⇔P∨(Q∨R)(4)交换律：P∧Q⇔Q∧P，P∨Q⇔Q∨P(5)分配律：P∧(Q∨R)⇔(P∧Q)∨(P∧R)，P∨(Q∧R)⇔(P∨Q)∧(P∨R)(6)德·摩根律：⌝ (P∧Q) ⌝⇔P∨⌝Q，⌝ (P∨Q) ⌝⇔P∧⌝Q(7)吸收律：P∧(P∨Q)⇔P，P∨(P∧Q)⇔P(8)同一律：P∧T⇔P，P∨F⇔P(9)零律：P∧F⇔F，P∨T⇔T(10)否定律：P∧⌝P⇔F，P∨⌝P⇔T(11) 条件式转化律：P→Q⌝⇔P∨Q，P→Q⌝⇔Q→⌝P(12) 双条件式转化律：P↔Q ⇔(P→Q)∧(Q→P) ⇔(P∧Q)∨(⌝P∧⌝Q)⌝ (P↔Q) ⇔P⌝↔Q ⌝⇔P↔Q(13) 输出律(CP规则)：P→(Q→R) ⇔(P∧Q)→R重点：等价式的证明、基本等价式1.5 重言式与蕴含式重言式或永真公式定义1-5.1 给定一命题公式，若无论对分量作怎样的指派，其对应的真值永为真，则称该命题公式为重言式或永真公式。

离散数学自考第二章

定义 1.辖域（作用域）：紧接在量词后面括号内的谓词公式。辖域（辖域作用域）
例： ∀xP(x) , ∃x(P(x) ∧Q(x)) 。若量词后括号内为原子谓词公式，则括号可以省去。
2.指导变元（作用变元）：紧接在量词后面括号内的X。指导变元（作用变元）指导变元 3.约束变元：在量词的辖域内，且与量词下标相同的变元。约束变元：约束变元 4.自由变元：当且仅当不受量词的约束。自由变元：自由变元
例：张华是学生，李明是学生。则可把它表示成： H:表示“是学生”，j:表示“张华”，m:表示“李明”，则可用下列符号表示上述二个命题：H(j)，H(m)。
1. 命题函数
客体在谓词表达式中可以是任意的名词。例：C—“总是要死的。” j：张三；t：老虎；e：桌子。则C(j), C(t), C(e)均表达了命题。在上面的例子中，C：表示“总是要死的”；x：表示变元（客体变元），则C(x)表示“x总是要死的”，则称C(x)为命题函数。定义》《定义》由一个谓词字母和一个非空的客体变元的集合所组成的表达式，称为命题函数。
2.区别是命题还是命题函数的方法（a）若谓词公式中出现自由变元，则该公式为命题函数；（b）若谓词公式中的变元均为约束出现，则该公式为命题。
例： ∀xP(x,y,z)是二元谓词， ∃y∀xP(x,y,z)是一元谓词，而谓词公式中如果没有自由变元出现，则该公式是一个命题。
3.代入规则：对公式中的自由变元的更改叫做代入。代入规则：代入规则 (a)对公式中出现该自由变元的每一处进行代入， (b)用以代入的变元与原公式中所有变元的名称不能相同。
∃x (A(x) ∨B(x)) ⇔ ∃xA(x) ∨ ∃xB(x) ∀x(A(x)∧B(x)) ⇔ ∀xA(x)∧ ∀xB(x) (∃x (A(x) → B(x)) ⇔ ∀xA(x) → ∃xB(x) ∀xA(x) ∨ ∀xB(x) ⇒ ∀x(A(x) ∨ B(x)) x(A(x) ∧ B(x)) ⇒ ∃ x（A(x) ∧ B(x)） ∃xA(x) → ∀xB(x) ⇒ ∀x(A(x) → B(x))

2-5谓词演算的等价式和蕴含式2-6前束范式

(x)（(y)(F(x)∧G(y)H(x,y))）
(x)(y)（(F(x)∧G(y))H(x,y)）
(x)(y)（（F(x)∧G(y))∨H(x,y)）
(x)(y)（（F(x)∧G(y)）∧ H(x,y)）
(x)(y)（F(x)∧G(y)∧ H(x,y)）
解： (x) F(x) ∧ (x) G(x)
(x) F(x) ∧ (x) G(x)
(x) (F(x) ∧ G(x)) 或 (x) F(x) ∧ (x) G(x) (x) F(x) ∧ (x) G(x) (x) F(x) ∧ (y) G(y)
(量词否定等价式)
因此A(a), B(a)皆为假, 所以(x)A(x)和(x)B(x)为假，即 (x)A(x)∨(x)B(x)为假。
故(x)A(x)∨(x)B(x)(x)(A(x)∨B(x))
证明
(x)(A(x)→B(x))(x)A(x)→(x)B(x)
(x)(A(x)→B(x)) ∧(x)A(x)
离散数学Ⅰ
Discrete Mathematics Ⅰ
封筠
fengjun@ ftp://202.206.41.4:8821/ User: Student.fengjun
12-04
课程回顾
变元约束的概念：指导变元、作用域、约束变元、自由变元、闭式约束变元换名、自由变元代入谓词公式的赋值、谓词公式的等价谓词公式的分类：永真、永假、可满足谓词演算的等价式和蕴含式：命题公式的推广、量词否定等价式（谓词演算中的对偶原理）、量词扩张/收缩律、量词与命题联结词之间的一些等价式（量词分配律）
(x){(y) A( x, y) (x)(y)[B( x, y) (y)(A( y, x) B( x, y))]}

离散数学谓词逻辑三段论逻辑推理例题证明

(3)(F(x，y)R(x，y))∧R(x，y)。
(4)xyF(x，y)xyF(x，y)。
2.5 谓词演算的等价式与蕴涵式
2.5.1 等价式 2.5.2 蕴涵式
2.5.1 等价式
定义2.13 设A和B是谓词公式，若AB为逻辑有效式，则称A和B是等价的，记为AB。
下面给出一些常见的基本谓词公式等价式。
2.4.2 谓词公式的分类
定义2.11 设A是一谓词公式，如A在任何解释下都是真的，称A为永真式或逻辑有效式；如A在任何解释下都是假的，称A为矛盾式；若至少存在一个解释使A为真，称A是可满足式。
例2 判断下列公式的类型(永真式、矛盾式、可满足式)：
(1)xF(x)xF(x)。
(2)xF(x)(xyG(x，y)xF(x))。
定理2.8 任何谓词公式的前束范式都存在。
例1 求下列公式的前束范式： (1)xF(x)∧xG(x)。 (2)xF(x)yG(x，y)。 (3)xF(x)xG(x)。 (4)xF(x)xG(x)。 (5)(xP(x)∨yQ(y))xR(x)。
1、全称量词消去规则(US)
若个体域为{a1，a2，…，an}，则有下式成立： (1)xA(x)A(a1)∧A(a2)∧…∧A(an)； (2)xA(x)A(a1)∨A(a2)∨…∨A(an)。
若个体域为{a1，a2，…，an}，则有下式成立： (1)xA(x)A(a1)∧A(a2)∧…∧A(an)； (2)xA(x)A(a1)∨A(a2)∨…∨A(an)。
例4 证明x(P(x)∨Q(x))，xP(x) ├ xQ(x)。
例5 (1)只要今天天气不好，就一定有考生不能提前进入考场，当且仅当所有考生提前进入考场，考试才能准时进行。所以，如果考试准时进行，那么天气就好。

离散数学第二章谓词逻辑

则xP和xP都是谓词公式
(5)当且仅当能够有限次地应用(1)－(4)所得到的
式子是谓词公式
二、谓词公式的概念

谓词公式是命题公式的扩展，约定最外层圆括号可以省略，但量词后面若有括号则不省略。

例如 (P(x,y)→(Q(x)→R(y,z)))
P(x,y,z)∧(P(x,y,z)→Q)
y((A(x)∧A(y))→F(x,y,0))
2.2 命题函数与量词

例2.2.6 翻译命题
甲村人与乙村人都同姓。
解设A(x)：x是甲村人。 B(y)：y是乙村人。 P(x,y)：x与y同姓。 (1)全总个体域 xy((A(x)∧B(y))→P(x,y)) (2)x的论域:甲村人 xy(P(x,y)) y的论域:乙村人
1.令F(x)：x是金属。G(y)：y是液体。H(x,y)：x可以溶解在y 中。则命题“任何金属可以溶解在某种液体中。”可翻译为（）。 A．x(F(x)∧y(G(y)∧H(x,y))) B．xy(F(x)→(G(y)→H(x,y))) C．x(F(x)→y(G(y)∧H(x,y))) D．x(F(x)→y(G(y)→H(x,y))) 2.令F(x)：x是火车。G(y)：y是汽车。H(x,y)：x比y快。则命题“某些汽车比所有火车慢。”可翻译为（）。 A.y(G(y)→x(F(x) ∧H(x,y))) B.y(G(y)∧x(F(x)→H(x,y))) C.xy(G(y)→(F(x)∧H(x,y))) D.y(G(y)→x(F(x)→H(x,y)))
由一个谓词常量或谓词变量A，n(n≥0)个个体变量 x1,x2,…,xn组成的表达式A(x1,x2,…,xn) 注意：0元谓词是命题，谓词逻辑是命题逻辑的扩展。

离散数学21.谓词演算的等价式

(x)(A(x)∨B(x)) (A(a1)∨B(a1))∨(A(a2)∨B(a2))∨…∨(A(an)∨B(an)) (A(a1)∨A(a2)∨...∨A(an))∨(B(a1)∨B(a2)∨...∨B(an)) (x)A(x)∨(x)B(x)
1. (x)P(x)(x)P(x)； 2. (x)P(x)(x)P(x). 对这两个公式可以证明如下：证明：设论域为{a1,a2,....,an}，则 (x)P(x)(P(a1)∧P(a2)∧...∧P(an))
P(a1)∨P(a2)∨...∨P(an)(x)P(x). 类似可以证明另一个公式.
(x)P(x)表示：不是所有人都是优等生.
(x) P(x)表示：有些人不是优等生.
(x)P(x)表示：没有人是优等生.
(x)P(x)表示：所有人都不是优等生.
显然：
“不是所有人都是优等生.”与“有些人不是优等生.”是等价的.
“没有人是优等生.”与“所有人都不是优等生.”是等价的.于是有：
从这两个公式，可以总结出如下规律：
将量词前的“”移到量词的后边，全称量词改成存在量词，存在量词改成全称量词;反之也要做相应改变.
4、量词作用域的扩张与收缩
在量词的作用域中，对于合取或者析取项，如果其中一个为命题，则可将该命题移直量词辖域外.
1. (x)(A(x)∨B)(x)A(x)∨B； 2. (x)(A(x)∧B)(x)A(x)∧B； 3. (x)(A(x)∨B)(x)A(x)∨B； 4. (x)(A(x)∧B)(x)A(x)∧B； 5. (x)A(x)→B(x)(A(x)→B)； 6. (x)A(x)→B(x)(A(x)→B)； 7. B→(x)A(x)(x)(B→A(x))；
谓词演算的等价式

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（x）（A(x)∧B）（x）A(x)∧ B
（x）（A(x)∨B）（x）A(x)∨B
（x）（A(x)∧B）（x）A(x)∧B
6
第二章谓词逻辑（Predicate Logic）
2.5谓词演算的等价式与蕴含式
• 量词辖域的扩张
（xA(x)B）（x) (A(x) B） (（x)A(x) B)(x) (A(x)B） (B (x)A(x)）（x)(B A(x)） (B (x)A(x))(x)(B A(x)) 另有多个公式见课本70页
• 2、量词与之间的关系（x）P(x) （x） P(x) （x）P(x）（x） P(x)
5
第二章谓词逻辑（Predicate Logic）
2.5谓词演算的等价式与蕴含式
• 3、量词辖域的扩张与收缩量词辖域中如果有合取或析取项，且其中有一个是命题，则可将该命题移至量词辖域之外。如：（x）（A(x)∨B）（x）A(x)∨B
• 4、量词分配等值式
设A(x)、B(x)是任意的含自由出现个体变元x的公式，则 (1) x(A(x)∧B(x)) x A(x) ∧ x B(x) (2)x(A(x)∨B(x)) x A(x) ∨ x B(x) (3)x(A(x)∨B(x)) ≠ x A(x)∨ x B(x) (4) x(A(x)∧B(x)) ≠ x A(x)∧ x B(x)
implications of predicate calculus)
2.6前束范式(Prenex normal form)
2.7谓词演算的推理理论(Inference theory of predicate calculus)
2
Байду номын сангаас
第二章谓词逻辑（Predicate Logic）
2.5谓词演算的等价式与蕴含式
2.5谓词演算的等价式与蕴含式(Equivalences &
calculus) 2.5.1谓词的等价和永真的概念 2.5.2谓词演算的等价式与蕴含式
implications of predicate
3
第二章谓词逻辑（Predicate Logic）
2.5谓词演算的等价式与蕴含式
2.5.1谓词的等价和永真的概念定义2.5.1:给定任意的谓词公式A,其个体域为E,对于A的所有赋值,公式A都为真,则称A在E上是永真的(或有效的);若对于A的所有赋值,公式A都为假,则称A在E上是永假的(或不可满足的);若至少存在着一种赋值使得公式A为真,则称A在E上是可满足的. • 定义2.5.2:给定任何两个谓词公式A、B，设它们有共同的个体域E，若对A和B的任一组变元进行赋值，所得命题的真值相同，则称谓词公式A和B在E上等价，并记为A B
离散数学(Discrete Mathematics)
1
第二章谓词逻辑（Predicate Logic）
2.1谓词的概念与表示(Predicate and its expression) 2.2命题函数与量词(Propositional functions & Quantifiers) 2.3谓词公式与翻译(Predicate formulae) 2.4变元的约束(Bound of variable) 2.5谓词演算的等价式与蕴含式(Equivalences &
7
第二章谓词逻辑（Predicate Logic）
2.5谓词演算的等价式与蕴含式
• 小结：本节介绍了约束变元、自由变元的概念，重点掌握约束变元的换名与自由变元的代入. 作业: P66 (4)a，（5）b
8
4
第二章谓词逻辑（Predicate Logic）
2.5谓词演算的等价式与蕴含式
• 1、命题公式的推广在命题公式中成立的式子，用谓词公式去代换其中相应的命题变元，得到的公式依然成立如： x( P(x)Q(x))
P(x)
∨

x( P(x)
∨
Q(x))
Q(x)
（P(x) ∧ Q(x)）等

离散数学(2.5谓词演算的等价式与蕴含式)

合集下载