立体几何公理定理推论汇总

立体几何公理及定理一、空间点、线、面之间的关系1、两条直线的位置关系有：2、两个平面的位置关系有：公理1、如果一条直线上的两点在一个平面内，那么这条直线在此平面内。

公理2、过不在一条直线上的三点，有且只有一个平面。

推论1、一组平行直线确定唯一一个平面。

推论2、一条直线及直线外一点确定唯一一个平面。

公理3、如果有两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

公理4（平行公理）、平行于同一直线的两直线平行。

二、平行关系直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

直线与平面平行的性质定理：一条直线与一个平面平行，则过这条直线的任意平面与此平面的交线与该直线平行。

平面与平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

平面与平面平行的性质定理：1、如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

2、两平面平行，其中一个平面内的任一直线平行于另一个平面。

3、夹在两个平行平面间的平行线段相等。

4、平行于同一平面的两个平面平行。

三、垂直关系直线与平面垂直的判定定理：一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直。

直线与平面垂直的性质定理：1、垂直于同一个平面的两条直线互相平行。

2、如果一条直线垂直一个平面，那么这条直线垂直于平面内的所有直线。

平面与平面垂直的判定定理：如果一个平面过另一个平面的垂线，那么这两个平面垂直。

平面与平面垂直的性质定理：如果两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。

三角公式汇总一、任意角的三角函数1. ①与α终边相同的角的集合（角α与角β的终边重合）：{}Z k k ∈+⨯=,360|αββ ②终边在x 轴上的角的集合： {}Z k k ∈⨯=,180| ββ③终边在y 轴上的角的集合：{}Z k k ∈+⨯=,90180| ββ ④终边在坐标轴上的角的集合：{}Z k k ∈⨯=,90| ββ⑤ 若角α与角β的终边在一条直线上，则角α与角β的关系：βα+=k 180 2. 角度与弧度的互换关系：360°=2π 180°=π弧度与角度互换公式： 1rad ＝π180°≈57.30° 1°＝180π3、弧长公式：r l ⋅=||α. 扇形面积公式：211||22s lr r α==⋅扇形 4、三角函数在各象限的符号：（一全二正弦，三切四余弦）正切、余切余弦、正割正弦、余割5、在角α的终边上任取．．一点),(y x P ，记：22y x r +=，正弦：r y =αsin 余弦：r x =αcos 正切：xy=αtan 二、同角三角函数的基本关系式 商数关系：αααcos sin tan = 平方关系：1cos sin22=+αα，2211tan cos αα+=，212sin cos (sin cos )αααα+=+ 212sin cos (sin cos )αααα-=-三、诱导公式⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值，等于α的同名函数值，前面加上一个把α看成．．锐角时原函数值的符号。

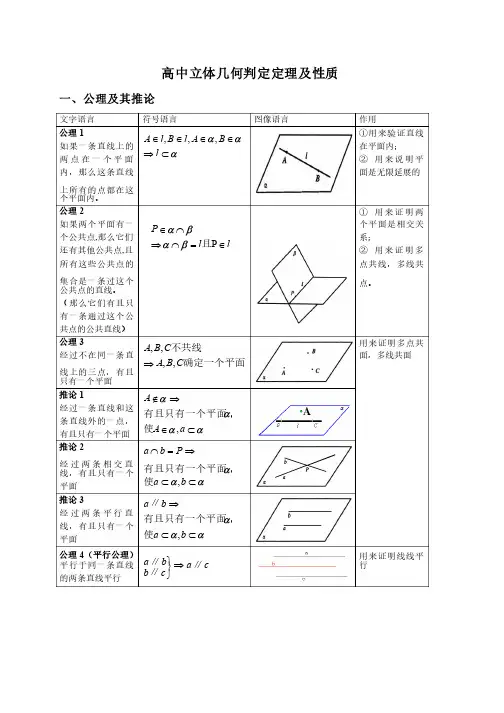
高中立体几何判定定理及性质一、公理及其推论文字语言文字语言 符号语言符号语言图像语言图像语言作用作用公理1如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内。

aaa ÌÞÎÎÎÎl B A l B l A ,,,①用来验证直线在平面内；在平面内； ② 用来说明平面是无限延展的面是无限延展的公理2 如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。

公共点的直线。

（那么它们有且只有一条通过这个公共点的公共直线）共点的公共直线） ll P Î=ÇÞÇÎP 且b a ba① 用来证明两个平面是相交关系；系；② 用来证明多点共线，多线共点。

点。

公理3 经过不在同一条直线上的三点，有且只有一个平面只有一个平面 确定一个平面不共线C B A C B A ,,,,Þ用来证明多点共面，多线共面面，多线共面推论1 经过一条直线和这条直线外的一点，有且只有一个平面有且只有一个平面 a a a a ÌÎÞÏa A A ,使，有且只有一个平面推论2 经过两条相交直线，有且只有一个平面平面 aa a ÌÌÞ=Çb a P b a ,使，有且只有一个平面推论3 经过两条平行直线，有且只有一个平面平面aa a ÌÌÞb a b a ,使，有且只有一个平面∥公理4 （平行公理）平行于同一条直线的两条直线平行的两条直线平行c a c b b a ∥∥∥Þþýü用来证明线线平行文字语言文字语言 符号语言符号语言 图像语言图像语言作用作用 （1）公理4 （平行公理） 平行于同一条直线的两条直线平行的两条直线平行c a c b b a ∥∥∥Þþýü（2）线面平行的判定定理 如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。

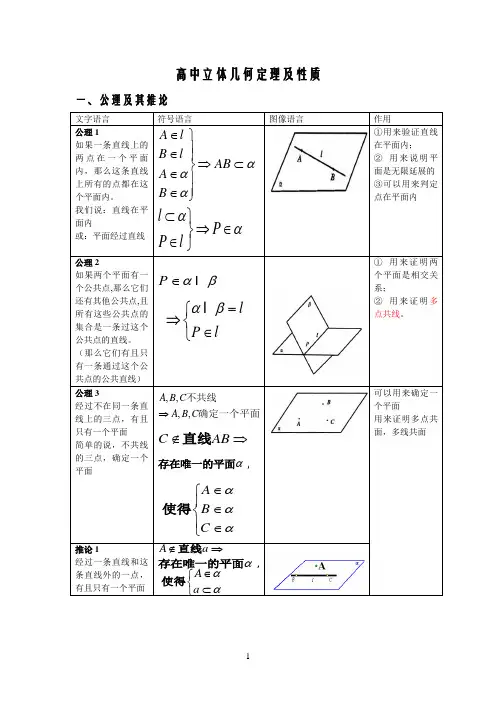
立体几何的性质,公理及定理下面是解立体几何一些简单的公式定例：公理1：如果一条直线上的两点在一个平面内，那么这条直线上的所有点都在这个平面内。

（1）判定直线在平面内的依据（2）判定点在平面内的方法公理2：如果两个平面有一个公共点，那它还有其它公共点，这些公共点的集合是一条直线。

（1）判定两个平面相交的依据（2）判定若干个点在两个相交平面的交线上公理3：经过不在一条直线上的三点，有且只有一个平面。

（1）确定一个平面的依据（2）判定若干个点共面的依据推论1：经过一条直线和这条直线外一点，有且仅有一个平面。

（1）判定若干条直线共面的依据（2）判断若干个平面重合的依据（3）判断几何图形是平面图形的依据推论2：经过两条相交直线，有且仅有一个平面。

推论3：经过两条平行线，有且仅有一个平面。

立体几何直线与平面空间二直线平行直线公理4：平行于同一直线的两条直线互相平行等角定理：如果一个角的两边和另一个角的两边分别平行，并且方向相同，那么这两个角相等。

异面直线空间直线和平面位置关系（1）直线在平面内——有无数个公共点（2）直线和平面相交——有且只有一个公共点（3）直线和平面平行——没有公共点立体几何直线与平面直线与平面所成的角（1）平面的斜线和它在平面上的射影所成的锐角，叫做这条斜线与平面所成的角（2）一条直线垂直于平面，定义这直线与平面所成的角是直角（3）一条直线和平面平行，或在平面内，定义它和平面所成的角是0度的角三垂线定理在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它和这条斜线垂直三垂线逆定理在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它和这条斜线的射影垂直空间两个平面两个平面平行判定性质（1）如果一个平面内有两条相交直线平行于另一个平面，那么这两个平面平行（2）垂直于同一直线的两个平面平行（1）两个平面平行，其中一个平面内的直线必平行于另一个平面（2）如果两个平行平面同时和第三个平面相交，那么它们的交线平行（3）一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面相交的两平面二面角：从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫二面角的线，这两个半平面叫二面角的面二面角的平面角：以二面角的棱上任一点为端点，在两个面内分另作垂直棱的两条射线，这两条射线所成的角叫二面角的平面角平面角是直角的二面角叫做直二面角两平面垂直判定性质如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直（1）若二平面垂直，那么在一个平面内垂直于它们的交线的直线垂直于另一个平面（2）如果两个平面垂直，那么经过第一个平面内一点垂直于第二个平面的直线，在第一个平面内立体几何多面体、棱柱、棱锥多面体定义由若干个多边形所围成的几何体叫做多面体。

立体几何初步公理、定理及推论1、连接两点的线中，线段最短；2、过两点有一条直线，并且只有一条直线；3、如果一条直线上的两点在一个平面内，那么这条直线上所有点都在这个平面内；4、经过不在同一条直线上的三点，有且只有一个平面；（不共线的三点确定一个平面）5、如果不重合的两个平面有一个公共点，那么它们有且只有一条过这个点的公共直线；6、经过直线和直线外一点，有且只有一个平面；7、经过两条相交直线，有且只有一个平面；8、经过两条平行直线，有且只有一个平面；9、过直线外一点有且只有一条直线和已知直线平行；10、平行于同一条直线的两条直线平行；11、如果一个角的两边与另一个角的两边分别对应平行，并且方向相同，那么这两个角相等；12、如果不在一个平面内的一条直线与平面内的一条直线平行，那么这条直线和这个平面平行；13、如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和两个平面的交线平行；14、如果一个平面内有两条相交直线平行于另一个平面，那么这两个平面平行；15、如果一个平面内有两条相交直线分别平行于另一个平面的两条直线，则这两个平面平行；16、如果两个平行平面同时与第三个平面相交，那么它们的交线平行；17、如果一条直线垂直于一个平面，那么它就和平面内任何一条直线垂直；18、如果一条直线与平面内的两条相交直线垂直，则这条直线与平面垂直；19、如果两条平行线中，有一条垂直于平面，那么另一条直线也垂直于这个平面；20、如果两条直线垂直于同一个平面，那么这两条直线平行；21、如果一个平面过另一个平面的一条垂线，则这两个平面互相垂直；22、如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。

立体几何中基本概念、公理、定理、推论1. 三个公理和三条推论：（1）公理1：一条直线的两点在一个平面内，那么这条直线上的所有的点都在这个平面内.这是判断直线在平面内的常用方法.（2）公理2：如果两个平面有一个公共点，它们有无数个公共点，而且这无数个公共点都在同一条直线上.这是判断几点共线（证这几点是两个平面的公共点）和三条直线共点（证其中两条直线的交点在第三条直线上）的方法之一.（3）公理3：经过不在同一直线上的三点有且只有一个平面.推论1：经过直线和直线外一点有且只有一个平面.推论2：经过两条相交直线有且只有一个平面.推论3：经过两条平行直线有且只有一个平面.公理3和三个推论是确定平面的依据.2. 直观图的画法（斜二侧画法规则）：在画直观图时，要注意：（1）使045x o y '''∠=(或0135)，x o y '''所确定的平面表示水平平面.（2）已知图形中平行于x 轴和z 轴的线段，在直观图中保持长度和平行性不变，平行于y 轴的线段平行性不变，但在直观图中其长度为原来的一半.3. 公理4：平行于同一直线的两直线互相平行.(即平行直线的传递性)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. (此定理说明角平移后大小不变) 若无“方向相同”,则这两个角相等或互补.4. 空间直线的位置关系：（1）相交直线――有且只有一个公共点.（2）平行直线――在同一平面内，没有公共点.（3）异面直线――不在同一平面内，也没有公共点.5. 异面直线⑴异面直线定义:不同在任何一个平面内的两条直线叫做异面直线.⑵异面直线的判定：连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.⑶异面直线所成的角：已知两条异面直线a 、b ,经过空间任一点O 作直线a '、b ',使//a a '、//b b ',把a '与b '所成的锐角(或直角)叫做异面直线a 、b 所成的角(或夹角).⑷异面直线所成的角的求法：首先要判断两条异面直线是否垂直，若垂直，则它们所成的角为900；若不垂直，则利用平移法求角，一般的步骤是“作（找）—证—算”.注意，异面直线所成角的范围是π0,2⎛⎤⎥⎝⎦；求异面直线所成角的方法：计算异面直线所成角的关键是平移（中点平移，顶点平移以及补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，以便易于发现两条异面直线间的关系）转化为相交两直线的夹角. ⑸两条异面直线的公垂线：①定义：和两条异面直线都垂直且相交的直线，叫做异面直线的公垂线；两条异面直线的公垂线有且只有一条.而和两条异面直线都垂直的直线有无数条，因为空间中，垂直不一定相交.②证明：异面直线公垂线的证明常转化为证明公垂线与两条异面直线分别垂直.⑹两条异面直线的距离：两条异面直线的公垂线在这两条异面直线间的线段的长度.6. 直线与平面的位置关系：（1）直线在平面内；（2）直线与平面相交.其中，如果一条直线和平面内任何一条直线都垂直，那么这条直线和这个平面垂直.注意：任一条直线并不等同于无数条直线；（3）直线与平面平行.其中直线与平面相交、直线与平面平行都叫作直线在平面外.平面与平面的位置关系：（1）平行――没有公共点；（2）相交――有一条公共直线.7.线面平行、面面平行⑴直线与平面平行的判定定理: 如果不在一个平面(α)内的一条直线(l )和平面(α)内的一条直线(m )平行，那么这条直线(l )和这个平面(α)平行.,,////l m l m l ααα⊄⊂⇒ (作用:线线平行⇒线面平行)⑵直线与平面平行的性质定理:如果一条直线(l )和一个平面(α)平行,经过这条直线(l )的平面(β)和这个平面(α)相交(设交线是m ),那么这条直线(l )和交线(m )平行.//,,//l l m l m αβαβ⊂⋂=⇒ (作用: 线面平行⇒线线平行)⑶平面与平面平行的判定定理:如果一个平面(β)内有两条相交直线(,a b )分别平行于另一个平面(α),那么这两个平面(,βα)平行.,,,//,////a b a b P a b ββααβα⊂⊂⋂=⇒ (作用:线面平行⇒面面平行)推论:如果一个平面(β)内有两条相交直线(,a b )分别平行于另一个平面(α)内的两条直线(,a b ''), 那么这两个平面(,βα)平行.,,,,,//,////a b a b P a b a a b b ββααβα''''⊂⊂⋂=⊂⊂⇒(作用: 线线平行⇒面面平行) ⑷平面与平面平行的性质定理:如果两个平行平面(,αβ)同时与第三个平面(γ)相交(设交线分别是,a b ),那么它们的交线(,a b )平行.//,,//a b a b αβαγβγ⋂=⋂=⇒ (作用: 面面平行⇒线线平行)推论:如果两个平面(,αβ)平行,则一个平面(α)内的一条直线(a )平行于另一个平面(β). //,//a a αβαβ⊂⇒ (作用: 面面平行⇒线面平行)8.线线垂直、线面垂直、面面垂直⑴直线与平面垂直的判定定理:如果一条直线(l )和一个平面(α)内的两条相交直线(,m n )都垂直,那么这条直线(l )垂直于这个平面(α).,,,,l m l n m n m n P l ααα⊥⊥⊂⊂⋂=⇒⊥ (作用: 线线垂直⇒线面垂直)⑵直线与平面垂直的性质定理:如果一条直线(l )和一个平面(α)垂直,那么这条直线(l )和这个平面(α)内的任意一条直线(m )垂直.,l m l m αα⊥⊂⇒⊥ .⑶三垂线定理: 其作用是证两直线异面垂直和作二面角的平面角①定理: 在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直.②逆定理：在平面内的一条直线，如果它和这个平面的一条斜线，那么它也和这条斜线在平面内的射影垂直.(作用: 线线垂直⇒线线垂直)⑷平面与平面垂直的判定定理: 如果一个平面(α)经过另一个平面(β)的一条垂线(l )，那么这两个平面(,αβ)互相垂直.,l l βααβ⊥⊂⇒⊥ (作用: 线面垂直⇒面面垂直)⑸平面与平面垂直的性质定理:如果两个平面(,αβ)垂直，那么在一个平面(α)内垂直于它们交线(m )的直线(l )垂直于另一个平面(β).,,,m l l m l αβαβαβ⊥⋂=⊂⊥⇒⊥ (作用: 面面垂直⇒线面垂直)9. 直线和平面所成的角⑴最小角定理:平面的斜线和它在平面内的射影所成的角,是这条斜线和这个平面内任意一条直线所成的角中最小的角.满足关系式:12cos cos cos θθθ=⋅θ是平面的斜线与平面内的一条直线所成的角；1θ是平面的斜线与斜线在平面内的射影所成的角；2θ是斜线在平面内的射影与平面内的直线所成的角.⑵直线和平面所成的角: 平面的一条斜线和它在平面内的射影所成的锐角，叫这条直线和这个平面所成的角. 范围：[0,90]10.二面角⑴二面角的定义:从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,每个半平面叫做二面角的面.棱为l ,两个面分别是α、β的二面角记为l αβ--.二面角的范围：[0,]π⑵二面角的平面角:在二面角的棱上取一点,在二面角的面内分别作两条垂直于棱的射线,这两条射线所成的角叫做二面角的平面角.11.空间距离⑴点到平面的距离:一点到它在一个平面内的正射影的距离.⑵直线到与它平行平面的距离:一条直线上的任一点到与它平行的平面的距离.⑶两个平行平面的距离:两个平行平面的公垂线段的长度.⑷异面直线的距离12. 多面体有关概念：（1）多面体：由若干个平面多边形围成的空间图形叫做多面体.围成多面体的各个多边形叫做多面体的面.多面体的相邻两个面的公共边叫做多面体的棱.（2）多面体的对角线：多面体中连结不在同一面上的两个顶点的线段叫做多面体的对角线.（3）凸多面体：把一个多面体的任一个面伸展成平面，如果其余的面都位于这个平面的同一侧，这样的多面体叫做凸多面体.13.棱柱⑴棱柱的定义: 有两个面互相平行，其余每相邻两个面的交线互相平行，这样的多面体叫棱柱.两个互相平行的面叫棱柱的底面（简称底）；其余各面叫棱柱的侧面；两侧面的公共边叫棱柱的侧棱；两底面所在平面的公垂线段叫棱柱的高（公垂线段长也简称高）.⑵棱柱的分类：侧棱不垂直于底面的棱柱叫斜棱柱.侧棱垂直于底面的棱柱叫直棱柱.底面是正多边形的直棱柱叫正棱柱.棱柱的底面可以是三角形、四边形、五边形……这样的棱柱分别叫三棱柱、四棱柱、五棱柱……⑶棱柱的性质：①棱柱的各个侧面都是平行四边形，所有的侧棱都相等，直棱柱的各个侧面都是矩形，正棱柱的各个侧面都是全等的矩形.②与底面平行的截面是与底面对应边互相平行的全等多边形.③过棱柱不相邻的两条侧棱的截面都是平行四边形.⑷平行六面体、长方体、正方体：底面是平行四边形的四棱柱是平行六面体．侧棱与底面垂直的平行六面体叫直平行六面体，底面是矩形的直平行六面体叫长方体，棱长都相等的长方体叫正方体．⑸①平行六面体的任何一个面都可以作为底面；②平行六面体的对角线交于一点，并且在交点处互相平分；③平行六面体的四条对角线的平方和等于各棱的平方和；④长方体的一条对角线的平方等于一个顶点上三条棱长的平方和．14.棱锥⑴棱锥的定义: 有一个面是多边形，其余各面是有一个公共顶点的三角形，这样的多面体叫棱锥其中有公共顶点的三角形叫棱锥的侧面；多边形叫棱锥的底面或底；各侧面的公共顶点()S ，叫棱锥的顶点，顶点到底面所在平面的垂线段()SO ，叫棱锥的高（垂线段的长也简称高）．⑵棱锥的分类：（按底面多边形的边数）分别称底面是三角形，四边形，五边形……的棱锥为三棱锥，四棱锥，五棱锥…… ⑶棱锥的性质：定理：如果棱锥被平行于底面的平面所截，那么所得的截面与底面相似，截面面积与底面面积比等于顶点到截面的距离与棱锥高的平方比． 中截面：经过棱锥高的中点且平行于底面的截面，叫棱锥的中截面⑷正棱锥：底面是正多边形，顶点在底面上的射影是底面的中心的棱锥叫正棱锥． ⑸正棱锥的性质:①正棱锥的各侧棱相等，各侧面都是全等的等腰三角形，各等腰三角形底边上的高（叫斜高）也相等。

立体几何中的公理、定理和常用结论一、定理1．公理1如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内．若A∈l，B∈l，A∈α，B∈α,则l⊂α．2．公理2如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是经过这个公共点的一条直线．P∈α，P∈α⇒α∩β＝l，且P∈l．3．公理3经过不在同一条直线上的三点，有且只有一个平面．推论1经过一条直线和这条直线外的一点,有且只有一个平面．推论2经过两条相交直线,有且只有一个平面．推论3经过两条平行直线，有且只有一个平面．4．异面直线的判定定理:连接平面内一点与平面外一点的直线，和这个平面内不经过此点的直线是异面直线．（若a⊂α，A 错误!α，B∈α，B错误!a,则直线AB和直线a是异面直线．) 5．公理4（空间平行线的传递性）:平行于同一条直线的两条直线互相平行．6．等角定理：如果一个角的两边和另一角的两边分别平行并且方向相同，那么这两个角相等．7．定理：如果一条直线垂直于两条平行线中的一条直线,那么它也垂直于另一条直线．若b∥c,a⊥b，则a⊥c．8．直线与平面平行的判定定理：如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行．若a错误!α，b⊂α，a∥b,则a∥α．9．直线与平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行．若a∥α，a⊂β，α⋂β＝b，则a∥b．10．直线与平面垂直的判定定理：如果一条直线和平面内的两条相交直线垂直，这条直线和这个平面垂直．若m⊂α，n⊂α，m⋂n＝O，l⊥m，l⊥n，则l⊥α．11．：若两条平行直线中的一条垂直于一个平面，那么另一条直线也和这个平面垂直．若a∥b，a⊥α，则b⊥α．12．直线与平面垂直的性质定理:若两条直线同时垂直于一个平面，那么这两条直线平行．若a⊥α，b⊥α，则a∥b．13．平面与平面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行．若a⊂α，b⊂α，a⋂b＝A，a∥β，b∥β，则α∥β．14．平面与平面平行的性质定理：如果两个平行平面同时与第三个平面相交，那么它们的交线平行．若α∥β，α∩γ＝a，β∩γ＝b，则a∥b．15．定理：如果一条直线垂直于两个平行平面中的一个平面，那么它也垂直于另一个平面．若α∥β，a⊥α,则a⊥β．16．两个平面垂直的判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直．若l⊥α，l⊂β，则α⊥β．17．两个平面垂直的性质定理：如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面．若α⊥β，α∩β＝l，a⊂α，a⊥l，则a⊥β．18．两个平面垂直的性质定理：如果两个平面互相垂直，那么过一个平面内一点且垂直于第二个平面的直线在第一个平面内．若α⊥β，P∈α，P∈a，a⊥β，则a⊂α．19．长方体的体积公式：V长方体＝abc，其中a，b，c分别为长方体的长、宽、高．20．祖暅原理：两个等高（夹在两个平行平面之间）的几何体，如果在任何等高处的截面积都相等，那么这两个几何体的体积相等．二、常识1．过空间一点，与已知平面垂直的直线有且只有一条．2．过空间一点，与已知直线垂直的平面有且只有一个．3．经过平面外一点有且只有一个平面和已知平面平行．三、常用结论（可用来解决选择、填空题）1．空间四点A、B、C、D，若直线AB与CD异面，则AC 与BD，AD与BC也一定异面．2．如果过平面内一点的直线平行于与此平面平行的一条直线，那么这条直线在此平面内．3．如果过平面内一点的直线垂直于与此平面垂直的一条直线,那么这条直线在此平面内．4．夹在两个平行平面间的平行线段相等．5．经过两条异面直线中的一条，有且只有一个平面与另一条直线平行．6．若直线a同时平行于两个相交平面，则a一定也平行于这两个相交平面的交线．7．如果一条直线垂直于一个三角形的两边，那么它也垂直于第三边．8．如果一个角所在平面外一点到角的两边距离相等，那么这一点在平面内的射影在这个角的平分线所在直线上．9．如果一个平面内有两条相交直线和另一个平面内的两条相交直线分别平行，那么这两个平面平行．10．平行于同一平面的两个平面平行．11．空间四面体A－BCD中，若有两对对棱互相垂直，则第三对对棱也互相垂直，且顶点A在平面BCD内的射影是△BCD 的垂心(类似地，顶点B在平面ACD内的射影是ΔACD的垂心，…）．12．空间四面体P－ABC中,若P A、PB、PC两两垂直，则①点P在平面ABC内的射影是ΔABC的垂心；②△ABC的垂心O也是点P在平面ABC内的射影（PO⊥平面ABC）．13．空间四面体P－ABC中，①若P A＝PB＝PC，则点P在平面ABC内的射影是△ABC的外心．②若三个侧面上的斜高PH1＝PH2＝PH3，则点P在平面ABC 内的射影是△ABC的内心．14．如果两个平面同时垂直于第三个平面，那么这两个平面的交线垂直于第三个平面．若α⊥β，P∈α，P∈a，a⊥β，则a⊂α．。

立体几何公理及定理一、公理公理1：如果一条直线上的两点在一个平面内，那么这条直线上的所有点都在这个平面内。

公理2：如果两个平面有一个公共点，那么它们有且仅有一条经过该点的公共直线。

（1）判定两个平面相交的依据（2）判定若干个点在两个相交平面的交线上公理3：经过不在一条直线上的三点，有且只有一个平面。

推论1：经过一条直线和这条直线外一点，有且仅有一个平面。

推论2：经过两条相交直线，有且仅有一个平面。

推论3：经过两条平行线，有且仅有一个平面。

公理4：平行于同一直线的两条直线互相平行二、定理○1等角定理：如果一个角的两边和另一个角的两边分别平行，并且方向相同，那么这两个角相等○2三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它和这条斜线垂直○3三垂线逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它和这条斜线的射影垂直○4直线与平面垂直的判定定理（1）：如果直线与平面上的两条相交直线都垂直，那么直线与这个平面垂直。

○5直线与平面垂直的判定定理（2）：如果两条平行直线中的其中一条垂直于一个平面，则另一条也垂直于这个平面。

○6直线和平面垂直的性质定理：如果两条直线同垂直于一个平面，那么这两条直线平行。

○7直线与平面平行的判定定理：如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。

○8直线与平面平行的性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

○9直线与平面平行的性质扩充定理：如果一条直线与两个相交平面都平行，那么这条直线与这两个平面的交线平行。

○10面面平行的判定定理: （1） 一个平面内的两条相交直线与另一个平面平行，则这两个平面平行（2） 一个平面内的两条相交直线与另一个平面内的两条直线平行，则这两个平面平行○11面面平行的性质定理： 如果两个平行平面同时和第三个平面相交，那么他们的交线平行○12面面垂直的判定定理： 一个平面过另一个平面的垂线，则这两个平面垂直○13面面垂直的性质定理： 两个平面垂直。

一空间直线和平面9.1平面公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内公理2:如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线公理3经过不在同一条直线上的三点,有且只有一个平面推论1:经过一条直线和这条直线外的一点,有且有一个平面推论2:经过两条相交直线,有且只有一个平面推论3:经过两条平行直线,有且只有一个平面9.2空间直线平行公理:平行于同一条直线的两条直线互相平行定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(直角)相等异面直线1如果两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直. 也记作a垂直b 2.和两条异面直线都垂直相交的直线,叫做两条异面直线的公垂线3两条异面直线的公开线在这两要异面直线间的线段(公垂线段)的长度,叫做两条异面直线的距离.9.3直线与平面平行的判定和性质定义:如果一条直线和一个平面没有公共点,那么我们说这条直线和这个平面平行2直线和平面平行的判定直线和平面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.3直线和平面平行的性质直线和平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.9.4直线与平面垂直的判定和性质1.直线和平面垂直的定义定义:如果一条直线L和一个平面α内的任意一个直线都垂直,我们就说直线L和平面α互相垂直,记作L垂直α直线和平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.从平面外一点引这个平面的垂线,这个点和垂足间的距离叫做这个点到这个平面的距离2.一条直线和一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线和这个平面的距离.斜线在平面内的射影1.这一点向平面引垂线,垂足叫做这点在这个平面内的射影.这点与垂足间的经段叫做这个点到这个平面的垂线段.2.一条直线和一个平面相交但不和这个平面垂直时,这条直线就叫做这个平面的斜线.斜线和平面的交点叫做斜足.从平面外一点向平面引斜线.这点与斜线和平面的交点叫做斜足.从平面外一点向平面引斜线,这点与斜足间的线段叫做这点到这个平面的斜线段3.从斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面内的射影,垂足与斜足间的线段叫做这点到平面的斜线段在这个平面内的射影.定理:从平面外一点向这个平面所引的垂线段和斜线段中1.射影相等的两条斜线段相等,射影较长的斜线段也较长2.相等的斜线段的射影相等,较长的斜线段的射影也较长3.垂线段比任何一条斜线段都短直线和平面所成的角平面的一条斜线和它在这个平面内的射影所成的锐角,叫做这个直线和这个平面所成的角可以证明,斜线和平面所成的角,是这条斜线和这个平面内经过斜足的直线所成的一切角中最小的角斜线和平面所成的角,是这条斜线和这个平面内的直线所成的一切角中最小的角三垂线定理三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直.9.5两个平面平行的判定和性质两个平面的位置关系如果两个平面没有公共点,我们就说这两个平面互相平行.两个平面平行的判定两个平面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.两个平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.和两个平行平面同时垂直的直线,叫做这两个平行平面的公垂线,它夹在这两个平行平面间的部分,叫做这两个平行平面的公垂线段.两个平行平面的公垂线段都相等,我们把公垂线段的长度叫做两个平行平面的距离9.6两个平面垂直的判定和性质以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条两射线所成的角叫做二面角的平面角平面角是直角的二面角叫做直二面角.两个平面垂直的判定一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.两个平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.两个平面垂直的性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面9.7棱柱棱柱的概念有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫做棱柱两个互相平行的面叫做棱柱的底面,其余各面叫做棱柱的侧面;两个面的公共边叫做棱柱的棱,其中两个侧面的公共边叫做棱柱的棱柱的侧棱,侧面与底面的公共顶点叫做棱柱的顶点,不在同一个面上的两个顶点在连线叫做棱柱的对角线,两个底面的距离叫做棱柱的高.侧棱不垂直于底面的棱柱叫做斜棱柱.直于底面的棱柱叫做直棱柱底面是正多边形的直棱柱叫做正棱柱棱柱的性质1侧棱都相等,侧面是平行四边形;2.两个底面与平行于底面的截面是全等的多边形3过不相邻的两条侧棱的截面是平行四边形定理:长方体一条对角线的长的平方等于一个顶点上三条棱的长的平方和.棱锥的性质定理:如果棱锥被平行于底面的平面所截,那么截面和底面相,并且它们面积的比等于截得的棱锥的高与已知棱锥的高的平方比.正棱锥有下面一些性质;1各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等,它叫做正棱锥的斜高.2棱锥的高,斜高和斜高在底面内的射影组成一个直角三角形;棱锥的高,侧棱和侧棱在底面内的射影也组成一个直角三角形.9.10球1球心和截面圆心的连线垂直于截面2球心到截面的距离d与球的半径R及截面的半径r有下面的关系:球面被经过球心的平面截得的圆叫做大圆,被不经过球心的截面截得的圆叫做小圆.定理:半径是R的球的体积.v=（4/3）πR3定理半径是R的球的表面积S=4πR2必修2立体几何知识点复习平面, 空间, 立体几何, 知识点立体几何复习知识点平面.1. 经过不在同一条直线上的三点确定一个面.注：两两相交且不过同一点的四条直线必在同一平面内.2. 两个平面可将平面分成3或4部分.（①两个平面平行，②两个平面相交）3. 过三条互相平行的直线可以确定1或3个平面.（①三条直线在一个平面内平行，②三条直线不在一个平面内平行）[注]：三条直线可以确定三个平面，三条直线的公共点有0或1个.4. 三个平面最多可把空间分成 8 部分.（X、Y、Z三个方向）空间直线.1. 空间直线位置分三种：相交、平行、异面. 相交直线—共面有反且有一个公共点；平行直线—共面没有公共点；异面直线—不同在任一平面内[注]：①两条异面直线在同一平面内射影一定是相交的两条直线.（×）（可能两条直线平行，也可能是点和直线等）②直线在平面外，指的位置关系：平行或相交③若直线a、b异面，a平行于平面，b与的关系是相交、平行、在平面内.④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点.⑤在平面内射影是直线的图形一定是直线.（×）（射影不一定只有直线，也可以是其他图形）⑥在同一平面内的射影长相等，则斜线长相等.（×）（并非是从平面外一点向这个平面所引的垂线段和斜线段）⑦是夹在两平行平面间的线段，若，则的位置关系为相交或平行或异面.2. 异面直线判定定理：过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.（不在任何一个平面内的两条直线）3. 平行公理：平行于同一条直线的两条直线互相平行.4. 等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等（如下图）.（二面角的取值范围）（直线与直线所成角）（斜线与平面成角）（直线与平面所成角）（向量与向量所成角推论：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成锐角（或直角）相等.5. 两异面直线的距离：公垂线的长度.空间两条直线垂直的情况：相交（共面）垂直和异面垂直.是异面直线，则过外一点P，过点P且与都平行平面有一个或没有，但与距离相等的点在同一平面内. （或在这个做出的平面内不能叫与平行的平面）直线与平面平行、直线与平面垂直.1. 空间直线与平面位置分三种：相交、平行、在平面内.2. 直线与平面平行判定定理：如果平面外一条直线和这个平面内一条直线平行，那么这条直线和这个平面平行.（“线线平行，线面平行”）[注]：①直线与平面内一条直线平行，则∥. （×）（平面外一条直线）②直线与平面内一条直线相交，则与平面相交. （×）（平面外一条直线）③若直线与平面平行，则内必存在无数条直线与平行. （√）（不是任意一条直线，可利用平行的传递性证之）④两条平行线中一条平行于一个平面，那么另一条也平行于这个平面. （×）（可能在此平面内）⑤平行于同一直线的两个平面平行.（×）（两个平面可能相交）⑥平行于同一个平面的两直线平行.（×）（两直线可能相交或者异面）⑦直线与平面、所成角相等，则∥.（×）（、可能相交）3. 直线和平面平行性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.（“线面平行，线线平行”）平面平行与平面垂直.1. 空间两个平面的位置关系：相交、平行.2. 平面平行判定定理：如果一个平面内有两条相交直线都平行于另一个平面，哪么这两个平面平行.（“线面平行，面面平行”）推论：垂直于同一条直线的两个平面互相平行；平行于同一平面的两个平面平行.[注]：一平面间的任一直线平行于另一平面.3. 两个平面平行的性质定理：如果两个平面平行同时和第三个平面相交，那么它们交线平行.（“面面平行，线线平行”）4. 两个平面垂直性质判定一：两个平面所成的二面角是直二面角，则两个平面垂直. 两个平面垂直性质判定二：如果一个平面与一条直线垂直，那么经过这条直线的平面垂直于这个平面.（“线面垂直，面面垂直”）。

公理1：如果一条直线上有两点在一个平面上，那么这条直线上所有的点都在这个平面上。

公理2：不在同一直线上的三点确定一个平面。

推论1：一条直线和这条直线外的一点确定一个平面。

推论2：两条相交直线确定一个平面.推论3：两条平行直线确定一个平面公理3：如果两个不同的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等。

公理4：平行于同一条直线的两条直线互相平行。

推论1 ：如果一个角的两边和另一个角的两边分别平行，那么这两个角相等或者互补推论2：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角(或直角)相等.异面直线判定定理：过平面外一点与平面上一点的直线，和此平面上不经过该点的任何一条直线都是异面直线。

直线与平面平行的判定定理：如果不在平面上的一条直线与这个平面上的一条直线平行，那么该直线与这个平面平行．直线与平面平行的性质定理：如果一条直线与一个平面平行，过这条直线的一个平面与此平面相交，那么其交线必与该直线平行．直线与平面垂直的判定定理：如果一条直线与一个平面上的两条相交直线都垂直，那么此直线与该平面垂直。

推论：如果一组平行线中的一条与一个平面垂直，那么其他平行线也都与这个平面垂直直线与平面垂直的性质定理：垂直于同二个平面的两条直线互相平行.推论1：过一点有且只有一个平面与给定的直线垂直推论2过一点有且只有一条直线与给定的平面垂直．三垂线定理：平面上的一条直线和这个平面的一条斜线垂直的充要条件是它和这条斜线在平面上的投影垂直．两个平面平行的判定定理：如果一个平面上的两条相交直线与另一个平面平行，那么这两个平面平行。

两个平面非行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

平面与平面垂直的判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面垂直。

平面与平面垂直的性质定理：如果两个平面垂直，那么其中一个平面上垂直于两平面交线的线与另一个平面垂直.。