- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5. 函数值分布:
当x=1时,y=0。 减函数
0<a<1:
0<a<1:
23.03.2022
Hale Waihona Puke 当:x>1, 图像在y轴下方; 当:x>1, 则y<0
当 0<x<1, 图像在对轴数函上数方; 当0<x<1, 则y>0;
11
图像的特征
函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占
满了整个y轴;
对数函数
2
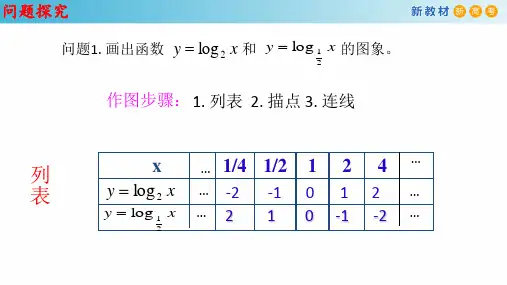
现在有一张纸,我把这张纸对折一次就变成了两层; 我对折两次纸就变成了四层;如果我们设把纸对折的次 数为x,对折后纸的层数为y,那么,试建立y关于x的函数 关系式。
解:y 2x
提问:如果我发现对折后的纸有4层,那么我对折了多少次? 2次
如果我发现对折后的纸有8层,那么我对折了多少次? 3次
x<0, y>1
y ax
y loga x
23.03.2022
对数函数
y loga x
(0, )
(,)
a>1, 增函数 0<a<1, 减函数 a>1: x>1, y>0
0<x<1, y<0 0<a<1: x>1, y<0
0<x<1, 14
按要求回答问题 (1) y=log3 (x- 2) (2) y=log2(x2 +1)
23.03.2022
对数函数
7
Y
5
Y=X
4
3
●
2● ●
1●
-1 O -1
● ●yax(0a1) 12 3 4 5 6 ●
7X
-2
●ylogax(0a1)
23.03.2022
对数函数
8
y 2x yx
y log2 x
1
1
y (1)x 2
1 1
yx
y log 1 x
2
a>1
0<a<1
请同学们:
根据对数函数的图象描述对数函数的性质:
3. 过(1.0)点
值域: R 当x=1时,y=0。
4. 单调性: a>1时,图像上升;
增函数
0<a<1时,图像下降;
减函数
5. 函数值分布:
a>1:
a>1:
当:x>1时, 图像在y轴上方;
当x>1,
则 y>0,
当0<x<1时,图像在下方;
当0<x<1, 则y<0;
0<a<1:
0<a<1:
当:x>1, 图像在y轴下方; 当:x>1, 则y<0
对数函数
(0, )
R
(1, 0 )
减函数
当x>1, 则y<0; 当0<x<1, 则y>0:
13
名称
指数函数与对数函数对比
指数函数
对数函数
一般形式 定义域
y ax
(,)
值域 单调性
函数值 变
化情况
(0, )
a>1, 增函数 0<a<1, 减函数 a>1: x>0, y>1
x<0, 0<y<1 0<a<1: x>0, 0<y<1
……
16层呢,32层呢 … …
我们可以发现:x关于y也可以建立一个函数。
你能写出这个X关于Y的函数的关系表达式吗?
解: y 2x 指数式化对数式
23.03.2022
xlog2 y 这个就是我们要的函数关系
ylog2 x 交换X和Y,以符合习惯
对数函数
3
对数函数的定义
一般地,函数 ylo gax(a0 ,a1 ) 就叫做对数函数。x为它的自变 量,函数的定义域为 (0,).
y log5 x, y log1 x
3
以上两个函数也是对数函数!
23.03.2022
对数函数
4
我们知道,函数 y 2x 和 ylog2 x互为反函数。 提问:
函数 y a x 和 y loga x 是什么关系呢? 函数 y a x 和 y loga x 互为反函数!
23.03.2022
对数函数
5
2.利用对称性画图.
因为指数函数y=ax (0<a≠1) 与对数函数y=logax(0<a≠1)的图 象关于直线y=x对称.
23.03.2022
对数函数
6
Y
Y=ax (a>1)
5
Y=X
● 4
3
●
2
●
●
● 1●
●
●
-1 O -1
●1
2
3
● Y=logax (a>1) 4 5 6 7X
-2
23.03.2022
对数函数
16
课堂小结:
1. 对数函数是指数函数的反函数,对数 函数的定义域、值域分别为相应的指数函数的值
域和定义域,它们的图象关于y x 成轴对称.
2. 当a>1, y loga x 在 (0, ) 为增函数. 当0<a<1, y loga x 在 (0, ) 为减函数.
23.03.2022
对数函数
1
回顾指数函数图象及性质
a>1
0<a<1
图
象
1.定义域:R
2.值域:(0,+∞)
性
3.过定点(0,1),即x=0时,y=1
质 4. 当x>0时, y>1;
当x<0时,0<y<1; 5.在 R上是增函数
当x>0时,0<y<1; 当x<0时,y>1;
在R上是减函数
23.03.2022
当 0<x<1, 图像在轴上方; 当0<x<1, 则y>0;
23.03.2022
对数函数
12
对数函数图像及性质
a 1
0 a 1
图
y loga x
y loga x
象
x 1
x 1
性 质
23.03.2022
定义域: 值域: 特殊点:
单调性:
函 数值 的
分布
(0, )
R
(1, 0 )
增函数
当x>1, 则y>0; 当0<x<1, 则y<0 :
23.03.2022
对数函数
17
作业:
习题2.8 第1题.(2),(4),(6),(8). 第2题.
23.03.2022
对数函数
18
23.03.2022
对数函数
19
以下函数是对数函数吗?
23.03.2022
对数函数
9
a 1
y loga x
x 1
图像的特征
函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占满了整个y轴; 值域: R
3. 过(1.0)点
当x=1时,y=0。
4. 单调性: a>1时,图像上升;
增函数
5. 函数值分布:
a>1:
a>1:
当:x>1时, 图像在y轴上方;
当x>1, 则 y>0,
23.03.2022
当0<x<1时,图像在对数y轴函数下方;
当0<x<1, 则y<0; 10
0 a 1 y loga x
x 1
图像的特征
函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占满了整个y轴; 值域: R
3. 过(1.0)点
4. 单调性: 0<a<1时,图像下降;
(1)以上函数的定义域。
(2)以上函数如果底数为 a(a>0且a ≠1)时,函数必过那一点。
23.03.2022
对数函数
15
例二:判断下列各组数中两个 值的大小:
(1) log30.8, (2) log0.54.2, (3) loga5.9,
log33.7 log0.52.9 loga3.1 (0<a≠1)