高中物理竞赛 动力学例题精选

，求电子从 运动到
的过程中，核的吸引力所做的
功。
f 试分别用动能定理和牛顿第二定律求物体A自静止落下
时的速度。
a (m m )g m g 求解第一三 ：次物拉体伸从和B到第C二的次过拉程伸中弹机簧械A时能做守功恒的，比F值做B。的功即物体重力势能C和弹力势能的增加量。
C
T
(m m m ) （1）求物体C与水平桌面的摩擦系数；
的过程中，核的吸引力所做的
F 7.P 0 7i 7.0i714 .1i1 t 0.05
2-11. 一质量为m的滑块，沿图示轨道以初速度 v0 2 Rg 无摩擦地滑动，求滑块由A运动到B的过程中所受的冲量。
解：根据动能定理，
12mB 2v12m02vmgR
y
vB
代入数据解得：vB 2Rg
建立如图直角坐标系，
12 1 l
2
22 2
0 2 m v kx m d ( 1 x v l)k k( 2 ) 1
比较（1）（2）式解得：l 1 2
取其中的正解得：l0.414cm
2-17. 如图，物体A和B的质量分别为 m Am B0.0k 5g ， 物体B与桌面的滑动摩擦系数为 k 0.1 。试分别用动能
1
l
v0 22g(lco1 s)
2-8. 长为l的轻绳，一端固定，另一端系一质量为m的小
球，使小球从悬挂着的位置以水平初速度 v 0 开始运动，
求小球沿逆时针转过 角度时的角速度和绳子张力。
解：法向方程
Tmcgosm2l
mv022g(lcos1) l
l
m
v0
Tmvl022g3gcos
2-9. 质量均为M的三条小船以相同的速率 v沿一直线同 向航行，从中间的小船向前后两船同时以相同速率 u （相对于该船）抛出质量同为 m的小包。从小包被抛出

t1 t2
I
t1
Fd t p2p1
2
t2
I Fd t p2p1
t1
上式表明: 质点所受合外力的冲量等于质点动量 的增量。这一结论称为质点动量定理（积分形式）。
适用条件：惯性系
注意：
恒I力 Ft
1、力的冲量是矢量：
变力I
t2
Fdt
t1
在碰撞、冲击、爆炸等现象中，冲力大，作用时间
短，常用平均冲力。
代入下式就得
y 2
30o
o
x
30o
1
F
mt (2
1
)
m
m2co s30 o j
3m
j
t
t
30o 30o 1
2
大小: F 3 m ,方向: j (y轴正方向)。
t
8
例题 煤粉自高h=0.8m处的料斗口自由落在传送带 A上。设料斗口连续卸煤的流量为qm=40kg/s, 传送带A
的速度=3m/s。求卸煤的过程中，煤粉对传送带A的
平均作用力的大小和方向。(不计相对传送带静止的煤 粉质量，取g=10m/s2）
解 煤粉下落h时的速度 o 2gh4m/s
取在时间dt内落下的煤粉dm=qmdt 为研究对象,由动量定理有
dm :Fd dt m d m 0 h
dm
平 dt q均 m : F 4 0,4 冲 ( 0 力 0)
0
mi
M
zcm 1zm 11m m 2z22 ... .. .m m ii zi. .....o
ri rc
mi zi
x
m1 y
24
M
质心坐标为:
mi xi
mi yi

全国中学生高中物理竞赛第16届—22届预赛动力学试题集锦（含答案）一、第16届预赛题. （15分）一质量为M 的平顶小车，以速度0v 沿水平的光滑轨道作匀速直线运动。

现将一质量为m 的小物块无初速地放置在车顶前缘。

已知物块和车顶之间的动摩擦系数为μ。

1. 若要求物块不会从车顶后缘掉下，则该车顶最少要多长？2. 若车顶长度符合1问中的要求，整个过程中摩擦力共做了多少功？ 参考解答1. 物块放到小车上以后，由于摩擦力的作用，当以地面为参考系时，物块将从静止开始加速运动，而小车将做减速运动，若物块到达小车顶后缘时的速度恰好等于小车此时的速度，则物块就刚好不脱落。

令v 表示此时的速度，在这个过程中，若以物块和小车为系统，因为水平方向未受外力，所以此方向上动量守恒，即0()Mv m M v =+ （1） 从能量来看，在上述过程中，物块动能的增量等于摩擦力对物块所做的功，即2112mv mg s μ= （2） 其中1s 为物块移动的距离。

小车动能的增量等于摩擦力对小车所做的功，即22021122Mv mv mgs μ-=- （3） 其中2s 为小车移动的距离。

用l 表示车顶的最小长度，则21l s s =- （4） 由以上四式，可解得22()Mv l g m M μ=+ （5）即车顶的长度至少应为202()Mv l g m M μ=+。

2．由功能关系可知，摩擦力所做的功等于系统动量的增量，即22011()22W m M v Mv =+- （6）由（1）、（6）式可得22()mMv W m M =-+ （7）二、第16届预赛题.（20分）一个大容器中装有互不相溶的两种液体，它们的密度分别为1ρ和2ρ（12ρρ<）。

现让一长为L 、密度为121()2ρρ+的均匀木棍，竖直地放在上面的液体内，其下端离两液体分界面的距离为34L ，由静止开始下落。

试计算木棍到达最低处所需的时间。

假定由于木棍运动而产生的液体阻力可以忽略不计，且两液体都足够深，保证木棍始终都在液体内部运动，未露出液面，也未与容器相碰。

2
2
dT cos dq N 0,
2
N 2T sin dq dT sin dq 0.
2
2
q T1
T0
y
N
f
1 2
dq
T
1 2
dq
1 2
dq
x
1 2
dq
T+dT
O
dq很小,sin
dq
2
dq
2
,
cos
dq
2
1.
dT N 0,
dT N,
N Tdq 1 dTdq 0.
2
N Tdq.
T
r
T 1 M 2 (L2 r 2 )
2L
T T+dT L
练习：匀弹簧在离心力场中的伸长问题。 M, k
（2010 IYPT题目）
T dT T 2 xdm,
dm
M L
dx0
x0
~L k k
dx0
T (x)
k~(dx dx0 )
dx k L(
dx0
1)
T
dT
kLd( dx dx0
1)
IPhO21-3中子星的旋转(p258)
毫秒脉冲星是宇宙中的一类辐射源，它们发射间隔周期为一到几毫 秒的持续时间非常短的脉冲。这种辐射在无线电波长范围内，一台合适的 无线电接收器便可用来检测各个脉冲，由此精确地测定其发射周期。
这些无线电脉冲来自于一种特殊的，称之为中子星的星体表面。中 子星非常密实，它们的质量与太阳的质量有相同数量级，而半径只有数十 公里。它们非常快地自旋。由于高速旋转，中子星稍被压扁（假定表面形 状是长、短轴几乎相等的旋转椭球面）。
R Mg N cosq 0

第一讲 平衡问题典题汇总类型一、物体平衡种类的问题一般有两种方法解题，一是根据平衡的条件从物体受力或力矩的特征来解题，二是根据物体发生偏离平衡位置后的能量变化来解题。

1、如图1—4所示，均匀杆长为a ，一端靠在光滑竖直墙上，另一端靠在光滑的固定曲面上，且均处于Oxy 平面内．如果要使杆子在该平面内为随遇平衡，试求该曲面在Oxy 平面内的曲线方程．分析和解：本题也是一道物体平衡种类的问题，解此题显然也是要从能量的角度来考虑问题，即要使杆子在该平面内为随遇平衡，须杆子发生偏离时起重力势能不变，即杆子的质心不变，y C 为常量。

又由于AB 杆竖直时12C y a =， 那么B 点的坐标为 sin x a θ=111cos (1cos )222y a a a θθ=-=- 消去参数得222(2)x y a a +-=类型二、物体系的平衡问题的最基本特征就是物体间受力情况、平衡条件互相制约，情况复杂解题时一定要正确使用好整体法和隔离法，才能比较容易地处理好这类问题。

例3．三个完全相同的圆柱体，如图1一6叠放在水平桌面上，将C 柱放上去之前，A 、B 两柱体之间接触而无任何挤压，假设桌面和柱体之间的摩擦因数为μ0，柱体与柱体之间的摩擦因数为μ，若系统处于平衡，μ0与μ必须满足什么条件？分析和解：这是一个物体系的平衡问题，因为A 、B 、C 之间相互制约着而有单个物体在力系作用下处于平衡，所以用隔离法可以比较容易地处理此类问题。

设每个圆柱的重力均为G ，首先隔离C 球，受力分析如 图1一7所示，由∑Fc y ＝0可得111)2N f G += ① 再隔留A 球，受力分析如图1一8所示，由∑F Ay =0得1121022N f N G +-+= ② 由∑F Ax =0得211102f N N -= ③ 由∑E A ＝0得12f R f R = ④ 由以上四式可得12f f ===112N G =，232N G =而202f N μ≤，11f N μ≤0μ≥2μ≥类型三、物体在力系作用下的平衡问题中常常有摩擦力，而摩擦力F f 与弹力F N 的合力凡与接触面法线方向的夹角θ不能大于摩擦角，这是判断物体不发生滑动的条件．在解题中经常用到摩擦角的概念．例4．如图1一8所示，有两根不可伸长的柔软的轻绳，长度分别为1l 和2l ，它们的下端在C 点相连接并悬挂一质量为m 的重物，上端分别与质量可忽略的小圆环A 、B 相连，圆环套在圆形水平横杆上．A 、B 可在横杆上滑动，它们与横杆间的动摩擦因数分别为μ1和μ2，且12l l <。

1.如图3—80所示，C 为一放在固定的粗糙水平桌面上的双斜面，其质量c m =6.5kg,顶端有一定滑轮，滑轮的质量及轴处的摩擦皆不可计。

A 和B 是两个滑块，质量分别为A m =3.0kg,B m =0.50kg,由跨过定滑轮的不可伸长的轻绳相连。

开始时，设法抓住A 、B 和C ，使它们都处于静止状态，且滑轮两边的轻绳恰好伸直。

今用一等于26.5N 的水平推力F 作用于C ，并同时释放A 、B 和C ，若C 沿桌面向左滑行，其加速度a =3.02/m s ,B 相对于桌面无水平方向的位移（绳子一直是绷紧的）。

试求C 与左面间的动摩擦因素μ。

（图中a =37°，β=53°，已知sin37°=0.6，重力加速度g=102/m s ）图3—80解：设A a 、B a 与'A a 、'B a 分别为A 、B 相对于桌面的加速度的大小和相对于C 的加速度的大小，设水平向右的x 轴的正方向，竖直向上的y 轴的正方向。

因为B 开始时相对于桌面静止，以后相对于桌面无水平方向的位移，可知B a 沿水平方向的分量为0，即Bx a ='Bx a -a =0由此得'Bx a =a =32/m s因此绳不可伸长，又不是绷紧的，固有'A a ='B a 。

它们的方向分别沿所在的斜面，方向如图3—81所示。

各分量的大小为xy37°a ’B图3—81'Bx a ='B a cos53°'By a ='B a sin53°'Ax a ='A a cos37°'Ay a =-'A a sin37°由此得'B a ='A a =52/m s ，'By a =42/m s 。

'Ax a =42/m s'Ay a =-32/m s 。

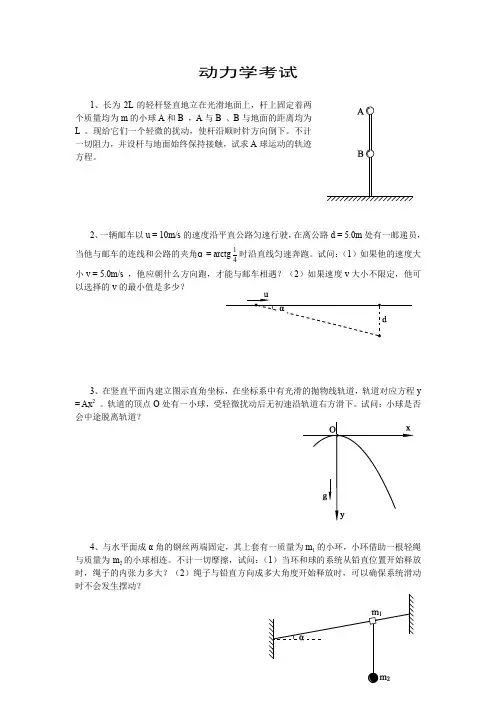
动力学考试1、长为2L 的轻杆竖直地立在光滑地面上，杆上固定着两个质量均为m 的小球A 和B ，A 与B 、B 与地面的距离均为L 。

现给它们一个轻微的扰动，使杆沿顺时针方向倒下。

不计一切阻力，并设杆与地面始终保持接触，试求A 球运动的轨迹方程。

2、一辆邮车以u = 10m/s 的速度沿平直公路匀速行驶，在离公路d = 5.0m 处有一邮递员，当他与邮车的连线和公路的夹角α= arctg 41时沿直线匀速奔跑。

试问：（1）如果他的速度大小v = 5.0m/s ，他应朝什么方向跑，才能与邮车相遇？（2）如果速度v 大小不限定，他可以选择的v 的最小值是多少？3、在竖直平面内建立图示直角坐标，在坐标系中有光滑的抛物线轨道，轨道对应方程y = Ax 2 。

轨道的顶点O 处有一小球，受轻微扰动后无初速沿轨道右方滑下。

试问：小球是否会中途脱离轨道？4、与水平面成α角的钢丝两端固定，其上套有一质量为m 1的小环，小环借助一根轻绳与质量为m 2的小球相连。

不计一切摩擦，试问：（1）当环和球的系统从铅直位置开始释放时，绳子的内张力多大？（2）绳子与铅直方向成多大角度开始释放时，可以确保系统滑动时不会发生摆动？5、质量为m 、倾角分别为α和β的双斜面体放在水平面上，另有质量分别为m 1和m 2的滑块通过轻滑轮跨过双斜面（两边的绳子和斜面平行）。

不计一切摩擦，静止释放整个系统，试求双斜面体．．．．的加速度。

《动力学考试》提示与答案1、提示：整体质心无水平位移。

建右图所示的坐标，并引入参数θ ，然后消去即可。

答案：22)2L (x + 22)L 2(y = 1 ，轨迹为椭圆。

2、提示——（1）对图示的灰色三角形用正弦定理，有βsin ut = αsin vt 得 β = arcsin 17172 （2）以β为未知，看v （β）函数 v = βαsin sin u 显然 v min = usin α答案：（1）与公路夹角θ = arctg 41+ arcsin 17172（约14.0°+ 29.0°= 43.0°）；（2）2.43m/s 。

(1)木块的下滑过程 (2)碰撞过程
m
9
解 (1)木块的下滑过程
(M+m+地球)：机械能守恒。选弹簧原长处为零 势点，则有
求得
方向沿斜面向下。
m
1
10
(2)碰撞过程 (M+m): 只有沿斜面方向系统动量守恒:
M1-m cos=(M+m)2 解出: 2=-0.89m/s。
负号表示此速度的方向沿斜面向上。
质点动力学习题
1
例题 半球面(R 、M) , 球面和地光滑， m、M静 止，若在角处m开始脱离球面，试求：
(1) 角满足的关系式； (2)分别讨论m/M<<1和m/M>>1时cos的取值。
解 (1)小物体脱离球面的条 件是：N=0。
m相对球面作圆运动， m
离开球面的瞬间球面是惯性
系，于是沿法向有
Vx
N
m
1
11
例题 要从地面以初速o发射卫星m进入离 地心为r的圆轨道，求o =？(地球: me、Re，
不计空气阻力)
解 圆轨道： 机械能守恒：
12
例题 质点作园周运动，半径为r，受力： (k为常量) ，方向指向园心。取无穷远为零势 点，求该质点的机械能。
解 r
o
机械能
13
讨论：(1)当r=Re时,
中的x、是m对地的速度。
m
R M
N
mg r
4
由速度合成定理: (4)
(5)
(1)
y
解上述式子得:
(2)
x m

N
(3)
Vx
R
M mg r
5
(2) 当m/M<<1，即M>>m时,

高中物理竞赛习题专题：刚体动力学1.均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动，如图所示，今使棒从水平位置由静止开始自由下落，在棒摆到竖直位置的过程中，下述说法正确的是()(A)角速度从小到大，角加速度不变(B)角速度从小到大，角加速度从小到大(C)角速度从小到大，角加速度从大到小(D)角速度不变，角加速度为零2.假设卫星环绕地球中心作椭圆运动，则在运动过程中，卫星对地球中心的()(A)角动量守恒，动能守恒(B)角动量守恒，机械能守恒(C)角动量不守恒，机械能守恒(D)角动量不守恒，动量也不守恒(Ｅ)角动量守恒，动量也守恒3.水分子的形状如图所示，从光谱分析知水分子对AA′轴的转动惯量JAA′＝1.93×10-47 kg·m2，对BB′轴转动惯量JBB′＝1.14×10-47kg·m2，试由此数据和各原子质量求出氢和氧原子的距离D和夹角θ．假设各原子都可当质点处理．4.用落体观察法测定飞轮的转动惯量，是将半径为R的飞轮支承在O点上，然后在绕过飞轮的绳子的一端挂一质量为m的重物，令重物以初速度为零下落，带动飞轮转动(如图)．记下重物下落的距离和时间，就可算出飞轮的转动惯量．试写出它的计算式．(假设轴承间无摩擦)．5.质量为m1和m2的两物体A、B分别悬挂在图(a)所示的组合轮两端.设两轮的半径分别为R和r，两轮的转动惯量分别为J1和J2，轮与轴承间、绳索与轮间的摩擦力均略去不计，绳的质量也略去不计.试求两物体的加速度和绳的张力.6.如图所示，一通风机的转动部分以初角速度ω0绕其轴转动，空气的阻力矩与角速度成正比，比例系数C为一常量.若转动部分对其轴的转动惯量为J，问：(1)经过多少时间后其转动角速度减少为初角速度的一半？(2)在此时间内共转过多少转？7.如图所示，一长为2l的细棒AB，其质量不计，它的两端牢固地联结着质量各为m的小球，棒的中点O焊接在竖直轴z上，并且棒与z轴夹角成α角.若棒在外力作用下绕z轴(正向为竖直向上)以角直速度ω＝ω0(1－e－t)转动，其中ω0为常量.求(1)棒与两球构成的系统在时刻t对z轴的角动量；(2)在t＝0时系统所受外力对z轴的合外力矩.8.在光滑的水平面上有一木杆，其质量m1＝1.0kg，长l＝40cm，可绕通过其中点并与之垂直的轴转动.一质量为m2＝10g的子弹，以v＝2.0×102m·s－1的速度射入杆端，其方向与杆及轴正交.若子弹陷入杆中，试求所得到的角速度.9.半径分别为r1、r2的两个薄伞形轮，它们各自对通过盘心且垂直盘面转轴的转动惯量为J1和J2.开始时轮Ⅰ以角速度ω0转动，问与轮Ⅱ成正交啮合后(如图所示)，两轮的角速度分别为多大？10.一质量为1.12kg，长为1.0m的均匀细棒，支点在棒的上端点，开始时棒自由悬挂.以100N的力打击它的下端点，打击时间为0.02s.(1)若打击前棒是静止的，求打击时其角动量的变化；(2)棒的最大偏转角.（3）打击瞬间O点杆收到的作用力。

第三章 动力学例题：如图所示，光滑斜面倾角为θ，在水平地面上加速运动。

斜面上用一条与斜面平行的细绳系一质量为m 的小球，当斜面加速度为a 时（a ＜cot θ），小球保持相对斜面静止。

求此时绳子的拉力T 。

解一、沿加速度a 方向建x 轴，与a 垂直的方向上建y 轴ΣFx = ma ，即Tx － Nx = maΣFy = 0 ， 即Ty + Ny = mg 代入数据，以上两式成为T cos θ－N sin θ = ma T sin θ + Ncos θ = mg解两式得：T = mgsin θ + ma cos θ解二、将正交分解的坐标选择为：x ——斜面方向，y ——和斜面垂直的方向。

这时，在分解受力时，只分解重力G 就行了，但值得注意，加速度a 不在任何一个坐标轴上，是需要分解的。

T － mg sin θ = m acos θ显然，独立解T 值是成功的。

结果与解法一相同。

T= mgsin θ + ma cos θ注意：当a ＞cot θ时，从支持力的结果N = mgcos θ－ma sin θ看小球脱离斜面的条件，脱离斜面后，θ条件已没有意义。

此时，T = m 22a g +例题：如图，二物之间的摩擦因数为μ，地面光滑。

（1）、二物相对静止的F 的条件 （2）、二物相对滑动时的系统牛顿第二定律 （3）、如果地面不光滑，二处的摩擦因数分别为1μ和2μ。

分析在不同F 下的运动情况解：（1）设二物相对静止。

则()12/a F m m =+静摩擦力 1112m Ff m a m m ==+最大静摩擦力 1m f m g μ=∵m f f ≤ ∴1112m Fm g m m μ+≥相对静止的条件 ()12F m m g μ+≤（2） 1122122F m a m a m g m a μ=+=+ （3）m 1和m 2之间的最大静摩擦力 111m f m g μ= m 2和地面之间的最大静摩擦力 ()2212m f m m g μ=+ 当2m F f ≤时，m 1和m 2均静止。

匀加速直线运动时。
解：（1）小车水平加速 y
运动时，摆锤的受力如图。 在如图坐标系中有
T1 m m
a1
x方向： T1 sin ma1 O
x
mg
y方向： T1 cos mg 0
T1 m g 2 a12
解得
tan a1
g
arctan
a1 g
当a1 0时， 0；当a1较大时，较大。
于平衡,其平衡方程的法向分
量式为
T+dT
(T dT )sin d T sin d N 0(1)
2
2
切向分量式为
N f
d
T
(T dT) cos d T cos d f 0(2)
2
2
由于dθ很小,可取sin(dθ/2)=dθ/2,cos(dθ/2)=1, 再略去高价无穷小量,上述两式变为
N Td (3)
F0 mg
2L
2g
(2n / 60)2 L
2g
4 2 400 2 5.97
2 9.8 60 2
534
g cos
g cos
若α=0，a2=a1,即为情况（1）T2 T1, 。
若a2= -gsinα,即为小车沿斜面自由下滑的情况，
此时 T2 mg cos mg， ，
可见此时悬线方向与斜面垂直。
利用一个系统中的单摆悬线的取向，可测定这个系 统直线运动时的加速度。
例题2.如图所示，在水平转台上放置一质量为M=2kg 的小物块A，物块与转台间的静摩擦系数μ=0.2，一条 光滑的绳子一端系在物块A上，另一端则由转台中心 处的小孔穿下并悬一质量为m=0.8kg的物块B。转台 以ω=4πrad/s的角速度绕竖直中心轴转动，求：转台 上面的物块A与转台相对静止时，物块转动半径的最 大值和最小值。

近期高中物理竞赛试题及答案试题一：牛顿第二定律的应用题目描述：一个质量为5kg的物体，在水平面上受到一个水平向右的力F=10N。

如果摩擦系数为0.2，求物体的加速度。

答案：首先计算摩擦力：f = μN = 0.2 × 5kg × 9.8m/s² = 9.8N。

然后应用牛顿第二定律：F - f = ma。

将已知数值代入：10N - 9.8N = 5kg × a。

解得加速度：a = 0.02m/s²。

试题二：动能定理的应用题目描述：一个质量为2kg的物体从静止开始，经过5秒后，速度达到10m/s。

求物体所受的恒定力。

答案：根据动能定理：F × s = 1/2 × m × v² - 0。

首先计算物体的动能变化：1/2 × 2kg × (10m/s)² = 100J。

然后根据位移公式：s = 1/2 × a × t²，其中a为加速度，t为时间。

由于v = at，可得a = v/t = 10m/s / 5s = 2m/s²。

代入位移公式：s = 1/2 × 2m/s² × (5s)² = 25m。

最后将动能变化和位移代入动能定理：F × 25m = 100J。

解得力：F = 100J / 25m = 4N。

试题三：理想气体状态方程题目描述：一个理想气体的初始状态为：压强P₁=1.0atm，体积V₁=2m³，温度T₁=300K。

当压强增加到P₂=2.0atm，温度不变，求气体的体积V₂。

答案：根据理想气体状态方程：P₁V₁/T₁ = P₂V₂/T₂。

由于温度不变，T₁=T₂，方程简化为：P₁V₁ = P₂V₂。

代入已知数值：1.0atm × 2m³ = 2.0atm × V₂。

全国中学生物理竞赛集锦（力学）第21届预赛（2004.9.5）二、（15分）质量分别为m1和m2的两个小物块用轻绳连结，绳跨过位于倾角α＝30︒的光滑斜面顶端的轻滑轮，滑轮与转轴之间的磨擦不计，斜面固定在水平桌面上，如图所示。

第一次，m1悬空，m2放在斜面上，用t表示m2自斜面底端由静止开始运动至斜面顶端所需的时间。

第二次，将m1和m2位置互换，使m2悬空，m1放在斜面上，发现m1自斜面底端由静止开始运动至斜面顶端所需的时间为t/3。

求m l与m2之比。

七、（15分）如图所示，B是质量为m B、半径为R的光滑半球形碗，放在光滑的水平桌面上。

A是质为m A的细长直杆，被固定的光滑套管C约束在竖直方向，A可自由上下运动。

碗和杆的质量关系为：m B＝2m A。

初始时，A杆被握住，使其下端正好与碗的半球面的上边缘接触（如图）。

然后从静止开始释放A，A、B便开始运动。

设A杆的位置用θ表示，θ为碗面的球心O至A杆下端与球面接触点的连线方向和竖直方向之间的夹角。

求A与B速度的大小（表示成θ的函数）。

九、（18分）如图所示，定滑轮B 、C 与动滑轮D 组成一滑轮组，各滑轮与转轴间的摩擦、滑轮的质量均不计。

在动滑轮D 上，悬挂有砝码托盘A ，跨过滑轮组的不可伸长的轻线的两端各挂有砝码2和3。

一根用轻线（图中穿过弹簧的那条坚直线）拴住的压缩轻弹簧竖直放置在托盘底上，弹簧的下端与托盘底固连，上端放有砝码1（两者未粘连）。

已加三个砝码和砝码托盘的质量都是m ，弹簧的劲度系数为k ，压缩量为l 0，整个系统处在静止状态。

现突然烧断栓住弹簧的轻线，弹簧便伸长，并推动砝码1向上运动，直到砝码1与弹簧分离。

假设砝码1在以后的运动过程中不会与托盘的顶部相碰。

求砝码1从与弹簧分离至再次接触经历的时间。

第21届复赛二、(20分) 两颗人造卫星绕地球沿同一椭圆轨道同向运动，它们通过轨道上同一点的时间相差半个周期．已知轨道近地点离地心的距离是地球半径R 的2倍，卫星通过近地点时的速度R GM 43=v ，式中M 为地球质量，G 为引力常量．卫星上装有同样的角度测量仪，可测出卫星与任意两点的两条连线之间的夹角．试设计一种测量方案，利用这两个测量仪测定太空中某星体与地心在某时刻的距离．（最后结果要求用测得量和地球半径R 表示）六、(20分)如图所示，三个质量都是m 的刚性小球A 、B 、C 位于光滑的水平桌面上（图中纸面），A 、B 之间，A BCπ-α DEB 、C 之间分别用刚性轻杆相连，杆与A 、B 、C 的各连接处皆为“铰链式”的（不能对小球产生垂直于杆方向的作用力）．已知杆AB 与BC 的夹角为π-α ，α < π/2．DE 为固定在桌面上一块挡板，它与AB 连线方向垂直．现令A 、B 、C 一起以共同的速度v 沿平行于AB 连线方向向DE 运动，已知在C 与挡板碰撞过程中C 与挡板之间无摩擦力作用，求碰撞时当C 沿垂直于DE 方向的速度由v 变为0这一极短时间内挡板对C 的冲量的大小．第二十届预赛（2003年9月5日）五、(20分)有一个摆长为l 的摆（摆球可视为质点，摆线的质量不计），在过悬挂点的竖直线上距悬挂点O 的距离为x 处（x ＜l ）的C 点有一固定的钉子，如图所示，当摆摆动时，摆线会受到钉子的阻挡．当l 一定而x 取不同值时，阻挡后摆球的运动情况将不同．现将摆拉到位于竖直线的左方（摆球的高度不超过O 点），然后放手，令其自由摆动，如果摆线被钉子阻挡后，摆球恰巧能够击中钉子，试求x 的最小值．六、(20分)质量为M 的运动员手持一质量为m 的物块，以速率v 0沿与水平面成a 角的方向向前跳跃（如图）．为了能跳得更远一点，运动员可在跳远全过程中的某一位置处，沿某一方向把物块抛出．物块抛出时相对运动员的速度的大小u 是给定的，物块抛出后，物块和运动员都在同一竖直平面内运动．(1)若运动员在跳远的全过程中的某时刻t o 把物块沿与x 轴负方向成某θ角的方向抛出，求运动员从起跳到落地所经历的时间．v 0(2)在跳远的全过程中，运动员在何处把物块沿与x轴负方向成θ角的方向抛出，能使自己跳得更远？若v0和u一定，在什么条件下可跳得最远？并求出运动员跳的最大距离．第二十届复赛三、（20分）有人提出了一种不用火箭发射人造地球卫星的设想．其设想如下：沿地球的一条弦挖一通道，如图所示．在通道的两个出口处A和B，分别将质量为M的物体和质量为m的待发射卫星同时自由释放，只要M比m足够大，碰撞后，质量为m的物体，即待发射的卫星就会从通道口B冲出通道；设待发卫星上有一种装置，在待发卫星刚离开出口B时，立即把待发卫星的速度方向变为沿该处地球切线的方向，但不改变速度的大小．这样待发卫星便有可能绕地心运动，成为一个人造卫星．若人造卫星正好沿地球表面绕地心做圆周运动，则地心到该通道的距离为多少？己知M＝20m，地球半径R＝6400 km．假定地球是质量均匀分布的球体，通道是光滑的，两物体间的碰撞是弹性的．五、(22分)有一半径为R 的圆柱A ，静止在水平地面上，并与竖直墙面相接触．现有另一质量与A 相同，半径为r 的较细圆柱B ，用手扶着圆柱A ，将B 放在A 的上面，并使之与墙面相接触，如图所示，然后放手．己知圆柱A 与地面的静摩擦系数为0.20，两圆柱之间的静摩擦系数为0.30．若放手后，两圆柱体能保持图示的平衡，问圆柱B 与墙面间的静摩擦系数和圆柱B 的半径r 的值各应满足什么条件？七、(25分)如图所示，将一铁饼状小物块在离地面高为h 处沿水平方向以初速0v抛出．己知物块碰地弹起时沿竖直方向的分速度的大小与碰前沿竖直方向的分速度的大小之比为e （＜1）．又知沿水平方向物块与地面之间的滑动摩擦系数为μ（≠0）：每次碰撞过程的时间都非常短，而且都是“饼面”着地．求物块沿水平方向运动的最远距离．第十九届预赛（2002年9月5日）一、（15分）今年3月我国北方地区遭遇了近10年来最严重的沙尘暴天气．现把沙尘上扬后的情况简化为如下情景：v 为竖直向上的风速，沙尘颗粒被扬起后悬浮在空中（不动）．这时风对沙尘的作用力相当于空气不动而沙尘以速度v 竖直向下运动时所受的阻力．此阻力可用下式表达2f Av αρ=其中α为一系数，A 为沙尘颗粒的截面积，ρ为空气密度．（1）若沙粒的密度 33S 2.810kg m ρ=⨯⋅－，沙尘颗粒为球形，半径42.510m r =⨯－，地球表面处空气密度30 1.25kg m ρ=⋅－，0.45α=，试估算在地面附近，上述v 的最小值1v ．（2）假定空气密度ρ随高度h 的变化关系为0(1)Ch ρρ=-，其中0ρ为0h =处的空气密度，C 为一常量，411.1810m C -=⨯－，试估算当19.0m s v =⋅－时扬沙的最大高度．（不考虑重力加速度随高度的变化）三、（20分）据新华社报道，为了在本世纪初叶将我国的航天员送上太空，2002年3月25日22时15分，我国成功地发射了一艘无人试验飞船。

例 9 图示的均质杆 OA 的质量为 30kg，杆在铅垂位置时弹簧处于自然状态。设 弹簧常数 k =3kN/m，为使杆能由铅直位置 OA 转到水平位置 OA'，在铅直位置时 的角速度至少88.4(J )
1 2 2 1 W ( F ) P 1.2 k ( 1 2 ) 309.81.2 3000[02 ( 2.4 1.2 2 ) 2 ] 2 2 1 1 T1 302.4 2 0 2 28.8 0 2 , 由 T2 0 T2 T1 W ( F ) 2 3
t 时，由图 6 x c2
因为 xc1 xc2
解得： x
说明电机沿水平方向作简谐振动，振幅为 2 ）
电 机 未 跳 起 时 ， Fy 仍 可 用 上 例 所 求 结 果 ， 即
F y m1 m2 g m2 e 2 sin t
令 F y 0 ，求的电机的角速度为： 讨论：当 sin t 1 ，即 t 的最小角速度为： min
图 18 解：选系统为研究对象
W ( F ) 2mg S sin f mgS cos mg S (2sin f cos )
T2 1 mv 2 1 mv 2 1 1 mr 2 2 2 2 2 2 运动学关系： v r T2 5 mv 2 4 T1 0
图5 解： 1．研究对象：电动机整体
2．分析受力（如图示）
图6
O1 O1 0 ；转子作匀速圆周运动，其法线加速度 3．分析运动：定子不动 x y
n aO e 2 2
4．列动力学方程求解：
m a
i
ix
Fix Fiy
m1 0 m 2 e 2 cos t Fx

1、（本题20分）如图6所示，宇宙飞船在距火星表面H 高度处作匀速圆周运动，火星半径为R R 。

当飞。

当飞船运行到P 点时，点时，在极短时间内向外侧点喷气，在极短时间内向外侧点喷气，在极短时间内向外侧点喷气，使飞船获得一径向速度，使飞船获得一径向速度，使飞船获得一径向速度，其大小为原来速度的其大小为原来速度的α倍。

因α很小，所以飞船新轨道不会与火星表面交会。

飞船喷气质量可以不计。

（1）试求飞船新轨道的近火星点A 的高度h 近和远火星点B 的高度h 远 ；（2）设飞船原来的运动速度为v 0 , ,试计算新轨道的运行周期试计算新轨道的运行周期T T 。

2，(20分)有一个摆长为l 的摆（摆球可视为质点，摆线的质量不计），在过悬挂点的竖直线上距悬挂点O 的距离为x 处（x ＜l ）的C 点有一固定的钉子，如图所示，当摆摆动时，摆线会受到钉子的阻挡．当l 一定而x 取不同值时，阻挡后摆球的运动情况将不同．现将摆拉到位于竖直线的左方（摆球的高度不超过O 点），然后放，然后放 手，令其自由摆动，如果摆线被钉子阻挡后，摆球恰巧能够击中钉子，试求x 的最小值．的最小值．3，（20分）如图所示，如图所示，一根长为一根长为L 的细刚性轻杆的两端分别连结小球a 和b ，它们的质量分别为m a 和 m b . 杆可绕距a 球为L/4处的水平定轴O 在竖直平面内转动．在竖直平面内转动．初始时杆处于竖直位置．初始时杆处于竖直位置．初始时杆处于竖直位置．小球小球b 几乎接触桌面．在杆的右边水平桌面上，紧挨着细杆放着一个质量为m 的立方体匀质物块，图中ABCD 为过立方体中心且与细杆共面的截面．现用一水平恒力F 作用于a 球上，使之绕O 轴逆时针转动，求当a 转过a 角时小球b 速度的大小．设在此过程中立方体物块没有发生转动，且小球b 与立方体物块始终接触没有分离．不计一切摩擦．离．不计一切摩擦．4、把上端A 封闭、下端B 开口的玻璃管插入水中,放掉部分空气后放手,玻璃管可以竖直地浮在水中(如下图).设玻璃管的质量m=40克,横截面积S=2厘米2,水面以上部分的长度b=1厘米,大气压强P 0=105帕斯卡.玻璃管壁厚度不计,管内空气质量不计.(1)求玻璃管内外水面的高度差h. (2)用手拿住玻璃管并缓慢地把它压入水中,当管的A 端在水面下超过某一深度时,放手后玻璃管不浮起.求这个深度. (3)上一小问中,放手后玻璃管的位置是否变化?如何变化?(计算时可认为管内空气的温度不变) 5、一个光滑的圆锥体固定在水平的桌面上,其轴线沿竖直方向,母线与轴线之间的夹角θ=30°(如右图).一条长度为l 的绳(质量不计),一端的位置固定在圆锥体的顶点O 处,另一端拴着一个质量为m 的小物体(物体可看作质点,绳长小于圆锥体的母线).物体以速率v 绕圆锥体的轴线做水平匀速圆周运动(物体和绳在上图中都没画出). a b A B C D F 6、(13(13分分) ) 一辆车通过一根跨过定滑轮的绳一辆车通过一根跨过定滑轮的绳一辆车通过一根跨过定滑轮的绳PQ PQ PQ提升井中质量为提升井中质量为提升井中质量为m m 的物体的物体,,如图所示绳的绳的P P 端拴在车后的挂钩上后的挂钩上,Q ,Q ,Q端拴在物体上端拴在物体上端拴在物体上..设绳的总长不变设绳的总长不变,,绳的质量、定滑轮的质量和尺寸、滑轮上的摩擦都忽略不计都忽略不计. .开始时开始时,,车在车在A A 点,左右两侧绳都已绷紧并且是竖直的,左侧绳长为左侧绳长为H.H.H.提升时提升时提升时,,车加速向左运动运动,,沿水平方向从沿水平方向从A A 经过经过B B 驶向驶向C.C.C.设设A 到B 的距离也为的距离也为H,H,H,车过车过车过B B 点时的速度为点时的速度为v v B .求在车由求在车由A A 移到移到B B 的过程中的过程中,,绳Q 端的拉力对物体做的功端的拉力对物体做的功. .7.7.在两端封闭、内径均匀的直玻璃管内在两端封闭、内径均匀的直玻璃管内,有一段水银柱将两种理想气体a 和b 隔开隔开..将管竖立着将管竖立着,,达到平衡时达到平衡时,,若温度为若温度为T,T,T,气柱气柱气柱a a 和b 的长度分别为的长度分别为l l a 和l b ;若温度为若温度为T T ＇,长度分别为长度分别为l l 抋和抋和l l 抌.然后将管平放在水平桌面上后将管平放在水平桌面上,,在平衡时在平衡时,,两段气柱长度分别为两段气柱长度分别为l l 攁和攁和l l 攂.已知已知T T 、T 挕8．如图所示，质量为Kg M9=的小车放在光滑的水平面上，其中AB 部分为半径R=0.5m 的光滑41圆弧，圆弧，BC BC 部分水平且不光滑，长为L=2m L=2m，一小物块质量，一小物块质量m=6Kg m=6Kg，由，由A 点静止释放，刚好滑到C 点静止（取g=102s m ），求：，求：①物块与BC 间的动摩擦因数间的动摩擦因数②物块从A 滑到C 过程中，小车获得的最大速度9.9.．如图所示，在光滑水平面上放一质量为．如图所示，在光滑水平面上放一质量为M 、边长为l 的正方体木块，木块上搁有一长为L 的轻质光滑棒，棒的一端用光滑铰链连接于地面上O 点，棒可绕O 点在竖直平面内自由转动，另一端固定一质量为m 的均质金属小球．开始时，棒与木块均静止，棒与水平面夹角为a 角．当棒绕O 点向垂直于木块接触边方向转动到棒与水平面间夹角变为b 的瞬时，求木块速度的大小．H R GM+2220)v (v a +21a +HR GM+mRωθ rA F θv 0r P = v A r A ④解①②③④四式可得：解①②③④四式可得： r A =a++1H R同理，对P 和B 用能量关系和开普勒第二定律，可得：r B =a-+1HR 椭圆的长半轴：椭圆的长半轴：a = a =2rrBA+=21HR a -+最后对圆轨道和椭圆轨道用开普勒第三定律可得椭圆运动的周期。

高中物理竞赛试题及答案1. 题目：一物体从静止开始做匀加速直线运动，第3秒内通过的位移为15米，求物体的加速度。

答案：根据匀加速直线运动的位移公式，第3秒内的位移为\(\frac{1}{2}a(3^2) - \frac{1}{2}a(2^2) = 15m\)，解得\(a =4m/s^2\)。

2. 题目：一个质量为2kg的物体在水平面上以10m/s的速度做匀速直线运动，若受到一个大小为5N的水平力作用，求物体的加速度。

答案：根据牛顿第二定律，\(F = ma\)，所以\(a = \frac{F}{m} =\frac{5N}{2kg} = 2.5m/s^2\)。

3. 题目：一个质量为1kg的物体从10m高处自由下落，忽略空气阻力，求物体落地时的速度。

答案：根据自由落体运动的公式，\(v^2 = 2gh\)，代入\(g =9.8m/s^2\)和\(h = 10m\)，解得\(v = \sqrt{2 \times 9.8 \times 10} = 14.1m/s\)。

4. 题目：一物体在水平面上以10m/s的速度做匀速圆周运动，半径为5m，求物体所受的向心力。

答案：根据向心力公式，\(F = \frac{mv^2}{r}\)，代入\(m = 1kg\)，\(v = 10m/s\)，\(r = 5m\)，解得\(F = \frac{1 \times 10^2}{5}= 20N\)。

5. 题目：一物体从高度为20m的斜面顶端以10m/s的初速度滑下，斜面倾角为30°，求物体滑到斜面底端时的速度。

答案：根据能量守恒定律，\(mgh + \frac{1}{2}mv_0^2 =\frac{1}{2}mv^2\)，代入\(g = 9.8m/s^2\)，\(h = 20m\)，\(v_0 = 10m/s\)，\(\theta = 30°\)，解得\(v = \sqrt{2gh\cos\theta + v_0^2} = \sqrt{2 \times 9.8 \times 20 \times\frac{\sqrt{3}}{2} + 10^2} = 22.6m/s\)。

动力学1、如图1所示，在光滑的固定斜面上，A 、B 两物体用弹簧相连，被一水平外力F 拉着匀速上滑。

某瞬时，突然将F 撤去，试求此瞬时A 、B 的加速度a A 和a B 分别是多少（明确大小和方向）。

已知斜面倾角θ= 30°，A 、B 的质量分别为m A = 1kg 和m B = 2kg ，重力加速度g = 10m/s 2。

（a A = 0 ；a B = 7.5m/s 2，沿斜面向下。

）2倾角为α的固定斜面上，停放质量为M 的大平板车，它与斜面的摩擦可以忽略不计。

平板车上表面粗糙，当其上有一质量为m 的人以恒定加速度向下加速跑动时，发现平板车恰能维持静止平衡。

试求这个加速度a 值。

3：光滑水平桌面上静置三只小球，m 1=1kg 、m 2=2kg 、m 3=3kg ，两球间有不可伸长的轻绳相连，且组成直角三角形，α=37°.若在m 1上突然施加一垂直于m 2、m 3连线的力F =10N ，求此瞬时m 1受到的合力，如图1所示.αa图 5mM4：图4所示。

为斜面重合的两楔块ABC及ADC，质量均为M，AD、BC两面成水平，E为质量等于m的小滑块，楔块的倾角为a，各面均光滑，系统放在水平平台角上从静止开始释放，求两斜面未分离前E的加速度。

5 长分别为l1和l2的不可伸长的轻绳悬挂质量都是m的两个小球，如图4所示，它们处于平衡状态。

突然连接两绳的中间小球受水平向右的冲击(如另一球的碰撞)，瞬间内获得水平向右的速度v0，求这瞬间连接m2的绳的拉力为多少？图5 6：定滑轮一方挂有m1=5kg的物体，另一方挂有轻滑轮B，滑轮B两方挂着m2=3kg与m3=2kg的物体(图5)，求每个物体的加速度。

7：如图9所示，两个木块A和B间的接触面垂直于图中纸面且与小平成θ角.A、B间的接触面是光滑的，但它们与水平桌面间有摩擦，静摩擦因数和动摩擦因数均为μ.开始时A、B都静止，现施一水平推力F于A，要使A、B向右加速运动且A、B之间不发生相对滑动，则：(1)μ的数值应满足什么条件？(2)推力F的最大值不能超过多少？(只考虑平动，不考虑转动问题)8：如图11所示，C为一放在固定的粗糙水平桌面上的双斜面，其质量m c=6.5kg，顶端有一定滑轮，滑轮的质量及轴处的摩擦皆可不计.A和B是两个滑块，质量分别为m A=3.0kg，m B=0.50kg，由跨过定滑轮的不可伸长的轻绳相连.开始时，设法抓住A、B和C，使它们都处于静止状态，且滑轮两边的轻绳恰好伸直.今用一大小等于26.5N的水平推力F作用于C，并同时释放A、B和C.沿桌面向左滑行，其加速度a=3.0m/s2，B相对于桌面无水平方向的位移(绳子一直是绷紧的).试求C与桌面间的动摩擦因数μ.(图中α=37°，β=53°，已知sin37°=0.6，重力加速度g=10m/s2)9：如图2所示，质量为m的物体C用两根绳子系住，两绳分别跨过同一高度的滑轮O1和O2后与滑块A、B相连.滑块A的质量为m，滑块B的质量为2m，分别放在倾角为60°和30°的固定光滑斜面上.当系统平衡时，在物体C上无初速地放上另一质量也为m的物体D，并且C、D立刻粘在一起.试求刚放上D的瞬时物体A和B的加速度.。