物理：地球表面的重力与重力加速度2

物理知识总结重力与重力加速度重力与重力加速度物理学中，重力是一个重要的概念，它是描述物体之间相互吸引力的特性。

重力对于我们理解自然界中的各种现象以及应用于工程和科学研究中的计算都起着至关重要的作用。

本文将从重力的定义、重力的计算公式以及重力加速度等方面进行总结和讨论。

一、重力的定义重力是指地球或其他天体对物体产生的吸引力，是物体质量相互作用的结果。

根据牛顿第三定律，一个物体受到的万有引力等于其质量乘以重力加速度。

重力的方向始终指向两个物体的中心。

二、重力的计算公式重力的计算公式由引力定律给出，其公式为：F =G * (m1 * m2) / r^2其中，F是两个物体之间的重力，m1和m2分别是两个物体的质量，r是两个物体之间的距离，G是重力常数。

三、重力加速度的概念重力加速度指的是物体在重力作用下的加速度。

根据牛顿第二定律，物体所受合力等于物体质量与加速度的乘积，即 F = m * a。

在地球表面附近，重力加速度常被记作 g，其大小约为9.8 m/s^2。

在其他天体上，重力加速度的大小会有所不同。

四、重力与物体质量的关系重力与物体质量成正比，即质量越大，重力就越大。

这可以从重力公式中得出，其中的质量作为乘数与重力成正比关系。

所以，地球对质量更大的物体会施加更大的重力。

五、重力与距离的关系重力与距离的平方成反比关系，即距离越远，重力越弱。

这可以从重力公式中推导得出，距离的平方作为分母与重力成反比关系。

因此，两个物体之间的距离增加，重力减小。

六、重力与物体的自由落体运动重力对物体的自由落体运动有重要影响。

根据物体质量和重力的关系，所有物体在同一加速度下都会以相同的速度自由落体。

这解释了为什么不同质量的物体在同一高度时会同时落地。

七、重力对轨道运动的影响重力对行星、卫星和人造卫星等天体的轨道运动也起着重要的作用。

根据万有引力定律，轨道运动是一个平衡力系统，以重力提供的向心力平衡物体想要沿直线运动的趋势。

物理中g的取值在物理学中，g通常代表重力加速度，是地球表面单位质量物体在重力场中受到的加速度大小。

下面就g的取值进行一些介绍：一、地球表面g的取值1. 标准重力加速度标准重力加速度是指实验室中测量得到的g值，其取值为9.80665米/秒²。

它是指在国际计量单位系统中作为重力加速度的标准值。

这个值是指在标准温度、标准大气压下，经由标准测量方法得出的一种平均值。

2. 实测重力加速度地球表面的实测重力加速度通常会因为地球的离心力、地形地貌、海拔高度以及地球自转等因素而有所不同。

在赤道地区，由于离心力的影响，地球实测重力加速度为9.780327米/秒²。

在北极地区，由于地球自转而造成的离心力的减弱，加上海拔高度较高，地球实测重力加速度只有9.8322米/秒²。

二、天体g的取值1. 太阳表面g的取值太阳的表面重力加速度约为274米/秒²。

2. 其他行星g的取值行星和卫星的重力加速度与其体积、密度、质量、半径以及自转等特性有关。

例如，火星的重力加速度为3.71米/秒²，木星为24.79米/秒²，土星为10.44米/秒²，月球为1.62米/秒²。

三、其他g的取值在一些特殊环境下，g的取值也会有所不同。

1. 空间站g的取值在国际空间站内，由于微重力环境，其g值约为0.006米/秒²。

为了维持人体生理的正常状态，可以通过运动、健身等手段来增加身体的负荷，保持骨骼肌肉的力量和健康。

2. 加速度g的取值在高速列车和飞机等运行过程中，由于加速度的作用，人体将受到不同的g值。

一般来说，人体能承受的最大g值是5~6g，超过这个范围后，人体就会出现失重、晕眩、甚至休克等症状。

而宇航员在火箭的发射和返回过程中，所受的g值可以高达20g以上，需要通过特殊的训练来适应这种极端环境。

以上就是关于g在物理学中的不同取值的介绍，可以看出g值的大小不仅与地球表面的位置有关，还与天体的特性和环境有关。

重力加速计算公式重力加速计算公式：g = G * M / r^2人们常常说，地球是我们的家园。

对于地球的重力，我们并不陌生。

它是地球与我们之间的一种吸引力，让我们紧紧地与地球相连，不会飘向宇宙的深处。

重力的大小与我们所处的位置有关。

在地球表面上，重力加速度的大小是9.8 m/s^2。

这个数值是怎么来的呢？我们可以通过一个简单的公式来计算。

这个公式是这样的：g = G * M / r^2。

其中，g代表重力加速度，G 代表万有引力常数，M代表地球的质量，r代表地球到我们所处位置的距离。

万有引力常数G是一个固定的值，约等于6.67 * 10^-11 N(m/kg)^2。

地球的质量M是一个大约为5.97 * 10^24 kg的数值。

地球到我们所处位置的距离r可以近似看作地球半径R，约为6371 km。

我们可以将这些数值代入公式中计算，就可以得到地球表面上的重力加速度。

将G、M和r代入公式，计算得到的结果是9.8 m/s^2。

这就是我们所熟悉的地球表面上的重力加速度。

重力加速度的大小对我们的日常生活有很大影响。

它决定了物体下落的速度和力量。

当我们抛出一个物体时，它会受到地球的重力作用，以9.8 m/s^2的加速度向下运动。

这也是为什么我们需要小心把握力度，以免物体过快地下落。

重力加速度还决定了我们的体重。

因为体重是由地球对我们的吸引力所决定的，所以不同的地方体重也会有所不同。

比如，在月球上，重力加速度只有地球的六分之一左右，所以我们会感觉轻飘飘的，仿佛在梦游一样。

重力加速度是我们生活中不可或缺的一部分。

它让我们与地球紧密相连，让我们感受到地球的温暖和安全。

虽然我们无法看见重力，但它却始终存在，并且时刻影响着我们的生活。

所以，让我们感恩地球给予我们的重力，让我们与地球一同旋转，一同舞动。

在这个宇宙中，地球是我们独一无二的家园，而重力则是我们与地球之间的纽带。

让我们珍惜这份纽带，保护好我们的家园。

重力加速度方程
在物理学中，重力加速度（g）是描述物体在地球表面附近自由下落时加速度的量。

其值为约9.81 m/s²（在标准状况下）。

根据牛顿的第二运动定律，重力加速度可以通过物体的质量（m）和重力（mg）之间的关系来表示。

具体来说，方程可以表示为：
mg = G * (m / r²)
其中，g是重力加速度，G是万有引力常数（约6.67259×10^-11 m³ kg⁻¹ s⁻²），m是物体的质量，r是地球半径（约6371 km）。

这个方程可以用于计算不同高度和纬度下的重力加速度值。

由于地球不是完美的球体，所以重力加速度在地球表面不同位置会有所变化。

此外，由于地球自转的影响，重力加速度也会随着纬度的变化而有所差异。

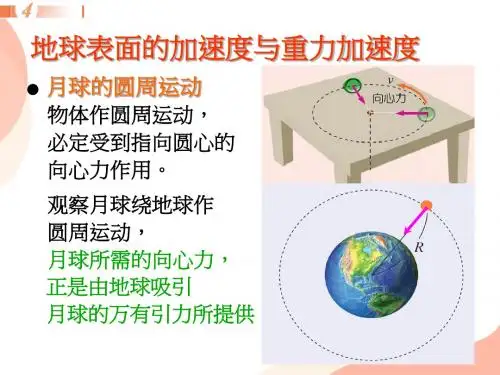
水平面重力加速度
水平面重力加速度在物理学中被广泛地指定为g，数值为9.8m/s2。

重力加速度的概念最初由伽利略提出，它代表地球表面上的对象自然受到的微小的力，又称重力力。

水平面重力加速度（g）是地球表面上所有物体受到的重力力的总和，由地球
表面上每一单位体积的物体产生的重力力叠加而得到。

根据牛顿第二定律，如果一个物体受到力，它会受到逆力，等于它受到的力的大小。

以此为基础，重力加速度可以作为物体受到任何重力力（摩擦力或弯矩）的反作用力的参考。

在当今的科学研究中，引力场的强度在任何一个地区都因地理位置而异，即由空间变量改变。

根据地球的磁场，强度以数十米的距离会表现出极大的变化，从而导致水平面重力加速度也会变化。

水平面重力加速度对于空间所有重力力研究有极其重要的作用，科学家们也确实利用该理论进行量化分析。

因此，由于涉及到了相关的复杂物理数学，不仅仅是机械等研究地面上的物体或者行为，其他的研究领域也会用的到水平面重力加速度，例如交通工程、建筑学。

虽然重力力在我们日常生活中是融入其中的，不能被直接感受，但它对于人类社会乃至宇宙中所有物理性质都有极其重要的作用，不容小觑。

正是水平面重力加速度（g），让我们更多地理解世界，进而更好地去应用知识，改善生活。

总而言之，水平面重力加速度（g）对我们的宇宙体系了解至关重要，成为研
究宇宙科学的基石。

这个基本概念的发现为人类的进步提供了重要的参考，并促使我们更好地把握宇宙的奥秘以及如何从中最大化加以利用。

地球上的重力加速度地球上的重力加速度（g）是指物体在地球表面上受到的重力作用所导致的加速度。

它是地球引力场中的一个重要参数，不仅影响物体的运动和行为，也对天文学、物理学等科学研究具有重要意义。

本文将详细介绍地球上的重力加速度以及它的影响。

一、重力加速度的概念及计算方法重力加速度是指物体在自由下落过程中，每秒钟速度增加的数值。

在地球表面上，重力加速度的平均值约等于9.8米/秒²。

这个数值是根据大量观测数据的统计结果得出的，具有一定的精确性。

计算重力加速度的常用公式为：g = G * M / R²其中，g表示重力加速度，G表示万有引力常量，M表示地球的质量，R表示地球的半径。

根据这个公式，可得到地球上的重力加速度约为9.8米/秒²。

二、重力加速度的测定方法为了准确测定地球上的重力加速度，科学家们使用了多种方法。

以下介绍几种常用的测定方法：1. 自由落体实验法：通过测量物体自由下落的时间和下落距离，计算出重力加速度的数值。

2. 重力震荡仪测量法：利用重力震荡仪观测出物体在重力场中的振荡周期，从而得到重力加速度的数值。

3. 弹簧测力计法：利用弹簧测力计的原理，测量物体在重力作用下所受到的力，进而计算得出重力加速度。

通过这些测定方法，科学家们得出了地球上的重力加速度约等于9.8米/秒²的结论。

三、重力加速度的影响地球上的重力加速度对物体的运动和行为有着重要影响。

以下列举几个常见的例子：1. 物体的自由下落速度：重力加速度决定了物体自由下落的速度。

在地球上，物体每秒钟下落的速度将增加9.8米。

2. 物体在斜面上的滑动：重力加速度决定了物体在斜面上滑动的速度。

斜面越陡峭，物体下滑的速度越快。

3. 影响天体运动：重力加速度是导致行星、卫星、彗星等天体绕轨道运动的重要因素。

它决定了天体之间的相互吸引和行星公转的速度。

4. 海洋潮汐的形成：重力加速度与月球和太阳的相互作用，导致了海洋潮汐的形成。

地球引力与重力加速度的计算地球引力是指地球对物体产生的引力，是因为地球质量大而产生的。

而重力加速度是指物体在地球表面上由于地球引力作用下所受到的加速度。

本文将探讨地球引力与重力加速度的计算方法以及相关的物理原理。

一、地球引力的计算地球引力的计算可以使用牛顿万有引力定律。

根据该定律，两个物体之间的引力与它们的质量和距离的平方成正比，与它们的质量和距离的平方成反比。

具体计算公式如下：F =G * (m1 * m2) / r^2其中，F表示两个物体之间的引力，G为万有引力常数，m1和m2分别为两个物体的质量，r为它们之间的距离。

以地球引力为例，我们可以将地球的质量记为M，地球上的物体质量记为m，地球半径记为R。

根据上述公式，地球对物体产生的引力可以表示为：F =G * (M * m) / R^2二、重力加速度的计算重力加速度是指物体在地球表面上由于地球引力作用下所受到的加速度。

重力加速度的计算可以通过地球引力和物体质量之间的关系得出。

根据牛顿第二定律，物体所受到的力与其质量和加速度成正比。

在地球表面上，物体所受到的力就是地球引力，加速度即为重力加速度。

因此，我们可以得到以下公式：F = m * g其中，F为物体所受到的力，m为物体的质量，g为重力加速度。

将地球引力的计算公式代入上述公式中，可以得到：G * (M * m) / R^2 = m * g进一步化简，可以得到：g = G * M / R^2这就是重力加速度的计算公式。

三、地球引力与重力加速度的数值根据已知的物理常数和地球的参数，我们可以计算出地球引力和重力加速度的数值。

万有引力常数G约等于6.67430 × 10^-11 N·(m/kg)^2，地球质量M约等于5.972 × 10^24 kg，地球半径R约等于6.371 × 10^6 m。

将这些数值代入公式中，可以得到地球引力和重力加速度的数值：地球引力：F = G * (M * m) / R^2重力加速度：g = G * M / R^2根据计算，地球引力约等于9.8 N，重力加速度约等于9.8 m/s^2。

如何测出地球的质量测量地球质量是一个复杂的过程，涉及到多种不同的方法和技术。

下面将介绍几种常用的测量地球质量的方法。

一、测量地球引力方法：最常见的测量地球质量的方法是利用地球引力的原理。

通过测量在地球表面的重力加速度，可以计算出地球的质量。

1.重力加速度测量：在地球表面的一些地点，可以使用重力计测量重力加速度。

根据牛顿第二定律可以知道，地球表面的重力加速度与地球质量成正比。

通过测量重力加速度，可以得到地球质量的近似值。

2.重力梯度测量：重力场存在垂直于地球表面的梯度变化，同时也与地球质量相关。

通过测量不同位置的重力梯度变化，可以得到地球质量的更精确估计。

二、测量地球对其他天体的引力方法：1.月球轨道运动观测：通过监测月球对地球引力的作用，可以计算出地球对月球引力的大小。

利用牛顿万有引力定律，可以推算出地球质量的估计值。

2.人造卫星轨道运动观测：人造卫星的轨道也受到地球引力的作用。

通过监测卫星的轨道参数，如半长轴、偏心率、周期等，可以计算出地球对卫星引力的大小，从而得到地球质量的估计值。

三、地震波传播速度方法：1.探测地震波传播速度：地震波在地球内部传播速度与地球的密度密切相关，因此可以利用地震波传播速度来推算地球的质量。

测量地震波P波和S波的传播速度，并结合地震学理论，可以推算出地球内部的密度分布，从而得到地球质量的估计值。

四、引潮力方法：1.观测潮汐引力：地球上的潮汐现象是由于月球和太阳的引力作用所导致的。

通过观测和计算潮汐现象，可以推算出地球的质量。

2.观测地球自转引起的形变：地球自转会引起地球的形变，形变的大小与地球质量有关。

利用地壳形变观测和计算，可以得到地球质量的估计值。

通过上述方法和技术的综合运用，可以得到地球质量的相对精确估计值。

需要注意的是，不同的测量方法都有一定的误差范围，因此得出的地球质量值也会有一定的误差。

此外，地球的质量在不同时间和地点也会有微小的变化，因此需要使用尽可能多的观测数据进行分析和计算，以获得更精确的结果。

万有引力求重力加速度公式
重力加速度是指物体受到地球引力作用时的加速度。

根据万有引力定律，物体之间的引力与它们的质量成正比，与它们之间的距离的平方成反比。

重力加速度公式可以简单地表示为：g = G * M / r^2。

在这个公式中，g代表重力加速度，G代表引力常数，M代表地球的质量，r代表物体与地球中心的距离。

我们可以通过这个公式来计算物体在地球表面上的重力加速度。

地球的质量约为 5.97×10^24千克，引力常数G约为 6.67×10^-11 N·m^2/kg^2。

将这些数值代入公式中，我们可以得到地球表面上的重力加速度大约为9.8 m/s^2。

重力加速度的大小决定了物体受到的重力力度。

例如，当我们把物体从高处自由下落时，重力加速度的作用会使物体加速下落。

而当我们把物体往上抛时，重力加速度的作用会使物体减速直至最终落地。

重力加速度公式的推导过程涉及到复杂的数学计算和物理原理，但我们不必深入研究这些细节。

重要的是理解重力加速度的概念以及它在物体运动中的作用。

通过理解重力加速度公式，我们可以更好地理解物体在地球上的运动规律，例如自由落体、抛体运动等。

这些运动规律在日常生活中无处不在，深刻影响着我们的生活。

重力加速度是物体受到地球引力作用时的加速度，可以用公式g = G * M / r^2来计算。

它决定了物体受到的重力力度，影响着物体的运动规律。

通过理解重力加速度的概念和公式，我们可以更好地理解物体在地球上的运动。

力学综合题【原卷】1．（2021届福建省莆田一中高三期中）如图，质量为M=4kg 的木板AB静止放在光滑水平面上，木板右端B点固定一根轻质弹簧，弹簧自由端在C点，C到木板左端的距离L=0.5m，质量为m=1kg 的小木块（可视为质点）静止放在木板的左端，木块与木板间的动摩擦因数为μ=0.2，木板AB受到水平向左的恒力F=14N，作用一段时间后撤去，恒力F撤去时木块恰好到达弹簧自由端C处，此后运动过程中弹簧最大压缩量x=5cm，g=10m/s2．求：(1)水平恒力F作用的时间t；(2)撤去F后，弹簧的最大弹性势能E P；(3)整个过程产生的热量Q．2．（2021届福建省三明市一中高三期中）用长L ＝0.6 m的绳系着装有m ＝0.5 kg水的小桶，在竖直平面内做圆周运动，成为“水流星”．G ＝10 m/s2．求：(1) 最高点水不流出的最小速度为多少？(2) 若过最高点时速度为3 m/s，此时水对桶底的压力多大？3．（2021届福建省三明市一中高三期中）一种氢气燃料的汽车，质量为3m=⨯，发动机的额定输出功率为80kW，行驶在平直公路上时所受阻力恒2.010kg为车重的0.1倍．若汽车从静止开始先匀加速启动，加速度的大小为2a=．达1.0m/s到额定输出功率后，汽车保持功率不变又加速行驶了800m，直到获得最大速度后才匀速行驶，g取210m/s．试求：（1）汽车的最大行驶速度；（2）汽车匀加速启动阶段结束时的速度；（3）汽车从静止到获得最大行驶速度所用的总时间．4．（2021届福建省三明市一中高三期中）传送带在工农业生产和日常生活中都有着广泛的应用．如图甲，倾角为θ的传送带以恒定速率逆时针转动，现将2kgm=的货物放在传送带上的A点，货物与传送带的速度v随时间t变化的图像如图乙，整个过程传送带是紧绷的，货物经过1.2s到达B点．(重力加速度2g=)10m/s（1）A、B两点间的距离L；（2）货物从A运动到B的过程中，货物与传送带间因摩擦产生的热量Q．5．（2021届福建省三明市一中高三期中）如图所示，固定斜面的倾角θ=30°，物体A与斜面之间的动摩擦因数μ=3，轻弹簧下端固定在斜面底端，弹簧处于原长时上端位于C点．用一根不可伸长的轻绳通过轻质光滑的定滑轮连接物体A 和B，滑轮右侧绳子与斜面平行，A的质量为2m，B的质量为m，初始时物体A 到C点的距离为L.现给A、B一初速度v0(v0>gL)，使A开始沿斜面向下运动，B向上运动，物体A将弹簧压缩到最短后又恰好能弹到C点．已知重力加速度为g，不计空气阻力，整个过程中，轻绳始终处于伸直状态，求：(1)物体A向下运动刚到C点时的速度大小；(2)弹簧的最大压缩量；(3)弹簧的最大弹性势能．6．（2021届广东省华南师大附中高三综合测试）粗糙的水平面上，一物体在水平方向拉力作用下做直线运动，水平拉力F及运动速度v随时间变化的图线如图中（甲）（乙）所示，取重力加速度g=10m/s2，求物体与地面间的动摩擦因数 。

重力加速度推导公式全文共四篇示例，供读者参考第一篇示例：重力加速度是指在自由下落过程中物体的速度不断增加的加速度。

重力是地球吸引物体的力，其大小与物体的质量有关，通常用g来表示，单位是米每秒平方，即m/s²。

在地球表面，重力加速度的大小约等于9.8m/s²。

重力加速度推导公式可以通过牛顿第二定律来推导。

牛顿第二定律公式可以表示为F=ma，其中F是受力，m是物体的质量，a是物体的加速度。

在重力作用下，物体会受到重力的作用，重力的大小可以表示为F=mg，其中g是重力加速度。

根据牛顿第二定律和重力公式可以得到：F=ma=mg将上面两个公式相等进行整合，可以得到：ma=mg由此可以得到：a=g即重力加速度的大小等于g，这就是重力加速度推导公式。

在地球表面，重力加速度的大小约等于9.8m/s²。

这个数值是通过实验测量得到的，可以用来计算物体自由下落的速度。

如果一个物体从静止开始自由下落，经过1秒钟，它的速度会增加9.8m/s；经过2秒钟，速度会增加19.6m/s；经过3秒钟，速度会增加29.4m/s，依此类推。

在一些特殊情况下，重力加速度可能会发生变化。

在月球表面，重力加速度约为1.6m/s²；在火星表面，重力加速度约为3.7m/s²。

在不同的天体表面，重力加速度会有所不同，需要根据实际情况进行计算。

重力加速度推导公式可以通过牛顿第二定律和重力公式推导得到。

重力加速度的大小与物体的质量无关，只与物体所在的天体和位置有关。

重力加速度的大小约为9.8m/s²，在物体自由下落的过程中起着重要作用。

通过重力加速度推导公式，可以计算物体在自由下落过程中的速度变化，帮助我们更好地理解重力的作用。

第二篇示例：重力加速度是一个在地球上非常普遍的现象，它是指物体在受重力作用下加速向地面运动的速度。

在地球表面，重力加速度的大小约为9.8米/秒²，这意味着一个物体在自由落体状态下每秒钟会增加9.8米的速度。

世界各地的重力加速度分别是多少一些城市的纬度和重力加速度地点纬度重力加速度附注赤道9.780 m/s2新加坡北纬1°17′9.7807马尼拉北纬14°35′9.7836南宁北纬22°43′9.7876广州北纬23°06′9.7883福州北纬28°02′ 9.7916杭州北纬30°16′ 9.7930武汉北纬30°33′ 9.7936上海北纬31°12′ 9.7940东京北纬35°42′ 9.7980海拔18m华盛顿北纬38°53′ 9.8011北京北纬39°56′ 9.8012罗马北纬41°54′ 9.8035海拔59m巴黎北纬48°50′ 9.8094海拔61m格林威治北纬51°29′ 9.81188伦敦北纬51°31′ 9.81199海拔30m柏林北纬52°31′ 9.8128海拔30m莫斯科北纬55°45′9.8156海拔139m好望角南纬33°56′9.7963海拔11m爪哇南纬6°9.7820北极909.832由于g随纬度变化不大，因此国际上将在纬度45°的海平面精确测得物体的重力加速度g=9.80665米／秒^2作为重力加速度的标准值。

在解决地球表面附近的问题中，通常将g作为常数，在一般计算中可以取g=9.80米／秒^2。

理论分析及精确实验都表明，随纬度的提高，重力加速度g的数值略有增大，如赤道附近g=9.780米／秒^2，北极地区g=9.832米／秒^2。

地球各点重力加速度近似计算公式:g=g0(1-0.00265cos&)/1+(2h/R)g0:地球标准重力加速度9.80665(m/平方秒)&:测量点的地球纬度 h:测量点的海拔高度 R:地球的平均半径(R=6370km) s:时间参考资料：/ 其他回答chenbinghui1988 2008-11-05 14:45:22地点纬度重力加速度附注赤道9.780 m/s2新加坡北纬1°17′9.7807马尼拉北纬14°35′9.7836南宁北纬22°43′9.7876广州北纬23°06′9.7883福州北纬28°02′ 9.7916杭州北纬30°16′ 9.7930武汉北纬30°33′ 9.7936上海北纬31°12′ 9.7940东京北纬35°42′ 9.7980海拔18m华盛顿北纬38°53′ 9.8011北京北纬39°56′ 9.8012罗马北纬41°54′ 9.8035海拔59m巴黎北纬48°50′ 9.8094海拔61m格林威治北纬51°29′ 9.81188伦敦北纬51°31′ 9.81199海拔30m柏林北纬52°31′ 9.8128海拔30m莫斯科北纬55°45′9.8156海拔139m好望角南纬33°56′9.7963海拔11m爪哇南纬6°9.7820北极909.832由于g随纬度变化不大，因此国际上将在纬度45°的海平面精确测得物体的重力加速度g=9.80665米／秒^2作为重力加速度的标准值。