计算机组成原理6-运算方法-加法
- 格式:ppt
- 大小:656.50 KB
- 文档页数:35


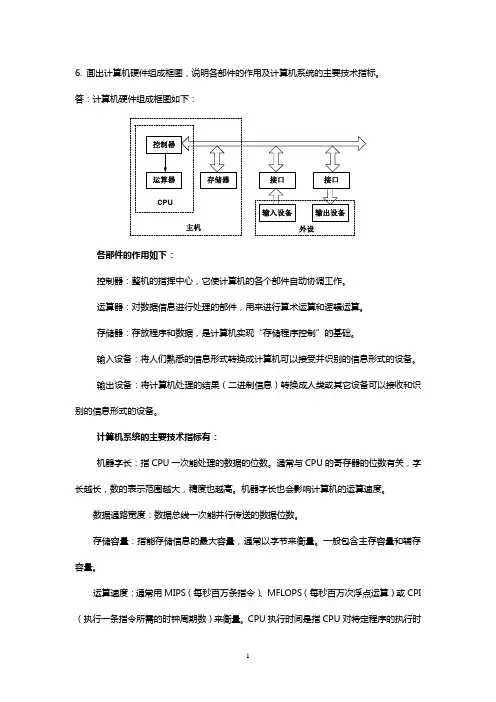
6. 画出计算机硬件组成框图,说明各部件的作用及计算机系统的主要技术指标。
答:计算机硬件组成框图如下:控制器运算器CPU主机存储器输入设备接口输出设备接口外设各部件的作用如下:控制器:整机的指挥中心,它使计算机的各个部件自动协调工作。
运算器:对数据信息进行处理的部件,用来进行算术运算和逻辑运算。
存储器:存放程序和数据,是计算机实现“存储程序控制”的基础。
输入设备:将人们熟悉的信息形式转换成计算机可以接受并识别的信息形式的设备。
输出设备:将计算机处理的结果(二进制信息)转换成人类或其它设备可以接收和识别的信息形式的设备。
计算机系统的主要技术指标有:机器字长:指CPU一次能处理的数据的位数。
通常与CPU的寄存器的位数有关,字长越长,数的表示范围越大,精度也越高。
机器字长也会影响计算机的运算速度。
数据通路宽度:数据总线一次能并行传送的数据位数。
存储容量:指能存储信息的最大容量,通常以字节来衡量。
一般包含主存容量和辅存容量。
运算速度:通常用MIPS(每秒百万条指令)、MFLOPS(每秒百万次浮点运算)或CPI (执行一条指令所需的时钟周期数)来衡量。
CPU执行时间是指CPU对特定程序的执行时间。
主频:机器内部主时钟的运行频率,是衡量机器速度的重要参数。
吞吐量:指流入、处理和流出系统的信息速率。
它主要取决于主存的存取周期。
响应时间:计算机系统对特定事件的响应时间,如实时响应外部中断的时间等。
9. 画出主机框图,分别以存数指令“STA M”和加法指令“ADD M”(M均为主存地址)为例,在图中按序标出完成该指令(包括取指令阶段)的信息流程(如→①)。
假设主存容量为256M*32位,在指令字长、存储字长、机器字长相等的条件下,指出图中各寄存器的位数。
解:主机框图如P13图1.11所示。
(1)STA M指令:PC→MAR,MAR→MM,MM→MDR,MDR→IR,OP(IR)→CU,Ad(IR)→MAR,ACC→MDR,MAR→MM,WR(2)ADD M指令:PC→MAR,MAR→MM,MM→MDR,MDR→IR,OP(IR)→CU,Ad(IR)→MAR,RD,MM→MDR,MDR→X,ADD,ALU→ACC,ACC→MDR,WR假设主存容量256M*32位,在指令字长、存储字长、机器字长相等的条件下,ACC、X、IR、MDR寄存器均为32位,PC和MAR寄存器均为28位。



池州学院数学计算机科学系实验报告专业:计算机科学与技术班级:11计本(2)班实验课程:计算机组成原理姓名:惠昊学号:110312210 实验室:硬件实验室同组同学:邓晓煜刘广东时应东于小波黄震朱斌斌钟建强王凤侠王敏实验时间:2013年3月20日指导教师签字:何向荣成绩:基本运算器实验:加法运算一实验目的和要求1.了解运算器的组成结构。
2.掌握运算器的工作原理。
二实验环境PC机一台,TD-CMA 实验系统一套三实验步骤及实验记录(1)按图连接电路,并检查无误。
(2)将时序与操作台单元的开关KK2 置为‘单拍’档, 开关KK1 、KK3 置为‘运行’档。
(3) 打开电源开关,然后按动CON单元的CLR 按钮,将运算器的A、B 和FC、FZ清零。
(4) 用输入开关向暂存器A 置数①拨动CON单元的SD27…SD20 数据开关,形成二进制数,数据显示亮为‘1 ’,灭为‘0 ’。
②置LDA=1,LDB=0,连续按动时序单元的 ST 按钮,产生一个 T4上沿,则将二进制数置入暂存器 A 中,暂存器A 的值通过ALU单元的A7…A0八位 LED 灯显示。
(5) 用输入开关向暂存器B 置数。
①拨动CON单元的SD27…SD20 数据开关,形成二进制数。
②置LDA=0,LDB=1,连续按动时序单元的 ST 按钮,产生一个T4上沿,则将二进制数置入暂存器B 中,暂存器 B 的值通过 ALU单元的B7…B0八位LED 灯显示(6)改变运算器的功能设置,观察运算器的输出。
置ALU_B=0、LDA=0、LDB=0,置 S3、S2、S1、S0为1001 ,运算器作加法运算四实验结果与分析。


计算机组成原理逻辑运算逻辑运算是计算机组成原理中非常重要的一部分,它通过对输入的逻辑值进行组合和操作,得到输出的逻辑值。
计算机中最基本的逻辑运算包括与、或、非三种运算。
与运算,又被称为逻辑乘法,它有两个输入,如果两个输入都是1,那么输出为1,否则输出为0。
其真值表如下:输入A,输入B,输出Y-------,-------,-------0,0,00,1,01,0,01,1,1或运算,又被称为逻辑加法,它有两个输入,如果两个输入中有至少一个是1,那么输出为1,否则输出为0。
其真值表如下:输入A,输入B,输出Y-------,-------,-------0,0,00,1,11,0,11,1,1非运算,又被称为逻辑反演,它只有一个输入,如果输入是1,那么输出为0;如果输入是0,那么输出为1、其真值表如下:输入A,输出Y-------,-------0,11,0除了这三种基本的逻辑运算,还有其他一些常用的逻辑运算,如异或(XOR)、与非(NAND)、或非(NOR)等。
这些逻辑运算可以通过基本的逻辑门电路进行实现。
基本的逻辑门电路主要包括与门(AND Gate)、或门(OR Gate)、非门(NOT Gate)、与非门(NAND Gate)、或非门(NOR Gate)、异或门(XOR Gate)等。
这些逻辑门电路可以通过逻辑电路图进行表示。
例如,与门的逻辑电路图如下所示:```_____A--AND,---B---,_____```图中A和B是输入端口,Y是输出端口,AND是与门。
根据与门的定义,只有当A和B的输入同时为1时,输出Y才会是1、否则,输出Y为0。
通过组合这些基本逻辑门电路,可以实现复杂的逻辑运算。
例如,通过与门和非门的组合,可以实现与非门的功能;通过或门和非门的组合,可以实现或非门的功能。
逻辑运算在计算机组成原理中广泛应用,包括算术逻辑单元(ALU),寄存器,控制单元等等。
这些逻辑运算的实现方式和原理都是基于逻辑门电路和逻辑电路图的。


计算机组成原理--运算⽅法:加减乘除补码加减法补码加法公式:[x+y]补=[x]补+[y]补补码减法:为了将减法转变为加法,需证明公式: [x-y]补=[x]补+[-y]补(证明)为了求得同时[-y]补,需要证明[-y]补=[y]补+2^-n(意义是[-y]补等于[y]补取反,末位加1)溢出检测溢出的检测可能产⽣溢出的情况两正数加,变负数,上溢(⼤于机器所能表⽰的最⼤数)两负数加,变正数,下溢(⼩于机器所能表⽰的最⼩数)定点原码乘法定点乘法原理n位乘n位积可能为2n位.乘积的最后是所有部分积之和,有n个数相加,⽽FA只有两个输⼊端,机器⼀次只能进⾏两个数的相加,不能进⾏多个数据的加法。
⼿⼯计算中,乘数的每⼀位是0还是1都可直接看见,⽽在计算机中,采⽤放乘数的寄存器的每⼀位直接决定本次相加数是被乘数还是0是很不⽅便的,若采⽤该寄存器的最低⼀位来执⾏这种判断就简便了。
计算机中执⾏乘法时,积的符号位由被乘数和乘数的符号位通过⼀个半加器(即异或门)实现。
数值部分的运算规则是:从最低位Y0开始,当乘数Yi为1时,将上次部分积加上被乘数的绝对值,然后右移⼀位,得到新的部分积;当Yi为0时,则写下全0。
然后再对乘数Y的⾼⼀位进⾏类似乘法运算。
重复“加—右移”操作N次,可得到最后的乘积。
R0存放部分积,R2存放被乘数,R1存放乘数R0清零,R2存放被乘数,R1存放乘数。
乘法开始时,“启动”信号时控制CX置1,于是开启时序脉冲T,当乘数寄存器R1最末位为“1“时,部分积Z和被乘数X在加法器中相加,其结果输出⾄R0的输⼊端。
⼀旦控制脉冲T到来,控制信号LDR0使部分积右移1位,与此同时,乘数寄存其R1也在控制信号LDR1作⽤下右移⼀位,且计数器I记数⼀次;将步骤三重复执⾏N次当计数器I=n时,计数器I的溢出信号使控制触法器CX置0,关闭时序脉冲T,乘法宣告结束原码算法存在的缺点:⼀是符号位需要单独运算,最后给运算结构以正确的符号;⼆是对于采⽤补码存储的机器,从存储器中取出的是操作数的补码,需先将其转换成原码,这样很不⽅便,⽽且影响速度。

加法原理计算机
加法原理是一种计算组合问题的方法。
它可以用来计算多个事件的总数。
加法原理的核心思想是将多个独立事件的可能性相加,以得出总数。
在使用加法原理时,需要注意以下几点:
1. 事件必须是互斥的,即一个事件发生时,其他事件不能同时发生。
例如,投掷一枚硬币,结果只能是正面或反面。
2. 事件之间不能有重叠。
每个事件都必须是独立的,不会同时发生。
例如,选择一张牌,不能同时选择红心和黑桃。
3. 每个事件都有相同的可能性。
每个事件发生的概率相等,否则加法原理不适用。
例如,从一副花色平均分布的扑克牌中选择一张,每种花色的概率都相等。
根据加法原理,如果有m个事件,每个事件发生的可能性数分别为n1、n2、...、nm,则总可能性数为n1 + n2 + ... + nm。
举个例子,假设有一家餐厅提供三种主菜和两种甜点供客人选择。
客人可以选择其中一种主菜和一种甜点。
根据加法原理,总共有3种主菜的选择 + 2种甜点的选择 = 5种不同的套餐组合。
加法原理在计算机科学中具有广泛的应用。
它可以用来计算不同组合、排列和选择的总数,帮助解决各种实际问题。
不论是
在编程、算法设计还是数据处理中,加法原理都是一个重要的工具。
第2章数据的表示和运算主要内容:(一)数据信息的表示1.数据的表示2.真值和机器数(二)定点数的表示和运算1.定点数的表示:无符号数的表示;有符号数的表示。
2.定点数的运算:定点数的位移运算;原码定点数的加/减运算;补码定点数的加/减运算;定点数的乘/除运算;溢出概念和判别方法。
(三)浮点数的表示和运算1.浮点数的表示:浮点数的表示范围;IEEE754标准2.浮点数的加/减运算(四)算术逻辑单元ALU1.串行加法器和并行加法器2.算术逻辑单元ALU的功能和机构2.3 浮点数的表示和运算2.3.1 浮点数的表示(1)浮点数的表示范围•浮点数是指小数点位置可浮动的数据,通常以下式表示:N=M·RE其中,N为浮点数,M为尾数,E为阶码,R称为“阶的基数(底)”,而且R为一常数,一般为2、8或16。
在一台计算机中,所有数据的R都是相同的,于是不需要在每个数据中表示出来。
浮点数的机内表示浮点数真值:N=M ×2E浮点数的一般机器格式:数符阶符阶码值 . 尾数值1位1位n位m位•Ms是尾数的符号位,设置在最高位上。
•E为阶码,有n+1位,一般为整数,其中有一位符号位EJ,设置在E的最高位上,用来表示正阶或负阶。
•M为尾数,有m位,为一个定点小数。
Ms=0,表示正号,Ms=1,表示负。
•为了保证数据精度,尾数通常用规格化形式表示:当R=2,且尾数值不为0时,其绝对值大于或等于0.5。
对非规格化浮点数,通过将尾数左移或右移,并修改阶码值使之满足规格化要求。
浮点数的机内表示阶码通常为定点整数,补码或移码表示。
其位数决定数值范围。
阶符表示数的大小。
尾数通常为定点小数,原码或补码表示。
其位数决定数的精度。
数符表示数的正负。
浮点数的规格化字长固定的情况下提高表示精度的措施:•增加尾数位数(但数值范围减小)•采用浮点规格化形式尾数规格化:1/2≤M <1 最高有效位绝对值为1浮点数规格化方法:调整阶码使尾数满足下列关系:•尾数为原码表示时,无论正负应满足1/2 ≤M <1即:小数点后的第一位数一定要为1。